Abstract
The objective of the compressed baryonic matter (CBM) experiment at the future Facility for Antiproton and Ion Research (FAIR) in Darmstadt, Germany, is the investigation of the fundamental properties of strongly interacting matter. Of particular interest for our understanding of compact stellar objects is the determination of the equation-of-state (EOS) at high baryon densities and the exploration of the microscopic degrees-of-freedom under these conditions. The results of these laboratory experiments will complement astronomical observations, which also constrain the high-density EOS. Recent results of QCD-based calculations suggest that a possible first-order chiral phase transition should be observable in heavy-ion collisions at FAIR energies. This article reviews relevant observables from heavy-ion collisions and describes the detector configuration and the physics performance of the CBM experiment.
1. Introduction
The fundamental properties of strongly interacting matter at high net baryon density, as it prevails in massive stellar objects, are still poorly understood. Recent astronomical observations, such as the determination of the mass and radii of neutron stars [1] and the detection of gravitational waves emitted from neutron star mergers [2], have provided some constraints on the high-density equation-of-state (EOS) of up to about four times the saturation density ρ0 [1]. Similar densities can be produced in the laboratory in the reaction volume of heavy-ion collisions at intermediate beam energies. Figure 1 illustrates the densities reached in central Au + Au collisions at a beam kinetic energy of 5A GeV and 10A GeV, as calculated by different microscopic transport models and by a 3 fluid hydrodynamics code [3]. According to the model calculations, densities of about five and 8 times the saturation density ρ0 are reached over a time span of 7 fm/c and 5 fm/c in collisions at 5A and 10A GeV, respectively. The expansion of the compressed reaction volume results in collective phenomena such as the flow of protons, which has been measured in experiments and analyzed by microscopic transport models in order to extract information on the EOS of symmetric matter [4]. In order to contribute to our understanding of neutron stars, the symmetry energy must also be determined.
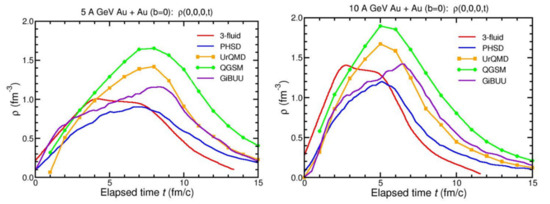
Figure 1.
Central net baryon density ρ(t) versus time calculated by various microscopic transport models and by a 3 fluid hydrodynamics code for central Au + Au collision at 5A GeV (left) and at 10A GeV (right) [3].
Another fundamental question concerns the matter composition at neutron star core density. As the neutron and proton chemical potentials very rapidly increase as functions of the density, the nucleons may decay via weak interactions into hyperons. This process reduces the pressure and softens the EOS and, hence, prevents the formation of very massive neutron stars, which, however, have been observed. This “hyperon puzzle” might be overcome by introducing repulsive two-body ΛN interactions and three-body ΛNN or ΛΛN interactions, which shift the decay into Λ hyperons at very high densities [5]. Experimentally, these interactions can be studied through the femtoscopy correlations between these particles [6] and by the measurement of (double-) Λ hypernuclei, which are produced in heavy-ion collisions, most abundantly at beam energies between 5A and 10A GeV [7].
At baryon densities above about 5 ρ0, it is very likely that nucleons start to percolate and dissolve into their elementary constituents, quarks and gluons. Such a phase transition is also predicted to occur in the core of massive neutron stars, either as a smooth crossover transition [8] or as a first-order transition with a mixed phase [9]. It is very difficult, if not impossible, to extract information on the microscopic degrees-of-freedom of high-density matter from astronomical observations. In laboratory experiments with heavy-ion collisions, however, various observables are expected to be sensitive to a possible phase transition in dense QCD matter.
In this article, the available information on the EOS, as provided by heavy-ion data, is reviewed and future experimental prospects in this field are outlined. Moreover, the status of and perspectives for the experimental search for indications of elementary degrees-of-freedom emerging in matter at high net baryon densities are discussed. Finally, the plans for the future compressed baryonic matter (CBM) experiment at the Facility for Antiproton and Ion Research are presented, including the results of physics performance studies for the relevant observables in heavy-ion collisions at Au-beam energies from 2A to 11A GeV, including rare probes such as (multi-)strange (anti-) hyperons, (double Λ) hypernuclei and lepton pairs.
2. The High-Density Equation-of-State of Nuclear Matter
The EOS relates pressure to density, volume, temperature and isospin. For a constant temperature, the pressure can be written as P = ρ2 d(E/A)/dρ, with ρ the density and the binding energy per nucleon E/A(ρ,δ) = E/A(ρ,0) + Esym(ρ)·δ2 + O(δ4). The first term, E/A(ρ,0), refers to isospin-symmetric nuclear matter and the symmetry energy Esym must be added in order to describe neutron-rich matter with an isospin asymmetry parameter δ = (ρn − ρp)/ρ. The EOS for isospin symmetric matter, which is relevant for nuclei and nuclear collisions, can be characterized by the nuclear incompressibility Knm = 9ρ2 δ2(E/A)/δρ2. Knm describes the curvature of E/A at saturation density ρ0, where the minimum E/A is -16 MeV. From the experimental study of giant monopole resonances in heavy nuclei, i.e., for saturation density, a value of Knm (ρ0) = 240 ± 20 MeV has been extracted as predicted by the majority of mean-field models, although a somewhat higher value in the range Knm (ρ0) = 250–315 MeV is not excluded [10].
The nuclear matter EOS beyond saturation density has been studied in heavy-ion collisions at beam energies around 1A GeV. In these experiments, a very important observable sensitive to the EOS is the collective flow of particles, which is driven by the pressure gradient in the reaction volume and, hence, serves a barometer. At GSI, the FOPI collaboration has performed detailed investigations of the elliptic flow of protons and light fragments in Au + Au collisions at energies from 0.4 to 1.5A GeV, where densities of up to 2 ρ0 are reached [11]. These data have been reproduced by IQMD model calculations assuming a nuclear incompressibility of Knm = 190 ± 30 MeV. It is important to note that this model takes into account momentum-dependent interactions and in-medium cross-sections in order to agree with the data.
A complementary approach to the study of the EOS of symmetric matter in heavy-ion collisions is the measurement of subthreshold strangeness production. This method has been developed by the KaoS collaboration at GSI, which measured K+ mesons in Au + Au collisions at beam energies from 0.8A GeV to 1.5A GeV [12]. In order to produce a K+ meson in the reaction p + p → K+ Λp, a proton kinetic energy of 1.58 GeV is required. In heavy-ion collisions at lower energies per nucleon, the production of K+ mesons proceeds via sequential collisions of hadrons, including hadron resonances. These processes are density-dependent and the yield of the created K+ mesons turns out to be an observable sensitive to the EOS. In order to reduce the influence of medium effects such as Fermi motion and of systematic errors on the kaon production, C + C collisions have been studied as a function of beam energy as the reference system. According to microscopic transport model calculation, the ratio of the K+ multiplicities in Au + Au over C + C collisions can be reproduced by assuming a nuclear incompressibility of Knm ≈ 200 MeV [13,14]. In this comparison, the remaining uncertainties in the modelling of momentum dependent interactions and in-medium cross sections, which also affect subthreshold kaon production, are reduced. According to transport simulations, the kaon production processes at GSI-SIS18 beam energies occur predominantly at densities above twice the saturation density.
In order to study the EOS at net baryon densities well above 2 ρ0, heavy-ion collisions at higher beam energies must be investigated. Such experiments have been performed at the AGS in Brookhaven, where the transverse and elliptic flow of protons has been measured in Au + Au collisions at beam kinetic energies from 2A GeV to 11A GeV [15]. At these beam energies, net baryon densities of more than 5 ρ0 corresponding to the density in the core of neutron stars, can be reached (see Figure 1). When analyzing the experimental results using relativistic transport model calculations, the transverse flow data can be reproduced assuming a soft EOS (Knm = 210 MeV), while the reproduction of the elliptic flow data requires a stiff EOS (Knm = 300 MeV) [4]. Figure 2 depicts a synopsis of the existing theoretical analysis of the experimental data on the EOS for symmetric nuclear matter, plotted as pressure versus baryon density. The AGS data are represented by the grey-hatched area [4,15] and the GSI data correspond to the yellow area [11,12,13,14]. For comparison, a soft and a hard EOS are shown, illustrated by the blue and red line, respectively [4]. It is worthwhile to note that Figure 2 still represents the constraint of the high-density EOS for symmetric nuclear matter, based on the analysis of heavy-ion data.
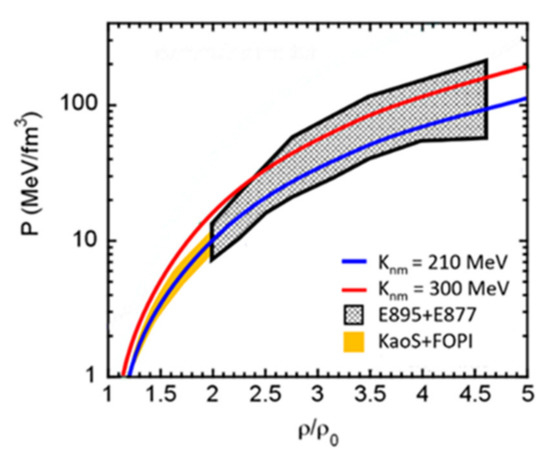
Figure 2.
Pressure versus net baryon density for symmetric nuclear matter. Grey hatched area: proton flow data taken at AGS [4,15]. Yellow area: proton flow, fragment flow and kaon data taken at GSI [11,12,13,14]. Red line: hard EOS, blue line: soft EOS [4].
In order to contribute to our understanding of the EOS of neutron stars, the symmetry energy Esym must be determined in addition to the EOS for symmetric matter. In order to contribute to our understanding of the EOS for neutron stars, the symmetry energy Esym must be determined in addition to the EOS for symmetric matter. From a variety of laboratory experiments that measure, for example, the neutron skin thickness of heavy nuclei, an average value for the symmetry energy at saturation density of Esym(ρ0) = 31.6 ± 2.66 MeV has been extracted [16]. Moreover, the density dependence of the symmetry energy L(ρ) = 3ρ ∂Esym/∂ρ has been deduced from the data and a value of L(ρ0) = 58.9 ± 16 MeV was determined [16]. In order to directly determine the symmetry energy at higher densities, the ASY-EOS collaboration at GSI recently performed a measurement of the elliptic flow both for protons and neutrons in Au + Au collisions at a beam energy of 0.4A GeV [17]. It was found that the ratio of neutrons to proton elliptic flow is one of the observables sensitive to Esym. According to UrQMD transport calculations, which reproduce the measured flow data, the density-dependent symmetry energy increases from Esym ≈ 32 MeV at ρ0 to Esym = 55 ± 5 MeV at 2 ρ0 [17]. These values for Esym must be added to the EOS for symmetric matter in order to obtain the EOS for neutron star matter. The result is shown as nucleon binding energy versus baryon density by the upper green area in Figure 3, together with the EOS for symmetric matter represented by the lower green area. In addition to the experimental results, Figure 3 also contains the results of various theoretical calculations for isospin symmetric (lower curves) and for neutron matter (upper curves) [18]. The figure illustrates that, in particular, the relativistic Dirac-Brueckner-Hartree-Fock (DBHF) approach (red line) is in good agreement with the experimental results. This calculation features a soft EOS up to densities of about 2ρ0 and a hard EOS at high density, which is required for the existence of very massive neutron stars [19]. The ASY-EOS collaboration proposed a follow-up experiment at GSI with the goal of measuring the flow of protons and neutrons in Au + Au collisions up to an energy of 1A GeV, using a new large-area neutron time-of-flight detector, which has been built for experiments at the future FAIR facility.
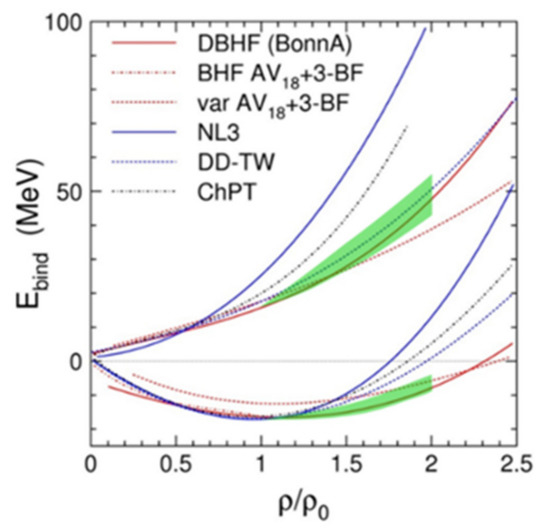
Figure 3.
Binding energy versus baryon density. Lower set of curves: symmetric nuclear matter. Upper set of curves: neutron matter [18]. Green areas: analysis of experimental data obtained at GSI [11,12,13,14,15,17], see text.
As illustrated in Figure 2 by the grey-hatched area, the high-density EOS is still weakly constrained; only very hard and very soft EOS are excluded. In order to further constrain the EOS for symmetric matter, future experiments at FAIR will perform precision measurements of the directed and elliptic flow of protons and light fragments. The idea, to study the EOS by subthreshold particle production, will be extrapolated towards higher densities by detailed experimental investigations of multi-strange (anti-) hyperon production at beam energies between 2A and 11A GeV. The first calculations with the new PHQMD event generator indicate that in Au + Au collisions at an energy of 4A GeV the yields of Ξ± and Ω±, hyperons are about a factor of 2 higher when assuming a soft instead of a hard EOS [20].
In order to compare the EOS extracted from heavy-ion collisions to results from neutron star observations, the symmetry energy must also be measured at high densities. As discussed above, one sensitive probe of Esym is the ratio of the elliptic flow of neutrons over the flow of protons. Moreover, the spectral pion ratio π−/π is expected to be sensitive to Esym. Pioneering experiments measured this ratio as a function of transverse momentum in the neutron-rich collision system 132Sn + 124Sn and extracted information on Esym at densities slightly above saturation density [21]. Promising observables sensitive to Esym at high baryon densities are particles with large masses and with the opposite third component of the isospin I3 = ±1, such as Σ−(dds) and Σ+(uus) hyperons, which reflect the density of neutrons (ddu) and protons (uud) [22]. Similarly, the production of excited Σ*−(dds) and Σ*+(uus) hyperons, which decay into Λπ pairs, will be systematically studied in heavy-ion collisions at the future FAIR facility sign.
3. The QCD Phase Diagram at High Baryon Densities
A sketch of the QCD phase diagram, expressed as temperature T versus baryon-chemical potential μb, is presented in Figure 4 [23]. The plot contains data points for the freeze-out temperature extracted from particle yields measured in heavy-ion collisions at LHC, RHIC, SPS, AGS and GSI. The black dotted line represents the parameterization of the freeze-out curve, which is based on the assumption of an average kinetic energy of 1 GeV per nucleon [24]. For the highest energies available at LHC, a freeze-out temperature of 156.5 ± 1.5 MeV (with μB = 0.7 ± 3.8 MeV) was derived from the ALICE data [25]. This value coincides with the pseudo-critical temperature of a smooth chiral crossover between quark and hadronic matter, calculated by lattice QCD (LQCD) [26,27]. Recently, LQCD calculations were performed in order to determine the temperature of a critical point of a first-order chiral phase transition. As an upper bound for such a temperature, a value of Tc0 = 132 + 3−6 MeV was found in the chiral limit, i.e., for massless quarks and for μB = 0 MeV [28]. For finite quark masses and finite baryon-chemical potential, the critical temperature is expected to be even lower, if a critical point exists at all. The upper limit of a possible critical temperature is sketched as the horizontal blue-shaded area in Figure 4. The QCD phase structure at finite temperature and chemical potential was studied recently with a combination of the functional renormalization group (FRG) and Dyson-Schwinger equations (DSE), which found a critical endpoint at TCEP = 93 MeV and μb = 672 MeV, as illustrated by the full red dot in Figure 4 [29].
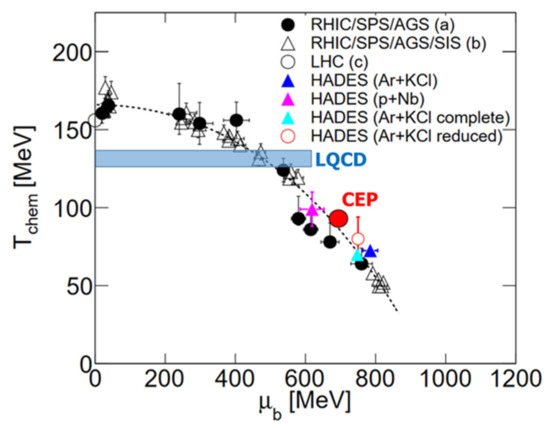
Figure 4.
A sketch of the two-dimensional phase diagram of strongly interacting matter in the plane temperature versus baryon chemical potential μb. The data points are extracted from particle yields measured at different energies using a statistical model [23]. The black dashed line illustrates a freeze-out curvature [24]. The upper limit for the chiral critical point T0c = 132 + 3−6 MeV predicted by lattice QCD calculations is shown as a blue-shaded area [28]. The critical endpoint CEP predicted by DSE-FRG calculations at TCEP = 93 MeV and μb = 672 MeV is marked by a full red dot [29].
The location of the critical endpoint of a possible first-order chiral phase transition in the QCD phase diagram, as predicted by the LQCD and the FRG-DSE calculations, will be accessible in heavy-ion collisions with beam kinetic energies at FAIR. This creates the opportunity to discover not only signatures of the onset of deconfinement and of the mixed phase, but even of the critical endpoint, if it exists in nature. Below, a selection of the most promising observables sensitive to a phase transition in dense nuclear matter is discussed.
3.1. Fluctuations of Net-Proton Number Distribution as Signature of the Critical Endpoint
The search for the critical endpoint in dense QCD matter is one of the major goals of contemporary high-energy, heavy-ion physics. Analogously to critical opalescence in classical binary systems, it is also expected that in nuclear matter, the correlation length will diverge when approaching the critical endpoint. An observable sensitive to the correlation length are moments of the conserved net baryon number distribution. Therefore, it was proposed to search for a non-monotonic variation of these moments as a function of collision energy, as an indication of the critical point [30]. Since the signatures of a critical point may be diluted by the dynamical evolution and finite size of the fireball, it was suggested to study higher moments, which depend even more strongly on the correlation length. As a proxy for the baryons, the STAR collaboration at RHIC studied in detail the net proton multiplicity distribution event-by-event in Au + Au collisions within the energy scan program. It was observed that the fourth to the second cumulant C4/C2 (=kurtosis×variance κσ2) exhibit a non-monotonic variation with a significance of 3.1σ at the lowest collision energy of √sNN = 7.7 GeV [31]. Whether this variation rises and again falls towards lower beam energies and, hence, finally indicates the possible location of a critical point, remains to be clarified by further experiments, which will be performed at STAR using a stationary target and at the future facilities NICA and FAIR. It is worthwhile to note that the divergence of the correlation length is also expected to cause critical fluctuations in the yields of light nuclei, which might appear in the ratio Nt∙Np/Nd2 [32].
3.2. Chemical Equilibration of Multi-Strange (Anti-) Hyperons as Signature of the Onset of Deconfinement
As mentioned above, the particle yields measured in heavy-ion collisions can be reproduced by statistical hadronization models through the variation of the freeze-out temperature, the baryon chemical potential and the volume. For ultra-relativistic collision energies, the freeze-out temperature coincides with the pseudo-critical temperature of a chiral crossover transition, as predicted by LQCD calculations. It was also found that (multi-) strange (anti) hyperons freeze out at the same temperature as the other particles, in spite of the very small hyperon–nucleon scattering cross section, which should prevent chemical equilibration in the short lifetime of the hadronic phase. In order to explain this observation, it was argued that (multi-) strange hyperons are born into equilibrium during hadronization [33]. Hence, chemically equilibrated hyperons may be regarded as a signature of a phase transition. In heavy-ion collisions down to beam energies of 30A GeV, the yields of Ξ− and Ξ+ hyperons are still found to be in chemical equilibrium with all the other particles [34]. However, the Ξ− hyperon yield measured in Ar + KCl collisions at an energy of 1.76A GeV exceeds the statistical model prediction obtained from the fit to the yield of the rest of the hadrons by a factor of 24 ± 9 [35]. The research program of the CBM experiment at FAIR includes the precise measurement of Ξ± and Ω± hyperons in Au + Au collisions from beam energies of 2A GeV to 11A GeV, in order to determine the freeze-out temperature and the baryon-chemical potential where multi-strange (anti-) hyperons are chemically equilibrated, which might indicate the onset of deconfinement.
3.3. Tracing the Caloric Curve by Detecting Dilepton Radiation
Dileptons observed in heavy-ion collisions provide unperturbed insight into the hot and dense fireball, as they are not affected by final-state interaction. The invariant mass spectrum of e+e− or μ+μ− pairs contains contributions from vector mesons decaying in lepton pairs and from thermal radiation from the fireball. The invariant mass range below about 1 GeV/c2 is dominated by contributions from pion Dalitz decays and decays of vector mesons, such as ω, ρ and ϕ. If the vector mesons decay inside the fireball, as in the case of the short-lived ρ meson, it is possible to determine the in-medium mass distribution, which is affected by the restoration of chiral symmetry in dense matter. The experimental challenge, however, is the correction for the combinatorial background of uncorrelated e+e− or μ+μ− pairs, which dominates the dilepton yield.
Invariant mass spectra above 1 GeV/c2 are only slightly contaminated by vector meson decays and are dominated by thermal radiation, reflecting the average temperature of the fireball [36]. It is important to note that the dilepton invariant mass spectrum is not distorted by the radial expansion of the fireball, which contributes to the transverse momentum spectra of the hadrons. The method of determining the average fireball temperature was pioneered by the NA60 experiment at CERN in In + In collisions at 158A GeV. After the subtraction of the contribution from uncorrelated μ+μ− pairs using the mixed-event technique, the contributions from known sources, such as vector mesons and Dalitz decays, were removed; eventually, the remaining thermal spectrum was corrected for experimental acceptance [37]. Above an invariant mass of 1 GeV/c2, this spectrum exhibits an exponential shape ∝exp(−M/T) with T = 205 ± 12 MeV, corresponding to the space-time averaged temperature over the course of the system. The HADES collaboration measured the e+e− invariant mass spectrum up to masses of about 1 GeV/c2 in Au + Au collisions at an energy of 1.23A GeV; after the subtraction of the combinatorial background and of contributions from known di-electron sources, a slope parameter of T = 72 ± 2 MeV was extracted [38]. It is worthwhile to note that these temperatures are well above the respective freeze-out temperatures of the different collision systems. In conclusion, the precise measurement of the invariant mass spectrum of dileptons in heavy-ion collisions for different beam energies creates the opportunity to discover the caloric curve of QCD matter and, hence, the onset of deconfinement and the critical endpoint of a possible first-order phase transition, if it exists.
3.4. Probing Dense Nuclear Matter by Subthreshold Charmonium Production
Since the earliest experiments with heavy-ion collisions at ultra-relativistic energies, Charmonium has played a prominent role as a probe of the QGP. The anomalous suppression of J/ψ mesons due to color screening in deconfined matter has been proposed as an unambiguous signature of the QGP [39]. Indeed, the NA50 collaboration at SPS found indications of a decrease in the J/ψ yield in central Pb + Pb collisions at 158A GeV, an effect that could be also explained by the interaction of J/ψ mesons with hadrons in central collisions and with co-moving particles [40]. In further systematic measurements, the NA50 collaboration confirmed the observation of a strong decrease in the charmonium yield as a function of energy density above a value of ε ≈ 2.5 GeV/fm3 and attributed this decline to the suppression of J/ψ mesons in the QGP [41]. Calculations based on the statistical hadronization model (SHM) explained the SPS data by assuming the direct production of charm quarks in hard scattering processes, followed by thermalization in the QGP and, finally, the formation of charmed hadrons by statistical hadronization at the phase boundary [42]. Instead of a suppression, the SHM model predicted an enhanced production of J/ψ mesons in heavy-ion collisions at LHC energies, with respect to a superposition of independent nucleon–nucleon collisions [42,43]. However, the ALICE experiment still observed a suppression of J/ψ mesons in Pb + Pb collisions at LHC energies, albeit less pronounced than at SPS or RHIC energies [44].
The SHM model has also been used to calculate the production yields of J/ψ mesons, D mesons and Λc hyperons in heavy-ion collisions down to threshold beam energies [43]. Because in this model the production of c and c-bar quarks is decoupled from the hadronization into charmed hadrons, the ratio of (J/ψ)/(D + D-bar) mesons is almost independent of beam energy, whereas in hadronic scenarios, such as the hadron string dynamics (HSD) transport code, the ratio of (J/ψ)/(D + D-bar) strongly increases towards the threshold beam energy [45]. The reason for this effect is that J/ψ features a lower production threshold than D or D-bar mesons. In hadronic models, the charmed hadrons are created in processes such as pp → J/ψ pp, pp → D-bar Λc p and pp→ D D-bar pp, with threshold energies of 11.3 GeV, 12.6 GeV and 14.9 GeV, respectively. Currently, no data exist on charm production in heavy-ion collisions close to threshold. At the FAIR facility, Au beams are only available up to the J/ψ production threshold, but higher energies will be available for lighter nuclei, which will allow us to study open charm production in nuclear collisions close to threshold.
Calculations with the UrQMD event generator predict a charm production mechanism in heavy-ion collisions at subthreshold beam energies [46]. Within this model, heavy N* resonances are excited via multiple hadron–hadron collisions and then decay with a certain branching ratio into mesons containing charm quarks, through processes such as N*→J/ψ+N and N*→Λc+D-bar. According to these calculations, the charm production threshold might be lowered substantially and would make it possible to observe both hidden and open charm mesons in Au + Au collisions at FAIR. A feasibility study of such a measurement is discussed in the next chapter. An intriguing consequence of the discovery of subthreshold charm production and its explanation by multiple hadron collisions would be that the existence of deconfined matter at the energies and densities under investigation would be ruled out. In any case, the observation of charm particles at FAIR energies would elucidate the charm production mechanisms in heavy-ion collisions and would provide a new probe of dense baryonic matter.
4. The CBM Experiment at FAIR
4.1. The Facility for Antiproton and Ion Research
The future “Facility for Antiproton and Ion Research” (FAIR), which is presently under construction in Darmstadt, Germany, will be equipped with a synchrotron of 100 Tm magnetic rigidity (SIS100), storage rings, a superconducting fragment separator (SFRS) and several experimental areas. SIS100 provides a variety of particle beams: high-energy antiproton beams with momenta up to 15 GeV/c and intensities of up to 1011/s, proton beams up to energies of 29 GeV with intensities up to 3 × 1013/s 30 GeV, heavy ion beams with energies from 2A–11A GeV for Au or U nuclei (up to 14A GeV for N = Z nuclei), intensities up to 1010/s and secondary rare isotope beams with energies up to 2A GeV [47]. These unstable isotopes were selected by the SFRS and transported downstream to experimental setups, which measure their lifetimes and masses in order to shed light on the origin of heavy elements by identifying the isotopes that take part in the r-process path produced in supernova explosions and neutron star mergers. The research program on hadron physics will be executed with high-energy antiproton beams by the PANDA experiment, which is located in the High-Energy Storage Ring (HESR). Moreover, there will be experiments on atomic physics, plasma physics, radiation biology and material science. The properties of dense baryonic matter, i.e., the EOS and the degrees-of-freedom at high densities, will be investigated through the compressed baryonic matter (CBM) experiment, which will study the relevant observables including those discussed in the previous chapter. A review of the research programs at FAIR is presented in [48]. The photograph of the FAIR construction site in September 2021 is shown in Figure 5 [49]. Below, the layout of the CBM experiment and the results of physics performance studies are presented.
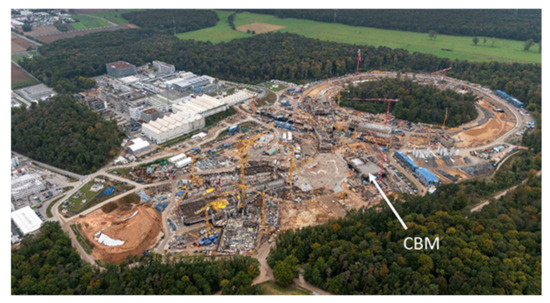
Figure 5.
Photograph of the FAIR construction site, September 2021 [49]. The underground synchrotron tunnel building is already covered with soil. Furthermore, the shell construction of the CBM cave is ready.
4.2. Layout of the CBM Experiment
The CBM experiment is designed to be operated at reaction rates of up to 10 MHz, in order to measure rare diagnostic probes of dense baryonic matter with unprecedented statistics and precision. This performance will be achieved through the development of fast detectors and a triggerless data readout and acquisition system, which requires online event reconstruction and selection. A micro-vertex detector (MVD) and a silicon tracking system (STS), located in the field of a large acceptance superconducting dipole, provide information on vertices and tracks and, hence, on particle momentum. The MVD comprises four stations equipped with monolithic active pixel silicon sensors (MAPS) positioned between 5 and 20 cm downstream of the target, while the STS consists of eight stations with 900 double-sided micro-strip silicon sensors, located between 25 cm and 100 cm downstream the target. For electron identification, a ring imaging Cherenkov (RICH) detector is installed behind the STS followed by a transition radiation detector (TRD). The RICH can be replaced by a muon chamber (MuCh) system, which comprises up to five hadron absorbers sandwiching tracking chamber triplets. The first two stations consist of GEM detectors and the third and fourth station are built from resistive plate chambers (RPC). In this configuration, the TRD provides additional information on the muon tracks. A time-of-flight (TOF) wall with an active area of 120 m2 consisting of multi-gap resistive plate chambers (MRPC) is positioned about 8 m downstream of the target. The CBM setup accepts polar angles between 3° and 25°, which is sufficient to cover midrapidity for FAIR beam energies. The final detector, located about 10 m downstream of the target, is the project spectator detector (PSD), a hadronic calorimeter, which provides information on the orientation of the reaction plane by measuring projectile fragments. As an upgrade option, the new large-area neutron time-of-flight detector, which has been built for the nuclear reaction experiments at FAIR, might be installed in the CBM cave, in order to measure simultaneously the collective flow of s and protons and to investigate the symmetry energy at high densities. A sketch of the CBM experiment is shown in the right part of Figure 6, while in the left part of the figure the high-acceptance di-electron spectrometer (HADES) is shown. HADES is a running experiment at GSI-SIS18 with a large polar angle acceptance from 18° to 85° and is well suited for reference measurements of proton-induced reactions.
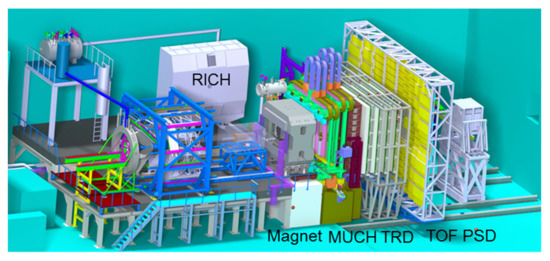
Figure 6.
The CBM setup (right) and the HADES detector (left), which will be operated alternately, with the beam coming from left. The CBM micro-vertex detector (MVD) and the silicon tracking system (STS) are located inside the CBM magnet, followed by the muon detection system (MUCH), while the electron detector (RICH) is in parking position. Downstream of the MUCH, the transition radiation detector (TRD), the time-of-flight wall (TOF) and the projectile spectator detector (PSD) are located. The HADES beam dump in front of the CBM magnet will be removed for CBM operation.
4.3. Physics Performance Studies for the CBM Experiment
The detector system of the CBM experiment described above has been developed for the measurement of hadrons and leptons at the highest possible heavy-ion collision rates. Extensive simulations based on realistic detector geometries and materials have been performed in order to optimize the detector configurations and the reconstruction and analysis software packages. An example of the simulation results is shown in Figure 7, which illustrates the identification of strange particles in central Au + Au collisions at a beam energy of 11A GeV. The calculation is based on 5 million events generated by the UrQMD event generator and transported through the CBM setup using the GEANT 3 transport engine. In this case, only the STS has been used for track reconstruction and the TOF wall for identification of the decay particles such as (anti-)protons and pions [50]. The beam energy of 11A GeV is below threshold for the production of Ω+ hyperons; therefore, their yield is too low to be detected in 5 million events. However, it is worthwhile to note that the beam time required to collect the spectra shown in Figure 7 will be about 5 s only.
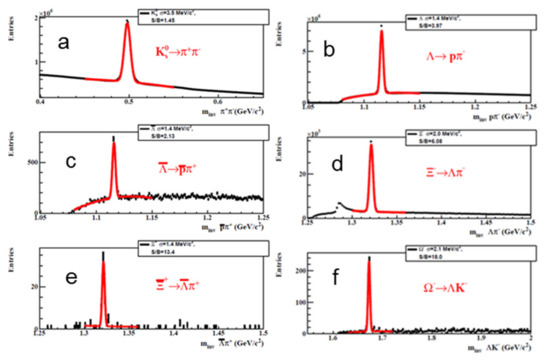
Figure 7.
Reconstructed invariant mass distribution of K0 (a), Λ (b), anti-Λ (c), Ξ− (d), Ξ+ (e) and Ω− (f) in central Au + Au collisions at a beam energy of 11A GeV. The red lines indicate the signal together with the background fit by a polynomial plus Gaussian functions. The signal width, the signal-to-background ratio and the total reconstruction efficiency are indicated [50].
As mentioned in the introduction, the precise measurement of the lifetimes and binding energies of (double-) lambda hypernuclei will shed light on ΛN, ΛNN and ΛΛN interactions, which determine the behavior of hyperons in dense nuclear matter. Statistical model calculations predict that hypernuclei are abundantly produced in heavy-ion collisions at FAIR [7]. According to these calculations, the hypernuclei yield exhibits a maximum around a collision energy of about √sNN = 4 GeV, which is within the FAIR energy range. In the CBM experiment, hypernuclei will be reconstructed via the tracks of their decay products, such as pions, kaons, protons and light fragments, which are measured by the MVD and the STS, together with the TOF for particle identification. The quality of reconstruction of double-lambda hypernuclei in central Au + Au collisions at 10A GeV/c is presented in Figure 8 for the decays 4ΛΛH → 4ΛHe π− and 4ΛΛH → 3ΛH p π−. The experimental task is the stepwise reconstruction of the decay topology, first of the secondary decays 4ΛHe → 3He p π− and 3ΛH → 3He π−, respectively, then of the primary decays. Finally, it must be verified that the 4ΛΛH hypernucleus originates from the primary vertex of the reaction [51].
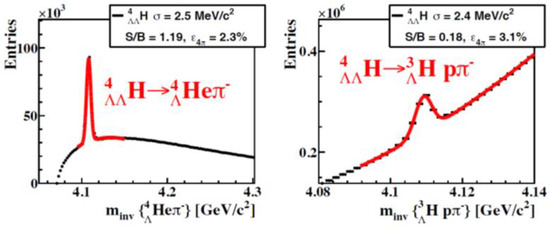
Figure 8.
The double-lambda 4ΛΛH hypernucleus identified via the reconstructed invariant mass spectra of 4ΛHe π− (a) and 3ΛHe p π− (b) in 1012 central Au + Au collisions at 10A GeV. The red lines indicate the signal plus background fit by a polynomial plus Gaussian function [51].
The measurement of dilepton invariant mass spectra creates the possibility to investigate the in-medium modifications of hadrons and to discover the caloric curve of dense nuclear matter. The experimental challenge is to suppress the combinatorial background, which differs for e+e− and μ+μ− pairs. Therefore, the CBM experiment is equipped with both electron and muon detection systems, as described in the previous section. For the simulations of electron measurements, the RICH, TRD and TOF detectors are used for electron and positron identification. The STS measures the curvature of the tracks and the MVD provides suppression electron-positron pairs with small opening angles, which are predominantly produced through the pair conversion of gamma-quanta in the target and contribute to the background in the di-electron spectra. The background is further reduced by using thin targets, such as 25 μm thick Au foils. The left panel in Figure 9 depicts the e+e− invariant mass spectrum simulated for central Au + Au collisions at 8A GeV/c. In the simulations, the UrQMD event generator was used for the calculation of the background and in each event, a di-electron pair from one of the following sources was embedded via the thermal PLUTO code: ω, φ and in-medium ρ decays into e+e−, ω-Dalitz decays or radiation from QGP [52]. The multiplicity of the signals is taken from a statistical model. The obtained signal-to-background ratio is in the order of 0.1 and allows the extraction of the signal in the experiment. The dimuon invariant mass spectrum, also simulated for central Au + Au collisions at 8A GeV/c, is shown in the right panel of Figure 9 [53]. The calculations took into account the information provided by the STS, MuCh, TRD and TOF detectors. In this case, the MuCh comprises four tracking detector stations and five hadron absorber blocks, while the TRD was used for track reconstruction. For muon measurements, an Au target of 250 μm thickness is used, corresponding to an interaction probability of 1%. The contributions of η, ω, φ and ρ meson, as well as from the QGP, are calculated in the same way as those of electrons. Similarly to the electron invariant mass spectrum, the dimuon distribution exhibits a signal-to-background ratio of about 0.1. In conclusion, both the electron and the muon detectors of the CBM experiment are very well suited for dilepton measurements in heavy-ion collisions at FAIR energies; their combination will help to reduce the systematic errors of the dilepton spectrum after subtraction of the combinatorial background.
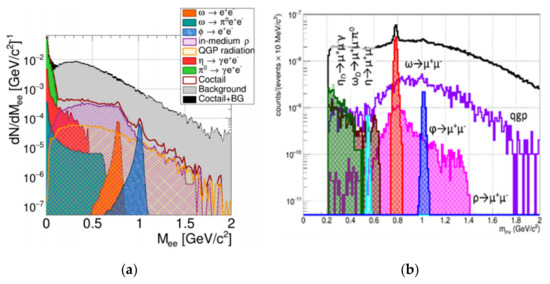
Figure 9.
Invariant mass spectrum of electron positron pairs (a) (adapted from [52]) and of dimuon pairs (b) [53] reconstructed from simulations of central Au + Au collisions at 8A GeV.
The subthreshold production of charmonium created in hadronic reactions via the decay of nucleonic excitations such as N∗ → J/ψ+N was studied in simulations of central Au + Au collisions. The background was generated using the UrQMD code, the J/ψ multiplicity of 10−6 per central Au + Au event was taken from [46] and the J/ψ momentum distribution was calculated using the PLUTO code. The J/ψ mesons are identified via their decay into μ+μ− pairs, which are identified by the CBM muon detection system (MuCh), including the fifth iron absorber of 1 m thickness behind the last tracking station. In addition, the CBM muon setup is comprised of the silicon tracking system (STS), the transition radiation detector (TRD) and the time-of-flight Detector (TOF) for particle identification. Figure 10 depicts the resulting dimuon invariant mass spectrum in the left panel and the reconstruction efficiency as a function of momentum in the right panel [54]. As mentioned above, the identification of J/ψ mesons in heavy-ion collisions at beam energies well below the production threshold would strongly support a hadronic scenario.
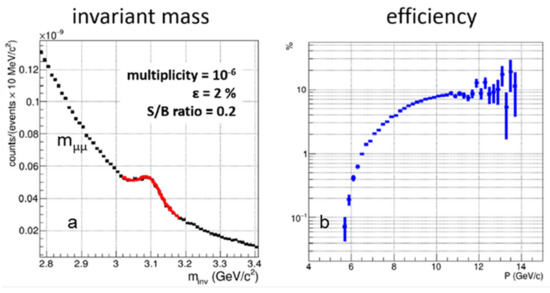
Figure 10.
Dimuon invariant mass spectrum calculated for central Au + Au collisions at 8A GeV/c (a) [54]. The background was generated using the UrQMD code, the J/ψ multiplicity was taken from [46]. J/ψ reconstruction efficiency as function of momentum (b).
5. Summary
The nuclear matter equation-of-state is a fundamental ingredient in our understanding of the structure of neutron stars, the dynamics of core-collapse supernovae and neutron star mergers. Recent astronomical measurements of masses and radii of neutron stars, as well as of gravitational waves from neutron star mergers, provide some constraints on the EOS up to about four times the saturation density ρ0. In laboratory experiments, information on the EOS has been obtained up to densities of about 2 ρ0 from the analysis of the elliptic flow of protons, neutrons and fragments, as well as from subthreshold kaon production measured in heavy-ion collisions up to beam kinetic energies of 1.5A GeV. The analysis of the collective flow of protons in heavy-ion collisions at energies from 2A to 10A GeV, corresponding to densities up to about 5 ρ0, excludes only very hard and very soft EOS. In this energy range, the CBM experiment at FAIR will provide precision data on the collective flow of identified particles, as well as on the yields and spectra of multi-strange (anti-) hyperons and hypernuclei, in order to determine the high-density EOS and to shed light on the ΛN and ΛΛN interaction. Moreover, the CBM research program is devoted to the investigation of the QCD phase diagram at large baryon densities, particularly to the search for signatures of a phase transition from hadronic to quark-gluon matter. The strategy is to measure observables, which are supposed to be sensitive to such a phase transition but that have not been studied before in this energy range, such as dilepton pairs and subthreshold charm production. In conclusion, the proposed laboratory measurements will complement astronomical observations in order to constrain the EOS and elucidate the elementary structure of matter at neutron star core densities.
Funding
This research received no external funding.
Acknowledgments
The author acknowledges support from the Europeans Union’s Horizon 2020 research and innovation program under grant agreement No. 871072, and from RFBR according to the research project No. 18-02-40086 by the Ministry of Science and Higher Education of the Russian Federation, Project “Fundamental properties of elementary particles and cosmology” No 0723-2020-0041.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- LIGO and Virgo Collaborations. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Arsene, I.C.; Bravina, L.V.; Cassing, W.; Ivanov, Y.B.; Larionov, A.; Randrup, J.; Russkikh, V.N.; Toneev, V.D.; Zeeb, G.; Zschiesche, D. Dynamical phase trajectories for relativistic nuclear collisions. Phys. Rev. C 2007, 75, 24902. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef]
- Logoteta, D.; Vidana, L.; Bombaci, I. Impact of chiral hyperonic three-body forces on neutron stars. Eur. Phys. J. A 2019, 55, 207. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Study of the Λ–Λ interaction with femtoscopy correlations in pp and p–Pb collisions at the LHC. Phys. Lett. B 2019, 797, 134822. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stöcker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Fukushima, K.; Kojo, T.; Weise, W. Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter. Phys. Rev. D 2020, 102, 096017. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Le Fèvre, A.; Leifels, Y.; Reisdorf, W.; Aichelin, J.; Hartnack, C. Constraining the nuclear matter equation of state around twice saturation density. Nucl. Phys. A 2016, 945, 112–133. [Google Scholar] [CrossRef]
- Sturm, C.; Böttcher, I.; Dȩbowski, M.; Förster, A.; Grosse, E.; Koczoń, P.; Kohlmeyer, B.; Laue, F.; Mang, M.; Naumann, L.; et al. Evidence for a soft nuclear equation of state from kaon production in heavy ion collisions. Phys. Rev. Lett. 2001, 86, 39. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.-M. Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 1974. [Google Scholar] [CrossRef] [PubMed]
- Hartnack, C.; Aichelin, J. Analysis of kaon production around the threshold. J. Phys. G 2002, 28, 1649. [Google Scholar] [CrossRef]
- Pinkenburg, C.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L. Elliptic Flow: Transition from Out-of-Plane to In-Plane Emission in Au + Au Collisions. Phys. Rev. Lett. 1999, 83, 1295. [Google Scholar] [CrossRef]
- Li, B.-A. Nuclear Symmetry Energy Extracted from Laboratory Experiments. Nucl. Phys. News 2017, 27, 7. [Google Scholar] [CrossRef]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F. Results of the ASY-EOS experiment at GSI: The symmetry energy at supra-saturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Fuchs, C. The Nuclear Equation of State at High Densities. In Collective Motion and Phase Transitions in Nuclear Systems; World Scientific Publishing Company: Singapore, 2006. [Google Scholar]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, M.; Demorest, P.D.; Stairs, H. Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. arXiv 2021, arXiv:2104.00880. [Google Scholar] [CrossRef]
- Aichelin, J.; Bratkovskaya, E.; Fevre, A.L.; Kireyeu, V.; Kolesnikov, V.; Leifels, Y.; Voronyuk, V. Parton-Hadron-Quantum-Molecular Dynamics (PHQMD)—A Novel Microscopic N-Body Transport Approach for Heavy-Ion Collisions, Dynamical Cluster Formation and Hypernuclei Production. Phys. Rev. C 2020, 101, 044905. [Google Scholar] [CrossRef]
- Estee, J.; Lynch, W.G.; Tsang, C.Y.; Barney, J.; Jhang, G.; Tsang, M.B.; Wang, R.; Kaneko, M.; Lee, J.W.; Isobe, T.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Zhao, E.; Gupta, R.K. Σ−/Σ+ ratio as a candidate for probing the density dependence of the symmetry potential at high nuclear densities. Phys. Rev. C 2005, 71, 054907. [Google Scholar] [CrossRef]
- Agakishiev, G.; Arnold, O.; Balanda, A.; Belver, D.; Belyaev, A.; Berger-Chen, J.C.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Cabanelas, P.; et al. Statistical model analysis of hadron yields in proton-nucleus and heavy-ion collisions at SIS 18 energies. arXiv 2015, arXiv:1512.07070. [Google Scholar]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Endrődi, G.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; De Tar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Lahiri, A.; Li, S.T.; Mukherjee, S.; Ohno, H.; Petreczky, P.; Schmidt, C.; et al. (HotQCD Collaboration). Chiral Phase Transition Temperature in (2 + 1)-Flavor QCD. Phys. Rev. Lett. 2019, 123, 062002. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Pawlowski, J.M. QCD phase structure from functional methods. Phys. Rev. D 2020, 102, 034027. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Event-by-event fluctuations in heavy ion collisions and the QCD critical point. Phys. Rev. D 1990, 60, 114028. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; STAR Collaboration. Net-proton number fluctuations and the Quantum Chromodynamics critical point. Phys. Rev. Lett. 2021, 126, 092301. [Google Scholar] [CrossRef] [PubMed]
- Shuryak, E.; Torres-Rincon, J.M. Light-nuclei production and search for the QCD critical point. Eur. Phys. J. A 2020, 56, 241. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J.; Wetterich, C. Chemical Freeze-out and the QCD Phase Transition Temperature. Phys. Lett. B 2004, 596, 6. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions. Acta Phys. Pol. B 2009, 40, 1005. [Google Scholar]
- Agakishiev, G.; Balanda, A.; Bannier, B.; Bassini, R.; Belver, D.; Belyaev, A.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Cabanelas, P.; et al. (HADES Collaboration) Hyperon production in Ar + KCl collisions at 1.76A GeV. Eur. Phys. J. A 2001, 47, 21. [Google Scholar] [CrossRef]
- Rapp, R.; van Hees, H. Thermal Dileptons as Fireball Thermometer and Chronometer. Phys. Lett. B 2016, 753, 586. [Google Scholar] [CrossRef]
- Specht, H.J. Thermal Dileptons from Hot and Dense Strongly Interacting Matter. AIP Conf. Proc. 2010, 1322, 1–10. [Google Scholar] [CrossRef]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M.; et al. Probing baryon-rich matter with virtual photons, The HADES Collaboration. Nat. Phys. 2019, 15, 1040–1045. [Google Scholar] [CrossRef]
- Matsui, T.; Satz, H. J/ψ suppression by quark-gluon plasma formation. Phys. Lett. B 1986, 178, 416. [Google Scholar] [CrossRef]
- Gavin, S.; Vogt, R. Charmonium Suppression by Comover Scattering in Pb + Pb Collisions. Z. Phys. C 1994, 61, 351. [Google Scholar] [CrossRef]
- Abreu, M.C.; Alessandro, B.; Alexa, C.; Arnaldi, R.; Atayan, M.; Baglin, C.; Baldit, A.; Bedjidian, M.; Beolè, S.; Boldea, V.; et al. NA50 Collaboration Evidence for deconfinement of quarks and gluons from the J/ψ suppression pattern measured in Pb–Pb collisions at the CERN-SPS. Phys. Lett. B 2000, 477, 28–36. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J. (Non)Thermal Aspects of Charmonium Production and a New Look at J./ψ Suppression. Phys. Lett. B 2000, 490, 196–202. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Charmonium and open charm production in nuclear collisions at SPS/FAIR energies and the possible influence of a hot hadronic medium. Phys. Lett. B 2008, 659, 149. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. ALICE Collaboration. J/ψ suppression at forward rapidity in Pb–Pb collisions at √sNN = 5.02 TeV. Phys. Lett. B 2017, 766, 212. [Google Scholar] [CrossRef]
- Linnyk, O.; Bratkovskaya, E.L.; Cassing, W.; Stöcker, H. Charmonium dynamics in heavy ion collisions. Nucl. Phys. A 2007, 786, 183. [Google Scholar] [CrossRef][Green Version]
- Steinheimer, J.; Botvina, A.; Bleicher, M. Sub-threshold charm production in nuclear collisions. Phys. Rev. C 2017, 95, 014911. [Google Scholar] [CrossRef]
- FAIR—Facility for Antiproton and Ion Research in Europe. Available online: https://fair-center.de (accessed on 14 July 2021).
- Durante, M.; Indelicato, P.; Jonson, B.; Koch, V.; Langanke, K.; Meißner, U.G.; Nappi, E.; Nilsson, T.; Stöhlker, T.; Widmann, E.; et al. All the Fun of the FAIR: Fundamental physics at the Facility for Antiproton and Ion Research. Phys. Scr. 2019, 94, 033001. [Google Scholar] [CrossRef]
- GSI Helmholtzzentrum für Schwerionenforschung. Photo: D. Fehrenz, GSI/FAIR. Available online: https://www.gsi.de/en/researchaccelerators/fair/fair_civil_construction/photos_and_videos (accessed on 14 July 2021).
- Vassiliev, I.; Kisel, I. Multi-Strange Hyperon Reconstruction with the CBM Light Setup; GSI Helmholtzzentrum für Schwerionenforschung GmbH: Darmstadt, Germany, 2019; ISBN 978-3-9815227-8-5. [Google Scholar]
- Vassiliev, I.; Kisel, I.; Zyzak, M. Hypernuclei Reconstruction at the CBM Experiment; GSI Helmholtzzentrum für Schwerionenforschung GmbH: Darmstadt, Germany, 2016; ISBN 978-3-9815227-4-7. [Google Scholar]
- Feier-Riesen, C.; Lebedev, S.; Höhne, C. Investigation on Impact of Higher Material Budget in STS on LMVM; GSI Helmholtzzentrum für Schwerionenforschung GmbH: Darmstadt, Germany, 2021; ISBN 978-3-9815227-9-2. [Google Scholar]
- Senger, A.; (Facility for Antiproton and Ion Research, Darmstadt, Germany). Private communication, 2021.
- Senger, A.; Senger, P. Probing dense QCD matter: Muon measurements with the CBM experiment at FAIR. Particles 2021, 4, 19. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).