Trojan Horse Investigation for AGB Stellar Nucleosynthesis
Abstract
1. Introduction
2. Indirect Methods in Nuclear Astrophysics
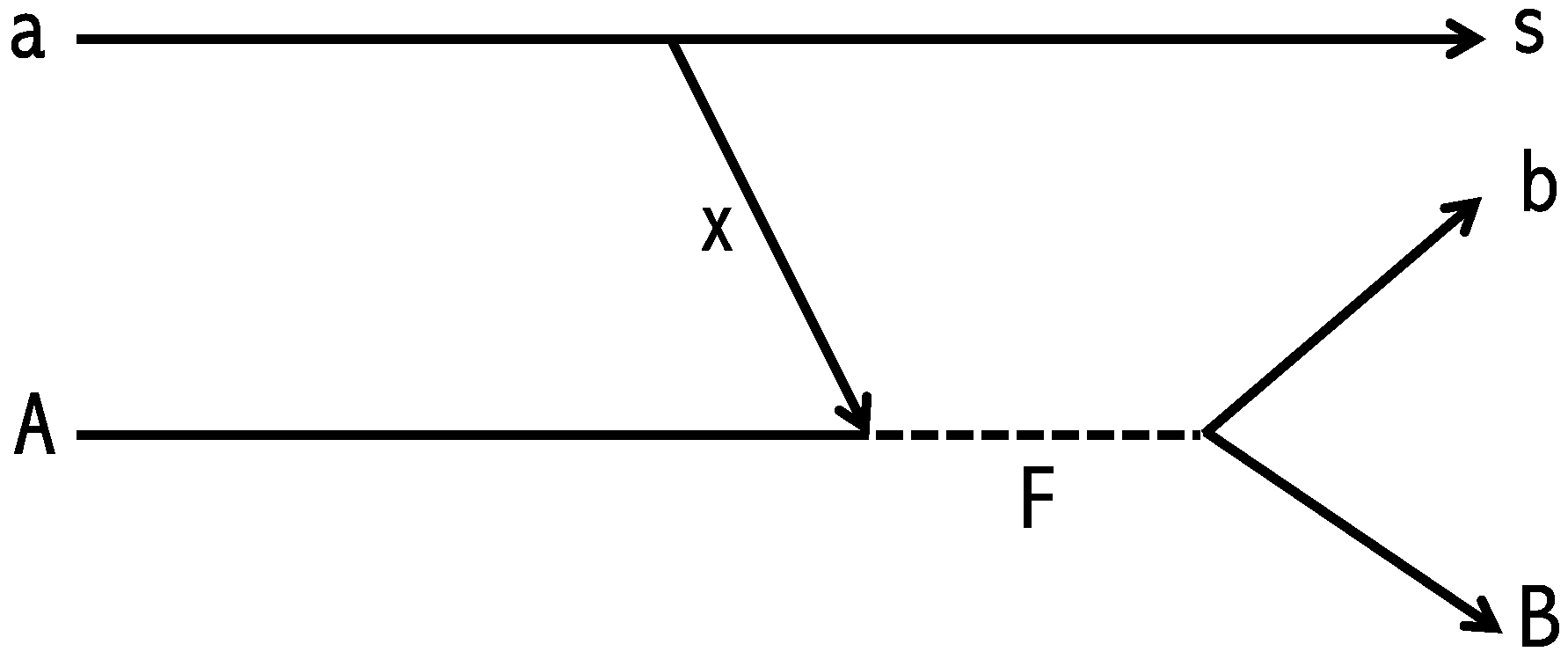
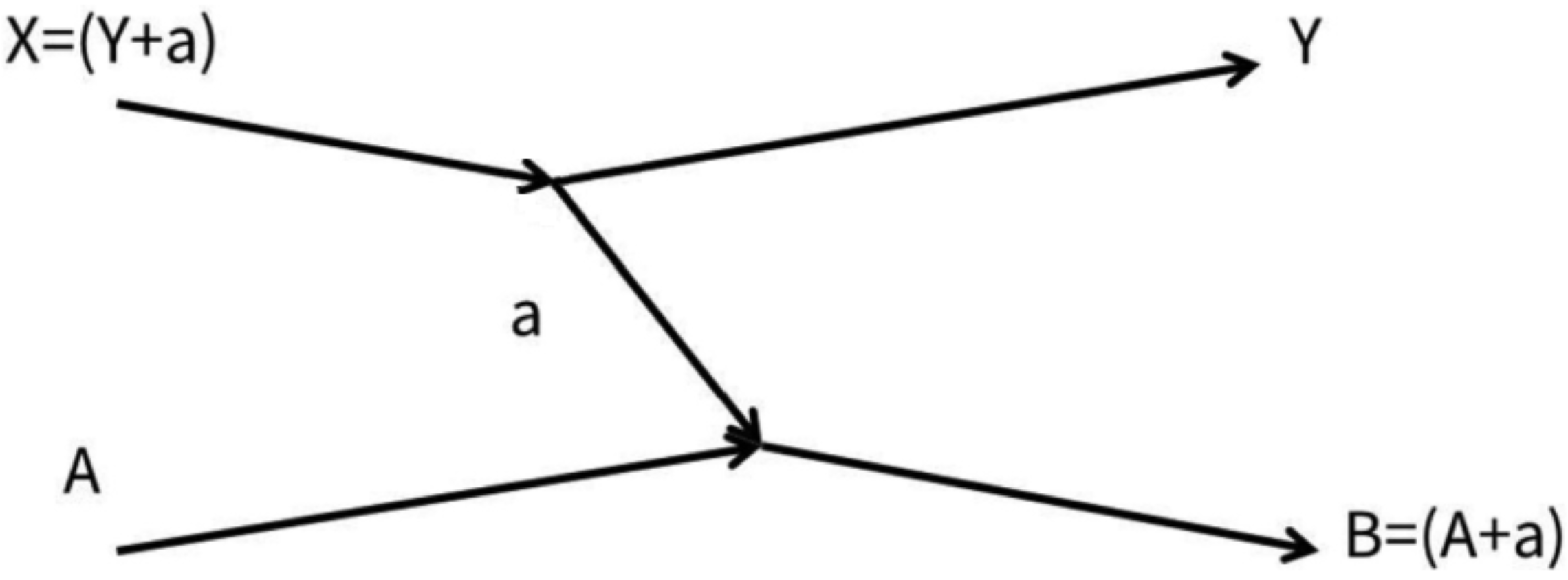
2.1. The Trojan Horse Method
2.2. The Asymptotic Normalization Coefficient
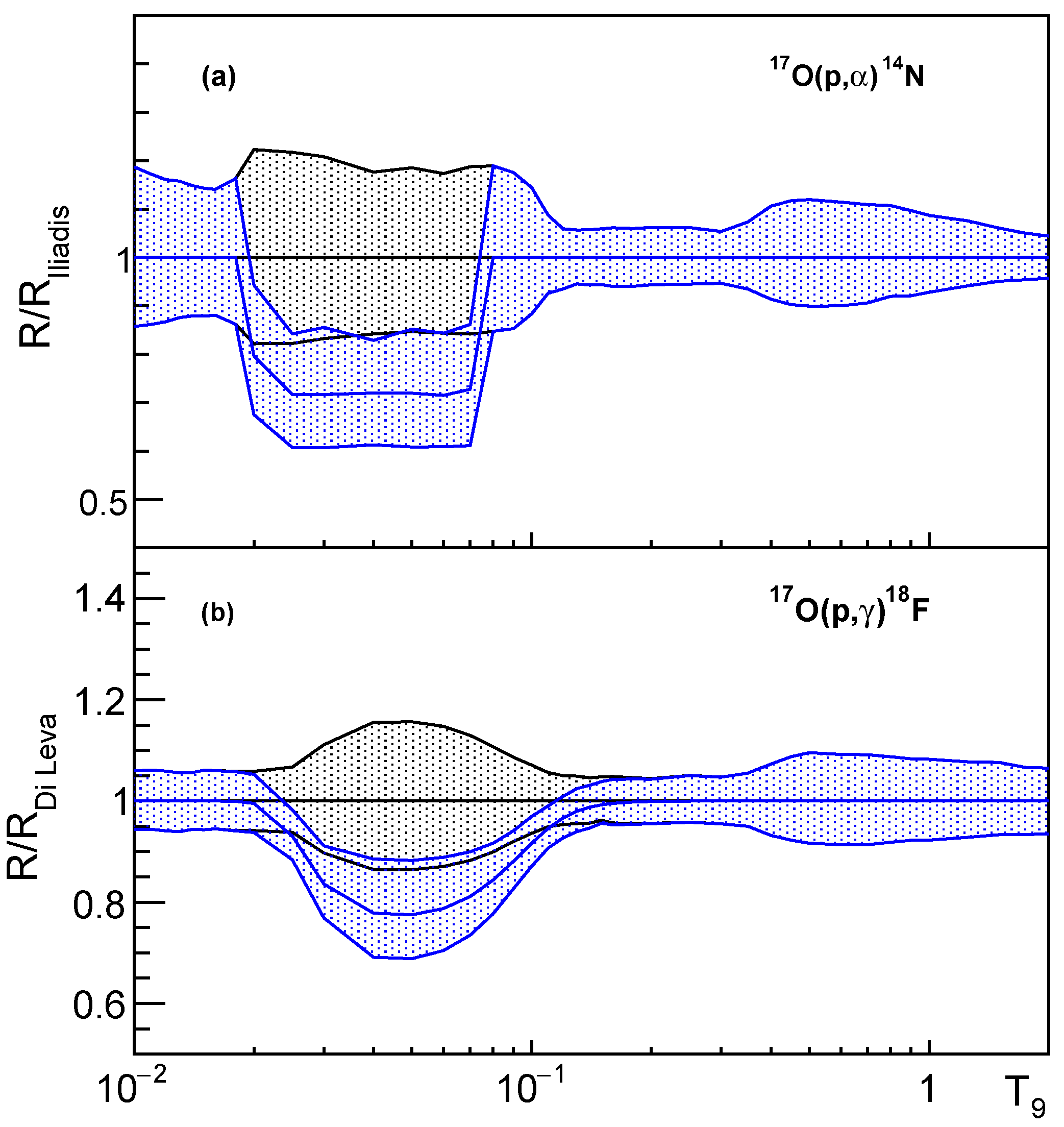
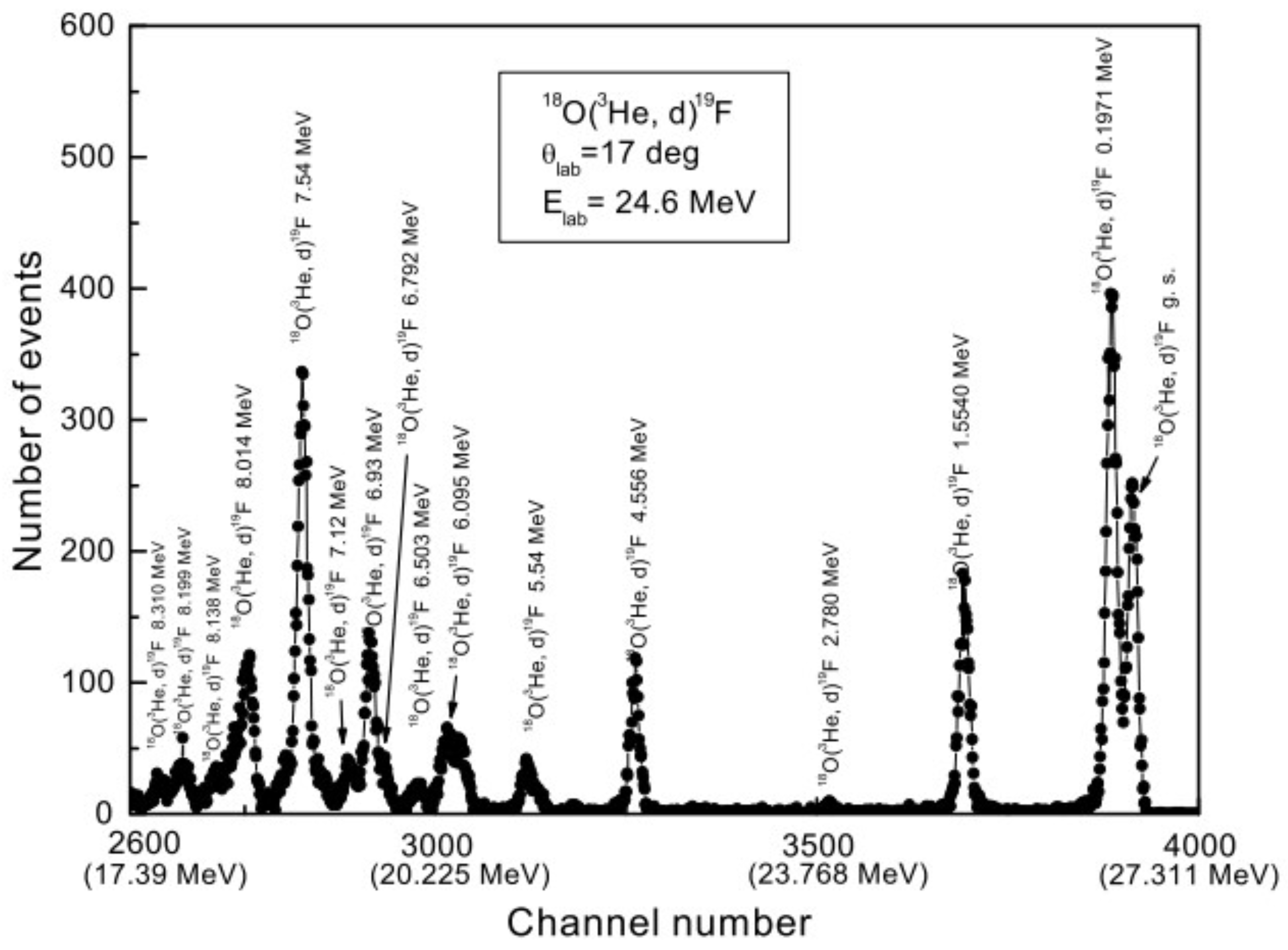
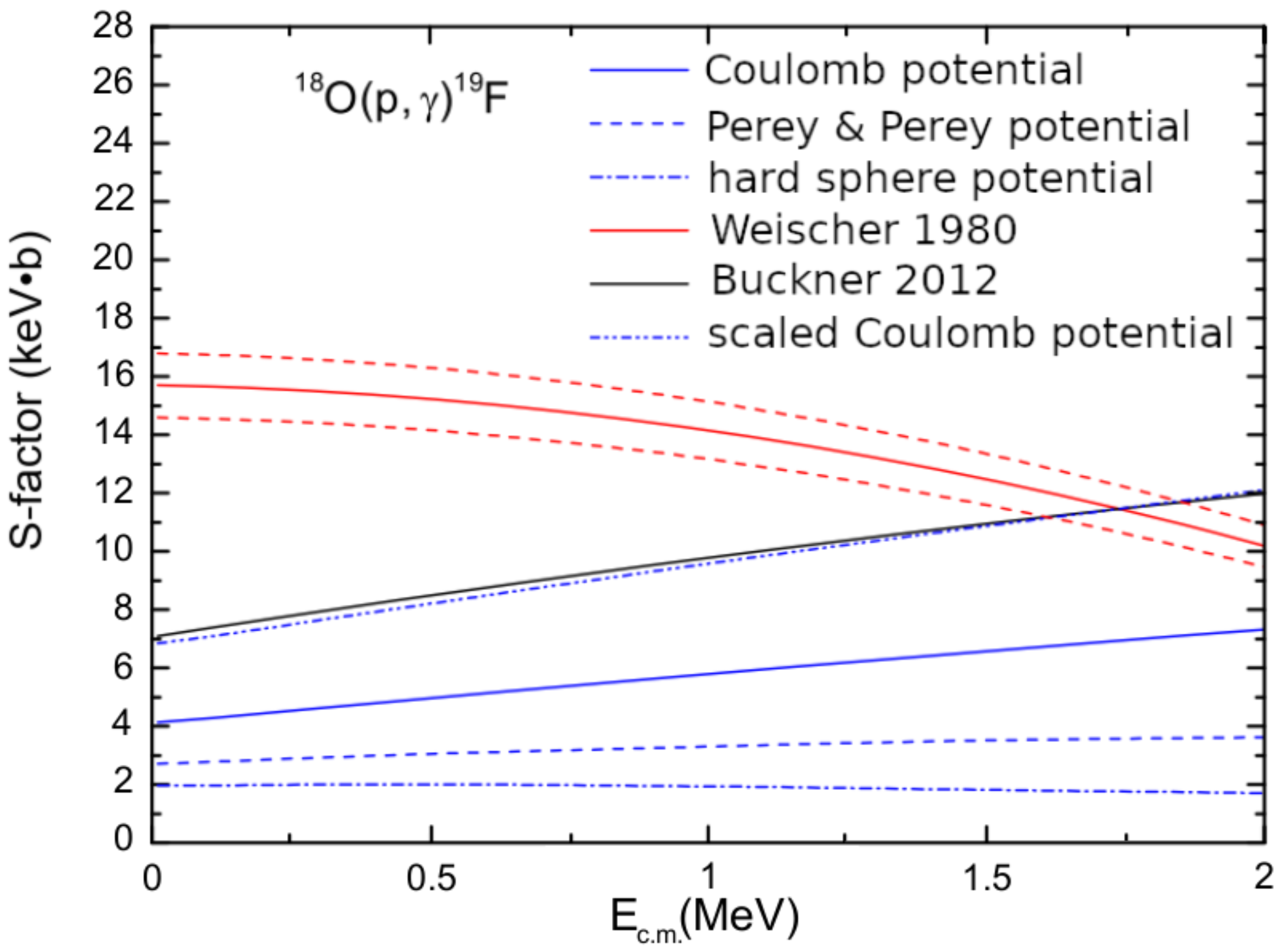
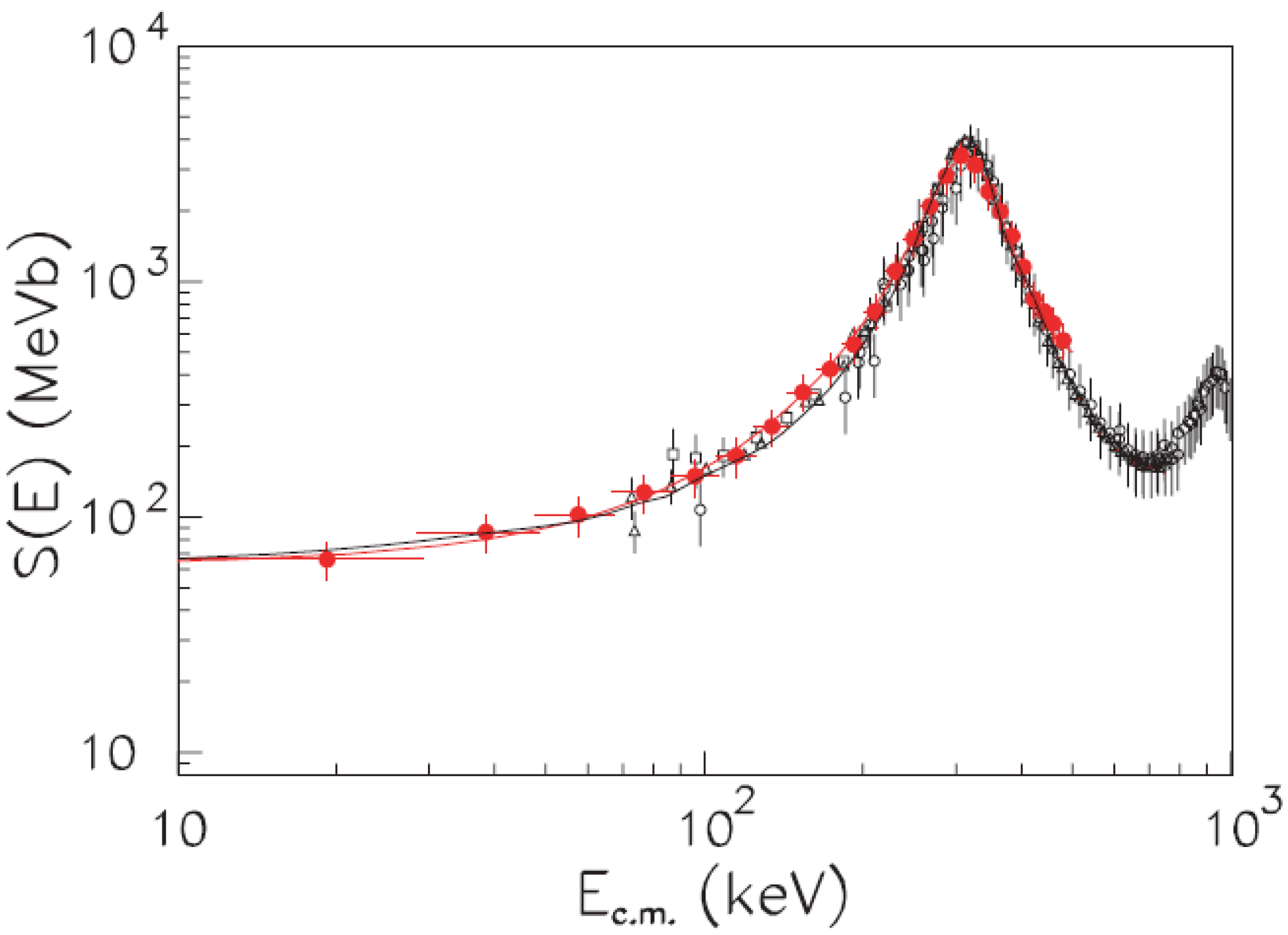
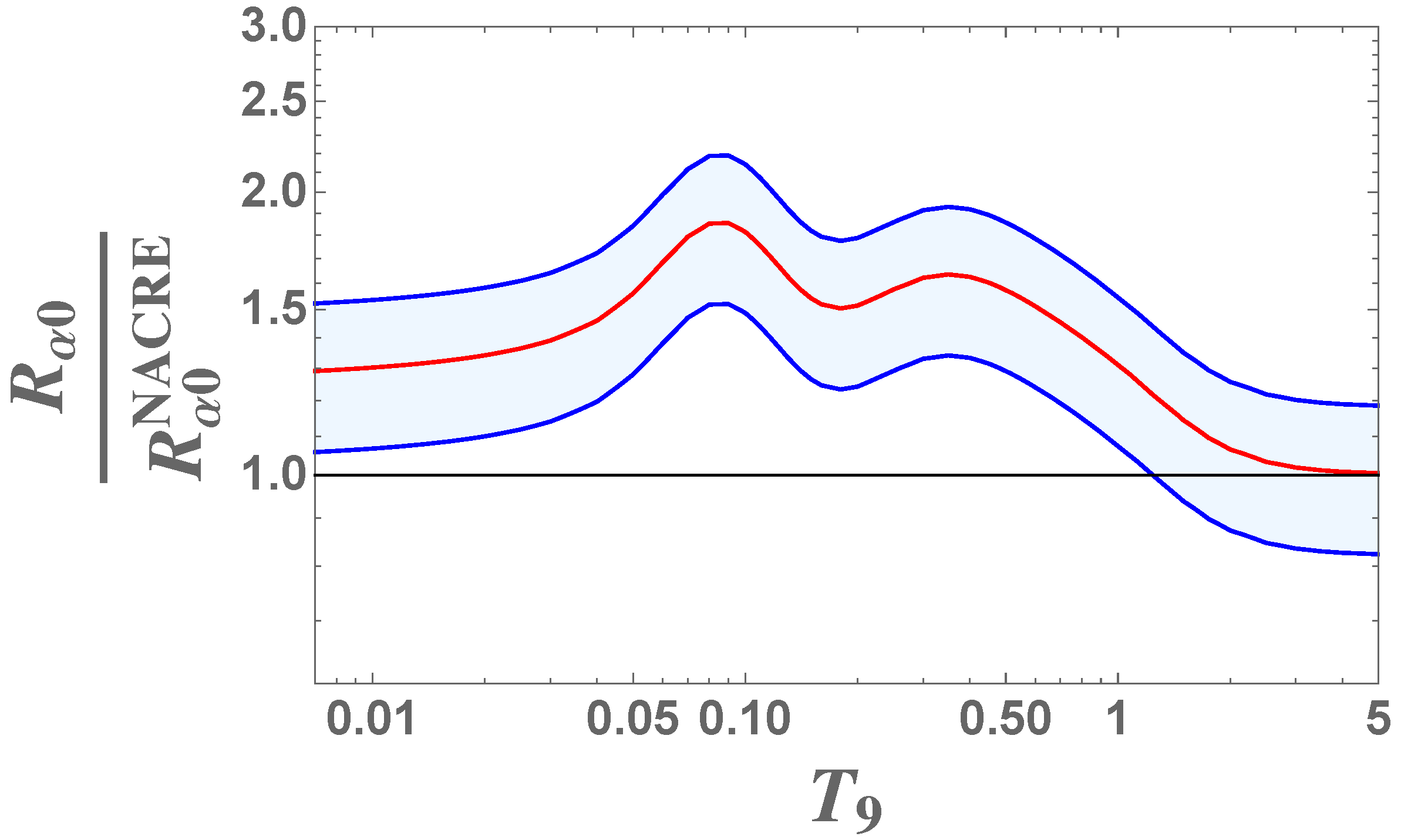
3. The O(p,)N and O(p,)F Reactions
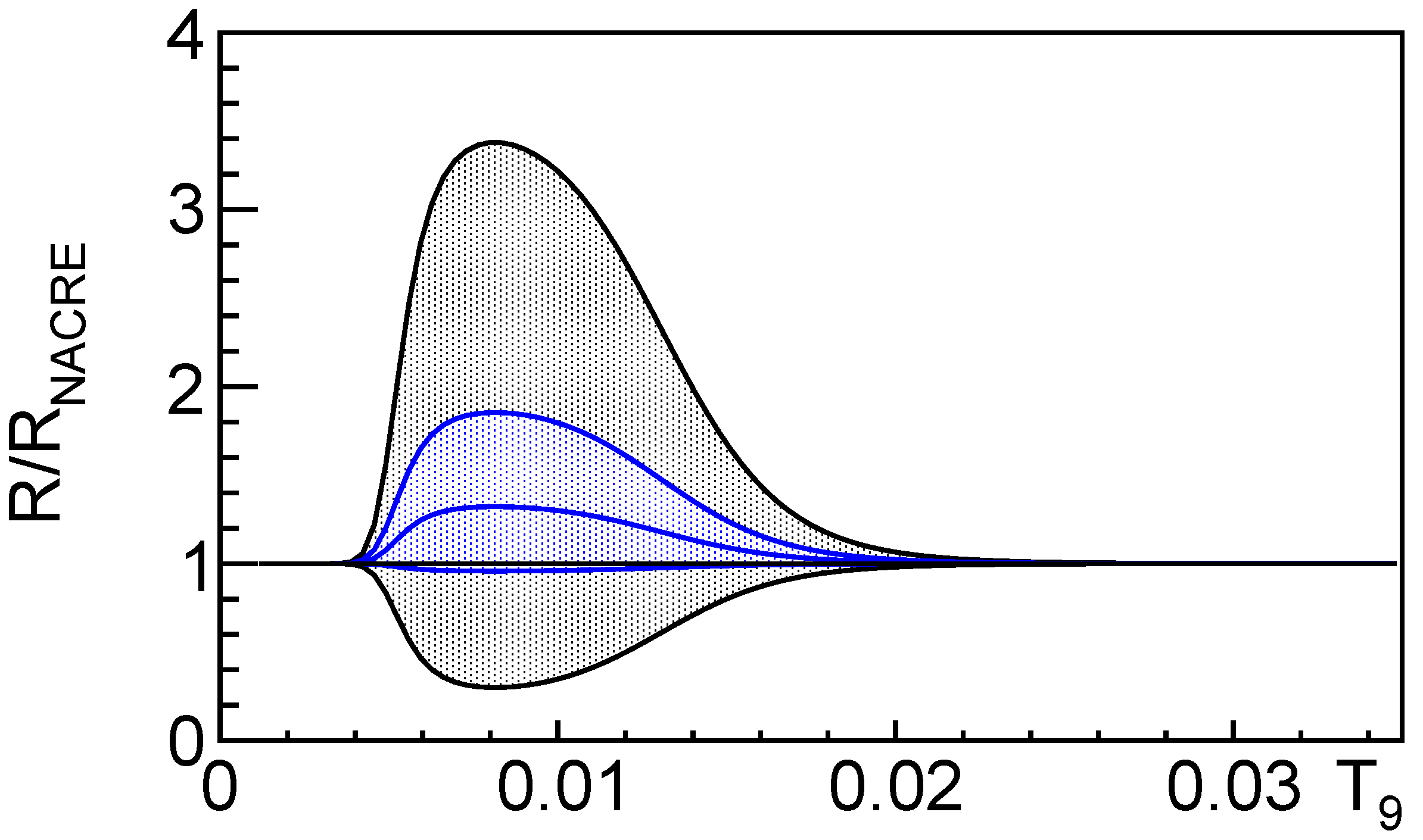
4. The N(p,)C Reaction
5. The Fluorine Problem: Study of the F(p,)O and F(,p)Ne Reactions
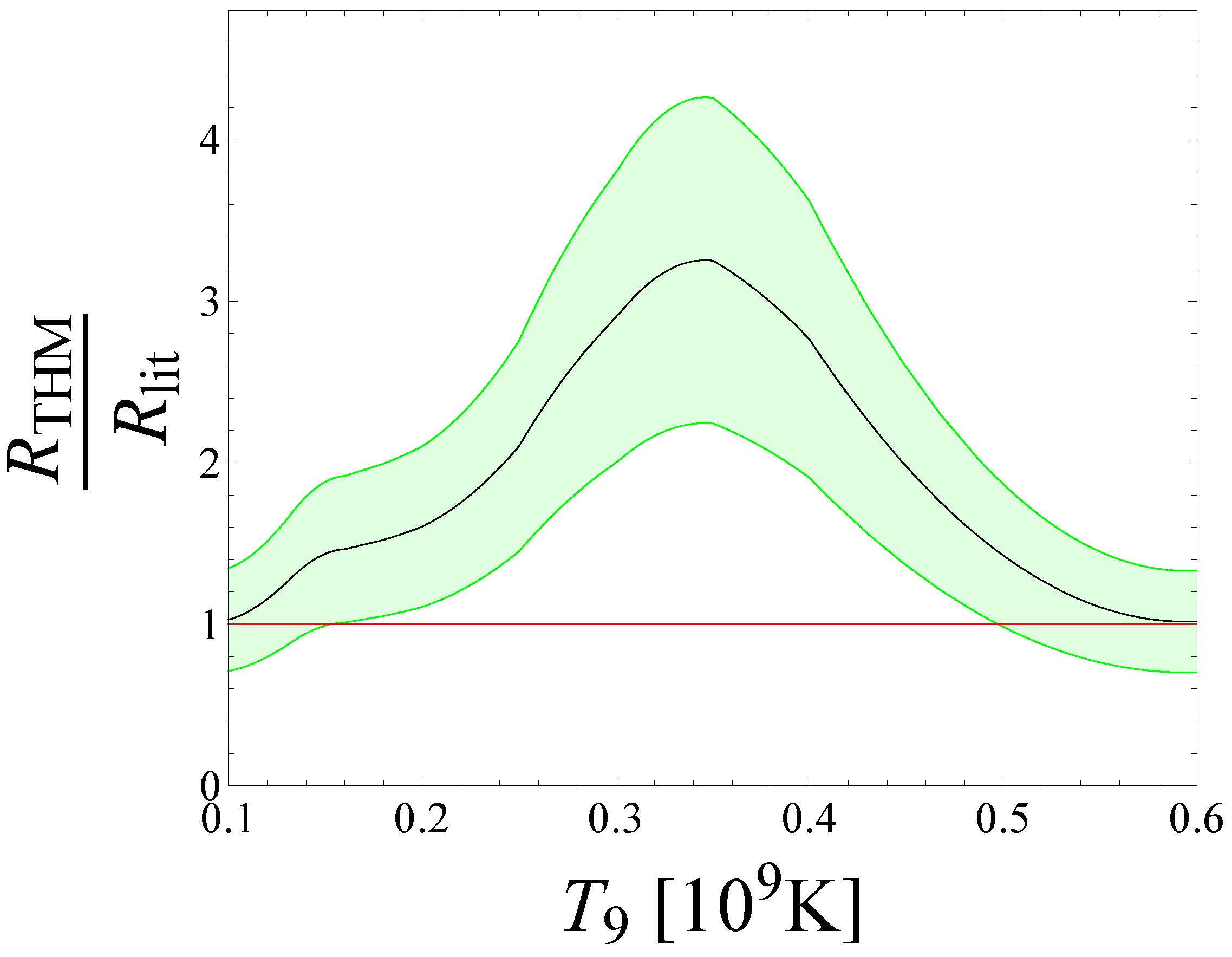
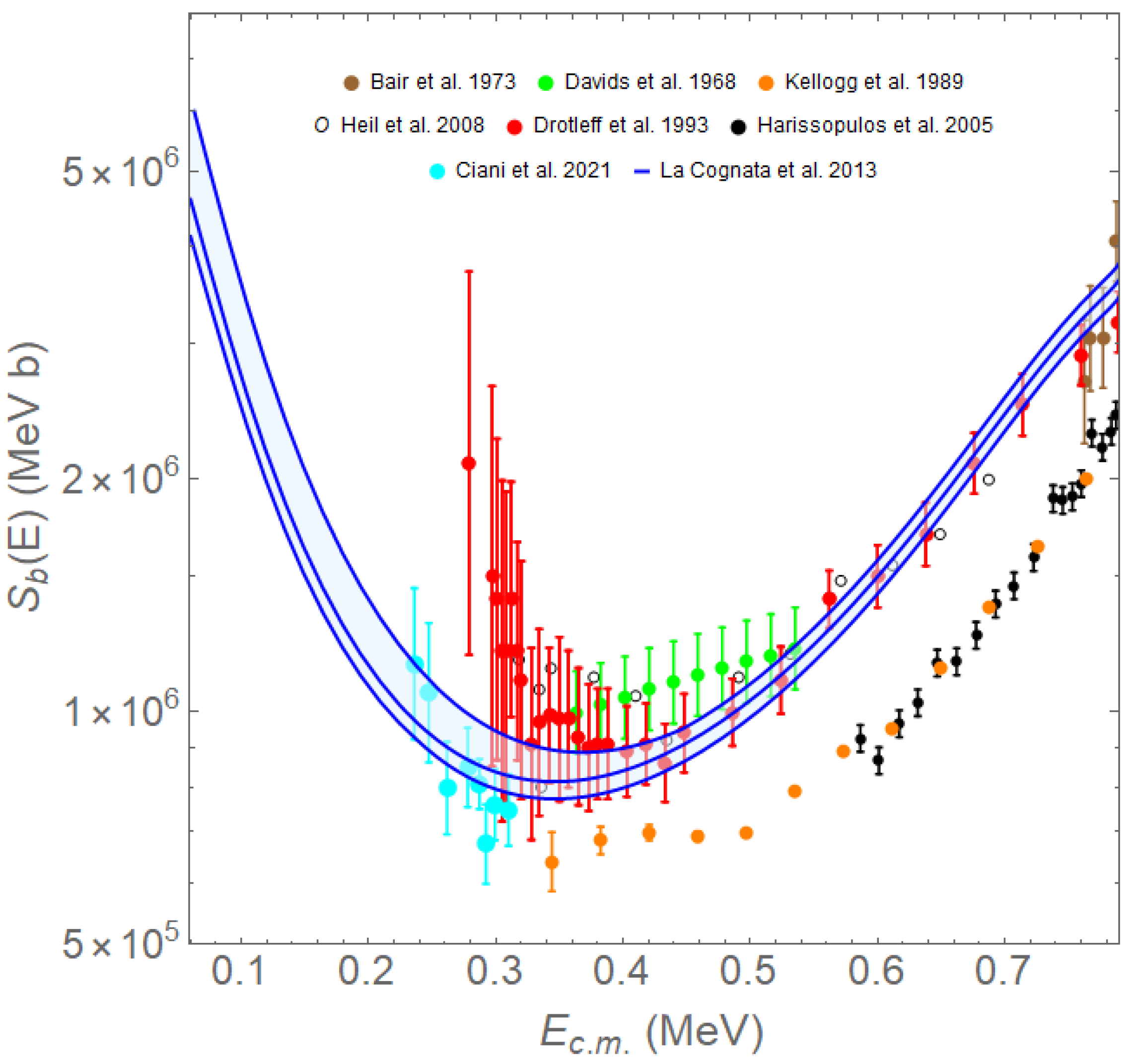
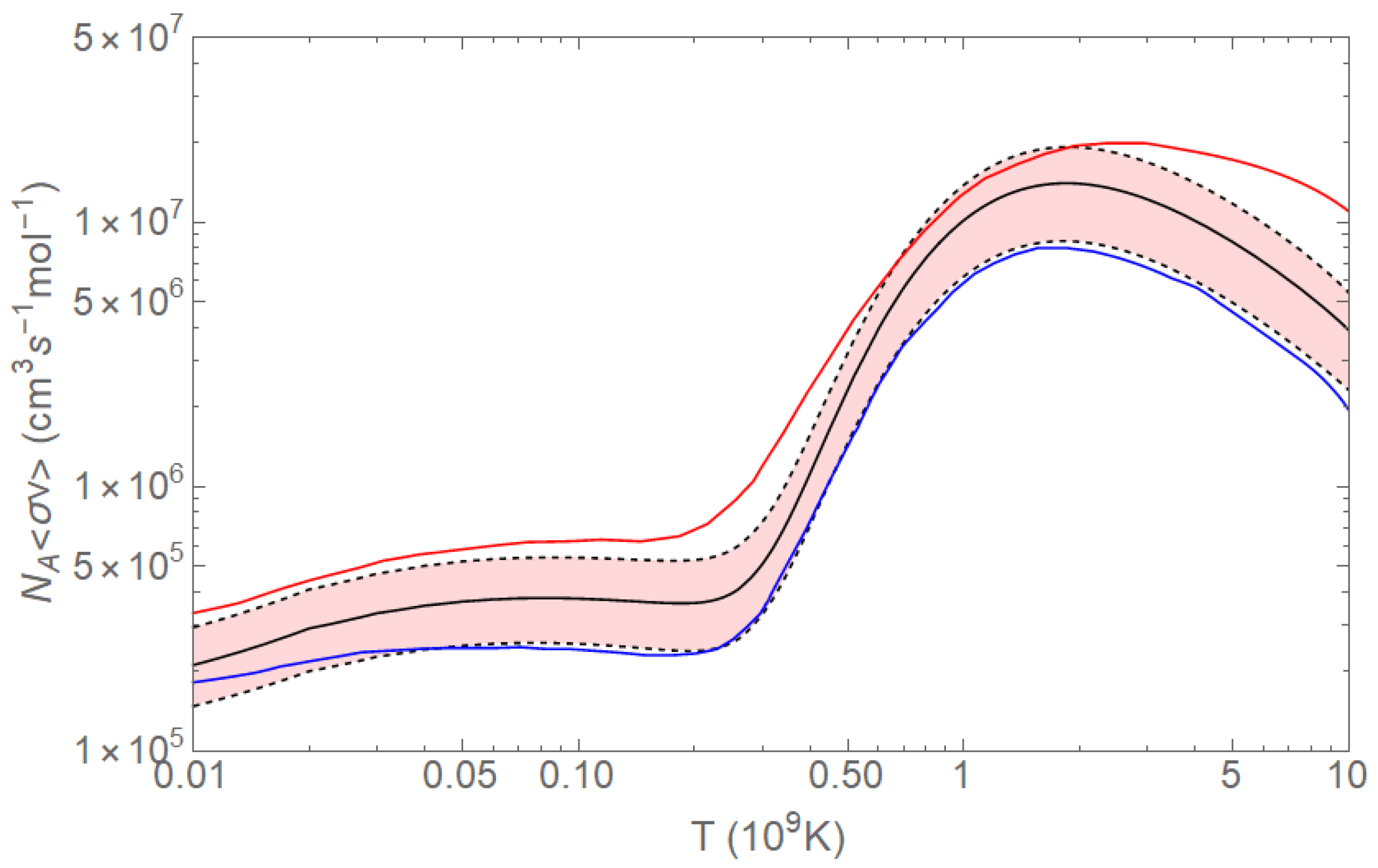
6. Neutron Sources for s-Processes: The C(,n)O Reaction
7. Neutron Poison Reactions: The O(n,)C and the N(n,p)C
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 |
References
- Herwig, F. Evolution of Asymptotic Giant Branch Stars Formation. Annu. Rev. Astron. Astroph. 2005, 43, 435. [Google Scholar] [CrossRef]
- Iliadis, C. Nuclear Physics of Stars; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Busso, M.; Gallino, R.; Wasserburg, G.J. Nucleosynthesis in Asymptotic Giant Branch Stars: Relevance for Galactic Enrichment and Solar System Formation. Annu. Rev. Astron. Astroph. 1999, 37, 239. [Google Scholar] [CrossRef]
- Cristallo, S.; La Cognata, M.; Massimi, C.; Best, A.; Palmerini, S.; Straniero, O.; Trippella, O.; Busso, M.; Ciani, G.F.; Mingrone, F.; et al. The Importance of the 13C(α,n)16O Reaction in Asymptotic Giant Branch Stars. Astroph. J. 2018, 859, 14. [Google Scholar] [CrossRef]
- Palmerini, S.; Trippella, O.; Busso, M.; Vescovi, D.; Petrelli, M.; Zucchini, A.; Frondini, F. s-Processing from MHD-induced mixing and isotopic abundances in presolar SiC grains. Geochim. Cosmochim. Acta 2018, 221, 21. [Google Scholar] [CrossRef]
- Busso, M.; Vescovi, D.; Palmerini, S.; Cristallo, S.; Antonuccio-Delogu, V. s-processing in AGB Stars Revisited. III. Neutron Captures from MHD Mixing at Different Metallicities and Observational Constraints. Astroph. J. 2021, 908, 55. [Google Scholar] [CrossRef]
- Woosley, S.E.; Haxton, W.C. Supernova neutrinos, neutral currents and the origin of fluorine. Nature 1988, 334, 45. [Google Scholar] [CrossRef]
- Goriely, S.E.; Jorrissen, A.; Arnould, M. On the Mechanism of 19F Production. In Proceedings of the 5th Workshop on Nuclear Astrophysics, Tegernsee, Germany, 30 January–4 February 1989. [Google Scholar]
- Meynet, G.; Arnould, M. Synthesis of 19F in Wolf-Rayet stars. Astron. Astrophys. 2000, 355, 176. [Google Scholar]
- Palacios, A.; Arnould, M.; Meynet, G. The thermonuclear production of 19F by Wolf-Rayet stars revisited. Astron. Astrophys. 2005, 443, 243. [Google Scholar] [CrossRef]
- Longland, R.; Lorén-Aguilar, P.; José, J.; García-Berro, E.; Althaus, L.G.; Isern, J. Nucleosynthesis during the Merger of White Dwarfs and the Origin of R Coronae Borealis Stars. Astrophys. J. Lett. 2011, 737, L34. [Google Scholar] [CrossRef]
- Vescovi, D.; Cristallo, S.; Palmerini, S.; Abia, C.; Busso, M. Magnetic-buoyancy-induced mixing in AGB stars: Fluorine nucleosynthesis at different metallicities. Astron. Astrophys. 2021, 652, 7. [Google Scholar] [CrossRef]
- Lucatello, S.; Masseron, T.; Johnson, J.A.; Pignatari, M.; Herwig, F. Fluorine and Sodium in C-rich Low-metallicity Stars. Astrophys. J. 2011, 729, 1. [Google Scholar] [CrossRef]
- Lattanzio, J.C.; Frost, C.A.; Cannon, R.C.; Wood, P.R. Hot Bottom Burning Nucleosynthesis in 6 Msolar Stellar Models. Nuc. Phys. A 1997, 621, 435. [Google Scholar] [CrossRef]
- Wasserburg, G.J.; Boothroyd, A.I.; Sackmann, I.-J. Deep Circulation in Red Giant Stars: A Solution to the Carbon and Oxygen Isotope Puzzles? Astroph. J. Lett. 1995, 447, 37. [Google Scholar] [CrossRef]
- Palmerini, S.; Trippella, O.; Busso, M. A deep mixing solution to the aluminum and oxygen isotope puzzles in pre-solar grains. Mon. Not. R. Astron. Soc. 2017, 467, 1193. [Google Scholar]
- Lugaro, M.; Karakas, A.I.; Bruno, C.G.; Aliotta, M.; Nittler, L.R.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; Caciolli, A.; et al. Origin of meteoritic stardust unveiled by a revised proton-capture rate of 17O. Nat. Astron. 2017, 1, 0027. [Google Scholar] [CrossRef]
- Palmerini, S.; Cristallo, S.; Busso, M.; La Cognata, M.; Sergi, M.L.; Vescovi, D. Low mass stars or intermediate mass stars? The stellar origin of presolar oxide grains revealed by their isotopic composition. Front. Astron. Space Sci. 2020, 7, 103. [Google Scholar] [CrossRef]
- Tribble, R.E.; Bertulani, C.A.; Mukhamedzhanov, A.M.; Spitaleri, C. Indirect techniques in nuclear astrophysics: A review. Rep. Prog. Phys. 2014, 77, 106901. [Google Scholar] [CrossRef]
- Spitaleri, C.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Tumino, A. Astrophysics studies with the Trojan Horse Method. Eur. Phys. J. A 2019, 55, 161. [Google Scholar] [CrossRef]
- Tumino, A.; Bertulani, A.C.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Romano, S.; Typel, S. The Trojan Horse Method: A Nuclear Physics Tool for Astrophysics. Ann. Rev. Nuc. Part. Sci. 2021, 71, 345–376. [Google Scholar] [CrossRef]
- Blokhintsev, L.D.; Borbely, I.; Dolinskii, E.I. Nuclear vertex constants. Sov. J. Part. Nucl. 1977, 8, 485. [Google Scholar]
- Mukhamedzhanov, A.M.; Timofeyuk, N.K. Astrophysical S-factor for the reaction 7Be+p→8B+γ. J. Exp. Theor. Phys. Lett. 1990, 51, 282. [Google Scholar]
- Xu, H.M.; Gagliardi, C.A.; Tribble, R.E.; Mukhamedzhanov, A.M.; Timofeyuk, N.K. Overall Normalization of the Astrophysical S Factor and the Nuclear Vertex Constant for 7Be(p,γ)8B Reactions. Phys. Rev. Lett. 1994, 73, 2027. [Google Scholar] [CrossRef]
- Rolfs, C.E.; Rodney, W.S. Cauldrons in the Cosmos; The University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Jain, M.; Roos, P.G.; Pugh, H.G.; Holmgren, H.D. The (p,pα) and (α, 2α) reactions on 6Li and 7Li at 60 MeV. Nucl. Phys. A 1970, 153, 49. [Google Scholar] [CrossRef]
- Tumino, A.; Spitaleri, C.; Mukhamedzhanov, A.; Rapisarda, G.G.; Campajola, L.; Cherubini, S.; Crucillá, V.; Elekes, Z.; Fülop, Z.; Gialanella, L.; et al. Off-energy-shell p-p scattering at sub-Coulomb energies via the Trojan horse method. Phys. Rev. C 2008, 78, 064001. [Google Scholar] [CrossRef]
- Dolinsky, E.I.; Dzhamalov, P.O.; Mukhamedzhanov, A.M. Peripheral-Model Approach to Stripping into Resonant States. Nucl. Phys. A 1973, 202, 97. [Google Scholar] [CrossRef]
- Mukhamedzhanov, A.M.; Blokhintsev, L.D.; Irgaziev, B.F.; Kadyrov, A.S.; La Cognata, M.; Spitaleri, C.; Tribble, R.E. Trojan Horse as an indirect technique in nuclear astrophysics. J. Phys. G Nucl. Part. Phys. 2008, 35, 014016. [Google Scholar] [CrossRef][Green Version]
- La Cognata, M.; Spitaleri, C.; Mukhamedzhanov, A.M.; Irgaziev, B.; Tribble, R.E.; Banu, A.; Cherubini, S.; Coc, A.; Crucillá, V.; Goldberg, V.Z.; et al. A Measurement of the 20 and 90 keV Resonances in the 18O(p,α)15N Reaction via the Trojan Horse Method. Phys. Rev. Lett. 2008, 101, 152501. [Google Scholar] [CrossRef]
- La Cognata, M.; Goldberg, V.Z.; Mukhamedzhanov, A.M.; Spitaleri, C.; Tribble, R.E. Improved determination of the astrophysical S(O) factor of the 15N(p,α)12C reaction. Phys. Rev. C. 2009, 80, 012801. [Google Scholar] [CrossRef]
- La Cognata, M.; Spitaleri, C.; Mukhamedzhanov, A.; Banu, A.; Cherubini, S.; Coc, A.; Crucillà, V.; Goldberg, V.; Gulino, M.; Irgaziev, B.; et al. A Novel Approach to Measure the Cross Section of the 18O(p,α)15N Resonant Reaction in the 0–200 keV Energy Range. Astrophys. J. 2010, 708, 796. [Google Scholar] [CrossRef]
- La Cognata, M.; Spitaleri, C.; Mukhamedzhanov, A.; Goldberg, V.; Irgaziev, B.; Lamia, L.; Pizzone, R.G.; Sergi, M.L.; Tribble, R.E. DWBA momentum distribution and its effect on THM. Nucl. Phys. A 2010, 834, 658. [Google Scholar] [CrossRef]
- Lamia, L.; La Cognata, M.; Spitaleri, C.; Irgaziev, B.; Pizzone, R.G. Influence of the d-state component of the deuteron wave function on the application of the Trojan horse method. Phys. Rev. C 2012, 85, 025805. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Spitaleri, C.; Cherubini, S.; La Cognata, M.; Lamia, L.; Miljanic, D.; Musumarra, A.; Romano, S.; Tumino, A.; Tudisco, S.; et al. Influence of the α-d motion in 6Li on Trojan Horse applications. Phys. Rev. C 2005, 71, 058801. [Google Scholar] [CrossRef]
- Tumino, A.; Spartá, R.; Spitaleri, C.; Mukhamedzhanov, A.M.; Typel, S.; Pizzone, R.G.; Tognelli, E.; Degl’Innocenti, S.; Burjan, V.; Kroha, V.; et al. New determination of the 2H(d,p)3H and 2H(d,n)3He reaction rates at astrophysical energies. Astrophys. J. 2014, 785, 96. [Google Scholar] [CrossRef]
- Tumino, A.; Spitaleri, C.; La Cognata, M.; Cherubini, S.; Guardo, G.L.; Gulino, M.; Hayakawa, S.; Indelicato, I.; Lamia, L.; Petrascu, H.; et al. An increase in the 12C+12C fusion rate from resonances at astrophysical energies. Nature 2018, 557, 687. [Google Scholar] [CrossRef] [PubMed]
- Tumino, A.; Spitaleri, C.; Mukhamedzhanov, A.; Rapisarda, G.G.; Cherubini, S.; Crucillá, E.Z.; Fülöp, Z.; Gulino, M.; Gyürky, G. Suppression of the Coulomb interaction in the Off-Energy-Shell p-p scattering from the p+d→p+p+n Reaction. Phys. Rev. Lett. 2007, 98, 252502. [Google Scholar] [CrossRef]
- Spitaleri, C.; Bertulani, C.A.; Fortunato, L.; Vitturi, A. The electron screening puzzle and nuclear clustering. Phys. Lett. B 2016, 755, 275. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Bertulani, C.A.; Lamia, L.; La Cognata, M.; Sergi, M.L.; Spartá, R.; Tumino, A. Clusters and their fundamental role for Trojan Horse Method. Eur. Phys. J. A 2020, 56, 283. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Spartá, R.; Bertulani, C.A.; Spitaleri, C.; La Cognata, M.; Lalmansingh, L.; Lamia, L.; Mukhamedzhanov, A.; Tumino, A. Big Bang Nucleosynthesis revisited via Trojan Horse Method measurements. Astrophys. J. 2014, 786, 112. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Spampinato, C.; Spartá, R.; Couder, M.; Tan, W.; Burjan, V.; D’Agata, G.; Guardo, G.L.; La Cognata, M.; Lamia, L.; et al. Indirect measurement of the 3He(n,p)3H reaction cross section at Big Bang energies. Eur. Phys. J. 2020, A56, 199. [Google Scholar] [CrossRef]
- Aliotta, M.; Spitaleri, C.; Lattuada, M.; Musumarra, A.; Pizzone, R.G.; Tumino, A.; Rolfs, C.; Strieder, F. Improved information on electron screening in 7Li(p,α)α using the Trojan-horse method. Eur. Phys. J. A 2000, 9, 435. [Google Scholar] [CrossRef]
- Lamia, L.; Spitaleri, C.; La Cognata, M.; Palmerini, S.; Pizzone, R.G. Recent evaluation of the 7Li(p,α)4He reaction rate at astrophysical energies via the Trojan Horse Method. Astron. Astrophys. 2012, 541, A158. [Google Scholar] [CrossRef]
- Romano, S.; Lamia, L.; Spitaleri, C.; Li, C.; Cherubini, S.; Gulino, M.; La Cognata, M.; Pizzone, R.G.; Tumino, A. Study of the 9Be(p,α)6Li reaction via the Trojan Horse Method. Eur. Phys. J. A 2006, 27, 221. [Google Scholar] [CrossRef]
- Lamia, L.; Spitaleri, C.; Tognelli, E.; Degl’Innocenti, S.; Pizzone, R.G.; Moroni, P.G.P. Astrophysical impact of the updated 9Be(p,α)6Li and 10B(p,α)7Be reaction rates as deduced by THM. Astrophy. J. 2015, 811, 99. [Google Scholar] [CrossRef]
- Cvetinović, A.; Spitaleri, C.; Spartá, R.; Rapisarda, G.G.; Puglia, S.M.R.; La Cognata, M.; Cherubini, S.; Guardo, G.L.; Gulino, M.; Lamia, L.; et al. Trojan horse measurement of the 10B(p,α0)7Be cross section in the energy range from 3 keV to 2.2 MeV. Phys. Rev. C 2018, 97, 065801. [Google Scholar] [CrossRef]
- Rapisarda, G.G.; Spitaleri, C.; Cvetinović, A.; Spartá, R.; Cherubini, S.; Guardo, G.L.; Gulino, M.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; et al. Study of the 10B(p,α1)7Be reaction by means of the Trojan Horse Method. Eur. Phys. J. A 2018, 54, 189. [Google Scholar] [CrossRef]
- Sergi, M.L.; Guardo, G.L.; La Cognata, M.; Gulino, M.; Mrázek, J.; Palmerini, S.; Spitaleri, C.; Wiescher, M. Indirect measurements of n- and p- induced reactions of astrophysical interest on oxygen isotopes. Front. Astron. Space Sci. 2020, 7, 60. [Google Scholar] [CrossRef]
- Guardo, G.L.; Spitaleri, C.; Lamia, L.; Gulino, M.; La Cognata, M.; Tang, X.; deBoer, R.; Fang, X.; Goldberg, V.; Mrázek, J.; et al. Assessing the near threshold cross section of the 17O(n,α)14C reaction by means of the Trojan horse method. Phys. Rev. C 2017, 95, 025807. [Google Scholar] [CrossRef]
- Guardo, G.L.; Spitaleri, C.; Lamia, L.; Spartá, R.; Carlin, N.; Cherubini, S.; Gimenez Del Santo, G.; Indelicato, I.; La Cognata, M.; Lattuada, D.; et al. The 10B(n,α)7Li cross sections at ultra-low energy through the Trojan Horse Method applied to the 2H(10B,α7Li)1H. Eur. Phys. J. A 2019, 55, 211. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Roeder, B.T.; McCleskey, M.; Trache, L.; Tribble, R.E.; Spitaleri, C.; Bertulani, C.A.; Cherubini, S.; Gulino, M.; Indelicato, I.; et al. Trojan Horse measurement of the 18F(p,α)15O astrophysical S(E)-factor. Eur. Phys. J. A 2016, 52, 24. [Google Scholar] [CrossRef]
- La Cognata, M.; Pizzone, R.G.; José, J.; Hernanz, M.; Cherubini, S.; Gulino, M.; Rapisarda, G.G.; Spitaleri, C. A Trojan Horse approach to the production of 18F in novae. Astr. J. 2017, 65, 846. [Google Scholar]
- Lamia, L.; Spitaleri, C.; Bertulani, C.A.; Hou, S.Q.; La Cognata, M.; Pizzone, R.G.; Romano, S.; Sergi, M.L.; Tumino, A. On the Determination of the 7Be(n,α)4He Reaction Cross Section at BBN Energies. Astrophys. J. 2017, 850, 175. [Google Scholar] [CrossRef]
- Lamia, L.; Mazzocco, M.; Pizzone, R.G.; Hayakawa, S.; La Cognata, M.; Spitaleri, C.; Bertulani, C.A.; Boiano, A.; Boiano, C.; Broggini, C.; et al. Cross-section measurement of the cosmologically relevant 7Be(n,α)4He reaction over a broad energy range in a single experiment. Astrophys. J. 2019, 879, 23. [Google Scholar] [CrossRef]
- Burjan, V.; Hons, Z.; Kroha, V.; Mrázek, J.; Piskoř, Š.; Mukhamedzhanov, A.M.; Trache, L.; Tribble, R.E.; La Cognata, M.; Lamia, L.; et al. The determination of the astrophysical S-factor of the direct 18O(p,γ)19F capture by the ANC method. Eur. Phys. J. A 2019, 55, 114. [Google Scholar] [CrossRef]
- Mukhamedzhanov, A.M.; Burjan, V.; Gulino, M.; Hons, Z.; Kroha, V.; McCleskey, M.; Mrázek, J.; Nguyen, N.; Nunes, F.M.; Piskoř, Š.; et al. Asymptotic normalization coefficients from the 14C(d,p)15C reaction. Phys. Rev. C 2011, 84, 024616. [Google Scholar] [CrossRef]
- Kiss, G.G.; La Cognata, M.; Spitaleri, C.; Yarmukhamedov, R.; Wiedenhöver, I.; Baby, L.T.; Cherubini, S.; Cvetinovic, A.; D’Agata, G.; Figuera, P.; et al. Astrophysical S-factor for the 3He(α,γ)7Be reaction via the asymptotic normalization coefficient (ANC) method. Phys. Lett. B 2020, 807, 135606. [Google Scholar] [CrossRef]
- Timofeyuk, N.K.; Johnson, R.C.; Mukhamedzhanov, A.M. Relation between Proton and Neutron Asymptotic Normalization Coefficients for Light Mirror Nuclei and its Relevance to Nuclear Astrophysics. Phys. Rev. Lett. 2003, 91, 232501. [Google Scholar] [CrossRef]
- Trache, L.; Azhari, A.; Carstoiu, F.; Clark, H.L.; Gagliardi, C.A.; Liu, Y.W.; Mukhamedzhanov, A.M.; Tang, X.; Timofeyuk, N.K.; Tribble, R.E. Asymptotic normalization coefficients for 8B→7Be+p from a study of 8Li→7Li+p. Phys. Rev. C 2003, 67, 062801. [Google Scholar] [CrossRef]
- McCleskey, M.; Mukhamedzhanov, A.M.; Trache, L.; Tribble, R.E.; Banu, A.; Eremenko, V.; Goldberg, V.Z.; Lui, Y.-W.; McCleskey, E.; Roeder, B.T.; et al. Determination of the asymptotic normalization coefficients for 14C+n→15C, the 14C(n,γ)15C reaction rate, and evaluation of a new method to determine spectroscopic factors. Phys. Rev. C 2014, 89, 044605. [Google Scholar] [CrossRef]
- D’Agata, G.; Kilic, A.I.; Burjan, V.; Mrázek, J.; Glagolev, V.; Kroha, V.; Guardo, G.L.; La Cognata, M.; Lamia, L.; Palmerini, S.; et al. 26Si(p,γ)27P direct proton capture by means of the asymptotic normalization coefficients method for mirror nuclei. Phys. Rev. C 2021, 103, 015806. [Google Scholar] [CrossRef]
- Mukhamedzhanov, A.M.; Clark, H.L.; Gagliardi, C.A.; Liu, Y.W.; Trache, L.; Tribble, R.E.; Xu, H.M.; Zhou, X.G.; Burjan, V.; Cejpek, J.; et al. Asymptotic normalization coefficients for 10B→9Be+p. Phys. Rev. C 1997, 56, 1302. [Google Scholar] [CrossRef]
- Liu, Z.H.; Lin, C.J.; Zhang, H.Q.; Li, Z.C.; Zhang, J.S.; Wu, Y.W.; Yang, F.; Ruan, M.; Liu, J.C.; Li, S.Y.; et al. Asymptotic normalization coefficients and neutron halo of the excited states in 12B and 13C. Phys. Rev. C 2001, 64, 034312. [Google Scholar] [CrossRef]
- Mukhamedzhanov, A.M.; Nunes, F.M. Combined method to extract spectroscopic information. Phys. Rev. C 2005, 72, 017602. [Google Scholar] [CrossRef]
- Belyaeva, T.L.; Perez-Torres, R.; Ogloblin, A.A.; Demyanova, A.S.; Ershov, S.N.; Goncharov, S.A. Determination of neutron halo radii in the first excited states of 13C and 11Be with the asymptotic normalization coefficients method. Phys. Rev. C 2014, 90, 064610. [Google Scholar] [CrossRef]
- Yang, J.; Capel, P. Systematic analysis of the peripherality of the 10Be(d,p)11Be transfer reaction and extraction of the asymptotic normalization coefficient of 11Be bound states. Phys. Rev. C 2018, 98, 054602. [Google Scholar] [CrossRef]
- Mukhamedzhanov, A.M.; Bém, P.; Burjan, V.; Gagliardi, C.A.; Goldberg, V.Z.; Hons, Z.; La Cognata, M.; Kroha, V.; Mrázek, J.; Novák, J.; et al. New astrophysical S factor for the 15N(p,γ)16O reaction via the asymptotic normalization coefficient (ANC) method. Phys. Rev. C 2008, 78, 015804. [Google Scholar] [CrossRef]
- Kiss, G.G.; La Cognata, M.; Yarmukhamedov, R.; Tursunmakhatov, K.I.; Wiedenhover, I.; Baby, L.T.; Cherubini, S.; Cvetinovic, A.; D’Agata, G.; Figuera, P.; et al. Indirect determination of the astrophysical S factor for the 6Li(p,γ)7Be reaction using the asymptotic normalization coefficient method. Phys. Rev. C 2021, 104, 015807. [Google Scholar] [CrossRef]
- Burjan, V.; Mrázek, J.; D’Agata, G. ANC from experimental perspective. Front. Astron. Space Sci. 2020, 7, 562466. [Google Scholar] [CrossRef]
- Palmerini, S.; Sergi, M.L.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Spitaleri, C. The RGB and AGB star nucleosynthesis in light of the recent 17O(p,α)14N and 18O(p,α)15N reaction rate determination. Astrophys. J. 2013, 764, 128. [Google Scholar] [CrossRef]
- Chafa, A.; Tatischeff, V.; Aguer, P.; Barhoumi, S.; Coc, A.; Garrido, F.; Hernanz, M.; José, J.; Kiener, J.; Lefebvre-Schuhl, A.; et al. Experimental determination of the 17O(p,α)14N and 17O(p,γ)18F reaction rates. Phys. Rev. C 2007, 75, 035810. [Google Scholar] [CrossRef]
- Iliadis, C.; Longland, R.; Champagne, A.E.; Coc, A.; Fitzgerald, R. Charged-particle thermonuclear reaction rates: II. Tables and graphs of reaction rates and probability density functions. Nucl. Phys. A 2010, 841, 31–250. [Google Scholar] [CrossRef]
- Newton, J.R.; Iliadis, C.; Champagne, A.E.; Longland, R.; Ugalde, C. Remeasurement of the 193 keV resonance in 17O(p,α)14N. Phys. Rev. C 2007, 75, 055808. [Google Scholar] [CrossRef]
- Moazen, B.H.; Bardayan, D.W.; Blackmon, J.C.; Chae, K.Y.; Chipps, K.; Domizioli, C.P.; Fitzgerald, R.; Greife, U.; Hix, W.R.; Jones, K.L.; et al. Measurement of the 183 keV resonance in O17(p,α)N14 using a novel technique. Phys. Rev. C 2007, 75, 065801. [Google Scholar] [CrossRef]
- Sergi, M.L.; Spitaleri, C.; La Cognata, M.; Coc, A.; Mukhamedzhanov, A.; Burjan, S.V.; Cherubini, S.; Crucillá, V.; Gulino, M.; Hammache, F.; et al. New high accuracy measurement of the 17O(p,α)14N reaction rate at astrophysical temperatures. Phys. Rev. C 2010, 82, 032801. [Google Scholar] [CrossRef]
- Sergi, M.L.; Spitaleri, C.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Rapisarda, G.G.; Tang, X.D.; Bucher, B.; Couder, M.; Davies, P.; et al. Improvement of the high-accuracy 17O(p,α)14N reaction rate measurement via the Trojan Horse method for application to 17O nucleosynthesis. Phys. Rev. C 2015, 91, 065803. [Google Scholar] [CrossRef]
- Di Leva, A.; Scott, D.A.; Caciolli, A.; Formicola, A.; Strieder, F.; Aliotta, M.; Anders, M.; Bemmerer, D.; Broggini, C.; Corvisiero, P.; et al. LUNA Collaboration Underground study of the 17O(p,γ)18F reaction relevant for explosive hydrogen burning. Phys. Rev. C 2014, 89, 015803. [Google Scholar] [CrossRef]
- Bruno, C.G.; Scott, D.A.; Aliotta, M.; Formicola, A.; Best, A.; Boeltzig, A.; Bemmerer, D.; Broggini, C.; Caciolli, A.; Cavanna, F.; et al. Improved Direct Measurement of the 64.5 keV Resonance Strength in the 17O(p,α)14N Reaction at LUNA. Phys. Rev. Lett. 2016, 117, 142502. [Google Scholar] [CrossRef]
- Fox, C.; Iliadis, C.; Champagne, A.E.; Fitzgerald, R.P.; Longland, R.; Newton, J.; Pollanen, J.; Runkle, R. Thermonuclear reaction rate of 17O(p,γ)18F. Phys. Rev. C 2005, 71, 055801. [Google Scholar] [CrossRef]
- Adelberger, E.G.; García, A.; Hamish Robertson, R.G.; Snover, K.A.; Balantekin, A.B.; Heeger, K.; Ramsey-Musolf, M.J.; Bemmerer, D.; Junghans, A.; Bertulani, C.A.; et al. Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Mod. Phys. 2011, 83, 195. [Google Scholar] [CrossRef]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3–183. [Google Scholar] [CrossRef]
- Champagne, A.E.; Pitt, M.L. The destruction of 18O in red giants: A search for a sub-threshold resonance in the 18O+p system. Nuc. Phys. A 1986, 457, 367. [Google Scholar] [CrossRef]
- Wiescher, M.; Becker, H.W.; Görres, J.; Kettner, K.U.; Trautvetter, H.P.; Kieser, W.E.; Rolfs, C.; Azuma, R.E.; Jackson, K.P.; Hammer, J.W. Nuclear and astrophysical aspects of 18O(p,γ)19F. Nucl. Phys. A 1980, 349, 165. [Google Scholar] [CrossRef]
- La Cognata, M.; Spitaleri, C.; Mukhamedzhanov, A.M. Effect of the high-energy resonances on the 18O(p,α)15N reaction rate at AGB and Post-AGB relevant temperatures. Astrophys. J. 2010, 723, 1512. [Google Scholar] [CrossRef]
- Becker, H.W.; Bahr, M.; Berheide, M.; Borucki, L.; Buschmann, M.; Rolfs, C.; Roters, G.; Schmidt, S.; Schulte, W.H.; Mitchell, G.E.; et al. Hydrogen depth profiling using 18O ions. Z. Phys. A 1995, 351, 453. [Google Scholar] [CrossRef]
- Bruno, C.G.; Aliotta, M.; Descouvemont, P.; Best, A.; Davinson, T.; Bemmerer, D.; Boeltzig, A.; Broggini, C.; Caciolli, A.; Cavanna, F.; et al. Improved astrophysical rate for the 18O(p,α)15N reaction by underground measurements. Phys. Lett. B 2019, 790, 237–242. [Google Scholar] [CrossRef]
- Vogelaar, R.B.; Wang, T.R.; Kellog, S.E.; Kavanagh, R.W. Low-energy reaction yields for 18O(p,γ) and 18O(α,γ). Phys. Rev. C 1990, 42, 753. [Google Scholar] [CrossRef] [PubMed]
- Pantaleo, F.R.; Boeltzig, A.; Best, A.; Perrino, R.; Aliotta, M.; Balibrea-Correa, J.; Barile, F.; Bemmerer, D.; Broggini, C.; Bruno, C.G. Low-energy resonances in the 18O(p,γ)19F reaction. Phys. Rev. C 2021, 104, 025802. [Google Scholar] [CrossRef]
- Buckner, M.Q.; Iliadis, C.; Cesaratto, J.M.; Howard, C.; Clegg, T.B.; Champagne, A.E.; Daigle, S. Thermonuclear reaction rate of 18O(p,γ)19F. Phys. Rev. C 2012, 86, 065804. [Google Scholar] [CrossRef]
- Vernotte, J.; Berrier-Ronsin, G.; Kalifa, J.; Tamisier, R. Optical model analysis of 3He elastic scattering from s-d shell nuclei at 25 MeV. Nucl. Phys. A 1982, 390, 285. [Google Scholar] [CrossRef]
- Trost, H.J.; Lezoch, P.; Strohbusch, U. Simple optical model treatment of the elastic 3He scattering. Nucl. Phys. A 1987, 462, 333. [Google Scholar] [CrossRef]
- Perey, C.M.; Perey, F.G. Compilation of phenomenological optical-model parameters 1954–1975. At. Data Nucl. Data Tables 1976, 17, 1–101. [Google Scholar] [CrossRef]
- Brida, I.; Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo calculations of spectroscopic overlaps in A ≤ 7 nuclei. Phys. Rev. C 2011, 84, 024319. [Google Scholar] [CrossRef]
- Lugaro, M.; Ugalde, C.; Karakas, A.I.; Görres, J.; Wiescher, M.; Lattanzio, J.C.; Cannon, R.C. Reaction Rate Uncertainties and the Production of 19F in Asymptotic Giant Branch Stars. Astrophys. J. 2004, 615, 934. [Google Scholar] [CrossRef]
- Schardt, A.; Fowler, W.A.; Lauritsen, C.C. The Disintegration of 15N by Protons. Phys. Rev. 1952, 86, 527–535. [Google Scholar] [CrossRef]
- Zyskind, J.L.; Parker, P.D. Remeasurement of the low-energy cross section for the 15N(p,α0)12C reaction. Nucl. Phys. A 1979, 320, 404–412. [Google Scholar] [CrossRef]
- Redder, A.; Becker, H.W.; Lorenz-Wirzba, H.; Rolfs, C.; Schmalbrock, P.; Trautvetter, H.P. The 15N(p,α0)12C reaction at stellar energies. Z. Phys. A 1982, 305, 325–333. [Google Scholar] [CrossRef]
- La Cognata, M.; Romano, S.; Spitaleri, C.; Cherubini, S.; Crucillá, V.; Gulino, M.; Lamia, L.; Pizzone, R.G.; Tumino, A.; Tribble, R.; et al. Astrophysical S(E) factor of the 15N(p,α)12C reaction at sub-Coulomb energies via the Trojan horse method. Phys. Rev. C. 2007, 76, 065804. [Google Scholar] [CrossRef]
- Palmerini, S.; La Cognata, M.; Cristallo, S.; Busso, M. Deep Mixing in Evolved Stars. I. The Effect of Reaction Rate Revisions from C to A. Astrophys. J. 2011, 729, 3. [Google Scholar] [CrossRef]
- Spyrou, K.; Chronidou, C.; Harissopulos, S.; Kossionides, S.; Paradellis, T.; Rolfs, C.; Schulte, W.H.; Borucki, L. The title of the cited article. Eur. Phys. J. A 2000, 7, 79–85. [Google Scholar] [CrossRef]
- Breuer, G. Messung und Analyse von Winkelverteilung und Wirkungsquerschnitt der Reaktion 19F( p,α0)16O im Energiebereich 0.4 bis 0.72 MeV. Z. Phys. 1959, 154, 339–351. [Google Scholar] [CrossRef]
- Lombardo, I.; Dell’Aquila, D.; Di Leva, A.; Indelicato, I.; La Cognata, M.; La Commara, M.; Ordine, A.; Rigato, V.; Romoli, M.; Rosato, E.; et al. Toward a reassessment of the 19F( p,α0)16O reaction rate at astrophysical temperatures. Phys. Lett. B 2015, 748, 178–182. [Google Scholar] [CrossRef]
- La Cognata, M.; Mukhamedzhanov, A.M.; Spitaleri, C.; Indelicato, I.; Aliotta, M.; Burjan, V.; Cherubini, S.; Coc, A.; Gulino, M.; Hons, Z.; et al. The Fluorine Destruction in Stars: First Experimental Study of the 19F( p,α0)16O Reaction at Astrophysical Energies. Astrophys. J. Lett. 2011, 739, L54. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Su, J.; He, J.J.; Wiescher, M.; deBoer, R.J.; Kahl, D.; Chen, Y.J.; Li, X.Y.; Wang, J.G.; Zhang, L.; et al. Direct Measurement of the Astrophysical 19F(p,αγ)16O Reaction in the Deepest Operational Underground Laboratory. Phys. Rev. Lett. 2021, 127, 152702. [Google Scholar] [CrossRef] [PubMed]
- Pizzone, R.G.; Spitaleri, C.; Lamia, L.; Bertulani, C.A.; Mukhamedzhanov, A.M.; Blokhintsev, L.; Burjan, V.; Cherubini, S.; Hons, Z.; Kiss, G.G.; et al. Trojan horse particle invariance studied with the 6Li(d,α)4He and 7Li(p,α)4He reactions. Phys. Rev. C 2011, 83, 045801. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Spitaleri, C.; Bertulani, C.A.; Mukhamedzhanov, A.M.; Blokhintsev, L.; La Cognata, M.; Lamia, L.; Rinollo, A.; Spartá, R.; Tumino, A. Updated evidence of the Trojan horse particle invariance for the 2H(d,p)3H reaction. Phys. Rev. C 2013, 87, 025805. [Google Scholar] [CrossRef]
- La Cognata, M.; Palmerini, S.; Spitaleri, C.; Indelicato, I.; Mukhamedzhanov, A.M.; Lombardo, I.; Trippella, O. Updated THM Astrophysical Factor of the 19F( p,α)16O Reaction and Influence of New Direct Data at Astrophysical Energies. Astroph. J. 2015, 805, 128. [Google Scholar] [CrossRef]
- Indelicato, I.; La Cognata, M.; Spitaleri, C.; Burjan, V.; Cherubini, S.; Gulino, M.; Hayakawa, S.; Hons, Z.; Kroha, V.; Lamia, L.; et al. New Improved Indirect Measurement of the 19F(p, α)16O 19F( p,α)16O Reaction at Energies of Astrophysical Relevance. Astroph. J. 2017, 845, 19. [Google Scholar] [CrossRef]
- Lombardo, I.; Dell’Aquila, D.; Campajola, L.; Rosato, E.; Spadaccini, G.; Vigilante, M. Analysis of the 19F( p,α0)16O reaction at low energies and the spectroscopy of 20Ne. J. Phys. G Nucl. Partic. 2013, 40, 125102. [Google Scholar] [CrossRef]
- Palmerini, S.; D’Agata, G.; La Cognata, M.; Indelicato, I.; Pizzone, R.G.; Trippella, O.; Vescovi, D. 19F(p, α)16O and 19F(α,p)22Ne Reaction Rate Measured via THM and Fluorine Nucleosynthesis in AGB stars. J. Phys. Conf. Ser. 2019, 1308, 012016. [Google Scholar] [CrossRef]
- Cristallo, S.; Di Leva, A.; Imbriani, G.; Piersanti, L.; Abia, C.; Gialanella, L.; Straniero, O. Effects of nuclear cross sections on 19F nucleosynthesis at low metallicities. Astron. Astrophys. 2014, 570, 46. [Google Scholar] [CrossRef][Green Version]
- Ugalde, C.; Azuma, R.E.; Couture, A.; Görres, J.; Lee, H.Y.; Stech, E.; Strandberg, E.; Tan, W.; Wiescher, M. Thermonuclear rate for the19F(α,p)22Ne reaction at stellar temperatures. Phys. Rev. C. 2008, 77, 035801. [Google Scholar] [CrossRef]
- Pizzone, R.G.; D’Agata, G.; La Cognata, M.; Indelicato, I.; Spitaleri, C.; Blagus, S.; Cherubini, S.; Figuera, P.; Grassi, L.; Guardo, G.L.; et al. First Measurement of the 19F(α, p)22Ne Reaction at Energies of Astrophysical Relevance. Astrophys. J. 2017, 836, 57. [Google Scholar] [CrossRef]
- D’Agata, G.; Pizzone, R.G.; La Cognata, M.; Indelicato, I.; Spitaleri, C.; Palmerini, S.; Trippella, O.; Vescovi, D.; Blagus, S.; Cherubini, S.; et al. The 19F(α,p)22Ne Reaction at Energies of Astrophysical Relevance by Means of the Trojan Horse Method and Its Implications in AGB Stars. Astrophys. J. 2018, 860, 61. [Google Scholar] [CrossRef]
- Trippella, O.; Busso, M.; Maiorca, E.; Käppler, F.; Palmerini, S. s-processing in AGB Stars revisited. I. Does the main component constrain the neutron source in the 13C pocket? Astrophys. J. 2014, 787, 41. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Origin of Anomalous Abundances of the Elements in Giant Stars. Astron. J. 1955, 121, 144. [Google Scholar] [CrossRef]
- Cameron, A.G.W. New Neutron Sources of Possible Astrophysical Importance. Astron. J. 1960, 65, 485. [Google Scholar] [CrossRef]
- Clayton, D.D.; Fowler, W.A.; Hull, T.E.; Zimmerman, B.A. Neutron capture chains in heavy element synthesis. Ann. Phys. 1961, 12, 331. [Google Scholar] [CrossRef]
- Faestermann, T.; Mohr, P.; Hertenberger, R.; Wirth, H.-F. Broad levels in 17O and their relevance for the astrophysical s-process. Phys. Rev. C 2015, 92, 052802(R). [Google Scholar] [CrossRef]
- La Cognata, M.; Spitaleri, C.; Trippella, O.; Kiss, G.G.; Rogachev, G.V.; Mukhamedzhanov, A.M.; Avila, M.; Guardo, G.L.; Koshchiy, E.; Kuchera, A.; et al. Measurement of the -3 keV resonance in the reaction 13C(α,n)16O of importance in the s-process. Phys. Rev. Lett. 2012, 109, 23. [Google Scholar] [CrossRef]
- La Cognata, M.; Spitaleri, C.; Trippella, O.; Kiss, G.G.; Rogachev, G.V.; Mukhamedzhanov, A.M.; Avila, M.; Guardo, G.L.; Koshchiy, E.; Kuchera, A.; et al. On the measurement of the 13C(α, n)16O S-Factor at negative energies and its influence on the s-process. Astrophys. J. 2013, 777, 143. [Google Scholar] [CrossRef][Green Version]
- Trippella, O.; La Cognata, M. Concurrent Application of ANC and THM to assess the 13C(α, n)16O Absolute Cross Section at Astrophysical Energies and Possible Consequences for Neutron Production in Low-mass AGB Stars. Astrophys. J. 2017, 837, 41. [Google Scholar] [CrossRef]
- Davids, C.N. A study of (α,n) reactions on 9Be and 13C at low energies. Nucl. Phys. A 1968, 110, 3. [Google Scholar] [CrossRef]
- Bair, J.K.; Haas, F.X. Total Neutron Yield from the Reactions 13C(α,n)16O and 17,18O(α,n)20,21Ne. Phys. Rev. C 1973, 7, 1356. [Google Scholar] [CrossRef]
- Kellogg, S.; Vogelaar, R.; Kavanagh, R.W. 13C(α,n) and 14C(p,n): Astrophysical Neutron Sources and Sinks. BAPS 1989, 34, 1192. [Google Scholar]
- Drotleff, H.W.; Denker, A.; Knee, H.; Soine, M.; Wolf, G.; Hammer, J.W.; Greife, U.; Rolfs, C.; Trautvetter, H.P. Reaction Rates of the s-Process Neutron Sources 22Ne(α, n)25Mg and 13C(α, n)16O. Astrophys. J. 1993, 414, 735. [Google Scholar] [CrossRef]
- Harissopulos, S.; Becker, H.W.; Hammer, J.W.; Lagoyannis, A.; Rolfs, C.; Strieder, F. Cross section of the 13C(α,n)16O reaction: A background for the measurement of geo-neutrinos. Phys. Rev. C 2005, 72, 062801(R). [Google Scholar] [CrossRef]
- Heil, M.; Detwiler, R.; Azuma, R.E.; Couture, A.; Daly, J.; Görres, J.; Käppeler, F.; Reifarth, R.; Tischhauser, P.; Ugalde, C.; et al. The 13C(α,n) reaction and its role as a neutron source for the s process. Phys. Rev. C 2008, 78, 025803. [Google Scholar] [CrossRef]
- Ciani, G.F.; Csedreki, L.; Rapagnani, D.; Aliotta, M.; Balibrea-Correa, J.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; et al. Direct Measurement of the 13C(α,n)16O Cross Section into the s-Process Gamow Peak. Phys. Rev. Lett. 2021, 127, 152701. [Google Scholar] [CrossRef]
- Käppeler, F.; Gallino, R.; Bisterzo, S.; Wako, A. The s-process: Nuclear physics, stellar models, and observations. Rev. Mod. Phys. 2011, 83, 157. [Google Scholar] [CrossRef]
- Mohr, P.; Heinz, C.; Pignatari, M.; Dillmann, I.; Mengoni, A.; Käppeler, F. Re-evaluation of the 16O(n, γ)17O Cross Section at Astrophysical Energies and Its Role as a Neutron Poison in the s-process. Astrophys. J. 2016, 827, 29. [Google Scholar] [CrossRef]
- Pignatari, M.; Gallino, R.; Heil, M.; Wiescher, M.; Käppeler, F.; Herwig, F.; Bisterzo, S. The weak s-process in massive stars and its dependence on the neutron capture cross sections. Astrophys. J. 2010, 710, 1557. [Google Scholar] [CrossRef]
- Sanders, M.R. Study of the 14C(p,n)14N and 14C(α,n)17O Reactions. Phys. Rev. 1956, 104, 1434. [Google Scholar] [CrossRef]
- Koehler, P.E.; Graff, S.M. 17O(n,α)14C cross section from 25 meV to approximately 1 MeV. Phys. Rev. C 1991, 44, 2788. [Google Scholar] [CrossRef] [PubMed]
- Schatz, H.; Kaeppeler, F.; Koehler, P.E.; Wiescher, M.; Trautvetter, H.P. 17O(n,α)14C: Closure of a Primordial CNO Bi-Cycle? Astrophys. J. 1993, 413, 750. [Google Scholar] [CrossRef]
- Wagemans, J.; Wagemans, C.; Goeminne, G.; Serot, O.; Loiselet, M.; Gaelens, M. The 17O(n,α)14C reaction from subthermal up to approximately 350 keV neutron energy. Phys. Rev. C 2002, 65, 034614. [Google Scholar] [CrossRef]
- Avila, M.L.; Rogachev, G.V.; Goldberg, V.Z.; Johnson, E.D.; Kemper, K.W.; Tchuvil’sky, Y.M.; Volya, A.S. α-cluster structure of 18O. Phys. Rev. C 2014, 90, 024327. [Google Scholar] [CrossRef]
- Ajzenberg-Selove, F. Energy levels of light nuclei A = 18–20. Nuc. Phys. A 1987, 475, 1–198. [Google Scholar] [CrossRef]
- Gulino, M.; Spitaleri, C.; Tang, X.D.; Guardo, G.L.; Lamia, L.; Cherubini, S.; Bucher, B.; Burjan, V.; Couder, M.; Davies, P.; et al. Suppression of the centrifugal barrier effects in the off-energy-shell neutron+17O interaction. Phys. Rev. C 2013, 87, 012801(R). [Google Scholar] [CrossRef]
- Oliva, A.A.; Guardo, G.L.; Lamia, L.; Cherubini, S.; Cvetinovic, A.; D’Agata, G.; de Sereville, N.; Di Pietro, A.; Figuera, P.; Gulino, M.; et al. Study of the neutron-induced reaction 17O(n,α)14C at astrophysical energies via the Trojan Horse Method. Il Nuovo Cimento C 2020, 111, 1–9. [Google Scholar] [CrossRef][Green Version]
- Brehm, K.; Becker, H.W.; Rolfs, C.; Trautvetter, H.P.; Kappeler, F.; Ratynski, W. The cross section of 14N(n,p)14C at stellar energies and its role as a neutron poison for S-process nucleosynthesis. Z. Phys. A 1988, 330, 167. [Google Scholar]
- Koehler, P.E.; O’Brien, H.A. 14N(n,p)14C cross section from 61 meV to 34.6 keV and its astrophysical implications. Phys. Rev. C 1989, 39, 1655. [Google Scholar] [CrossRef] [PubMed]
- Koehler, P.E. 14N(n,p)14C cross section near thermal energy. Phys. Rev. C 1993, 48, 439. [Google Scholar] [CrossRef] [PubMed]
- Gledenov, Y.M.; Salatski, V.I.; Sedyshev, P.V.; Sedysheva, M.V.; Pshenichnyj, V.A.; Andrzejewski, J. Cross sections of the 14N(n,p)14C reaction at 24.5, 53.5 and 144 keV. Z. Phys. A 1994, 348, 199. [Google Scholar] [CrossRef]
- Sanami, T.; Baba, M.; Matsuyama, I.; Matsuyama, S.; Kiyosumi, T.; Nauchi, Y.; Hirakawa, N. Measurement of 14N(n,p)14C cross section for kT = 25.3 keV Maxwellian neutrons using gridded ionization chamber. Nuclear Instrum. Methods Phys. Res. A 1997, 394, 368. [Google Scholar] [CrossRef]
- Kii, T.; Shima, T.; Sato, H.; Baba, T.; Nagai, Y. Cross section of the 14N(n,p)14C reaction from 10 to 100 keV measured by a gas scintillation drift chamber. Phys. Rev. C 1999, 59, 3397. [Google Scholar]
- Wagemans, J.; Wagemans, C.; Goeminne, G.; Geltenbort, P. Experimental determination of the 14N(n,p)14C reaction cross section for thermal neutrons. Phys. Rev. C 2000, 61, 064601. [Google Scholar] [CrossRef]
- D’Agata, G.; Pizzone, R.G.; La Cognata, M.; Indelicato, I.; Spitaleri, C.; Burjan, V.; Cherubini, C.; Di Pietro, A.; Guardo, G.L.; Gulino, M.; et al. The 19F(α,p)22Ne and 23Na(p,α)20Ne reaction in AGB nucleosynthesis via THM. EPJ Web Conf. 2018, 184, 02003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergi, M.L.; D’Agata, G.; Guardo, G.L.; Rapisarda, G.G.; Burjan, V.; Cherubini, S.; Gulino, M.; Indelicato, I.; La Cognata, M.; Lamia, L.; et al. Trojan Horse Investigation for AGB Stellar Nucleosynthesis. Universe 2022, 8, 128. https://doi.org/10.3390/universe8020128
Sergi ML, D’Agata G, Guardo GL, Rapisarda GG, Burjan V, Cherubini S, Gulino M, Indelicato I, La Cognata M, Lamia L, et al. Trojan Horse Investigation for AGB Stellar Nucleosynthesis. Universe. 2022; 8(2):128. https://doi.org/10.3390/universe8020128
Chicago/Turabian StyleSergi, Maria Letizia, Giuseppe D’Agata, Giovanni Luca Guardo, Giuseppe Gabriele Rapisarda, Vaclav Burjan, Silvio Cherubini, Marisa Gulino, Iolanda Indelicato, Marco La Cognata, Livio Lamia, and et al. 2022. "Trojan Horse Investigation for AGB Stellar Nucleosynthesis" Universe 8, no. 2: 128. https://doi.org/10.3390/universe8020128
APA StyleSergi, M. L., D’Agata, G., Guardo, G. L., Rapisarda, G. G., Burjan, V., Cherubini, S., Gulino, M., Indelicato, I., La Cognata, M., Lamia, L., Lattuada, D., Mrázek, J., Oliva, A. A., Pizzone, R. G., Romano, S., Spartá, R., Trippella, O., & Tumino, A. (2022). Trojan Horse Investigation for AGB Stellar Nucleosynthesis. Universe, 8(2), 128. https://doi.org/10.3390/universe8020128








