Diffeomorphisms in Momentum Space: Physical Implications of Different Choices of Momentum Coordinates in the Galilean Snyder Model

Abstract

It has been pointed out that different choices of momenta can be associated to the same noncommutative spacetime model. The question of whether these momentum spaces, related by diffeomorphisms, produce the same physical predictions is still debated. In this work, we focus our attention on a few different momentum spaces that can be associated to the Galilean Snyder noncommutative spacetime model and show that they produce different predictions for the energy spectrum of the harmonic oscillator.

1. Introduction

The Snyder noncommutative spacetime model was proposed in Ref. [1] with the aim of removing the divergencies emerging in the quantum field theory. The main idea was that spacetime coordinates could acquire a discrete spectrum characterized by a fundamental length scale without breaking Lorentz invariance. This was the first time noncommuting coordinates were considered in the literature, and this paper anticipated the development of noncommutative geometry by several decades 1. While this is well-known, it was recently made explicit [3,4,5,6] that this model was also the first instance were spacetime noncommutativity is linked to momentum space curvature.

In fact, in Snyder’s construction, the momentum manifold has a de Sitter geometry, and spacetime coordinates are identified with the translation generators over such a manifold. Then, spacetime noncommutativity can simply be understood as a consequence of the curvature of the momentum manifold.

Such a feature has recently emerged as a general implication of noncommutative spacetime models [7,8], including those where relativistic symmetries are described by a (Planck-scale) deformation of the standard Lorentz transformations [9,10,11,12,13]. These developments converged in the relative locality proposal [14,15], which pointed out that locality of interactions becomes an observer-dependent statement in these models, thus motivating a shift of focus from spacetime to momentum space, at least for what concerns phenomenological applications [16,17,18,19].

Because of the prominent role played by momentum space geometry in uncovering the phenomenology of noncommutative spacetime models and of quantum gravity in general, it is important to understand whether diffeomorphisms on momentum space, which induce a change of coordinates on the manifold, have physically relevant implications. When importing the intuition from general relativity, where spacetime diffeomorphisms do not modify the physics, one is led to think that this should also be the case for momentum space [20,21,22]. However, while one can indeed identify a duality between features of models with curved momentum space and models with curved spacetime [23], the two constructions have fundamental differences, due to the different role played in physics by spacetime and momentum space. For instance, while we know that the evolution of spacetime geometry is governed by Einstein’s equations, at the moment we have no strong motivation to introduce dynamics on momentum space. Additionally, it seems difficult to link momentum diffeomorphisms to a change of observer, which is contrary to the interpretation of coordinate invariance in general relativity.

In this paper, we aim to contribute to the understanding of this issue by focussing on the phenomenological consequences of different choices of momentum coordinates for the Snyder model. While the canonical momenta in the Snyder model are given by the Beltrami projective coordinates on the de Sitter manifold, in recent work [5,6] it was noted that, in fact, any choice of projective coordinates on the manifold provides viable momentum coordinates, which are commutative and behave classically under the Lorentz transformations. Because the phase space algebra associated to any such set of coordinates is different, in Refs. [5,6] it was suggested that indeed, the physical predictions of the Snyder model would depend on this choice, but no explicit example was provided. The possibility of generalizing a Snyder model was already noticed in Refs. [24,25] from an algebraic point of view, but its phenomenology was not investigated, except in the context of the field theory.

Here, we fill this gap by focussing on what could be considered the simplest nontrivial example, namely that of a one-dimensional harmonic oscillator. Because this is a quantum-mechanical setting, we will work in the nonrelativistic limit of the Snyder model 2. Until recently, this limit was usually taken by simply considering the three-dimensional Euclidean version of the model, thus neglecting the role of the time coordinate [27,28,29,30,31,32]. However, in the Ref. [5] it was shown that explicitly taking the limit for $c\to \infty$ gives rise to more complicated relations, where a mix between time and space variables is still present. The resulting model has been called a Galilean Snyder model, to emphasize that it is invariant under Galilean transformations. This is reviewed in Section 2, where we also discuss the different sets of momentum space coordinates that will be used in our analysis. These are the Beltrami projective coordinates, which we mentioned earlier, the Poincaré projective coordinates, and the embedding coordinates of the de Sitter manifold. In Section 3 and Section 4, we derive, for each of these three sets of coordinates, the deformed Schrödinger equation for the harmonic oscillator and its eigenvalues. We find that indeed, the energy levels differ in the various cases. We comment on our results in the concluding Section 6.

In this work, we shall limit our investigation to the Snyder model, with a positive coupling constant, but similar calculations can be performed for the anti-Snyder model [27], taking into account its different properties. We work with a mostly plus metric, Latin uppercase indices run from 0 to 4, Greek lowercase indices run from 0 to 3, and Latin lowercase indices run from 1 to 3.

2. The Snyder Model and Its Galilean Limit

As we mentioned, Lorentz invariance of the Snyder model is guaranteed by the fact that spacetime coordinates are identified with the translation generators over a curved manifold with de Sitter geometry. In $3+1$ dimensions, the full algebra of symmetries over such manifold is given in terms of boosts $K_i$, rotations $J_i$, and translations $P_{\alpha }$ as follows:

$$\begin{array}{ccc}[J_i,J_j]={ϵ}_{ijk}{J}_k,\hfill & [J_i,P_j]={ϵ}_{ijk}{P}_k,\hfill & [J_i,K_j]={ϵ}_{ijk}{K}_k,\hfill \\ {\displaystyle [K_i,P_0]=P_i,}\hfill & [K_i,P_j]=\frac{1}{c^2}{\delta }_{ij}{P}_0,\hfill & [K_i,K_j]=-\frac{1}{c^2}{ϵ}_{ijk}{J}_k,\hfill \\ [P_0,P_i]=-{\beta }^2{K}_i,\hfill & [P_i,P_j]={\beta }^2\frac{1}{c^2}{ϵ}_{ijk}{J}_k,\hfill & [P_0,J_i]=0.\hfill \end{array}$$

(1)

Following Ref. [5], we write the speed of light c explicitly in order to be able to easily perform the Galilean limit. Here, ${\beta }^2$ plays the role of curvature of the de Sitter manifold.

The Snyder noncommutative spacetime parametrized by the coordinates $x_{\mu }$ is then obtained upon the identification

$$x_0:=-\frac{1}{c}{P}_0,x_i:=-c{P}_i,$$

(2)

so that spacetime coordinates satisfy the following commutation relations induced by the curvature of the de Sitter manifold:

$$\left[x_0,x_i\right]=-{\beta }^2{K}_i,\left[x_i,x_j\right]={\beta }^2{ϵ}_{ijk}{J}_k.$$

(3)

In the Snyder model, momenta live on the de Sitter manifold. However, the specific choice of coordinates on this manifold to be identified with the physical momenta is not univocal. Indeed, several options, described in detail in Ref. [6], satisfy the basic properties of being commutative and transforming classically under Lorentz transformations. The starting point is given by the ambient coordinates on the de Sitter manifold, ${\eta }_A$, that satisfy the constraint

$${\eta }_4^2-{\beta }^2{\eta }_0^2+\frac{{\beta }^2}{c^2}\left({\eta }_1^2+{\eta }_2^2+{\eta }_3^2\right)=1.$$

(4)

The canonical choice for physical momenta, also used in the original paper by Snyder [1], is given by the (appropriately rescaled) Beltrami projective coordinates, related to the ambient coordinates as follows:

$$p_0:=c\frac{{\eta }_0}{{\eta }_4},p_i:=\frac{1}{c}\frac{{\eta }_i}{{\eta }_4}.$$

(5)

With this choice of physical momenta, and turning coordinates and momenta into Hermitian operators, ${\widehat{x}}_{\mu }\equiv i\hslash x_{\mu }$, ${\widehat{p}}_{\nu }\equiv p_{\nu }$, that act on the space of functions of momenta $\psi \left(p\right)$, the Snyder phase space commutation relations read:

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ {\displaystyle \left[{\widehat{x}}_0,{\widehat{p}}_{\alpha }\right]=i\hslash (-{\delta }_{0\alpha }+\frac{{\beta }^2}{c^2}{\widehat{p}}_0{\widehat{p}}_{\alpha }),}\hfill & \left[{\widehat{x}}_i,{\widehat{p}}_0\right]=i\hslash {\beta }^2{\widehat{p}}_0{\widehat{p}}_i,\hfill \\ \left[{\widehat{x}}_i,{\widehat{p}}_j\right]=i\hslash ({\delta }_{ij}+{\beta }^2{\widehat{p}}_i{\widehat{p}}_j),\hfill & \left[{\widehat{p}}_{\alpha },{\widehat{p}}_{\beta }\right]=0,\hfill \end{array}$$

(6)

with boost and rotation generators given by

$${\widehat{K}}_i=-{\widehat{x}}_0{\widehat{p}}_i+\frac{1}{c^2}{\widehat{x}}_i{\widehat{p}}_0,{\widehat{J}}_i={ϵ}_{ijk}{\widehat{x}}_j{\widehat{p}}_k.$$

(7)

It is easy to check that these phase space commutators are invariant under Lorentz transformations and that both spacetime coordinates and momenta transform classically under Lorentz symmetries.

In Ref. [6], different choices for the physical momenta were analyzed. In particular, it was noted that any set of projective coordinates for the de Sitter manifold would have the required properties and so be a viable option, all choices being related by a momentum space diffeomorphism. For example, one could define momenta via the Poincaré projective coordinates:

$${\tilde{p}}_0:=c\frac{2{\eta }_0}{1+{\eta }_4},{\tilde{p}}_i:=\frac{1}{c}\frac{2{\eta }_i}{1+{\eta }_4}.$$

(8)

These momenta are related to the Beltrami momenta via the following diffeomorphism:

$${\tilde{p}}_{\alpha }=\frac{2p_{\alpha }}{1+\sqrt{1-\frac{{\beta }^2}{c^2}{p}_0^2+{\beta }^2(p_1^2+p_2^2+p_3^2)}},p_{\alpha }=\frac{{\tilde{p}}_{\alpha }}{1+\frac{{\beta }^2}{4c^2}{\tilde{p}}_0^2-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)}.$$

(9)

Using as physical momenta the ones related to the Poincaré coordinates, the resulting Snyder phase space is

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ {\displaystyle \left[{\widehat{x}}_0,{\tilde{p}}_{\alpha }\right]=i\hslash \left(-{\delta }_{0\alpha }\left(1+\frac{{\beta }^2}{4c^2}{\tilde{p}}_0^2-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)\right)-\frac{{\beta }^2}{2c^2}{\tilde{p}}_0{\tilde{p}}_{\alpha }\right),}\hfill & \left[{\widehat{x}}_i,{\tilde{p}}_0\right]=i\hslash \frac{{\beta }^2}{2}{\tilde{p}}_0{\tilde{p}}_i,\hfill \\ {\displaystyle \left[{\widehat{x}}_i,{\tilde{p}}_j\right]=i\hslash \left({\delta }_{ij}\left(1+\frac{{\beta }^2}{4c^2}{\tilde{p}}_0^2-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)\right)+\frac{{\beta }^2}{2}{\tilde{p}}_i{\tilde{p}}_j\right),}\hfill & \left[{\tilde{p}}_{\alpha },{\tilde{p}}_{\beta }\right]=0,\hfill \end{array}$$

(10)

where we omitted the hat on the ${\tilde{p}}_{\alpha }$ operators in order to simplify the notation. The Lorentz boosts and rotations now take the form

$${\widehat{K}}_i=\frac{-{\widehat{x}}_0{\tilde{p}}_i+\frac{1}{c^2}{\widehat{x}}_i{\tilde{p}}_0}{1+\frac{{\beta }^2}{4c^2}{\tilde{p}}_0^2-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)},{\widehat{J}}_i=\frac{{ϵ}_{ijk}{\widehat{x}}_j{\tilde{p}}_k}{1+\frac{{\beta }^2}{4c^2}{\tilde{p}}_0^2-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)}.$$

(11)

Finally, one can obtain a quasi-canonical structure for the Snyder phase space by adopting physical momenta that are more directly related to the de Sitter ambient coordinates:

$${\pi }_0:=c{\eta }_0,{\pi }_i:=\frac{1}{c}{\eta }_i.$$

(12)

In this case, the Snyder phase space algebra reads:

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ \left[{\widehat{x}}_{\alpha },{\widehat{\pi }}_{\beta }\right]=i\hslash {\eta }_{\alpha \beta }\sqrt{1+\frac{{\beta }^2}{c^2}{\widehat{\pi }}_0^2-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)},\hfill & \left[{\widehat{\pi }}_{\alpha },{\widehat{\pi }}_{\beta }\right]=0,\hfill \end{array}$$

(13)

and the Lorentz generators are given by

$${\widehat{K}}_i=\frac{-{\widehat{x}}_0{\widehat{\pi }}_i+\frac{1}{c^2}{\widehat{x}}_i{\widehat{\pi }}_0}{\sqrt{1+\frac{{\beta }^2}{c^2}{\widehat{\pi }}_0^2-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)}},{\widehat{J}}_i=\frac{{ϵ}_{ijk}{\widehat{x}}_j{\widehat{\pi }}_k}{\sqrt{1+\frac{{\beta }^2}{c^2}{\widehat{\pi }}_0^2-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)}}.$$

(14)

Having kept track of the factors of c throughout our brief summary, it is easy to work out the Galilean limit $c\to \infty$ of the Snyder model in either set of momentum coordinates. Using the Beltrami momenta, the Galilean limit gives the following phase space relations:

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ {\displaystyle \left[{\widehat{x}}_0,{\widehat{p}}_{\alpha }\right]=-i\hslash {\delta }_{0\alpha },}\hfill & \left[{\widehat{x}}_i,{\widehat{p}}_0\right]=i\hslash {\beta }^2{\widehat{p}}_0{\widehat{p}}_i,\hfill \\ \left[{\widehat{x}}_i,{\widehat{p}}_j\right]=i\hslash ({\delta }_{ij}+{\beta }^2{\widehat{p}}_i{\widehat{p}}_j),\hfill & \left[{\widehat{p}}_{\alpha },{\widehat{p}}_{\beta }\right]=0,\hfill \end{array}$$

(15)

where now the boost generator is the Galilean one:

$${\widehat{K}}_i=-{\widehat{x}}_0{\widehat{p}}_i.$$

(16)

Using the momenta given by the Poincaré projective coordinates, the phase space algebra in the Galilean limit reads:

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ {\displaystyle \left[{\widehat{x}}_0,{\tilde{p}}_{\alpha }\right]=-i\hslash {\delta }_{0\alpha }\left[1-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)\right],}\hfill & \left[{\widehat{x}}_i,{\tilde{p}}_0\right]=i\hslash \frac{{\beta }^2}{2}{\tilde{p}}_0{\tilde{p}}_i,\hfill \\ {\displaystyle \left[{\widehat{x}}_i,{\tilde{p}}_j\right]=i\hslash \left[{\delta }_{ij}\left(1-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)\right)+\frac{{\beta }^2}{2}{\tilde{p}}_i{\tilde{p}}_j\right],}\hfill & \left[{\tilde{p}}_{\alpha },{\tilde{p}}_{\beta }\right]=0,\hfill \end{array}$$

(17)

with Galilean boost and rotation generators:

$${\widehat{K}}_i=\frac{-{\widehat{x}}_0{\tilde{p}}_i}{1-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)},{\widehat{J}}_i=\frac{{ϵ}_{ijk}{\widehat{x}}_j{\tilde{p}}_k}{1-\frac{{\beta }^2}{4}({\tilde{p}}_1^2+{\tilde{p}}_2^2+{\tilde{p}}_3^2)}.$$

(18)

Finally, using the momenta given by ambient coordinates, the Galilean phase space reads:

$$\begin{array}{cc}\left[{\widehat{x}}_0,{\widehat{x}}_i\right]=-i\hslash {\beta }^2{\widehat{K}}_i,\hfill & \left[{\widehat{x}}_i,{\widehat{x}}_j\right]=i\hslash {\beta }^2{ϵ}_{ijk}{\widehat{J}}_k,\hfill \\ \left[{\widehat{x}}_{\alpha },{\widehat{\pi }}_{\beta }\right]=i\hslash {\eta }_{\alpha \beta }\sqrt{1-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)},\hfill & \left[{\widehat{\pi }}_{\alpha },{\widehat{\pi }}_{\beta }\right]=0,\hfill \end{array}$$

(19)

with Galilean boost and rotation generators

$${\widehat{K}}_i=\frac{-{\widehat{x}}_0{\widehat{\pi }}_i}{\sqrt{1-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)}},{\widehat{J}}_i=\frac{{ϵ}_{ijk}{\widehat{x}}_j{\widehat{\pi }}_k}{\sqrt{1-{\beta }^2({\widehat{\pi }}_1^2+{\widehat{\pi }}_2^2+{\widehat{\pi }}_3^2)}}.$$

(20)

As was already emphasized in Ref. [5], the Galilean limit does not remove the mixing between space and time components of the phase space, as is instead the case in standard mechanics. In the following sections we shall study the spectrum of the harmonic oscillator in this limit and compare it with the case of classical quantum mechanics and the Euclidean Snyder model.

3. The Snyder–Galilei Harmonic Oscillator in Embedding Coordinates

We can now embark into the investigation of the one-dimensional quantum harmonic oscillator in the framework of the Galilean Snyder model, starting from the simplest case which is given by the embedding coordinates. First of all, we observe that the phase space coordinates ${\widehat{x}}_{\mu }$ and ${\widehat{\pi }}_{\mu }$ can be realized in terms of canonical coordinates ${\overline{x}}_{\mu }$ and ${\overline{p}}_{\mu }$ such that 3

$$\left[{\overline{x}}_{\mu },{\overline{x}}_{\nu }\right]=0,\left[{\overline{x}}_{\mu },{\overline{p}}_{\nu }\right]=i\hslash {\eta }_{\mu \nu }\left[{\overline{p}}_{\mu },{\overline{p}}_{\nu }\right]=0,$$

(21)

the realization being given by:

$${\widehat{x}}_{\mu }=\sqrt{1-{\beta }^2{\overline{p}}_k^2}{\overline{x}}_{\mu },{\widehat{\pi }}_{\mu }={\overline{p}}_{\mu }.$$

(22)

Starting from this realization, we can easily define a momentum representation for the phase space operators, setting ${\overline{p}}_1\to p$, ${\overline{x}}_1\to i\hslash \frac{\partial }{\partial p}$, ${\overline{p}}_0\to E$, ${\overline{x}}_0\to -i\hslash \frac{\partial }{\partial E}$, so that

$$\begin{array}{ccc}& & {\widehat{\pi }}_1=p,{\widehat{x}}_1=i\hslash \sqrt{1-{\beta }^2{p}^2}\frac{\partial }{\partial p},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & {\widehat{\pi }}_0=E,{\widehat{x}}_0=-i\hslash \sqrt{1-{\beta }^2{p}^2}\frac{\partial }{\partial E},\hfill \end{array}$$

(24)

and the relevant Hilbert space is a (1+1)-dimensional space given by square integrable functions $\psi (p,E)$ of p and E.

We assume that the Hamiltonian for the harmonic oscillator takes the standard form in terms of the Snyder spacetime coordinates and physical momenta:

$$H=\frac{{\widehat{\pi }}_1^2}{2m}+\frac{m{\omega }^2}{2}{\widehat{x}}_1^2.$$

(25)

In the representation (23) and (24) the associated Schrödinger equation reduces to

$$E\psi =\frac{1}{2m}\left[-{\hslash }^2{m}^2{\omega }^2\left((1-{\beta }^2{p}^2)\frac{{\partial }^2}{\partial p^2}-{\beta }^{2}p\frac{\partial }{\partial p}\right)+p^2\right]\psi .$$

(26)

The energy coordinate E completely decouples from the equation, so one can set $\psi =\psi \left(p\right)$, with Hilbert space measure

$$d\mathsf{\Omega }=\frac{dp}{\sqrt{1-{\beta }^2{p}^2}},$$

(27)

so that the space coordinate operator ${\widehat{x}}_1$ in (23) is Hermitian.

The Schrödinger equation can be solved exactly in terms of Mathieu functions. In fact, after defining a new variable $z={\beta }^{-1}arcsin\beta p$, which induces a trivial measure in the Hilbert space, $d\mathsf{\Omega }=dz$, the Schrödinger equation reads:

$$\frac{d^2\psi }{d{z}^2}-\frac{1}{{\alpha }^2}\left(\frac{{sin}^2\beta z}{{\beta }^2}-2mE\right)\psi =0,\mathrm{with}\alpha =\hslash m\omega .$$

(28)

After another change of variables, defining $y=\beta z$, Equation (28) can be further simplified and written in the standard form of a Mathieu equation:

$$\frac{d^2\psi }{d{y}^2}+(a-2qcos2y)\psi =0,\mathrm{with}q=-\frac{1}{4{\alpha }^2{\beta }^4},a=\frac{-1+4{\beta }^{2}mE}{2{\alpha }^2{\beta }^4}.$$

(29)

The dimensionless variable q so defined is very large, and in this regime the eigenvalues of (29) can be obtained from Equation (20.2.30) of [33], giving

$$E_n=\hslash \omega \left[\left(n+\frac{1}{2}\right)-\frac{\alpha {\beta }^2}{4}\left(n^2+n+\frac{1}{2}\right)+o\left({\alpha }^2{\beta }^4\right)\right].$$

(30)

Alternatively, corrections to the standard energy spectrum for small $\beta$ can be found via a perturbative approach, writing

$$\frac{{sin}^2\beta z}{{\beta }^2}=z^2-\frac{{\beta }^2}{3}{z}^4+o\left({\beta }^4\right),$$

(31)

so that the Schrödinger Equation (28) simplifies to

$$\frac{d^2\psi }{d{z}^2}-\frac{1}{{\alpha }^2}\left(z^2-\frac{{\beta }^2}{3}{z}^4-2mE\right)\psi =0.$$

(32)

This is the equation of an anharmonic oscillator and can be treated using standard perturbation theory. The solutions of the unperturbed equation are

$${\psi }_n=\frac{1}{\sqrt{\sqrt{\pi \alpha }{2}^{n}n!}}{e}^{-z^2/2\alpha }{H}_n\left(\frac{z}{\sqrt{\alpha }}\right),E_n=\hslash \omega \left(n+\frac{1}{2}\right),$$

(33)

and the corrections to the spectrum to first order in ${\beta }^2$ are given by

$$\mathsf{\Delta }{E}_n=-\frac{\hslash \omega {\beta }^2}{3{\alpha }^2}({\psi }_n,z^4{\psi }_n)=-\frac{\hslash \omega \alpha {\beta }^2}{8}\left(n^2+n+\frac{1}{2}\right).$$

(34)

Hence the energy levels of the harmonic oscillator read:

$$E_n=\hslash \omega \left[\left(n+\frac{1}{2}\right)-\frac{\alpha {\beta }^2}{4}\left(n^2+n+\frac{1}{2}\right)+o\left({\alpha }^2{\beta }^4\right)\right],$$

(35)

and one recovers (30).

4. The Snyder–Galilei Harmonic Oscillator in Beltrami Coordinates

As we mentioned, we are interested in comparing the physical predictions of the Snyder model when different choices for the physical momenta are taken. To this aim, in this section we derive the energy spectrum of the harmonic oscillator using a different set of momentum space coordinates than the one of the previous section, namely those associated to the Beltrami projective coordinates, defined in Equation (5).

Following the same steps as in the previous section, we start by identifying a realization of the Galilean Snyder phase space (15) in terms of canonical coordinates (21):

$${\widehat{x}}_0={\overline{x}}_0,{\widehat{x}}_i={\overline{x}}_i+{\beta }^2{\overline{p}}_i{\overline{p}}_{\alpha }{\overline{x}}_{\alpha },{\widehat{p}}_{\mu }={\overline{p}}_{\mu }.$$

(36)

In 1 + 1 dimensions this reduces to

$${\widehat{x}}_0={\overline{x}}_0,{\widehat{x}}_1=(1+{\beta }^2{\overline{p}}_1^2){\overline{x}}_1-{\beta }^2{\overline{p}}_1{\overline{p}}_0{\overline{x}}_0,{\widehat{p}}_{\mu }={\overline{p}}_{\mu },$$

(37)

and allows us to find a representation on momentum space:

$${\widehat{p}}_1=p,{\widehat{x}}_1=i\hslash (1+{\beta }^2{p}^2)\frac{\partial }{\partial p}+i\hslash {\beta }^{2}pE\frac{\partial }{\partial E},$$

(38)

$${\widehat{p}}_0=E,{\widehat{x}}_0=-i\hslash \frac{\partial }{\partial E}.$$

(39)

The Hilbert space of these operators is that of square integrable functions $\psi (p,E)$ of p and E. With the choice (38) of operator ordering, the measure in this Hilbert space is 4

$$d\mathsf{\Omega }=\frac{dpdE}{{(1+{\beta }^2{p}^2)}^{3/2}}.$$

(40)

As before, we write the Hamiltonian for the harmonic oscillator in the standard form in terms of the Snyder spacetime coordinates and physical momenta, which are now the Beltrami momenta:

$$H=\frac{{\widehat{p}}_1^2}{2m}+\frac{m{\omega }^2}{2}{\widehat{x}}_1^2.$$

(41)

Using the representation (38) and (39), the Schrödinger equation can be written as

$$\left[E-\frac{p^2}{2m}\right]\psi =-\frac{{\alpha }^2}{2m}\left[{(1+{\beta }^2{p}^2)}^2\frac{{\partial }^2}{\partial p^2}+2{\beta }^2(1+{\beta }^2{p}^2)p\frac{\partial }{\partial p}\left(1+E\frac{\partial }{\partial E}\right)+\left(E^2\frac{{\partial }^2}{\partial E^2}+2E\frac{\partial }{\partial E}\right){\beta }^4{p}^2+{\beta }^{2}E\frac{\partial }{\partial E}\right]\psi ,$$

(42)

with $\alpha$ defined in (28). Because on the r.h.s. of this equation the terms that contain E are homogeneous, a possible ansatz for the eigenstate $\psi$ is

$$\psi (E,p)=E^{\mu }\varphi \left(p\right).$$

(43)

In this case, Equation (42) reduces to an ordinary Schrödinger equation for $\varphi \left(p\right)$:

$$\left[{(1+{\beta }^2{p}^2)}^2\frac{{\partial }^2}{\partial p^2}+2(1+\mu )(1+{\beta }^2{p}^2){\beta }^{2}p\frac{\partial }{\partial p}+\left(\frac{2Em}{{\alpha }^2{\beta }^2}+\mu \right){\beta }^2+\left({\mu }^2+\mu -\frac{1}{{\alpha }^2{\beta }^4}\right){\beta }^4{p}^2\right]\varphi =0.$$

(44)

An equation of this form has been solved in the Ref. [34] in the way we sketch in the following. Changing variables

$$z=\frac{p}{\sqrt{1+{\beta }^2{p}^2}},\mathrm{with}{}^{\prime }=\frac{d}{dz},$$

(45)

and defining

$$\varphi ={(1-{\beta }^2{z}^2)}^{\lambda /2}f\left(\beta z\right),$$

(46)

one obtains

$$(1-{\beta }^2{z}^2)f^{″}-(1-2\mu +2\lambda )\beta z{f}^{\prime }+\left(\mu -\lambda +\frac{2Em}{{\alpha }^2{\beta }^2}\right)f+\left({\mu }^2+\mu +{\lambda }^2-\lambda -2\lambda \mu -\frac{1}{{\alpha }^2{\beta }^4}\right)\frac{{\beta }^2{z}^2}{1-{\beta }^2{z}^2}f=0.$$

(47)

To have a normalizable solution the last term must vanish, fixing the value of $\lambda$ to

$$\lambda =\mu +\frac{1}{2}\left(1\pm \sqrt{1+\frac{4}{{\alpha }^2{\beta }^4}}\right).$$

(48)

Choosing the positive sign for the square root, Equation (47) reduces to a Gegenbauer equation with eigenvalues

$$E_n=\hslash \omega \left[\left(n+\frac{1}{2}\right)\left(\sqrt{1+\frac{{\alpha }^2{\beta }^4}{4}}+\frac{\alpha {\beta }^2}{2}\right)+\frac{n^2}{2}\alpha {\beta }^2\right],$$

(49)

and the solution $\psi$ of the Schrödinger Equation (42) is:

$$\psi (E,p)=\mathrm{const}\times E_n^{\mu }{(1-{\beta }^2{z}^2)}^{\lambda /2}{C}_n^{\lambda }\left(\beta z\right).$$

(50)

An important result is that in spite of the explicit dependence on the energy of the Schrödinger equation, its eigenvalues only depend on the parameters $\alpha$ and $\beta$. Thus, $E_n$ is independent of $\mu$, which can therefore be chosen arbitrarily. The most natural choice is $\mu =0$, namely $\lambda =\frac{1}{2}\left(1+\sqrt{1+\frac{4}{{\alpha }^2{\beta }^4}}\right)$, so that the solution $\psi$ of the Schrödinger equation becomes independent of E and can be normalized.

5. The Snyder–Galilei Harmonic Oscillator in Poincaré Coordinates

The final set of coordinates we will use in order to compare predictions of different choices for the physical momenta in the Snyder model is that associated to the Poincaré projective coordinates, defined in Equation (8). In 1 + 1 dimensions, Poincaré coordinates lead to calculations rather similar to the previous case.

The realization of the Galilean Snyder phase space (17) in terms of canonical coordinates (21) reads:

$${\widehat{x}}_{\mu }=\left(1-\frac{{\beta }^2}{4}{\overline{p}}_{\alpha }^2\right){\overline{x}}_{\mu }+\frac{{\beta }^2}{2}{\overline{p}}_{\mu }{\overline{p}}_{\alpha }{\overline{x}}^{\alpha },{\tilde{p}}_{\mu }={\overline{p}}_{\mu }.$$

(51)

In 1 + 1 dimensions this reduces to

$${\widehat{x}}_0={\overline{x}}_0,{\widehat{x}}_1=\left(1+\frac{{\beta }^2}{4}{\overline{p}}_1^2\right){\overline{x}}_1-\frac{{\beta }^2}{2}{\overline{p}}_1{\overline{p}}_0{\overline{x}}_0,{\tilde{p}}_{\mu }={\overline{p}}_{\mu },$$

(52)

and allows us to find the following representation on momentum space:

$${\tilde{p}}_1=p,{\widehat{x}}_1=i\hslash \left(1+\frac{{\beta }^2}{4}{p}^2\right)\frac{\partial }{\partial p}+i\hslash \frac{{\beta }^2}{2}pE\frac{\partial }{\partial E},$$

(53)

$${\tilde{p}}_0=E,{\widehat{x}}_0=-i\hslash \frac{\partial }{\partial E}.$$

(54)

The Hilbert space of these operators is that of square integrable functions $\psi (p,E)$ of p and E. With the choice (53) of operator ordering, the measure in this Hilbert space is

$$d\mathsf{\Omega }=\frac{dpdE}{{\left(1+\frac{{\beta }^2}{4}{p}^2\right)}^{3/2}}.$$

(55)

We again choose the standard Hamiltonian for the harmonic oscillator, written now in terms of the Snyder-Poincaré coordinates:

$$H=\frac{{\tilde{p}}_1^2}{2m}+\frac{m{\omega }^2}{2}{\widehat{x}}_1^2.$$

(56)

Using the representation (53) and (54), the resulting Schrödinger equation can be written as

$$\begin{array}{c}\hfill \left(E-\frac{p^2}{2m}\right)\psi =-\frac{{\alpha }^2}{2m}[{\left(1+\frac{{\beta }^2}{4}{p}^2\right)}^2\frac{{\partial }^2}{\partial p^2}+\frac{{\beta }^2}{2}\left(1+\frac{{\beta }^2}{4}{p}^2\right)p\frac{\partial }{\partial p}\left(1+2E\frac{\partial }{\partial E}\right)\\ \hfill +\left(E^2\frac{{\partial }^2}{\partial E^2}+\frac{3}{2}E\frac{\partial }{\partial E}\right)\frac{{\beta }^4}{4}{p}^2+\frac{{\beta }^2}{2}E\frac{\partial }{\partial E}]\psi ,\end{array}$$

(57)

with $\alpha$ defined in (28). Following the same steps as in the previous section, we make the ansatz

$$\psi (E,p)=E^{\mu }\varphi \left(p\right),$$

(58)

so that the Schrödinger Equation (57) reduces to

$$\left[{\left(1+\frac{{\beta }^2}{4}{p}^2\right)}^2\frac{{\partial }^2}{\partial p^2}+\frac{1+2\mu }{2}\left(1+\frac{{\beta }^2}{4}{p}^2\right){\beta }^{2}p\frac{\partial }{\partial p}+\left(\frac{2Em}{{\alpha }^2{\beta }^2}+\frac{\mu }{2}\right){\beta }^2+\left({\mu }^2+\frac{\mu }{2}-\frac{4}{{\alpha }^2{\beta }^4}\right)\frac{{\beta }^4}{4}{p}^2\right]\varphi =0.$$

(59)

This can be solved as in the previous case by changing variables as

$$z=\frac{p}{2\sqrt{1+\frac{{\beta }^2}{4}{p}^2}},\mathrm{with}{}^{\prime }=\frac{d}{dz},$$

(60)

and defining

$$\varphi ={\left(1-{\beta }^2{z}^2\right)}^{\lambda /2}f\left(\beta z\right).$$

(61)

Then Equation (59) reads

$$(1-{\beta }^2{z}^2)f^{″}-(1-4\mu +2\lambda )\beta z{f}^{\prime }+\left(2\mu -\lambda +\frac{8Em}{{\alpha }^2{\beta }^2}\right)f+\left(4{\mu }^2+2\mu +{\lambda }^2-\lambda -4\mu \lambda -\frac{16}{{\alpha }^2{\beta }^4}\right)\frac{{\beta }^2{z}^2}{1-{\beta }^2{z}^2}f=0.$$

(62)

Again, the solution is normalizable if the last term vanishes, namely

$$\lambda =2\mu +\frac{1}{2}\left(1\pm \sqrt{1+\frac{64}{{\alpha }^2{\beta }^4}}\right).$$

(63)

Choosing the positive sign in (63), Equation (62) reduces to a Gegenbauer equation with eigenvalues

$$E_n=\hslash \omega \left[\left(n+\frac{1}{2}\right)\left(\sqrt{1+\frac{{\alpha }^2{\beta }^4}{64}}+\frac{\alpha {\beta }^2}{8}\right)+\frac{n^2}{8}\alpha {\beta }^2\right],$$

(64)

and the eigenfunction of the Schrödinger Equation (57) is

$$\psi (E,p)=\mathrm{const}\times E_n^{\mu }{(1-{\beta }^2{z}^2)}^{\lambda /2}{C}_n^{\lambda }\left(\beta z\right).$$

(65)

Also in this case $E_n$ is independent of $\mu$, and we can choose $\mu =0$, namely $\lambda =\frac{1}{2}\left(1+\sqrt{1+\frac{64}{{\alpha }^2{\beta }^4}}\right)$, so that $\psi$ becomes independent of E and normalizable.

6. Conclusions

The goal of this work was to investigate whether different choices of momentum space coordinates associated to the same noncommutative spacetime models are physically relevant. We did so by focussing on the well-known Snyder model, for which spacetime coordinates can be identified with the translation generators over a de Sitter manifold and momenta with coordinates on such manifold. We derived the energy spectrum of the harmonic oscillator in three different cases corresponding to the following choices of physical momenta, related to each other by a momentum space diffeomorphism: one where the physical momenta are those related to the embedding coordinates of the de Sitter manifold, one where they are related to the Beltrami projective coordinates, and finally, one where they are related to the Poincaré projective coordinates. We found that these different choices of physical momenta indeed imply different behaviours of the energy spectrum. In fact, the leading order contributions, up to $\mathcal{O}\left({\beta }^2\right)$, can be written as

$$E_n=\hslash \omega \left[\left(n+\frac{1}{2}\right)+ϵ\alpha {\beta }^2\left(n^2+n+\frac{1}{2}\right)\right],$$

(66)

where $ϵ=-\frac{1}{4}$ for embedding coordinates, $ϵ=\frac{1}{2}$ for Beltrami coordinates, and $ϵ=\frac{1}{8}$ for Poincaré coordinates. In all cases, the leading corrections are qualitatively similar, but the coefficients of the correction terms beyond the standard contribution are different, confirming that different parametrizations of the momentum space give rise to nonequivalent physical models.

Let us remark that this result was obtained by considering changes in the momentum space coordinates as active diffeomorphisms on the momentum space, to use the terminology of [35,36] 5. In fact, for each set i of momentum space coordinates, $p_{\alpha }^{\left(i\right)}$, we take the Hamiltonian of the harmonic oscillator to be written in the standard form in terms of these, namely $H=\frac{p^{\left(i\right)}{}^2}{2m}+\frac{m{\omega }^2}{2}{\widehat{x}}_1^2$. The $p_{\alpha }^{\left(i\right)}$ are thus identified with the physical momenta. Our results confirm, in a completely different setting and using a different model, the conclusions of the Ref. [35], that active diffeomorphisms lead to different physical predictions. Of course, if we were to start from a Hamiltonian that takes a standard form in terms of some momentum space coordinates $p_{\alpha }^{\left(i\right)}$ and then simply mapped to some new momenta $p_{\alpha }^{\left(j\right)}$ by writing $p^{\left(i\right)}\left(p^{\left(j\right)}\right)$, we would be doing a mere change of variables, or a passive diffeomorphism, using the terminology of [35,36]. In this case, the Hamiltonian would take a different, non-standard, form in terms of the new momenta $p_{\alpha }^{\left(j\right)}$, $H=\frac{p^{\left(i\right)}\left(p^{\left(j\right)}\right){}^2}{2m}+\frac{m{\omega }^2}{2}{\widehat{x}}_1^2$, but then we would not expect to see physically relevant differences.

As an additional result of our analysis, we were able to start comparing the predictions of the Galilean limit of the Snyder model, which we used in this work, to the predictions of the Euclidean Snyder model [27], where only spatial coordinates are affected by noncommutativity. The latter had been widely used to describe the modifications induced by Snyder-like spacetime noncommutativity on non-relativistic systems, see for example, Refs. [27,28,29,31,32]. In Ref. [5] it was shown that the proper non-relativistic limit of the Snyder model leads, in fact, to the Galilean Snyder model, which differs from the Euclidean one because of a residual noncommutativity between the space and time coordinates. However, this difference might not be significant in the simple model we considered here, since the energy levels of the harmonic oscillator in the Euclidean Snyder model [27] coincide with those obtained here with the Beltrami coordinates, Equation (30), which are also the coordinates used in Ref. [27]. This can be traced back to the fact that, in the representation used here for the Beltrami coordinates, the spatial coordinate does depend on energy and its derivative, but in a homogeneous way. Thus, the solutions to the Schrödinger equation are separable and the part depending on momenta satisfies the same Schrödinger equation as the solutions in the Euclidean model. One may wonder whether this is true also for the other choices of parametrization of the phase space considered in this paper or for less elementary models. The first option does not seem to be the case. In fact, we notice that for the Poincaré coordinates we can make a similar remark to the one that applies to the Beltrami coordinates. Moreover, the representation of the embedding coordinates does not mix spatial momenta and energy. We thus conjecture that the second option is more likely, since the only way to have effects different from the Euclidean case would be to have a time-dependent Hamiltonian, so that the time coordinate introduces terms that are not homogeneous in the energy.

From a phenomenological point of view, one may estimate the size of the corrections to the quantum mechanical spectrum. These are of order $\hslash \omega {\beta }^2$. As usual with the Snyder model, if one identifies $\beta$ with the Planck length, the corrections are very small and hence not detectable experimentally. For example, if one considers an atomic-size oscillator with $m\omega \sim {10}^{21}$ kg/s, they are of order ${10}^{-14}$. However, one cannot exclude that the parameter $\beta$ has a much greater value [37,38] (see also discussion in Ref. [39] and references therein).

A simple application of our results is given by the computation of the partition function for the different models. This is given by

$$Z=\sum _{n=0}^{\infty }{e}^{-\frac{E_n}{T}},$$

(67)

where T is the temperature and we have set to 1 the Boltzmann constant. Using the spectrum (66) and expanding to the first order in $\alpha {\beta }^2$, one obtains

$$Z\approx \sum _{n=0}^{\infty }{e}^{-\frac{\hslash \omega }{T}(n+\frac{1}{2})}\left[1-ϵ\alpha {\beta }^2\left(n^2+n+\frac{1}{2}\right)\right]=\frac{2}{sinh\frac{\hslash \omega }{2T}}\left[1-ϵ\alpha {\beta }^2\frac{\hslash \omega }{2T}{coth}^2\frac{\hslash \omega }{2T}\right].$$

(68)

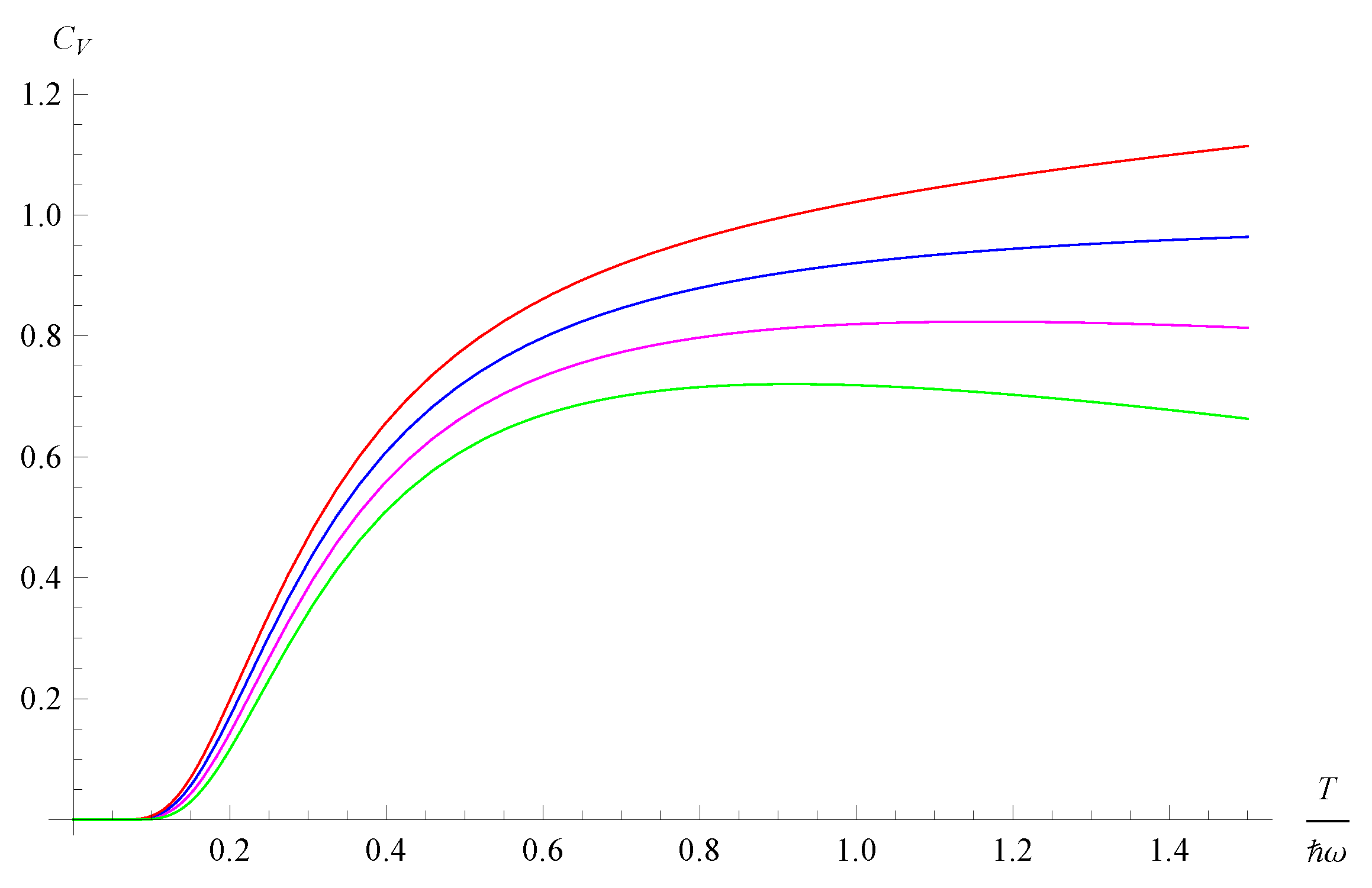
From the partition function one can obtain the specific heat of the oscillator as $C_V=\frac{1}{T^2}\frac{{\delta }^{2}Z}{\delta {(1/T)}^2}$. Its behavior is similar to that of the anharmonic oscillator [40] and is displayed in Figure 1 for the various models. For $T\to 0$ it is analogous to the standard harmonic oscillator, but for high values of T it is rather different. In particular, in the case of Beltrami or Poincaré coordinates it decreases for high temperature, while in embedding coordinates it increases. This behavior can be compared to the standard case, where it tends to a constant value. This property could lead to interesting phenomenological consequences.

It would be interesting to further investigate the issues raised in the present paper, possibly considering other physical frameworks, especially in three spatial dimensions, such as the hydrogen atom, which could be compared with the results obtained in the Ref. [29] in the case of the Euclidean Snyder model.