Constraints on Barrow Entropy from M87* and S2 Star Observations
Abstract
:1. Introduction
2. Black Holes with Barrow Entropy
3. Barrow Entropy Effect on Black Hole Shadows
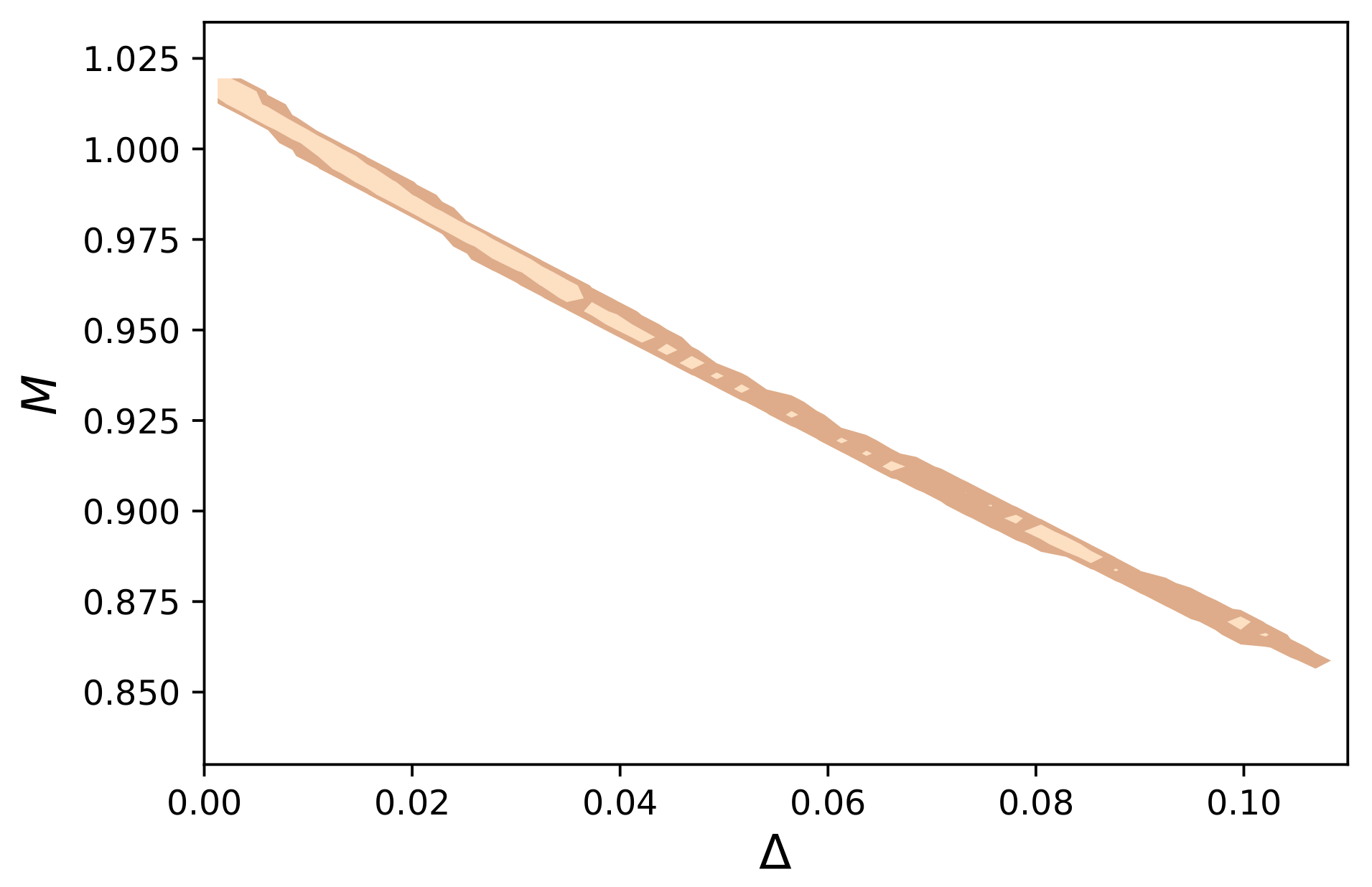
4. Observational Constraints on the Barrow Parameter
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Accretion of Matter onto Black Holes with Barrow Entropy
Appendix A.1. Isothermal Fluids
Appendix A.2. Polytropic Fluids
Appendix A.3. Correspondence: The Critical Point versus the Photon Sphere
References
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Akiyama, K. et al. [Event Horizon Telescope] First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett. 2019, 875, L2. [Google Scholar]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. arXiv 2021, arXiv:2111.05659. [Google Scholar]
- Shaikh, R. Black hole shadow in a general rotating spacetime obtained through Newman-Janis algorithm. Phys. Rev. D 2019, 100, 024028. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.W.; Zou, Y.C.; Liu, Y.X.; Mann, R.B. Curvature radius and Kerr black hole shadow. J. Cosmol. Astropart. Phys. 2019, 1908, 030. [Google Scholar] [CrossRef] [Green Version]
- Moffat, J.W.; Toth, V.T. Masses and shadows of the black holes Sagittarius A* and M87* in modified gravity. Phys. Rev. D 2020, 101, 024014. [Google Scholar] [CrossRef] [Green Version]
- Firouzjaee, J.T.; Allahyari, A. Black hole shadow with a cosmological constant for cosmological observers. Eur. Phys. J. C 2019, 79, 930. [Google Scholar] [CrossRef]
- Banerjee, I.; Mandal, B.; SenGupta, S. Does black hole continuum spectrum signal f(R) gravity in higher dimensions? Phys. Rev. D 2020, 101, 024013. [Google Scholar] [CrossRef] [Green Version]
- Long, F.; Wang, J.; Chen, S.; Jing, J. Shadow of a rotating squashed Kaluza-Klein black hole. J. High Energy Phys. 2019, 1910, 269. [Google Scholar] [CrossRef] [Green Version]
- Zhu, T.; Wu, Q.; Jamil, M.; Jusufi, K. Shadows and deflection angle of charged and slowly rotating black holes in Einstein-Æther theory. Phys. Rev. D 2019, 100, 044055. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Zhidenko, A. Analytical representation for metrics of scalarized Einstein-Maxwell black holes and their shadows. Phys. Rev. D 2019, 100, 044015. [Google Scholar] [CrossRef] [Green Version]
- Contreras, E.; Rincón, Á.; Panotopoulos, G.; Bargueño, P.; Koch, B. Black hole shadow of a rotating scale–dependent black hole. Phys. Rev. D 2020, 101, 064053. [Google Scholar] [CrossRef] [Green Version]
- Li, P.C.; Guo, M.; Chen, B. Shadow of a Spinning Black Hole in an Expanding Universe. Phys. Rev. D 2020, 101, 084041. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G.; Wang, A. Gravitational deflection of light and shadow cast by rotating Kalb-Ramond black holes. Phys. Rev. D 2020, 101, 104001. [Google Scholar] [CrossRef]
- Pantig, R.C.; Rodulfo, E.T. Rotating dirty black hole and its shadow. Chin. J. Phys. 2020, 68, 236. [Google Scholar] [CrossRef]
- Xavier, S.V.M.C.B.; Cunha, P.V.P.; Crispino, L.C.B.; Herdeiro, C.A.R. Shadows of charged rotating black holes: Kerr–Newman versus Kerr–Sen. Int. J. Mod. Phys. D 2020, 29, 2041005. [Google Scholar] [CrossRef]
- Guo, M.; Li, P.C. Innermost stable circular orbit and shadow of the 4D Einstein–Gauss–Bonnet black hole. Eur. Phys. J. C 2020, 80, 588. [Google Scholar] [CrossRef]
- Roy, R.; Chakrabarti, S. Study on black hole shadows in asymptotically de Sitter spacetimes. Phys. Rev. D 2020, 102, 024059. [Google Scholar] [CrossRef]
- Jin, X.H.; Gao, Y.X.; Liu, D.J. tStrong gravitational lensing of a 4-dimensional Einstein–Gauss–Bonnet black hole in homogeneous plasma. Int. J. Mod. Phys. D 2020, 29, 2050065. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, R.; Ghosh, S.G. Gravitational lensing by black holes in the 4D Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2020, 2009, 030. [Google Scholar] [CrossRef]
- Chen, C.Y. Rotating black holes without Z2 symmetry and their shadow images. J. Cosmol. Astropart. Phys. 2020, 5, 040. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Schee, J.; Ovchinnikov, D. Shadow of the magnetically and tidally deformed black hole. arXiv 2020, arXiv:2008.04118. [Google Scholar]
- Belhaj, A.; Benali, M.; Balali, A.E.; Hadri, W.E.; Moumni, H.E.; Torrente-Lujan, E. Black Hole Shadows in M-theory Scenarios. arXiv 2021, arXiv:2008.09908. [Google Scholar] [CrossRef]
- Long, F.; Chen, S.; Wang, M.; Jing, J. Shadow of a disformal Kerr black hole in quadratic DHOST theories. arXiv 2020, arXiv:2009.07508. [Google Scholar]
- Contreras, E.; Rincón, Á.; Panotopoulos, G.; Bargueño, P. Geodesic analysis and black hole shadows on a general non–extremal rotating black hole in five–dimensional gauged supergravity. arXiv 2021, arXiv:2010.03734. [Google Scholar] [CrossRef]
- Shao, W.H.; Chen, C.Y.; Chen, P. Generating Rotating Spacetime in Ricci-Based Gravity: Naked Singularity as a Black Hole Mimicker. arXiv 2021, arXiv:2011.07763. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Kumar, R.; Islam, S.U. Parameters estimation and strong gravitational lensing of nonsingular Kerr-Sen black holes. arXiv 2021, arXiv:2011.08023. [Google Scholar] [CrossRef]
- Glampedakis, K.; Pappas, G. Can supermassive black hole shadows test the Kerr metric? arXiv 2021, arXiv:2011.08023. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Shadows of parametrized axially symmetric black holes allowing for separation of variables. Phys. Rev. D 2021, 103, 104033. [Google Scholar] [CrossRef]
- Wang, H.M.; Wei, S.W. Shadow cast by Kerr-like black hole in the presence of plasma in Einstein-bumblebee gravity. arXiv 2021, arXiv:2106.14602. [Google Scholar]
- Khodadi, M.; Lambiase, G.; Mota, D.F. No-hair theorem in the wake of Event Horizon Telescope. J. Cosmol. Astropart. Phys. 2021, 09, 028. [Google Scholar] [CrossRef]
- Frion, E.; Giani, L.; Miranda, T. Black Hole Shadow Drift and Photon Ring Frequency Drift. arXiv 2021, arXiv:2107.13536. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, T. Shadow of the wormhole-like static aether solution. arXiv 2021, arXiv:2109.08463. [Google Scholar]
- Heydari-Fard, M.; Heydari-Fard, M.; Sepangi, H.R. On null geodesics and shadow of hairy black holes in Einstein-Maxwell-dilaton. arXiv 2021, arXiv:2110.02713. [Google Scholar]
- Jusufi, K.; Saurabh. Black hole shadows in Verlinde’s emergent gravity. Mon. Not. Roy. Astron. Soc. 2021, 503, 1310. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Denton, P.B. Ultralight Boson Dark Matter and Event Horizon Telescope Observations of M87*. Phys. Rev. Lett. 2019, 123, 021102. [Google Scholar] [CrossRef] [Green Version]
- Bar, N.; Blum, K.; Lacroix, T.; Panci, P. Looking for ultralight dark matter near supermassive black holes. J. Cosmol. Astropart. Phys. 2019, 1907, 045. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Jamil, M.; Salucci, P.; Zhu, T.; Haroon, S. Black Hole Surrounded by a Dark Matter Halo in the M87 Galactic Center and its Identification with Shadow Images. Phys. Rev. D 2019, 100, 044012. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A. Shadow of a black hole surrounded by dark matter. Phys. Lett. B 2019, 795, 1. [Google Scholar] [CrossRef]
- Narang, A.; Mohanty, S.; Kumar, A. Test of Kerr-Sen metric with black hole observations. arXiv 2020, arXiv:2002.12786. [Google Scholar]
- Sau, S.; Banerjee, I.; SenGupta, S. Imprints of the Janis-Newman-Winicour spacetime on observations related to shadow and accretion. Phys. Rev. D 2020, 102, 064027. [Google Scholar] [CrossRef]
- Belhaj, A.; Benali, M.; Balali, A.E.; Moumni, H.E.; Ennadifi, S.E. Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions. Class. Quant. Grav. 2020, 37, 215004. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Ghosh, S.G. Testing Rotating Regular Metrics as Candidates for Astrophysical Black Holes. Astrophys. J. 2020, 896, 89. [Google Scholar] [CrossRef]
- Zeng, X.X.; Zhang, H.Q. Influence of quintessence dark energy on the shadow of black hole. Eur. Phys. J. C 2020, 80, 1058. [Google Scholar] [CrossRef]
- Saurabh, K.; Jusufi, K. Imprints of dark matter on black hole shadows using spherical accretions. Eur. Phys. J. C 2021, 81, 490. [Google Scholar] [CrossRef]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef] [Green Version]
- Haroon, S.; Jusufi, K.; Jamil, M. Shadow Images of a Rotating Dyonic Black Hole with a Global Monopole Surrounded by Perfect Fluid. Universe 2020, 6, 23. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R.; Joshi, P.S. Can we distinguish black holes from naked singularities by the images of their accretion disks? J. Cosmol. Astropart. Phys. 2019, 1910, 064. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. EHT constraint on the ultralight scalar hair of the M87 supermassive black hole. Universe 2019, 5, 220. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, I.; Chakraborty, S.; SenGupta, S. Silhouette of M87*: A New Window to Peek into the World of Hidden Dimensions. Phys. Rev. D 2020, 101, 041301. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.H.; Lu, H. On the size of rotating black holes. Eur. Phys. J. C 2020, 80, 551. [Google Scholar] [CrossRef]
- Yan, S.F.; Li, C.; Xue, L.; Ren, X.; Cai, Y.F.; Easson, D.A.; Yuan, Y.F.; Zhao, H. Testing the equivalence principle via the shadow of black holes. Phys. Rev. Res. 2020, 2, 023164. [Google Scholar] [CrossRef]
- Allahyari, A.; Khodadi, M.; Vagnozzi, S.; Mota, D.F. Magnetically charged black holes from non-linear electrodynamics and the Event Horizon Telescope. J. Cosmol. Astropart. Phys. 2020, 2002, 003. [Google Scholar] [CrossRef] [Green Version]
- Rummel, M.; Burgess, C.P. Constraining Fundamental Physics with the Event Horizon Telescope. J. Cosmol. Astropart. Phys. 2020, 2005, 051. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Bambi, C.; Visinelli, L. Concerns regarding the use of black hole shadows as standard rulers. Class. Quant. Grav. 2020, 37, 087001. [Google Scholar] [CrossRef] [Green Version]
- Khodadi, M.; Allahyari, A.; Vagnozzi, S.; Mota, D.F. Black holes with scalar hair in light of the Event Horizon Telescope. J. Cosmol. Astropart. Phys. 2020, 2009, 026. [Google Scholar] [CrossRef]
- Chang, Z.; Zhu, Q.H. Does the shape of the shadow of a black hole depend on motional status of an observer? Phys. Rev. D 2020, 102, 044012. [Google Scholar] [CrossRef]
- Kruglov, S.I. The shadow of M87* black hole within rational nonlinear electrodynamics. Mod. Phys. Lett. A 2020, 35, 2050291. [Google Scholar] [CrossRef]
- Ghosh, D.; Thalapillil, A.; Ullah, F. Astrophysical hints for magnetic black holes. arXiv 2020, arXiv:2009.03363. [Google Scholar] [CrossRef]
- Psaltis, D.etal. [Event Horizon Telescope Collaboration]. Gravitational Test Beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole. Phys. Rev. Lett. 2020, 125, 141104. [Google Scholar] [CrossRef]
- Hu, Z.; Zhong, Z.; Li, P.C.; Guo, M.; Chen, B. QED effect on a black hole shadow. Phys. Rev. D 2021, 103, 044057. [Google Scholar] [CrossRef]
- Li, C.; Zhao, H.; Cai, Y.F. New test on the Einstein equivalence principle through the photon ring of black holes. Phys. Rev. D 2021, 104, 064027. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Barrow, J.D. The Area of a Rough Black Hole. Phys. Lett. B 2020, 808, 135643. [Google Scholar] [CrossRef]
- Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 123525. [Google Scholar] [CrossRef]
- Saridakis, E.N. Modified cosmology through spacetime thermodynamics and Barrow horizon entropy. J. Cosmol. Astropart. Phys. 2020, 7, 031. [Google Scholar] [CrossRef]
- Mamon, A.A.; Paliathanasis, A.; Saha, S. Dynamics of an Interacting Barrow Holographic Dark Energy Model and its Thermodynamic Implications. Eur. Phys. J. Plus 2021, 136, 134. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, H.; Xu, B.; Tu, F.; Chen, J. Dynamical analysis and statefinder of Barrow holographic dark energy. Eur. Phys. J. C 2021, 81, 686. [Google Scholar] [CrossRef]
- Rani, S.; Azhar, N. Braneworld Inspires Cosmological Implications of Barrow Holographic Dark Energy. Universe 2021, 7, 268. [Google Scholar] [CrossRef]
- Adhikary, P.; Das, S.; Basilakos, S.; Saridakis, E.N. Barrow Holographic Dark Energy in non-flat Universe. Phys. Rev. D 2021, 104, 123519. [Google Scholar] [CrossRef]
- Sheykhi, A. Barrow Entropy Corrections to Friedmann Equations. Phys. Rev. D 2021, 103, 123503. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A. Some statistical approaches in the apparent horizon entropy and the generalized second law of thermodynamics. arXiv 2021, arXiv:2107.04869. [Google Scholar]
- Sharma, U.K.; Varshney, G.; Dubey, V.C. Barrow agegraphic dark energy. Int. J. Mod. Phys. D 2021, 30, 2150021. [Google Scholar] [CrossRef]
- Lymperis, A.; Basilakos, S.; Saridakis, E.N. Modified cosmology through Kaniadakis horizon entropy. Eur. Phys. J. C 2021, 81, 1037. [Google Scholar] [CrossRef]
- Drepanou, N.; Lymperis, A.; Saridakis, E.N.; Yesmakhanova, K. Kaniadakis holographic dark energy. arXiv 2021, arXiv:2109.09181. [Google Scholar]
- Telali, E.C.; Saridakis, E.N. Power-law holographic dark energy and cosmology. arXiv 2021, arXiv:2109.09181. [Google Scholar]
- Abreu, E.M.C.; Neto, J.A. Barrow black hole corrected-entropy model and Tsallis nonextensivity. Phys. Lett. B 2020, 810, 135805. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A. Thermal features of Barrow corrected-entropy black hole formulation. Eur. Phys. J. C 2020, 80, 776. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Barboza, E.M., Jr. Barrow’s black hole entropy and the equipartition theorem. Europhys. Lett. 2020, 130, 40005. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Faraoni, V. Area-law versus Rényi and Tsallis black hole entropies. arXiv 2021, arXiv:2109.05315. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Khodadi, M.; Saridakis, E.N. Einstein-Æther gravity in the light of event horizon telescope observations of M87*. Phys. Dark Univ. 2021, 32, 100835. [Google Scholar] [CrossRef]
- Jusufi, K. Quasinormal Modes of Black Holes Surrounded by Dark Matter and Their Connection with the Shadow Radius. Phys. Rev. D 2020, 101, 084055. [Google Scholar] [CrossRef] [Green Version]
- Cuadros-Melgar, B.; Fontana, R.D.B.; de Oliveira, J. Analytical correspondence between shadow radius and black hole quasinormal frequencies. Phys. Lett. B 2020, 811, 135966. [Google Scholar] [CrossRef]
- Narayan, R.; Johnson, M.D.; Gammie, C.F. The Shadow of a Spherically Accreting Black Hole. Astrophys. J. Lett. 2019, 885, L33. [Google Scholar] [CrossRef] [Green Version]
- Zeng, X.X.; Zhang, H.Q.; Zhang, H. Shadows and photon spheres with spherical accretions in the four-dimensional Gauss-Bonnet black hole. Eur. Phys. J. C 2020, 80, 872. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the galactic center. Astrophys. J. Lett. 2000, 528, L13. [Google Scholar] [CrossRef] [Green Version]
- Bambi, C. Can the supermassive objects at the centers of galaxies be traversable wormholes? The first test of strong gravity for mm/sub-mm very long baseline interferometry facilities. Phys. Rev. D 2013, 87, 107501. [Google Scholar] [CrossRef] [Green Version]
- Gillessen, S.; Eisenhauer, F.; Fritz, T.K.; Bartko, H.; Dodds-Eden, K.; Pfuhl, O.; Ott, T.; Genzel, R. The orbit of the star S2 around SgrA* from VLT and Keck data. Astrophys. J. Lett. 2009, 707, L114–L117. [Google Scholar] [CrossRef] [Green Version]
- Abuter, R. et al. [GRAVITY Collaboration] Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar]
- Walsh, J.L.; Barth, A.J.; Ho, L.C.; Sarzi, M. The M87 Black Hole Mass from Gas-dynamical Models of Space Telescope Imaging Spectrograph Observations. Astrophys. J. 2013, 770, 86. [Google Scholar] [CrossRef] [Green Version]
- Shahzadi, M.; Kolosš, M.; Stuchlík, Z.; Habib, Y. Testing alternative theories of gravity by fitting the hot-spot data of Sgr A*. arXiv 2022, arXiv:2201.04442. [Google Scholar]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’Neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic center supermassive black hole. Science 2019, 365, 664–668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becerra-Vergara, E.A.; Arguelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Geodesic motion of S2 and G2 as a test of the fermionic dark matter nature of our Galactic core. Astron. Astrophys. 2020, 641, A34. [Google Scholar] [CrossRef]
- Nampalliwar, S.; Kumar, S.; Jusufi, K.; Wu, Q.; Jamil, M.; Salucci, P. Modeling the Sgr A* Black Hole Immersed in a Dark Matter Spike. Astrophys. J. 2021, 916, 116. [Google Scholar] [CrossRef]
- Jusufi, K.; Kumar, S.; Azreg-Aïnou, M.; Jamil, M.; Wu, Q.; Bambi, C. Constraining Wormhole Geometries using the Orbit of S2 Star and the Event Horizon Telescope. arXiv 2021, arXiv:2106.08070. [Google Scholar]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Observational constraints on Barrow holographic dark energy. Eur. Phys. J. C 2020, 80, 826. [Google Scholar] [CrossRef]
- Leon, G.; Na, J.M.; Hernández-Almada, A.; García-Aspeitia, M.A.; Verdugo, T.; Motta, V. Barrow Entropy Cosmology: An observational approach with a hint of stability analysis. arXiv 2021, arXiv:2108.10998. [Google Scholar] [CrossRef]
- Barrow, J.D.; Basilakos, S.; Saridakis, E.N. Big Bang Nucleosynthesis constraints on Barrow entropy. Phys. Lett. B 2021, 815, 136134. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A. An upper limit on the spin of SgrA* based on stellar orbits in its vicinity. Astrophys. J. Lett. 2020, 901, L32. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Maartens, R.; MacCallum, M.A.H. Relativistic Cosmology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Azreg-Aïnou, M. Cyclic and heteroclinic flows near general static spherically symmetric black holes: Semi-cyclic flows—Addendum and corrigendum. Eur. Phys. J. C 2017, 77, 36. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.K.; Azreg-Aïnou, M.; Faizal, M.; Jamil, M. Cyclic and heteroclinic flows near general static spherically symmetric black holes. Eur. Phys. J. C 2016, 76, 280. [Google Scholar] [CrossRef] [Green Version]
- Azreg-Aïnou, M.; Ahmed, A.K.; Jamil, M. Spherical accretion by normal and phantom Einstein–Maxwell–dilaton black holes. Class. Quant. Grav. 2018, 35, 235001. [Google Scholar] [CrossRef] [Green Version]
- Bahamonde, S.; Jamil, M. Accretion Processes for General Spherically Symmetric Compact Objects. Eur. Phys. J. C 2015, 75, 508. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.K.; Camci, U.; Jamil, M. Accretion on Reissner–Nordström–(anti)-de Sitter black hole with global monopole. Class. Quant. Grav. 2016, 33, 215012. [Google Scholar] [CrossRef] [Green Version]
- Aslam, A.; Jamil, M.; Myrzakulov, R. Noether gauge symmetry for the Bianchi type I model in f(T) gravity. Phys. Scr. 2013, 88, 025003. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Available online: https://www.amazon.com/Gravitation-Cosmology-Principles-Applications-Relativity/dp/0471925675 (accessed on 12 November 2021).
- Kumar, R.; Islam, S.U.; Ghosh, S.G. Gravitational lensing by charged black hole in regularized 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, 80, 1128. [Google Scholar] [CrossRef]
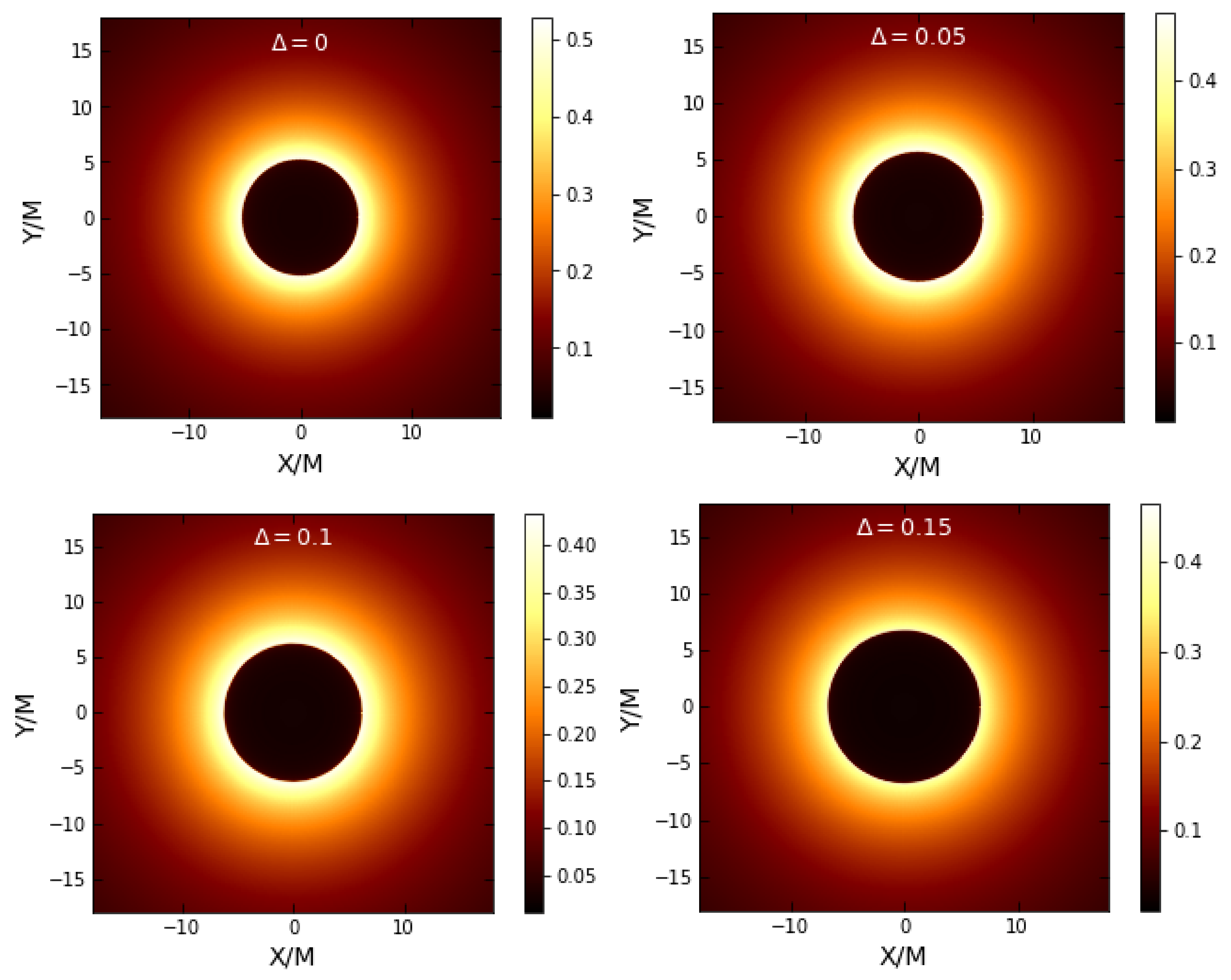
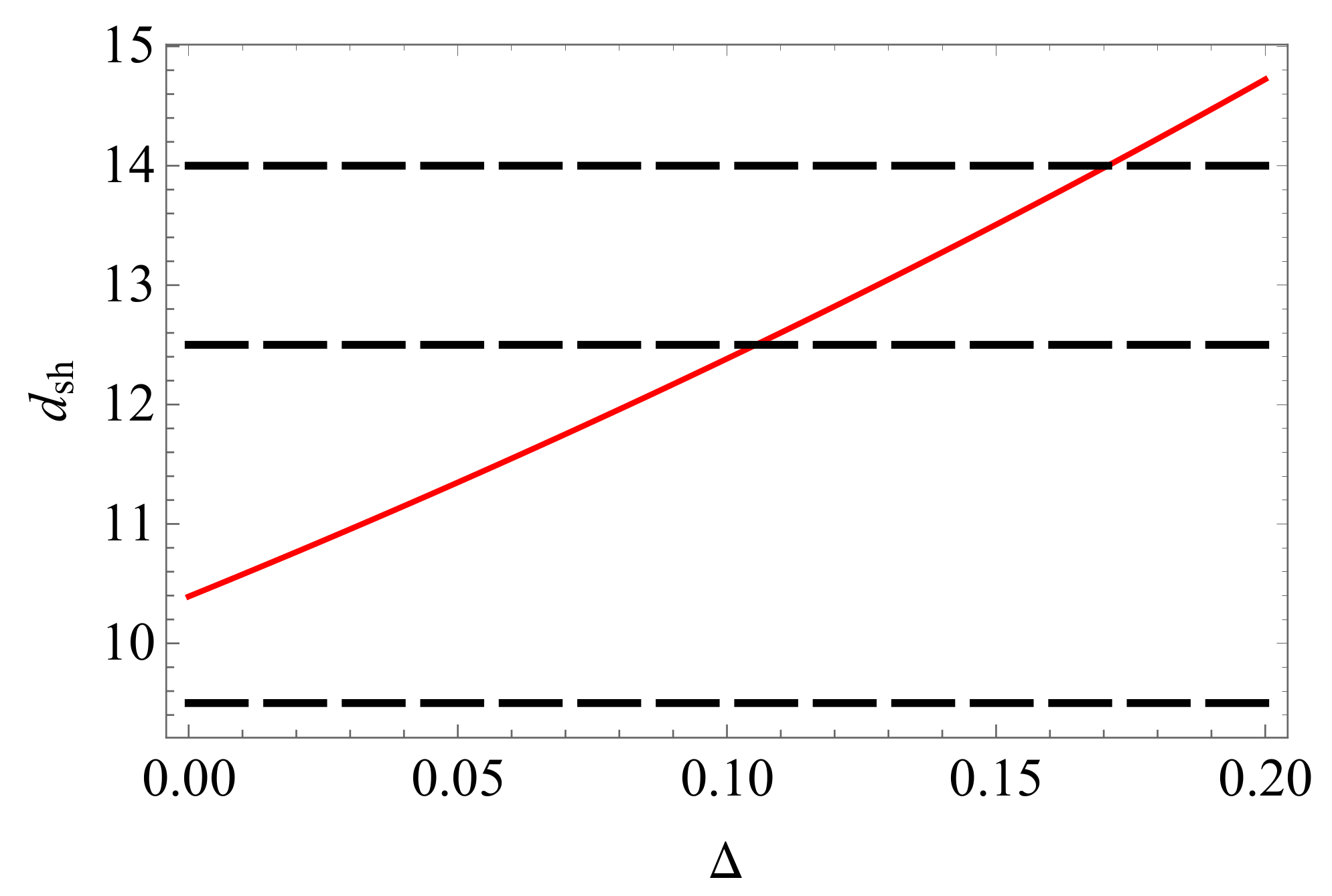
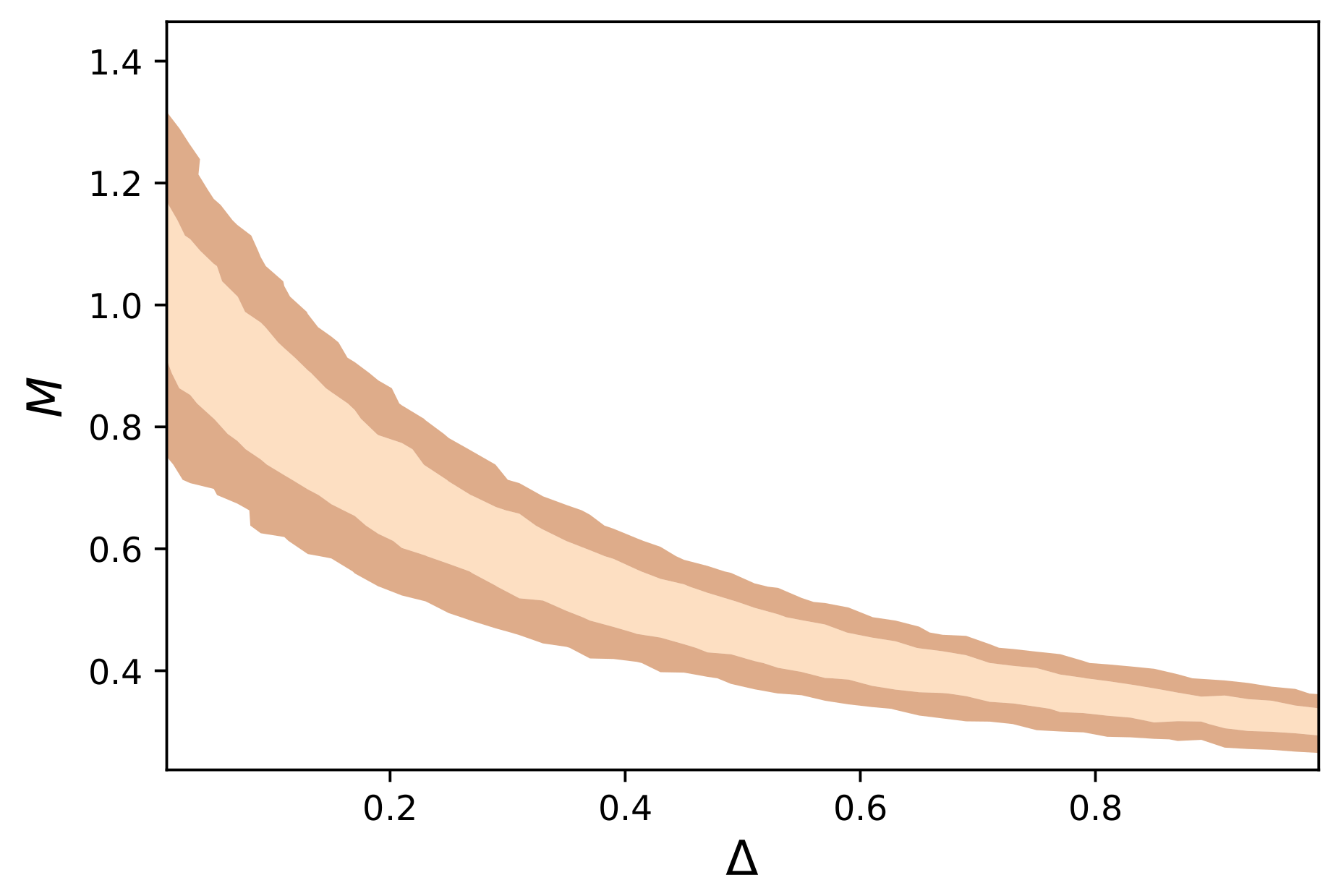
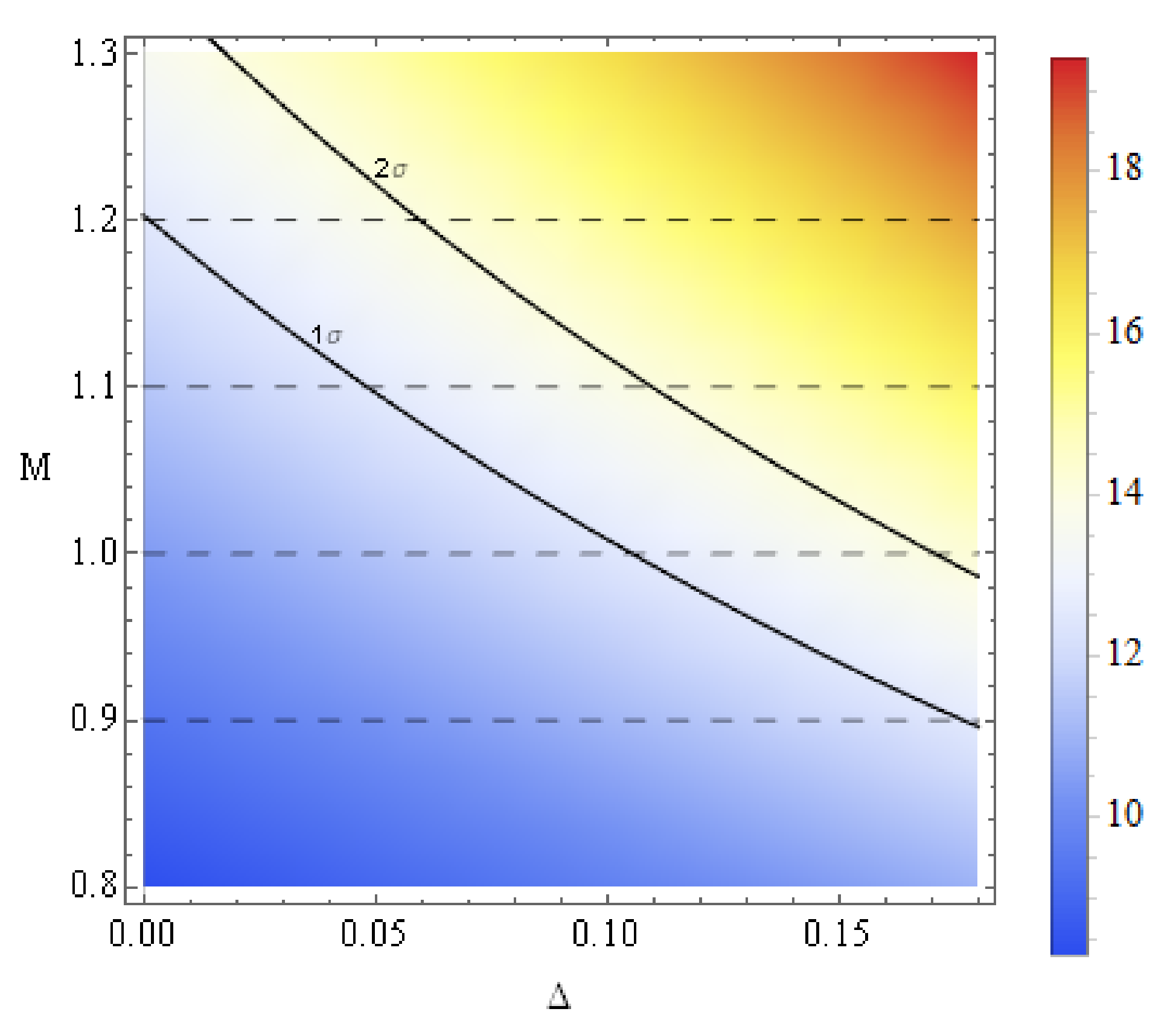

| 0 | 3 | 5.196152424 | 0.5000000000 |
| 0.001 | 3.005300838 | 5.205333745 | 0.4991180853 |
| 0.005 | 3.026590476 | 5.242208479 | 0.4956071896 |
| 0.008 | 3.042648663 | 5.270022075 | 0.4929915236 |
| 0.010 | 3.053397641 | 5.288639851 | 0.4912560290 |
| 0.030 | 3.162827055 | 5.478177156 | 0.4742592542 |
| 0.050 | 3.275860255 | 5.673956398 | 0.4578949904 |
| 0.080 | 3.452414952 | 5.979758107 | 0.4344784798 |
| 0.100 | 3.574958849 | 6.192010363 | 0.4195852494 |
| 0.120 | 3.701516690 | 6.411214974 | 0.4052392912 |
| 0.150 | 3.899154632 | 6.753533931 | 0.3846987723 |
| 0.170 | 4.036303659 | 6.991083014 | 0.3716271436 |
| 0.200 | 4.250450140 | 7.361995599 | 0.3529037985 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jusufi, K.; Azreg-Aïnou, M.; Jamil, M.; Saridakis, E.N. Constraints on Barrow Entropy from M87* and S2 Star Observations. Universe 2022, 8, 102. https://doi.org/10.3390/universe8020102
Jusufi K, Azreg-Aïnou M, Jamil M, Saridakis EN. Constraints on Barrow Entropy from M87* and S2 Star Observations. Universe. 2022; 8(2):102. https://doi.org/10.3390/universe8020102
Chicago/Turabian StyleJusufi, Kimet, Mustapha Azreg-Aïnou, Mubasher Jamil, and Emmanuel N. Saridakis. 2022. "Constraints on Barrow Entropy from M87* and S2 Star Observations" Universe 8, no. 2: 102. https://doi.org/10.3390/universe8020102
APA StyleJusufi, K., Azreg-Aïnou, M., Jamil, M., & Saridakis, E. N. (2022). Constraints on Barrow Entropy from M87* and S2 Star Observations. Universe, 8(2), 102. https://doi.org/10.3390/universe8020102









