A Short Review on Clustering Dark Energy
Abstract
1. Introduction
2. Linear Perturbations
3. Dark Energy Models
3.1. Quintessence
3.2. Tachyon
3.3. Clustering DE
4. The Spherical Collapse Model
4.1. Einstein-de-Sitter Universe
4.2. Spherical Collapse Model with Homogeneous Dark Energy
4.3. Spherical Collapse Model with Inhomogeneous Dark Energy
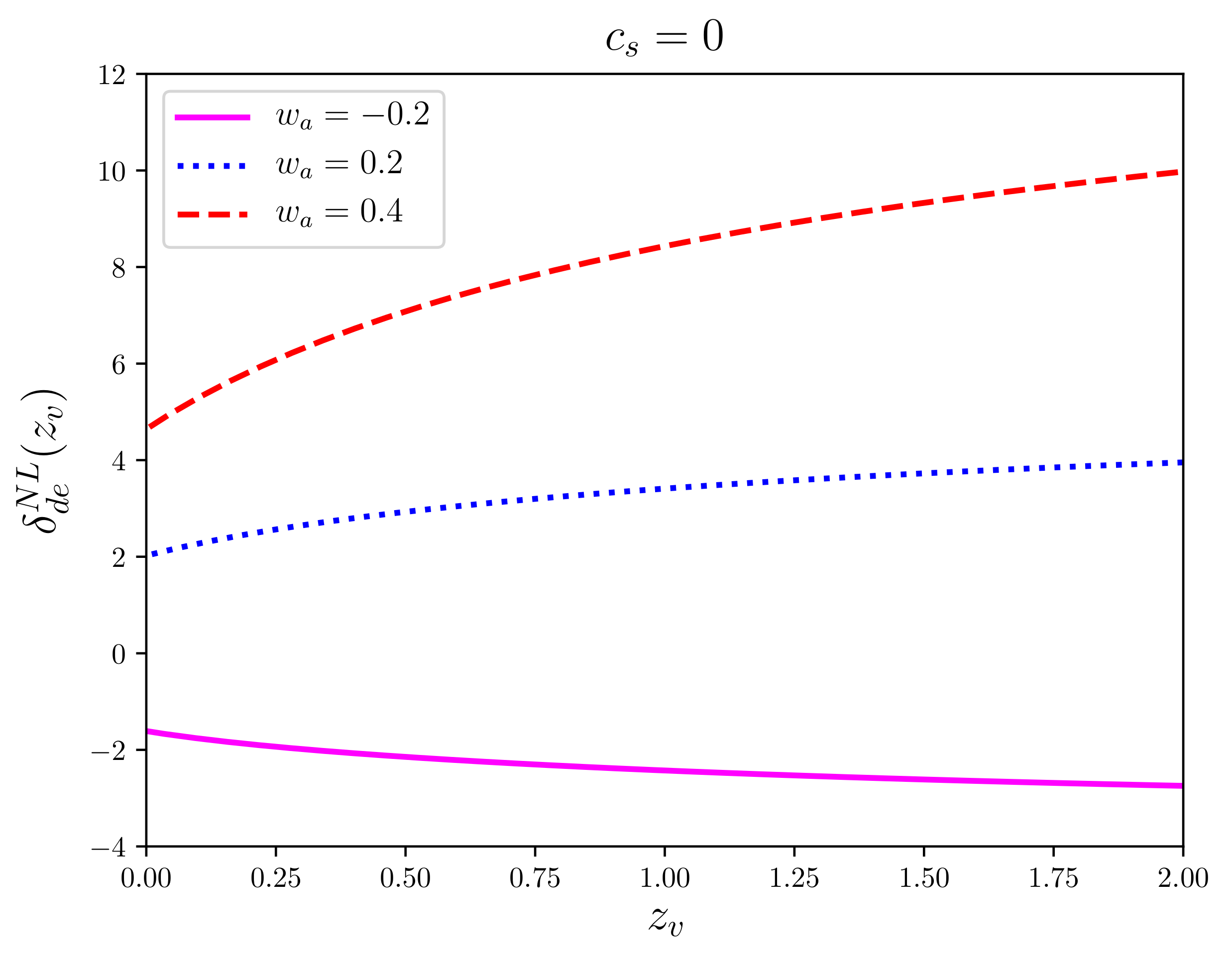
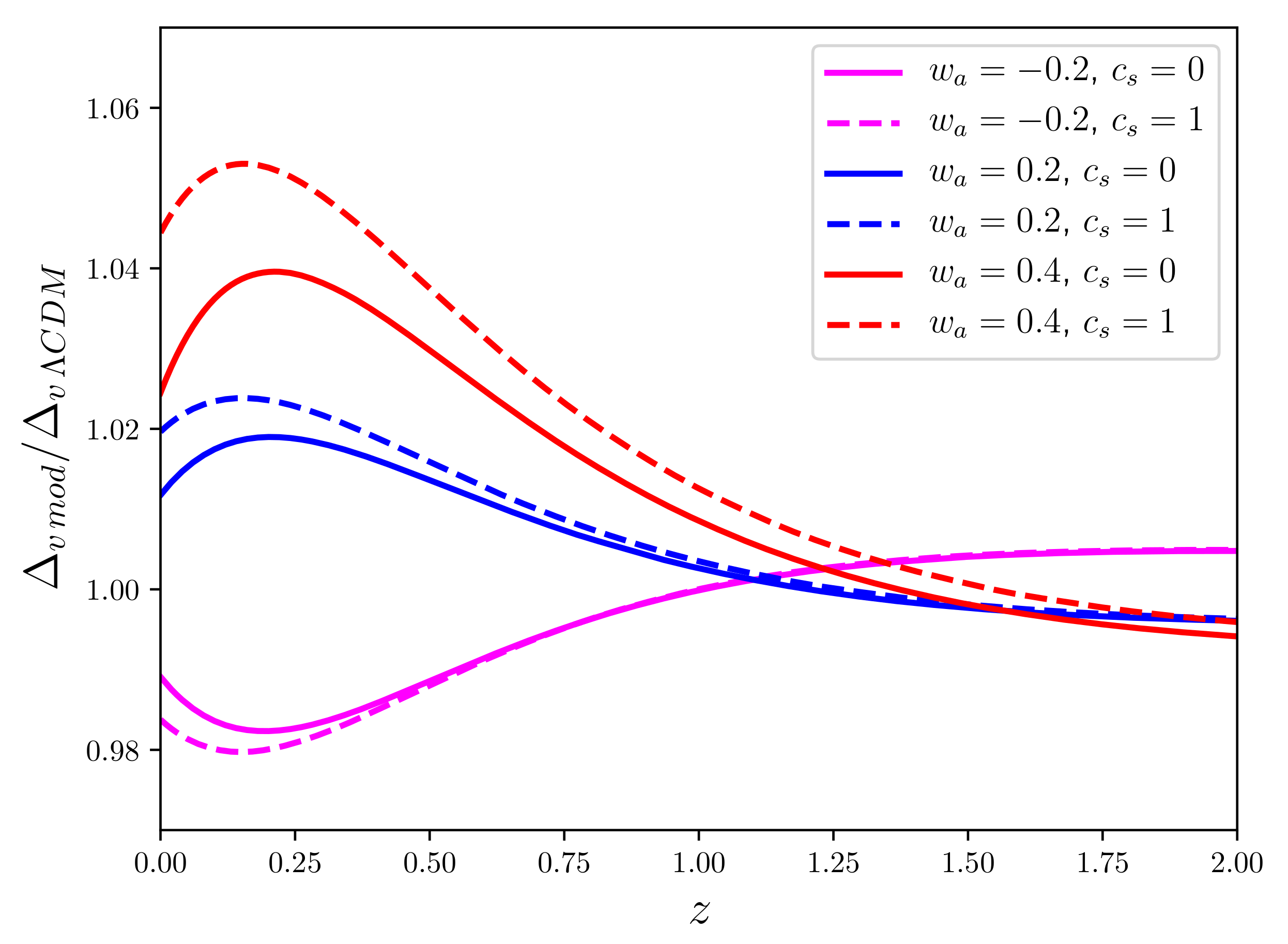
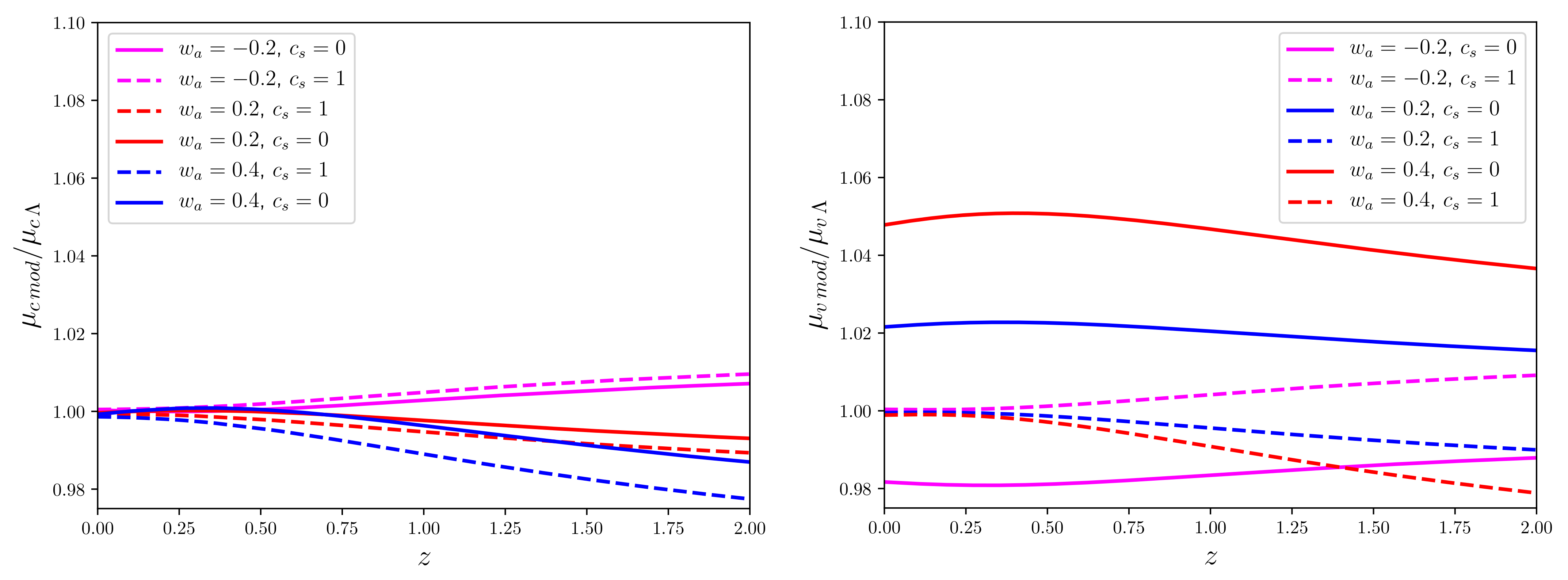
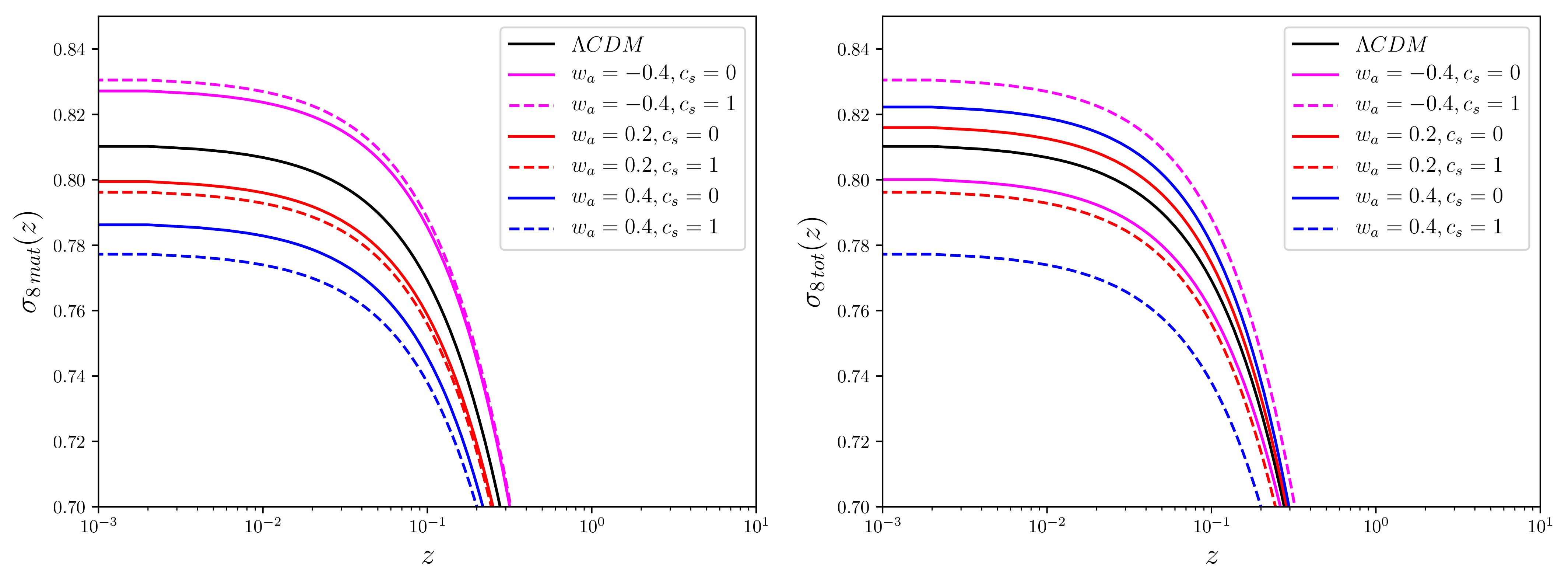
- The number DE fluctuations strongly depends on the evolution of w.
- DE fluctuations impact the nonlinear evolution of and virialization of halos.
- The local EoS of DE can be distinct from w due to DE fluctuations.
4.4. Other Generalizations of the Spherical Collapse Model
5. Spherical Collapse Model in the Pseudo-Newtonian Cosmology
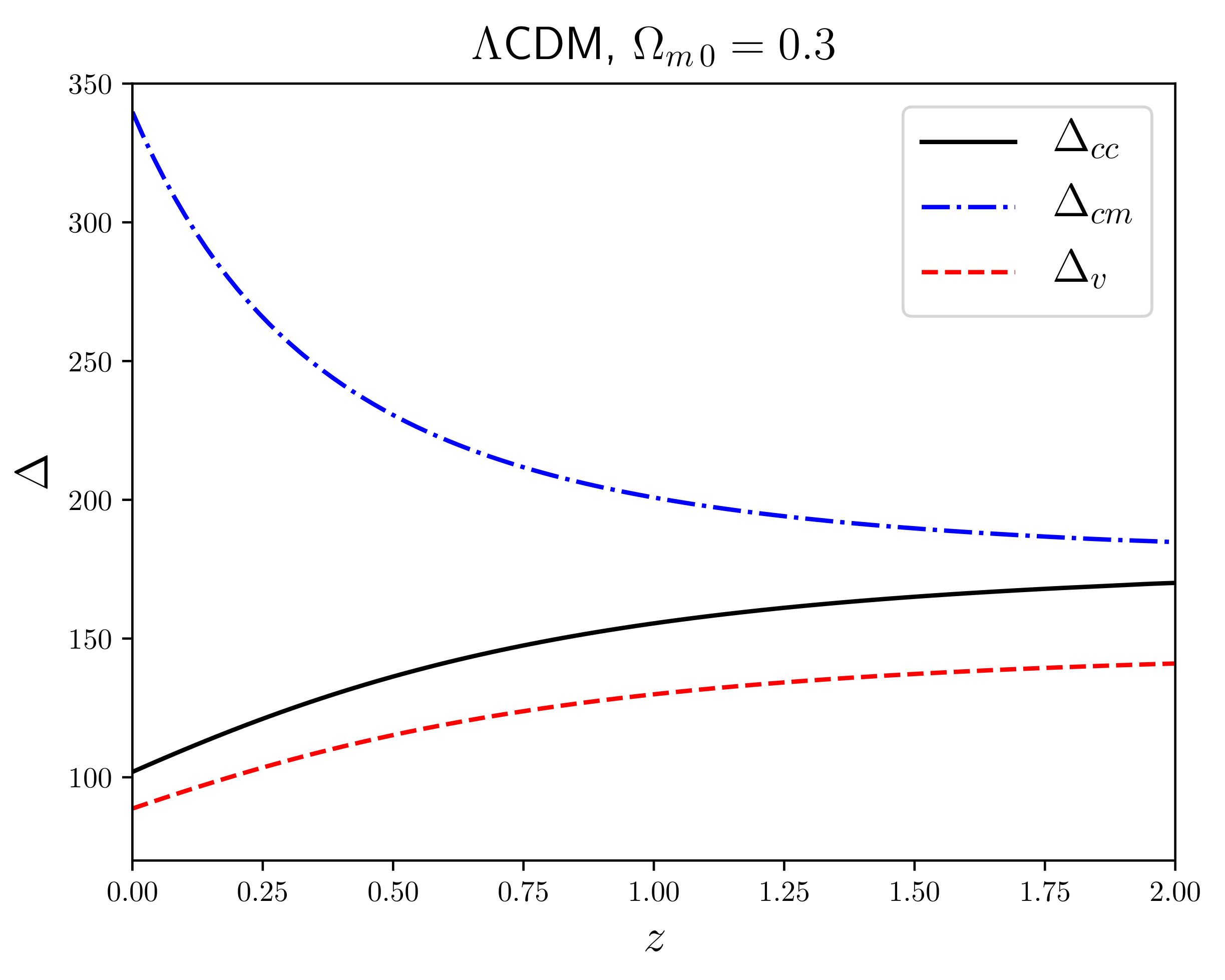
6. Density Threshold Definitions
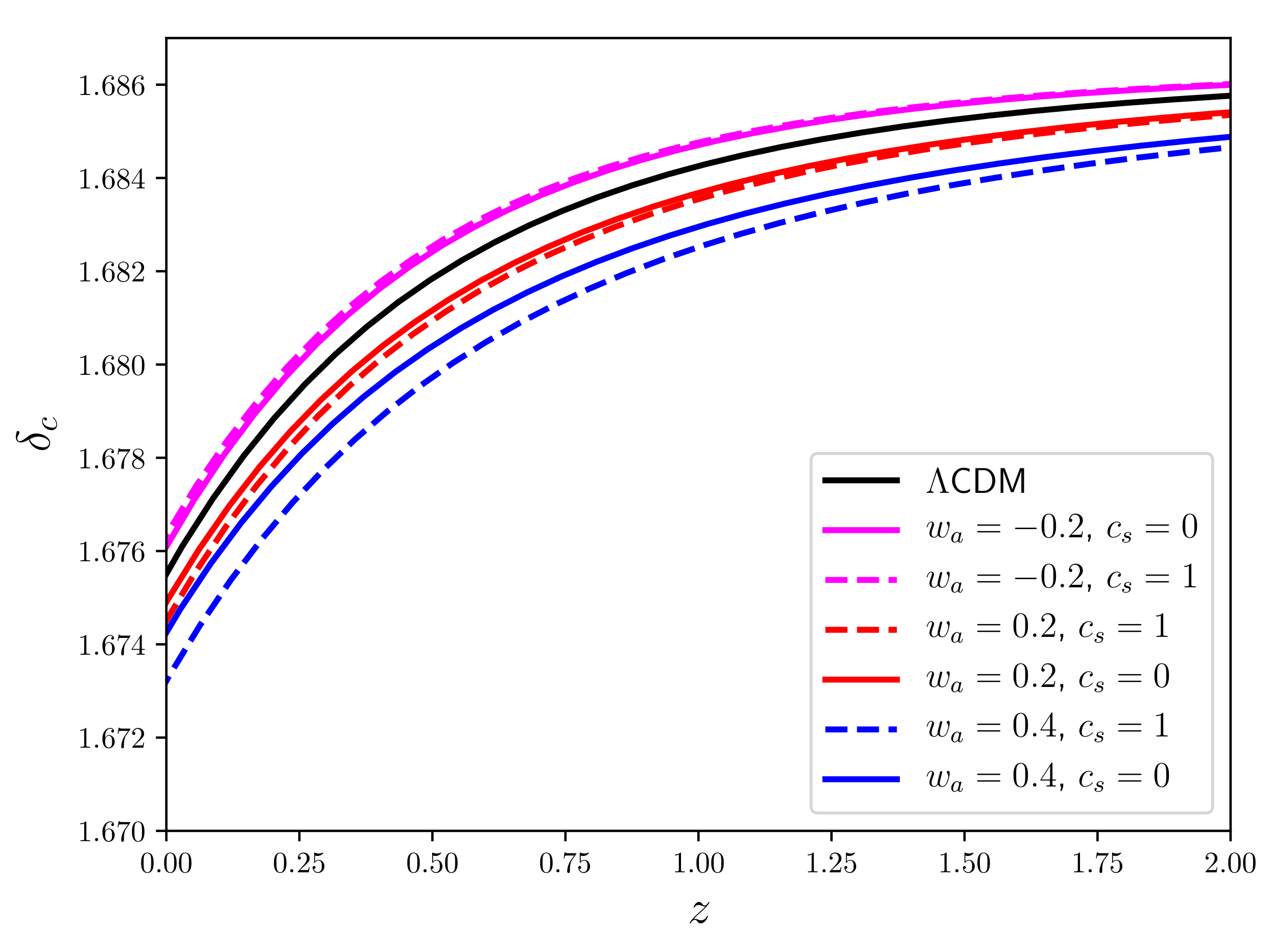
6.1. Collapse Threshold,
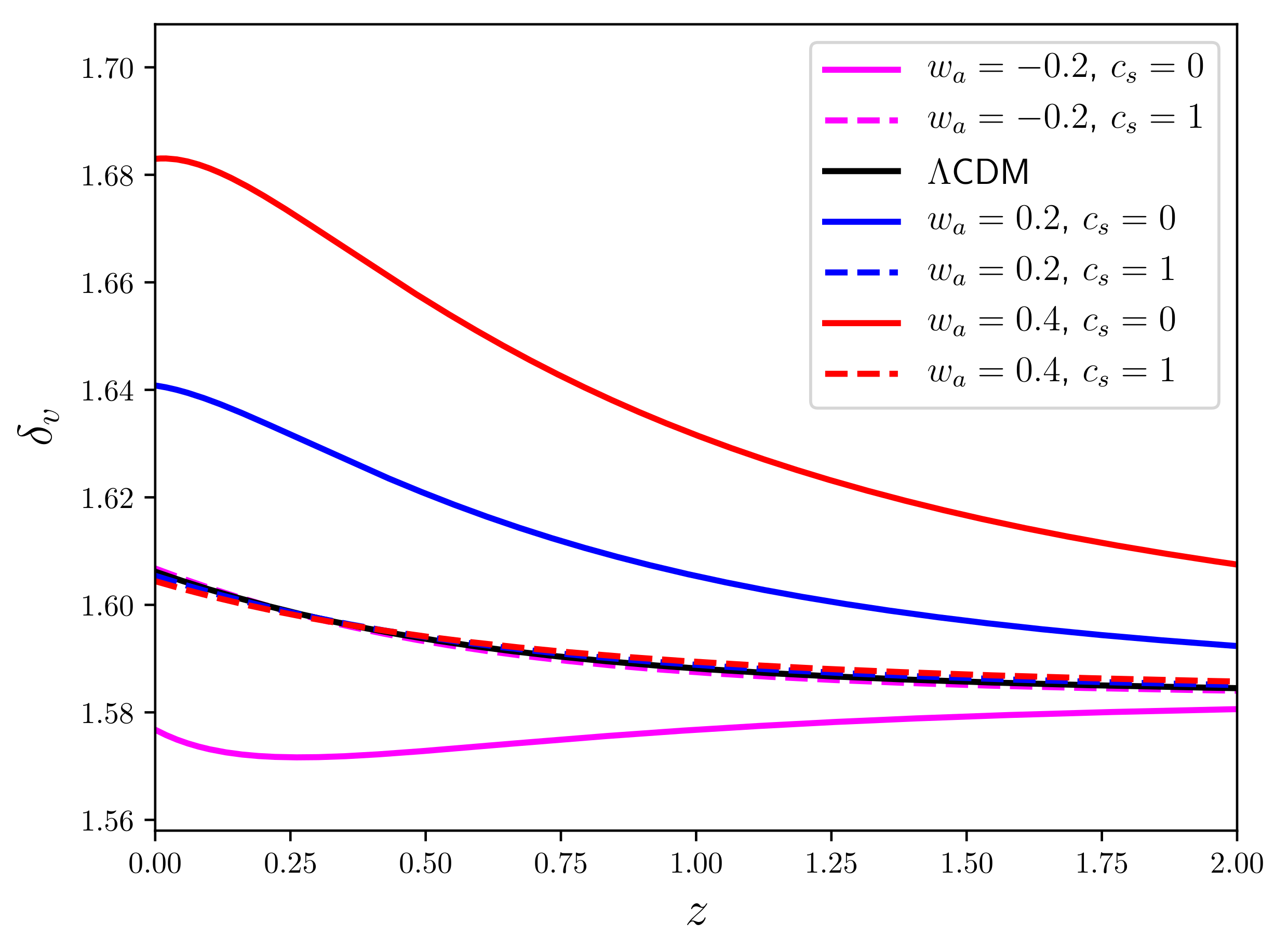
6.2. Virialization Threshold,
7. Halo Mass Functions
Numerical Simulations
8. Cosmological Observables
8.1. CMB and Large Scale Structure
8.2. Higher Order Perturbation Theory
8.3. Weak Lensing
8.4. Cluster Abundances
8.5. Internal Structure of Galaxy Clusters
8.6. Tension and Growth Rate
9. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2021, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark Energy Survey Year 3 Results: Cosmological Constraints from Galaxy Clustering and Weak Lensing. Phys. Rev. D 2021, 98, 043526. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stölzner, B.; Tröster, T.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev.Mod.Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Schöneberg, N.; Franco Abellán, G.; Pérez Sánchez, A.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. arXiv 2021, arXiv:2107.10291. [Google Scholar]
- Peebles, P.J.E.; Ratra, B. Cosmology with a Time Variable Cosmological ’Constant’. Astrophys. J. 1988, 325, L17. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the Fate of Dilatation Symmetry. Nucl. Phys. 1988, B302, 668. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological Imprint of an Energy Component with General Equation-of-State. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.M.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Ma, C.P.; Caldwell, R.R.; Bode, P.; Wang, L.M. The mass power spectrum in quintessence cosmological models. Astrophys. J. 1999, 521, L1–L4. [Google Scholar] [CrossRef][Green Version]
- Brax, P.; Martin, J.; Riazuelo, A. Exhaustive study of cosmic microwave background anisotropies in quintessential scenarios. Phys. Rev. D 2000, 62, 103505. [Google Scholar] [CrossRef]
- DeDeo, S.; Caldwell, R.R.; Steinhardt, P.J. Effects of the sound speed of quintessence on the microwave background and large scale structure. Phys. Rev. D 2003, 67, 103509. [Google Scholar] [CrossRef]
- Sen, A. Field theory of tachyon matter. Mod. Phys. Lett. A 2002, 17, 1797–1804. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Bagla, J.S.; Jassal, H.K.; Padmanabhan, T. Cosmology with tachyon field as dark energy. Phys. Rev. D 2003, 67, 063504. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I. Maximal freedom at minimum cost: Linear large-scale structure in general modifications of gravity. J. Cosmol. Astropart. Phys. 2014, 2014, 050. [Google Scholar] [CrossRef]
- Gubitosi, G.; Piazza, F.; Vernizzi, F. The Effective Field Theory of Dark Energy. J. Cosmol. Astropart. Phys. 2013, 2013, 032. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Rel. 2018, 21, 2. [Google Scholar] [CrossRef]
- Kodama, H.; Sasaki, M. Cosmological Perturbation Theory. Prog. Theor. Phys. Suppl. 1984, 78, 1–166. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Ma, C.P.; Bertschinger, E. Cosmological perturbation theory in the synchronous and conformal Newtonian gauges. Astrophys. J. 1995, 455, 7–25. [Google Scholar] [CrossRef]
- Dakin, J.; Hannestad, S.; Tram, T.; Knabenhans, M.; Stadel, J. Dark energy perturbations in N-body simulations. J. Cosmol. Astropart. Phys. 2019, 2019, 013. [Google Scholar] [CrossRef]
- Hassani, F.; Adamek, J.; Kunz, M.; Vernizzi, F. k-evolution: A relativistic N-body code for clustering dark energy. J. Cosmol. Astropart. Phys. 2019, 2019, 011. [Google Scholar] [CrossRef]
- Hassani, F.; Adamek, J.; Kunz, M. Clustering dark energy imprints on cosmological observables of the gravitational field. Mon. Not. R. Astron. Soc. 2020, 500, 4514–4529. [Google Scholar] [CrossRef]
- Mota, D.F.; van de Bruck, C. On the spherical collapse model in dark energy cosmologies. Astron. Astrophys. 2004, 421, 71–81. [Google Scholar] [CrossRef]
- Abramo, L.; Batista, R.; Liberato, L.; Rosenfeld, R. Structure formation in the presence of dark energy perturbations. J. Cosmol. Astropart. Phys. 2007, 2007, 012. [Google Scholar] [CrossRef]
- Creminelli, P.; D’Amico, G.; Norena, J.; Senatore, L.; Vernizzi, F. Spherical collapse in quintessence models with zero speed of sound. J. Cosmol. Astropart. Phys. 2010, 2010, 027. [Google Scholar] [CrossRef]
- Basse, T.; Bjaelde, O.E.; Wong, Y.Y.Y. Spherical collapse of dark energy with an arbitrary sound speed. J. Cosmol. Astropart. Phys. 2011, 2011, 038. [Google Scholar] [CrossRef][Green Version]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. 2001, D10, 213–224. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Bean, R.; Dore, O. Probing dark energy perturbations: The dark energy equation of state and speed of sound as measured by WMAP. Phys. Rev. D 2004, 69, 083503. [Google Scholar] [CrossRef]
- Linder, E.V.; Scherrer, R.J. Aetherizing Lambda: Barotropic Fluids as Dark Energy. Phys. Rev. D 2009, 80, 023008. [Google Scholar] [CrossRef]
- Unnikrishnan, S.; Sriramkumar, L. A note on perfect scalar fields. Phys. Rev. D 2010, 81, 103511. [Google Scholar] [CrossRef]
- Ballesteros, G.; Lesgourgues, J. Dark energy with non-adiabatic sound speed: Initial conditions and detectability. J. Cosmol. Astropart. Phys. 2010, 2010, 014. [Google Scholar] [CrossRef]
- Abramo, L.; Batista, R.; Liberato, L.; Rosenfeld, R. Physical approximations for the nonlinear evolution of perturbations in inhomogeneous dark energy scenarios. Phys. Rev. D 2009, 79, 023516. [Google Scholar] [CrossRef]
- Sapone, D.; Kunz, M.; Kunz, M. Fingerprinting Dark Energy. Phys. Rev. D 2009, 80, 083519. [Google Scholar] [CrossRef]
- Creminelli, P.; D’Amico, G.; Norena, J.; Vernizzi, F. The Effective Theory of Quintessence: The w<-1 Side Unveiled. J. Cosmol. Astropart. Phys. 2009, 2009, 018. [Google Scholar] [CrossRef]
- Batista, R.; Pace, F. Structure formation in inhomogeneous Early Dark Energy models. J. Cosmol. Astropart. Phys. 2013, 2013, 044. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yoo, J.; Watanabe, Y. Theoretical Models of Dark Energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Grav. 2013, 30, 214003. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Erickson, J.K.; Caldwell, R.; Steinhardt, P.J.; Armendariz-Picon, C.; Mukhanov, V.F. Measuring the speed of sound of quintessence. Phys. Rev. Lett. 2002, 88, 121301. [Google Scholar] [CrossRef] [PubMed]
- Chan Hwang, J.; Noh, H. Quintessential perturbations during scaling regime. Phys. Rev. D 2001, 64, 103509. [Google Scholar] [CrossRef]
- Sen, A. Rolling tachyon. J. High Energy Phys. 2002, 04, 048. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Choudhury, T.R. Can the clustered dark matter and the smooth dark energy arise from the same scalar field? Phys. Rev. D 2002, 66, 081301. [Google Scholar] [CrossRef]
- Abramo, L.R.W.; Finelli, F. Cosmological dynamics of the tachyon with an inverse power- law potential. Phys. Lett. B 2003, 575, 165–171. [Google Scholar] [CrossRef]
- Abramo, L.R.; Finelli, F.; Pereira, T.S. Constraining Born-Infeld models of dark energy with CMB anisotropies. Phys. Rev. D 2004, 70, 063517. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Sandvik, H.; Tegmark, M.; Zaldarriaga, M.; Waga, I. The end of unified dark matter? Phys. Rev. D 2004, 69, 123524. [Google Scholar] [CrossRef]
- Makler, M.; Quinet de Oliveira, S.; Waga, I. Constraints on the generalized Chaplygin gas from supernovae observations. Phys. Lett. B 2003, 555, 1. [Google Scholar] [CrossRef]
- Bento, M.d.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas and CMBR constraints. Phys. Rev. D 2003, 67, 063003. [Google Scholar] [CrossRef]
- Amendola, L.; Finelli, F.; Burigana, C.; Carturan, D. WMAP and the generalized Chaplygin gas. J. Cosmol. Astropart. Phys. 2003, 2003, 005. [Google Scholar] [CrossRef]
- Reis, R.R.R.; Makler, M.; Waga, I. Skewness as a test for quartessence. Phys. Rev. D 2004, 69, 101301. [Google Scholar] [CrossRef]
- Sahni, V.; Wang, L.M. A New cosmological model of quintessence and dark matter. Phys. Rev. D 2000, 62, 103517. [Google Scholar] [CrossRef]
- Bilic, N.; Tupper, G.B.; Viollier, R.D. Unification of dark matter and dark energy: The inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
- Bertacca, D.; Bartolo, N.; Matarrese, S. Unified Dark Matter Scalar Field Models. Adv. Astron. 2010, 2010, 1–29. [Google Scholar] [CrossRef]
- Kunz, M.; Nesseris, S.; Sawicki, I. Using dark energy to suppress power at small scales. Phys. Rev. D 2015, 92, 063006. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely kinetic k-essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Unnikrishnan, S. Can cosmological observations uniquely determine the nature of dark energy? Phys. Rev. D 2008, 78, 063007. [Google Scholar] [CrossRef]
- Lim, E.A.; Sawicki, I.; Vikman, A. Dust of Dark Energy. J. Cosmol. Astropart. Phys. 2010, 2010, 012. [Google Scholar] [CrossRef]
- Gunn, J.E.; Gott, J.R.I. On the infall of matter into cluster of galaxies and some effects on their evolution. Astrophys. J. 1972, 176, 1–19. [Google Scholar] [CrossRef]
- Padmanabhan, T. Structure Formation in the Universe; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Sahni, V.; Coles, P. Approximation methods for nonlinear gravitational clustering. Phys. Rep. 1995, 262, 1–135. [Google Scholar] [CrossRef]
- Engineer, S.; Kanekar, N.; Padmanabhan, T. Nonlinear density evolution from an improved spherical collapse model. Mon. Not. R. Astron. Soc. 2000, 314, 279. [Google Scholar] [CrossRef]
- Shaw, D.J.; Mota, D.F. An Improved Semi-Analytical Spherical Collapse Model for Non-linear Density Evolution. Astrophys. J. Suppl. 2008, 174, 277. [Google Scholar] [CrossRef][Green Version]
- Despali, G.; Giocoli, C.; Angulo, R.E.; Tormen, G.; Sheth, R.K.; Baso, G.; Moscardini, L. The universality of the virial halo mass function and models for non-universality of other halo definitions. Mon. Not. R. Astron. Soc. 2016, 456, 2486–2504. [Google Scholar] [CrossRef]
- Lee, S.; Ng, K.W. Spherical collapse model with non-clustering dark energy. J. Cosmol. Astropart. Phys. 2010, 2010, 028. [Google Scholar] [CrossRef]
- Lahav, O.; Lilje, P.B.; Primack, J.R.; Rees, M.J. Dynamical effects of the cosmological constant. Mon. Not. R. Astron. Soc. 1991, 251, 128–136. [Google Scholar] [CrossRef]
- Lacey, C.; Cole, S. Merger rates in hierarchical models of galaxy formation. Mon. Not. R. Astron. Soc. 1993, 262, 627–649. [Google Scholar] [CrossRef]
- Kitayama, T.; Suto, Y. Semianalytical predictions for statistical properties of X-ray clusters of galaxies in cold dark matter universes. Astrophys. J. 1996, 469, 480. [Google Scholar] [CrossRef]
- Wang, L.M.; Steinhardt, P.J. Cluster Abundance Constraints on Quintessence Models. Astrophys. J. 1998, 508, 483–490. [Google Scholar] [CrossRef]
- Weinberg, N.N.; Kamionkowski, M. Constraining dark energy from the abundance of weak gravitational lenses. Mon. Not. R. Astron. Soc. 2003, 341, 251. [Google Scholar] [CrossRef]
- Mainini, R.; Maccio, A.V.; Bonometto, S.A. Non-linear predictions from linear theories on models with dark energy. New Astron. 2003, 8, 173–178. [Google Scholar] [CrossRef]
- Nunes, N.J.; Mota, D.F. Structure Formation in Inhomogeneous Dark Energy Models. Mon. Not. R. Astron. Soc. 2006, 368, 751–758. [Google Scholar] [CrossRef]
- Mota, D.F.; Shaw, D.J.; Silk, J. On the Magnitude of Dark Energy Voids and Overdensities. Astrophys. J. 2007, 675, 29. [Google Scholar] [CrossRef]
- Wang, Q.; Fan, Z. Dynamical evolutin of quintessence dark energy in collapsing dark matter halos. Phys. Rev. D 2009, 79, 123012. [Google Scholar] [CrossRef]
- Manera, M.; Mota, D.F. Cluster number counts dependence on dark energy inhomogeneities and coupling to dark matter. Mon. Not. R. Astron. Soc. 2006, 371, 1373. [Google Scholar] [CrossRef]
- Wintergerst, N.; Pettorino, V. Clarifying spherical collapse in coupled dark energy cosmologies. Phys. Rev. D 2010, 82, 103516. [Google Scholar] [CrossRef]
- Martino, M.C.; Stabenau, H.F.; Sheth, R.K. Spherical Collapse and Modified Gravity. Phys. Rev. D 2009, 79, 084013. [Google Scholar] [CrossRef]
- Schaefer, B.M.; Koyama, K. Spherical collapse in modified gravity with the Birkhoff-theorem. Mon. Not. R. Astron. Soc. 2008, 385, 411–422. [Google Scholar] [CrossRef]
- Schmidt, F.; Hu, W.; Lima, M. Spherical Collapse and the Halo Model in Braneworld Gravity. Phys. Rev. D 2010, 81, 063005. [Google Scholar] [CrossRef]
- Brax, P.; Rosenfeld, R.; Steer, D.A. Spherical Collapse in Chameleon Models. J. Cosmol. Astropart. Phys. 2010, 2010, 033. [Google Scholar] [CrossRef]
- Borisov, A.; Jain, B.; Zhang, P. Spherical Collapse in f(R) Gravity. Phys. Rev. D 2012, 85, 063518. [Google Scholar] [CrossRef]
- Barreira, A.; Li, B.; Baugh, C.M.; Pascoli, S. Spherical collapse in Galileon gravity: Fifth force solutions, halo mass function and halo bias. J. Cosmol. Astropart. Phys. 2013, 2013, 056. [Google Scholar] [CrossRef]
- Kopp, M.; Appleby, S.A.; Achitouv, I.; Weller, J. Spherical collapse and halo mass function in f(R) theories. Phys. Rev. D 2013, 88, 084015. [Google Scholar] [CrossRef]
- Lopes, R.C.C.; Voivodic, R.; Abramo, L.R.; Sodré, L., Jr. Turnaround radius in f(R) model. J. Cosmol. Astropart. Phys. 2018, 2018, 010. [Google Scholar] [CrossRef]
- Lopes, R.C.C.; Voivodic, R.; Abramo, L.R.; Sodré, L. Relation between the Turnaround radius and virial mass in f(R) model. J. Cosmol. Astropart. Phys. 2019, 2019, 026. [Google Scholar] [CrossRef]
- Frusciante, N.; Pace, F. Growth of non-linear structures and spherical collapse in the Galileon Ghost Condensate model. Phys. Dark Univ. 2020, 30, 100686. [Google Scholar] [CrossRef]
- Basilakos, S.; Plionis, M.; Sola, J. The spherical collapse model in time varying vacuum cosmologies. Phys. Rev. D 2010, 82, 083512. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Spherical collapse model with shear and angular momentum in dark energy cosmologies. Mon. Not. R. Astron. Soc. 2013, 430, 628–637. [Google Scholar] [CrossRef]
- Pace, F.; Batista, R.C.; Del Popolo, A. Effects of shear and rotation on the spherical collapse model for clustering dark energy. Mon. Not. R. Astron. Soc. 2014, 445, 648. [Google Scholar] [CrossRef]
- Mehrabi, A.; Pace, F.; Malekjani, M.; Del Popolo, A. Constraints on shear and rotation with massive galaxy clusters. Mon. Not. R. Astron. Soc. 2017, 465, 2687–2697. [Google Scholar] [CrossRef][Green Version]
- Velten, H.; Caramês, T.R.P.; Fabris, J.C.; Casarini, L.; Batista, R.C. Structure formation in a Λ viscous CDM universe. Phys. Rev. D 2014, 90, 123526. [Google Scholar] [CrossRef]
- McCrea, W.H. Relativity Theory and the Creation of Matter. R. Soc. Lond. Proc. Ser. A 1951, 206, 562–575. [Google Scholar]
- Harrison, E.R. Cosmology without general relativity. Ann. Phys. 1965, 35, 437–446. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a cosmological model and angular variations of the microwave background. Astrophys. J. 1967, 147, 73–90. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Zanchin, V.; Brandenberger, R.H. On the Newtonian cosmology equations with pressure. Mon. Not. R. Astron. Soc. 1997, 291, L1–L4. [Google Scholar] [CrossRef]
- Reis, R.R.R. Domain of validity of the evolution of perturbations in Newtonian cosmology with pressure. Phys. Rev. D 2003, 67, 087301. [Google Scholar] [CrossRef]
- Chan Hwang, J.; Noh, H. Newtonian versus relativistic nonlinear cosmology. Gen. Rel. Grav. 2006, 38, 703–710. [Google Scholar]
- Fabris, J.C.; Goncalves, S.V.B.; Velten, H.E.S.; Zimdahl, W. Matter Power Spectrum for the Generalized Chaplygin Gas Model: The Newtonian Approach. Phys. Rev. D 2008, 78, 103523. [Google Scholar] [CrossRef]
- Velten, H.; Schwarz, D.; Fabris, J.; Zimdahl, W. Viscous dark matter growth in (neo-)Newtonian cosmology. Phys. Rev. D 2013, 88, 103522. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H.; Fabris, J.; Piattella, O.F.; Zimdahl, W. Newtonian hydrodynamic equations with relativistic pressure and velocity. J. Cosmol. Astropart. Phys. 2016, 2016, 046. [Google Scholar] [CrossRef][Green Version]
- Herrera, D.; Waga, I.; Jorás, S.E. Calculation of the critical overdensity in the spherical-collapse approximation. Phys. Rev. D 2017, 95, 064029. [Google Scholar] [CrossRef]
- Pace, F.; Meyer, S.; Bartelmann, M. On the implementation of the spherical collapse model for dark energy models. J. Cosmol. Astropart. Phys. 2017, 2017, 040. [Google Scholar] [CrossRef]
- Batista, R.C.; Marra, V. Clustering dark energy and halo abundances. J. Cosmol. Astropart. Phys. 2017, 2017, 048. [Google Scholar] [CrossRef]
- Basse, T.; Bjaelde, O.E.; Hannestad, S.; Wong, Y.Y.Y. Confronting the sound speed of dark energy with future cluster surveys. arXiv 2012, arXiv:1205.0548. [Google Scholar]
- Ichiki, K.; Takada, M. The impact of massive neutrinos on the abundance of massive clusters. Phys. Rev. D 2012, 85, 063521. [Google Scholar] [CrossRef]
- LoVerde, M. Spherical collapse in νΛCDM. Phys. Rev. D 2014, 90, 083518. [Google Scholar] [CrossRef]
- Abramo, L.R.W.; Batista, R.; Liberato, L.; Rosenfeld, R. Dynamical Mutation of Dark Energy. Phys. Rev. D 2008, 77, 067301. [Google Scholar] [CrossRef]
- Saridakis, E.N. Do we need soft cosmology? Phys. Lett. B 2021, 822, 136649. [Google Scholar] [CrossRef]
- Heneka, C.; Rapetti, D.; Cataneo, M.; Mantz, A.B.; Allen, S.W.; von der Linden, A. Cold dark energy constraints from the abundance of galaxy clusters. Mon. Not. R. Astron. Soc. 2018, 473, 3882–3894. [Google Scholar] [CrossRef]
- Sefusatti, E.; Vernizzi, F. Cosmological structure formation with clustering quintessence. J. Cosmol. Astropart. Phys. 2011, 2011, 047. [Google Scholar] [CrossRef]
- Maor, I.; Lahav, O. On Virialization with Dark Energy. J. Cosmol. Astropart. Phys. 2005, 2005, 003. [Google Scholar] [CrossRef]
- Meyer, S.; Pace, F.; Bartelmann, M. Relativistic virialization in the Spherical Collapse model for Einstein-de Sitter and ΛCDM cosmologies. Phys. Rev. D 2012, 86, 103002. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of galaxies and clusters of galaxies by selfsimilar gravitational condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Sheth, R.K.; Tormen, G. Large-scale bias and the peak background split. Mon. Not. R. Astron. Soc. 1999, 308, 119–126. [Google Scholar] [CrossRef]
- Warren, M.S.; Abazajian, K.; Holz, D.E.; Teodoro, L. Precision determination of the mass function of dark matter halos. Astrophys. J. 2006, 646, 881–885. [Google Scholar] [CrossRef]
- Tinker, J.L.; Kravtsov, A.V.; Klypin, A.; Abazajian, K.; Warren, M.S.; Yepes, G.; Gottlober, S.; Holz, D.E. Toward a halo mass function for precision cosmology: The Limits of universality. Astrophys. J. 2008, 688, 709–728. [Google Scholar] [CrossRef]
- Cooray, A.; Sheth, R.K. Halo Models of Large Scale Structure. Phys. Rep. 2002, 372, 1–129. [Google Scholar] [CrossRef]
- Peacock, J.A.; Heavens, A.F. Alternatives to the Press-Schechter cosmological mass function. Mon. Not. R. Astron. Soc. 1990, 243, 133–143. [Google Scholar] [CrossRef]
- Bond, J.R.; Cole, S.; Efstathiou, G.; Kaiser, N. Excursion set mass functions for hierarchical Gaussian fluctuations. Astrophys. J. 1991, 379, 440. [Google Scholar] [CrossRef]
- Efstathiou, G.; Fall, S.M.; Hogan, C. Self-similar gravitational clustering. Mon. Not. R. Astron. Soc. 1979, 189, 203–220. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Lucchin, F.; Matarrese, S. The Mass function from local density maxima. Groups and clusters of galaxies. Astrophys. J. 1989, 345, 3–11. [Google Scholar] [CrossRef]
- Gelb, J.M.; Bertschinger, E. Cold dark matter. 1: The Formation of dark halos. Astrophys. J. 1994, 436, 467. [Google Scholar] [CrossRef]
- Narayan, R.; White, S.D.M. Gravitational lensing in a cold dark matter universe. Mon. Not. R. Astron. Soc. 1988, 231, 97–103. [Google Scholar] [CrossRef]
- Lilje, P.B. Abundance of Rich Clusters of Galaxies: A Test for Cosmological Parameters. Astrophys. J. Lett. 1992, 386, L33. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Eisenstein, D.J.; Hu, W. Baryonic features in the matter transfer function. Astrophys. J. 1998, 496, 605. [Google Scholar] [CrossRef]
- Percival, W.J. Cosmological structure formation in a homogeneous dark energy background. Astron. Astrophys. 2005, 443, 819. [Google Scholar] [CrossRef]
- Le Delliou, M. Dynamical quintessence fields Press-Schechter mass function: Detectability and effect on dark haloes. J. Cosmol. Astropart. Phys. 2006, 2006, 021. [Google Scholar] [CrossRef]
- Horellou, C.; Berge, J. Dark energy and the evolution of spherical overdensities. Mon. Not. R. Astron. Soc. 2005, 360, 1393–1400. [Google Scholar] [CrossRef]
- Liberato, L.; Rosenfeld, R. Dark energy parameterizations and their effect on dark halos. J. Cosmol. Astropart. Phys. 2006, 2006, 009. [Google Scholar] [CrossRef]
- Bartelmann, M.; Doran, M.; Wetterich, C. Non-linear Structure Formation in Cosmologies with Early Dark Energy. Astron. Astrophys. 2006, 454, 27–36. [Google Scholar] [CrossRef]
- Pace, F.; Waizmann, J.C.; Bartelmann, M. Spherical collapse model in dark energy cosmologies. Mon. Not. R. Astron. Soc. 2010, 406, 1865. [Google Scholar] [CrossRef]
- Pace, F.; Fedeli, C.; Moscardini, L.; Bartelmann, M. Structure formation in cosmologies with oscillating dark energy. Mon. Not. R. Astron. Soc. 2012, 422, 1186–1202. [Google Scholar] [CrossRef]
- Linder, E.V.; Jenkins, A. Cosmic Structure and Dark Energy. Mon. Not. R. Astron. Soc. 2003, 346, 573. [Google Scholar] [CrossRef]
- Grossi, M.; Springel, V. The impact of Early Dark Energy on non-linear structure formation. Mon. Not. R. Astron. Soc. 2009, 394, 1559–1574. [Google Scholar] [CrossRef]
- Basse, T.; Bjaelde, O.E.; Hamann, J.; Hannestad, S.; Wong, Y.Y.Y. Dark energy properties from large future galaxy surveys. J. Cosmol. Astropart. Phys. 2014, 2014, 021. [Google Scholar] [CrossRef][Green Version]
- Abramo, L.R.; Batista, R.C.; Rosenfeld, R. The signature of dark energy perturbations in galaxy cluster surveys. J. Cosmol. Astropart. Phys. 2009, 2009, 040. [Google Scholar] [CrossRef]
- Castro, T.; Marra, V.; Quartin, M. Constraining the halo mass function with observations. Mon. Not. R. Astron. Soc. 2016, 463, 1666–1677. [Google Scholar] [CrossRef]
- LoVerde, M.; Miller, A.; Shandera, S.; Verde, L. Effects of Scale-Dependent Non-Gaussianity on Cosmological Structures. J. Cosmol. Astropart. Phys. 2008, 2008, 014. [Google Scholar] [CrossRef]
- Velliscig, M.; van Daalen, M.P.; Schaye, J.; McCarthy, I.G.; Cacciato, M.; Le Brun, A.M.C.; Vecchia, C.D. The impact of galaxy formation on the total mass, mass profile and abundance of haloes. Mon. Not. R. Astron. Soc. 2014, 442, 2641–2658. [Google Scholar] [CrossRef]
- Weller, J.; Lewis, A.M. Large scale cosmic microwave background anisotropies and dark energy. Mon. Not. R. Astron. Soc. 2003, 346, 987–993. [Google Scholar] [CrossRef]
- Hannestad, S. Constraints on the sound speed of dark energy. Phys. Rev. D 2005, 71, 103519. [Google Scholar] [CrossRef]
- De Putter, R.; Huterer, D.; Linder, E.V. Measuring the Speed of Dark: Detecting Dark Energy Perturbations. Phys. Rev. D 2010, 81, 103513. [Google Scholar] [CrossRef]
- Takada, M. Can A Galaxy Redshift Survey Measure Dark Energy Clustering? Phys. Rev. D 2006, 74, 043505. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pal, S. Constraining Dark Energy Perturbations: The Role of Early Dark Energy. arXiv 2019, arXiv:1907.10946. [Google Scholar]
- Hu, W.; Scranton, R. Measuring dark energy clustering with CMB-galaxy correlations. Phys. Rev. D 2004, 70, 123002. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Giannantonio, T.; Melchiorri, A. Constraining dark energy with cross-correlated CMB and large scale structure data. Phys. Rev. D 2005, 71, 123521. [Google Scholar] [CrossRef]
- Pietrobon, D.; Balbi, A.; Marinucci, D. Integrated Sachs-Wolfe effect from the cross-correlation of WMAP 3 year and NVSS: New results and constraints on dark energy. Phys. Rev. D 2006, 74, 043524. [Google Scholar] [CrossRef]
- Li, H.; Xia, J.Q. Constraints on Dark Energy Parameters from Correlations of CMB with LSS. J. Cosmol. Astropart. Phys. 2010, 2010, 026. [Google Scholar] [CrossRef]
- D’Amico, G.; Sefusatti, E. The nonlinear power spectrum in clustering quintessence cosmologies. J. Cosmol. Astropart. Phys. 2011, 2011, 013. [Google Scholar] [CrossRef]
- Anselmi, S.; Ballesteros, G.; Pietroni, M. Non-linear dark energy clustering. J. Cosmol. Astropart. Phys. 2011, 2011, 014. [Google Scholar] [CrossRef][Green Version]
- Anselmi, S.; López Nacir, D.; Sefusatti, E. Nonlinear effects of dark energy clustering beyond the acoustic scales. J. Cosmol. Astropart. Phys. 2014, 2014, 013. [Google Scholar] [CrossRef][Green Version]
- Sapone, D.; Kunz, M.; Amendola, L. Fingerprinting Dark Energy II: Weak lensing and galaxy clustering tests. Phys. Rev. D 2010, 82, 103535. [Google Scholar] [CrossRef]
- Ayaita, Y.; Schaefer, B.M.; Weber, M. Investigating clustering dark energy with 3d weak cosmic shear. Mon. Not. R. Astron. Soc. 2012, 422, 3056–3066. [Google Scholar] [CrossRef][Green Version]
- Majerotto, E.; Sapone, D.; Schäfer, B.M. Combined constraints on deviations of dark energy from an ideal fluid from Euclid and Planck. Mon. Not. R. Astron. Soc. 2016, 456, 109–118. [Google Scholar] [CrossRef]
- Appleby, S.A.; Linder, E.V.; Weller, J. Cluster Probes of Dark Energy Clustering. Phys. Rev. D 2013, 88, 043526. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. Astron. Astrophys. 2015, 594, A24. [Google Scholar]
- Mantz, A.; Allen, S.W.; Rapetti, D.; Ebeling, H. The observed growth of massive galaxy clusters—I. Statistical methods and cosmological constraints. Mon. Not. R. Astron. Soc. 2010, 406, 1759–1772. [Google Scholar] [CrossRef]
- Kravtsov, A.; Borgani, S. Formation of Galaxy Clusters. Ann. Rev. Astron. Astrophys. 2012, 50, 353–409. [Google Scholar] [CrossRef]
- Mota, D.F. Probing Dark Energy at Galactic and Cluster Scales. J. Cosmol. Astropart. Phys. 2008, 2008, 006. [Google Scholar] [CrossRef]
- Basilakos, S.; Bueno Sanchez, J.C.; Perivolaropoulos, L. The spherical collapse model and cluster formation beyond the Λ cosmology: Indications for a clustered dark energy? Phys. Rev. D 2009, 80, 043530. [Google Scholar] [CrossRef]
- Batista, R.C. Impact of dark energy perturbations on the growth index. Phys. Rev. D 2014, 89, 123508. [Google Scholar] [CrossRef]
- Mehrabi, A.; Basilakos, S.; Pace, F. How clustering dark energy affects matter perturbations. Mon. Not. R. Astron. Soc. 2015, 452, 2930–2939. [Google Scholar] [CrossRef]
- Mehrabi, A.; Basilakos, S.; Malekjani, M.; Davari, Z. Growth of matter perturbations in clustered holographic dark energy cosmologies. Phys. Rev. D 2015, 92, 123513. [Google Scholar] [CrossRef]
- Mehrabi, A.; Malekjani, M.; Pace, F. Can observational growth rate data favor the clustering dark energy models? Astrophys. Space Sci. 2015, 356, 129–135. [Google Scholar] [CrossRef]
- Sawicki, I.; Saltas, I.D.; Amendola, L.; Kunz, M. Consistent perturbations in an imperfect fluid. J. Cosmol. Astropart. Phys. 2013, 2013, 004. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batista, R.C. A Short Review on Clustering Dark Energy. Universe 2022, 8, 22. https://doi.org/10.3390/universe8010022
Batista RC. A Short Review on Clustering Dark Energy. Universe. 2022; 8(1):22. https://doi.org/10.3390/universe8010022
Chicago/Turabian StyleBatista, Ronaldo C. 2022. "A Short Review on Clustering Dark Energy" Universe 8, no. 1: 22. https://doi.org/10.3390/universe8010022
APA StyleBatista, R. C. (2022). A Short Review on Clustering Dark Energy. Universe, 8(1), 22. https://doi.org/10.3390/universe8010022





