Continuous Gravitational Wave Emissions from Neutron Stars with Pinned Superfluids in the Core
Abstract
1. Introduction
2. Setting the Stage: Hydrodynamic Perturbations
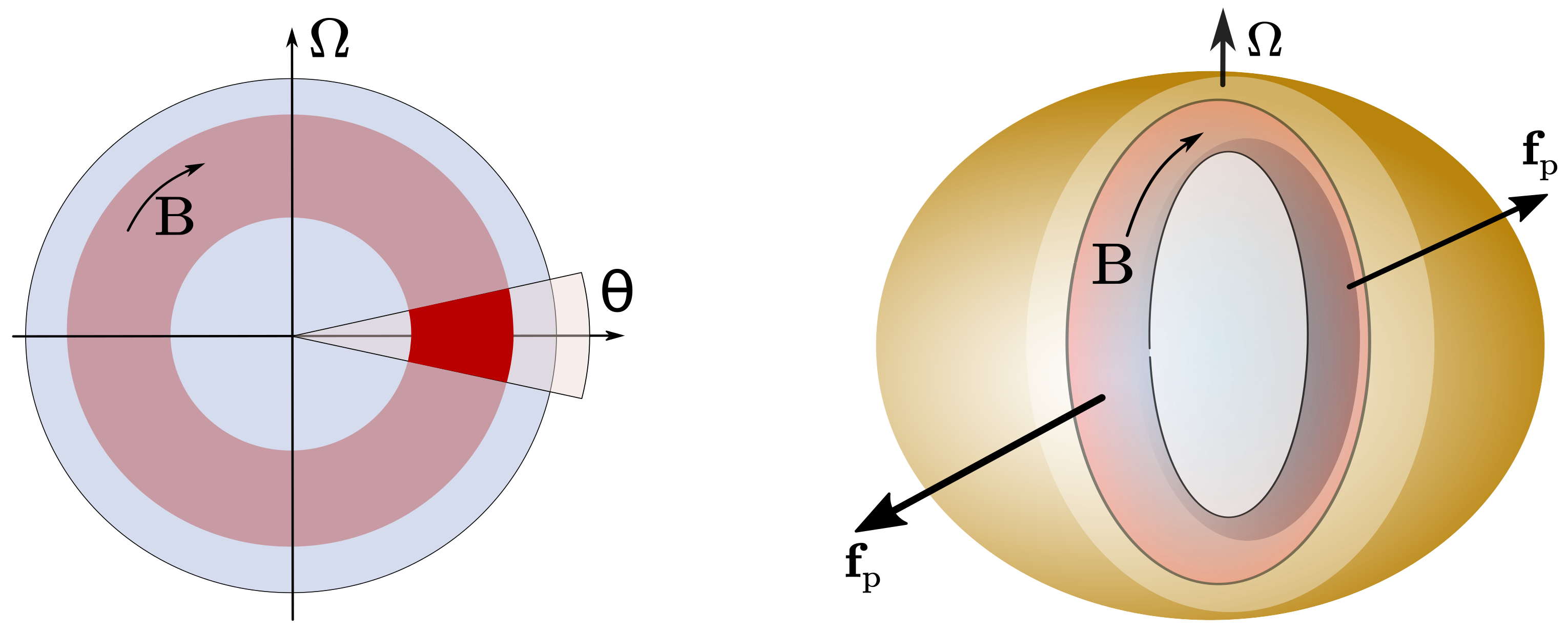
3. Magnetic Field and Pinning
4. Perturbation Equations for the Pinned Configuration
5. Continuous Wave Emission
6. Results
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Apart from the uncertainties regarding the extent of the S-wave gap for superfluidity, further reduction in the pinning strength may be due to the fact that the mutual orientation between a vortex and the fluxtubes is expected to fluctuate locally, thereby, giving rise to a decrease of the effective pinning force, similarly to what happens for vortices that are randomly oriented with respect to the principal axis of the Coulomb lattice in the inner crust [21]. |
References
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Güven, H.; Bozkurt, K.; Khan, E.; Margueron, J. Multimessenger and multiphysics Bayesian inference for the GW170817 binary neutron star merger. Phys. Rev. C 2020, 102, 015805. [Google Scholar] [CrossRef]
- Mondal, C.; Gulminelli, F. Can we decipher the composition of the core of a neutron star? Phys. Rev. D 2022, 105, 083016. [Google Scholar] [CrossRef]
- Lasky, P.D. Gravitational wave astronomy. In Multimessenger Astronomy in Practice: Celestial Sources in Action; Filipović, M.D., Tothill, N.F.H., Eds.; IOP Publishing: Bristol, UK, 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Piccinni, O.J. Status and Perspectives of Continuous Gravitational Wave Searches. Galaxies 2022, 10, 72. [Google Scholar] [CrossRef]
- Riles, K. Searches for Continuous-Wave Gravitational Radiation. arXiv 2022, arXiv:2206.06447. [Google Scholar]
- Lasky, P.D. Gravitational Waves from Neutron Stars: A Review. Publ. Astron. Soc. Austr. 2015, 32, e034. [Google Scholar] [CrossRef]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey. In Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Astrophysics and Space Science Library: Springer Cham, Switzerland, 2018; Volume 457, p. 673. [Google Scholar] [CrossRef]
- Haskell, B.; Schwenzer, K. Isolated Neutron Stars. In Handbook of Gravitational Wave Astronomy; Bambi, C., Ed.; Springer Nature: Cham, Switzerland, 2022; p. 12. [Google Scholar] [CrossRef]
- Bildsten, L. Gravitational Radiation and Rotation of Accreting Neutron Stars. Astrophys. J. Lett. 1998, 501, L89–L93. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: Emission by the magnetic-field-induced distortion. Astron. Astrophys. 1996, 312, 675–690. [Google Scholar]
- Singh, N.; Haskell, B.; Mukherjee, D.; Bulik, T. Asymmetric accretion and thermal `mountains’ in magnetized neutron star crusts. Mon. Not. R. Astron. Soc. 2020, 493, 3866–3878. [Google Scholar] [CrossRef]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2000, 319, 902–932. [Google Scholar] [CrossRef]
- Haskell, B.; Jones, D.I.; Andersson, N. Mountains on neutron stars: Accreted versus non-accreted crusts. Mon. Not. R. Astron. Soc. 2006, 373, 1423–1439. [Google Scholar] [CrossRef]
- Woan, G.; Pitkin, M.D.; Haskell, B.; Jones, D.I.; Lasky, P.D. Evidence for a Minimum Ellipticity in Millisecond Pulsars. Astrophys. J. Lett. 2018, 863, L40. [Google Scholar] [CrossRef]
- Mendell, G. Superfluid Hydrodynamics in Rotating Neutron Stars. II. Dissipative Effects. Astrophys. J. 1991, 380, 530. [Google Scholar] [CrossRef]
- Andersson, N.; Sidery, T.; Comer, G.L. Mutual friction in superfluid neutron stars. Mon. Not. R. Astron. Soc. 2006, 368, 162–170. [Google Scholar] [CrossRef]
- Antonelli, M.; Haskell, B. Superfluid vortex-mediated mutual friction in non-homogeneous neutron star interiors. Mon. Not. R. Astron. Soc. 2020, 499, 3690–3705. [Google Scholar] [CrossRef]
- Seveso, S.; Pizzochero, P.M.; Grill, F.; Haskell, B. Mesoscopic pinning forces in neutron star crusts. Mon. Not. R. Astron. Soc. 2016, 455, 3952–3967. [Google Scholar] [CrossRef]
- Alpar, M.A. Flux-Vortex Pinning and Neutron Star Evolution. J. Astrophys. Astron. 2017, 38, 44. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Ducci, L.; Pizzochero, P.M.; Doroshenko, V.; Santangelo, A.; Mereghetti, S.; Ferrigno, C. Properties and observability of glitches and anti-glitches in accreting pulsars. Astron. Astrophys. 2015, 578, A52. [Google Scholar] [CrossRef]
- Ray, P.S.; Guillot, S.; Ho, W.C.G.; Kerr, M.; Enoto, T.; Gendreau, K.C.; Arzoumanian, Z.; Altamirano, D.; Bogdanov, S.; Campion, R.; et al. Anti-glitches in the Ultraluminous Accreting Pulsar NGC 300 ULX-1 Observed with NICER. Astrophys. J. 2019, 879, 130. [Google Scholar] [CrossRef]
- Ruderman, M. Crust-breaking by neutron superfluids and the Vela pulsar glitches. Astrophys. J. 1976, 203, 213–222. [Google Scholar] [CrossRef]
- Jones, D.I. Gravitational waves from rotating strained neutron stars. Class. Quantum Gravity 2002, 19, 1255–1265. [Google Scholar] [CrossRef][Green Version]
- Keitel, D.; Woan, G.; Pitkin, M.; Schumacher, C.; Pearlstone, B.; Riles, K.; Lyne, A.G.; Palfreyman, J.; Stappers, B.; Weltevrede, P. First search for long-duration transient gravitational waves after glitches in the Vela and Crab pulsars. Phys. Rev. D 2019, 100, 064058. [Google Scholar] [CrossRef]
- Abadie, J. et al. [The LIGO Scientific Collaboration] Search for gravitational waves associated with the August 2006 timing glitch of the Vela pulsar. Phys. Rev. D 2011, 83, 042001. [Google Scholar] [CrossRef]
- Abbott, R. et al. [The LIGO Scientific Collaboration] Narrowband Searches for Continuous and Long-duration Transient Gravitational Waves from Known Pulsars in the LIGO-Virgo Third Observing Run. Astrophys. J. 2022, 932, 133. [Google Scholar] [CrossRef]
- Bennett, M.F.; van Eysden, C.A.; Melatos, A. Continuous-wave gravitational radiation from pulsar glitch recovery. Mon. Not. R. Astron. Soc. 2010, 409, 1705–1718. [Google Scholar] [CrossRef]
- Warszawski, L.; Melatos, A. Gravitational-wave bursts and stochastic background from superfluid vortex avalanches during pulsar glitches. Mon. Not. R. Astron. Soc. 2012, 423, 2058–2074. [Google Scholar] [CrossRef][Green Version]
- Melatos, A.; Douglass, J.A.; Simula, T.P. Persistent Gravitational Radiation from Glitching Pulsars. Astrophys. J. 2015, 807, 132. [Google Scholar] [CrossRef]
- Chamel, N. Neutron conduction in the inner crust of a neutron star in the framework of the band theory of solids. Phys. Rev. C 2012, 85, 035801. [Google Scholar] [CrossRef]
- Chamel, N. Entrainment in Superfluid Neutron-Star Crusts: Hydrodynamic Description and Microscopic Origin. J. Low Temp. Phys. 2017, 189, 328–360. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Ho, W.C.G.; Espinoza, C.M. Pulsar Glitches: The Crust is not Enough. Phys. Rev. Lett. 2012, 109, 241103. [Google Scholar] [CrossRef] [PubMed]
- Chamel, N. Crustal Entrainment and Pulsar Glitches. Phys. Rev. Lett. 2013, 110, 011101. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Haskell, B.; Pizzochero, P. Statistical Estimates of the Pulsar Glitch Activity. Universe 2021, 7, 8. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Pizzochero, P.M. The role of mass, equation of state, and superfluid reservoir in large pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 492, 4837–4846. [Google Scholar] [CrossRef]
- Haskell, B.; Khomenko, V.; Antonelli, M.; Antonopoulou, D. Crust or core? Insights from the slow rise of large glitches in the Crab pulsar. Mon. Not. R. Astron. Soc. 2018, 481, L146–L150. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Magistrelli, F.; Pizzochero, P.M. Bayesian estimate of the superfluid moments of inertia from the 2016 glitch in the Vela pulsar. Astron. Astrophys. 2020, 642, A223. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N. Force on a neutron quantized vortex pinned to proton fluxoids in the superfluid core of cold neutron stars. Mon. Not. R. Astron. Soc. 2020, 493, 382–389. [Google Scholar] [CrossRef]
- Gügercinoğlu, E.; Alpar, M.A. Vortex Creep Against Toroidal Flux Lines, Crustal Entrainment, and Pulsar Glitches. Astrophys. J. Lett. 2014, 788, L11. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N. Vortex pinning in the superfluid core of neutron stars and the rise of pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 493, L98–L102. [Google Scholar] [CrossRef]
- Pizzochero, P.M.; Montoli, A.; Antonelli, M. Core and crust contributions in overshooting glitches: The Vela pulsar 2016 glitch. Astron. Astrophys. 2020, 636, A101. [Google Scholar] [CrossRef]
- Ciolfi, R. Modelling the magnetic field configuration of neutron stars. Astron. Nachrichten 2014, 335, 624. [Google Scholar] [CrossRef]
- Lander, S.K. Magnetic Fields in Superconducting Neutron Stars. Phys. Rev. Lett. 2013, 110, 071101. [Google Scholar] [CrossRef] [PubMed]
- Sur, A.; Haskell, B. The impact of superconductivity and the Hall effect in models of magnetised neutron stars. Publ. Astron. Soc. Austr. 2021, 38, e043. [Google Scholar] [CrossRef]
- Sur, A.; Cook, W.; Radice, D.; Haskell, B.; Bernuzzi, S. Long-term general relativistic magnetohydrodynamics simulations of magnetic field in isolated neutron stars. Mon. Not. R. Astron. Soc. 2022, 511, 3983–3993. [Google Scholar] [CrossRef]
- Ruderman, M.; Zhu, T.; Chen, K. Neutron Star Magnetic Field Evolution, Crust Movement, and Glitches. Astrophys. J. 1998, 492, 267–280. [Google Scholar] [CrossRef]
- Ciolfi, R.; Rezzolla, L. Twisted-torus configurations with large toroidal magnetic fields in relativistic stars. Mon. Not. R. Astron. Soc. 2013, 435, L43–L47. [Google Scholar] [CrossRef]
- Jones, D.I. Gravitational wave emission from rotating superfluid neutron stars. Mon. Not. R. Astron. Soc. 2010, 402, 2503–2519. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Relativistic fluid dynamics: Physics for many different scales. Living Rev. Relativ. 2021, 24, 3. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Astrophysics and Space Science Library; Springer Nature: Cham, Switzerland, 2018; Volume 457, p. 401. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M. Thermodynamics of uncharged relativistic multifluids. Class. Quantum Gravity 2020, 37, 025014. [Google Scholar] [CrossRef]
- Graber, V.; Cumming, A.; Andersson, N. Glitch rises as a test for rapid superfluid coupling in neutron stars. ArXiv 2018, arXiv:astro-ph.HE/1804.02706. [Google Scholar] [CrossRef]
- Celora, T.; Khomenko, V.; Antonelli, M.; Haskell, B. The effect of non-linear mutual friction on pulsar glitch sizes and rise times. Mon. Not. R. Astron. Soc. 2020, 496, 5564–5574. [Google Scholar] [CrossRef]
- Charbonneau, J.; Zhitnitsky, A. Novel mechanism for type I superconductivity in neutron stars. Phys. Rev. C 2007, 76, 015801. [Google Scholar] [CrossRef]
- Link, B. Instability of superfluid flow in the neutron star core. Mon. Not. R. Astron. Soc. 2012, 421, 2682–2691. [Google Scholar] [CrossRef][Green Version]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Leinson, L.B. Vortex lattice in rotating neutron spin-triplet superfluid. Mon. Not. R. Astron. Soc. 2020, 498, 304–309. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. General relativistic models for rotating magnetized neutron stars in conformally flat space-time. Mon. Not. R. Astron. Soc. 2017, 470, 2469–2493. [Google Scholar] [CrossRef]
- Castillo, F.; Reisenegger, A.; Valdivia, J.A. Magnetic field evolution and equilibrium configurations in neutron star cores: The effect of ambipolar diffusion. Mon. Not. R. Astron. Soc. 2017, 471, 507–522. [Google Scholar] [CrossRef]
- Sur, A.; Haskell, B.; Kuhn, E. Magnetic field configurations in neutron stars from MHD simulations. Mon. Not. R. Astron. Soc. 2020, 495, 1360–1371. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in General Relativity under the Conformally Flat Condition. Mon. Not. R. Astron. Soc. 2014, 439, 3541–3563. [Google Scholar] [CrossRef]
- Khomenko, V.; Antonelli, M.; Haskell, B. Hydrodynamical instabilities in the superfluid interior of neutron stars with background flows between the components. Phys. Rev. D 2019, 100, 123002. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Haskell, B. Oscillations of dissipative superfluid neutron stars. Phys. Rev. D 2009, 79, 103009. [Google Scholar] [CrossRef]
- van Eysden, C.A.; Melatos, A. Gravitational radiation from pulsar glitches. Class. Quantum Gravity 2008, 25, 225020. [Google Scholar] [CrossRef]
- Sidery, T.; Passamonti, A.; Andersson, N. The dynamics of pulsar glitches: Contrasting phenomenology with numerical evolutions. Mon. Not. R. Astron. Soc. 2010, 405, 1061–1074. [Google Scholar] [CrossRef]
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299–339. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.G. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass-Radius Estimate of PSR J0740+6620 and Multimessenger Observations. Astrophys. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Jones, P.B. The Alignment of the Crab Pulsar Magnetic Axis. Ap&SS 1975, 33, 215–230. [Google Scholar] [CrossRef]
- Easson, I.; Pethick, C.J. Stress tensor of cosmic and laboratory type-II superconductors. Phys. Rev. D 1977, 16, 275–280. [Google Scholar] [CrossRef]
- Haskell, B.; Priymak, M.; Patruno, A.; Oppenoorth, M.; Melatos, A.; Lasky, P.D. Detecting gravitational waves from mountains on neutron stars in the advanced detector era. Mon. Not. R. Astron. Soc. 2015, 450, 2393–2403. [Google Scholar] [CrossRef]
- Giliberti, E.; Cambiotti, G.; Antonelli, M.; Pizzochero, P.M. Modelling strains and stresses in continuously stratified rotating neutron stars. Mon. Not. R. Astron. Soc. 2020, 491, 1064–1078. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haskell, B.; Antonelli, M.; Pizzochero, P. Continuous Gravitational Wave Emissions from Neutron Stars with Pinned Superfluids in the Core. Universe 2022, 8, 619. https://doi.org/10.3390/universe8120619
Haskell B, Antonelli M, Pizzochero P. Continuous Gravitational Wave Emissions from Neutron Stars with Pinned Superfluids in the Core. Universe. 2022; 8(12):619. https://doi.org/10.3390/universe8120619
Chicago/Turabian StyleHaskell, Brynmor, Marco Antonelli, and Pierre Pizzochero. 2022. "Continuous Gravitational Wave Emissions from Neutron Stars with Pinned Superfluids in the Core" Universe 8, no. 12: 619. https://doi.org/10.3390/universe8120619
APA StyleHaskell, B., Antonelli, M., & Pizzochero, P. (2022). Continuous Gravitational Wave Emissions from Neutron Stars with Pinned Superfluids in the Core. Universe, 8(12), 619. https://doi.org/10.3390/universe8120619







