Incorporating a Radiative Hydrodynamics Scheme in the Numerical-Relativity Code BAM
Abstract
:1. Introduction
2. Fundamental Equations
2.1. 3 + 1 Decomposition and Spacetime Evolution
2.2. General Relativistic Radiative Hydrodynamics
2.3. Neutrino Leakage
Underlying Hypotheses of the Neutrino Leakage Scheme
- For simplicity, we consider only electrons and positrons as representative leptons within the fluid.
- The considered neutrino flavors are electron neutrinos , electron antineutrinos , and heavy lepton neutrinos/antineutrinos , collectively grouped as a single species with statistical weight 4.
- Neutrinos obey the ultra-relativistic Fermi–Dirac distribution in local -equilibrium and have the same temperature as the matter. Hence, the relativistic chemical potentials (i.e., including rest-masses of protons, neutrons, and electrons) for electron-flavored neutrinos readwhere, for simplicity, we assume , given that heavy lepton neutrinos rarely interact with matter. This hypothesis is justified by the assumption that a possible non-equilibrium condition (induced, for instance, by a density oscillation) is rapidly driven to -equilibrium on a timescale that is much smaller than the timestep adopted to numerically evolve the matter and spacetime quantities. However, it is important to point out that reestablishing -equilibrium from a (short-lived) non-equilibrium state implies energy dissipation, which translates into damping of density oscillations by neutrinos bulk-viscosity [74,75].
- 4.
- The emission of neutrinos is isotropic in the fluid rest-frame and is given bywhere the total emissivity (energy per unit time and baryon) is the sum of emissivities for all neutrino flavorsTo see that Equation (18) corresponds to an isotropic emission, note that the projection of onto the hypersurface orthogonal to the fluid worldlines via the projector vanishes (i.e., ). Hence, neutrinos are emitted such that no net momentum flux is perceived in the fluid comoving frame.
- 5.
- The source term is given bywhere is the electron antineutrinos production rate, and is the electron neutrinos production rate. Then, the Equation above states that the creation of electron (anti-) neutrinos demand the (creation) annihilation of an (electron) positron in order to conserve the lepton family number.
- 6.
- Neutrinos are treated as a `test’ fluid. Hence, the projections of , which act as sources of spacetime curvature, are neglected.
2.4. Emissivities and Production Rates
- (i)
- Direct Urca process, comprised of positron capture by neutronsand electrons capture by protons
- (ii)
- Electron–positron pair annihilation
- (iii)
- Transversal plasmon decay
- (i)
- Neutrino-elastic scattering on a representative heavy nucleus X and atomic mass number A.
- (ii)
- Neutrino-elastic scattering on free nucleons
- (iii)
- Electron-flavor neutrino absorption on free nucleons
3. Numerical Implementation
3.1. Code Updates
- In our previous studies using the BAM code, we used mainly one-parameter piecewise polytropes EoSs together with an ideal-gas thermal contribution. Now, we have extended this infrastructure to enable the use of three-dimensional tables. In general, these tables have a finite range of validity defined as a domain withFor this purpose, EoS evaluations should only be performed within this domain (i.e., additional checks have to be incorporated into BAM).
- Previously adopted EoSs allowed us to use a simple and fast converging root-finding procedure for the conservative-to-primitive conversion. This is not the case for a three-parameter tabulated EoS, since numerical derivatives computed by trilinear interpolations are noisy. In our case, we use the methods outlined in [73,81] to ensure a robust conservative-to-primitive conversion.
- Once we employ three-parameter EoSs, we also have to solve Equation (24).
- We make use of a static and cold atmosphere to model vacuum, that is, grid points with (here, we use and ) are set toWe use in our TOV simulations to reproduce the conditions of the testbeds reported in the literature, and in our BNS runs so that the pressure of the atmosphere is lowest.
3.2. Free Emission Rates and Optical Depth Estimates
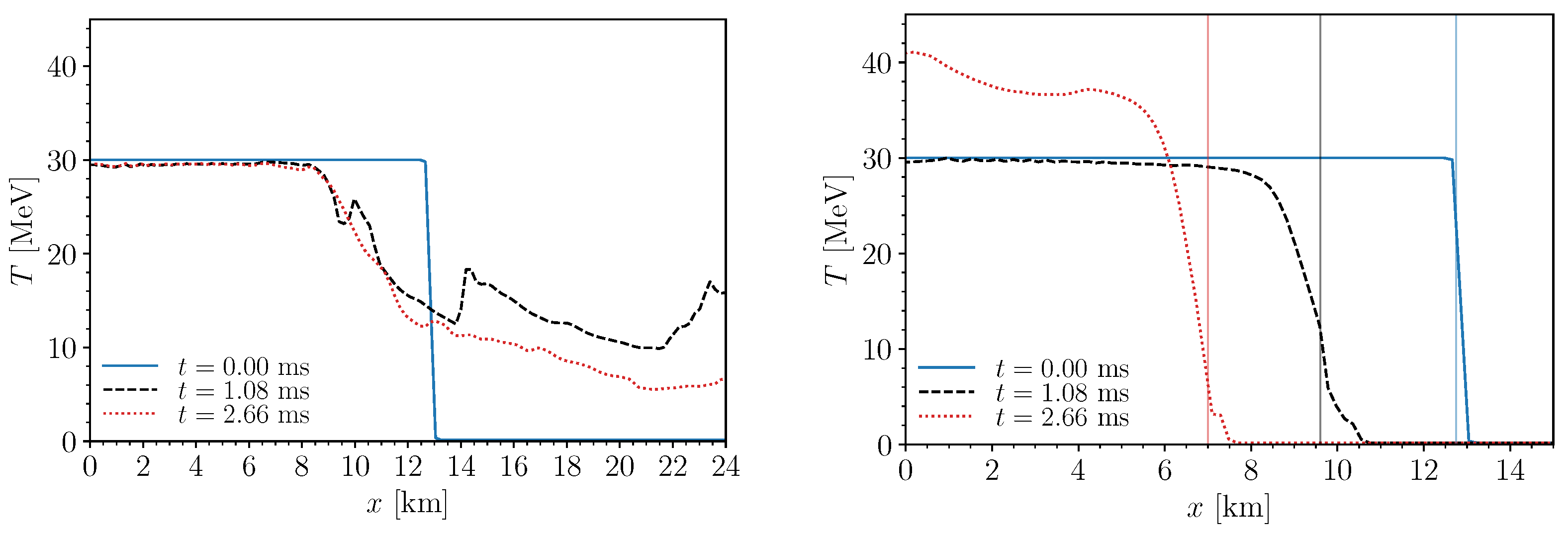
4. Neutrino-Induced Collapse of Single TOV Stars
5. BNS Simulations
5.1. Initial Data
5.2. Short Inspiral Simulations
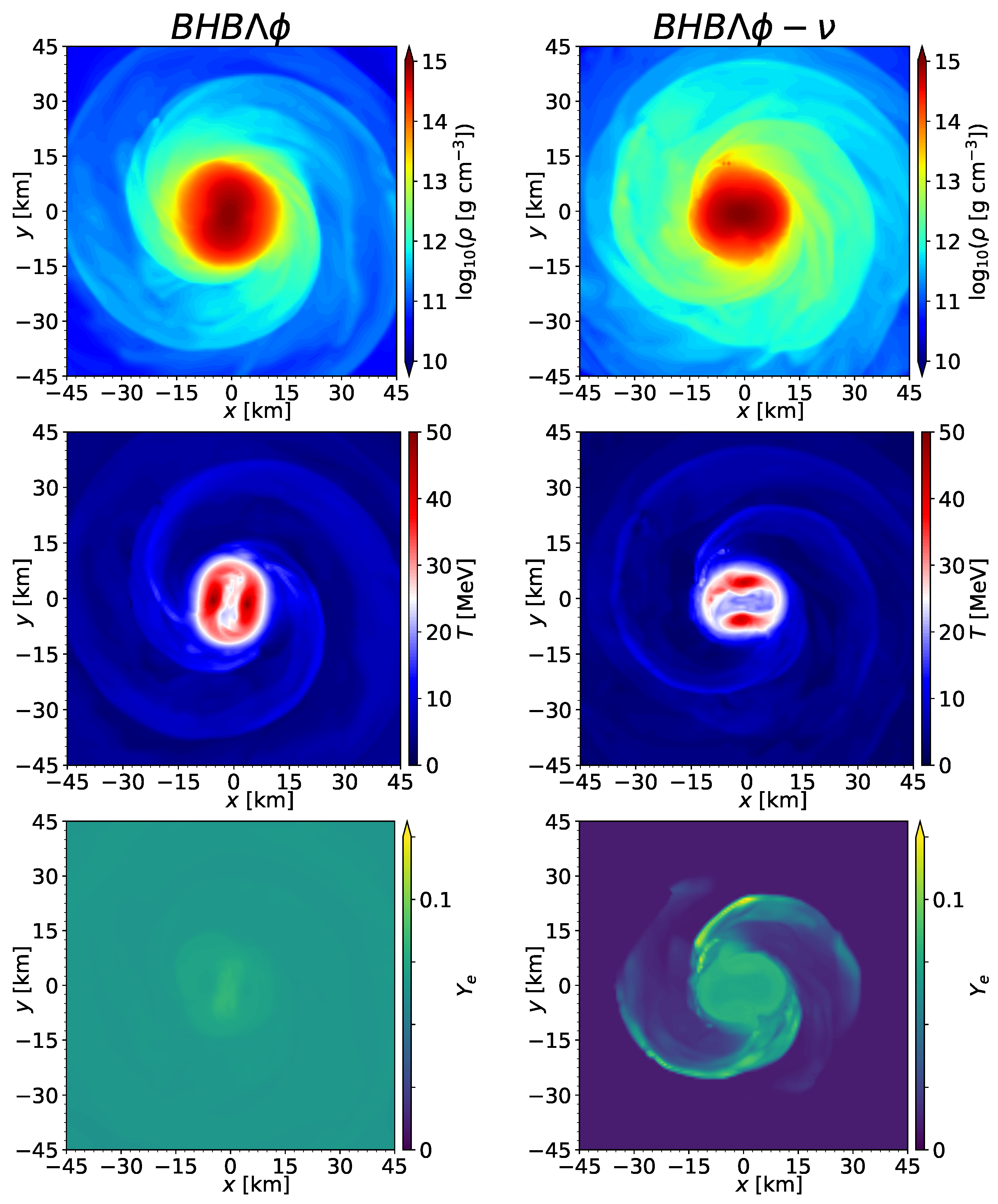
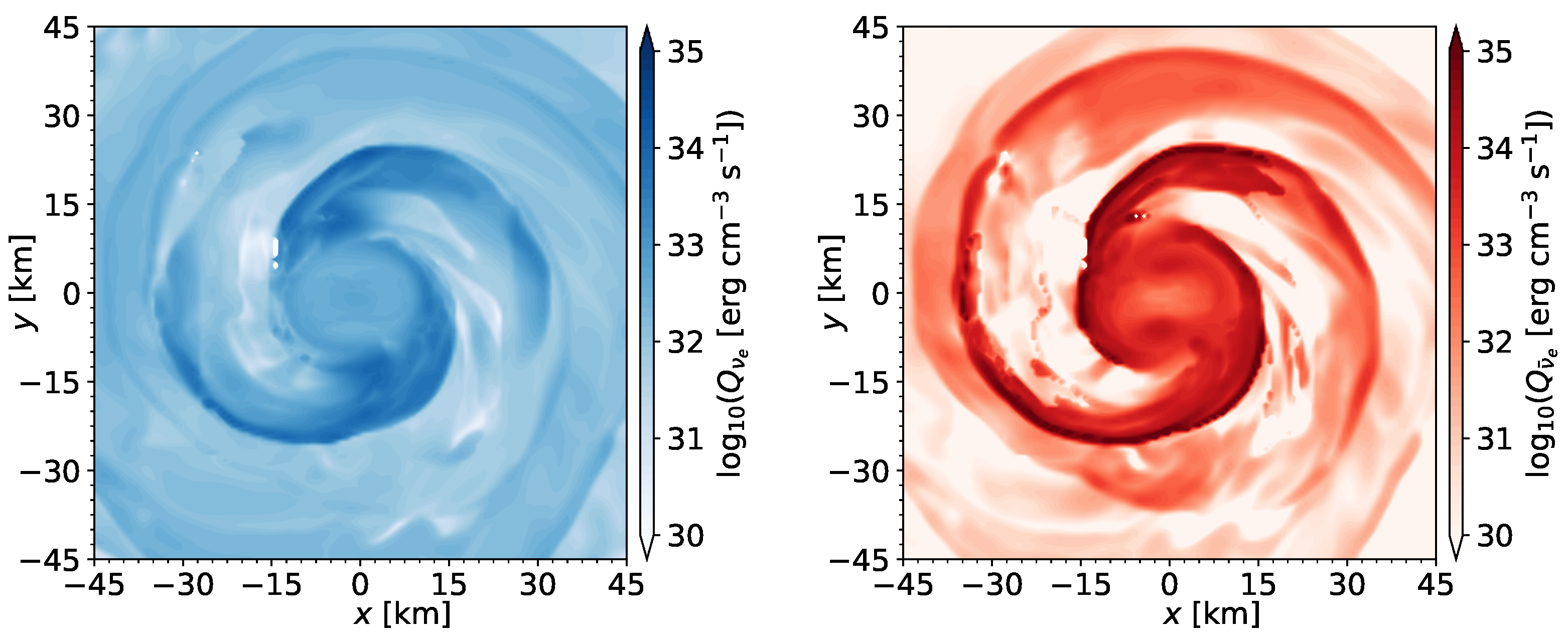
5.2.1. Post-Merger Stage
5.2.2. Spectrograms
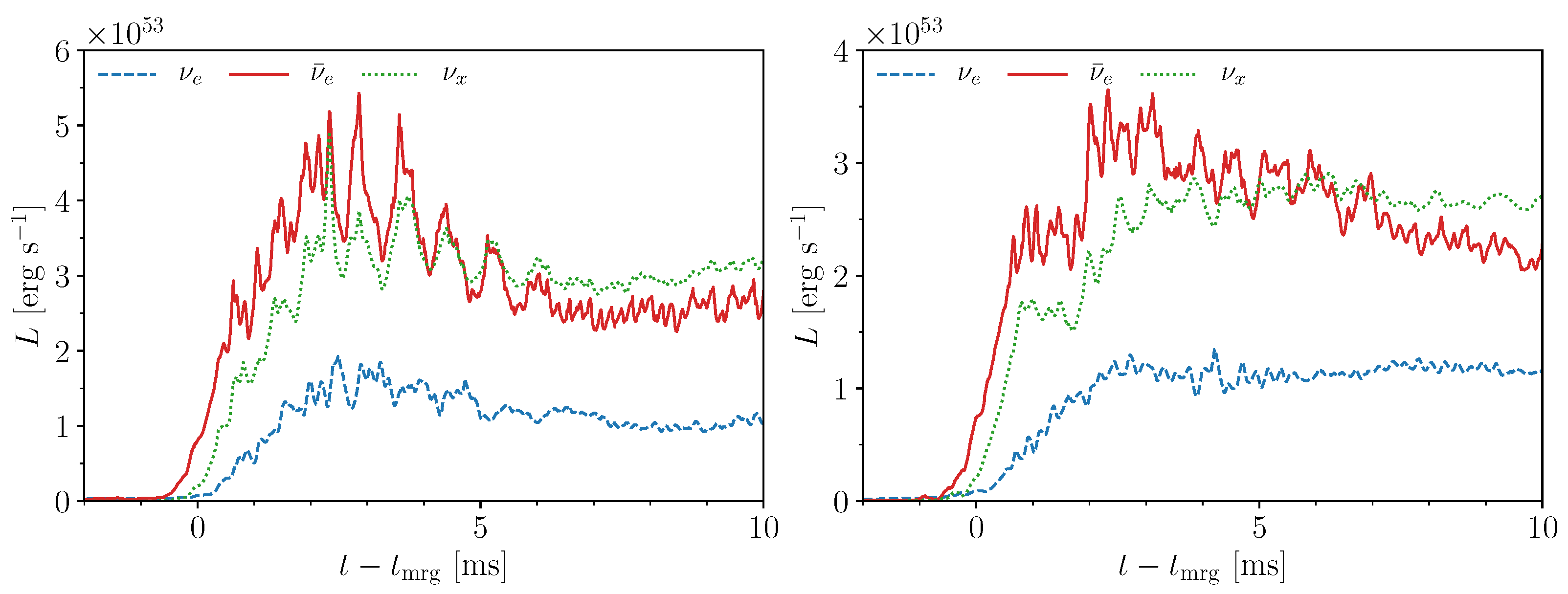
5.2.3. Neutrinos Emission
5.3. Long Inspiral Simulations
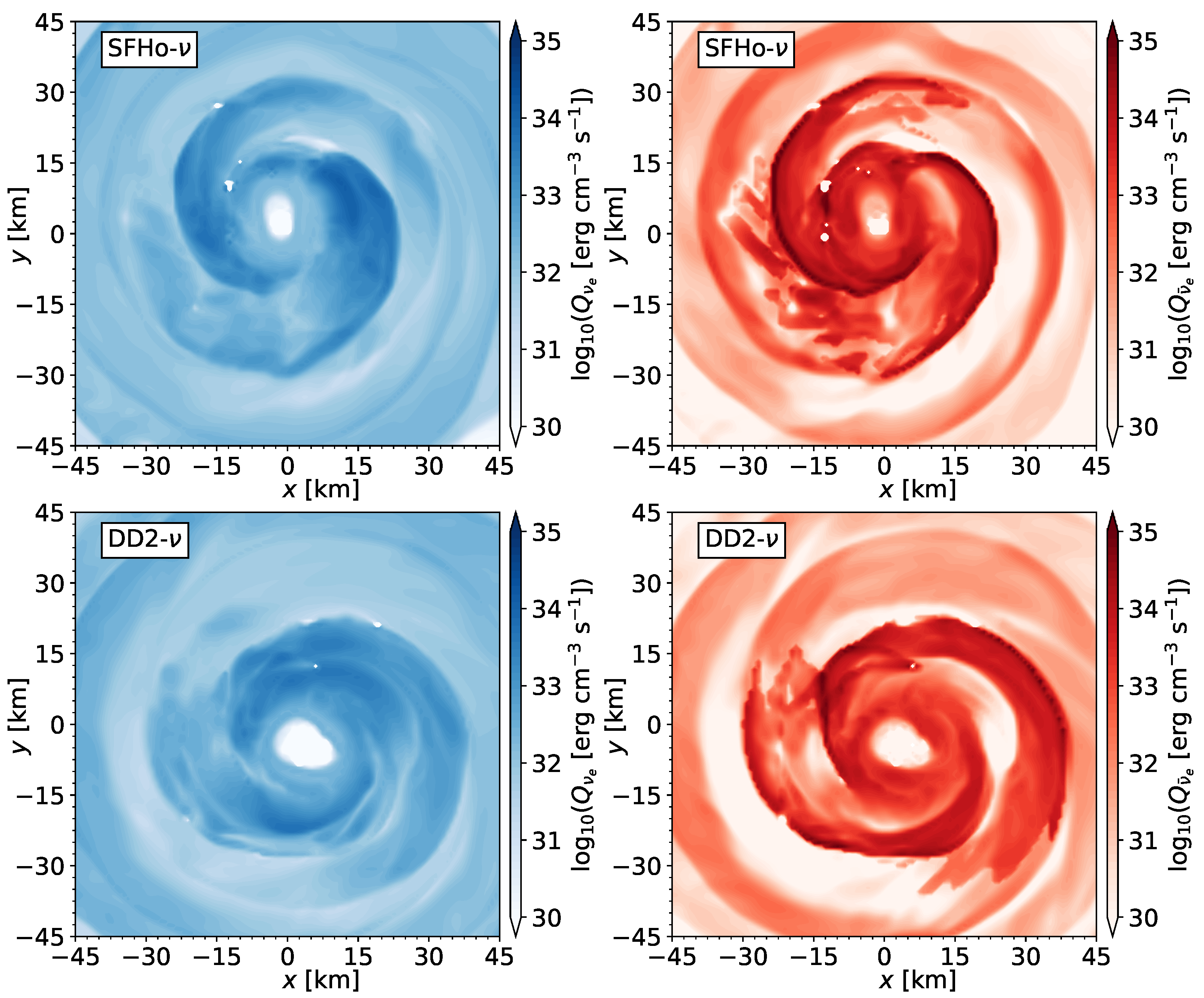
5.3.1. Post-Merger Stage
5.3.2. Neutrino Emissions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
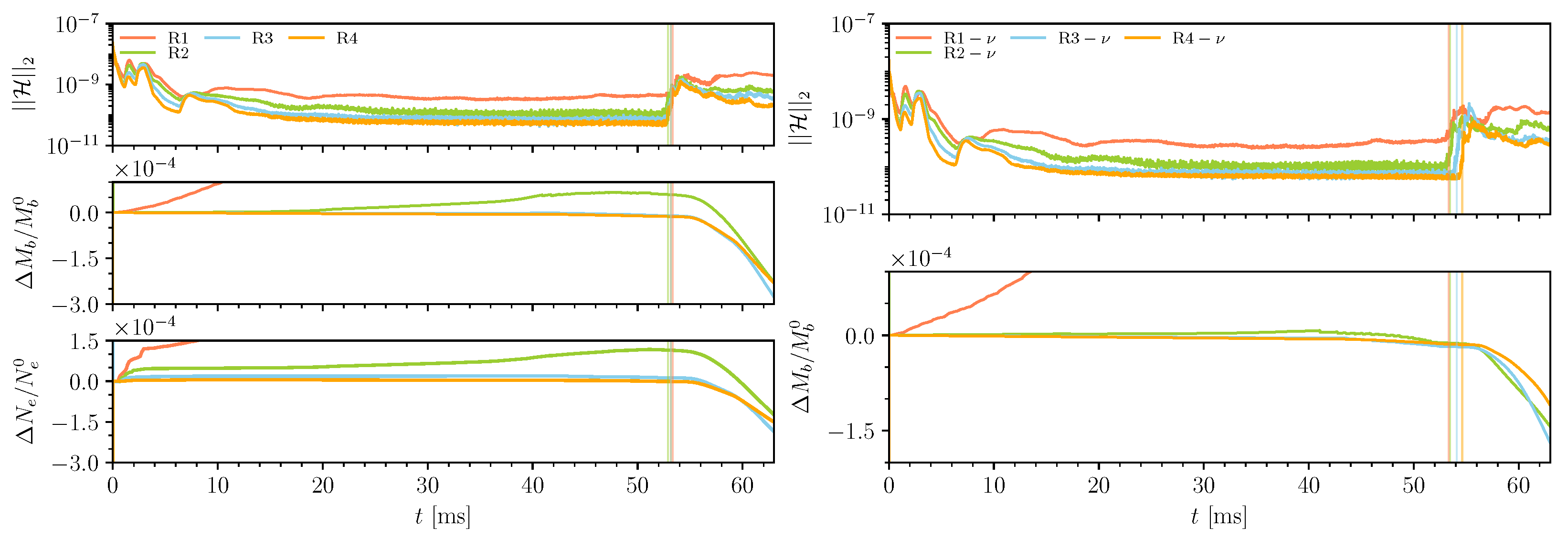
Appendix A. Convergence of the Code

References
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.A.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikaril, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Arcavi, I.; Hosseinzadeh, G.; Howell, D.A.; McCully, C.; Poznanski, D.; Kasen, D.; Barnes, J.; Zaltzman, M.; Vasylyev, S.; Maoz, D.; et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 2017, 551, 64. [Google Scholar] [CrossRef] [Green Version]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the Optical Counterpart to a Gravitational Wave Source. Science 2017, 358, 1556. [Google Scholar] [CrossRef] [Green Version]
- Lipunov, V.M.; Gorbovskoy, E.; Kornilov, V.G.; Tyurina, N.; Balanutsa, P.; Kuznetsov, A.; Vlasenko, D.; Kuvshinov, D.; Gorbunov, I.; Buckley, D.A.H.; et al. MASTER Optical Detection of the First LIGO/Virgo Neutron Star Binary Merger GW170817. Astrophys. J. Lett. 2017, 850, L1. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.Y.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Discovery of the Optical Counterpart Using the Dark Energy Camera. Astrophys. J. Lett. 2017, 848, L16. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-Rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. Lett. 2017, 848, L27. [Google Scholar] [CrossRef]
- Valenti, S.; Sand, D.J.; Yang, S.; Cappellaro, E.; Tartaglia, L.; Corsi, A.; Jha, S.W.; Reichart, D.E.; Haislip, J.; Kouprianov, V. The discovery of the electromagnetic counterpart of GW170817: Kilonova AT 2017gfo/DLT17ck. Astrophys. J. Lett. 2017, 848, L24. [Google Scholar] [CrossRef] [Green Version]
- Hajela, A.; Margutti, R.; Alexander, K.D.; Kathirgamaraju, A.; Baldeschi, A.; Guidorzi, C.; Giannios, D.; Fong, W.; Wu, Y.; MacFadyen, A.; et al. Two Years of Nonthermal Emission from the Binary Neutron Star Merger GW170817: Rapid Fading of the Jet Afterglow and First Constraints on the Kilonova Fastest Ejecta. Astrophys. J. Lett. 2019, 886, L17. [Google Scholar] [CrossRef]
- Hajela, A.; Margutti, R.; Bright, J.S.; Alexander, K.D.; Metzger, B.D.; Nedora, V.; Kathirgamaraju, A.; Margalit, B.; Radice, D.; Guidorzi, C.; et al. Evidence for X-Ray Emission in Excess to the Jet-afterglow Decay 3.5 yr after the Binary Neutron Star Merger GW 170817: A New Emission Component. Astrophys. J. Lett. 2022, 927, L17. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef] [Green Version]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass. Phys. Rev. D 2018, 97, 021501. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef] [Green Version]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef] [Green Version]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [Green Version]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef] [Green Version]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstr, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480, 3871–3878. [Google Scholar] [CrossRef] [Green Version]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multimessenger Bayesian parameter inference of a binary neutron star merger. Mon. Not. R. Astron. Soc. 2019, 489, L91–L96. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625–632. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef] [PubMed]
- Nedora, V.; Radice, D.; Bernuzzi, S.; Perego, A.; Daszuta, B.; Endrizzi, A.; Prakash, A.; Schianchi, F. Dynamical ejecta synchrotron emission as a possible contributor to the changing behaviour of GRB170817A afterglow. Mon. Not. R. Astron. Soc. 2021, 506, 5908–5915. [Google Scholar] [CrossRef]
- Huth, S.; Pang, P.T.; Tews, I.; Dietrich, T.; Le Fèvre, A.; Schwenk, A.; Trautmann, W.; Agarwal, K.; Bulla, M.; Coughlin, M.W.; et al. Constraining neutron-star matter with microscopic and macroscopic collisions. Nature 2022, 606, 276–280. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; The Las Cumbres Observatory Collaboration; The VINROUGE Collaboration; The MASTER Collaboration. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef] [Green Version]
- Guidorzi, C.; Margutti, R.; Brout, D.; Scolnic, D.; Fong, W.; Alexander, K.D.; Cowperthwaite, P.S.; Annis, J.; Berger, E.; Blanchard, P.K.; et al. Improved Constraints on H0 from a Combined Analysis of Gravitational-wave and Electromagnetic Emission from GW170817. Astrophys. J. Lett. 2017, 851, L36. [Google Scholar] [CrossRef] [Green Version]
- Hotokezaka, K.; Nakar, E.; Gottlieb, O.; Nissanke, S.; Masuda, K.; Hallinan, G.; Mooley, K.P.; Deller, A.T. A Hubble constant measurement from superluminal motion of the jet in GW170817. Nat. Astron. 2019, 3, 940–944. [Google Scholar] [CrossRef] [Green Version]
- Coughlin, M.W.; Dietrich, T.; Heinzel, J.; Khetan, N.; Antier, S.; Bulla, M.; Christensen, N.; Coulter, D.A.; Foley, R.J. Standardizing kilonovae and their use as standard candles to measure the Hubble constant. Phys. Rev. Res. 2020, 2, 022006. [Google Scholar] [CrossRef] [Green Version]
- Pérez-García, M.A.; Izzo, L.; Barba, D.; Bulla, M.; Sagués-Carracedo, A.; Pérez, E.; Albertus, C.; Dhawan, S.; Prada, F.; Agnello, A.; et al. Hubble constant and nuclear equation of state from kilonova spectro-photometric light curves. arXiv 2022, arXiv:2204.00022. [Google Scholar]
- Wang, H.; Giannios, D. Multimessenger parameter estimation of GW170817: From jet structure to the Hubble constant. Astrophys. J. 2021, 908, 200. [Google Scholar] [CrossRef]
- Bulla, M.; Coughlin, M.W.; Dhawan, S.; Dietrich, T. Multi-messenger constraints on the Hubble constant through combination of gravitational waves, gamma-ray bursts and kilonovae from neutron star mergers. Universe 2022, 8, 289. [Google Scholar] [CrossRef]
- Dietrich, T.; Hinderer, T.; Samajdar, A. Interpreting Binary Neutron Star Mergers: Describing the Binary Neutron Star Dynamics, Modelling Gravitational Waveforms, and Analyzing Detections. Gen. Rel. Grav. 2021, 53, 27. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quant. Grav. 2017, 34, 105014. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef] [Green Version]
- Nedora, V.; Schianchi, F.; Bernuzzi, S.; Radice, D.; Daszuta, B.; Endrizzi, A.; Perego, A.; Prakash, A.; Zappa, F. Mapping dynamical ejecta and disk masses from numerical relativity simulations of neutron star mergers. Class. Quant. Grav. 2022, 39, 015008. [Google Scholar] [CrossRef]
- Krüger, C.J.; Foucart, F. Estimates for Disk and Ejecta Masses Produced in Compact Binary Mergers. Phys. Rev. D 2020, 101, 103002. [Google Scholar] [CrossRef]
- Metzger, B.D.; Martinez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.V.; Zinner, N.T. Electromagnetic Counterparts of Compact Object Mergers Powered by the Radioactive Decay of R-process Nuclei. Mon. Not. R. Astron. Soc. 2010, 406, 2650. [Google Scholar] [CrossRef]
- Watson, D.; Hansen, C.J.; Selsing, J.; Koch, A.; Malesani, D.B.; Andersen, A.C.; Fynbo, J.P.; Arcones, A.; Bauswein, A.; Covino, S.; et al. Identification of strontium in the merger of two neutron stars. Nature 2019, 574, 497–500. [Google Scholar] [CrossRef] [Green Version]
- Bruegmann, B.; Gonzalez, J.A.; Hannam, M.; Husa, S.; Sperhake, U.; Tichy, W. Calibration of Moving Puncture Simulations. Phys. Rev. D 2008, 77, 024027. [Google Scholar] [CrossRef] [Green Version]
- Thierfelder, M.; Bernuzzi, S.; Bruegmann, B. Numerical relativity simulations of binary neutron stars. Phys. Rev. D 2011, 84, 044012. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Brügmann, B. Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. Phys. Rev. D 2015, 91, 124041. [Google Scholar] [CrossRef] [Green Version]
- Bernuzzi, S.; Dietrich, T. Gravitational waveforms from binary neutron star mergers with high-order weighted-essentially-nonoscillatory schemes in numerical relativity. Phys. Rev. D 2016, 94, 064062. [Google Scholar] [CrossRef] [Green Version]
- Ruffert, M.H.; Janka, H.T.; Schaefer, G. Coalescing neutron stars: A Step towards physical models. 1: Hydrodynamic evolution and gravitational wave emission. Astron. Astrophys. 1996, 311, 532–566. [Google Scholar]
- Rosswog, S.; Liebendoerfer, M. High resolution calculations of merging neutron stars. 2: Neutrino emission. Mon. Not. R. Astron. Soc. 2003, 342, 673. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Baumgarte, T.W.; Shapiro, S.L. On the numerical integration of Einstein’s field equations. Phys. Rev. D 1998, 59, 024007. [Google Scholar] [CrossRef] [Green Version]
- Hilditch, D.; Bernuzzi, S.; Thierfelder, M.; Cao, Z.; Tichy, W.; Bruegmann, B. Compact binary evolutions with the Z4c formulation. Phys. Rev. D 2013, 88, 084057. [Google Scholar] [CrossRef] [Green Version]
- Banyuls, F.; Font, J.A.; Ibanez, J.M.A.; Marti, J.M.A.; Miralles, J.A. Numerical 3+1 General Relativistic Hydrodynamics: A Local Characteristic Approach. Astrophys. J. 1997, 476, 221. [Google Scholar] [CrossRef] [Green Version]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Taniguchi, K.; Uryu, K. Merger of binary neutron stars with realistic equations of state in full general relativity. Phys. Rev. D 2005, 71, 084021. [Google Scholar] [CrossRef] [Green Version]
- Bruenn, S.W. Stellar core collapse—Numerical model and infall epoch. APJS 1985, 58, 771–841. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. A new open-source code for spherically symmetric stellar collapse to neutron stars and black holes. Class. Quantum Gravity 2010, 27, 114103. [Google Scholar] [CrossRef] [Green Version]
- O’Connor, E. An Open-Source Neutrino Radiation Hydrodynamics Code for Core-Collapse Supernovae. Astrophys. J. Suppl. 2015, 219, 24. [Google Scholar] [CrossRef] [Green Version]
- Deaton, M.B.; Duez, M.D.; Foucart, F.; O’Connor, E.; Ott, C.D.; Kidder, L.E.; Muhlberger, C.D.; Scheel, M.A.; Szilagyi, B. Black Hole-Neutron Star Mergers with a Hot Nuclear Equation of State: Outflow and Neutrino-Cooled Disk for a Low-Mass, High-Spin Case. Astrophys. J. 2013, 776, 47. [Google Scholar] [CrossRef] [Green Version]
- Foucart, F.; Deaton, M.B.; Duez, M.D.; O’Connor, E.; Ott, C.D.; Haas, R.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B. Neutron star-black hole mergers with a nuclear equation of state and neutrino cooling: Dependence in the binary parameters. Phys. Rev. D 2014, 90, 024026. [Google Scholar] [CrossRef] [Green Version]
- Foucart, F.; Haas, R.; Duez, M.D.; O’Connor, E.; Ott, C.D.; Roberts, L.; Kidder, L.E.; Lippuner, J.; Pfeiffer, H.P.; Scheel, M.A. Low mass binary neutron star mergers: Gravitational waves and neutrino emission. Phys. Rev. D 2016, 93, 044019. [Google Scholar] [CrossRef] [Green Version]
- Neilsen, D.; Liebling, S.L.; Anderson, M.; Lehner, L.; O’Connor, E.; Palenzuela, C. Magnetized Neutron Stars With Realistic Equations of State and Neutrino Cooling. Phys. Rev. D 2014, 89, 104029. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Kiuchi, K.; Sekiguchi, Y.i.; Suwa, Y. Truncated Moment Formalism for Radiation Hydrodynamics in Numerical Relativity. Prog. Theor. Phys. 2011, 125, 1255–1287. [Google Scholar] [CrossRef] [Green Version]
- Cardall, C.Y.; Endeve, E.; Mezzacappa, A. Conservative 3+1 General Relativistic Boltzmann Equation. Phys. Rev. D 2013, 88, 023011. [Google Scholar] [CrossRef] [Green Version]
- Foucart, F.; O’Connor, E.; Roberts, L.; Duez, M.D.; Haas, R.; Kidder, L.E.; Ott, C.D.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B. Post-merger evolution of a neutron star-black hole binary with neutrino transport. Phys. Rev. D 2015, 91, 124021. [Google Scholar] [CrossRef] [Green Version]
- Anninos, P.; Fragile, P.C. Multi-frequency General Relativistic Radiation-hydrodynamics with M1 Closure. Astrophys. J. 2020, 900, 71. [Google Scholar] [CrossRef]
- Foucart, F.; Duez, M.D.; Hebert, F.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A. Monte-Carlo neutrino transport in neutron star merger simulations. Astrophys. J. Lett. 2020, 902, L27. [Google Scholar] [CrossRef]
- Weih, L.R.; Olivares, H.; Rezzolla, L. Two-moment scheme for general-relativistic radiation hydrodynamics: A systematic description and new applications. Mon. Not. R. Astron. Soc. 2020, 495, 2285–2304. [Google Scholar] [CrossRef]
- Foucart, F.; Duez, M.D.; Hebert, F.; Kidder, L.E.; Kovarik, P.; Pfeiffer, H.P.; Scheel, M.A. Implementation of Monte Carlo Transport in the General Relativistic SpEC Code. Astrophys. J. 2021, 920, 82. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A.; Haas, R. A new moment-based general-relativistic neutrino-radiation transport code: Methods and first applications to neutron star mergers. Mon. Not. R. Astron. Soc. 2022, 512, 1499–1521. [Google Scholar] [CrossRef]
- Weih, L.R.; Gabbana, A.; Simeoni, D.; Rezzolla, L.; Succi, S.; Tripiccione, R. Beyond moments: Relativistic Lattice-Boltzmann methods for radiative transport in computational astrophysics. Mon. Not. R. Astron. Soc. 2020, 498, 3374–3394. [Google Scholar] [CrossRef]
- Ardevol-Pulpillo, R.; Janka, H.T.; Just, O.; Bauswein, A. Improved Leakage-Equilibration-Absorption Scheme (ILEAS) for Neutrino Physics in Compact Object Mergers. Mon. Not. R. Astron. Soc. 2019, 485, 4754–4789. [Google Scholar] [CrossRef]
- Perego, A.; Cabezón, R.; Käppeli, R. An advanced leakage scheme for neutrino treatment in astrophysical simulations. Astrophys. J. Suppl. 2016, 223, 22. [Google Scholar] [CrossRef] [Green Version]
- Gizzi, D.; O’Connor, E.; Rosswog, S.; Perego, A.; Cabezón, R.; Nativi, L. A multidimensional implementation of the Advanced Spectral neutrino Leakage scheme. Mon. Not. R. Astron. Soc. 2019, 490, 4211–4229. [Google Scholar] [CrossRef] [Green Version]
- Gizzi, D.; Lundman, C.; O’Connor, E.; Rosswog, S.; Perego, A. Calibration of the Advanced Spectral Leakage scheme for neutron star merger simulations, and extension to smoothed-particle hydrodynamics. Mon. Not. R. Astron. Soc. 2021, 505, 2575–2593. [Google Scholar] [CrossRef]
- Galeazzi, F.; Kastaun, W.; Rezzolla, L.; Font, J.A. Implementation of a simplified approach to radiative transfer in general relativity. Phys. Rev. D 2013, 88, 064009. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Harris, S.P. Damping of density oscillations in neutrino-transparent nuclear matter. Phys. Rev. C 2019, 100, 035803. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity of baryonic matter with trapped neutrinos. Phys. Rev. D 2019, 100, 103021. [Google Scholar] [CrossRef] [Green Version]
- Most, E.R.; Harris, S.P.; Plumberg, C.; Alford, M.G.; Noronha, J.; Noronha-Hostler, J.; Pretorius, F.; Witek, H.; Yunes, N. Projecting the likely importance of weak-interaction-driven bulk viscosity in neutron star mergers. Mon. Not. R. Astron. Soc. 2021, 509, 1096–1108. [Google Scholar] [CrossRef]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk Viscous Damping of Density Oscillations in Neutron Star Mergers. Particles 2020, 3, 500–517. [Google Scholar] [CrossRef]
- Takahashi, K.; El Eid, M.; Hillebrandt, W. Beta transition rates in hot and dense matter. Astron. Astrophys. 1978, 67, 185–197. [Google Scholar]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Shen, G.; Horowitz, C.J.; Teige, S. A New Equation of State for Astrophysical Simulations. Phys. Rev. C 2011, 83, 035802. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.L.; Ipser, J.R.; Sorkin, R.D. Turning point method for axisymmetric stability of rotating relativistic stars. Astrophys. J. 1988, 325, 722–724. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The Piecewise Parabolic Method (PPM) for Gas Dynamical Simulations. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef] [Green Version]
- Epstein, R.I. Lepton Driven Convection in Supernovae. Mon. Not. R. Astron. Soc. 1978, 188, 305–325. [Google Scholar] [CrossRef]
- Steiner, A.W.; Hempel, M.; Fischer, T. Core-collapse supernova equations of state based on neutron star observations. Astrophys. J. 2013, 774, 17. [Google Scholar] [CrossRef] [Green Version]
- Hempel, M.; Schaffner-Bielich, J. Statistical Model for a Complete Supernova Equation of State. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef] [Green Version]
- Banik, S.; Hempel, M.; Bandyopadhyay, D. New Hyperon Equations of State for Supernovae and Neutron Stars in Density-dependent Hadron Field Theory. Astrophys. J. Suppl. 2014, 214, 22. [Google Scholar] [CrossRef]
- Typel, S.; Oertel, M.; Klähn, T. CompOSE CompStar online supernova equations of state harmonising the concert of nuclear physics and astrophysics compose.obspm.fr. Phys. Part. Nucl. 2015, 46, 633–664. [Google Scholar] [CrossRef]
- CompOSE. Available online: https://compose.obspm.fr/ (accessed on 1 May 2021).
- Tichy, W. A New numerical method to construct binary neutron star initial data. Class. Quantum Gravity 2009, 26, 175018. [Google Scholar] [CrossRef] [Green Version]
- Tichy, W. Constructing quasi-equilibrium initial data for binary neutron stars with arbitrary spins. Phys. Rev. D 2012, 86, 064024. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, T.; Moldenhauer, N.; Johnson-McDaniel, N.K.; Bernuzzi, S.; Markakis, C.M.; Brügmann, B.; Tichy, W. Binary Neutron Stars with Generic Spin, Eccentricity, Mass ratio, and Compactness—Quasi-equilibrium Sequences and First Evolutions. Phys. Rev. D 2015, 92, 124007. [Google Scholar] [CrossRef] [Green Version]
- Tichy, W.; Rashti, A.; Dietrich, T.; Dudi, R.; Brügmann, B. Constructing binary neutron star initial data with high spins, high compactnesses, and high mass ratios. Phys. Rev. D 2019, 100, 124046. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.R.; Mathews, G.J. Instabilities in Close Neutron Star Binaries. Phys. Rev. Lett. 1995, 75, 4161–4164. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.R.; Mathews, G.J.; Marronetti, P. Relativistic numerical model for close neutron star binaries. Phys. Rev. 1996, D54, 1317–1331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- York, J.W., Jr. Conformal ‘thin sandwich’ data for the initial-value problem. Phys. Rev. Lett. 1999, 82, 1350–1353. [Google Scholar] [CrossRef] [Green Version]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Kyutoku, K.; Shibata, M.; Taniguchi, K. Reducing orbital eccentricity in initial data of binary neutron stars. Phys. Rev. D 2014, 90, 064006. [Google Scholar] [CrossRef] [Green Version]
- Chaurasia, S.V.; Dietrich, T.; Johnson-McDaniel, N.K.; Ujevic, M.; Tichy, W.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of large eccentricities. Phys. Rev. D 2018, 98, 104005. [Google Scholar] [CrossRef] [Green Version]
- Radice, D.; Bernuzzi, S.; Del Pozzo, W.; Roberts, L.F.; Ott, C.D. Probing Extreme-Density Matter with Gravitational Wave Observations of Binary Neutron Star Merger Remnants. Astrophys. J. Lett. 2017, 842, L10. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. Beta equilibrium in neutron star mergers. Phys. Rev. C 2018, 98, 065806. [Google Scholar] [CrossRef] [Green Version]
- Doulis, G.; Atteneder, F.; Bernuzzi, S.; Brügmann, B. Entropy-limited higher-order central scheme for neutron star merger simulations. arXiv 2022, arXiv:2202.08839. [Google Scholar] [CrossRef]
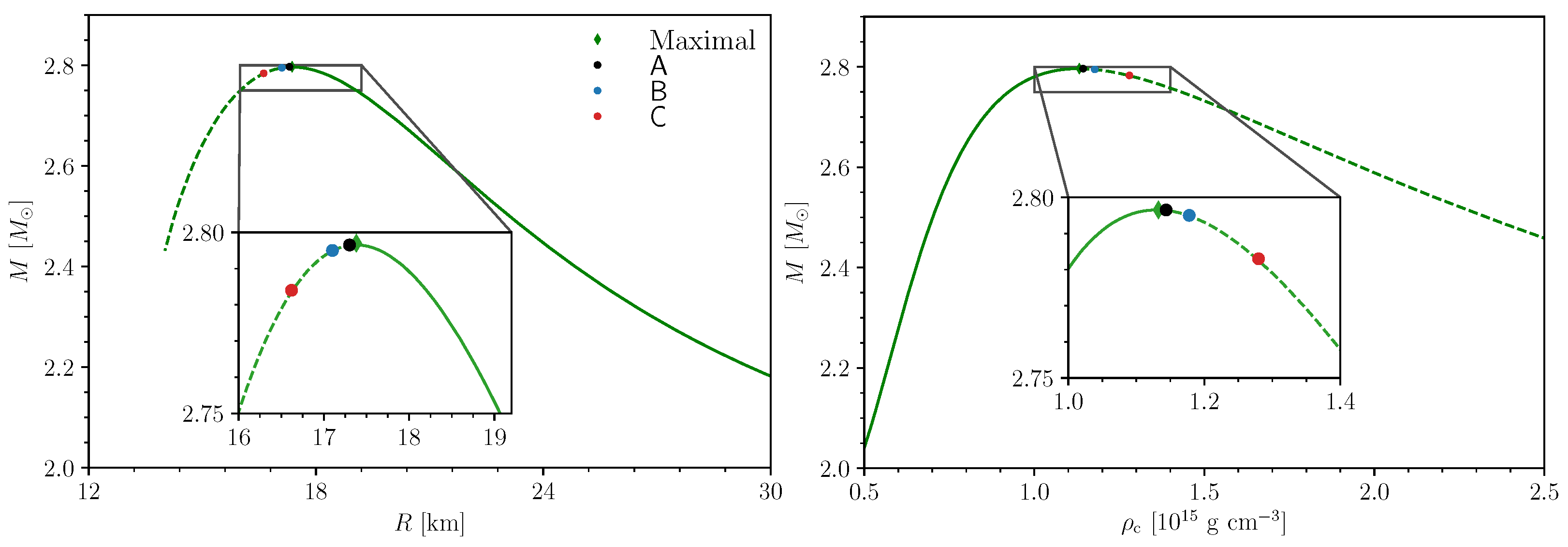
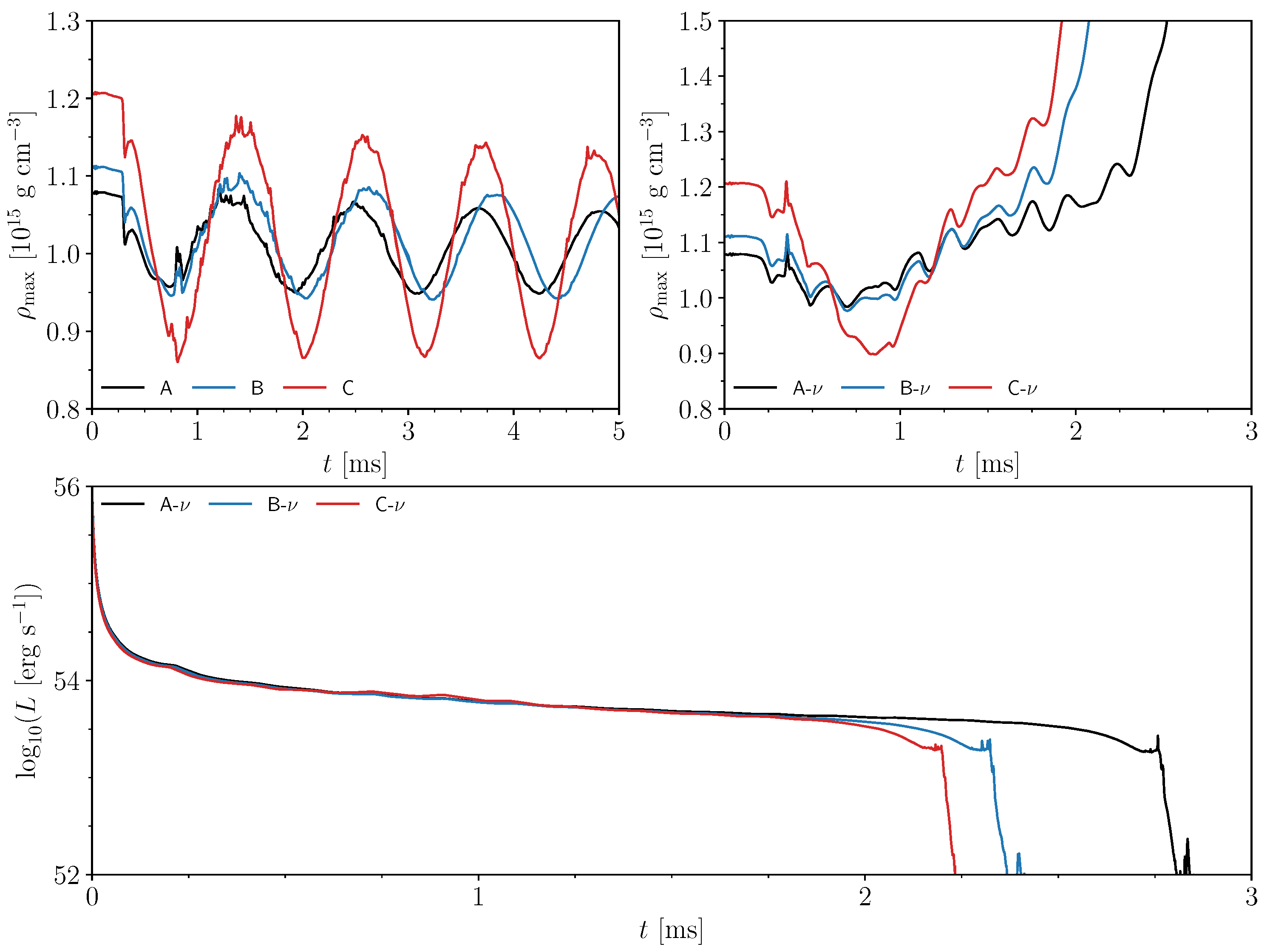
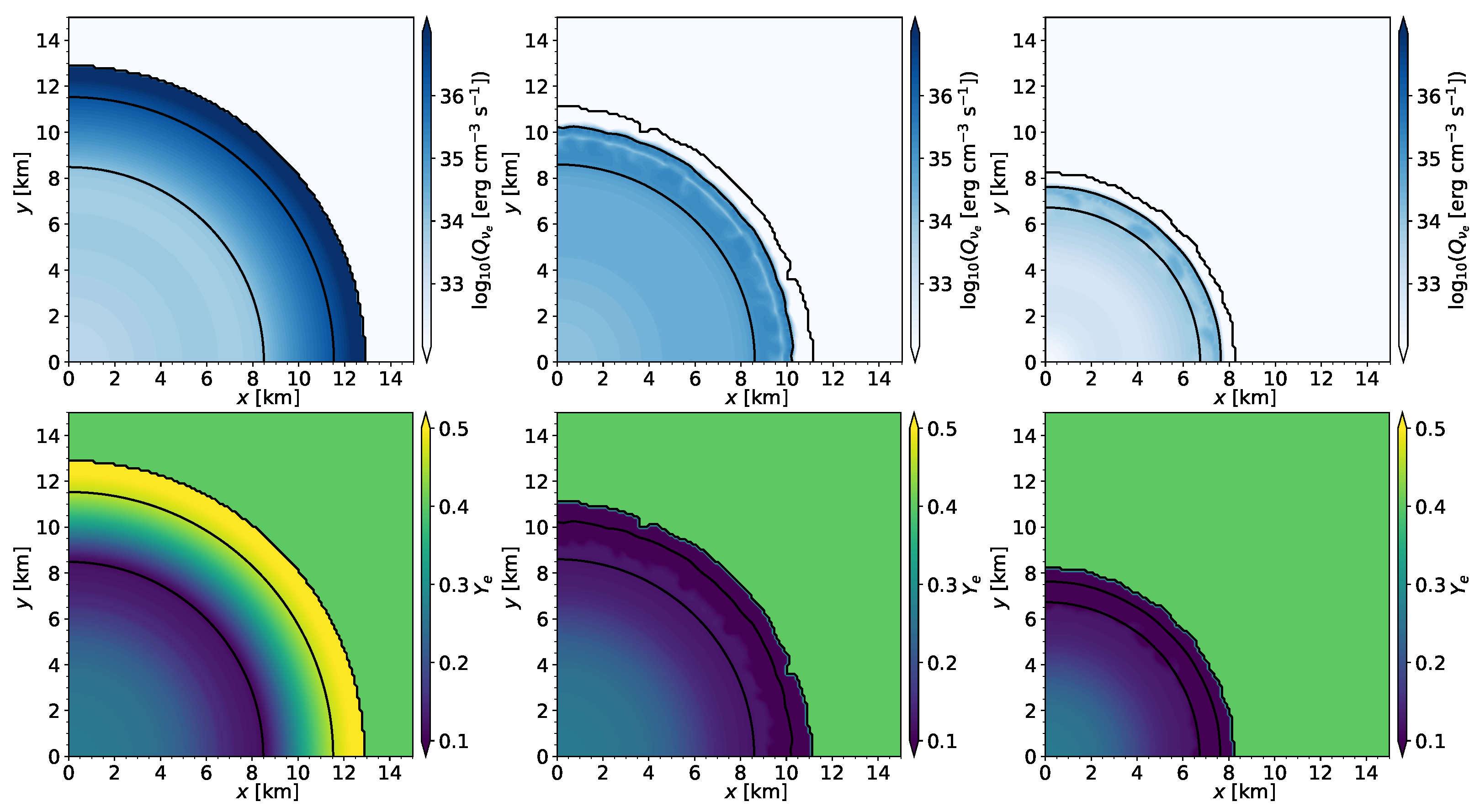
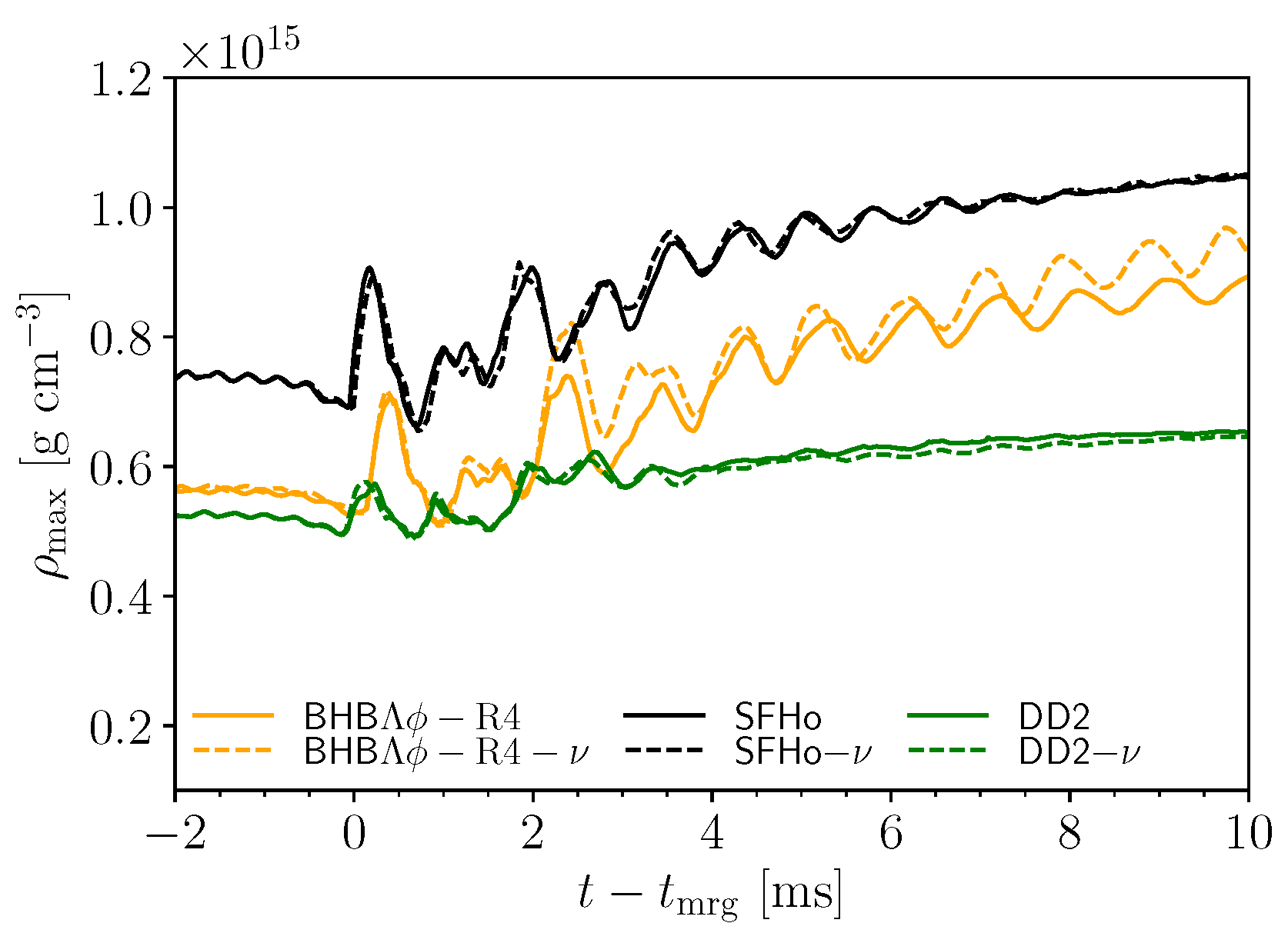
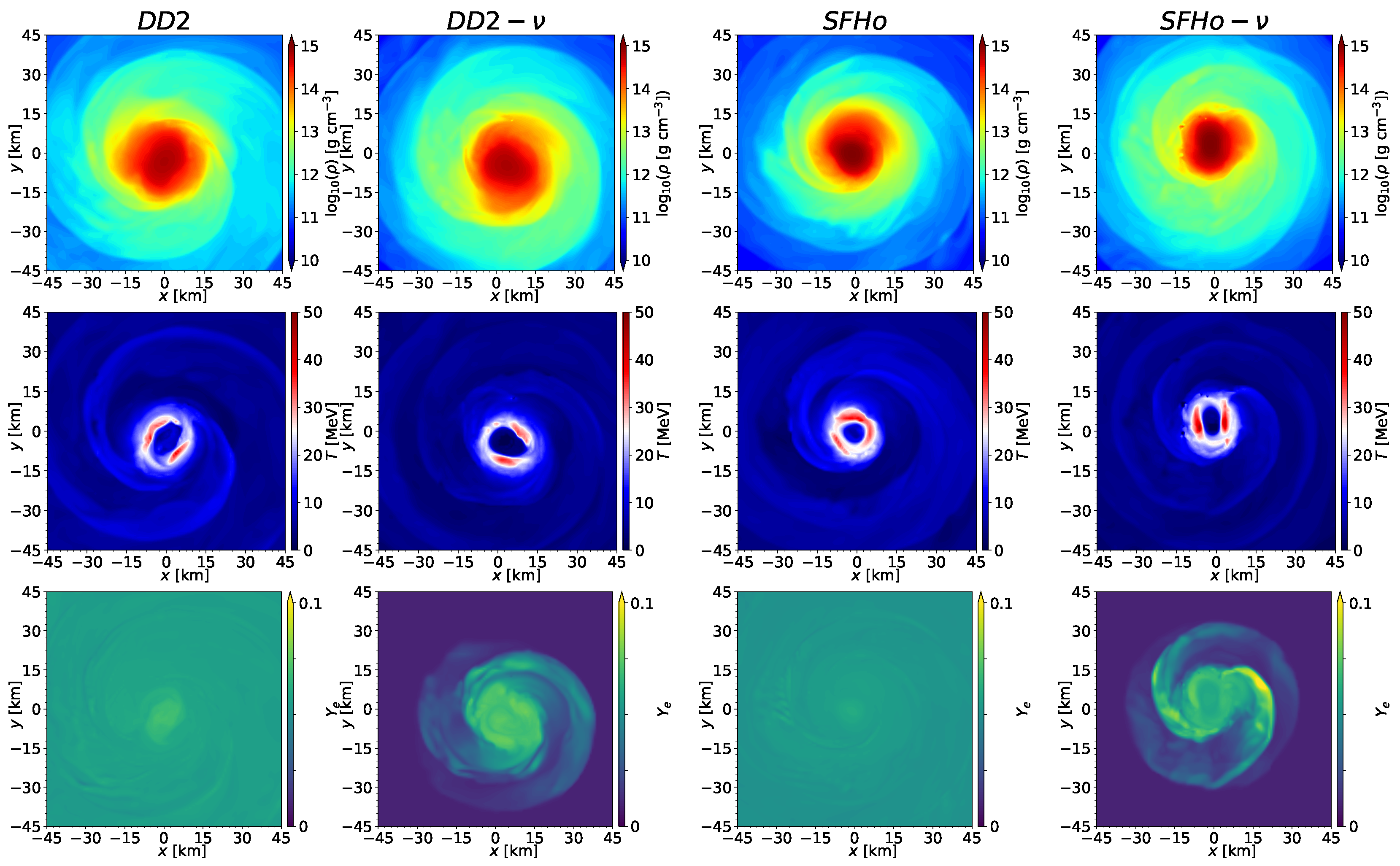
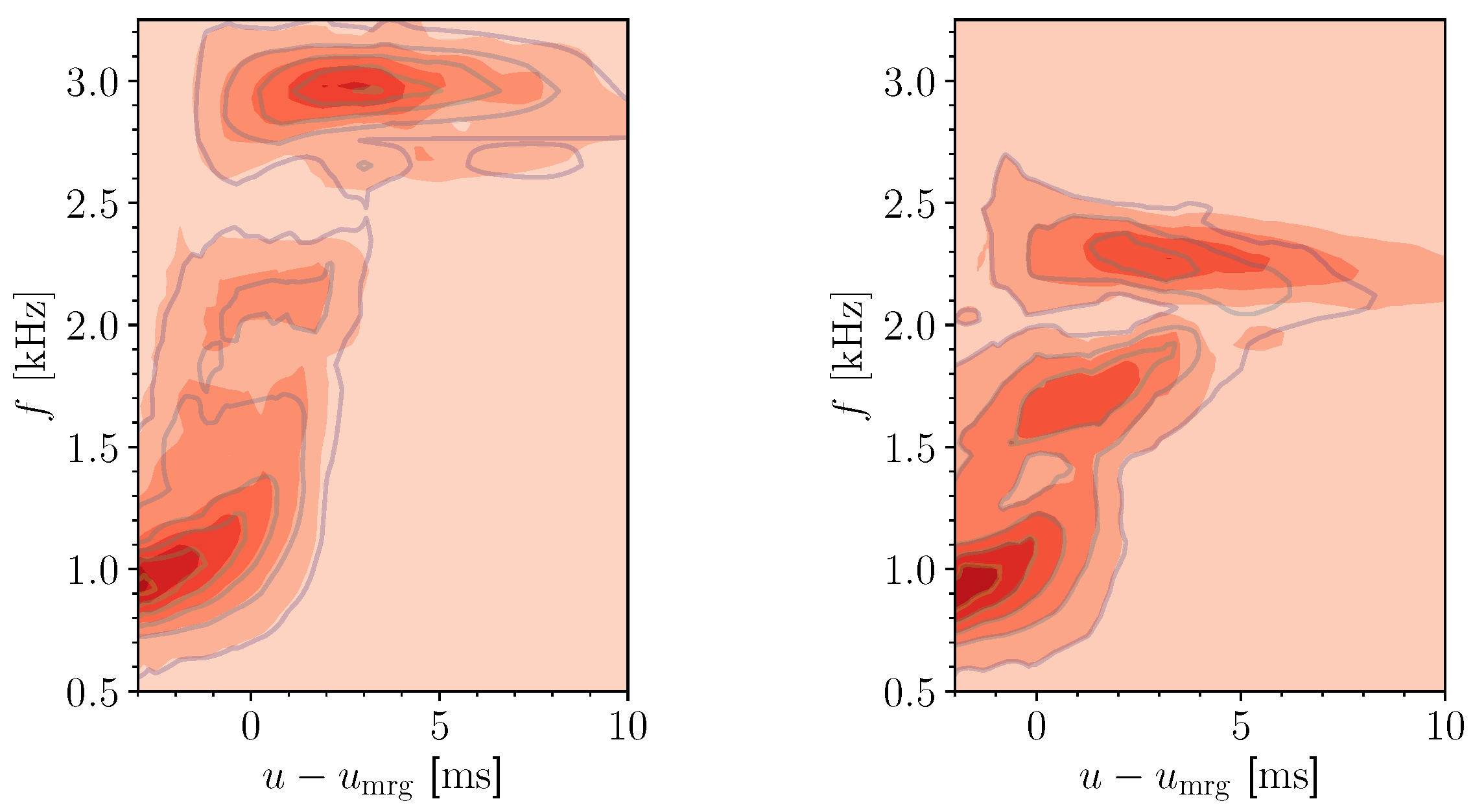

| Model | n | |||||
|---|---|---|---|---|---|---|
| Maximal | 1.068 | 2.797 | 3.506 | - | - | - |
| A | 1.079 | 2.797 | 3.310 | 2.433 | 256 | 111 |
| B | 1.111 | 2.796 | 3.309 | 2.191 | 256 | 111 |
| C | 1.218 | 2.784 | 3.293 | 2.075 | 256 | 111 |
| Model | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DD2 | 256 | 128 | ||||||||
| SFHo | 256 | 128 | ||||||||
| BHB | 128 | 64 | ||||||||
| BHB | 192 | 96 | ||||||||
| BHB | 256 | 128 | ||||||||
| BHB | 320 | 160 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gieg, H.; Schianchi, F.; Dietrich, T.; Ujevic, M. Incorporating a Radiative Hydrodynamics Scheme in the Numerical-Relativity Code BAM. Universe 2022, 8, 370. https://doi.org/10.3390/universe8070370
Gieg H, Schianchi F, Dietrich T, Ujevic M. Incorporating a Radiative Hydrodynamics Scheme in the Numerical-Relativity Code BAM. Universe. 2022; 8(7):370. https://doi.org/10.3390/universe8070370
Chicago/Turabian StyleGieg, Henrique, Federico Schianchi, Tim Dietrich, and Maximiliano Ujevic. 2022. "Incorporating a Radiative Hydrodynamics Scheme in the Numerical-Relativity Code BAM" Universe 8, no. 7: 370. https://doi.org/10.3390/universe8070370
APA StyleGieg, H., Schianchi, F., Dietrich, T., & Ujevic, M. (2022). Incorporating a Radiative Hydrodynamics Scheme in the Numerical-Relativity Code BAM. Universe, 8(7), 370. https://doi.org/10.3390/universe8070370






