Abstract
Einstein described the relationship between mass and energy using the theory of special relativity by a simple equation, . Mass–energy equivalence implies that mass can be converted into energy and vice versa. In this study, a virtual reality (VR) system was developed for learners to take a spacecraft travelling at nearly the speed of light to conduct space exploration and understand the concepts of special relativity and mass–energy equivalence. A teaching experiment was conducted to investigate the learning effectiveness and cognitive load of learners by recruiting 60 students as research samples. The experimental group (30 students) used the VR system and the control group (30 students) used physics textbooks for learning special relativity and mass–energy equivalence. The experimental results reveal that the learning effectiveness of the experimental group is higher than that of the control group while the cognitive load of the former is lower than that of the latter. The questionnaire results show that students of the control group had responded positively to learning content, cognitive usefulness, cognitive ease of use, and user satisfaction, indicating that they were satisfied with the learning experience of the VR system.
1. Introduction
In 1905, Einstein proposed the special theory of relativity, which overturned the ancient view that time and space do not affect each other. He believed that the temporal and spatial coordinates of any event would change according to the observer’s coordinate system. The theory of relativity is a theory of spacetime and gravity, and it can be divided into two parts: special relativity and general relativity. General relativity integrates Newton’s law of gravity with special relativity, where gravity is described as a geometric property (curvature) of space and time and it is related to the radiated energy and momentum of matter specified by Einstein’s field equations. It is generally accepted that the theory of special relativity deals with problems where gravity is absent or can be ignored, whereas the theory of general relativity covers the physics with gravity.
Before Einstein proposed the theory of special relativity, it was believed that time and space exist independently [1]. The concept of absolute time and space had been established since Galileo’s time, and Newton’s classical mechanics and kinematics were gradually developed based on this concept. Based on Newton’s classical mechanics and Maxwell’s classical electromagnetism [2], Einstein first proposed the concept of “four-dimensional spacetime”, which explained that time and space are not independent and there are 3 + 1 dimensions of space and time as a whole. Observers moving in spacetime can establish their own coordinate system with its own time and space, and the time and space defined by different observers can also be different. Starting from the two basic assumptions listed below, Einstein broke the misconception of Newton’s absolute time and space by proposing a new concept of relative time and space.
- Principle of special relativity: All inertial coordinate systems are homogeneous, and laws of physics are consistent in any inertial coordinate system (e.g., an observer in a stationary laboratory and an electron moving at nearly the speed of light).
- The speed of light is constant: The speed of light in a vacuum is constant in any coordinate system. In the International System of Units, the unit of length “meter” is defined as the distance traveled by light in a vacuum in 1/299,792,458 s.
Based on the aforementioned assumptions, Einstein derived the results of “time dilation” and “length contraction” caused by high-speed moving objects. Time dilation is a physical phenomenon in which the clock is slower in a stationary coordinate system than the clock in a moving coordinate system, but this description is correct only in the observer’s coordinate system. Length contraction is the phenomenon of length reduction seen by an observer when watching an object with a non-zero relative velocity, which is obvious only when the relative velocity is close to the speed of light and can only be observed in the moving direction of the observer.
The main areas for applying the theory of relativity include (1) high-speed motion (near the speed of light), and (2) strong gravity fields. Many hospitals have particle accelerators in their radiotherapy departments to generate energetic particles and produce isotopes for radiotherapy and medical imaging [3]. Because the speed of energetic particles is close to the speed of light, the design and use of a particle accelerator must take relativistic effects into account. The atomic clocks in a global positioning system (GPS) satellite are important for positioning accuracy, which may be affected by the time dilation effect due to high-speed motion (special relativity) and the weaker gravitational field above Earth’s surface (general relativity). Considering the combined effect of these two factors, the atomic clocks in the GPS satellite will move faster than the clocks on the ground. Therefore, the satellite must calculate and offset the relativistic effects to maintain the accuracy of GPS.
Many people find it difficult to imagine the spacetime concepts in special relativity. For example, the time measured in a coordinate system where the clock is stationary (proper time) or the length measured in a coordinate system where the observer is stationary (proper length) is different from the measured results in different coordinate systems. Similarly, the Lorentz transformations of velocities between different coordinate systems are different from the classical concepts of Newton’s laws of motion. These phenomena can only be observed and verified in an environment moving near the speed of light. Therefore, these concepts are very difficult to understand for physics beginners [4].
In 1905, Einstein proposed a theory based on the law of inertia and calculation of an object’s energy based on mass–energy equivalence, which states that mass can be converted into energy and energy can be converted into mass without violating the laws of conservation of mass and energy. The main idea of Einstein’s theory is that any object with mass has an invisible internal energy. If the relationship between mass and energy is described mathematically, the internal energy of a stationary object is equal to the mass of the object multiplied by the square of light speed. The relativistic energy expression is different from Newton’s expression for kinetic energy. The discovery of antimatter in 1936 led the scientific community to understanding that mass be converted into energy only when matter is exposed to antimatter.
Mass–energy equivalence reveals the existence of internal energy in an object. The total energy of the object can be described as . The total energy of the object is calculated as , where the mass of the object in motion is modified as ; is the Lorentz factor and is mathematically expressed as ). In the above equation, the internal energy of the object is and the kinetic energy can then be expressed as . In classical mechanics, the kinetic energy of an object is expressed as . When the moving speed of an object is much smaller than the speed of light, the kinetic energy of the object is very different from that of the object moving at nearly the speed of light.
Special relativity is an important breakthrough in modern physics and its spacetime concepts are often described as the violation of intuition in the real-life experience. Learning physics often involves conducting experiments, but it is almost impossible to conduct experiments for learning special relativity. As a result, many learners have difficulty in understanding the relativistic effects through classroom instruction [5]. In order to enable learners to understand relativity theory, instructors are trying to find a logical and easy-to-understand explanation [6].
The above literature survey shows that VR has been applied in many academic disciplines, and the research results reveal significant improvements in terms of learners’ achievement, interest, and motivation. Although VR is suitable for science education applications, only a few studies have been conducted on instructional design for learning relativistic concepts. Early simulations of relativity such as RelLab [7], Physlet [8], and simulation software [9,10,11] used 2D models to present relativistic concepts and provide visual effects that learners cannot experience in the real world. In recent years, more researchers have developed 3D simulation environments, such as CAVE [12,13], real-time relativity systems [14,15], and a software package [16] for learning relativity. Their findings showed that interactive simulation can enhance learning motivation, and visualization can concretize relativistic concepts.
Situated learning is a learner-centered approach where learners are placed in teaching and learning contexts to engage in action learning, reflective inquiry, and environmental feedback. The goal is to enable learners to interact in multiple contexts and to develop appropriate constructions of individual knowledge [17]. Contextual learning emphasizes that knowledge is a product of the interaction between learners and environments and is inherently influenced by learning activities and cultural contexts. The goal of this study is to create an interactive and immersive environment to enhance learners’ understanding of special relativity and mass–energy equivalence. The VR system combines relativistic concepts with a space exploration mission to provide learners with an interactive, observational, and problem-solving learning environment where they can control the spacecraft speed to observe and compare the effects of time dilation and length contraction in different coordinate systems. It is very helpful in constructing and understanding the concepts of special relativity and mass–energy equivalence.
Cognitive load refers to the amount of working memory resources used in cognition and was originally proposed by Sweller [18] in his research on problem solving. There are three types of cognitive load: (1) intrinsic cognitive load is the effort associated with a particular learning topic; (2) extraneous cognitive load occurs when information or tasks are presented to the learner; (3) germane cognitive load is the work done to create a permanent storage of knowledge (a base model). The research results of Andersen et al. [19] and Vesga et al. [20] showed that applying VR in teaching environments can help reduce the cognitive load of learners. In this study, the VR technology is used to develop a simulation environment suitable for learning special relativity in high school and university physics. The objective is to make abstract and complex concepts observable and more concrete so that learners can understand the physical nature and real-life application of relativity while reducing their cognitive load.
According to Alstein et al. [21], there are three learning objectives of special relativity: (1) to enhance conceptual understanding, (2) to foster understanding of the history and philosophy of science, and (3) to gain motivation and confidence toward special relativity and modern physics in general. The VR system developed in this study provides a scaffold for independent learning to facilitate conceptual change and to make abstract and complex concepts concrete, observable, and interesting. The instructional design of the VR system is based on the basic knowledge of special relativity and the deduction of principles, allowing learners to verify important concepts such as time dilation and length contraction through observation and interaction. Learners can wear head-mounted displays (HMD) for immersive learning to discover that special relativity is not so difficult to understand, and they are willing to take the initiative to learn it.
The VR system developed in this study can guide learners to experience the space exploration, enhance their willingness and motivation to learn, and understand the concepts of special relativity and mass–energy equivalence. A questionnaire survey was conducted based on learners’ satisfaction with the VR system, which can be used to further improve the user interface and learning content of the system. Based on the above research objectives, the research questions of this study are:
- What is the impact of VR on the learning achievement of special relativity and mass–energy equivalence?
- What is the impact of VR on the cognitive load of learning special relativity and mass–energy equivalence?
- What is the technology acceptance of learners after using the VR system?
2. Materials and Methods
The VR system developed in this study combines the situated learning theory and the important concepts of special relativity, allowing learners to simulate driving a spacecraft to explore the universe by travelling at nearly the speed of light. It also integrates the concepts of mass–energy equivalence into learning activities, which can enhance interest in learning and understanding the principle of relativity.
This study first analyzed the learning content and then conducted system planning and design according to the learning objectives. The main scenes of the VR system include: rocket launch station, control room, spacecraft, cockpit, scenes in outer space, and galaxies. The objects operated and observed by learners include: dashboard, clock, speed meter, and missiles. Among the above scenes and objects, Earth, the launch station, and the control room belong to the same coordinate system, while the spacecraft, the cockpit, the dashboard, and the alien spaceship belong to another coordinate system, each having its own clock. The change of time, length, and speed in individual coordinate systems can be seen on the screens of the control room and the spacecraft (Figure 1).
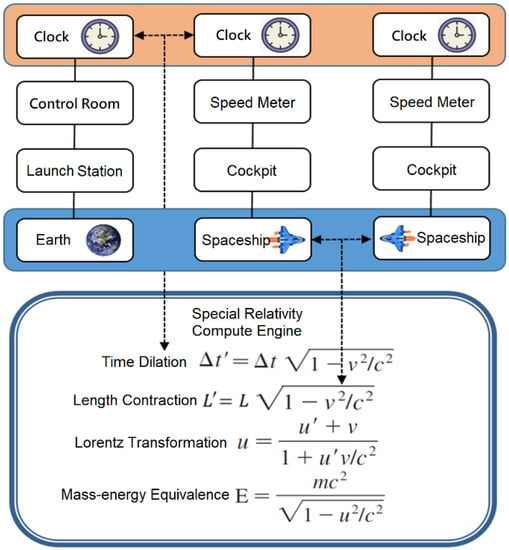
Figure 1.
System architecture of the virtual reality (VR) system.
This study used Microsoft Windows 10 as the development environment and Unity 3D as the tool for VR user interface design. Unity 3D has cross-platform capabilities and is often used to develop single-player games running on PC and Mac OS as well as multiplayer online games. The 3D models of objects and virtual scenes were created by Autodesk 3D Studio Max 2017, and then exported to Unity 3D as attachment files in FBX format. The relativity compute engine was designed using C#.
The development of a 3D object includes: creating the model (Figure 2), pasting material images, designing animation, and setting group assets and attributes. Because the spacecraft must be carried by a rocket into outer space, the launch station and rocket model must also be designed. The spacecraft has a dashboard and pilot seats. The pilot can control the direction and speed of the spacecraft, and observe the status of the spacecraft and the launch station on Earth (e.g., travelling distance and time) through the monitor on the dashboard. Before the mission starts, the clocks in the Earth and spacecraft coordinate systems are synchronous. As the speed of the spacecraft increases, the VR system will adjust the clock speed and the length of the scenes observed from the cockpit in the moving direction according to the calculation of the compute engine.
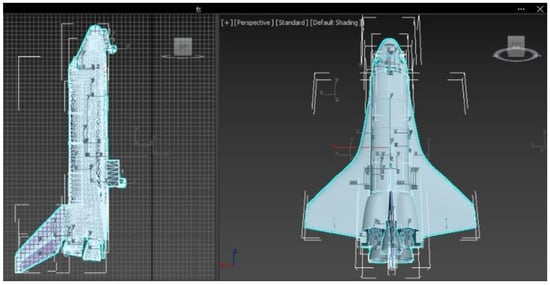
Figure 2.
Development of 3D objects in the VR system.
Unity 3D is a hierarchical and integrated development environment with the functions of visual editing, attribute setting, and dynamic game preview. It is a popular game development tool for designing 2D and 3D cross-platform games and interactive simulation environments. In this study, Unity 3D is used to import the objects created by 3ds Max into the virtual scenes, and the visual effects are enhanced by the built-in settings for scene design and light projection. The user interface of each scene is designed according to the stages of space exploration in the VR system, and the completed project is published by Unity 3D and converted into an executable file for installation on mobile devices such as tablets and smartphones. The learner can also wear an HMD and use controllers to access the VR system (Figure 3).

Figure 3.
Wearing a head-mounted display to access the VR system.
2.1. Relativity Compute Engine
The design of the relativity compute engine is based on the formulas of time dilation, length contraction, Lorentz transformation and mass–energy equivalence. S represents the Earth coordinate system and S’ represents the spacecraft coordinate system, and their X-axis and X′-axis overlap. When the spacecraft is moving along the X′-axis with a speed v, the observer on Earth will see the clock in the control room running normally but the clock in the spacecraft is slower due to time dilation, i.e.,
In the above equation, is the time interval that elapses on Earth and is the time interval that elapses in the spacecraft. If the distance between Earth and the target galaxy measured by the ground staff is L, then the distance measured by the spacecraft pilot will be shorter because the speed of the spacecraft increases due to length contraction, i.e.,
If the position in the spacecraft’s coordinate system along X-axis measured by an observer on Earth is x, then, according to the Lorentz transformation, the position of the spacecraft measured by the spacecraft pilot will be
In this study, we used C# to design a relativity compute engine in Unity 3D for time and length calculation according to the spacecraft speed. By setting objects in the same coordinate system as a group and using the same time and length ratios, we can calculate the time conversion between the two coordinate systems using the compute engine when the spacecraft speed changes. As shown in Figure 4, if the clock in the control room of the launch station is increased by 1 s each time, the spacecraft speed v is input to the compute engine and the conversion factor is calculated to determine the change of time and length observed from the spacecraft. Because the conversion factor is less than 1, the clock in the spacecraft will run slower than that in the control room.

Figure 4.
Relativity compute engine (switching to the Earth coordinate system).
If the relativity compute engine is switched back to the spacecraft coordinate system (Figure 5), the clock in the spacecraft is increased by 1 s each time. The compute engine uses the spacecraft speed v to calculate the conversion factor. It can then calculate the current time and length on the ground observed by the staff in the control room, and then change the length ratio (along X-axis direction) of all objects in the Earth group by the scale function. Because the conversion factor is less than 1, the clock in the control room on the ground will move faster than the clock in the spacecraft.
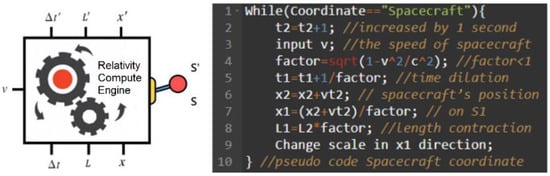
Figure 5.
Relativity compute engine (switching to the spacecraft coordinate system).
2.2. Mass–Energy Equivalence
Mass–energy equivalence states that mass and energy are the same property of an object and mass is the concentrated energy. All matter has mass, from galaxies, stars, and planets to molecules, atoms, and elementary particles. Mass is the fundamental property of all known matter, and its existence has a certain energy. All objects (regardless of their size) are attracted to each other in the universe. The total energy of an object is the sum of its rest energy and the energy in motion. Assuming that the mass of an object is 𝑚, the kinetic energy produced by the force on the object is
Applying the differential rule on multiplication, we have
According to the Lorentz transformation, if the mass of the object at rest is , then the equation for the transformation of mass based on the object’s velocity is
By moving the denominator on the right side of the equation above to the left side and then squaring both sides, we can obtain the following equation:
Differentiating both sides of the equation above yields
Moving the negative parts to the right side and dividing both sides by 2m, we have
The kinetic energy of the object can then be derived as
where the rest energy of the object is
The total energy of the object is equal to the sum of the kinetic energy of the object and the rest energy of the object , i.e.,
2.3. System Operation
The VR system allows learners to observe the changes in time and space in different coordinate systems caused by changing the spacecraft speed. The relativity compute engine performs the space-time transformation between different coordinate systems, and presents the respective scenes with 3D visual effects. Learners can play the roles of the spacecraft pilot and the control room staff to complete the mission of space exploration and understand the concepts of special relativity and mass–energy equivalence. When the spacecraft returns to Earth, learners can observe the clocks in the spacecraft and the launch station as well as the appearance of ground staffs to verify the time difference caused by the relative speed between the two different coordinate systems. During the space mission, the learners must answer questions correctly to verify the concepts of special relativity and mass–energy equivalence in each challenge stage.
This study used VR technology to create a learning environment and to design its virtual scenes and 3D object models based on the learning content. The VR system provides real-time feedback to facilitate learners’ exploration and manipulation in the virtual environment. The learner can press the “Start” button to enter the VR system, and the task of the first stage is to study the basic principles of special relativity. After reading the learning content on the screen, the learner must answer test questions correctly to launch the rocket and start the space exploration. In the second and the third stages, the learner must pilot the spacecraft and observe the space, time, and mass changes to understand the concepts of special relativity and mass–energy equivalence. In the last stage, the user will return to Earth and observe the appearances of ground staff in the control room. The flowchart of the VR system operation is shown in Figure 6.

Figure 6.
Flowchart of the VR system operation.
The scrip of the VR system is designed based on the mission of space exploration, in which the learner needs to complete the challenge stages by answering questions correctly. When the challenge of a stage is successful, the learner can enter the next stage. The first scene of the VR system is the control room (Figure 7) for launching the rocket, where the learner must become familiar with the controller’s functions. After reading the controller menu, the learner can click the “Start” button to enter the control room. The learner can complete the preparation task by reading the learning content of special relativity. After that, a button will pop up for the learner to launch the rocket.

Figure 7.
Virtual scene of the control room at the launch station.
If the learner answers a question incorrectly, they can choose to answer it again by reading the learning content on the screen of the control room for verification. After answering all questions correctly, the learner can enter the spacecraft to start the exploration mission. The rocket will carry the spacecraft slowly up into the sky, out of the range of gravity, and finally into outer space (Figure 8). The learner can adjust the speed and direction of the spacecraft and drive it towards the destination.

Figure 8.
Spacecraft reaching outer space after launching from Earth.
After entering the navigation stages, the monitor in front of the cockpit shows the current speed, the local time, and the remote time in the control room on Earth as well as the remaining nuclear fuel of the reactor (Figure 9). The learner can observe the difference between the running speed of the two clocks and compute the changes of time and space according to the spacecraft’s speed. For example, if the learner pilots the spacecraft at 0.9 times the speed of light to the destination, Proxima Centauri (about 4.3 light years from Earth), the challenge questions are: “How far is Earth away from Proxima Centauri as measured by the spacecraft pilot?” and “If the time in the control room on Earth passes by one minute, how long does the time in the spacecraft elapse?”.

Figure 9.
Control panel in the spacecraft cockpit.
Since the spacecraft travels at 0.9 times the speed of light, the distance between Earth and Proxima Centauri measured by the pilot in the spacecraft is calculated as
and the time elapsed in the spacecraft is only (seconds). The learner can also see the planet deforming as the speed of spacecraft increases (Figure 10).

Figure 10.
Deformation of planet as the spacecraft increasing its speed.
Before the spacecraft reaches Proxima Centauri, an alien spaceship will appear on the way to the destination. If the learner can correctly calculate the speed of the alien spaceship, they can avoid the enemy’s attack. If the calculation is incorrect, the spacecraft will be attacked by the enemy (Figure 11). For example, if the learner drives the spacecraft at 0.9 times the speed of light and the alien spaceship suddenly approaches at the same speed, relative to the Earth coordinate system, the challenge question is: “What is the speed of the alien spaceship measured by the human pilot?” According to the Lorentz transformation, the human pilot will measure the alien spaceship moving forward at the speed

Figure 11.
Alien spaceship attacking the human spacecraft.
Another challenge question is “If the enemy launches a missile at 0.95 times the speed of light relative to the alien spaceship, what is the velocity of the missile if measured in the control room of the launch station?” According to the Lorentz transformation, the speed of the missile measured in the control room on Earth is
If the human pilot shoots a laser beam towards the alien spaceship, what is the speed of the laser measured by the enemy? According to the special relativity, the speed of the laser beam measured by the enemy is still the speed of light, which can be verified as
The learner can confirm understanding the concepts of special relativity and mass–energy equivalence by answering questions in each stage of the mission. After the spacecraft returns to Earth, the learner can observe the clocks in the spacecraft and the control room as well as the appearance of the ground staff (Tom), who looks much older than the spacecraft pilot (Adam) even though they are twins (Figure 12).

Figure 12.
Adam returning to Earth after completing the mission.
3. Results
The VR system developed in this study combines the mission of space exploration with the learning content of special relativity. The learner starts by entering the rocket launch station to study basic knowledge of special relativity, and then goes through the mission to enhance the understanding of special relativity and mass–energy equivalence by interactive operation and observation. Each stage has test questions to confirm the learner’s understanding of the learning content. A teaching experiment was conducted to investigate learning effectiveness and cognitive load after using the VR system.
3.1. Experimental Design
In this study, a quasi-experiment with a pretest–posttest design was conducted by dividing learners into an experimental group and a control group, where the experimental group learned with the VR system and the control group learned with textbooks. This study recruited 60 students from a university in Hsinchu, Taiwan, with 50% (n = 30) males and 50% (n = 30) females. The educational background of participants was 46.67% in science and engineering and 53.33% in other fields. The research tools of the teaching experiment include the achievement test (pretest and posttest), cognitive-load scale, and system satisfaction questionnaire. The independent variable is the teaching method; the dependent variable is the learning effectiveness; the covariate is the background knowledge of special relativity; the control variables are the instructor, teaching time, and learning content. The variables of the teaching experiment are shown in Table 1.

Table 1.
Research variables of the teaching experiment.
The purpose of this teaching experiment is to analyze whether there is a significant difference in the effectiveness of using different methods for learning the concepts of special relativity and mass–energy equivalence. Before and after the treatment, students took the achievement test and they had to complete the cognitive load scale after the posttest. The experimental group also conducted a questionnaire survey to understand their satisfaction with the VR system (Figure 13). In addition, this study interviewed the instructor for his opinion on the application of VR in learning special relativity. The qualitative data can also be used as a reference for improving the VR system.
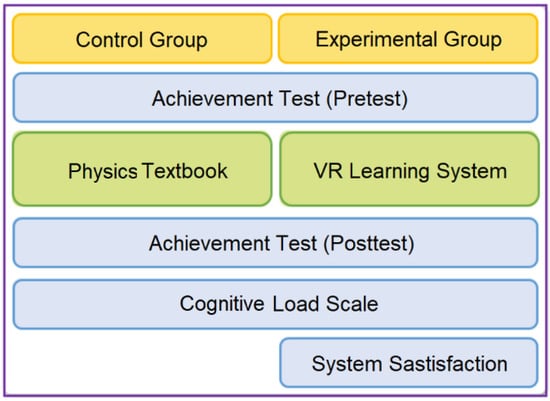
Figure 13.
Flowchart of the teaching experiment in this study.
3.2. Research Tools
The research tools used in this study include the learning achievement test (pretest and posttest), the cognitive load scale, and the system satisfaction survey. The design and content of these tools are described as follows:
- Achievement test
In order to investigate the learning effectiveness of participants using the VR system, this study developed the achievement test (pretest and posttest) and invited a physics teacher and two experts to analyze the difficulty of test questions and ensure their validity and consistency with the instructional objectives. An internal consistency analysis was conducted to remove unsuitable questions. After that, the achievement test contained 10 multiple-choice questions with three options to choose from. A higher score in the achievement test indicated a better performance in the learning result.
- Cognitive load scale
This scale was adapted from the scales developed by Chang et al. [22] and Thees et al. [23]. After the adaptation, three experts were invited to review the questions to ensure that the changes were consistent with the original topic and each question matched the main concepts for measuring cognitive load. The experts included a science educator, a physics expert, and a high school physics teacher to review and discuss the scale until they all agreed on the questions to ensure the validity. The scale is composed of two parts: “mental effort” and “mental load”, each containing 10 questions.
- System satisfaction survey
In order to understand learners’ satisfaction after using the VR system, this study developed a system satisfaction scale based on the teaching experience of and discussion with experts to ensure the correctness of the questionnaire. The survey contained 16 questions in four parts: “teaching content”, “cognitive usefulness”, “cognitive ease of use”, and “user satisfaction” based on a five-point Likert scale; the score ranged from “strongly agree = 5” to “strongly disagree = 1”. The questionnaire was reviewed by the experts for examining its validity with the Cronbach’s α = 0.939.
3.3. Experimental Results
The data collected from the teaching experiment consist of pretest and posttest scores of the achievement test as well as the results of the cognitive load scale and system satisfaction survey. In this study, descriptive statistics, paired sample t-tests, independent sample t-tests, and one-way analysis of covariance (ANCOVA) are used to perform statistical analyses on the experimental results.
- Learning effectiveness
According to the results in Table 2, the mean score of the experimental group is 45.67 with a standard deviation of 15.47 in the pretest and 57.67 with a standard deviation of 14.78 in the posttest. The mean score of the control group is 40.67 with a standard deviation of 11.72 in the pretest and 45.67 with a standard deviation of 16.75 in the posttest. The progress of the experimental group is higher than that of the control group.

Table 2.
Results of descriptive statistics on pretest and posttest scores.
Table 3 shows the difference between the pretest and posttest for the two groups through the analysis of pair samples t-tests. The difference between the two tests for the experimental group is −12.000 with a standard deviation of 18.670; the difference between the two tests for the control group is −5.000 with a standard deviation of 18.336. The analysis of the pair samples t-test for the experimental group shows t = −3.527 and p = 0.001 < 0.01, with a significant result. For the control group, the analysis of the pair samples t-test shows t = −1.494 and p = 0.146 > 0.05, without reaching the significant level. This means that the experimental group had effective learning but the control group did not.

Table 3.
Results of paired samples t-test on learning achievement for both groups.
In this study, a one-way ANCOVA is conducted to further compare the learning effectiveness of the two groups. Before conducting the ANCOVA, a Levene’s test is used to examine whether the two groups are homogeneous. If the p-value of the Levene’s test is greater than 0.05, the two groups are homogeneous. The test results are f = 0.997 and p = 0.322 > 0.05, without reaching the significant level, so the hypothesis of homogeneity is satisfied and the ANCOVA can therefore be performed.
In the ANCOVA, the pretest score is used as the covariate, the posttest score is used as the dependent variable, and the group is the independent variable to analyze whether there is a significant difference in the learning effectiveness between the two groups. The results in Table 4 show that the learning effectiveness between the two groups is significant, f = 6.909 and p = 0.011 < 0.05, indicating that there is a significant difference in the posttest scores for both groups depending on the learning method with a net correlation of η2 = 0.108, which is a high correlation strength.

Table 4.
ANCOVA results on learning achievement for both groups.
According to the ANCOVA results, the VR system is more effective than the textbook for improving the learning achievement because learners could conduct space exploration to enhance their understanding of relativistic concepts by observing the phenomena of time dilation and length contraction.
- Cognitive load
The cognitive load scale is divided into two parts, “mental effort” and “mental load”, each containing 10 questions. The questions 3, 4, 5, 6, and 7 of the “mental effort” scale are reversed, and all questions of the “mental load” scale are reversed except for questions 1, 2, and 7, of which the results are recoded. The results in Table 5 show that the mean score for the experimental group is 2.86 with a standard deviation of 0.592 and the mean score for the control group is 3.74 with a standard deviation of 0.695. The t-test results show that t = −5.249 and p < 0.001, indicating that the cognitive load of the experimental group is significantly lower than that of the control group. In other words, learning with the VR system incurred lower cognitive load than using the textbook. It can be inferred that the VR system was more interesting and caused less mental effort for learners because they could experience the fun of space exploration during the learning process, which was useful for reducing the cognitive load caused by abstract concepts.

Table 5.
Results of t-test on cognitive load for both groups.
The results of mental effort in Table 6 show that the experimental group has a mean score 3.18 with a standard deviation 0.60 and the control group has a mean score 3.75 with a standard deviation 0.64. The difference between the two groups is moderately significant with p = 0.001 < 0.01. For mental load, the mean score of the experimental group is 2.55 with a standard deviation 0.66, and the mean score of the control group is 3.73 with a standard deviation 0.80. The difference between the two groups is highly significant with p < 0.001, indicating that the VR system incurred lower mental effort and mental load and the effect of the latter was more significant than the former.

Table 6.
Dimensional analysis on cognitive load for both groups.
Table 7 shows the statistical results for the “mental effort” scale, in which the differences between the two groups for questions 2, 3, 4, 9, and 10 are not significant. It is inferred that special relativity itself is very difficult and there are more formulas and abstract concepts involved and thus require more mental effort in learning. Furthermore, learners needed to deal with many messages at the same time because the test questions involved multiple concepts in calculation. The major difference between the two groups shows that the experimental group spent less effort in learning relativistic concepts because the VR system provided an interactive environment for observation, thus the experimental group performed better than the control group and had a sense of accomplishment.

Table 7.
Mean, standard deviation, and significance of “mental effort” score for both groups.
Table 8 shows the statistical results for the “mental load” scale, in which the differences between the two groups for all items are significant. The scores of questions 5 and 6 are greater than three for the control group and greater than four for the control group with significant differences, indicating a higher cognitive load was incurred for both groups because special relativity and mass–energy equivalence are difficult learning subjects no matter which learning method was used. However, the concepts of special relativity were more abstract and difficult for learning using textbooks. Similarly, the concepts of mass–energy equivalence were difficult to understand and it could affect the learning interest of the control group, thus the experimental group spent less time to achieve a better performance and had more confidence to continue learning physics.

Table 8.
Mean, standard deviation, and significance of “mental load” scores for both groups.
- System satisfaction
According to the results in Table 9, the overall mean score of the system satisfaction is 4.04. Among the four dimensions, the mean score of “teaching content” is 3.83; the mean score of “cognitive usefulness” is 3.88; the mean score of “cognitive ease of use” is 4.27; the mean score of “user satisfaction” is 4.18. In general, the cognitive ease of the VR system is high, indicating that most learners were satisfied with the VR system. Among all questions, the scores of questions 3, 8, 9, 10, 12, 14, and 16 are higher, indicating that: the test questions are clearly described; the VR system can enhance the learning experience of special relativity; it is interesting to learn special relativity with the VR system; learning to use the system is easy; Overall, learners were satisfied with the VR system.

Table 9.
Mean score and standard deviation of system satisfaction survey.
4. Discussion
The research by Adams et al. [24] discovered that well-designed simulations can provide better understanding than traditional physics instruction. Chu et al. proposed that visual simulations are highly engaging and effective for learners because they are more likely to understand unfamiliar scientific concepts [25]. Windmiller et al. [26] developed immersive activities for the introductory astronomy course and laboratory, i.e., moon phases and stellar parallax. They tested the efficacy of these activities on a large cohort of general education astronomy students and reported that VR-based techniques performed comparably well against other teaching methods. They reported similar results between the VR group and the control group and emphasized the significant workload of developing the VR activities, as can be seen in this study.
A popular space flight simulation video game called Kerbal Space Program, developed by the Mexican developer Squad [27], intends to engage students to understand space mission design and associated physics through the game-based learning approach. The players have access to a number of parts to assemble a fully-functional spacecraft that flies based on realistic aerodynamic and orbital physics. This game features a realistic orbital physics engine, allowing for various real-life orbital maneuvers such as Hohmann transfer orbits and orbital rendezvous, and papers such as [28,29] discuss its use in schools and their results are similar to those obtained in this study.
In recent years, the rapid development of information and communications technology paved the way for immersive technologies such as virtual reality (VR) to emerge. In the virtual world, learners can use their visual, auditory, and other senses to feel as if situated in the real world, and they can communicate with others to experience an immersive feeling. VR is a 3D simulation technology that creates a virtual and highly interactive environment through special hardware interface by integrating with artificial intelligence, network parallel processing, computer graphics, computer simulation, display, and sensing technologies. VR has been applied in science, entertainment, education, and engineering because a virtual environment can achieve realistic effects without danger and consuming resources in the real environment.
In addition to VR, Mixed Reality (MR) represents an innovative tool for various sectors. MR is a combination of VR and Augmented Reality (AR), an immersive technology combining virtual objects and information with the real world based on position or image recognition. MR is often confused with AR, and the former is identified by the situation that users can interact with both virtual and real objects in real time, while these objects can also interact with each other simultaneously [30,31]. This “awareness of the environment” implies that not only do virtual objects act in the real environment, but real objects can also modify virtual elements, no matter where the experience is taking place.
McCloy and Stone [32] used VR to develop the Minimally Invasive Surgical Trainer (MIST) system, a surgical simulator for laparoscopic skills training. The MIST system provided objective assessment of psychomotor skills and could generate an overall score for performance based on errors made and time taken for training tasks. Burdea and Coiffet [33] illustrated the definition of VR through a number of interesting remote robotic applications, where a 3D space was simulated by computers to provide immediate feedback for the user after giving commands, which can stimulate the sense organs for the user to immerse in the 3D virtual space.
Dede et al. [34] conducted research on touch sensation for robotic design and optimization through structural analysis in a computer-aided design environment to improve the accuracy and sense of presence in remote operations. Lee and Wong [35] investigated the learning effectiveness of high school students in a virtual learning environment, including the effect of learners’ ability to interact with different spaces. Lopreiato [36] used various immersive 3D visual simulations to replicate real-life scenarios. These studies confirmed that VR can help learners acquire new learning experiences and information, change their cognition, and correct misconceptions.
VR has many advantages on learning scientific concepts, such as: learners can use virtual experiments as scaffolds to help construct complete scientific concepts [37]. It can also simulate dynamic phenomena to help learners understand abstract concepts [38]. VR allows learners to repeat experiments and analyze difficult scientific knowledge, principles, or concepts, and it can change viewing angles to enhance perception [39]. Virtual experiments can provide learners with repetitive and efficient operating procedures to shorten waiting time, save money, and reduce errors in the experimental process, which is helpful for improving learners’ experimental skills.
The study by Tarng et al. [40] found that learners’ interest in carbon nanotechnology was enhanced by using the virtual electron microscopy to observe carbon nanostructures. It could also improve their learning motivation and achievement in nanostructure analysis. Jacobson, Taylo, and Richards [41] investigated the effects of 3D virtual worlds and 2D virtual ecosystems on inquiry-based learning. They found that both groups were interested in the immersion of virtual worlds and the middle- and low-achievement learners improved more significantly than the high-achievement learners.
In this study, the three learning objectives of special relativity proposed by Alstein et al. [21] have been achieved using the VR system, i.e., (1) to enhance conceptual understanding, (2) to foster understanding of the history and philosophy of science, and (3) to gain motivation and confidence toward special relativity and modern physics in general because it allows learners to verify important concepts such as time dilation and length contraction through observation and interaction.
The VR system provides a scaffold for independent learning to facilitate conceptual change and to make abstract and complex concepts concrete, observable, and interesting. However, generalization from the experimental results should be cautious with the small sample sizes and lack of repetition over many cohorts. In the future, it is suggested that a more prudent study be conducted to test the hypothesis that VR students do not perform worse than the other cohort by using a larger sample size.
5. Conclusions
This study used the VR technology to develop a VR system by transforming abstract concepts of special relativity and mass–energy equivalence into an interesting and observable space exploration mission. The VR system provides an immersive and interactive environment for learners to explore the universe by driving the spacecraft at near light speed to observe the changes in time and space between different coordinate systems and understand that mass and energy can be converted to each other. VR can strengthen learning impressions through multiple and complementary perspectives, thus creating a more intuitive and realistic experience. Learners can understand the principles of special relativity and the concepts of mass–energy equivalence through interactive operation and observation. This study investigated the learning effectiveness and cognitive load of learners after using the VR system through a teaching experiment, and the findings of this study are as listed as follows:
- Learning effectiveness
The analytical results show that the experimental group performed better than the control group. There is a significant difference in learning effectiveness between the two groups, indicating using the VR system could improve the learning effectiveness on the concepts of special relativity and mass–energy equivalence.
- Cognitive load
The statistical results show that there is a significant difference in cognitive load between the experimental group and the control group, indicating that using the VR system to learn the concepts of special relativity and mass–energy equivalence could reduce the cognitive load of learners, especially the mental load.
- System satisfaction
The overall mean score of the satisfaction survey is higher than 4. The learners were more satisfied with the items “cognitive ease of use” and “user satisfaction”, and they thought the VR system was interesting and easy to use. Generally speaking, learners were satisfied with the overall performance of the VR system
In previous studies, the performance of VR in learning special relativity and mass–energy equivalence has seldom been investigated. The experimental results in this study reveal that using the VR system can enhance the learning effectiveness and reduce the cognitive load of learners in comparison with the traditional method (using textbooks). The concepts of special relativity and mass–energy equivalence are difficult to understand and therefore require more observation and thinking. It is recommended that the design of teaching materials should take the operating time into account to avoid affecting learners’ attention and incurring additional cognitive load because they may feel dizziness after wearing the HMD for a long time.
The results of this study can be used as a reference for future research on the design of virtual software for immersive learning and how to avoid user discomfort. The learning content of this study are mainly for high school and college students in science education. When extending the application to other age groups, it is recommended to adjust the difficulty of teaching materials in order to meet the needs of young learners.
The concept of metaverse emerged in recent years and has great potential for development in the areas of entertainment and education. The VR system developed in this study can only be accessed by a single user, and it is suggested that a multiplayer online mission could be created in the future to expand the social connection and achieve the effect of cooperative learning and peer discussion. The VR system developed in this study transforms abstract and difficult scientific concepts into an easy-to-understand learning experience. It is interesting and educational with low construction and maintenance costs. Further promotion activities will be conducted to achieve the goal of popularizing science. The goal is for learners to understand that relativistic concepts are not incomprehensible, and that they are willing to take the initiative to learn the new knowledge and have the ability to apply the knowledge to solve real-life problems.
6. Limitations and Future Works
Although VR is effective for improving learning achievement and reducing cognitive load, there are some limitations for extending its applications and findings obtained in this study, as described below:
- Restriction on learning equipment
This study used the HMD as learning equipment, but some participants felt uncomfortable after wearing it for a long time. To avoid the symptoms of dizziness and nausea due to motion sickness, it is suggested to take a rest if these symptoms occur. In the future, a preliminary test can be conducted before the experiment to exclude the participants suffering from physical discomfort due to wearing the HMD for a long time.
- Research variables
Because the learning effectiveness and cognitive load may be affected by the educational background, gender, and age of individual participants, it is suggested to include additional research variables to obtain more in-depth investigation and findings.
In this study, the VR system is developed for learning the concepts of special relativity and mass–energy equivalence. It is suggested that future studies may include the learning content of general relativity because special relativity is only a special case of general relativity. Specifically, general relativity reduces to special relativity in the case of negligible gravity or a flat spacetime—for example, in space far from any objects. VR can visualize gravity as the three-dimensional curvature of space and time, which is helpful for learners to understand the concepts of general relativity.
The VR system can also be developed for learning quantum mechanics, a physical theory describing the behavior of microscopic matter. It is the basis for understanding all basic forces (electromagnetic interaction, strong interaction, and weak interaction) except gravitation. Quantum mechanics has brought revolutionary changes to physics and, as well as relativity, it is considered as the foundation of modern physics. Many students find it difficult to understand that microscopic particles have both wave and particle properties due to the scale of the real world they see. Quantum mechanics deals with things that are very small, and the particle and wave phenomena at the microscopic scale are difficult to observe and understand. Therefore, the VR system can concretize and visualize the abstract concepts of quantum mechanics in the microscopic world.
Author Contributions
Investigation and formal analysis: Y.-C.L.; investigation and methodology: K.-L.O.; investigation, writing–review, and editing: W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science and Technology Council (NSTC), Taiwan under the grant numbers 111-2410-H-007-009 and 109-2511-H-007-006-MY3.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Research Ethics Committee of National Tsing Hua University, Taiwan (10905HT035, 16 July 2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beatty, M.F. Introduction to Advanced Dynamics. Principles of Engineering Mechanics; Springer: Boston, MA, USA, 2006. [Google Scholar]
- Knight, R.D. Physics for Scientists and Engineers: A Strategic Approach with Modern Physics; Pearson: London, UK, 2007. [Google Scholar]
- Fowler, J.S.; Ido, T. Initial and subsequent approach for the synthesis of 18FDG. Semin. Nucl. Med. 2002, 32, 6–12. [Google Scholar] [CrossRef] [PubMed]
- Dimitriadi, K.; Halkia, K. Secondary students’ understanding of basic ideas of special relativity. Int. J. Sci. Educ. 2012, 34, 2565–2582. [Google Scholar] [CrossRef]
- Scherr, R.E.; Shaffer, P.S.; Vokos, S. Student understanding of time in special relativity: Simultaneity and reference frames. Am. J. Phys. 2001, 69 (Suppl. 1), S24–S35. [Google Scholar] [CrossRef]
- Kustanto, H.; Oktova, R. The twin paradox in the theory on special relativity as an enrichment topic for high school physics. Berk. Fis. Indones. 2016, 8, 10–16. [Google Scholar]
- Horwitz, P.; Taylor, E.F.; Hickman, P. “Relativity readiness” using the RelLab program. Phys. Teach. 1994, 32, 81–86. [Google Scholar]
- Belloni, M.; Christian, W.; Dancy, M.H. Teaching special relativity using Physlets®. Phys. Teach. 2004, 42, 284–290. [Google Scholar] [CrossRef]
- Taylor, E.F. Space-time software: Computer graphics utilities in special relativity. Am. J. Phys. 1989, 57, 508–514. [Google Scholar] [CrossRef]
- Carr, D.N.; Bossomaier, T.; Lodge, K. Designing a computer game to teach Einstein’s Theory of Relativity. In Proceedings of the Computer Graphics, Imaging and Visualisation Conference, Bangkok, Thailand, 14–17 August 2007; IEEE Computer Society: Los Alamitos, CA, USA, 2007; pp. 109–114. [Google Scholar]
- Weiskopf, D.; Borchers, M.; Ertl, T.; Falk, M.; Fechtig, O.; Frank, R.; Grave, F.; King, A.; Kraus, U.; Muller, T. Explanatory and illustrative visualization of special and general relativity. IEEE Trans. Vis. Comput. Graph. 2006, 12, 522–534. [Google Scholar] [CrossRef]
- De Hosson, C.; Doat, T.; Kermen, I.; Parizot, E.; Vézien, J. Designing learning scenarios for a 3D virtual environment: The case of special relativity. Lat.-Am. J. Phys. Educ. 2012, 6, 27–33. [Google Scholar]
- De Hosson, C.; Kermen, I.; Maisch, C.; Parizot, E.; Doat, T.; Vézien, J.-M. Learning scenario for a 3D virtual environment: The case of special relativity. In Frontiers of Fundamental Physics and Physics Education Research; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Savage, C.M.; Searle, A.; McCalman, L. Real time relativity: Exploratory learning of special relativity. Am. J. Phys. 2007, 75, 791–798. [Google Scholar] [CrossRef]
- McGrath, D.; Wegener, M.; McIntyre, T.J.; Savage, C.; Williamson, M. Student experiences of virtual reality: A case study in learning special relativity. Am. J. Phys. 2010, 78, 862–868. [Google Scholar] [CrossRef]
- Savage, C.; Wegener, M.; McIntyre, T.; McGrath, D.; Williamson, M. Teaching physics using virtual reality: Special relativity. In Proceedings of the AIP 18th National Congress, Adelaide, Australia, 30 November–5 December 2008. [Google Scholar]
- Lave, J.; Wenger, E. Situated Learning. Legitimate Peripheral Participation; University of Cambridge Press: Cambridge, UK, 1991. [Google Scholar]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Andersen, S.A.W.; Frendø, M.; Sørensen, M.S. Effects on cognitive load of tutoring in virtual reality simulation training. MedEdPublish 2020, 9, 51. [Google Scholar] [CrossRef][Green Version]
- Vesga, J.B.; Xu, X.; He, H. The effects of cognitive load on engagement in a virtual reality learning environment. In Proceedings of the 2021 IEEE Virtual Reality and 3D User Interfaces (VR), Lisboa, Portugal, 27 March–1 April 2021; pp. 645–652. [Google Scholar]
- Alstein, P.; Krijtenburg-Lewerissa, K.; van Joolingen, W.R. Teaching and learning special relativity theory in secondary and lower undergraduate education: A literature review. Phys. Rev. Phys. Educ. Res. 2021, 17, 023101. [Google Scholar] [CrossRef]
- Chang, C.C.; Liang, C.; Chou, P.N.; Lin, G.Y. Is game-based learning better in flow experience and various types of cognitive load than non-game-based learning? Perspective from multimedia and media richness. Comput. Hum. Behav. 2017, 71, 218–227. [Google Scholar] [CrossRef]
- Thees, M.; Kapp, S.; Strzys, M.P.; Beil, F.; Lukowicz, P.; Kuhn, J. Effects of augmented reality on learning and cognitive load in university physics laboratory courses. Comput. Hum. Behav. 2020, 108, 106316. [Google Scholar] [CrossRef]
- Adams, W.K.; Paulson, A.; Wieman, C.E. What levels of guidance promote engaged exploration with interactive simulations? In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2008; Volume 1064, pp. 59–62. [Google Scholar]
- Chu, G.; Humer, I.; Eckhardt, C. Special relativity in immersive learning. In Proceedings of the International Conference on Immersive Learning, London, UK, 23–27 June 2019; Springer: Cham, Switzerland, 2019; pp. 16–29. [Google Scholar]
- Windmiller, G.; Blanco, P.; Welsh, W.F. Developing virtual reality activities for the Astro 101 Class and Lab, ASP2020: Embracing the Future: Astronomy Teaching and Public Engagement 2021. ASP Conf. Ser. 2021, 531, 285. [Google Scholar]
- Luke, V. “‘Kerbal Space Program’ Launches NASA ‘Asteroid Redirect Mission’ Update [VIDEO]”. International Business Times, 2 April 2014. Available online: https://www.ibtimes.com/kerbal-space-program-launches-nasa-asteroid-redirect-mission-update-video-1566556 (accessed on 19 November 2022).
- Rosenthal, S.; Ratan, R.A. Balancing learning and enjoyment in serious games: Kerbal Space Program and the communication mediation model. Comput. Educ. 2022, 182, 104480. [Google Scholar] [CrossRef]
- Ranalli, J.; Ritzko, J. Assessing the Impact of Video Game Based Design Projects in a First Year Engineering Design Course. In Proceedings of the IEEE Frontiers in Education, Oklahoma City, OK, USA, 23–26 October 2013. [Google Scholar] [CrossRef]
- Monterubbianesi, R.; Tosco, V.; Vitiello, F.; Orilisi, G.; Fraccastoro, F.; Putignano, A.; Orsini, G. Augmented, Virtual and Mixed Reality in Dentistry: A Narrative Review on the Existing Platforms and Future Challenges. Appl. Sci. 2022, 12, 877. [Google Scholar] [CrossRef]
- Flavián, C.; Ibáñez-Sánchez, S.; Orús, C. The impact of virtual, augmented and mixed reality technologies on the customer experience. J. Bus. Res. 2019, 100, 547–560. [Google Scholar] [CrossRef]
- McCloy, R.; Stone, R. Virtual reality in surgery. BMJ 2001, 323, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Burdea, G.C.; Coiffet, P. Virtual reality technology. Presence Teleoperators Virtual Environ. 2003, 12, 663–664. [Google Scholar] [CrossRef]
- Dede, M.İ.C.; Selvi, Ö.; Bilgincan, T.; Kant, Y. Design of a haptic device for teleoperation and virtual reality systems. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, SMC 2009, San Antonio, TX, USA, 11–14 October 2009. [Google Scholar]
- Lee, E.A.L.; Wong, K.W. Learning with desktop virtual reality: Low spatial ability learners are more positively affected. Comput. Educ. 2014, 79, 49–58. [Google Scholar] [CrossRef]
- Lopreiato, J.O. Healthcare Simulation Dictionary; Agency for Healthcare Research and Quality: Rockville, MD, USA, 2016.
- Lee, H.P. An example of the interaction between virtual and physical experiments in dynamics. Int. J. Mech. Eng. Educ. 2004, 32, 93–99. [Google Scholar] [CrossRef]
- Chen, C.H.; Yang, J.C.; Shen, S.; Jeng, M.C. A desktop virtual reality earth motion system in astronomy education. J. Educ. Technol. Soc. 2007, 10, 289–304. [Google Scholar]
- Lee, E.A.L.; Wong, K.W.; Fung, C.C. How does desktop virtual reality enhance learning outcomes? A structural equation modeling approach. Comput. Educ. 2010, 55, 1424–1442. [Google Scholar]
- Tarng, W.; Tsai, C.F.; Lin, C.M.; Lee, C.Y.; Liou, H.H. Development of an educational virtual transmission electron micro-scope laboratory. Virtual Real. 2015, 9, 33–44. [Google Scholar] [CrossRef]
- Jacobson, M.J.; Taylor, C.E.; Richards, D. Computational scientific inquiry with virtual worlds and agent-based models: New ways of doing science to learn science. Interact. Learn. Environ. 2016, 24, 2080–2108. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).