Hilltop Inflation and Generation of Helical Magnetic Field
Abstract
:1. Introduction and Motivation
2. Basic Field Equations: Setting Up the Stage
3. Hilltop Inflation with Quadratic Potential
4. Modified Maxwell’s Equations in Cosmological Background
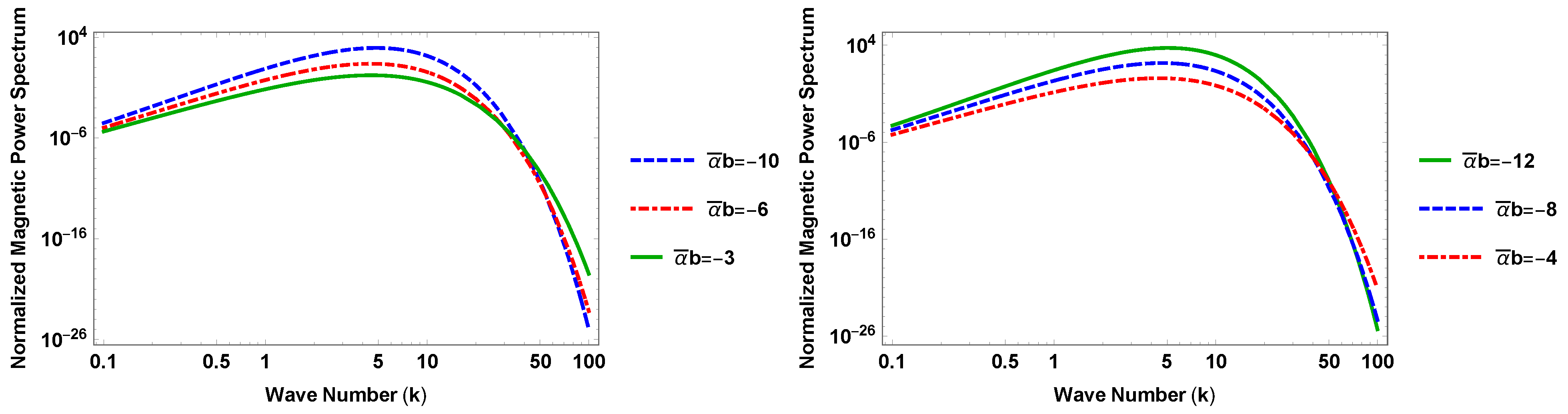
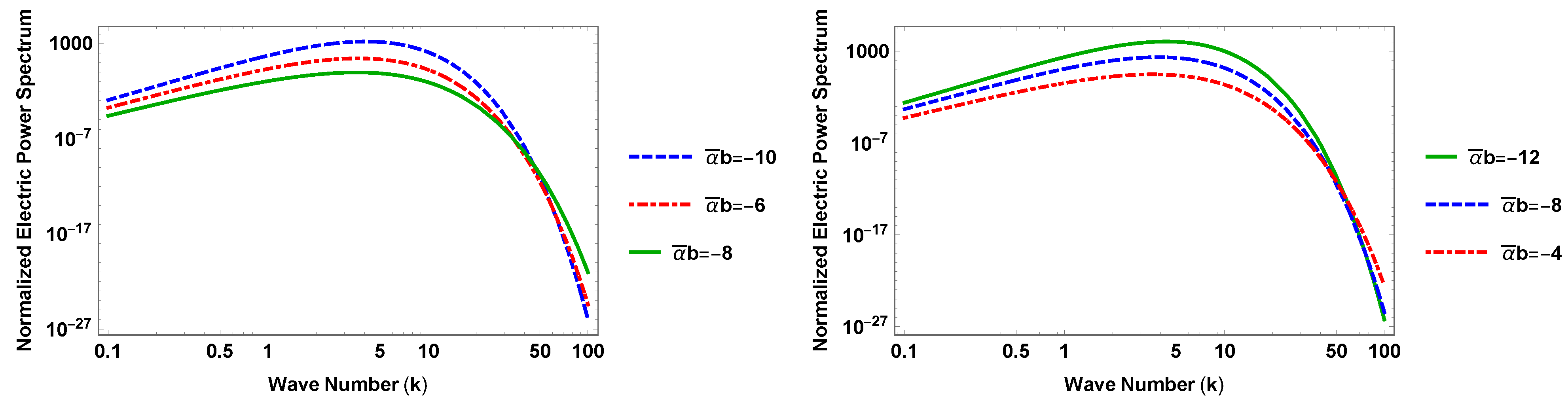
5. Power Spectra for Electric and Magnetic Fields
5.1. Power Spectra in Terms of Vector Potential
5.2. Solving for the Vector Potential
6. Strength of the Magnetic Field and Its Scale Dependance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
| 1 | To be precise the estimate of spatial curvature corresponds to from latest Planck 2018 data through TT, TE, EE + lowE + lensing + BAO data [35]. Here TT means temperature temperature cross-correlation of CMB data, TE means cross-correlation between temperature and electric type polarization of CMB data and finally BAO stands for Baryon Acoustic Oscillation. |
| 2 | In principle, one can also define an electric spectral index with similar arguments, but as it will turn out, the electric field strength is not going to play significant role here and hence, we will eventually ignore it. |
References
- Grasso, D.; Rubinstein, H.R. Magnetic fields in the early universe. Phys. Rept. 2001, 348, 163–266. [Google Scholar] [CrossRef] [Green Version]
- Beck, R. Galactic and extragalactic magnetic fields. Space Sci. Rev. 2001, 99, 243–260. [Google Scholar] [CrossRef]
- Widrow, L.M. Origin of galactic and extragalactic magnetic fields. Rev. Mod. Phys. 2002, 74, 775–823. [Google Scholar] [CrossRef] [Green Version]
- Kandus, A.; Kunze, K.E.; Tsagas, C.G. Primordial magnetogenesis. Phys. Rept. 2011, 505, 1–58. [Google Scholar] [CrossRef] [Green Version]
- Durrer, R.; Neronov, A. Cosmological Magnetic Fields: Their Generation, Evolution and Observation. Astron. Astrophys. Rev. 2013, 21, 62. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rept. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulsrud, R.M.; Zweibel, E.G. The Origin of Astrophysical Magnetic Fields. Rept. Prog. Phys. 2008, 71, 0046091. [Google Scholar] [CrossRef] [Green Version]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rept. 2005, 417, 1–209. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, K. Magnetic fields in the early universe. Astron. Nachr. 2010, 331, 110–120. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.; Jagannathan, S.; Seshadri, T.R.; Subramanian, K. Challenges in Inflationary Magnetogenesis: Constraints from Strong Coupling, Backreaction and the Schwinger Effect. Phys. Rev. 2017, D96, 083511. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.; Subramanian, K.; Seshadri, T.R. Generation of helical magnetic field in a viable scenario of inflationary magnetogenesis. Phys. Rev. 2018, D97, 083503. [Google Scholar] [CrossRef] [Green Version]
- Jain, R.K.; Sloth, M.S. Consistency relation for cosmic magnetic fields. Phys. Rev. 2012, D86, 123528. [Google Scholar] [CrossRef] [Green Version]
- Koley, R.; Samtani, S. Magnetogenesis in Matter-Ekpyrotic Bouncing Cosmology. J. Cosmol. Astropart. Phys. 2017, 1704, 030. [Google Scholar] [CrossRef] [Green Version]
- Durrer, R.; Hollenstein, L.; Jain, R.K. Can slow roll inflation induce relevant helical magnetic fields? J. Cosmol. Astropart. Phys. 2011, 1103, 037. [Google Scholar] [CrossRef] [Green Version]
- Kanno, S.; Soda, J.; Watanabe, M.A. Cosmological Magnetic Fields from Inflation and Backreaction. J. Cosmol. Astropart. Phys. 2009, 0912, 009. [Google Scholar] [CrossRef]
- Campanelli, L. Helical Magnetic Fields from Inflation. Int. J. Mod. Phys. 2009, D18, 1395–1411. [Google Scholar] [CrossRef] [Green Version]
- Martin, J.; Yokoyama, J. Generation of Large-Scale Magnetic Fields in Single-Field Inflation. J. Cosmol. Astropart. Phys. 2008, 0801, 025. [Google Scholar] [CrossRef] [Green Version]
- Demozzi, V.; Mukhanov, V.; Rubinstein, H. Magnetic fields from inflation? J. Cosmol. Astropart. Phys. 2009, 0908, 025. [Google Scholar] [CrossRef] [Green Version]
- Bamba, K.; Sasaki, M. Large-scale magnetic fields in the inflationary universe. J. Cosmol. Astropart. Phys. 2007, 0702, 030. [Google Scholar] [CrossRef]
- Ratra, B. Cosmological ‘seed’ magnetic field from inflation. Astrophys. J. 1992, 391, L1–L4. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 2016, 594, A19. [Google Scholar]
- Dolag, K.; Kachelriess, M.; Ostapchenko, S.; Tomas, R. Lower limit on the strength and filling factor of extragalactic magnetic fields. Astrophys. J. 2011, 727, L4. [Google Scholar] [CrossRef] [Green Version]
- Neronov, A.; Vovk, I. Evidence for strong extragalactic magnetic fields from Fermi observations of TeV blazars. Science 2010, 328, 73–75. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, D.; Sriramkumar, L.; Kamionkowski, M. Enhancing the cross-correlations between magnetic fields and scalar perturbations through parity violation. J. Cosmol. Astropart. Phys. 2018, 2018, 031. [Google Scholar] [CrossRef] [Green Version]
- Vachaspati, T. Magnetic fields from cosmological phase transitions. Phys. Lett. 1991, B265, 258–261. [Google Scholar] [CrossRef]
- Turner, M.S.; Widrow, L.M. Inflation Produced, Large Scale Magnetic Fields. Phys. Rev. 1988, D37, 2743. [Google Scholar] [CrossRef]
- Takahashi, K.; Ichiki, K.; Ohno, H.; Hanayama, H. Magnetic field generation from cosmological perturbations. Phys. Rev. Lett. 2005, 95, 121301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agullo, I.; Navarro-Salas, J. Conformal anomaly and primordial magnetic fields. arXiv 2013, arXiv:1309.3435. [Google Scholar]
- Ferreira, R.J.Z.; Jain, R.K.; Sloth, M.S. Inflationary magnetogenesis without the strong coupling problem. J. Cosmol. Astropart. Phys. 2013, 1310, 004. [Google Scholar] [CrossRef] [Green Version]
- Atmjeet, K.; Seshadri, T.R.; Subramanian, K. Helical cosmological magnetic fields from extra-dimensions. Phys. Rev. 2015, D91, 103006. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, D.; Sriramkumar, L.; Jain, R.K. Duality and scale invariant magnetic fields from bouncing universes. Phys. Rev. 2016, D94, 083512. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, D.; Sriramkumar, L.; Kamionkowski, M. Cross-correlations between scalar perturbations and magnetic fields in bouncing universes. J. Cosmol. Astropart. Phys. 2019, 2019, 048. [Google Scholar] [CrossRef] [Green Version]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2018, 641, A6. [Google Scholar]
- Bouchet, F.R. COrE (Cosmic Origins Explorer) A White Paper. arXiv 2011, arXiv:1102.2181. [Google Scholar]
- Matsumura, T.; Akiba, Y.; Borrill, J.; Chinone, Y.; Dobbs, M.; Fuke, H.; Ghribi, A.; Hasegawa, M.; Hattori, K.; Hattori, M.; et al. Mission design of LiteBIRD. J. Low Temp. Phys. 2013, 176, 733–740. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Ade, P.A.; Akiba, Y.; Alonso, D.; Arnold, K.; Aumont, J.; Baccigalupi, C.; Barron, D.; Basak, S.; Beckman, S.; et al. The LiteBIRD Satellite Mission - Sub-Kelvin Instrument. In Proceedings of the 17th International Workshop on Low Temperature Detectors (LTD 17), Kurume City, Japan, 17–21 July 2017. [Google Scholar]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- André, P.; Baccigalupi, C.; Banday, A.; Barbosa, D.; Barreiro, B.; Bartlett, J.; Bartolo, N.; Battistelli, E.; Battye, R.; Bendo, G.; et al. PRISM (Polarized Radiation Imaging and Spectroscopy Mission): An Extended White Paper. J. Cosmol. Astropart. Phys. 2014, 1402, 006. [Google Scholar] [CrossRef]
- Kogut, A.; Fixsen, D.J.; Chuss, D.T.; Dotson, J.; Dwek, E.; Halpern, M.; Hinshaw, G.F.; Meyer, S.M.; Moseley, S.H.; Seiffert, M.D.; et al. The Primordial Inflation Explorer (PIXIE): A Nulling Polarimeter for Cosmic Microwave Background Observations. J. Cosmol. Astropart. Phys. 2011, 1107, 025. [Google Scholar] [CrossRef] [Green Version]
- Taylor, A.M.; Vovk, I.; Neronov, A. Extragalactic magnetic fields constraints from simultaneous GeV-TeV observations of blazars. Astron. Astrophys. 2011, 529, A144. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Gravitation: Foundations and Frontiers; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fujita, T.; Mukohyama, S. Universal upper limit on inflation energy scale from cosmic magnetic field. J. Cosmol. Astropart. Phys. 2012, 1210, 034. [Google Scholar] [CrossRef] [Green Version]
- Caprini, C.; Sorbo, L. Adding helicity to inflationary magnetogenesis. J. Cosmol. Astropart. Phys. 2014, 1410, 056. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T. Primordial Magnetic Fields from the Post-Inflationary Universe. J. Cosmol. Astropart. Phys. 2014, 1405, 040. [Google Scholar] [CrossRef] [Green Version]
- Atmjeet, K.; Pahwa, I.; Seshadri, T.R.; Subramanian, K. Cosmological Magnetogenesis From Extra-dimensional Gauss Bonnet Gravity. Phys. Rev. 2014, D89, 063002. [Google Scholar] [CrossRef] [Green Version]
- Fujita, T.; Namba, R.; Tada, Y.; Takeda, N.; Tashiro, H. Consistent generation of magnetic fields in axion inflation models. J. Cosmol. Astropart. Phys. 2015, 1505, 054. [Google Scholar] [CrossRef] [Green Version]
- Campanelli, L. Lorentz-violating inflationary magnetogenesis. Eur. Phys. J. 2015, C75, 278. [Google Scholar] [CrossRef] [Green Version]
- Tasinato, G. A scenario for inflationary magnetogenesis without strong coupling problem. J. Cosmol. Astropart. Phys. 2015, 1503, 040. [Google Scholar] [CrossRef] [Green Version]
- Rajeev, K.; Chakraborty, S.; Padmanabhan, T. A comment on generalized Schwinger effect. Eur. Phys. J. C 2017, 78, 836. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, S. Multifaceted Schwinger effect in de Sitter space. Phys. Rev. 2017, D96, 025012. [Google Scholar] [CrossRef] [Green Version]
- Fröb, M.B.; Garriga, J.; Kanno, S.; Sasaki, M.; Soda, J.; Tanaka, T.; Vilenkin, A. Schwinger effect in de Sitter space. J. Cosmol. Astropart. Phys. 2014, 1404, 009. [Google Scholar] [CrossRef] [Green Version]
- Stahl, C.; Xue, S.S. Schwinger effect and backreaction in de Sitter spacetime. Phys. Lett. 2016, B760, 288–292. [Google Scholar] [CrossRef] [Green Version]
- Stahl, C. Schwinger effect impacting primordial magnetogenesis. Nucl. Phys. 2019, B939, 95–104. [Google Scholar] [CrossRef]
- Campanelli, L.; Cea, P.; Fogli, G.L.; Tedesco, L. Inflation-Produced Magnetic Fields in Nonlinear Electrodynamics. Phys. Rev. 2008, D77, 043001. [Google Scholar] [CrossRef] [Green Version]
- Koivisto, T.S.; Urban, F.R. Three-magnetic fields. Phys. Rev. 2012, D85, 083508. [Google Scholar]
- Urban, F.R. The anisotropy of a three- and a one-form. J. Cosmol. Astropart. Phys. 2013, 1308, 008. [Google Scholar] [CrossRef] [Green Version]
- Campanelli, L. Evolution of Magnetic Fields in Freely Decaying Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2007, 98, 251302. [Google Scholar] [CrossRef] [Green Version]
- Seto, N.; Taruya, A. Polarization analysis of gravitational-wave backgrounds from the correlation signals of ground-based interferometers: Measuring a circular-polarization mode. Phys. Rev. 2008, D77, 103001. [Google Scholar] [CrossRef] [Green Version]
- Byrnes, C.T.; Hollenstein, L.; Jain, R.K.; Urban, F.R. Resonant magnetic fields from inflation. J. Cosmol. Astropart. Phys. 2012, 1203, 009. [Google Scholar] [CrossRef]
- Lewis, A. CMB anisotropies from primordial inhomogeneous magnetic fields. Phys. Rev. 2004, D70, 043011. [Google Scholar] [CrossRef] [Green Version]
- Field, G.B.; Carroll, S.M. Cosmological magnetic fields from primordial helicity. Phys. Rev. D 2000, 62, 103008. [Google Scholar] [CrossRef] [Green Version]
- Anber, M.M.; Sorbo, L. N-flationary magnetic fields. J. Cosmol. Astropart. Phys. 2006, 10, 018. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory: Volume 2, Loop Amplitudes, Anomalies and Phenomenology; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Majumdar, P.; SenGupta, S. Parity violating gravitational coupling of electromagnetic fields. Class. Quant. Grav. 1999, 16, L89–L94. [Google Scholar] [CrossRef] [Green Version]
- Garretson, W.D.; Field, G.B.; Carroll, S.M. Primordial magnetic fields from pseudoGoldstone bosons. Phys. Rev. 1992, D46, 5346–5351. [Google Scholar]
- Adshead, P.; Giblin, J.T.; Scully, T.R.; Sfakianakis, E.I. Gauge-preheating and the end of axion inflation. J. Cosmol. Astropart. Phys. 2015, 1512, 034. [Google Scholar] [CrossRef] [Green Version]
- Adshead, P.; Giblin, J.T.; Scully, T.R.; Sfakianakis, E.I. Magnetogenesis from axion inflation. J. Cosmol. Astropart. Phys. 2016, 1610, 039. [Google Scholar] [CrossRef] [Green Version]
- Adshead, P.; Giblin, J.T.; Weiner, Z.J. Gravitational waves from gauge preheating. Phys. Rev. 2018, D98, 043525. [Google Scholar] [CrossRef] [Green Version]
- Boubekeur, L.; Lyth, D.H. Hilltop inflation. J. Cosmol. Astropart. Phys. 2005, 07, 010. [Google Scholar] [CrossRef] [Green Version]
- Bostan, N. Quadratic, Higgs and hilltop potentials in the Palatini gravity. Commun. Theor. Phys. 2020, 72, 085401. [Google Scholar] [CrossRef]
- Kohri, K.; Lin, C.M.; Lyth, D.H. More hilltop inflation models. J. Cosmol. Astropart. Phys. 2007, 12, 004. [Google Scholar] [CrossRef] [Green Version]
- Pal, B.K.; Pal, S.; Basu, B. Mutated Hilltop Inflation: A Natural Choice for Early Universe. J. Cosmol. Astropart. Phys. 2010, 01, 029. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Grøn, O. Predictions of Spectral Parameters by Several Inflationary Universe Models in Light of the Planck Results. Universe 2018, 4, 15. [Google Scholar] [CrossRef] [Green Version]
- Gomes, C.; Bertolami, O.; Rosa, J.A.G. Inflation with Planck data: A survey of some exotic inflationary models. Phys. Rev. D 2018, 97, 104061. [Google Scholar] [CrossRef] [Green Version]
- Thorne, K.S.; MacDonald, D. Electrodynamics in Curved Spacetime—3+1 Formulation. Mon. Not. Roy. Astron. Soc. 1982, 198, 339. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D.; Tsagas, C.G. Cosmological magnetic field survival. Mon. Not. R. Astron. Soc. 2011, 414, 512. [Google Scholar] [CrossRef] [Green Version]
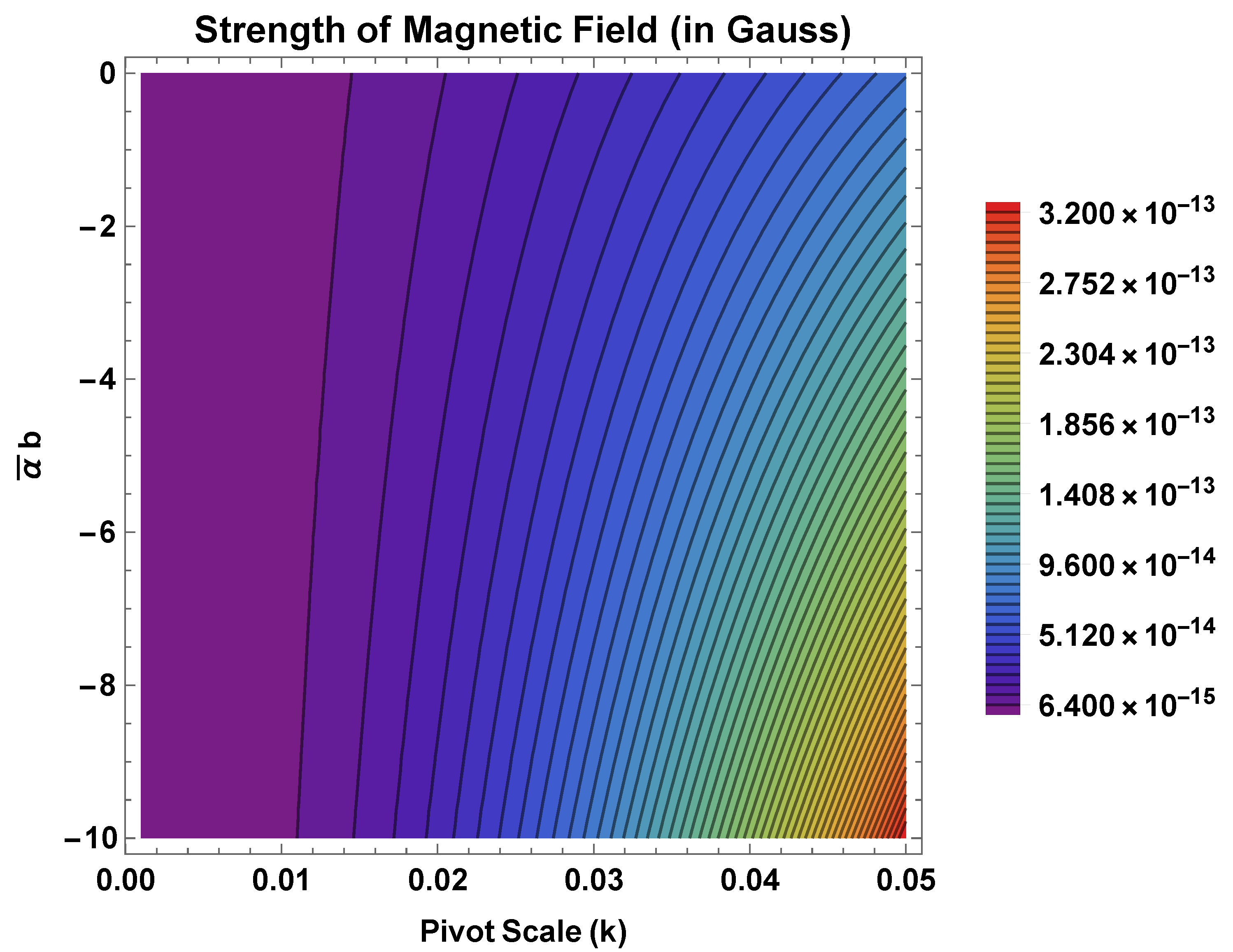
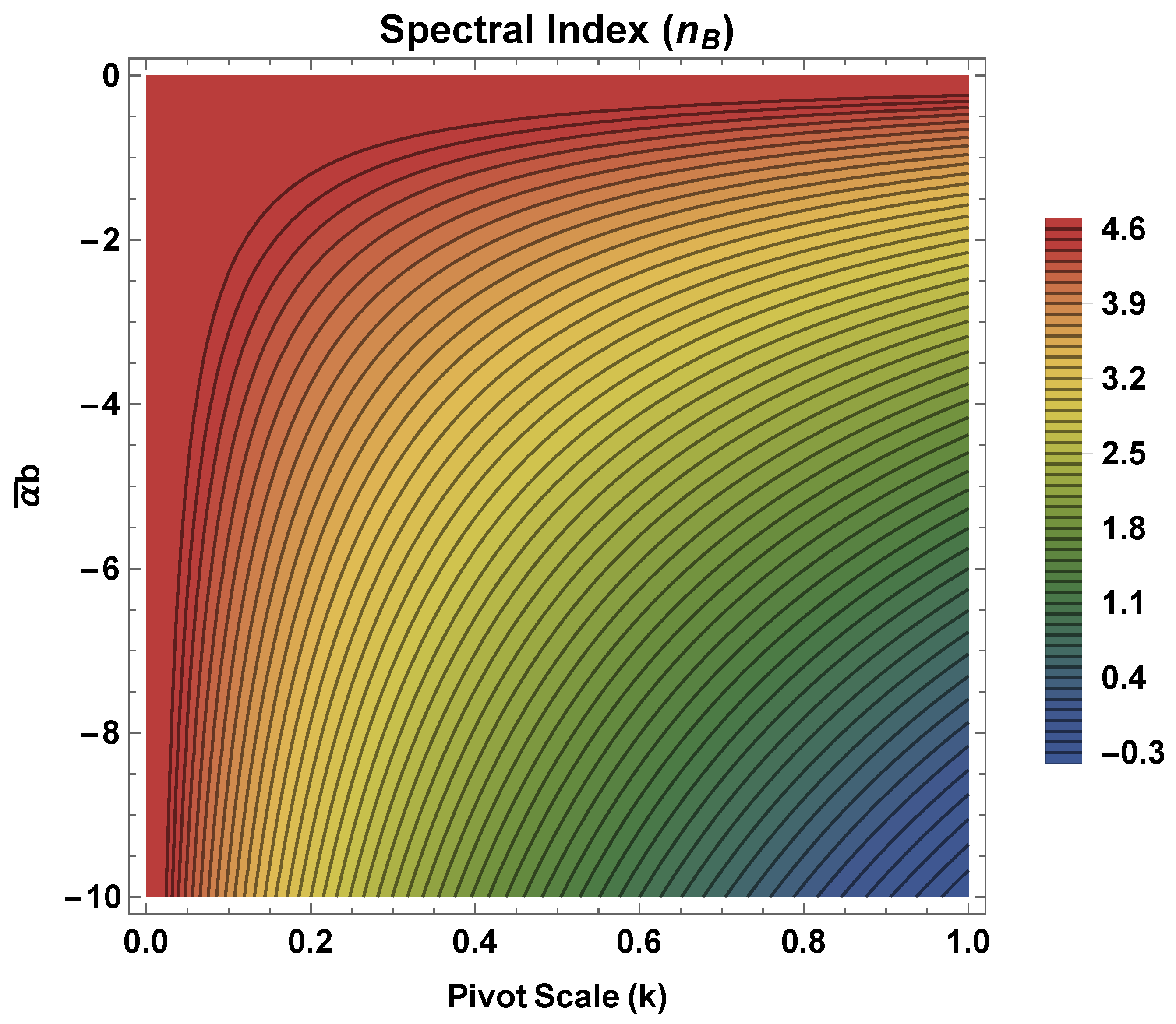
| Strength of Magnetic Field | ||||
|---|---|---|---|---|
| (Pivot Scale k = 0.09) | (Pivot Scale k = 0.05) | (Pivot Scale k = 0.01) | (Pivot Scale k = 0.005) | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| () | |
|---|---|
| 0.1 | |
| 0.5 | |
| 1 | |
| 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, S.; Pal, S.; SenGupta, S. Hilltop Inflation and Generation of Helical Magnetic Field. Universe 2022, 8, 26. https://doi.org/10.3390/universe8010026
Chakraborty S, Pal S, SenGupta S. Hilltop Inflation and Generation of Helical Magnetic Field. Universe. 2022; 8(1):26. https://doi.org/10.3390/universe8010026
Chicago/Turabian StyleChakraborty, Sumanta, Supratik Pal, and Soumitra SenGupta. 2022. "Hilltop Inflation and Generation of Helical Magnetic Field" Universe 8, no. 1: 26. https://doi.org/10.3390/universe8010026
APA StyleChakraborty, S., Pal, S., & SenGupta, S. (2022). Hilltop Inflation and Generation of Helical Magnetic Field. Universe, 8(1), 26. https://doi.org/10.3390/universe8010026






