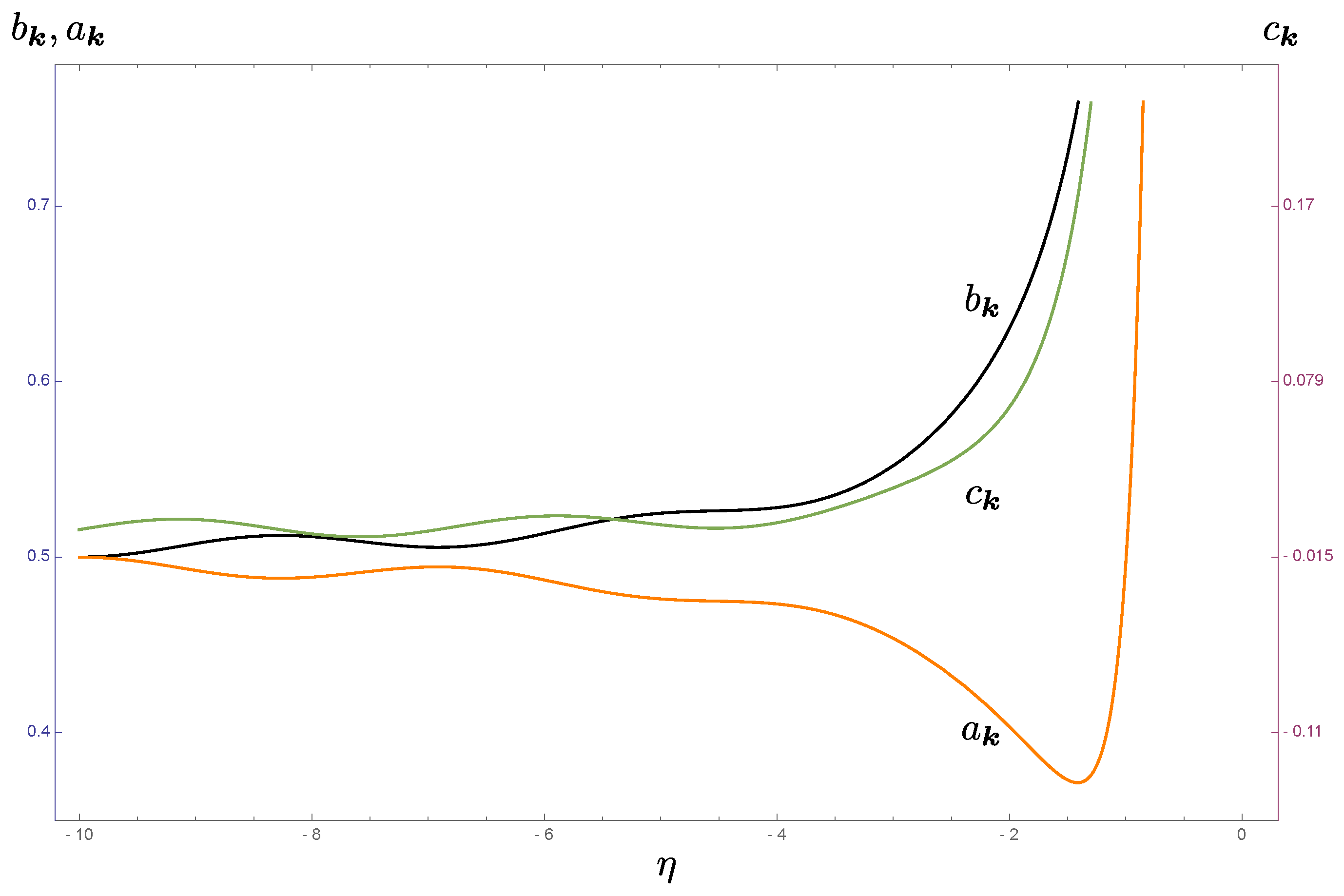Abstract
After a brief summary of the four main veins in the treatment of decoherence and quantum to classical transition in cosmology since the 1980s, we focus on one of these veins in the study of quantum decoherence of cosmological perturbations in inflationary universe, the case when it does not rely on any environment. This is what ‘intrinsic’ in the title refers to—a closed quantum system, consisting of a quantum field which drives inflation. The question is whether its quantum perturbations, which interact with the density contrast giving rise to structures in the universe, decohere with an inflationary expansion of the universe. A dominant view which had propagated for a quarter of a century asserts yes, based on the belief that the large squeezing of a quantum state after a duration of inflation renders the system effectively classical. This paper debunks this view by identifying the technical fault-lines in its derivations and revealing the pitfalls in its arguments which drew earlier authors to this wrong conclusion. We use a few simple quantum mechanical models to expound where the fallacy originated: The highly squeezed ellipse quadrature in phase space cannot be simplified to a line, and the Wigner function cannot be replaced by a delta function. These measures amount to taking only the leading order in the relevant parameters in seeking the semiclassical limit and ignoring the subdominant contributions where quantum features reside. Doing so violates the bounds of the Wigner function, and its wave functions possess negative eigenvalues. Moreover, the Robertson-Schrödinger uncertainty relation for a pure state is violated. For inflationary cosmological perturbations, in addition to these features, entanglement exists between the created pairs. This uniquely quantum feature cannot be easily argued away. Indeed, it could be our best hope to retroduce the quantum nature of cosmological perturbations and the trace of an inflation field. All this points to the invariant fact that a closed quantum system, even when highly squeezed, evolves unitarily without loss of coherence; quantum cosmological perturbations do not decohere by themselves.
1. Introduction
Long before the 1996 popular paper [1] by Polarski and Starobinsky (PS) on cosmological decoherence which commanded the attention of the cosmology community, there had already been intense activities on the issue of quantum decoherence: two major paradigms of consistent/decoherent histories [2,3,4,5,6,7,8,9] and the environment-induced decoherence [10,11,12,13,14] programs had been formulated, and the emergence of classical spacetime in quantum cosmology [15] investigated. The theoretical foundation for quantum decoherence, laid down from the early 1980s to the early 1990s, is essential for understanding the corresponding issues of cosmological perturbations in inflationary cosmology. Even the first step in the analysis, e.g., whether to take a closed quantum system, such as pursued by Hartle [16,17] or an open quantum system [18,19,20] viewpoint, makes a big difference. For a closed system we can just do quantum mechanics the usual way, as had been done earlier. What is different as presented in this paper is, we shall identify the fault-lines and pitfalls which caused some earlier authors to jump to wrong conclusions. From an open system perspective, it is a welcoming sign that in recent years nonequilibrium quantum field theory [21,22,23,24] developed in the 1980s–90s are increasingly recognized to be essential for a rigorous treatments of cosmological decoherence issues. To ensure that inexperienced researchers do not overlook the complexity of this issue arduously worked out by authors of that earlier period, and take an overly lighthearted attitude to this issue, we give an overview of the four stages and the four veins of quantum decoherence research in gravitation and cosmology in the 1980s and 90s, up to PS. Because of its pedagogical emphasis, we place it in a separate section, Section 2, with a remark that readers familiar with this historical development can skip over.
The main goal of this paper is to focus on one of these veins in the study of quantum decoherence of cosmological perturbations in inflationary universe, the case when one does not rely on an environment. This is what ‘intrinsic’ in the title refers to—a closed system. Namely, a quantum field which drives inflation by itself, the inflation, not the environment. In fact, a free field1 The cases of an interacting field, where one divides the high frequency modes from the low frequency modes, and examines how the former sector decoheres the latter, has been studied in detail before [25,26,27] and is gathering increasing momentum in recent papers (see, e.g., [28,29,30] and references therein). Despite its simplicity, the issue of decoherence for a free field is perhaps conceptually more challenging, not unlike defining the ‘intrinsic’ entropy of a quantum field (see, e.g., [31] and earlier references cited therein). This is because, if one adheres to the basic principles, a closed quantum system should evolve unitarily—there is no loss of quantum coherence. What makes this an issue is that there are papers by respectable authors which claim there is decoherence in this closed quantum system at late times, due to the inflationary expansion. Because PS offered an easy, simple, even faulty philosophically sophisticated explanation of decoherence (‘decoherence without decoherence’), it has attracted large numbers of followers. We want to show in this paper that this claim is ill-founded and this simplistic view is misleading2. We do this by working out in detail the three cases which had been studied before—a free particle [32], an inverted harmonic oscillator [33] and the inflationary universe [1]— pointing out the exact places where illegitimate jumps were made, which prompted these claims and promulgated this erroneous view.
With a simple quantum harmonic oscillator example, using both the Wigner function and the wave function, and an operator Heisenberg equation, we examine several commonly-used criteria of classicalization, including the commonplace , and the somewhat more sophisticated large n approximation. On the other hand, for a free particle, and inverted oscillator, we focus on the late time, highly squeezed, limit when the system is taken to behave classically by many authors. The squeezing under time evolution turns a quadrature ellipse in phase space into a very narrow and elongated shape. This is where many authors made a leap of faith and claim that the ellipse is like a line, replace it by a delta function in the expression of the corresponding Wigner function, which perfects a trajectory in phase space and proclaim classicalization is consummated. We point out that this act is illegitimate, because if they are treated in this way, negative eigenvalues and unphysical states arise.
For the inflationary universe, we follow the evolution of the squeezed quantum field, the inflation perturbation, with nonequilibrium quantum field theory treatment in terms of the Bogoliubov coefficients, and demonstrated that entanglement persists between the pair of particles that are created. Entanglement is a uniquely quantum feature absent in classical physics, there is unequivocal evidence that the system does not turn classical even at late times under severe inflation. An important criterion for all four examples we invoked is the Robertson-Schrödinger uncertainty relation (not the Schrödinger uncertainty as used in [33]), which is an invariant throughout the unitary evolution. Other criteria we have used include the non-commutativity of operators, boundedness of the Wigner function, and semi-positivity of the density matrix.
The contrast with PS is even clearer: while PS asserted that there is decoherence with a clever twist, we show that there is no decoherence, and no twist.
1.1. Gravitational and Quantum Field Perturbations—Some Clarifying Remarks
Because quantum cosmological perturbations involve both classical gravitational perturbations and quantum field fluctuations, some clarification remarks may be needed on a few basic issues related to the role of quantum field fluctuations in cosmological perturbations. This subsection provides the background for, and can be read as a preamble of, Section 5.
There are three parties involved in inflationary cosmological perturbations: (i) classical gravitation theory, based on general relativity, which governs cosmological evolution, (ii) a quantum field, the inflation, which drives the universe to inflationary expansion, and (iii) their perturbations/fluctuations: the scalar sector of gravitational perturbations is coupled to the quantum scalar field fluctuations, together governing the density contrasts which seed the structures in the universe, like galaxies.
Classical theories of cosmological structure formation are based on gravitational perturbation theory [34,35,36,37] where the density contrasts, the isocurvature perturbations, the vorticity and the primordial gravitational waves are described by the scalar, vector and tensor perturbations of the background spacetime. The gravity sector based on general relativity is classical throughout. We will comment on tensor perturbations and graviton physics separately.
The scalar (inflation) field is intrinsically quantum in nature. Often, a background field expansion is performed, where the background field is a mean field3 and are the quantum fluctuations (N.B. strictly speaking, quantum perturbations—see Section 1.1.3 below). To get compact equations of motion for the density contrasts, mixed metric perturbations + quantum scalar field variables are used, such as the gauge invariant Mukhanov-Sasaki variable. Now, with a mixed variable coming from classical gravity and quantum field, what do quantum cosmological perturbations refer to, and which variables are we targeting in their decoherence, or, which quantum variables become classical at late times—or do they?
1.1.1. Which Quantities in Cosmological Perturbations Are Intrinsically Quantum?
The mixed gravity + inflation variables can come in many shades depending on which gauge one chooses to use in the gravity sector and the apportioned weight of each sector. Regardless, the gravitational perturbations remain of classical origin. The scalar sector of the metric perturbations related to the Newtonian potential is a constraint, not a dynamical degree of freedom (the tensor modes are). Its nature is determined by (or ‘slaved’ [39,40] to) the matter source. In general relativity when the matter source is classical, this scalar sector of the metric perturbation is classical.
In an extreme case, one may conjure up situations where the quantum fluctuations of the scalar field are made to vanish, such as “choosing a (co-moving) gauge which for scalar perturbations makes the velocity perturbation vanish. For single field inflation, this means that the time coordinate is defined so that at any given time the scalar field equals its unperturbed value” (one is riding up and down with the scalar field’s fluctuations), “with all perturbations relegated to components of the metric” ([41], Sec. 5.3D). This does not mean that gravity has become quantum, only that the scalar perturbations now acquire a quantum nature by virtue of the presence of the inflation field. When there is no inflation, one returns to purely classical gravity. The Newtonian force is slaved to the source which is classical. There is no way for the gravitational perturbations to become quantum in this way, and there are no decoherence issues.
1.1.2. Tensor Perturbations: Gravitational Waves. Quantized Tensor Perturbations: Gravitons
The tensor sector of gravitational perturbations are not linked to the quantum field which drives inflation and thus there is no issue of quantumness by proxy with the inflation. They are intrinsically classical and carry gravity’s dynamical (or propagating) degrees of freedom. Primordial gravitational waves are described by the tensor sector of the gravitational metric perturbations. They have been studied at the classical level since 1946 by Lifshitz and others. One can consider quantizing the linearized tensor perturbations, whence they become the gravitons, like photons for QED4. Primordial gravitons created from the vacuum fluctuations in the early universe have been studied by many authors since the 70s [43,44]. The two polarizations each obey an equation of motion of the same form as a massless minimally-coupled scalar field. The normal mode amplitudes of each polarization obey an equation of motion of the same form as that of a parametric oscillator with time-dependent frequency determined by the expansion of the universe, as studied here and earlier (e.g., [31] and references therein). Decoherence of primordial gravitons and decoherence due to gravitons are important current subjects which we hope to return in conjunction with graviton detection [45,46,47] and gravitational decoherence [48,49,50] issues.
1.1.3. Perturbations: Deterministic Variables. Fluctuations: Stochastic Variables
It is of theoretical significance to make the distinction between quantized linear perturbations, which are believed to be the progenitors of galaxies and structures we see today, and vacuum fluctuations of a quantum field, which engender spontaneous creation of particle pairs, a subject fundamental in quantum field theory in curved spacetime. Note the former is a deterministic variable whereas the latter is a stochastic variable. What is customarily called quantum ‘fluctuations’ of the inflation field: the above should strictly speaking be called perturbations, because they are deterministic variable, obeying deterministic equations of motion It is important to make this distinction especially when people try to replace quantum field-theoretical variables by classical stochastic variables. The relation between a quantum variable and a classical stochastic variable is a nontrivial one. A lot depends on what constitutes the noise, how it is introduced and how it acts on a system. See, e.g., [9]. Some features of the former can be captured by the latter, but not all. For Gaussian systems it is easier to bridge the two, but still there remain differences. See discussions in, e.g., the last section of [31].
Fluctuations in (linear) quantum matter fields can be represented by the noise kernels (vacuum expectation values of the stress energy bitensor). When these fluctuations are included in addition to the expectation values of the stress-energy tensor (the mean) as sources driving the Einstein equation, they induce metric fluctuations (‘spacetime foam’). There, fluctuations are of the main concern, and the Einstein-Langevin equation is the centerpiece of semiclassical stochastic gravity.
1.2. Model Studies, Key Findings and Organization
Of the four veins of decoherence studies described in more detail in the next section we shall focus on one of these veins, the evolution of closed quantum systems. Two representative works are, the 1985 paper by Guth and Pi (GP) [33] which contains great detail, and the 1996 paper by Polarski and Starobinsky [1] which we mentioned earlier, together with subsequent joint papers with Kiefer along the same thread [51]. This vein does not require any environmental field to decohere the inflation perturbations, but focuses on the late time behavior in the evolution of the inflation field perturbations. Since both sets of papers use simple quantum mechanical models to illustrate their findings, the inverted harmonic oscillator (IHO) of GP, and the free particle of Kiefer et al., we shall do the same, so direct comparisons can be made to see the differences.
Before we delve into the details of the model systems studied in Section 4, we first use the simple harmonic oscillator model to point out relevant subtleties in taking the semi-classical limit. In particular, we (1) address whether/how the regions, in which the Wigner function assumes negative values, vary when the small ℏ limit is taken, (2) address the (in)compatibility between the different protocols of taking the semi-classical limits such as taking the large n (excitation) limit vs the small ℏ limit. This is especially pertinent to our subsequent analysis, warning against treating large squeezing as the classical limit, and (3) offer a pedagogical derivation to show how classical dynamics in phase space can indeed emerge, but only upon taking the proper semi-classical limit.
The model systems we investigate in this paper have a common feature that the ellipse in phase space formed by the dispersion of the canonical variables of the model system becomes exceedingly squashed in one quadrature but extremely stretched in another. Prior authors made the observation that for the leading order of the large squeezing parameter in their states, the ellipse reduces to a one-dimensional path in phase space. From this, they argue that an apparent classicality emerges from the quantum systems of these models. They also showed that the accompanying Wigner function is proportional to a delta function, and used this as a heuristic support for their claims. However, as we shall show in this paper, their claims are invalid. It is dangerous to keep only the dominant contributions in treating the semiclassical limit. Doing so will have the following unfortunate consequences:
- Such a Wigner function does not correspond to a physical state
- (a)
- it violates the bound of the Wigner function when ,
- (b)
- if the system started in a pure state, the final state is no longer pure even though the evolution is unitary,
- (c)
- the purity of the state is greater than unity,
- (d)
- this implies that the corresponding density matrix has negative eigenvalues,
- The Robertson-Schrödinger uncertainty relation for a pure state is violated,
- The commutator of the canonical operator, like , at different times becomes commutative,
- The equal-time commutation relation of the canonical variables vanishes so the canonical pair commutes.
These behaviors are contradictory to our understanding of how a closed quantum system undergoes unitary evolution. These fallacies could have been avoided if the sub-dominant contributions had been included in one’s consideration. Even though these subdominant terms are likely to be very small compared to the dominant ones, they are just what we need to keep things right. Coherence, which carries the quantum essence of the closed system, resides in these sub-dominant contributions. In addition, in the case of cosmological perturbations treated in Section 5, an irrefutable support that such a system remains quantum comes from the existence of quantum entanglement between the particle pairs produced in the process of parametric amplification due to the expansion of the universe.
In Section 2, we give a short review of the study of decoherence and quantum to classical transition in cosmology, in five stages of development, featuring four main veins of approach. This is the quantum backdrop necessary for the investigation of decoherence in inflationary cosmological perturbations. In Section 3, we start with an overview of the quantum mechanical tools used in the Gaussian dynamics of closed linear systems, and stress the unique role of the Robertson-Schrödinger uncertainty principle for pure quantum states. We then turn to the relevant properties of the Wigner function in the context of the quantum-to-classical transition, and show that the aforementioned pitfalls are quite generic when the limiting cases are taken without mindful discretion. In Section 4 we first use the harmonic oscillator model to shed light on the elusive points in taking the semi-classical limits. Then we use the free particle and the inverted harmonic oscillator models by previous authors to pinpoint where their seemingly plausible assumptions lead to adverse pitfalls in drawing conclusions regarding the emergence of classicality in these closed quantum systems under unitary evolution, and show how judicious measures lead to correct conclusions. Section 5 is dedicated to the quantum perturbations of the inflation field. In addition to the features of the quantum mechanical models studied in Section 3 and Section 4, a new feature pertaining to quantum fields arises, namely, quantum entanglement among particle pairs produced out of the field quanta by the expanding universe. This is an unmistakable signifier of the quantumness of the inflation field perturbations which cannot be erased by the simplistic arguments used by prior authors. We summarize the major findings of this paper in the Conclusion section. In Appendix A we show that the squeeze transformation does not modify the bound in the generalized uncertainty relation for the free, linear quantum scalar field. In Appendix B, we show the proper limits to take in a harmonic oscillator model to reach the correct semiclassical limit.
2. Decoherence in Cosmology: Highlights of Past Four Decades
Before one delves into a study of the decoherence for quantum inflationary perturbations it is useful to be conversant of the ways how decoherence is addressed in simpler settings in quantum mechanics and in more complex settings in quantum cosmology. There are about four decades of work on decoherence (counting from Zurek’s early papers [13,52]) and many approaches with very different emphasis. In this section, we shall outline the four main veins of decoherence, so inexperienced researchers can appreciate the complexity of the issues involved and become aware of the variety of methodologies used. It can also serve as a coordinate system for experienced practitioners to compare notes, to identify different set-ups, to define the issues they want to address and the approaches they wish to take. Readers already familiar with this subject can skip over this section and proceed to Section 3.
Background (5 Stages) and Methodology (4 Veins)
O. 1980s. The theoretical foundations were laid down in the 1980s. (A) Environment-induced decoherence, in the work of Zurek [13] and Joos and Zeh [14], aided by the 1983 Caldeira-Leggett master equation [53] for quantum Brownian motion for Markovian quantum processes. (B) Consistent histories of Griffiths [2] and Omnes [4].
I. 1985–1988, the first period of work on decoherence in inflationary cosmology, we mention two relevant papers: (1) Guth and Pi 1985 (GP) [33] used an uncertainty relation to demarcate between quantum and classical. We refer to this approach as the First Vein: closed quantum system to this issue, the vein pursued in this paper. (2) Starobinsky’s 1986 stochastic inflation [54] (see also Sakagami [55]) as a representative of the Second Vein: closed with partition (or with this symbol where a noninteracting scalar field is partitioned into a long wavelength (<, division according to wavevector : low refers to long wavelength modes) segment and a short wavelength segment (>). The latter is assumed to be a white noise in a Langevin equation which drives inflation. The long wavelength segment is assumed to be classical. Outstanding issues in this model include: (a) Does a sharp cutoff indeed generate white noise [56]; (b) with a shifting partition in space a proper treatment requires quantum field theory of half space with time-dependent Hilbert spaces, which is amiss; (c) Decoherence of the long wavelength sector. We shall continue this discussion along the Fourth Vein in the same spirit but with interacting quantum fields.
II. 1988–1992. Quantum cosmology, where decoherence is considered for the emergence of classical spacetimes. Decoherence in quantum cosmology was a major focus in the work of many authors in the late 1980s and early 1990s, notably, Gell-Mann and Hartle [7,8], Halliwell [15], Habib and Laflamme [57], Kiefer [58], Singh and Padmanabhan [59,60,61], Paz and Sinha [62,63] and others. Many papers invoke the Born-Oppenheimer approximation, in light of the discrepancy between the massive gravity sector and the lighter matter field sector, and introduce a WKB time in the Wheeler-DeWitt equation [64,65], enabling the wave functions of the universe to enter the semiclassical realm. Strictly speaking, the assumption is not decoherence. It is more in line with the slow variables of van Hove in statistical mechanics. The division between fast-slow variables, heavy-light masses, high-low energy sectors and treating them differently is the beginning step in an open quantum systems approach. Such a view is applied to the minisuperspace approximation in, e.g., [66,67,68].
III. 1990–96.
A. The consistent histories vein of the 1980s is continued in the decoherent histories of Gell-Mann and Hartle [7,8,9,69]. Of particular interest is how these authors use the existent conditions of cosmology as a closed system to construct a new interpretation of quantum physics, and then apply it to understand the quantum mechanics of spacetime [16,17]. Its value goes beyond the decoherence issues, probing deeper into the relations between quantum and gravitation.
B. Likewise, the Environment-induced decoherence program has seen significant developments with the derivation of a non-Markovian master equation for quantum Brownian motion [70,71] and applications to decoherence of model quantum systems [72]. For example, Zurek, Habib, and Paz [73] explained why the coherent state has the most ‘classical’ features, Hu and Zhang [74,75] derived an uncertainty relation at finite temperatures and use it to understand the quantum-classical demarcation. We shall invoke a generalized (Robertson-Schrödinger) uncertainty relation in this work. In 1994, Hu and Matacz [76] derived the HPZ equations for a parametric Brownian oscillator in a parametric oscillator bath—parametric refers to oscillators with time-dependent frequencies in their normal modes. This is useful for treating squeezed states in quantum optics and for cosmology. As we shall see, cosmological perturbations obey equations with a time-dependent effective mass, and cosmological particle creation can be seen as a manifestation of the quantum field being squeezed [77,78,79,80] by the expansion of the universe. With this connection one can investigate the entropy, decoherence and entanglement issues related to quantum cosmological perturbations. (For a brief description, see, e.g., [31] and the references therein).
C. For issues in inflationary cosmology, we mention three groups of papers in that period which exemplify the second vein and introduce two additional veins in the approaches to cosmological decoherence. As background on cosmological perturbations, decoherence and entropy issues, read the papers of Brandenberger, Laflamme, Mukhanov, Prokopec, Gasperini and Giovannini, et al. [81,82,83,84,85,86], and the recent mini-review [31] where many references can be found.
Third Vein: two-fields – non-Markovian master equation with colored noise. (1) The first serious study of cosmological decoherence based on non-Markovian master equations for a system quantum field and a bath quantum fields is in the 1992 paper by Hu, Paz and Zhang (HPZ) [87]. These authors consider two independent self-interacting scalar fields in de Sitter spacetime: depicting the system, and depicting the bath, and an interaction between them in the biquadratic form . (Note that a system interacting with an environment with an interaction action of the bilinear form such as used in Cornwall and Bruisma [88] would not decohere5.) These authors used this model to address two basic issues in the theory of galaxy formation from the fluctuations of quantum fields: (a) the nature and origin of noise and fluctuations and (b) the conditions which need to be met for using a classical stochastic equation for their description. Whether the stochastic inflation proposal [54] can fly depends critically on a satisfactory resolution of these two issues.
On the first issue, HPZ derived the influence functional for a field in a zero-temperature bath in de Sitter universe and obtained the correlators for the colored noises of vacuum fluctuations. This exemplifies a new mechanism for colored noise generation which can act as seeding for galaxy formation with non-Gaussian distributions. For the second issue, HPZ presented a (functional) master equation for the inflation field in de Sitter universe. By examining the form of the noise kernel they studied the decoherence of the long-wavelength sector and the conditions for it to behave classically. The more general case of the system field and bath field interacting with the form was deal with by Zhang in his thesis work [89], as reported in [90], based on the functional perturbative methods they used for the study of nonlinear QBM [71].
Fourth Vein: nonlinear fields – (2a) Decoherence of the mean field by quantum fluctuations. Instead of using a rather ad hoc splitting of a quantum field in stochastic inflation [54] into long and short wavelength segments, with the latter providing the noise which decoheres the former, Calzetta Hu in 1995 [25] treated a nonlinear field and examined the decoherence of the mean field by the interacting field’s own quantum fluctuations, or that of other fields it interacts with. Note, in spirit, this shares with the first vein for a closed quantum system. The quantum field by itself is a closed system. The decomposition of an interacting quantum field into a mean field and the fluctuation field is not enough to turn the mean field classical (which is commonly assumed in a background field expansion). One needs to specify the conditions when, the ways how, and how likely a mean field will be decohered. Interaction with its quantum fluctuations is one way this may happen.
(2b) Partitioning one interacting field into high and low frequency sectors. Starobinsky proposed this for a free field in his 1986 stochastic inflation model (See also Matacz [91]). We mentioned earlier the difficulties this model encounters as it is based on the partitioning of a free field, how the high frequency segment acts on the low frequency segment is not clear, and a proper quantum field theory treatment is not easy. Instead, for an interacting quantum field with partition, there are no such conceptual issues. Technically it may seem more challenging, but there are well-developed methods to handle it, known as the coarse-grained effective action [92,93,94], the closed-time-path or in-in [95,96,97,98] version of it is akin to the influence action [53,99,100]. This was carried out neatly by Lombardo and Mazzitelli [26] and applied to cosmological decoherence by Lombardo and Lopez-Nacir [27]. A natural partition is the horizon scale, in which case one can talk about entanglement entropy between the sub and super-horizon sectors. See, e.g., [28].
We see that the conceptual and technical foundation for the study of cosmological decoherence were quite well established from 1982 to 1996. They form the theoretical frameworks for continued investigations in the following 25 years.
IV. 1996–2008. Selected representative works include:
A. The 1996 paper by Polarski and Starobinsky (PS) [1]. It belongs to the first vein, similar to Guth and Pi, in that the authors assert that decoherence comes by naturally without any environment assistance (we shall refer to this as ‘intrinsic’). After Kiefer joined the collaboration [51,101,102] arguments were made more rigorous and connection with other work derived from theories with solid foundations was extended, such as for the entropy of gravitons with quantum open squeezed system [103].
B. Anderson et al. [104]. This paper can be read as the continuation of [105], which expounded the ideas of [106], a good representative of the First Vein. These authors showed that with respect to a second order adiabatic vacuum there is no decoherence in the setup of Polarski and Starobinsky.
C. Martineau and Brandenberger 2005 [107] investigated the gravitational backreaction of long wavelength (super-Hubble) scalar metric fluctuations on the perturbations themselves, due to the nonlinearity in the Einstein equations, for a large class of inflationary models. Martineau [108] considered gravitational backreaction and interactions due to nonlinearities in the matter evolution equation in the chaotic inflation model. Prokopec and Rigopoulos [109] used two decoupled massive fields to study the decoherence of curvature perturbations during inflation.
D. Campo and Parentani 2008 [110] begins with an interacting quantum field, but quickly truncate the correlation hierarchy at the Gaussian level, thus effectively acting like a free field. Their result of the entropy of cosmological perturbations in a closed system agrees with other approaches, such as in [31,103,111]. In the second paper [112], they use an open-quantum system approach, and obtain results which independent of the choice of gauge or basis, thus “pointer states appear not to be relevant to the discussion”, which seems counter to the claims in [101].
V. 2008–2020. A welcoming trend in the recent decade is a broader recognition that the concepts and methods of open quantum systems, effective field theory and nonequilibrium quantum field theory are essential to a more rigorous and thorough treatment which can provide a deeper and better understanding of cosmological quantum processes related to entropy, decoherence and entanglement. Representative papers are: Boyanovsky 2015 [113] employing techniques from nonequilibrium quantum field theory [21,114]. Working with two field models (Third Vein) he obtained a master equation from which he derived the corrections to the power spectrum, and drew implications for dark matter. Hollowood and McDonald [30] followed Boyanovksy’s pathway and studied the evolution of decoherence and the onset of classical stochastic behavior as modes exit the horizon. Burgess et al., 2015 [115], using effective field theory explored stochastic inflation via the Lindblad equation for Markovian processes. Nelson 2016 [29] considered the effect of gravitational nonlinearity from expanding the Einstein-Hilbert action to third order in the fluctuations and show that they provide a minimal mechanism for generating classical stochastic perturbations from inflation. This is in a similar spirit as [25] of the Fourth Vein. Allowing for changes in the partitioning of the frequency sectors separating the system from its bath, Shandera et al. [116] derived the evolution equation for the density matrix of a UV- and IR-limited band of comoving momentum modes of the canonically normalized scalar degree of freedom in two examples of nearly de Sitter universes. Finally, Brahma et al. [28] studied the entanglement entropy in cosmology with the super- and sub-horizon partition. It also contains a comprehensive list of references for work on these topics up to 2020.
3. Quantum States in a Closed System Do Not Turn Classical
In this section we ask the generic question whether and when a quantum state behaves classically in a closed system. We first give a short overview about the mathematical tools useful in the context of Gaussian states, discuss some important and often overlooked subtleties we will meet in the semi-classical limit.
Let be the pair of canonical variables of a closed Gaussian system, where p is the momentum conjugated to the position x. The system is assumed in a Gaussian state. In quantum mechanics, this canonical pair will be promoted to operators .
3.1. Heisenberg Equation
The Heisenberg picture offers insights into the non-commutativity of operators. The Heisenberg equations of operators offer a very intuitive way to investigate the quantum dynamics of linear (interacting) systems. For a Gaussian system, the evolution of its canonical-variable operators can be written as
in terms of their initial values, and at the initial time . The parameter m denotes mass if the system is a linear (harmonic/inverted) oscillator, or it is set to unity if the system describes the modes of a linear field. Here are a special set of homogeneous solutions to the equation of motion, called the fundamental solutions, satisfying
This allows us to readily write down various moments of the Gaussian system
and then
The dispersions follow similar structure with, for example, replaced by , where . We observer that
In general (7) does not vanish. That is, the operator at different times does not commute. Similarly we can show the equal-time canonical commutation relation is obeyed for all times
due to the Wronskian conditions of the fundamental solutions.
3.2. Gaussian Pure State
Now we go to the Schrödinger picture, and the dynamical evolution of the linear system is fully accounted for by the wave function. Consider a general time-dependent Gaussian pure state
The normalization condition enables us to write the wavefunction into the form
We see that only contributes to an overall spatially independent, but time-dependent phase, so it will not enter the calculations of the covariance matrix elements. We then find
and
The expressions of the coefficients , and can be determined by the Schrödinger equation. Note that the cross correlation between the canonical variables does not vanish unless .
If we use the pure state (10) to construct the density matrix elements, we have
Note that there is no term in the exponent. However this condition may not serve as a criterion that the state is pure. This is basis dependent. For example, if we change to the bases, Equation (14) becomes
The coefficient of the term is nonzero, but obviously it still describes a pure state.
3.3. Wigner Function and Density Matrix Elements
The covariance matrix turns out to be an convenient building blocks of the Gaussian system, and for a one-dimensional system it is defined as
Here is the operator counterpart of , and we have assumed that . If not, we simply replace in (16) by . The elements of the covariance matrix have specific meanings. Since they are
we see that b gives the position dispersion, a the momentum dispersion, and c is the correlation between the x and p quadratures. In general, they are time-dependent functions and in general . In terms of these elements, the Robertson-Schrödinger uncertainty relation is
Hereafter we will choose the units such that , but will put back ℏ if necessary. The unitary evolution of the quantum system will not change the value of the lefthand side of (18).
The density matrix elements of a Gaussian state takes the form
with the simplification that the mean position and momentum are zero, and
The variable gives a measure regarding the width of the off-diagonal elements perpendicular to the diagonal. In the absence of c, the parameter gives the width of the off-diagonal elements. However when , the interpretation becomes less transparent,
The variable still gives the width of the spread along the direction, but the other orthogonal quadrature veers off the diagonal to , whose physical meaning is not transparent in this picture but will be better seen in terms of the Wigner function. Often we are interested in a quantity call purity, defined by . From (19), we find
Thus, when , we have . It indicates that the density matrix describes a pure state6. The trace of (22) gives
For a pure state, we find , while for a mixed state, we have , so we find . This mixed state can be the reduced density matrix of a bi-partite pure entangled state.
The Wigner function of a Gaussian system is given by
with
It can be shown that
In particular we note that (27) shows a correspondence between operator in Weyl ordering and its classical expression. The Wigner function provides an alternative formulation of quantum mechanics in terms of the phase space variables. In (24), the Wigner function is positive definite in phase space. Thus it is often chosen as the candidate of a classical probability distribution, according to this observation. In fact, in general, it is not a positive definite, and can have negative values over regions, the area of each of which is of order ℏ in a two-dimensional phase space [117,118,119]. We will provide a few examples at the end of this section.
When we write (24) explicitly in terms of covariance matrix elements,
we observe that if , the exponent describes an ellipse whose semi-axes are x and p axes, and have lengths proportional to and . Thus the case corresponds to a rotated ellipse.
When we investigate the distortion of quadratures, that is, squeezing or stretching, due to evolution, it is not easy to see the extent of distortion when because a and b do not tell the lengths of semi-axes. It proves convenient to co-rotate with the quadrature ellipse, that is, using the axes defined by the eigenvectors of the covariance matrix elements. The eigenvalues of the covariance matrix elements are given by
if , and the eigenvectors are
Note that since the elements of the covariance matrix do not carry the same dimension, it is customary to append appropriate dimensional parameters to make expressions in (29) and (30) dimensionally consistent.
The covariance matrix can be diagonalized by the matrix formed from the eigenvectors
such that
It means the covariance matrix formed by a new canonical operator pair, ,
is automatically diagonal, i.e., . By means of , the Wigner function (24) becomes
with
The new canonical operator pair is rotated from by an angle
in phase space such that . Thus and give us information about the semi-axes of the ellipse, and in turns, the extent of squeezing and stretching of the quadrature ellipse during the evolution.
Let us take a special case . We can use the formula
to write the Wigner function into
where we have put back the mean values . In this limit we find
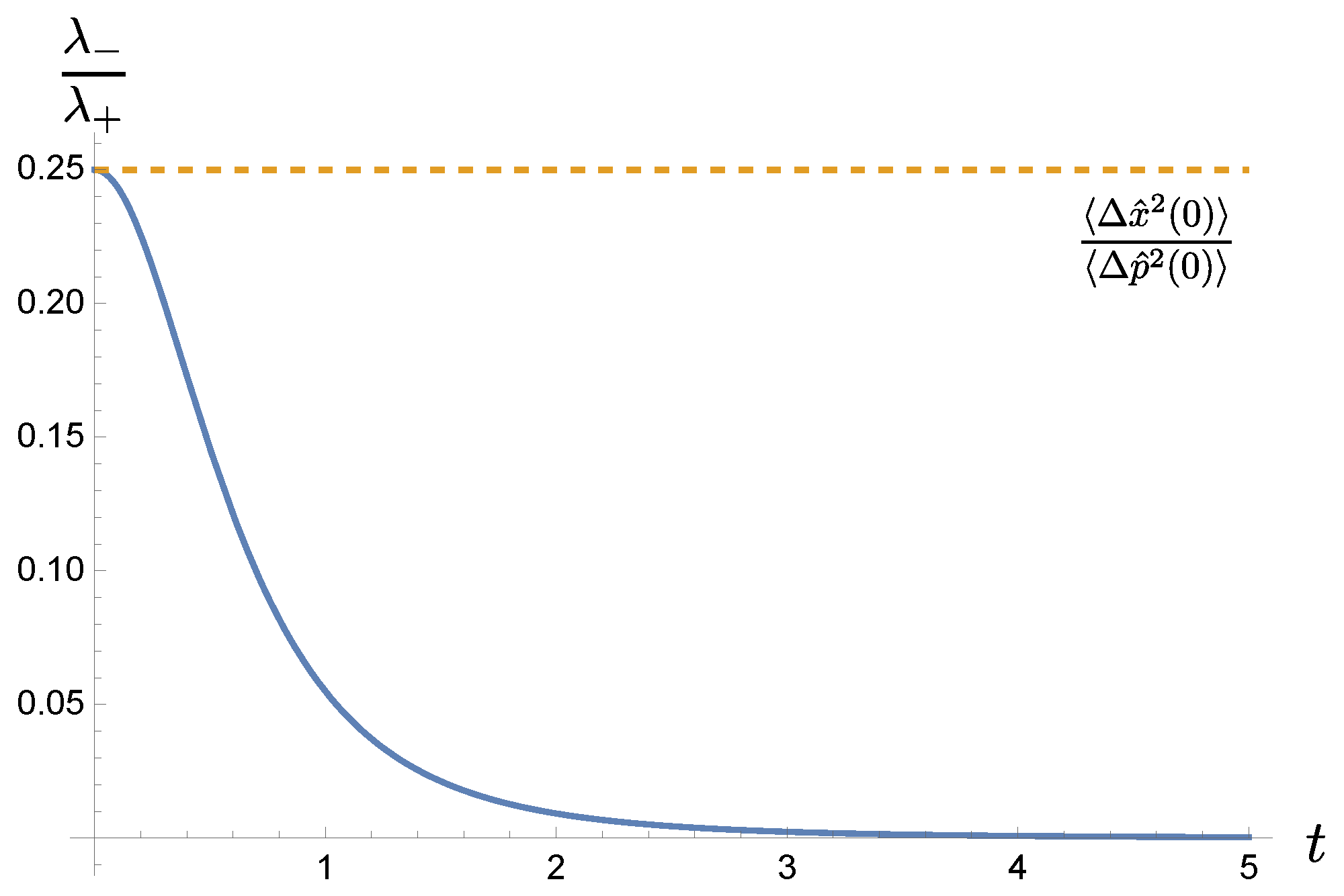
as shown in Figure 1
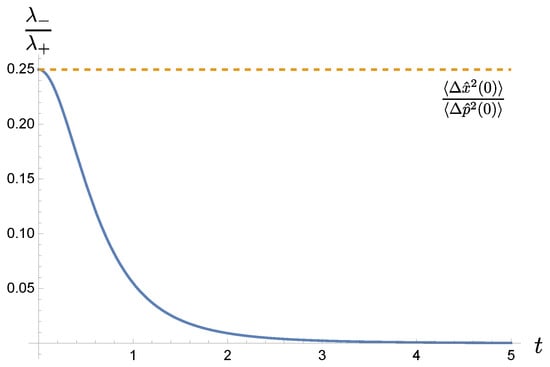
Figure 1.
The time variation of the ratio of the eigenvalues of the covariance matrix. it shows the squeezing and stretching of the quadratures. In this case, the position dispersion is highly squeezed but the momentum is stretched. For a free particle of mass m and initial position dispersion , the ratio is asymptotically given by , and for the inverted harmonic oscillator, it behaves like , where the notations are explained in Section 4.
If we take the limit according to (37) literally, then (39) describes an ellipse which is extremely squeezed in one quadrature but extremely stretched in another. In particular the Wigner function (38) has an extremely sharp peak about and thus is often interpreted as a (quasi-)probability distribution along the one-dimensional path defined by the delta function, instead of over two-dimensional phase space. It is often claimed that in this case the Wigner function gives a classical probability description of a Gaussian state along a well-defined classical trajectory. Nonetheless, it does not meet our expectation that in the (semi-)classical limit, the system, averagely speaking, should follow the trajectory described by the mean position , the expectation value of the canonical coordinate operator . The classical trajectory in phase space is a straight line parallel to the x axis, different from the line defined by one of the semi-axes of the rotated ellipse, inferred by (38).
It is also interesting to observe that if we use the Wigner function (34) to construct the density matrix elements, we find
The limit implies that or . We then find that the density matrix elements in terms of these rotated variables and depict a highly localized, delta-function-like packet on the – plane or – plane,
even though the cross section of the quadrature profile in phase space is still an ellipse with the same area , a consequence of invariance of the symplectic eigenvalues of the covariance matrix. This does not imply that the wavepacket is also localized in the x– plane because in the limit the dispersion is essentially infinite. Note that so far we do not take , and the limit is purely dynamical. Thus, obtaining a result like (41) sounds odd. In fact, it has been shown [120] that the Wigner function is bounded for a finite value of ℏ
so using (37) too literally introduces the artefacts to the Wigner function (38), and makes it violate the bounds.
In the limit , we obtain
with the help of (37). This also shows the violation of (42), and if we compute the density matrix elements, denoted by , from (44), then we find
where is given in (19). Three observations [121] are made on (45): a) the density matrix elements do not satisfy
for . That is, does not describe a pure state, and not only that, b) the purity diverges
in contradiction to the fact that for a generic quantum state , its purity satisfies the bound
The purity of the pure state is equal to 1, while the mixed state has purity less than unity. Recall that we do not take yet. c) It is further argued in [121] that since
some of the eigenvalues of must be negative. It renders the von Neumann entropy associated with ill defined. Thus the state corresponds to the form of the Wigner function in (44) is unphysical. This example points out the subtleties in treating the limiting form of the Wigner function.
4. Quantum Mechanical Examples
The Planck constant ℏ, a hallmark of quantum physics, does not reside in the classical descriptions of physical, chemical or the biological processes, so the limit in the formalism offers an unambiguous reduction from the quantum regime to the classical regime. However, in the operational sense, since ℏ is a constant, taking this limit is not practically useful. We often turn to other parameters that are tunable and may be qualified for describing the quantum to classical transition of the system of our interest. One relevant to the discussion in this paper is the large n limit, where n can be the number of the constituents in the system, or represents the highly excited state of the system, such as an Rydberg atom [122]. This limit seems consistent with our mundane experience that a macroscopic system behaves classically. However here, as an appetizer, we will first use a simple example of quantum harmonic oscillator to illustrate the inequivalence of two limits.
4.1. Harmonic Oscillator: Semiclassical Limit
Consider the excited states of the harmonic oscillator, whose Hamiltonian is given by
in which m is the mass and is the oscillating frequency. The wavefunction of the excited state is
The probability density of finding the oscillator in this excited state is
where is the Hermite polynomial of the order. The probability distribution is always non-negative. In the classically allowed region, the probability function is oscillatory and the number of nodes is equal to n, but into the classically forbidden region, the probability exponentially decays, as shown in Figure 2.

Figure 2.
(a) shows the probability distribution and the Wigner function of the ground state of a harmonic oscillator. Both are positive definite. (b) For the excited state . It is clearly seen that the Wigner function becomes indefinite in sign. The Wigner function is evaluated at .
The Wigner function of excited state of the harmonic oscillator is given by
Introduce new variables
and the Wigner function reduces to
With the help of the identity [123]
for , where is the generalized Laguerre polynomial, we obtain
and then the Wigner function of excited state of the harmonic oscillator becomes
where
The ratio is related to action variable and is an adiabatic invariant in classical mechanics. In quantum physics, the relation
roughly defines the boundary between the classically allowed and forbidden regions for the excited state. That is, the phase-space point such that will fall in the classically forbidden region. The Wigner function can be negative when , in contrast to the probability density , which in fact is related to the Wigner function by an integral relation
Qualitatively speaking, from Figure 3, the Wigner function of the excited state of the harmonic oscillator will have negative values in the regions that form n among concentric annuli centered at the origin of the phase space. Each annulus has an area roughly order of , so that the total area of negative-value region is of order . This has a few interesting implications. First in the limit , the areas where the Wigner function takes on negative values have measure zero. Hence essentially the Wigner function becomes non-negative. This seems consistent with the interpretation of identifying the Wigner function as a probability distribution. On the other hand, as , the total area of the regions the Wigner function takes on negative values increases with n, so the Wigner function still keeps the quantum features, and it can never serve as a probability distribution. Hence here we see an example that the large n limit does not always lead to a classical description. In this case, the disparity can be seen from (58) that n and ℏ do not always appear together as a ratio of the form, say, .
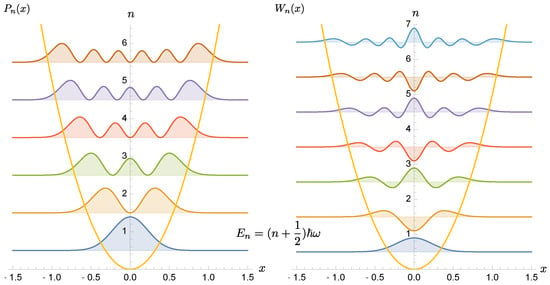
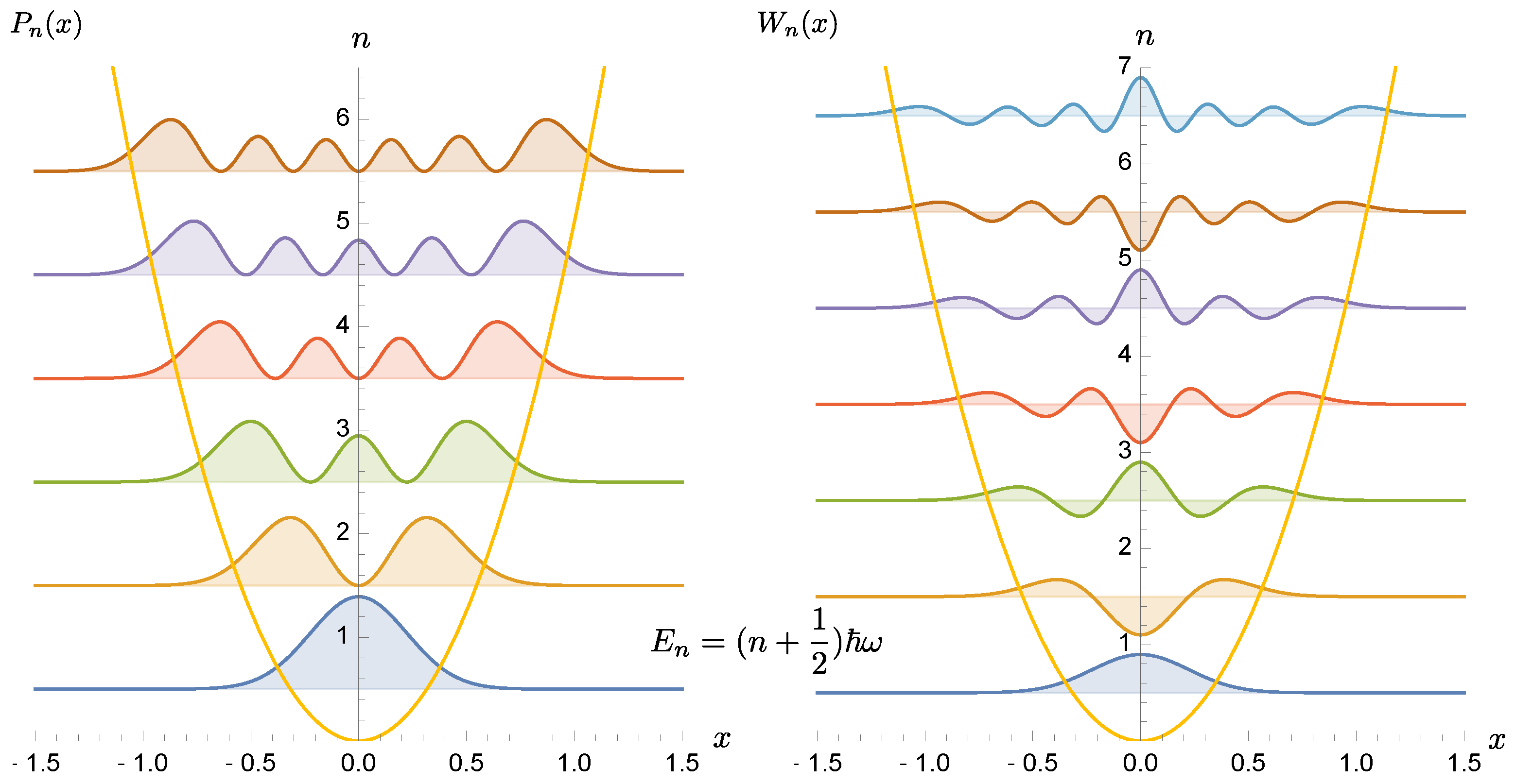
Figure 3.
Comparison of the probability distribution and the Wigner function of a harmonic oscillator from the ground state up to 5th excited state. A few distinguished features of the Wigner function can be easily identified, such as and the number of the regions where the Wigner function is negative. Both exhibit exponential decay into the classically forbidden regimes.
Quantitatively in the limit , the Wigner function is approximately give by
for a highly excited state, as long as q, p are not too close to the boundary defined by (60), which is related to the turning points of the harmonic potential. Again, it shows that the Winger function remains oscillatory between the positive and negative values within the classically allowed region, even in the limit. In comparison, we check the large limit, that is, the large energy limit
This consistently describes the behavior of the Wigner function in the classically forbidden region. The probability is exponentially suppressed.
The semi-classical limit is rather tricky, and the rigorous treatment of the Wigner function in the semi-classical limit can be found in [124,125]. Here we merely discuss a few subtlety in taking the semi-classical limit. Although the total area of the regions where the Wigner function is negative approaches zero in this limit, the transition is rather extreme. From the functional form of (58), we observe that when ℏ is shrunk by a factor , the lateral dimension, as seen in Figure 2b, will be squeezed into of what it was, but the oscillation amplitude is blown up by a factor . For a fixed n, the number of oscillations does not change with varying ℏ.
Naïvely expanding the Wigner function with respect to small ℏ will yield an expression like (62), which is already positive. Then taking leads to a limiting form that is proportional to , with the sign of the proportionality constant independent of n. This is rather perplexing because we know . Either the intermediate Taylor expansion (62) or the final limiting form of the Wigner function do not correctly describe the aforementioned scaling behavior of the Wigner function. Physically, we would expect that if the Wigner function were indeed to give a consistent (semi-)classical description of the quantum harmonic oscillator in phase space when , it would sharply peak at the ellipse, defined by (60). Clearly, the aforementioned scaling behavior does not signal that either. In fact, an implicit feature hints that way. Since the Wigner function is normalized to unity, it means there will be an excess of positive part of the Wigner function over its negative part. The surplus resides on the positive ridge, which is independent of n, roughly along the boundary of the classically allowed/forbidden regimes, as seen in Figure 3. In addition, it has been raised that the more satisfactory way to take the semi-classical limit is to simultaneously require that , but should be fixed. It has been shown [126] that in such a limit the Wigner function (58) does reduce to
consistent with the classical expectation. To be thorough, we include the derivation of (64) in Appendix B. Here we have used the harmonic oscillator to illustrate the subtleties in and the inequivalence between different approaches of taking the classical limit. Next we will move on to the models that have been used in the context of classicality of cosmological perturbations. In contrast to the harmonic oscillator, they do not have a confining potential, so their canonical coordinate or momentum dispersion tends to grow indefinitely.
4.2. Free Particle
The free particle is used in [32] to highlight features of cosmological perturbation in inflationary spacetime.
Suppose we have a free particle of mass m and it has an initial momentum at , and we further assume that initially its wave function is described by a Gaussian wavepacket such that
The parameter denotes the initial width of the state. Then in the Heisenberg picture, By solving the Heisenberg equation
the position and the momentum operators evolve with time according to
where
Together we can explicitly show that the Robertson-Schrödinger uncertainty relation is invariant with time
a necessary requirement of a pure quantum state under unitary evolution, where ,
This is of particular importance because it stresses that nothing is lost about the quantumness of the system during the evolution.
The mean position follows the trajectory of the classical free particle and the mean momentum is a constant. They are all consistent with the classical theory. On the other hand, The wavepacket spreads out rapidly in space, which is a very quantum mechanical feature. The position uncertainty grows quadratically indefinitely with time, but the momentum uncertainty remains constant. They, together with the correlation between and , ensure that the uncertainty function remains independent of time. It is important to have this correlation involved. Without it, the product grows without bounds.
We also observe that the wavepacket becomes increasingly more squeezed in with time because the ratio rapidly diminishes in time even though remains a constant. Strictly speaking, here we have , so and are not orthogonal and they are correlated, so to better describe the deformation of the wavepacket we will find two orthogonal quadratures. They can be determined by the eigenvectors of the covariance matrix for the canonical variables . Following the procedures outlined in (29)–(36) and using the new set of canonical operator pair , we find that always but in the large time limit
while in the short-time limit, we have
Thus the wavepacket, according to the Wigner function in phase space, is squeezed in the quadrature but stretched in the quadrature. It peaks at , and in particular . On the other hand, since the ellipse defined by these quadratures becomes extremely thin in the direction but strung out in the direction. The ellipse seems morphed into a well defined path. However, it does not coincide with the bona fide classical path of a free particle in phase space. Alternatively, since the Wigner function of a free particle can be given by (43), with a, b, and c in (72), at late times we have , and we can apply the limit in (44). Nonetheless, we note that the path defined by the delta function7
again in general is not equal to the phase-space path of the free particle, with an exception of and . This special case identically satisfies (77). Finally, according the discussion following (44), we learn that the resulting Wigner function is not physical because (1) the pure state is not pure any more after we take the limit, (2) the purity of the state is greater than unity, and (3) the corresponding von Neumann entropy is ill defined. Thus the assumed emergence of a well-defined path in phase space at late times does not lead to a description consistent with the known classical dynamics. What is worse is that the corresponding Wigner function does not even describe a legitimate physical state of a quantum-mechanical system.
The ratio of the square root of the position uncertainty and the mean position gives a measure about the strength of the quantum fluctuations. This is clearly seen from the definition of the position uncertainty. For the free particle, it is given by
At large times, the ratio reaches to a nonzero constant
so the system still possesses a quantum-fluctuation feature. Since this measure works also for the non-Gaussian state, it cannot be fully accounted for by assuming the Wigner function as a classical probability distribution.
Equation (68) offers an intuitive way to examine the non-commutativity of, say , at different times. In the free-particle case, we have
from (7). The righthand side is far from being zero, so at different times are strongly non-commuting. From the aforementioned Together with the equal-time commutation relation
for all times, we find that the free-particle system remains quantum mechanical throughout the unitary evolution, and the assertion that transition to its classical counterpart at late times cannot be fully justified.
Oftentimes one might resort to the arguments that since at late times, one might write
at late times, such that one would conclude
and claim that the operators becomes commuting. A more careful analysis based on (80) plainly shows that the approximation used in (82) is misleading and the subsequent conclusion is then illusory.
Next we will examine the quantum inverted oscillator used in [33], which in some sense mimics the runaway behavior of the cosmological perturbations in the de Sitter space.
4.3. Inverted Linear Oscillator
The inverted oscillator’s potential has an opposite sign to the harmonic potential, so the Heisenberg equation takes the form
Strictly speaking, its motion is not oscillatory, so the parameter does not bear the meaning of oscillation frequency. In general, the classical inverted oscillator has unstable, runaway dynamics, except for the occasion that the initial conditions satisfy . An example is the case when the system initially rests at the top of the potential. The quantum inverted oscillator is susceptible to its own quantum fluctuations, so its dynamics are more prone to run away.
The fundamental solutions to (84) are
Suppose the initial conditions are given by
The parameters , are chosen such that [33]
The former is associated with the width of the initial wavefunction, and comparing with (66), we may identify . The mean energy of the system is conserved and is given by
in which the kinetic energy and the potential energy are
Since the potential is unbounded below, we expect the kinetic energy of the inverted oscillator will also increase without bound.
Thus although averagely speaking, the mean position of the quantum inverted oscillator remains at the top of the potential, its position dispersion spreads exponentially fast. This means that, when we try to measure the coordinate operator , it is more than often that we will obtain a nonzero value, and with increasing time, the typical measured value grows indefinitely, rolling down under either side of the inverted potential. Therefore, in the coordinate representation, the wavefunction is widely spread about the mean trajectory. The same conclusion applies to the measurement of the canonical momentum operator . These also hold true even when the initial conditions are such that the system rolls downs that potential. From (3) and (85), we see that the mean position will increase exponentially, but the position dispersion grows equally fast. Even the system has such a runaway behavior, its uncertainty function remains a constant value
Again we emphasize that this reveals that the quantum nature of the system never loses and decoherence does not happen, even though the system may seem to show classical behavior in some partial measures. In contrast, if one uses the approximated forms of the covariance matrix elements in (87)–(89), one will obtain a zero value for the uncertainty function, which violates unitarity. It would be misleading if one uses this as the criterion to claim the emergence of classicality due to a loss of quantum coherence. This example also tells us that one should be mindful of the contributions of the subdominant contributions in the covariant matrix elements.
The Wigner function takes the standard form for the Gaussian state we used,
with . However, in contrast to the free-particle case; here, the momentum uncertainty also increases indefinitely with time. Thus, it is interesting to examine the behavior of the Wigner function to see whether it will define a highly squeezed ellipse at late times. Discussions in the previous sections indicate that the ratio of the two orthogonal quadratures can provide the information about the extent of squeezing of the ellipse during the course of evolution. From (29), we find the ratio given by
at late times. It falls to zero extremely fast, so we end up with a highly stretched and highly squeezed ellipse. As a reminder, even the ratio takes on such an extreme value, the product remains , a rephrasing of the Robertson-Schrödinger uncertainty relation for the orthogonal quadratures. Since from (44), if we take the limit too literally, the Wigner function contains a delta function that defined a path in phase space8,
This, in the current case when , , clearly does not match the classical counterpart even in the limit . One may find this example too atypical, so let us consider the initial conditions of the inverted oscillator such that its classical counterpart does roll down that potential. The mean position and momentum are given by
Equation (99) becomes
This does not resemble the classical path in phase space. Following our discussions in the free-particle case in treating a highly squeezed ellipse, one should not fall into the trap of misinterpreting this as the emergence of classicality of the quantum system. Here we would like to stress again that no matter how one deforms the quadrature ellipse in phase space by squeezing and stretching, it is always a two-dimensional geometric object, having an invariant area , a dictum of the quantum uncertainty principle and unitary evolution of a closed system. Nonetheless, when one jumps to reducing the ellipse to a line in phase space, the areas go to zero, and unitarity is violated.
Here it is also interesting to note that suppose we have two “density matrix elements”, and they differ by
for some real number and have the property . Then these two density matrix elements will give the same probability distribution and satisfy the same normalization condition, but they may not all be physical. They may not be guaranteed to be semi-positive definite.
Finally we examine the commutator of the position operator at different times
The commutator is far from being zero, so they do not commute. For the motion of the inverted oscillator having the mean position and momentum, given by (100), the effects of quantum fluctuation effect are not negligible, because the ratio
approaches a constant of order unity, as . Therefore as in the free particle case, we conclude that the quantum inverted oscillator remains quantal throughout its evolution.
To summarize the salient features in our model studies discussed in this section we refer the reader back to Section 1.2, for an itemized list of pivotal findings.
In the next section we shall discuss the evolution of a quantum field in an inflationary universe. After a long duration of inflation the quantum state has undergone a high degree of squeezing. This is the reason why some authors felt justified enough to adopt the leading-order approximation, and, without providing any convincing explanation, ignored the sub-leading terms. With the help of the simpler quantum mechanical models studied in this and the previous section, we have pin-pointed where the pitfalls are with regard to the classicalization issue where the fallacy of the prior claims resides. In the same vein, for the case of inflation studied in the next section we shall show that viewed as a closed system, quantum cosmological perturbations do not decohere. In addition, the existence of quantum entanglement lends support to our thesis that closed quantum systems do not turn classical just because they are badly squeezed.
5. Inflation Field
Cosmological perturbations in an inflationary universe, in an appropriate gauge, follows the linear perturbations of the inflation field [31], so we will just follow the unitary evolution of the perturbations of the inflation field.
The perturbation of the inflation field can be described by a minimally coupled scalar field in spatially flat de Sitter space, whose line element in the conformal time frame is given by
Here, is the scale factor that depends only on the conformal time . Thus the Lagrangian takes the form
where we decompose the field into its modes, and the temporal dependence is included in
It is convenient to make a change of variable , and write the Lagrangian as9
The last term is a total time derivative, so its contribution can be discarded. Thus the canonical momentum conjugated to is given by
and then the equation of motion is
Each mode essentially behaves like a linear parametric oscillators, so its evolution remains Gaussian if the initial state of such a system is a Gaussian. If the initial state is a pure state like the vacuum state, then it will evolve to a two-mode squeezed (vacuum) state [31]. Creation of particle pairs will accompany such a parametric evolution.
If with , then the mode function is given by
normalized by the Wronksian condition . After we promote the canonical variables to operators, they can be expanded by the mode function ,
and . In the limit , the mode function corresponds to the positive-frequency mode
However, we may consider a more general case that the inflation starts at . We then require that and . Thus the positive-frequency mode function takes a rather complicated form
and the fundamental solutions are given by
with
Then the general evolution of can be constructed in the same way as outlined in Section 3 by
such that
At the initial time the mode operator can be expressed in terms of the creation and annihilation operators of the modes,
Then we can express at any time in terms of the creation and annihilation operators at the initial times,
Compared with (112) we arrive at a convenient relation
between the mode function and the fundamental solutions to the differential Equation (110).
5.1. Canonical Variables Remain Noncommutating
From (118), we may compute the commutators of at different times10
but
independent of , so the same expression even if . The commutator Equation (125) for the superhorizon mode , in general does not vanish. It is approximately given by
and will approach zero only if additional limits and are imposed. Thus in general these two operators do not commute.
Notice that if one opts to keep only the growing part contribution of for the superhorizon modes, then without additional requirement and . This is where some prior authors wrongly conclude that these two operators commute for superhorizon modes at any time.
Different from the previous examples, given a fixed k, we can always find, in the inflation field case, a sufficiently small and to make the commutator as close to zero as possible. This is not a typical scenario. On the other hand, the equal-time commutation relation between the canonical variables is always nonzero, given by
A spurious argument is also often used for the equal-time commutation relation in this context: For a finite , if one keeps only the dominant contributions of for the superhorizon modes
then one will obtain
because both have the same form of dependence. Thus one again incorrectly concludes that
and wrongly proclaim that the quantum-to-classical transition has implicitly occurred. Equation (130) is clearly in contradiction with (127). In addition, all the issues concerning the Wigner function11 discussed in Section 4 apply here. The extreme squeezing of the state, caused by the exponential expansion of the background spacetime, offers a strong temptation for authors of this persuasion to dispense with the subleading terms, and to draw physical conclusions based only on the dominant contributions. Thus, the salient lesson we have learned so far is that the subdominant contributions may not be wantonly discarded and must be treated carefully. Then we will correctly find that the non-commutativity between the canonical operators are intact and robust.
5.2. Particle Creation: Numbers and Coherence
The inflation field perturbation has a distinguished quantum feature that is absent in the examples in Section 4. The particles in the modes are created in pair over the parametric evolution driven by the expanding spacetime. These particles are not created incoherently. In fact they are entangled. Even though particles are copiously produced and entangled, the state of the perturbation remains pure without entropy production [31,111].
Let us look into this aspect in more detail. In the Heisenberg picture, the time evolution of the linear field operator can be expressed as a mapping of the operators in terms of the squeezed transformation
with the two-mode squeeze operator
and the rotation transformation
with the rotation operator
The squeeze parameter and the rotation angle are time-dependent functions, reflecting the time evolution of the operator in this case. At a later time, the operator at the initial time is formally mapped to
with
The Bogoliubov coefficients , obey the Wronskian condition
Two useful combinations of the Bogoliubov coefficients are
where we have assumed [31,127] that the squeeze parameters , and the rotation angle depend only on the magnitude of . Equation (138) gives the number density of the pair-created particles, while (139) is a measure of coherence between the created particle [128].
The Bogoliubov coefficients can be related to the fundamental solutions by [31,127]
Thus we readily find that for the mode function (114), we have
It is oscillatory with frequency when , but the amplitude is proportional to roughly . On the other hand, if it gradually stops oscillating and transits to a monotonic increase as like . That is, the number density of created particles of each mode oscillates with time when its physical wavelength is smaller than the horizon width, but when the physical wavelength becomes greater than the horizon, it grows monotonically.
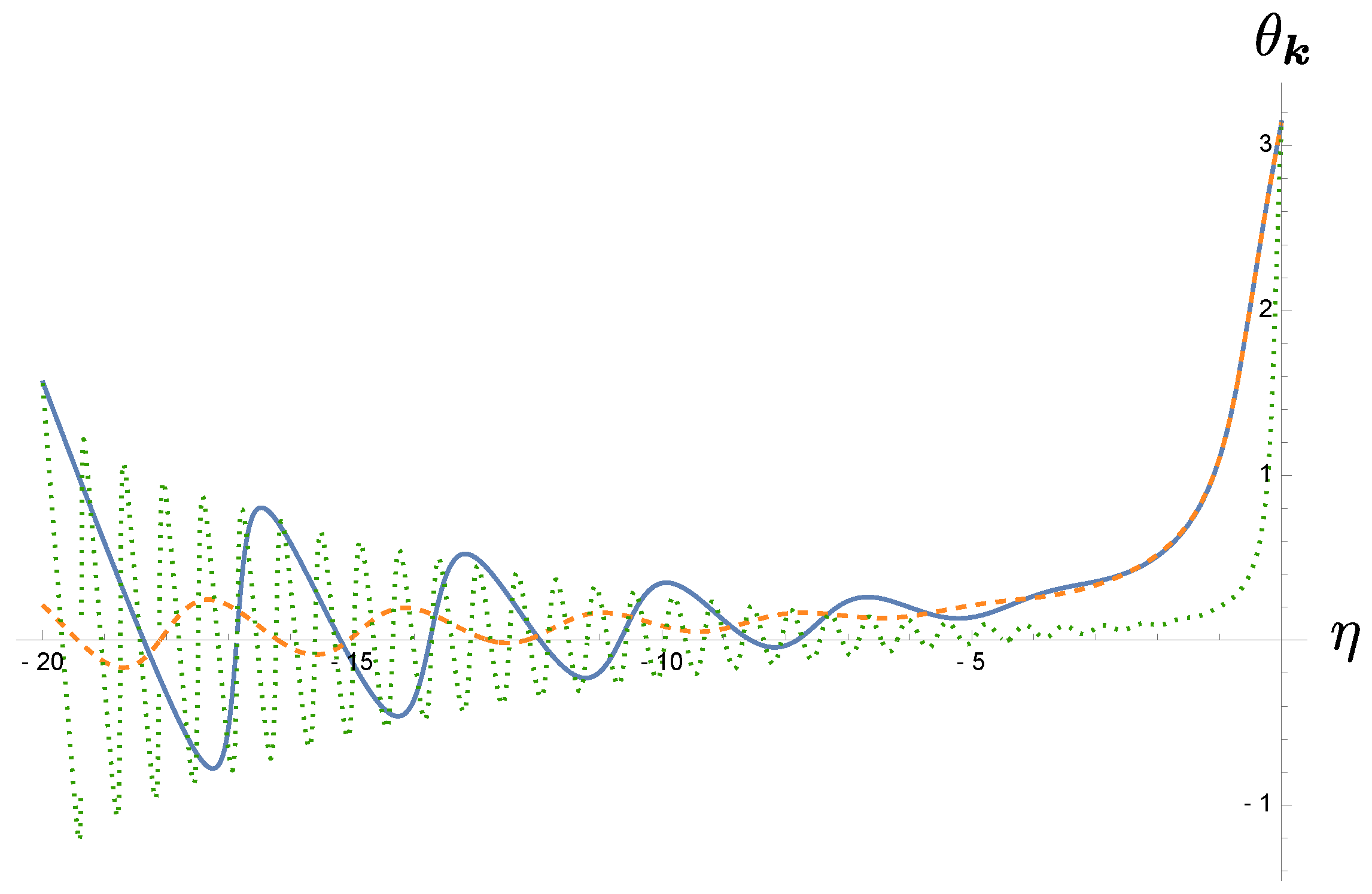
Similar behavior is observed for the coherence between the created particles . However, two points are worth emphasizing. First, this quantity is not positive definite like the particle number density. Moreover, its phase will come to a constant , as shown in Figure 4.
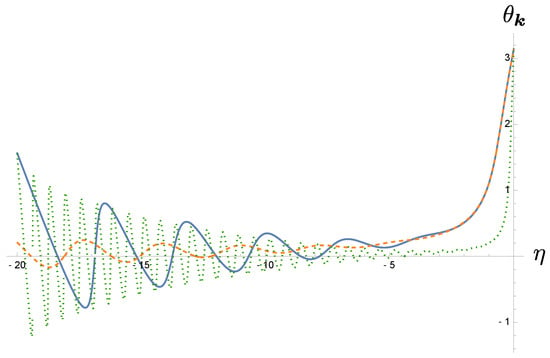
Figure 4.
The time variation of the phase in coherence for mode . The blue solid curve has the initial time is and , the orange dashed curve and , and the green dotted curve and .
This can be seen from the expansion of about
In Figure 4, it is interesting to note that for sufficiently close to , the blue solid curve and the green dotted curve follow the same envelope. However, when , the blue curve more or less overlap with the red dashed curve, independent of the initial time, as has ben shown in (143). We also observe that the initial phase is , seemingly contradictory to the fact that and . It may be resolved by their Taylor expansions around
Thus, the value of the phase angle in fact comes from the first-order contribution of .
The covariance matrix elements are given by
As shown in Figure 5, on the subhorizon scales, they oscillates with time, but once the physical wavelength of the mode crosses the Hubble horizon, they increase monotonically and indefinitely.
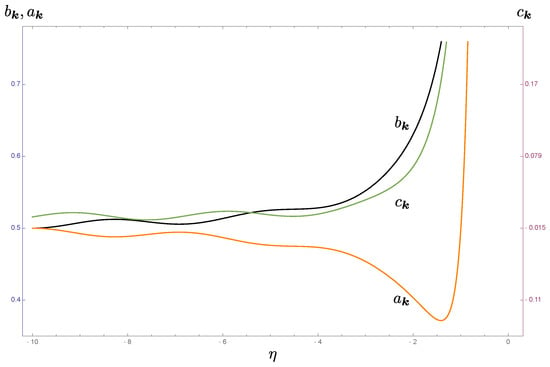
Figure 5.
The time variation of the covariance matrix elements for mode . The blue solid curve denotes , the orange dashed curve , and the green dotted curve . We choose the parameter and . Hence, their behaviors are qualitatively different, when , where the corresponding mode has a physical wavelength greater than the Hubble horizon.
Roughly, there is a trend that will lie between and in the super-horizon regime although it is not accurately portrayed in Figure 5 because different vertical scales are used. In addition, the element seems always positive for the superhorizon modes
for , and the dominant contribution is independent of . That is, for , we always have when . For comparison, in the superhorizon regime, we have
The trend is then clearly seen. We emphasize again that similar to the inverted oscillator, if we use the exact, full expressions of the covariance matrix elements, we always have
a signature of the unitary evolution of the pure Gaussian state. If one uses the approximated expressions (149) and (150) for the superhorizon modes, one would find
If one uses this condition to argue for the classicalization of inflationary cosmological perturbations, one would miserably be doomed because it violates the Robertson-Schrödinger uncertainty relation
5.3. Entanglement: An Indelible Signifier of Quantumness
If each mode of the inflation field perturbation starts in a vacuum state, then the evolution will lead it to a two-mode squeezed vacuum, which remains a pure state. To examine whether there exists quantum entanglement between states of modes , an easily computable entanglement measure for such a bi-partite pure Gaussian state is their reduced von Neumann entropy [111,129,130]. This is the von Neumann entropy of the reduced density matrix, which is obtained after we coarse-grain one party of the bi-partite pure Gaussian state associated with modes . As is shown in [31,111], the entanglement measure takes the form
with the created particle number density being . Following earlier discussions on , we learn that it would change monotonically once the mode crosses the horizon, meaning that the physical wavelength of the mode is greater than the horizon. Therefore the pair-created particles are unambiguously entangled even for the superhorizon modes. This is a very strong evidence that the inflation field perturbation remains quantum-mechanical. Together with the arguments presented earlier, we can say that the inflation field perturbation never drops its quantum nature, and decoherence does not occur during the unitary evolution of the perturbation. Similar consideration has been carried out by [131], who investigate the quantum discord in the bi-partite state among the modes . They showed that for a pure state, the quantum discord takes the same form as the reduced von Neumann entropy, discussed above. We concur with their conclusion that ‘… the CMB is placed in a state which is “very quantum”. This means that it is certainly impossible to reproduce all the correlation functions in a classical picture …’.
Finally, in this context we mention the take-home message of our recent companion paper [31], that the entropy of the bipartite state for modes is zero throughout the unitary evolution because it continues to be a pure state and the created particles are entangled. If somehow we lose track of one partner of the pair in mode or , we will end up having nonzero entropy given by (154). Thus implies that entropy production in cosmological particle creation does not result from particle creation per se, but is a consequence of the loss of complete information of the field.
6. Conclusions
In this paper we adopt the Heisenberg picture to re-derive some earlier results pertaining to the classicalization issue of closed linear quantum systems where the free particle [32] and the inverted oscillator [33] models have been used as analogues to the quantum cosmological perturbations in inflationary universe. The advantage of the Heisenberg equations in treating the analog models systems lies in its physical transparency and proximity to the classical equations of motion, so one can directly identify the dynamical features of the systems in question.
The classical or semi-classical limit of a closed quantum system is subtler than what one might think. The cut- and-dry rule of thumb of simply taking alone may not be the proper way to reach a classical limit even though it is well-known that classical physics does not contain ℏ. Neither is the large n limit alone, as prescribed by the correspondence principle: A highly excited system is often expected to show classical behavior because the energy difference of the neighboring states are small compared with the mean energy of the system. It is often stated that the quantum, discrete nature becomes increasingly obscure and a classical description becomes viable. We use a harmonic oscillator as an example to show that taking the large n (excitation number) limit does not produce equivalent results as compared to a vanishing ℏ. To refresh these basic points we have included a pedagogical derivation in Appendix B to show the conditions how the Wigner function in a phase-space formulation of the quantum harmonic oscillator can, in the suitable semi-classical limit, describe the corresponding paths in phase space of a classical harmonic oscillator—namely, and while keeping the total energy fixed.
A closed system should remain quantum mechanical throughout its unitary evolution. For the un-confined linear quantum systems such as the free particle, inverted oscillator and cosmological perturbations in the inflationary universe, they have a common feature, that is, the dispersions of the canonical variables tend to grow unbounded over the unitary evolution, so that at late times the quadrature ellipse becomes extremely squeezed in one direction and stretched in another direction. It is then often claimed or implicitly argued that in this limit the ellipse can reduce to a well-defined path in phase space, and the Wigner function will be proportional to a delta function that defines the path and the proportionality factor gives the classical probability of the system along the emergent phase-space path. Since in this argument ℏ remains finite, the resulting Wigner function clearly violates the requirement that a proper Wigner function is bounded both from above and below. Further, the density matrix elements converted from this delta-function like Wigner function is unphysical: (1) It does not correspond to a pure state if the closed system starts in pure state; (2) It does not describe a mixed state either because the purity of the state is greater than unity, (3) the density matrix has negative eigenvalues, violating unitarity, leading to negative probability and ill-defined von Neumann entropy; and 4) the Robertson-Schrödinger uncertainty relation is not respected.
Furthermore, regarding the evolution of the quantum operator, for unbounded motion, an approximation is often used where only the leading order contribution is kept. One would then show that the (canonical) operator at different times commute and even the equal-time commutation relation vanishes, and, voila, classicality emerges. This is another gaffe in the folklore. As a matter of fact, if one considers the full contribution, even just keeping the subleading contribution, one can unambiguously demonstrate that the aforementioned operator does not commute, and the commutation relation is preserved.
Therefore, it is an oversimplification to regard the large squeezing limit as a classical limit because the quantum features of this closed system remain intact, and discounting or dismantling them leads to ill-defined mathematical properties and unphysical consequences. This is perspicuously seen if we perform an unsqueezing via an unitary transformation. The quantum coherence of the system can be restored. Finally, in cosmological perturbations, there is a more compelling argument for the preservation of quantumness. The particle pairs created during the inflationary universe are entangled. Entanglement is a uniquely quantum feature, and its existence is especially important if one wishes to trace back the quantum origin of cosmological perturbations using quantum information-theoretical tools.
Author Contributions
J.-T.H. and B.-L.H. contributed equally to the conceptualization, methodology, investigation and writing of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
J.-T. Hsiang is supported by the Ministry of Science and Technology of Taiwan under Grant No. MOST 110-2811-M-008-522.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Preservation of the Uncertainty Function under Squeeze Transformation
Here we show that the squeeze transformation does not modify the bound in the generalized uncertainty relation for the free, linear quantum scalar field. Since the free quantum scalar field in flat space can be viewed as a collection of quantum harmonic oscillators, we will use a harmonic oscillator to illustrate this point. Suppose that the oscillator is in an arbitrary normalized state . The generalized uncertainty relation can be expressed as
where the displacement and the conjugated momentum of the oscillator are respectively
such that
with , , and .
If we apply the squeeze operator on the state , then its associated actions on can be given by
with . We then have
such that
It then shows that in general the squeezing does not modify the generalized uncertainty relation; it only distorts the quadratures in the relation.
Appendix B. Semiclassical Limit of the Harmonic Oscillator
It is well-known that the motion of a classical harmonic oscillator traces out an ellipse in the phase space of its canonical variables . Thus it is quite naturally to ask whether the Wigner function for a quantum harmonic oscillator in the phase space formulation of quantum mechanics can, in a suitable semi-classical limit, reveal the same feature. That is, can one show that in the semi-classical limit, the Wigner function reduces to
which is consistent with classical expectation. The following discussion is largely based on the work [126], with notations adapted to this paper. Suppose the oscillator has an energy , which is held fixed when the semi-classical limit is reached. Thus the excitation number n will grow accordingly.
It turns out more convenient to use the double Fourier transform, the characteristic function, of the Wigner function
In particular, the characteristic function of a pure state can be written as
For the excited state of the harmonic oscillator,
we have
Here is the Hermite polynomial of order n. To evaluate this, we first form the generating function of by
with the help of
for . We then write (A10) into
with
and compare it with the generating function of the Laguerre polynomials
We find
Now we explore an asymptotic expression of the generalized Laguerre polynomial for sufficiently large n,
valid for , with
and the Bessel function of first kind . When , we have
and . In the limit , we find
and thus
which is valid for , or with
Going in parallel, we check the double Fourier transformation of the delta function
Thus we have
Following our previous arguments, we would like to fix while taking the limit , so (A25) becomes
Therefore we find that when both limits are taken together, the Wigner function reduces to a form that is consistent with the classical dynamics of the harmonics oscillator. We next examine the normalization condition
and check that it is satisfied.
Notes
| 1 | Here, the center of attention is the quantum perturbations of the inflation field, that is, (see next subsection); the mean field is governed by a potential which engineers the inflationary dynamics, such as ‘slow-roll’, etc. |
| 2 | There is plenty of truth in the idiom,“truth is always simple, but simplicity is not always the truth”. |
| 3 | The background field is often assumed to be classical, but this needs to be proven rather than assumed to be automatically valid. The regarded as a mean field keeps its quantum nature. (The difference between a mean field and a classical field is explained in, e.g., [38].) One can show how readily the mean field is decohered by its quantum fluctuations, such as treated in [25]. |
| 4 | Note gravitational waves are weak metric perturbations. Gravitons are quantized short wavelength linear perturbations off of a smooth spacetime manifold, in the nature of collective excitations. Gravitons are governed by general relativity, a low energy theory for the macroscopic structure of spacetime, a far cry from quantum gravity, defined as theories for the microscopic structures of spacetime functional at the Planck scale [42] |
| 5 | Despite the similarity in form with the bilinear type of coupling between a quantum Brownian oscillator interacting with a bath of many modes, when two fields are bilinearly coupling, only one mode of the system field interacts with one mode of the bath field, the physics is totally different. It is like two equal subsystems interacting. One would not see dissipation or decoherence; the energy and phase information only pass from one to another back and forth. A large number of modes in the bath is needed to see dissipation and decoherence in the system. |
| 6 | For a pure state , the density matrix operator is . We thus have . In addition, any pure Gaussian state can be reached from the vacuum state by a suitable unitary transformation. Since the vacuum has minimal uncertainty, that is, and since the unitary transformation preserve the Robertson-Schrödinger uncertainty principle, the resulting pure Gaussian state then has . |
| 7 | Although in [32], the authors did not explicitly write the Wigner function into a form proportional to a delta function for the free particle case, their Equation (63) and Figure 1 served the same end. Besides, the Wigner function of the cosmological perturbations in their Equation (29) takes the delta-function form. They obtained their Equations (15) and (16) by keeping only the dominant contributions. According to the analysis in our Section 3 these results in [32] are thus problematic. |
| 8 | In [33], only the dominant contribution is kept, so the derived Wigner function of a quantum inverted oscillator in their Equation (2.13) contains a delta function. It does not describe a physical state, according to [121] and the reasoning in our Section 3. |
| 9 | Or instead of representation, we may use the representation,
|
| 10 | |
| 11 | For example, in [1], the Wigner funciton of the cosmological perturbations in its Equation (46) is written into a delta function form, and when only the leading term of what is resulting in its Equation (51) is kept, the conclusion of ‘decoherence without decoherence’ is conveniently yet haphazardly drawn. |
References
- Polarski, D.; Starobinsky, A.A. Semiclassicality and decoherence of cosmological perturbations. Class. Quant. Grav. 1996, 13, 377. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent histories and the interpretation of quantum mechanics. J. Stat. Phys. 1984, 36, 219. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent Quantum Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Omnes, R. Logical reformulation of quantum mechanics, I. Foundations. J. Stat. Phys. 1998, 53, 893. [Google Scholar] [CrossRef]
- Omnes, R. Consistent interpretations of quantum mechanics. Rev. Mod. Phys. 1992, 339, 64. [Google Scholar] [CrossRef]
- Omnes, R. The Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Quantum mechanics in the light of quantum cosmology. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Westview Press: Boulder, CO, USA, 1990. [Google Scholar]
- Hartle, J.B. The quantum mechanics of cosmology. In Quantum Cosmology and Baby Universes; World Scientific: Singapore, 1990. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Classical equations for quantum systems. Phys. Rev. D 1993, 47, 3345. [Google Scholar] [CrossRef] [PubMed]
- Joos, E.; Zeh, H.D.; Kiefer, C.; Giulini, D.J.; Kupsch, J.; Stamatescu, I.O. Decoherence and the Appearance of a Classical World in Quantum Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2004, 76, 1267. [Google Scholar] [CrossRef]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1. [Google Scholar] [CrossRef]
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, H.D. The emergence of classical properties through interaction with the environment. Z. Phys. B 1985, 59, 223. [Google Scholar] [CrossRef]
- Halliwell, J.J. Decoherence in quantum cosmology. Phys. Rev. D 1989, 39, 2912. [Google Scholar] [CrossRef]
- Hartle, J.B. The quantum mechanics of closed systems. In Directions in General Relativity, Vol. 1; Hu, B.L., Ryan, M.P., Vishveswara, C.V., Eds.; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Hartle, J.B. The reduction of the state vector and limitations on measurement in the quantum mechanics of closed systems. In Directions in General Relativity, Vol. 2; Hu, B.L., Jacobson, T.A., Eds.; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems, 2nd ed.; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Rivas, A.; Huelga, S.F. Open Quantum Systems: An Introduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Rammer, J. Quantum Field Theory of Non-Equilibrium States; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kamenev, A. Field Theory of Non-Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems, 4th ed.; World Scientific: Singapore, 2012. [Google Scholar]
- Calzetta, E.A.; Hu, B.L. Nonequilibrium Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Calzetta, E.A.; Hu, B.L. Quantum fluctuations, decoherence of the mean field, and structure formation in the early universe. Phys. Rev. D 1995, 52, 6770. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Mazzitelli, F.D. Coarse graining and decoherence in quantum field theory. Phys. Rev. D 1996, 53, 2001. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Nacir, D.L. Decoherence during inflation: The generation of classical inhomogeneities. Phys. Rev. D 2005, 72, 063506. [Google Scholar] [CrossRef]
- Brahma, R.; Alaryani, O.; Brandenberger, R.H. Entanglement entropy of cosmological perturbations. Phys. Rev. D 2020, 102, 043529. [Google Scholar] [CrossRef]
- Nelson, E. Quantum decoherence during inflation from gravitational nonlinearities. JCAP 2016, 3, 022. [Google Scholar] [CrossRef]
- Hollowood, T.J.; McDonald, J.I. Decoherence, discord, and the quantum master equation for cosmological perturbations. Phys. Rev. D 2017, 95, 103521. [Google Scholar] [CrossRef]
- Hsiang, J.-T.; Hu, B.L. Intrinsic entropy of squeezed quantum fields and nonequilibrium quantum dynamics of cosmological perturbations. Entropy 2021, 23, 1544. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, C.; Polarski, D. Emergence of classicality for primordial fluctuations: Concepts and analogies. Ann. Phys. 1998, 3, 137. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.-Y. Quantum mechanics of the scalar field in the new inflationary universe. Phys. Rev. D 1985, 32, 1899. [Google Scholar] [CrossRef]
- Lifshitz, E.M. On the gravitational stability of the expanding universe. J. Phys. 1946, 10, 116. [Google Scholar]
- Lifshitz, E.M.; Khalatnikov, I.M. Investigations in relativistic cosmology. Adv. Phys. 1963, 12, 185. [Google Scholar] [CrossRef]
- Hawking, S.W. Perturbations of an expanding universe. Astrophys. J. 1966, 145, 544. [Google Scholar] [CrossRef]
- Bardeen, J.M. Gauge invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882. [Google Scholar] [CrossRef]
- Chou, C.-H.; Hu, B.L.; Subasi, Y. Macroscopic quantum phenomena from the large N perspective. J. Phys. Conf. Ser. 2011, 306, 012002. [Google Scholar] [CrossRef]
- Anastopoulos, C.; Hu, B.L. Comment on “A spin entanglement witness for quantum gravity” and on “Gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity?”. arXiv 2018, arXiv:1804.11315. [Google Scholar]
- Anastopoulos, C.; Hu, B.L. Quantum superposition of two gravitational cat states. Class. Quant. Grav. 2020, 37, 235012. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Hu, B.L. Emergent/quantum gravity: Macro/micro structures of spacetime. J. Phys. Conf. Ser. 2009, 174, 012015. [Google Scholar] [CrossRef]
- Grishchuk, L.P. Amplification of gravitational waves in an isotropic universe. Zhurnal Eksp. Teor. Fiz. 1974, 67, 825. [Google Scholar]
- Ford, L.H.; Parker, L. Quantized gravitational wave perturbations in Robertson-Walker universes. Phys. Rev. D 1977, 16, 1601. [Google Scholar] [CrossRef]
- Parikh, M.; Wilczek, F.; Zahariade, G. The noise of gravitons. arXiv 2020, arXiv:2005.07211. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J.; Tokuda, J. Noise and decoherence induced by gravitons. Phys. Rev. D 2021, 103, 044017. [Google Scholar] [CrossRef]
- Cho, H.T.; Hu, B.L. Quantum noise of gravitons and stochastic force on geodesic separations. arXiv 2021, arXiv:2112.08174. [Google Scholar]
- Bassi, A.; Großardt, A.; Ulbricht, H. Gravitational Decoherence. Class. Quant. Grav. 2017, 34, 193002. [Google Scholar] [CrossRef]
- Anastopoulos, C.; Hu, B.L. Gravitational decoherence: A thematic overview. arXiv 2021, arXiv:2111.02462. [Google Scholar]
- Bao, N.; Chatwin-Davies, A.; Pollack, J.; Remmen, G.N. Cosmological decoherence from thermal gravitons. JHEP 2020, 8, 65. [Google Scholar] [CrossRef]
- Kiefer, C.; Polarski, D.; Starobinsky, A.A. Quantum-to-classical transition for fluctuations in the early universe. Int. J. Mod. Phys. D 1998, 7, 455. [Google Scholar] [CrossRef]
- Zurek, W.H. Preferred states, predictability, classicality and the environment-induced decoherence. Prog. Theor. Phys. 1993, 89, 281. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Path integral approach to quantum Brownian motion. Physica A 1983, 121, 587. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Stochastic de Sitter (inflationary) stage in the early universe. In Field Theory, Quantum Gravity and Strings; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1986; Volume 246. [Google Scholar]
- Sakagami, M.A. Evolution from pure states into mixed states in de Sitter space. Prog. Theor. Phys. 1988, 79, 442. [Google Scholar] [CrossRef]
- Winitzki, S.; Vilenkin, A. Effective noise in a stochastic description of inflation. Phys. Rev. D 2000, 61, 084008. [Google Scholar] [CrossRef]
- Habib, S.; Laflamme, R. Wigner function and decoherence in quantum cosmology. Phys. Rev. D 1990, 42, 4056. [Google Scholar] [CrossRef]
- Kiefer, C. Interpretation of the decoherence functional in quantum cosmology. Class. Quant. Grav. 1991, 8, 379. [Google Scholar] [CrossRef]
- Singh, T.P.; Padmanabhan, T. Notes on semiclassical gravity. Ann. Phys. 1989, 196, 296. [Google Scholar] [CrossRef]
- Padmanabhan, T. Decoherence in the density matrix describing quantum three geometries and the emergence of classical space-time. Phys. Rev. D 1989, 39, 2924. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Singh, T.P. On the semiclassical limit of the Wheeler–DeWitt equation. Class. Quant. Grav. 1997, 7, 411. [Google Scholar] [CrossRef]
- Paz, J.P.; Sinha, S. Decoherence and back reaction: The origin of the semiclassical Einstein equations. Phys. Rev. D 1991, 44, 1038. [Google Scholar] [CrossRef]
- Paz, J.P.; Sinha, S. Decoherence and back reaction in quantum cosmology: Multidimensional minisuperspace examples. Phys. Rev. D 1992, 45, 2823. [Google Scholar] [CrossRef] [PubMed]
- DeWitt, B.S. Quantum theory of gravity. 1. The canonical theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
- Wheeler, J.A. Superspace and the nature of quantum geometrodynamics. In Batelles Rencontres; DeWitt, B.S., Wheeler, J.A., Eds.; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Misner, C.W. Minisuperspace. In Magic without Magic: John Archibald Wheeler; W. H. Freeman: San Francisco, CA, USA, 1972. [Google Scholar]
- Kiefer, C. Continuous measurement of mini-superspace variables by higher multipoles. Class. Quant. Grav. 1987, 4, 1369. [Google Scholar] [CrossRef]
- Hu, B.L.; Paz, J.P.; Sinha, S. Minisuperspace as a quantum open system. In Directions in General Relativity, Vol. 1; Hu, B.L., Ryan, M.P., Vishveswara, C.V., Eds.; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Hartle, J.B. Spacetime quantum mechanics and the quantum mechanics of spacetime. In Gravitation and Quantizations; North-Holland: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Hu, B.L.; Paz, J.P.; Zhang, Y. Quantum Brownian motion in a general environment: Exact master equation with nonlocal dissipation and colored noise. Phys. Rev. D 1992, 45, 2843. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.L.; Paz, J.P.; Zhang, Y. Quantum Brownian motion in a general environment II. Nonlinear coupling and perturbative approach. Phys. Rev. D 1993, 47, 1576. [Google Scholar] [CrossRef] [PubMed]
- Paz, J.P.; Habib, S.; Zurek, W.H. Reduction of the wave packet: Preferred observable and decoherence time scale. Phys. Rev. D 1993, 47, 488. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H.; Habib, S.; Paz, J.P. Coherent states via decoherence. Phys. Rev. Lett. 1993, 70, 1187. [Google Scholar] [CrossRef]
- Hu, B.L.; Zhang, Y. Squeezed states and uncertainty relation at finite temperature. Mod. Phys. Lett. A 1993, 8, 3575. [Google Scholar] [CrossRef]
- Hu, B.L.; Zhang, Y. Uncertainty relation for a quantum open system. Int. J. Mod. Phys. A 1995, 10, 4537. [Google Scholar] [CrossRef]
- Hu, B.L.; Matacz, A. Quantum Brownian motion in a bath of parametric oscillators: A model for system-field interactions. Phys. Rev. D 1994, 49, 6612. [Google Scholar] [CrossRef]
- Grishchuk, L.P.; Sidorov, Y.V. Squeezed quantum states of relic gravitons and primordial density fluctuations. Phys. Rev. D 1990, 42, 3413. [Google Scholar] [CrossRef]
- Hu, B.L.; Kang, G.; Matacz, A. Squeezed vacua and the quantum statistics of cosmological particle creation. Int. J. Mod. Phys. A 1994, 9, 991. [Google Scholar] [CrossRef]
- Prokopec, T. Entropy of the squeezed vacuum. Class. Quant. Grav. 1993, 10, 2295. [Google Scholar] [CrossRef]
- Albrecht, A.; Ferreira, P.; Joyce, M.; Prokopec, T. Inflation and squeezed quantum states. Phys. Rev. D 1994, 50, 4807. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Mukhanov, V.F.; Prokopec, T. Entropy of a classical stochastic field and cosmological perturbations. Phys. Rev. Lett. 1992, 69, 3606. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Prokopec, T.; Mukhanov, V.F. The entropy of the gravitational field. Phys. Rev. D 1993, 48, 2443. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Laflamme, R.; Mijic, M. Classical perturbations from decoherence of quantum fluctuations in the inflationary universe. Mod. Phys. Lett. A 1990, 5, 2311. [Google Scholar] [CrossRef]
- Gasperini, M.; Giovannini, M. Entropy production in the cosmological amplification of the vacuum fluctuations. Phys. Lett. B 1993, 301, 334. [Google Scholar] [CrossRef]
- Gasperini, M.; Giovannini, M. Quantum squeezing and cosmological entropy production. Class. Quant. Grav. 1993, 10, L133. [Google Scholar] [CrossRef]
- Hu, B.L.; Paz, J.P.; Zhang, Y. Quantum origin of noise and fluctuations in cosmology. In The Origin of Structure in the Universe; Gunzig, E., Nardone, P., Eds.; NATO ASI Series; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Cornwall, J.M.; Bruinsma, R. Quantum evolution of an unstable field in a de Sitter-space thermal bath. Phys. Rev. D 1988, 38, 3146. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Stochastic Properties of Interacting Quantum Fields. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 1990. [Google Scholar]
- Hu, B.L. Quantum statistical field theory in gravitation and cosmology. In Thermal Field Theory, Proceedings of the Canadian Summer School for Theoretical Physics and the Third International Workshop on Thermal Field Theories and Applications, Banff, AL, Canada, 15–28 August 1993; Kobes, R., Kunstatter, G., Eds.; World Scientific: Singapore, 1994. [Google Scholar]
- Matacz, A. A new theory of stochastic inflation. Phys. Rev. D 1997, 55, 1860. [Google Scholar] [CrossRef]
- Hu, B.L. Coarse-graining and backreaction in inflationary and minisuperspace cosmology. In Relativity and Gravitation: Classical and Quantum; D’Olivio, J., Nahmad, E., Rosenbaum, M., Ryan, M.P., Urrutia, L.F., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- Johnson, P.R.; Hu, B.L. Stochastic theory of relativistic particles moving in a quantum field: I. Influence functional and Langevin equation. arXiv 2000, arXiv:quant-ph/0012137. [Google Scholar]
- Calzetta, E.A.; Hu, B.L.; Mazzitelli, F.D. Coarse-grained effective action and renormalization group theory in semiclassical gravity and cosmology. Phys. Rep. 2001, 352, 459. [Google Scholar] [CrossRef][Green Version]
- Schwinger, J.S. Brownian motion of a quantum oscillator. J. Math. Phys. 1961, 2, 407. [Google Scholar] [CrossRef]
- Keldysh, L. Diagram technique for nonequilibrium processes. Zhurnal Eksp. Teor. Fiz. 1964, 47, 1515. [Google Scholar]
- Chou, K.-C.; Su, Z.-B.; Hao, B.-L.; Yu, L. Equilibrium and non-equilibrium formalisms made unified. Phys. Rep. 1985, 118, 1. [Google Scholar] [CrossRef]
- Calzetta, E.; Hu, B.L. Nonequilibrium quantum fields: Closed-time-path effective action, Wigner function and Boltzmann equation. Phys. Rev. D 1988, 37, 2878. [Google Scholar] [CrossRef]
- Feynman, R.P.; Vernon, F.L. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 1963, 281, 547. [Google Scholar] [CrossRef]
- Grabert, H.; Schramm, P.; Ingold, G.L. Quantum Brownian motion: The functional integral approach. Phys. Rep. 1988, 168, 115. [Google Scholar] [CrossRef]
- Kiefer, C.; Lohmar, I.; Polarski, D.; Starobinsky, A.A. Pointer states for primordial fluctuations in inflationary cosmology. Class. Quant. Grav. 2007, 24, 1699. [Google Scholar] [CrossRef]
- Kiefer, C.; Polarski, D.; Starobinsky, A.A. Entropy of gravitons produced in the early universe. Phys. Rev. D 2000, 62, 043518. [Google Scholar] [CrossRef]
- Koks, D.; Matacz, A.; Hu, B.L. Entropy and uncertainty of squeezed quantum open systems. Phys. Rev. D 1997, 55, 5917. [Google Scholar] [CrossRef]
- Anderson, P.R.; Molina-Paris, C.; Mottola, E. Short distance and initial state effects in inflation: Stress tensor and decoherence. Phys. Rev. D 2005, 72, 043515. [Google Scholar] [CrossRef]
- Kluger, Y.; Mottola, E.; Eisenberg, J.M. Quantum Vlasov equation and its Markov limit. Phys. Rev. D 1998, 58, 125015. [Google Scholar] [CrossRef]
- Hu, B.L.; Pavon, D. Intrinsic measures of field entropy in cosmological particle creation. Phys. Lett. B 1986, 180, 329. [Google Scholar] [CrossRef]
- Martineau, P.; Brandenberger, R.H. The effects of gravitational back-reaction on cosmological perturbations. Phys. Rev. D 2005, 72, 023507. [Google Scholar] [CrossRef]
- Martineau, P. On the decoherence of primordial fluctuations during inflation. Class. Quant. Grav. 2007, 24, 5817. [Google Scholar] [CrossRef]
- Prokopec, T.; Rigopoulos, G.I. Decoherence from isocurvature perturbations in inflation. JCAP 2007, 11, 029. [Google Scholar] [CrossRef]
- Campo, D.; Parentani, R. Decoherence and entropy of primordial fluctuations. I. Formalism and interpretation. Phys. Rev. D 2008, 78, 065044. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Chou, C.-H.; Hu, B.L. Quantum entanglement and entropy in particle creation. Phys. Rev. D 2010, 81, 084018. [Google Scholar] [CrossRef]
- Campo, D.; Parentani, R. Decoherence and entropy of primordial fluctuations. II. The entropy budget. Phys. Rev. D 2008, 78, 065045. [Google Scholar] [CrossRef]
- Boyanovsky, D. Effective field theory during in inflation: Reduced density matrix and its quantum master equation. Phys. Rev. D 2015, 92, 023527. [Google Scholar] [CrossRef]
- Calzetta, E.A.; Hu, B.L. Correlations, decoherence, dissipation, and noise in quantum field theory. arXiv 1995, arXiv:hep-th/9501040. [Google Scholar]
- Burgess, C.P.; Holman, R.; Tasinato, G.; Williams, M. EFT beyond the horizon: Stochastic inflation and how primordial quantum fluctuations go classical. JHEP 2015, 3, 90. [Google Scholar] [CrossRef]
- Shandera, S.; Agarwal, N.; Kamal, A. Open quantum cosmological system. Phys. Rev. D 2018, 98, 083535. [Google Scholar] [CrossRef]
- Hilley, M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121. [Google Scholar] [CrossRef]
- Mückenheim, W.; Ludwig, G.; Dewdney, C.; Holland, P.R.; Kyprianidis, A.; Vigier, J.P.; Petroni, N.C.; Bartlett, M.S.; Jaynes, E.T. A review of extended probabilities. Phys. Rep. 1986, 133, 337. [Google Scholar] [CrossRef]
- Curtright, T.L.; Fairlie, D.B.; Zachos, C.K. A Concise Treatise on Quantum Mechanics in Phase Space; World Scientific: Singapore, 2014. [Google Scholar]
- Baker, G.A., Jr. Formulation of quantum mechanics based on the quasi-probability distribution induced on phase space. Phys. Rev. 1958, 109, 128. [Google Scholar] [CrossRef]
- Egusquiza, I.L.; Feinstein, A.; Sebastián, M.A.P.; Basagoiti, M.A.V. On the entropy and the density matrix of cosmological perturbations. Class. Quant. Grav. 1998, 15, 1927. [Google Scholar] [CrossRef]
- Kleppner, D.; Littman, M.G.; Zimmerman, M.L. Highly excited atoms. Sci. Am. 1981, 244, 130. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 8th ed.; Academic Press: Waltham, MA, USA, 2015. [Google Scholar]
- Berry, M.V. Semi-classical mechanics in phase space: A study of Wigner’s function. Philos. Trans. R. Soc. 1977, A287, 237. [Google Scholar]
- Berry, M.V.; Mount, K.E. Semiclassical approximations in wave mechanics. Rep. Prog. Phys. 1972, 35, 315. [Google Scholar] [CrossRef]
- Truman, H.; Zhao, H.Z. Semi-classical limit of wave functions. Proc. Am. Math. Soc. 2000, 128, 1003. [Google Scholar] [CrossRef]
- Hsiang, J.-T.; Hu, B.L. Fluctuation-dissipation relation for a quantum Brownian oscillator in a parametrically squeezed thermal field. Ann. Phys. 2021, 433, 168594. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. I. Phys. Rev. 1969, 183, 1057. [Google Scholar] [CrossRef]
- Serafini, A.; Illuminati, F.; de Siena, S. Symplectic invariants, entropic measures and correlations of Gaussian states. J. Phys. B 2003, 37, L21. [Google Scholar] [CrossRef]
- Addesso, G.; Ragy, S.; Lee, A.R. Continuous variable quantum information: Gaussian states and beyond. Open Sys. Inf. Dyn. 2014, 21, 144001. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Quantum discord of cosmic inflation: Can we show that CMB anisotropies are of quantum-mechanical origin? Phys. Rev. D 2016, 93, 023505. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).