Statistical Hauser-Feshbach Model Description of (n,α) Reaction Cross Sections for the Weak s-Process
Abstract
1. Introduction
2. Theory Framework
3. Results and Discussion
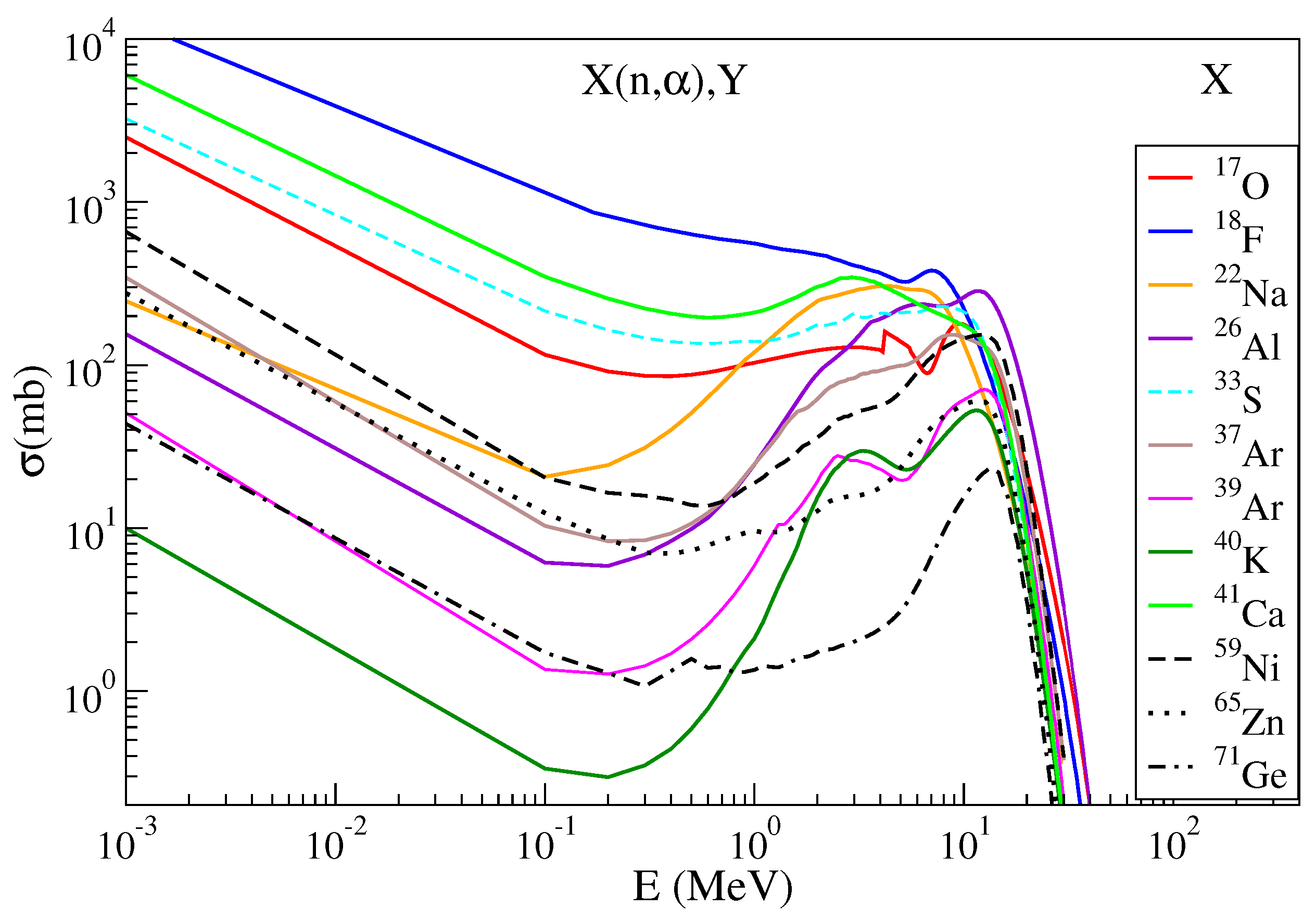
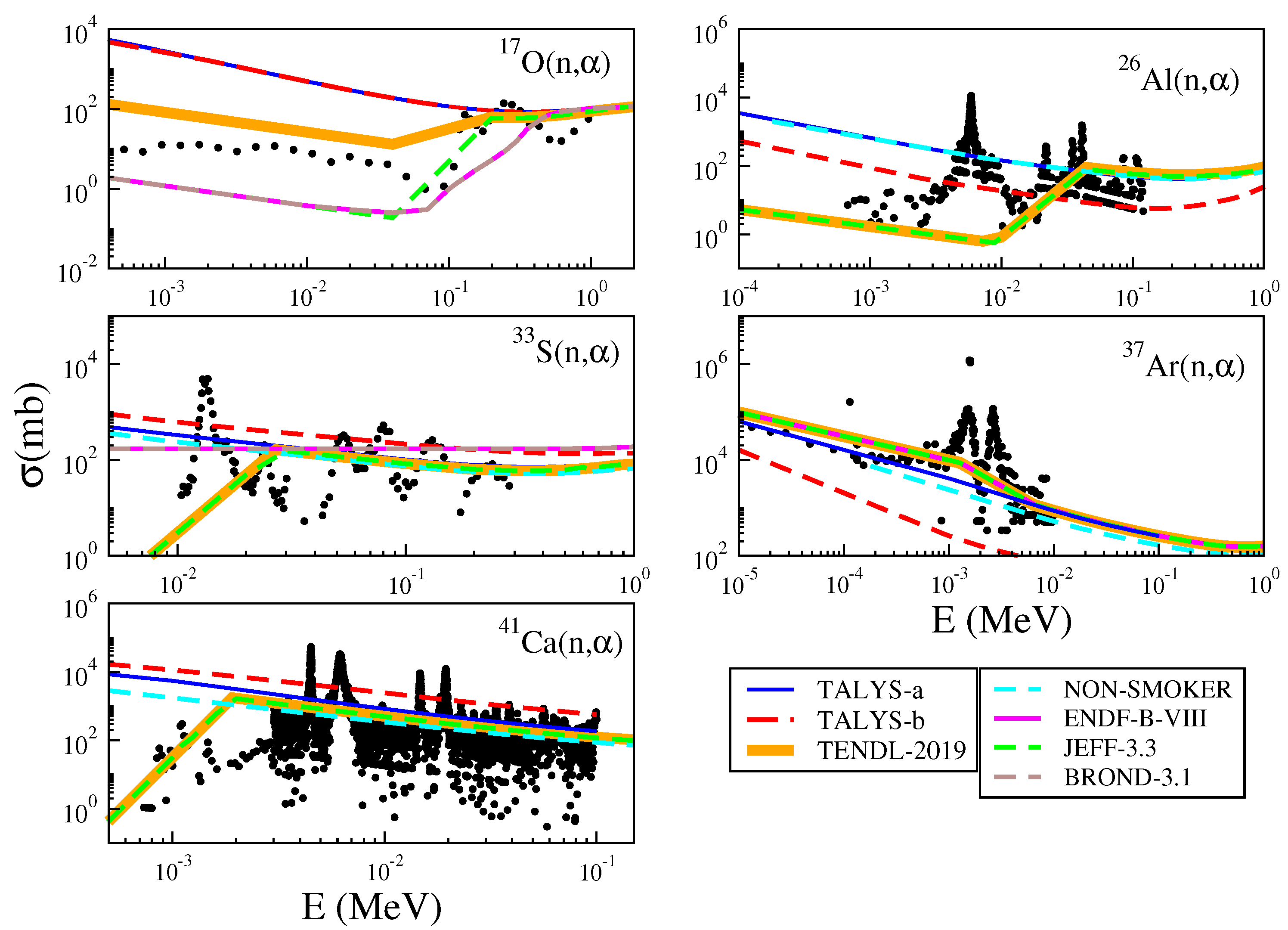
3.1. Reaction Cross Sections for s-Process Nuclei
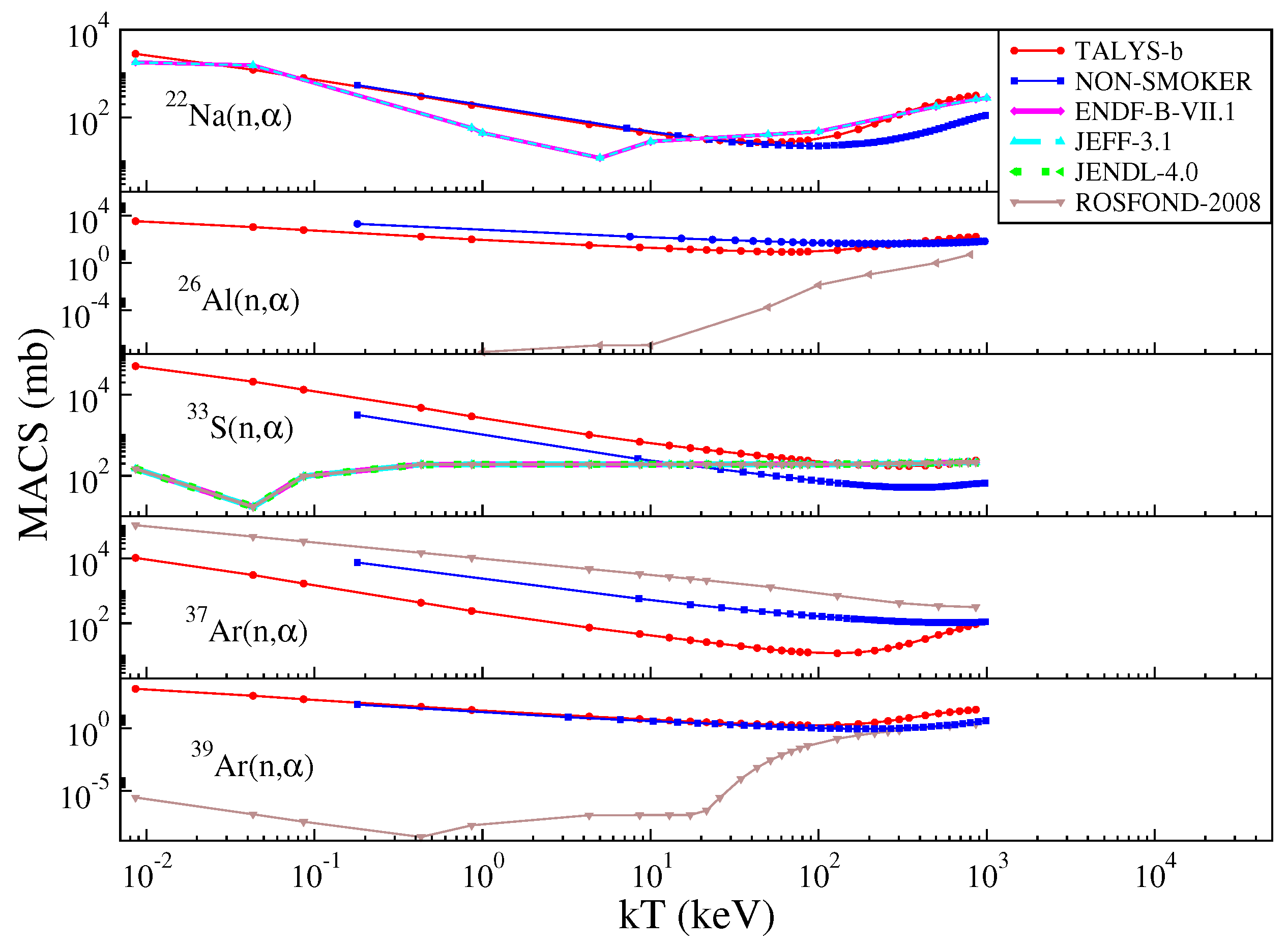
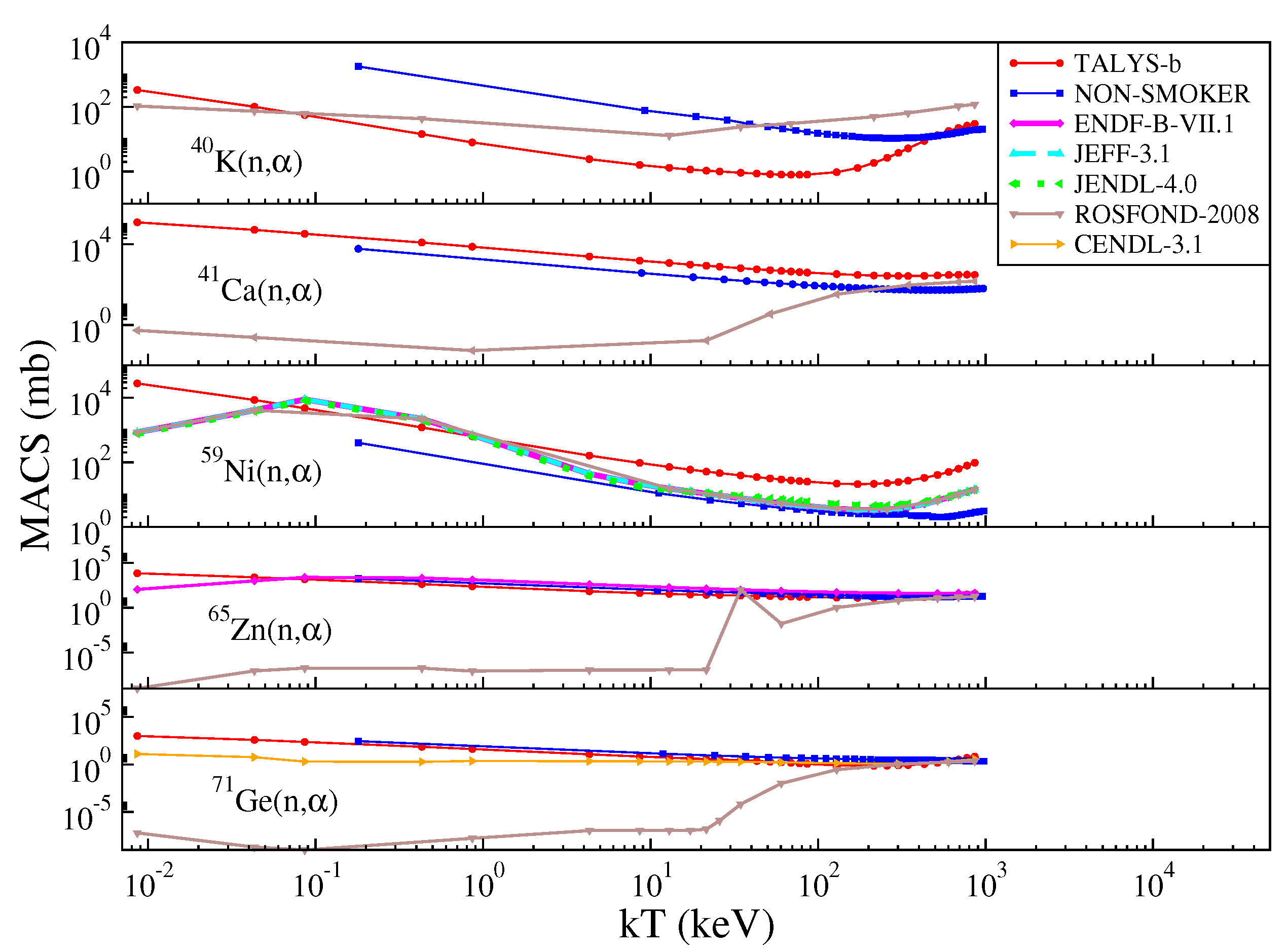
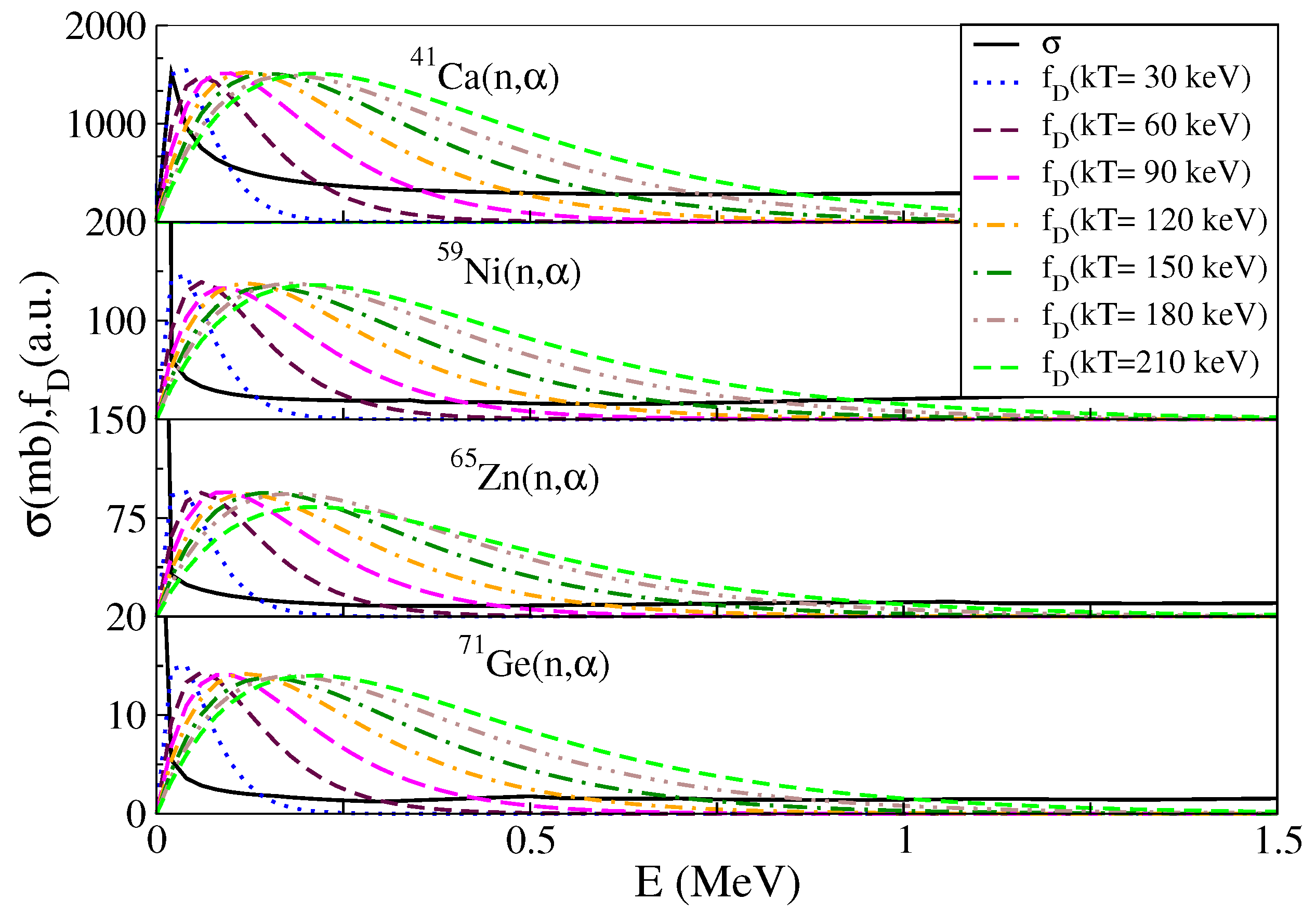
3.2. Astrophysically Relevant Neutron Energy Window for Reactions
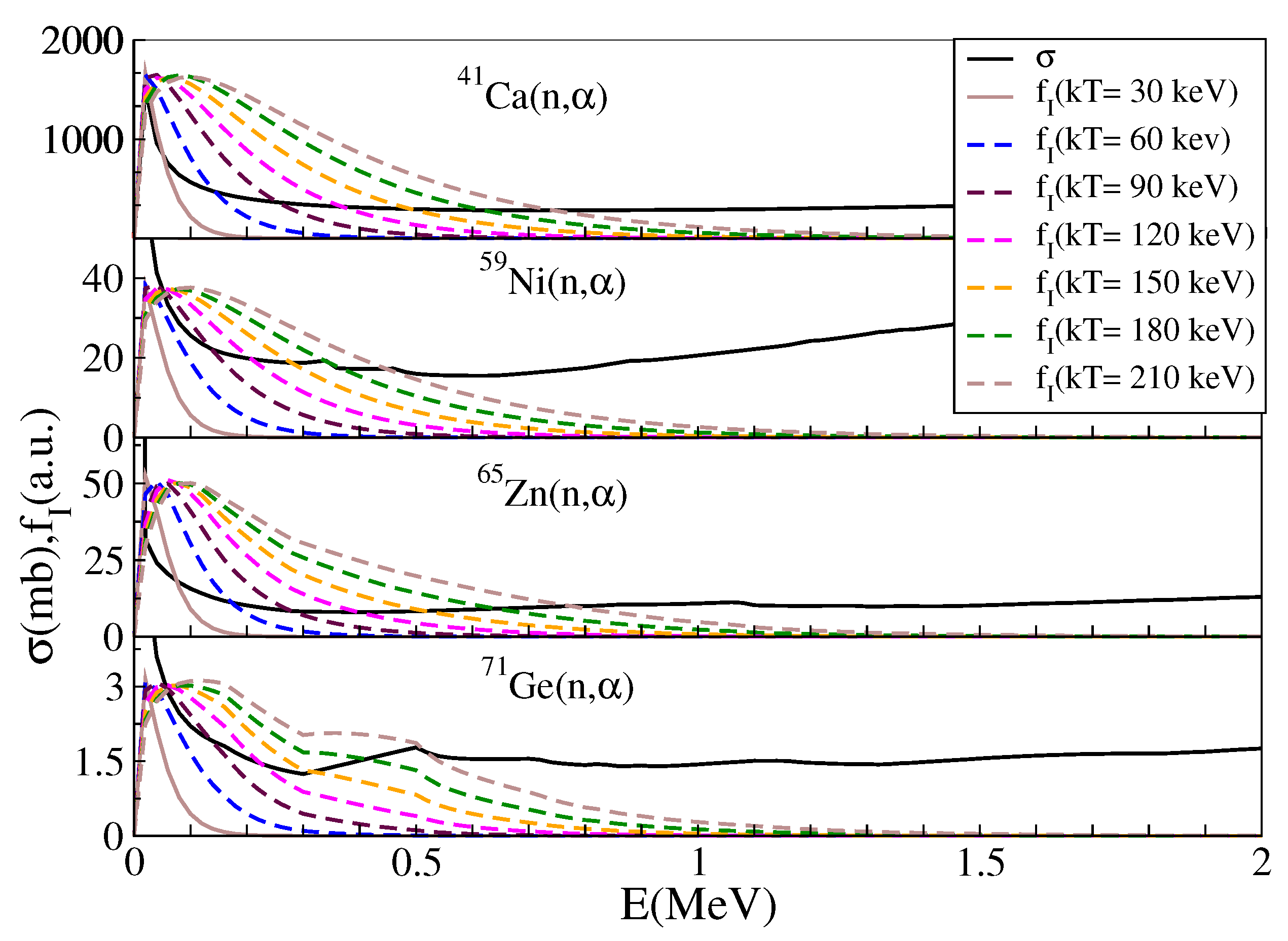
3.3. Astrophysically Relevant Neutron Energy Range for Reactions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Stellar Evolution, Nuclear Astrophysics, and Nucleogenesis; Chalk River Report; Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1957; Volume 41. [Google Scholar]
- Janka, H.T.; Langanke, K.; Marek, A.; Martínez-Pinedo, G.; Müller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef]
- José, J.; Iliadis, C. Nuclear astrophysics: The unfinished quest for the origin of the elements. Rep. Prog. Phys. 2011, 74, 096901. [Google Scholar] [CrossRef]
- Bracco, A.; Körner, G.E.; Krusche, B.; Nappi, E.; Maj, A.; Murphy, A.; Nystrand, J.; Widmann, E.; Dobeš, J.; Lewitowicz, M. (Eds.) NuPECC Long Range Plan 2017 Perspectives in Nuclear Physics; Nuclear Physics European Collaboration Committee: Caen, France, 2017; p. 236. Available online: https://www.esf.org/fileadmin/user_upload/esf/Nupecc-LRP2017.pdf (accessed on 28 November 2021).
- Otuka, N.; Dupont, E.; Semkova, V.; Pritychenko, B.; Blokhin, A.; Aikawa, M.; Babykina, S.; Bossant, M.; Chen, G.; Dunaeva, S.; et al. Towards a More Complete and Accurate Experimental Nuclear Reaction Data Library (EXFOR): International Collaboration Between Nuclear Reaction Data Centres (NRDC). Nucl. Data Sheets 2014, 120, 272–276. [Google Scholar] [CrossRef]
- Chadwick, M.B.; Herman, M.; Obložinský, P.; Dunn, M.E.; Danon, Y.; Kahler, A.C.; Smith, D.L.; Pritychenko, B.; Arbanas, G.; Arcilla, R.; et al. ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data. Nucl. Data Sheets 2011, 112, 2887–2996. [Google Scholar] [CrossRef]
- Rauscher, T.; Thielemann, F.K. Astrophysical Reaction Rates From Statistical Model Calculations. At. Data Nucl. Data Tables 2000, 75, 1–351. [Google Scholar] [CrossRef]
- Plompen, A.J.M.; Cabellos, O.; De Saint Jean, C.; Fleming, M.; Algora, A.; Angelone, M.; Archier, P.; Bauge, E.; Bersillon, O.; Blokhin, A.; et al. The joint evaluated fission and fusion nuclear data library, JEFF-3.3. Eur. Phys. J. A 2020, 56, 181. [Google Scholar] [CrossRef]
- Shibata, K.; Iwamoto, O.; Nakagawa, T.; Iwamoto, N.; Ichihara, A.; Kunieda, S.; Chiba, S.; Furutaka, K.; Otuka, N.; Ohsawa, T.; et al. JENDL-4.0: A New Library for Nuclear Science and Engineering. J. Nucl. Sci. Technol. 2011, 48, 1–30. [Google Scholar] [CrossRef]
- Andrianova, O.N.; Golovko, Y.Y.; Manturov, G.N. Verification of the ROSFOND/ABBN nuclear data based on the OECD/NEA benchmark on criticality safety of mox-fueled systems. Nucl. Energy Technol. 2019, 5, 91–96. [Google Scholar] [CrossRef]
- Ge, Z.; Zhao, Z.; Xia, H.; Zhuang, Y.; Liu, T.; Zhang, J.; Wu, H. The Updated Vversion of Chinese Evaluated Nuclear Data Library (CENDL-3.1). J. Korean Phys. Soc. 2011, 59, 1052–1056. [Google Scholar] [CrossRef]
- Bao, Z.; Käppeler, F. Neutron capture cross sections for s-process studies. At. Data Nucl. Data Tables 1987, 36, 411–451. [Google Scholar] [CrossRef]
- Käppeler, F.; Gallino, R.; Bisterzo, S.; Aoki, W. The s process: Nuclear physics, stellar models, and observations. Rev. Mod. Phys. 2011, 83, 157–193. [Google Scholar] [CrossRef]
- Banerjee, P.; Heger, A.; Qian, Y.Z. New s-process Mechanism in Rapidly Rotating Massive Population II Stars. Astrophys. J. 2019, 887, 187. [Google Scholar] [CrossRef]
- Mathews, G.J.; Cowan, J.J. New insights into the astrophysical r-process. Nature 1990, 345, 491–494. [Google Scholar] [CrossRef]
- Cowan, J.J.; Thielemann, F.K.; Truran, J.W. The R-process and nucleochronology. Phys. Rep. 1991, 208, 267–394. [Google Scholar] [CrossRef]
- Wanajo, S.; Tamamura, M.; Itoh, N.; Nomoto, K.; Ishimaru, Y.; Beers, T.C.; Nozawa, S. Ther-Process in Supernova Explosions from the Collapse of O-Ne-Mg Cores. Astrophys. J. 2003, 593, 968–979. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Arcones, A.; Käppeli, R.; Liebendörfer, M.; Rauscher, T.; Winteler, C.; Fröhlich, C.; Dillmann, I.; Fischer, T.; Martinez-Pinedo, G.; et al. What are the astrophysical sites for the r-process and the production of heavy elements? Prog. Part. Nucl. Phys. 2011, 66, 346–353. [Google Scholar] [CrossRef]
- Freiburghaus, C.; Rosswog, S.; Thielemann, F.K. r-Process in Neutron Star Mergers. Astrophys. J. 1999, 525, L121–L124. [Google Scholar] [CrossRef]
- Goriely, S.; Bauswein, A.; Janka, H.T. r-process nucleosynthesis in dynamically ejected matter of neutron star mergers. Astrophys. J. Lett. 2011, 738, L32. [Google Scholar] [CrossRef]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67–70. [Google Scholar] [CrossRef]
- Kajino, T.; Aoki, W.; Balantekin, A.; Diehl, R.; Famiano, M.; Mathews, G. Current status of r-process nucleosynthesis. Prog. Part. Nucl. Phys. 2019, 107, 109–166. [Google Scholar] [CrossRef]
- Litvinova, E.; Loens, H.; Langanke, K.; MartÃnez-Pinedo, G.; Rauscher, T.; Ring, P.; Thielemann, F.K.; Tselyaev, V. Low-lying dipole response in the relativistic quasiparticle time blocking approximation and its influence on neutron capture cross sections. Nucl. Phys. A 2009, 823, 26–37. [Google Scholar] [CrossRef][Green Version]
- Pignatari, M.; Gallino, R.; Heil, M.; Wiescher, M.; Käppeler, F.; Herwig, F.; Bisterzo, S. The weak s-process in massive stars and its dependence on the neutron capture cross sections. Astrophys. J. 2010, 710, 1557–1577. [Google Scholar] [CrossRef]
- Vermote, S.; Wagemans, C.; De Smet, L.; Lampoudis, C.; Van Gils, J. Experimental determination of the 41Ca(n,α)38Ar reaction cross section up to 80 keV, and calculation of the Maxwellian averaged cross section at stellar temperatures. Phys. Rev. C 2012, 85, 015803. [Google Scholar] [CrossRef]
- Woosley, S.; Fowler, W.A.; Holmes, J.; Zimmerman, B. Semiempirical thermonuclear reaction-rate data for intermediate-mass nuclei. At. Data Nucl. Data Tables 1978, 22, 371–441. [Google Scholar] [CrossRef]
- Schatz, H.; Kaeppeler, F.; Koehler, P.E.; Wiescher, M.; Trautvetter, H.P. 17O(n, alpha )14C: Closure of a Primordial CNO Bi-Cycle? Astrophys. J. 1993, 413, 750. [Google Scholar] [CrossRef]
- Bertulani, C.; Kajino, T. Frontiers in nuclear astrophysics. Prog. Part. Nucl. Phys. 2016, 89, 56–100. [Google Scholar] [CrossRef]
- Pritychenko, B.; Mughaghab, S.; Sonzogni, A. Calculations of Maxwellian-averaged cross sections and astrophysical reaction rates using the ENDF/B-VII.0, JEFF-3.1, JENDL-3.3, and ENDF/B-VI.8 evaluated nuclear reaction data libraries. At. Data Nucl. Data Tables 2010, 96, 645–748. [Google Scholar] [CrossRef][Green Version]
- Dan, M.; Singh, G.; Chatterjee, R.; Shubhchintak. Neutron capture rates of 18C. Phys. Rev. C 2019, 99, 035801. [Google Scholar] [CrossRef]
- Konobeyev, A.; Lunev, V.; Shubin, Y. Semi-empirical systematics for (n,α) reaction cross sections at the energy of 14.5 MeV. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1996, 108, 233–242. [Google Scholar] [CrossRef]
- Forrest, R.A. Systematics of Neutron-Induced Threshold Reactions with Charged Products at about 145 MeV; Technical Report AERE-R–12419; UKAEA Atomic Energy Research Establishment: Abingdon, UK, 1986.
- Fessler, A.; Wattecamps, E.; Smith, D.L.; Qaim, S.M. Excitation functions of (n,2n), (n,p), (n,np+pn+d), and (n,α) reactions on isotopes of chromium. Phys. Rev. C 1998, 58, 996–1004. [Google Scholar] [CrossRef]
- Smet, L.D.; Wagemans, C.; Goeminne, G.; Heyse, J.; Gils, J.V. Experimental determination of the 36Cl(n,p)36S and 36Cl(n,α)33P reaction cross sections and the consequences on the origin of 36S. Phys. Rev. C 2007, 75, 034617. [Google Scholar] [CrossRef]
- Gledenov, Y.M.; Koehler, P.E.; Andrzejewski, J.; Guber, K.H.; Rauscher, T. 147Sm(n,α) cross section measurements from 3 eV to 500 keV: Implications for explosive nucleosynthesis reaction rates. Phys. Rev. C 2000, 62, 042801. [Google Scholar] [CrossRef]
- Goeminne, G.; Wagemans, C.; Wagemans, J.; Serot, O.; Loiselet, M.; Gaelens, M. Investigation of the 37Ar(n,p)37Cl and 37Ar(n,α)34S reactions in the neutron energy range from 10 meV to 100 keV. Nucl. Phys. A 2000, 678, 11–23. [Google Scholar] [CrossRef]
- Weiß, C.; Guerrero, C.; Griesmayer, E.; Andrzejewski, J.; Badurek, G.; Chiaveri, E.; Dressler, R.; Ganesan, S.; Jericha, E.; Käppeler, F.; et al. The (n,α) Reaction in the s-process Branching Point 59Ni. Nucl. Data Sheets 2014, 120, 208–210. [Google Scholar] [CrossRef]
- Fotiades, N.; Devlin, M.; Haight, R.C.; Nelson, R.O.; Kunieda, S.; Kawano, T. α and 2p2n emission in fast neutron-induced reactions on 60Ni. Phys. Rev. C 2015, 91, 064614. [Google Scholar] [CrossRef]
- Barbagallo, M.; Musumarra, A.; Cosentino, L.; Maugeri, E.; Heinitz, S.; Mengoni, A.; Dressler, R.; Schumann, D.; Käppeler, F.; Colonna, N.; et al. 7Be(n,α)4He Reaction and the Cosmological Lithium Problem: Measurement of the Cross Section in a Wide Energy Range at nTOF at CERN. Phys. Rev. Lett. 2016, 117, 152701. [Google Scholar] [CrossRef] [PubMed]
- Gledenov, Y.M.; Sedysheva, M.V.; Khuukhenkhuu, G.; Bai, H.; Jiang, H.; Lu, Y.; Cui, Z.; Chen, J.; Zhang, G. Measurement of the cross sections of the 25Mg(n,α)22Ne reaction in the 4–6 MeV region. Phys. Rev. C 2018, 98, 034605. [Google Scholar] [CrossRef]
- Praena, J.; Sabaté-Gilarte, M.; Porras, I.; Quesada, J.M.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Bécares, V.; Barbagallo, M.; Bečvář, F.; et al. Measurement and resonance analysis of the 33S(n,α)30Si cross section at the CERN nTOF facility in the energy region from 10 to 300 keV. Phys. Rev. C 2018, 97, 064603. [Google Scholar] [CrossRef]
- Bai, H.; Jiang, H.; Lu, Y.; Cui, Z.; Chen, J.; Zhang, G.; Gledenov, Y.M.; Sedysheva, M.V.; Khuukhenkhuu, G.; Ruan, X.; et al. 56,54Fe(n,α)53,51Cr cross sections in the MeV region. Phys. Rev. C 2019, 99, 024619. [Google Scholar] [CrossRef]
- Helgesson, P.; Sjöstrand, H.; Rochman, D. Uncertainty-driven nuclear data evaluation including thermal (n,α) applied to 59Ni. Nucl. Data Sheets 2017, 145, 1–24. [Google Scholar] [CrossRef]
- Weiß, C.; Griesmayer, E.; Guerrero, C.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Badurek, G.; Barbagallo, M.; Bécares, V.; Bečvář, F.; et al. A new CVD diamond mosaic-detector for (n,α) cross-section measurements at the n_TOF experiment at CERN. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 732, 190–194. [Google Scholar] [CrossRef]
- Gyürky, G.; Fülöp, Z.; Käppeler, F.; Kiss, G.G.; Wallner, A. The activation method for cross section measurements in nuclear astrophysics. Eur. Phys. J. A 2019, 55, 41. [Google Scholar] [CrossRef]
- Al-Khasawneh, K.; Borris, E.; Bruückner, B.; Eberhardt, K.; Erbacher, P.; Fiebiger, S.; Gernhäauser, R.; Göobel, K.; Heftrich, T.; Kisselbach, T.; et al. NICE—Neutron Induced Charged particle Emission. J. Phys. Conf. Ser. 2020, 1668, 012021. [Google Scholar] [CrossRef]
- Hauser, W.; Feshbach, H. The Inelastic Scattering of Neutrons. Phys. Rev. 1952, 87, 366–373. [Google Scholar] [CrossRef]
- Moldauer, P.A. Why the Hauser-Feshbach formula works. Phys. Rev. C 1975, 11, 426–436. [Google Scholar] [CrossRef]
- Koning, A.; Hilaire, S.; Duijvestijn, M. TALYS1.0. In Proceedings of the International Conference on Nuclear Data for Science and Technology, Nice, France, 22–27 April 2007; EDP Sciences: Les Ulis, France, 2008; pp. 211–214. [Google Scholar]
- Koning, A.; Hilaire, S.; Goriely, S. TALYS-1.8 A Nuclear Reaction Program. User Manual; Nuclear Research and Consultancy Group (NRG): Petten, The Netherlands, 2015. [Google Scholar]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.; Thibault, C. The Ame2003 atomic mass evaluation: (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337–676. [Google Scholar] [CrossRef]
- Wapstra, A.; Audi, G.; Thibault, C. The Ame2003 atomic mass evaluation: (I). Evaluation of input data, adjustment procedures. Nucl. Phys. A 2003, 729, 129–336. [Google Scholar] [CrossRef]
- Newton, J.R.; Iliadis, C.; Champagne, A.E.; Coc, A.; Parpottas, Y.; Ugalde, C. Gamow peak in thermonuclear reactions at high temperatures. Phys. Rev. C 2007, 75, 045801. [Google Scholar] [CrossRef]
- Glorius, J.; Langer, C.; Slavkovská, Z.; Bott, L.; Brandau, C.; Brückner, B.; Blaum, K.; Chen, X.; Dababneh, S.; Davinson, T.; et al. Approaching the Gamow Window with Stored Ions: Direct Measurement of 124Xe(p,γ) in the ESR Storage Ring. Phys. Rev. Lett. 2019, 122, 092701. [Google Scholar] [CrossRef] [PubMed]
- Ciani, G.F.; Csedreki, L.; Rapagnani, D.; Aliotta, M.; Balibrea-Correa, J.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; et al. Direct Measurement of the 13C(α,n)16O Cross Section into the s-Process Gamow Peak. Phys. Rev. Lett. 2021, 127, 152701. [Google Scholar] [CrossRef]
- Rauscher, T. Relevant energy ranges for astrophysical reaction rates. Phys. Rev. C 2010, 81, 045807. [Google Scholar] [CrossRef]
- Fallis, J.; Akers, C.; Laird, A.; Simon, A.; Spyrou, A.; Christian, G.; Connolly, D.; Hager, U.; Hutcheon, D.; Lennarz, A.; et al. First measurement in the Gamow window of a reaction for the gamma-process in inverse kinematics: 76Se(alpha,gamma)80Kr. Phys. Lett. B 2020, 807, 135575. [Google Scholar] [CrossRef]
- Stoitsov, M.; Moré, J.; Nazarewicz, W.; Pei, J.C.; Sarich, J.; Schunck, N.; Staszczak, A.; Wild, S. Towards the universal nuclear energy density functional. J. Phys. Conf. Ser. 2009, 180, 012082. [Google Scholar] [CrossRef]
- Paar, N.; Papakonstantinou, P.; Ponomarev, V.; Wambach, J. Low-energy dipole excitations towards the proton drip-line: Doubly magic 48Ni. Phys. Lett. B 2005, 624, 195–202. [Google Scholar] [CrossRef][Green Version]
- Paar, N. The quest for novel modes of excitation in exotic nuclei. J. Phys. G Nucl. Part. Phys. 2010, 37, 064014. [Google Scholar] [CrossRef]
- Khan, E.; Paar, N.; Vretenar, D. Low-energy monopole strength in exotic nickel isotopes. Phys. Rev. C 2011, 84, 051301. [Google Scholar] [CrossRef]
- Samana, A.R.; Krmpotić, F.; Paar, N.; Bertulani, C.A. Neutrino and antineutrino charge-exchange reactions on 12C. Phys. Rev. C 2011, 83, 024303. [Google Scholar] [CrossRef]
- Fantina, A.F.; Khan, E.; Colò, G.; Paar, N.; Vretenar, D. Stellar electron-capture rates on nuclei based on a microscopic Skyrme functional. Phys. Rev. C 2012, 86, 035805. [Google Scholar] [CrossRef]
- Paar, N.; Moustakidis, C.C.; Marketin, T.; Vretenar, D.; Lalazissis, G.A. Neutron star structure and collective excitations of finite nuclei. Phys. Rev. C 2014, 90, 011304. [Google Scholar] [CrossRef]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comput. Phys. Commun. 2014, 185, 1808–1821. [Google Scholar] [CrossRef]
- Paar, N.; Vretenar, D.; Khan, E.; Colò, G. Exotic modes of excitation in atomic nuclei far from stability. Rep. Prog. Phys. 2007, 70, 691–793. [Google Scholar] [CrossRef]
- Gao, Y.; Dobaczewski, J.; Kortelainen, M.; Toivanen, J.; Tarpanov, D. Propagation of uncertainties in the Skyrme energy-density-functional model. Phys. Rev. C 2013, 87, 034324. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Colò, G.; Sagawa, H. New Skyrme energy density functional for a better description of the Gamow–Teller resonance. Phys. Scr. 2013, T154, 014011. [Google Scholar] [CrossRef]
- Washiyama, K.; Bennaceur, K.; Avez, B.; Bender, M.; Heenen, P.H.; Hellemans, V. New parametrization of Skyrme’s interaction for regularized multireference energy density functional calculations. Phys. Rev. C 2012, 86, 054309. [Google Scholar] [CrossRef]
- Yüksel, E.; Marketin, T.; Paar, N. Optimizing the relativistic energy density functional with nuclear ground state and collective excitation properties. Phys. Rev. C 2019, 99, 034318. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kohn, W. Nobel Lecture: Electronic structure of matter—wave functions and density functionals. Rev. Mod. Phys. 1999, 71, 1253–1266. [Google Scholar] [CrossRef]
- Goriely, S.; Hilaire, S.; Koning, A.J. Improved predictions of nuclear reaction rates with the TALYS reaction code for astrophysical applications. A&A 2008, 487, 767–774. [Google Scholar] [CrossRef]
- Avrigeanu, V.; Avrigeanu, M.; Mănăilescu, C. Further explorations of the α-particle optical model potential at low energies for the mass range A ≈ 45–209. Phys. Rev. C 2014, 90, 044612. [Google Scholar] [CrossRef]
- Koning, A.; Hilaire, S.; Goriely, S. New Edition-24 December 2019. Available online: https://tendl.web.psi.ch/tendl_2019/talys.html (accessed on 28 November 2021).
- Moldauer, P. Statistics and the average cross section. Nucl. Phys. A 1980, 344, 185–195. [Google Scholar] [CrossRef]
- Krane, K. Introductory Nuclear Physics, 2nd ed.; John Willey and Sons: New York, NY, USA, 1988. [Google Scholar]
- Koehler, P.E.; Graff, S.M. 17O(n,α)14C cross section from 25 meV to approximately 1 MeV. Phys. Rev. C 1991, 44, 2788–2793. [Google Scholar] [CrossRef] [PubMed]
- Koehler, P.; Harvey, J.; Hill, N. Two detectors for (n,p) and (n,α) measurements at white neutron sources. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 361, 270–276. [Google Scholar] [CrossRef]
- Wagemans, C.; Weigmann, H.; Barthelemy, R. Measurement and resonance analysis of the 33S(n,α) cross section. Nucl. Phys. A 1987, 469, 497–506. [Google Scholar] [CrossRef]
- Koning, A.; Rochman, D.; Sublet, J.C.; Dzysiuk, N.; Fleming, M.; van der Marck, S. TENDL: Complete Nuclear Data Library for Innovative Nuclear Science and Technology. Nucl. Data Sheets 2019, 155, 1–55. [Google Scholar] [CrossRef]
- Brown, D.; Chadwick, M.; Capote, R.; Kahler, A.; Trkov, A.; Herman, M.; Sonzogni, A.; Danon, Y.; Carlson, A.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Blokhin, A.I.; Gai, E.V.; Ignatyuk, A.V.; Koba, I.I.; Manokhin, V.N.; Pronyaev, V.N. New version of neutron evaluated data library BROND-3.1. Yad. Reak. Konst. 2016, 2, 62. [Google Scholar]
- Oginni, B.M.; Iliadis, C.; Champagne, A.E. Theoretical evaluation of the reaction rates for 26Al(n,p)26Mg and 26Al(n,α)23Na. Phys. Rev. C 2011, 83, 025802. [Google Scholar] [CrossRef]
- Herman, M.; Capote, R.; Carlson, B.; Oblozinsky, P.; Sin, M.; Trkov, A.; Wienke, H.; Zerkin, V. EMPIRE: Nuclear Reaction Model Code System for Data Evaluation. Nucl. Data Sheets 2007, 108, 2655–2715. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Küçüksucu, S.; Yiğit, M.; Paar, N. Statistical Hauser-Feshbach Model Description of (n,α) Reaction Cross Sections for the Weak s-Process. Universe 2022, 8, 25. https://doi.org/10.3390/universe8010025
Küçüksucu S, Yiğit M, Paar N. Statistical Hauser-Feshbach Model Description of (n,α) Reaction Cross Sections for the Weak s-Process. Universe. 2022; 8(1):25. https://doi.org/10.3390/universe8010025
Chicago/Turabian StyleKüçüksucu, Sema, Mustafa Yiğit, and Nils Paar. 2022. "Statistical Hauser-Feshbach Model Description of (n,α) Reaction Cross Sections for the Weak s-Process" Universe 8, no. 1: 25. https://doi.org/10.3390/universe8010025
APA StyleKüçüksucu, S., Yiğit, M., & Paar, N. (2022). Statistical Hauser-Feshbach Model Description of (n,α) Reaction Cross Sections for the Weak s-Process. Universe, 8(1), 25. https://doi.org/10.3390/universe8010025






