Abstract
Neutron-rich Sr nuclei around exhibit a sudden shape transition from a spherical ground state to strongly prolate-deformed. Recently, much new insight into the structure of Sr isotopes in this region has been gained through experimental studies of the excited levels, transition strengths, and spectroscopic factors. In this work, a “classic” shell model description of strontium isotopes from to is provided, using a natural valence space outside the Ni core. Both even–even and even–odd isotopes are addressed. In particular, spectroscopic factors are computed to shed more light on the structure of low-energy excitations and their evolution along the Sr chain. The origin of deformation at is mentioned in the context of the present and previous shell model and Monte Carlo shell model calculations.
1. Introduction
Strontium () and zirconium () isotopes exhibit a sharp shape transition from a spherical shape at to a strongly prolate-deformed shape at . Such a change is manifested by a decrease of the level energy from 0.8 MeV in Sr to 0.15 MeV in Sr and from 1.2 MeV in Zr to 0.2 MeV Zr. The corresponding value increases at the same time by about a factor of 10 when adding two neutrons only. The quest for the shape coexistence and quantum phase transition in shape of Zr isotopes was addressed in many theoretical approaches, including beyond mean-field ones with Gogny and Skyrme forces, the large-scale shell model (LSSM), the Monte Carlo shell model (MCSM), and the algebraic IBM model with configuration mixing; see [1] for a recent review.
Such rapid shape transitions are challenging for a theoretical description, which has to model to great detail the interplay between the stabilizing role of the shell gaps and the quadrupole correlations tending to deform the nucleus. The shell model approaches are well suited for an accurate description of such changes, provided a large enough model space can be handled numerically; it is usually the intruder orbitals coming down in the neutron-rich nuclei that are the source of necessary quadrupole correlations. Among the most successful examples of such spherical-to-deformed modelization one counts the islands of inversions at and ; see, e.g., [2,3,4,5,6].
In [7], the shape change in Zr isotopes was addressed in the shell model calculations employing a model space outside Ni with proton and neutron orbitals. The study permitted a good description of the spectra and transition rates of odd and even isotopes up to . In particular, it showed a better agreement with experiments as compared to an earlier work with the Sr core [8], which appeared too soft to be used in such calculations in the region [9]. Nevertheless, the framework of [7] encountered a difficulty in the description of the shape transition from to : while the decrease of the energy in Zr was reasonably given, the transition rate was underestimated severely in spite of using a large polarization charge. The problem was then addressed within the pseudo-SU3 [10,11,12] and quasi-SU3 models [13,14]. The extension of the model space to include quadrupole partners, i.e., the neutron and proton , was suggested to bring the necessary collectivity. Such calculations could not have been performed in the conventional shell model due to the intractable size of the configuration space. The challenge was later undertaken by the Tokyo group within Monte Carlo shell model calculations, permitting treating extremely large configuration spaces thanks to the application of the Metropolis algorithm and variational methods to optimize the single-particle basis vectors [15,16]. A beautiful agreement was achieved by experiments in Zr nuclei, and this as far as [17], using a large valence space with orbits from two major harmonic oscillator shells for both neutrons and protons. The authors of [17] also noticed that the abrupt change of the shape in the ground state of Zr isotopes can be defined as a quantum phase transition and discussed the role of shell evolution in the deformation-driving process. The connection between shape transition and quantum phase transition in Zr isotopes was further explored in the interacting boson model with configuration mixing in [1,18]. The MCSM framework was later applied to the Sr isotopes, but faced some difficulty, predicting the deformed configurations to appear at too low a neutron number [19].
In the present work, I revisit the approach of [7] and apply it to study the Sr isotopes, both even and odd between and . Stimulated by the wealth of new data in this region [19,20,21,22,23,24], the calculations of the low-energy spectra, transition rates, and spectroscopic factors are performed and discussed. The approach from [7] was previously applied in [25] to study Sr, with an emphasis on negative parity excitations. Recently, more shell model results within this approach were presented in [23], but the calculations were limited to even–even isotopes up to . The present work extends the application to the odd–even Sr isotopes and in terms of the configuration spaces employed. In addition, the monopole interactions beyond are improved based on the spectra of even–odd isotopes in the region. This permits investigating to what extent the coexistence of spherical and deformed states in Sr can be accounted for without the presence of intruders while having an up-to-date effective interaction.
The work is organized as follows. In Section 2, the shell model framework and numerical aspects of the calculations are presented. Then, I discuss the properties of even–odd Sr isotopes in Section 3.1. The even–even nuclei are described in Section 3.2. Finally, I address the nature of low-lying states and discuss the possible mechanisms driving the shape coexistence and deformation in this region in Section 3.3. Conclusions and the outlook are given in Section 4.
2. Shell Model Framework
As stated earlier, the calculations were performed in the model space outside Ni with proton and neutron orbitals. The effective interaction is based on the same Hamiltonian that was used for the study of Zr isotopes in [7] and in an earlier study of Sr isotopes in [25], focused on the description of low-energy states involving the excitations to the orbital. This interaction, dubbed Ni-I, was later replaced by the Ni-II version with a new fit of the proton–proton interaction optimized for the nuclei [26,27]. The new fit permitted reproducing better odd–even neutron-rich nuclei closer to the Ni core. However, the proton–neutron and neutron–neutron parts remaining unchanged, the physics of heavier Z, even–even nuclei between and does not vary between the two interactions. One should stress that the developments of both interactions were focused on nuclei with . In the present work, the monopole matrix elements , are additionally made more attractive to obtain a better agreement with experiments also in Sr. This modification has little or no effect for lighter Sr isotopes where the lowest excited states are dominated by the neutron interaction.
With two protons less than Zr, the Sr isotopes pose a greater challenge for the shell model diagonalizations in the same model space. In the present work, the non-public version of the ANTOINE code developed by E. Caurier was employed, which permits treating matrices up to size 10 [4,5,28]. Full-space diagonalizations were performed for Sr. For heavier isotopes, up to 8p-8h excitations with respect to the orbital for protons and from the neutron to the rest of the shell were allowed. A good convergence of the spectra of Sr was obtained this way. In Sr, 8p-8h truncation gives the matrix size 9.5, which requires the most time-consuming calculation performed in this work: computing the and states takes ∼188 CPU hours.
Alternatively, calculations in the seniority scheme were performed for the lowest states of even–even nuclei to provide more insight into the composition of the wave functions. The j-coupled code NATHAN was used for this purpose. A good convergence of the spectra was obtained with seniority eight in Sr (j-coupled dimension 28 ), while in Sr, a maximal seniority ten was reached for the states leading to the <200 keV convergence of all states. Converging three states in Sr (j-coupled dimension 87.5 ) took ∼130 h of CPU time. The feasibility of the calculations with relatively modest computing resources and CPU time is a big advantage of using the present valence space outside the Ni core. As will be discussed below, it permits interpreting the structure of Sr nuclei from to well, before the shape transition takes place and the model reaches its application limit.
3. Results
3.1. Properties of Odd–Even Sr Isotopes
In Figure 1 and Figure 2, the spectra of odd–even Sr isotopes are presented compared to the experimental data. Those were taken from ENSDF [29] for Sr, while the level schemes established recently for Sr in [22] are plotted in Figure 2, supplemented by the candidates for the characteristic excitation taken from [29].
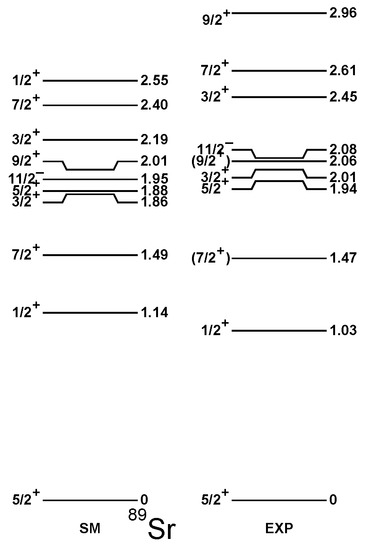
Figure 1.
Theoretical low-energy spectra of Sr and Sr in comparison to the experimental data from [29].
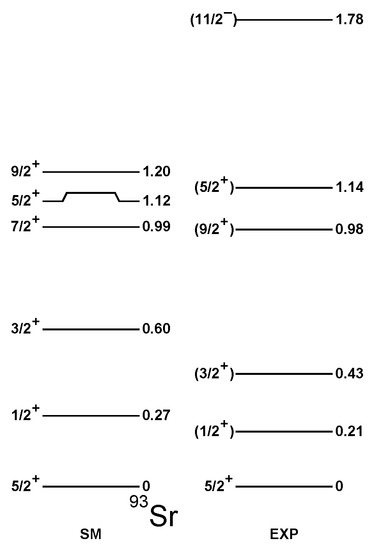
Figure 2.
Theoretical low-energy spectra of Sr in comparison to the experimental data from [22,29].
Each of the experimentally established levels finds its counterpart in the shell model calculations within a maximum of 250 keV. The rms deviation for the ensemble of levels shown in Figure 1, Figure 2, Figure 3 and Figure 4 is only 140 keV, which confirms the good quality of the present interaction. On the other hand, more levels are predicted by the theory than assigned experimentally, and various possibilities are not excluded for the spin/parity assignments of a few levels.
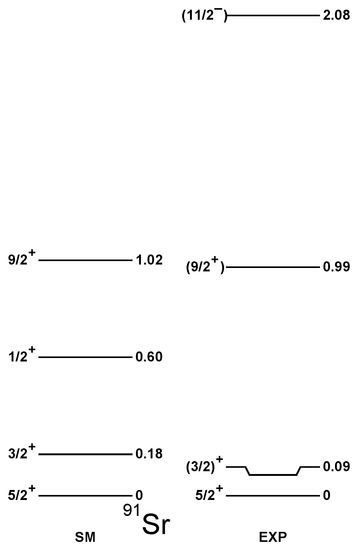
Figure 3.
Theoretical low-energy spectra of Sr in comparison to the experimental data from [29].
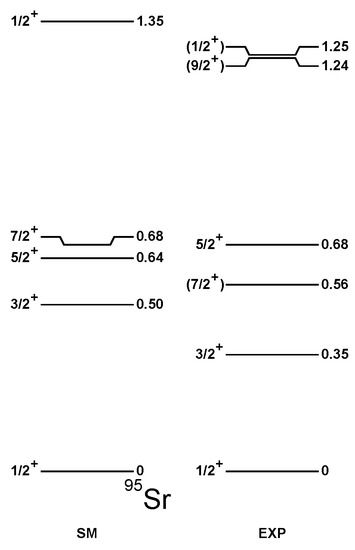
Figure 4.
Theoretical low-energy spectra of Sr in comparison to the experimental data from [22,29].
To investigate further the single-particle structures in Sr isotopes, the spectroscopic factors were computed in Sr, to be compared with the data obtained in [21,22,30]. They are summarized in Table 1. For Sr, two sets of data are listed (from different reactions), which correspond to one-neutron removal (first set) and one-neutron addition (second set) spectroscopic factors in the calculations.

Table 1.
Spectroscopic factors computed for Sr nuclei compared to the experimental data from [30] in Sr, Table II of [21] (1) and Table IV of [22] (2). See the text for more details.
As can be seen, the magnitude of the spectroscopic factors is fairly reproduced. One notices in particular that the first excited state in Sr is a core-coupled state, while the second, predicted at 2.40 MeV, carries a large spectroscopic factor. The magnitude of the spectroscopic factors in the states seems inverted between the shell model and experiment, but the “centers of gravity” based on these two states would be fairly similar. The calculated values are also close to the experiment in the case of Sr and for one-neutron addition data in Sr. The largest discrepancy was found for the and states in Sr, in the case of one-neutron removal. As the computed spectroscopic factors are too large, the occupation of these orbits in the wave function of the ground state of Sr are probably too large, as well, and higher orbitals should be better populated. The structure of the states of Sr isotopes is discussed in the next section.
In Table 2, the occupations of the proton and neutron orbitals are listed for the low-energy excitations with and spin/parity. In addition to the spectroscopic factors listed above, the magnetic moments were computed for all low-energy states (using 0.7 quenching on the spin part of the operator). They are listed along with the occupation numbers and compared to the experimental values from [29] when possible. The agreement between theoretical and experimental magnetic moments is fairly satisfying. Note that the 213 keV level in Sr was assigned as in ENSDF, while it was suggested to be in [22], which agrees better with shell model predictions.

Table 2.
Occupation numbers and magnetic moments in selected low-energy states in odd-Sr isotopes. The occupations lower than 0.01 particles are rounded to zero.
As can be noted, the neutron occupations reveal a clearly single-particle structure for the ground state and the first state in Sr. The occupation of the in the and of the in the is of the order of ; thus, those states mostly result from the coupling of the odd neutron to proton excited states. The first state, with no particle in , was predicted due to a coupling of the proton with the neutron with a probability. The occupation of the orbital grows to 0.7 particles in the second excited (not shown in the Table) predicted at 2.4 MeV. The energy of this orbital was estimated to be around 2 MeV in the Ni core, and its evolution with the neutron number is crucial for the development of the collectivity, as will be outlined below. Unfortunately, no experimental information on its position is currently available beyond from the experimentally available spectroscopic factors, as seen from Table 1. With the increasing neutron number, one observes an increase of the collectivity of the lowest states, manifested by more spread occupancies on both the proton and neutron sides. Still, up to , the lowest excitations are based on neutrons in orbitals. The mixing of neutrons from the and shells reflects the lack of a shell closure at in Sr isotopes, which can be inferred from the systematics. The occupation of the orbital in the level increases steadily from 0.3 to 1.0 particles at . However, no experimental information on the position of the excitation is available in this nucleus to confirm the predicted tendency. After passing the , also the first excited states and have around one particle in the and orbitals, respectively. Nevertheless, their wave functions remain spread over many components with probabilities less than 10%.
It is worth mentioning that similar shell model calculations were carried out in [20,21,22], exploring smaller configuration spaces. The present results for Sr and Sr seem more satisfactory in their prediction of the position of the first excited state (see Figures 13 and 16 of [22]). This state contains a considerable admixture of the proton orbital, crucial for a proper description of single-particle and collective excitations in this region of nuclei. Its exclusion from the model space used in [22] may be thus responsible for a too high position of the excited states in Sr.
3.2. Low-Energy Spectra of Even–Even Sr Isotopes
In Figure 5, Figure 6, Figure 7 and Figure 8, the low-energy spectra of even–even Sr between and are shown. The overall agreement with the experiment is very good in lighter Sr, with larger uncertainties at subshell closures. Nonetheless, the rms deviation for the levels shown is 300 keV, twice larger than for odd nuclei. In Sr, the shell model predicts the excitation 470 keV lower than the experiment, with of the configuration. The excitation is based on the same configuration (), but predicted closer to the experiment (within 290 keV). In addition, the excited level in the neighboring Rb (Z = 37) is predicted at 1366 keV to be compared to the experimental value of 1577.9 keV, and in Y (Z = 39), the theoretical value is 890 keV against 909 keV experimentally. The larger disagreement for the level should thus not be related to the position of the orbital or the monopole part of the interaction involving it.
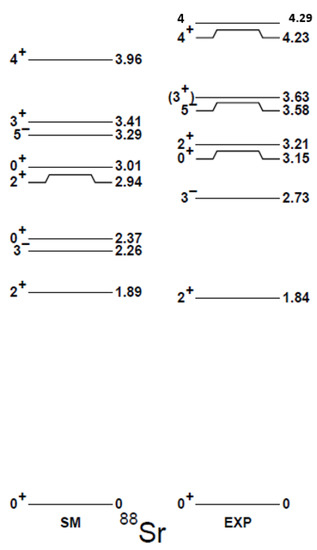
Figure 5.
Theoretical low-energy spectra of Sr in comparison to the experimental data from [29].
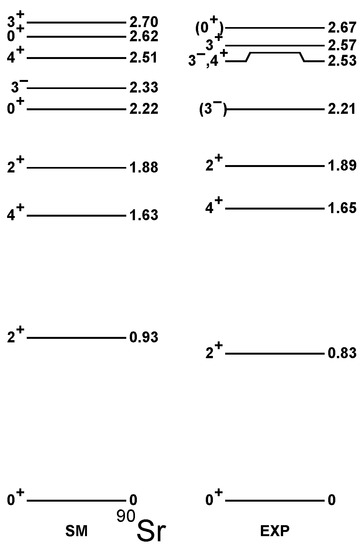
Figure 6.
The same as in Figure 5, but for Sr.
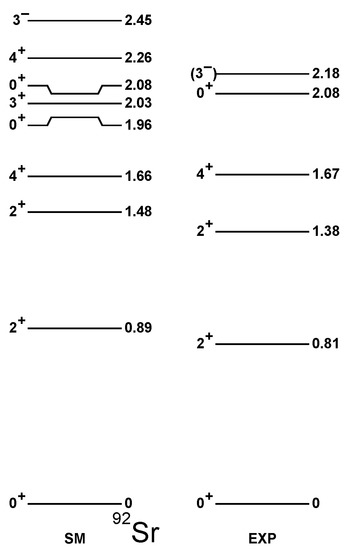
Figure 7.
The same as in Figure 5, but for Sr.
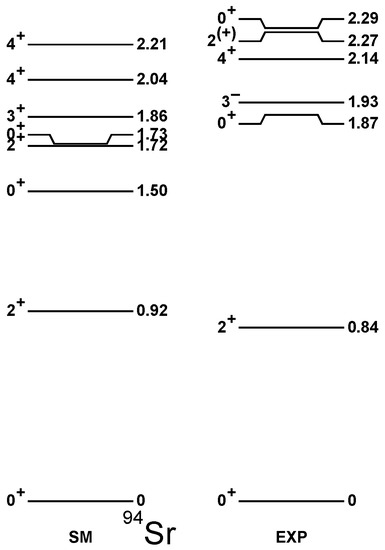
Figure 8.
The same as in Figure 5, but for Sr.
Interestingly, the state in Sr fits the experimental candidates much better, whether the first is the 2.21 MeV or 2.53 MeV level. Here, the component accounts for only , and one can note that the neutron configuration contributes to the wave function. The occupation of the grows from 0.21 at to 0.48 at in the states. The energy of this excitation deviates more and more with increasing neutron number, suggesting octupole collectivity starts playing a role in heavier Sr isotopes, as is the case in heavier-Z nuclei.
Another discrepancy in Sr concerns the first excited , predicted well below the first known state, while the second shell model fits the experiment very well. This situation propagates along the chain; see Figure 9. The systematics of the states was also discussed in the previous work (see Figure 11 of [23]), and a similar disagreement with the experiment was observed. The present calculations were performed with an improved shell model interaction, as described in Section 2, and provide an overall better agreement with the experiment in heavier Sr compared to the calculations from [23]. The problem of low-lying states remains anyway. As can be seen in Figure 9, it is the second excited from theory that closely follows the experimental data, while the first excited theoretical seems to have no counterpart.
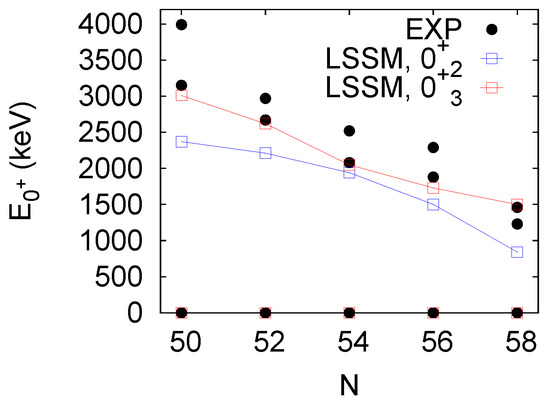
Figure 9.
Systematics of the states in Sr isotopes. Experimentally known levels are indicated in black, while shell model results in red and blue. Lines are added to guide the eye.
Based on the data from [23], it was not possible to clarify whether a low-energy excitation is systematically not observed in the experiment or the shell model underestimates the energy of the first excited state. To gain more insight into this issue, the distribution of one-particle removal spectroscopic factors was computed for the low-spin states in Sr. The values for the lowest states are shown in Table 3 along with the data from [21].

Table 3.
Spectroscopic factors in Sr; see the text for more details.
The agreement between the computed and experimental spectroscopic factors is fair for the states: though the value of the ground state is slightly overshot, the differences in the magnitude among the three states are particularly well reproduced. One can thus conclude that the first three LSSM states correspond indeed to their experimental partners. This is true at least in Sr, as no such spectroscopic factors are available for . The model underestimates excitation energies, which can be due to the inaccuracies of the diagonal and non-diagonal matrix elements of pairing interactions. Such a problem was avoided in Zr isotopes where the orbitals are mostly involved in the s, contrary to Sr with large mixing in the wave functions. I note, in passing that, in recent MCSM calculations in Sr nucleus, a triaxially deformed band predicted on the state was located below 1.5 MeV, thus at a similar energy as the first excited predicted in the present calculations.
The lowest s were also computed using the j-coupled code with seniority truncation, which is the most efficient scheme to converge multiple excitations in spite of the large sizes of the matrices. The composition of the states is shown in Figure 10. The seniority zero component decreases with mass; still, it is predicted to dominate in all states and in all isotopes between and . Seniority four does not exceed , while are minor. Seniority and higher components are negligible (and not shown in the figure), which explains the fast convergence of the computed states in terms of the number of broken nucleonic pairs. At , the higher seniority components are also minor for the first two states, but the third changes its structure: it is dominated by , and reach . This change of structure is consistent with the prediction that one of the excited states should be deformed at .
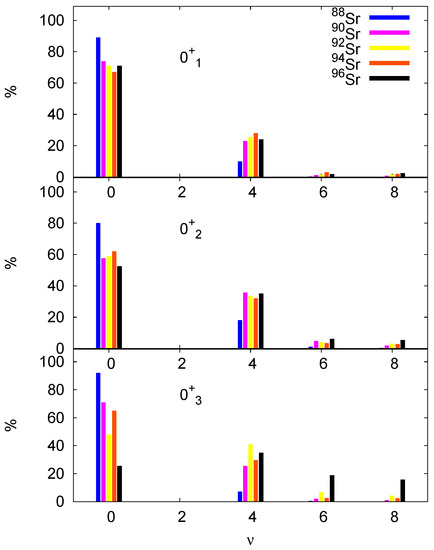
Figure 10.
Seniority composition of the states in Sr isotopes.
As for the dominating configurations, states in Sr are composed of: : of , : of , : of . Adding two neutrons in Sr, one finds the same proton components coupled to neutrons, in the same order, but with a smaller percentage. The situation changes in Sr, where an exchange of major configurations takes place: the first excited is now dominated by the component coupled to neutrons, while the second contains more of the configuration. The percentages of various components continue to drop with the neutron number until reaching less than for the dominating components in the ground state of Sr. All the states computed in this nucleus are based on the configuration with 9%, 27%, and 28%, respectively, and neutrons occupy mostly the and orbitals. It is interesting to notice that the ground state is the purest in terms of seniority, but the most fragmented over different configurations. At , the same structures in the wave functions can be found in the first two states with and . In the third , none of the configurations is privileged. Different particle–hole components do not exceed , confirming this state is the most collective of all the calculated s. At the same time, the occupation of the and orbitals doubles in this state with respect to the ground state, reaching 1.43 and 1.41 particles, respectively, a much smaller number than the occupation predicted in the deformed state in Zr within the MCSM, where the has more than three protons. Moving to , these occupations do not grow in the ground state, which is also dominated by the component, contrary to the expectations. This problem is discussed in the next section devoted to the shape change at .
Table 3 reports also the values of the spectroscopic factors for higher spin states compared to the data on Sr. The spectroscopic factor calculated here for the state is consistent with the experimental value, and the excitation energy of the state agrees very well. The largest discrepancy among the computed states concerns the first level: here, the theoretical energy is 550 keV too low and the spectroscopic factor twice too large; the LSSM calculations reported in [22] agree better in energy, but overestimate the spectroscopic factor by nearly a factor of three. The present calculations predict other excited states in the vicinity of the experimental value with much lower spectroscopic factors. Unfortunately, experimentally, no more unambiguous spin assignments are available for the states to compare the total strength and its distribution. As discussed before in [23], along the Sr chain, the lowest energy is predicted by the LSSM in Sr. It is also in this nucleus where the state bears some characteristics of the non-axially deformed state. On the contrary, at , the transitions from the state to the state are not particularly strong. No excitation was reported from the MCSM in [19], but one can expect a low-energy state along with the prediction of a triaxial band. It would be of high interest to investigate further whether triaxiality is present or not at and whether it could explain the magnitude of the spectroscopic factor of the extracted from the experiment.
3.3. Collectivity in the Sr Chain towards N = 60
The early shell model works of Federman and Pittel [31,32,33], in a small configuration space, pointed out the rapid decrease of the energy around in connection to the important role of the strong, attractive interaction (the so-called spin–orbit partners (SOPs) mechanism). The deformation should be then established by the proton–neutron pairs in the orbitals. This mechanism appeared however insufficient to explain the deformation in Zr isotopes in [7], so it was concluded that orbitals from adjacent shells play a significant role in shaping the nuclei of this region. The suggestion was to add to the model space the quadrupole-driving orbitals and to create quasi-SU3 blocks for neutrons and protons operating in addition to two pseudo-SU3 blocks formed by the lower shells. The addition of only one of the two orbitals was shown to be possibly sufficient to reproduce the enhancement of the value observed between Zr and Zr. Alternatively, it was debated if the increased population of the at can be due to the promotion of the particles from the extruder neutron orbital (across the gap); see [34] and the references therein. This relates also to the possibility of the mapping between the proxy-SU3 approximation to the spherical shell model basis, which results in replacing the intruders of opposite parity by their de Shalit–Goldhaber partners, i.e., the orbital by the orbital in the present case; see [35,36].
In fact, the MCSM calculations presented in [17] can provide an answer to these questions in the shell model context. The model space used in [17] contained both and , as well as orbitals. The authors discussed the role of configuration-dependent shell evolution, which confirms the original idea of Federman and Pittel on the important role of the SOP mechanism with the and attraction as the primary reason for the shape change. While it was not stated explicitly from which orbitals the additional quadrupole correlations came, the inspection of the effective single-particle energies (ESPEs) and occupation numbers displayed in Figure 3 of the same work provides the necessary insight. First, the proton occupation is non-zero in the deformed states. As was shown in the island of inversion study in [4], even a fractional occupancy of this orbital combined with a large population can bring a substantial increase of the collectivity. The (and to a lesser extent ) ESPEs are in the proximity of the rest of the shells as well, which fuels the quasi-SU3 mechanism suggested in [7]. The neutron is not shown, as it is located 12 MeV below . The necessity of higher intruder orbits to obtain the right degree of quadrupole correlations in the shell model framework was thus confirmed in Zr isotopes. On the contrary, the importance of the in the deformation-driving process could be ruled out based on those MCSM results.
In the previous section, the behavior of the states was discussed. The present model predicts a correct number of low-energy states and is sufficient to describe the systematics of the majority of yrast and non-yrast low-spin states from to included, as was shown in [23]. For completeness, the excitation energies are shown in Figure 11. The agreement is very good in the whole chain, with the maximum difference of only 90 keV. The calculation reproduces correctly the tendency without a shell closure effect at . One should bear in mind that the energy increases in the neighboring Zr, which is also present in the current calculations ( is located at 1.49 MeV). The origin of this increase and the connection to the subshell closure is however not obvious; see as well Figure 2 of [37] and the discussion therein. The possible origin of the increase of the energy in Zr was also discussed recently in [1].
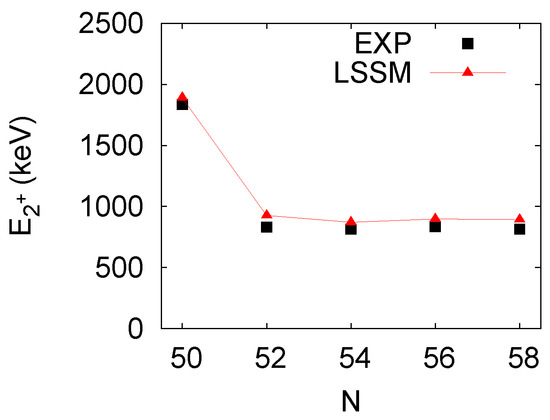
Figure 11.
excitation energy along the Sr chain: experiment vs. present calculations.
In Figure 12, the transitions are shown in comparison to the experimental data and other models taken from [19]. In the calculations of the reduced transition probabilities, a polarization charge was applied for both neutrons and protons. Note that in [7], a charge was employed, which appears to overestimate the transitions in Sr isotopes. One could fine-tune further the proton and neutron charges for a better agreement with the experiment on particular transitions. Nevertheless, the experimental errors are large in the transition region, and the major interest is to understand the relative differences in the magnitude of the transitions between the isotopes. The present calculations fit very well the data on lighter Sr isotopes. At , the predicted value is close to that of the MCSM and indicates an increase of collectivity with respect to . This comes from the large quadrupole matrix elements between the and orbitals, which are both well occupied due to the lack of the shell closure at . Such an increase is in contrast with the flat behavior of the experimental values, though the shell model ones still fall within the error bars. The from the 5DCH model with Gogny forces is three-times larger than the experiment at . In Sr, at , the deviations grow: the available experimental values differ greatly from one another, though they are consistent within the error bars. The 5DCH model predicts more collectivity at than at . The MCSM gives the largest of all values presented: as mentioned earlier, those calculations seem to predict the shape transition at a too low neutron number in Sr. Interestingly, the present calculation falls a bit down towards the lower of the two experimental values. Whether this behavior is correct can be further debated: as deduced before from the spectroscopic factors calculations, the ground state wave function of Sr may not be very accurate. More experimental and theoretical effort can still be performed to provide a comprehensive picture of the coexisting forms just before the shape change at .
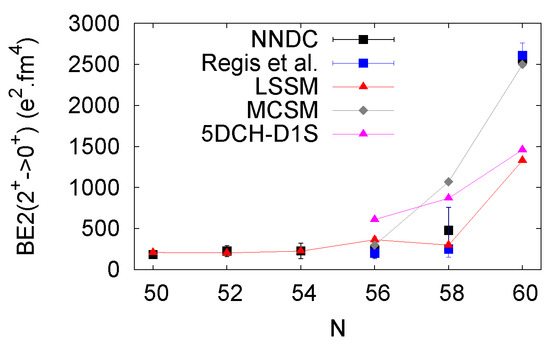
Figure 12.
reduced transitions probabilities as obtained within the present framework in comparison to available data and other models’ predictions. The LSSM value at is obtained in a fixed configuration calculation; see the text for details. The MCSM and 5DCH-D1S values are those reported along with the data in [19].
After the shape change takes place at , the MCSM value matches very well the experiment, while the 5DCH-D1S does not increase enough. In spite of that, the latter calculation reproduces correctly a set of other transitions in the same nucleus (see [19,24]). In the case of the present LSSM, only a fixed occupancy calculation was performed in Sr: The occupations of the spin–orbit partners were fixed to four and six particles, respectively, and seniority was allowed. The state in such a calculation is located at 284 keV, and the transition value, shown in Figure 12, is 1331fm. As seen, having an increased occupancy of these orbits (of a similar order as the resulting fully mixed MCSM calculations in Zr isotopes) leads to a great increase of the value compared to , but still not sufficient to match the experiment. In the state computed without imposing occupancies (at ), there are 0.45 particles in and 0.9 particles in , only. The transition is then one order of magnitude lower than in a fixed occupation calculation. Clearly, the interaction consistent with the properties of lighter Sr isotopes and a large number of other nuclei in the region does not favor configurations with many particles in the SOP to take over. This was also the case of Zr isotopes studied in the same framework, which confirms that the deformation origin is the same in both chains. The immediate conclusion is that its description requires an extra mechanism to populate the and orbitals. The second observation is that additional quadrupole collectivity is necessary, even if the SOPs are well occupied. Both points cannot be satisfied without extending the valence space, testifying to the crucial role of intruder orbitals in shaping nuclei in the region. It is now advisable to theoretically further investigate the shape coexistence around towards lighter Z nuclides. As in Kr and Se, the drops of the energies are not as pronounced as in Sr and Zr, it is of interest to uncover the origin of this difference and to track the evolution of the intruding orbits with decreasing proton number.
4. Conclusions
The properties of Sr isotopes described in a valence space outside the Ni core were discussed. The present calculations properly reproduced the excitation energies and wave functions of low-energy states between and and to some extent at , as was previously the case for Zr isotopes. Accounting fully for the abrupt shape change at appears impossible without the incorporation of the orbitals from adjacent harmonic oscillator shells.
Compared to the Zr isotopes, the strontiums appear more challenging for the present shell model description. While the structure of odd nuclei seems well reproduced and understood, the even–even ones revealed systematic differences with the experiment. In particular, the energies of excited states were underestimated, probably due to inaccuracies in the pairing interactions of several orbitals involved. The difficulty of reproducing the coexisting structures in Sr isotopes to a great detail seems common to the available shell model and other approaches. On the other hand, it is clear from the current and previous calculations that the origin of deformation in Zr and Sr isotopes should be the same. The famous attraction mechanism between neutrons in and protons in appears insufficient to yield enough of the collective enhancement in the values at . Additionally, the effective interaction reproducing the properties of a large number of nuclei in the region does not favor configurations with highly occupied SOPs to dominate the low-energy states. Thus, the presence of higher intruder orbitals cannot be neglected to describe the quadrupole collectivity in Sr and Zr with . As the lighter-Z isotopes do not reveal such abrupt changes in their structure when passing , it would be now of interest to provide a microscopic description of the shape coexistence of those nuclei in the same theoretical framework.
In spite of the recent experimental progress, there are still missing ingredients that could help to understand the structure of low-energy excitations in Sr and in neighboring isotopes. As an example, it is expected that the neutron orbital play an important role in driving the deformation in this region of nuclei, but there are no experimental constraints permitting following its evolution close to . Searching experimentally for spherical states including 1p-1h excitations to this orbital could be of interest for future theoretical developments. Furthermore, the understanding of the coexisting shapes before and the presence of the quantum shape transition in Sr isotopes could be deepened through two-neutron and transfer reactions. This would clearly help examine the pairing collectivity of the low-energy excitations and elucidate the wave function decomposition in Sr isotopes.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- García-Ramos, J.E.; Heyde, K. Quest of shape coexistence in Zr isotopes. Phys. Rev. C 2019, 100, 044315. [Google Scholar] [CrossRef] [Green Version]
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Otsuka, T.; Mizusaki, T.; Honma, M. Varying shell gap and deformation in N 20 unstable nuclei studied by the Monte Carlo shell model. Phys. Rev. C 1999, 60, 054315. [Google Scholar] [CrossRef]
- Lenzi, S.M.; Nowacki, F.; Poves, A.; Sieja, K. Island of inversion around Cr 64. Phys. Rev. C 2010, 82, 054301. [Google Scholar] [CrossRef]
- Nowacki, F.; Poves, A.; Caurier, E.; Bounthong, B. Shape Coexistence in 78Ni as the Portal to the Fifth Island of Inversion. Phys. Rev. Lett. 2016, 117, 272501. [Google Scholar] [CrossRef] [Green Version]
- Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Shimizu, N. Ab initio multishell valence-space Hamiltonians and the island of inversion. Phys. Rev. C 2020, 102, 034320. [Google Scholar] [CrossRef]
- Sieja, K.; Nowacki, F.; Langanke, K.; Martinez-Pinedo, G. Shell model description of zirconium isotopes. Phys. Rev. C 2009, 79, 064310. [Google Scholar] [CrossRef]
- Holt, A.; Engeland, T.; Hjorth-Jensen, M.; Osnes, E. Application of realistic effective interactions to the structure of the Zr isotopes. Phys. Rev. C 2000, 61, 064318. [Google Scholar] [CrossRef] [Green Version]
- Kumbartzki, G.J.; Benczer-Koller, N.; Burcher, S.; Ratkiewicz, A.; Rice, S.L.; Sharon, Y.Y.; Zamick, L.; Speidel, K.H.; Torres, D.A.; Sieja, K.; et al. Transition from collectivity to single-particle degrees of freedom from magnetic moment measurements on and . Phys. Rev. C 2014, 89, 064305. [Google Scholar] [CrossRef]
- Arima, A.; Harvey, M.; Shimuzi, K. Pseudo LS coupling and pseudo SU3 coupling schemes. Phys. Lett. B 1969, 30, 517–522. [Google Scholar] [CrossRef]
- Ratna Raju, R.; Draayer, J.; Hecht, K. Search for a coupling scheme in heavy deformed nuclei: The pseudo SU (3) model. Nucl. Phys. A 1973, 202, 433–466. [Google Scholar] [CrossRef] [Green Version]
- Draayer, J.; Weeks, K.; Hecht, K. Strength of the Qπ· Qv interaction and the strong-coupled pseudo-SU (3) limit. Nucl. Phys. A 1982, 381, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zuker, A.P.; Retamosa, J.; Poves, A.; Caurier, E. Spherical shell model description of rotational motion. Phys. Rev. C 1995, 52, R1741–R1745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuker, A.P.; Poves, A.; Nowacki, F.; Lenzi, S.M. Nilsson-SU3 self-consistency in heavy N = Z nuclei. Phys. Rev. C 2015, 92, 024320. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 2001, 47, 319–400. [Google Scholar] [CrossRef]
- Shimizu, N.; Abe, T.; Tsunoda, Y.; Utsuno, Y.; Yoshida, T.; Mizusaki, T.; Honma, M.; Otsuka, T. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 2012, 01A205. [Google Scholar] [CrossRef] [Green Version]
- Togashi, T.; Tsunoda, Y.; Otsuka, T.; Shimizu, N. Quantum phase transition in the shape of Zr isotopes. Phys. Rev. Lett. 2016, 117, 172502. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. Subtle connection between shape coexistence and quantum phase transition: The Zr case. Phys. Rev. C 2020, 102, 054333. [Google Scholar] [CrossRef]
- Régis, J.M.; Jolie, J.; Saed-Samii, N.; Warr, N.; Pfeiffer, M.; Blanc, A.; Jentschel, M.; Köster, U.; Mutti, P.; Soldner, T.; et al. Abrupt shape transition at neutron number N = 60: B (E 2) values in 94,96,98Sr from fast γ-γ timing. Phys. Rev. C 2017, 95, 054319. [Google Scholar] [CrossRef] [Green Version]
- Cruz, S.; Bender, P.; Krücken, R.; Wimmer, K.; Ames, F.; Andreoiu, C.; Austin, R.; Bancroft, C.; Braid, R.; Bruhn, T.; et al. Shape coexistence and mixing of low-lying 0+ states in 96Sr. Phys. Lett. B 2018, 786, 94–99. [Google Scholar] [CrossRef]
- Cruz, S.; Wimmer, K.; Bhattacharjee, S.S.; Bender, P.C.; Hackman, G.; Krücken, R.; Ames, F.; Andreoiu, C.; Austin, R.A.E.; Bancroft, C.S.; et al. Single-particle structure in neutron-rich Sr isotopes approaching the N=60 shape transition. Phys. Rev. C 2020, 102, 024335. [Google Scholar] [CrossRef]
- Cruz, S.; Wimmer, K.; Bender, P.C.; Krücken, R.; Hackman, G.; Ames, F.; Andreoiu, C.; Austin, R.A.E.; Bancroft, C.S.; Braid, R.; et al. Single-particle structure of neutron-rich Sr isotopes via 2H(94,95,96Sr, p) reactions. Phys. Rev. C 2019, 100, 054321. [Google Scholar] [CrossRef] [Green Version]
- Urban, W.; Sieja, K.; Rząca-Urban, T.; Wiśniewski, J.; Blanc, A.; Jentschel, M.; Mutti, P.; Köster, U.; Soldner, T.; de France, G.; et al. Structure of even-even Sr isotopes with 50 ≤ N ≤ 58 neutrons. Phys. Rev. C 2021, 104, 064309. [Google Scholar] [CrossRef]
- Clément, E.; Zielińska, M.; Görgen, A.; Korten, W.; Péru, S.; Libert, J.; Goutte, H.; Hilaire, S.; Bastin, B.; Bauer, C.; et al. Spectroscopic Quadrupole Moments in 96,98Sr: Evidence for Shape Coexistence in Neutron-Rich Strontium Isotopes at N = 60. Phys. Rev. Lett. 2016, 116, 022701. [Google Scholar] [CrossRef] [PubMed]
- Rzaca-Urban, T.; Sieja, K.; Urban, W.; Nowacki, F.; Durell, J.L.; Smith, A.G.; Ahmad, I. (h 11/2, g7/2)9- neutron excitation in 92,94,96Sr. Phys. Rev. C 2009, 79, 024319. [Google Scholar] [CrossRef]
- Litzinger, J.; Blazhev, A.; Dewald, A.; Didierjean, F.; Duchêne, G.; Fransen, C.; Lozeva, R.; Sieja, K.; Verney, D.; De Angelis, G.; et al. Transition probabilities in neutron-rich 84,86Se. Phys. Rev. C 2015, 92, 064322. [Google Scholar] [CrossRef] [Green Version]
- Czerwiński, M.; Rząca-Urban, T.; Urban, W.; Bączyk, P.; Sieja, K.; Nyakó, B.M.; Timár, J.; Kuti, I.; Tornyi, T.G.; Atanasova, L.; et al. Neutron-proton multiplets in the nucleus 88Br. Phys. Rev. C 2015, 92, 014328. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, A.; Sieja, K. Collectivity in the light xenon isotopes: A shell model study. Phys. Rev. C 2010, 82, 064304. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.nndc.bnl.gov/ensdf (accessed on 19 October 2021).
- Blok, H.; Zimmerman, W.; Kraushaar, J.; Batay-Csorba, B. Excitation of core coupled states in 87Sr and 89Sr via two-step processes in the 88Sr (p, d) and 88Sr (d, p) reactions. Nucl. Phys. A 1977, 287, 156–178. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Towards a unified microscopic description of nuclear deformation. Phys. Lett. B 1977, 69, 385–388. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Hartree-Fock-Bogolyubov study of deformation in the Zr Mo region. Phys. Lett. B 1978, 77, 29–32. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Unified shell-model description of nuclear deformation. Phys. Rev. C 1979, 20, 820–829. [Google Scholar] [CrossRef]
- Urban, W.; Rząca-Urban, T.; Wiśniewski, J.; Smith, A.G.; Simpson, G.S.; Ahmad, I. First observation of γ-soft and triaxial bands in Zr isotopes. Phys. Rev. C 2019, 100, 014319. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Assimakis, I.; Peroulis, S.; Sarantopoulou, S.; Minkov, N. Connecting the proxy-SU (3) symmetry to the shell model. EPJ Web Conf. 2021, 252, 02004. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.; Peroulis, S.; Sarantopoulou, S.; Cseh, J. Proxy-SU (3) symmetry in the shell model basis. Eur. Phys. J. A 2020, 56, 239. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F.; Blaum, K. Correlations of experimental isotope shifts with spectroscopic and mass observables. Phys. Rev. C 2010, 82, 061306. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).