Abstract
We consider axionlike particles as the most probable constituents of dark matter, the Yukawa-type corrections to Newton’s gravitational law and constraints on their parameters following from astrophysics and different laboratory experiments. After a brief discussion of the results by Prof. Yu. N. Gnedin in this field, we turn our attention to the recent experiment on measuring the differential Casimir force between Au-coated surfaces of a sphere and the top and bottom of rectangular trenches. In this experiment, the Casimir force was measured over an unusually wide separation region from 0.2 to m and compared with the exact theory based on first principles of quantum electrodynamics at nonzero temperature. We use the measure of agreement between experiment and theory to obtain the constraints on the coupling constant of axionlike particles to nucleons and on the interaction strength of a Yukawa-type interaction. The constraints obtained on the axion-to-nucleon coupling constant and on the strength of a Yukawa interaction are stronger by factors of 4 and 24, respectively, than those found previously from gravitational experiments and measurements of the Casimir force but weaker than the constraints following from a differential measurement where the Casimir force was nullified. Some other already performed and planned experiments aimed at searching for axions and non-Newtonian gravity are discussed, and their prospects are evaluated.
1. Introduction
The problem of dark matter has a long history [1]. As found by J. Oort in 1932 when studying stellar motion in the neighborhood of a galaxy, the galaxy mass must be well over than that of its visible constituents [2]. A year later, F. Zwicky [3] applied the virial theorem to the Coma cluster of galaxies in order to determine its mass. The obtained mass value turned out to be much larger than that found from the number of observed galaxies belonging to the Coma cluster multiplied by their mean mass. An excess mass, which reveals itself only gravitationally, received the name dark matter.
According to current concepts, dark matter contributes to approximately 27% of the energy of the universe although its physical nature remains unknown. There are many approaches to this problem based on the role of some hypothetical particles, such as axions, arions, massive neutrinos, weakly interacting massive particles (WIMP), barionic dark matter, modified gravity, etc. (see [1,4,5,6,7,8] for a review).
The model of dark matter that finds support from astrophysics and cosmology is referred to as cold dark matter. According to this model, dark matter consists of light hypothetical particles that are produced in the early universe and become nonrelativistic already at the first stages of its evolution. The most popular particle of this kind is an axion, i.e., a pseudoscalar Nambu–Goldstone boson introduced to solve the problem of strong CP violation in Quantum Chromodynamics (QCD) [9,10,11]. It has been known that the gauge invariant QCD vacuum depends on an angle , and that this dependence violates the CP invariance of QCD. However, experiments suggest that strong interactions are CP invariant and that the electric dipole moment of a neutron is equal to zero up to a high degree of accuracy. An introduction of the Peccei–Quinn symmetry and axions, which are connected with its violation, helps to solve this problem.
Axions and other axionlike particles that arise in many extensions to the Standard Model can interact both with photons and with fermions (electrons and nucleons). These interactions are used for an axion search and for constraining axion masses and coupling constants from observations of numerous astrophysical and cosmological processes as well as from various laboratory experiments (see reviews [1,4,5,6,7,8,12,13,14,15,16,17,18,19,20] of already obtained bounds on the axion mass and coupling constants to photons, electrons and nucleons).
Prof. Yuri N. Gnedin obtained many important results investigating the interaction of dark matter axions with photons in astrophysics and cosmology. He proposed [21] to employ the polarimetric methods for a search for axions and arions (i.e., the axions of zero mass [22]) in the emission from pulsars, X-ray binaries with low-mass components, and magnetic white dwarfs. For this purpose, he used the conversion process of photons into axions in the magnetic field of compact stars and in the interstellar and intergalactic space (i.e., the Primakoff effect). Next, Prof. Gnedin demonstrated an appearance of the striking feature in the polarized light of quasistellar objects due to the resonance magnetic conversion of photons into massless axions [23].
Using these results, Prof. Yu. N. Gnedin organized the axion search by the 6 m telescope at the Special Astronomical Observatory in Russia. Both the Primakoff effect and the inverse process of an axion decay into two photons were searched for in the integalactic light of clusters of galaxies and in the brightness of night sky due to axions in the halo of our galaxy [24]. Although no evidences of axions were found, it was possible to find the upper limit on the photon-to-axion coupling constant from the polarimetric observations of magnetic chemically peculiar stars of spectral type A possessing strong hydrogen Balmer absorption lines [24]. The above results, as well as the ground-based cavity experiments searching for galactic axions, searches of an axion decay in the galactic and extragalactic light, for the solar and stellar axions, and the limits obtained on the coupling constant of axions to photons, were discussed in a review [25].
In their further research on dark matter axions, Yu. N. Gnedin and his collaborators analyzed [26] the intermediate results of PVLAS experiments interpreted [27] as arising due to a conversion of photons into axions with a coupling constant to photons of the order of . By considering the astrophysical and cosmological constraints, they have shown [26] that this result is in contradiction with the data on stellar evolution that exclude the standard model of QCD axions.
Using the cosmic orientation of the electric field vectors of polarized radiation from distant quasars, Yu. N. Gnedin and his collaborators placed a rather strong limit on the coupling constant of axions to an electric field [28]. Numerous results related to the processes of axion decay into two photons, the transformation of photons into axions in the magnetic fields of stars and of interstellar or intergalactic media, and the transformation of axions generated in the cores of stars into X-ray photons were discussed in a review [29].
It has been known that the coupling constant of axionlike particles to fermions can be constrained in the laboratory experiments measuring the Casimir force between two closely spaced test bodies. This force is caused by the zero-point and thermal fluctuations of the electromagnetic field. It acts between any material surfaces—metallic, dielectric or semiconductor [30,31]. A constraint on the electron-arion coupling constant from old measurements of the Casimir force [32] was obtained in [33]. The competitive constraints on the coupling constants of axionlike particle to nucleons from different experiments measuring the Casimir interaction were obtained in [34,35,36,37,38,39,40,41]. All experiments used for obtaining these constraints have been performed in the separation range below m.
Starting from 1982 [42], measurements of the van der Waals and Casimir forces were also used for constraining the Yukawa-type corrections to Newton’s law of gravitation. These corrections arise due to an exchange of light scalar particles between atoms of two closely spaced macrobodies [43] and in the extra-dimensional unification schemes with a low-energy compactification scale [44,45,46,47]. A review of the most precise measurements of the Casimir interaction and constraints on non-Newtonian gravity obtained from them can be found in [20,48].
In this paper, we obtain new constraints on the coupling constant of axionlike particles to nucleons and on the Yukawa-type corrections to Newtonian gravity following from recent experiment measuring the differential Casimir force between two Au-coated bodies spaced at separations from 0.2 to m [49]. This experiment was performed by Prof. R. S. Decca by means of a micromechanical torsional oscillator. The differential Casimir force was measured between an Au-coated sapphire sphere and the top and bottom of Au-coated deep Si trenches. The measurement results were compared with the exact theory using the scattering approach and were found to be in good agreement with it over the entire measurement range with no fitting parameters under the condition that the relaxation properties of conduction electrons are not included in the computations. Another theoretical approach that takes into account the relaxation properties of conduction electrons was excluded by the measurement data over the range of separations from 0.2 to m [49].
We calculate additional forces arising in the experimental configuration due to an exchange of two axionlike particles between nucleons of the test bodies as well as due to the Yukawa-type correction to Newton’s gravitational potential. Taking into account that no extra force was observed, the constraints on the masses and coupling constants of axions and on the strength and interaction range of the Yukawa interaction were found from the extent of agreement between the measured and calculated Casimir forces.
According to our results, the obtained constraints on axionlike particles are up to a factor of 4 stronger than those from other measurements of the Casimir force. The new constraints on the Yukawa-type interaction are up to a factor of 24 stronger than those obtained previously when measuring the Casimir force. Stronger constraints on an axion [38] and non-Newtonian gravity [50] were obtained only from the experiment by R. S. Decca [50], where the Casimir force was completely nullified.
The paper is organized as follows. In Section 2, we consider the effective potentials due to an exchange of pseudoscalar and scalar particles. Section 3 is devoted to a brief discussion of recent experiments on measuring the differential Casimir force in the micrometer range. In Section 4, we calculate additional forces due to an exchange of two axionlike particles between nucleons and obtain constraints on the axion mass and coupling constant. The constraints on the Yukawa-type correction to Newtonian gravity are found in Section 5. In Section 6 and Section 7, the reader can find a discussion of the results obtained and our conclusions, respectively.
We use a system of units with .
2. Effective Potentials Due to Exchange of Pseudoscalar and Scalar Particles
An interaction of the field of originally introduced QCD axions [9,10,11], which describes the Nambu–Goldstone bosons, with the fermionic field is given by the pseudovector Lagrangian density [12,15]
where is the mass of an axion, with are the Dirac matrices, and g is the dimensionless coupling constant of the axions to fermionic particles of spin 1/2 (in our case a proton or a neutron).
The axionlike particles introduced in Grand Unified Theories (GUT) interact with fermions by means of the pseudoscalar Lagrangian density [12,15,51]
On a tree level, the Lagrangian densities (1) and (2) result in the same action and common effective potential due to an exchange of one axion or axionlike particle between two nucleons of mass m spaced at a distance [52,53]
where is the unit vector directed along the line connecting the two nucleons and are their spins. Here, we assume that the coupling constants of an axion to a neutron and a proton are equal and denote m as their mean mass.
Taking into account that the effective potential (3) is spin-dependent, the resulting additional force averages to zero when integrated over the volumes of unpolarized test bodies used in experiments on measuring the Casimir force. Therefore, the process of one-axion exchange cannot be used for the axion search in measurements of the Casimir force performed until now [31,54] (the proposed measurement of the Casimir force between two test bodies possessing the polarization of nuclear spins [55] is, however, quite promising for this purpose).
A process of the two-axion exchange between two nucleons deserves particular attention. If the pseudovector Lagrangian density (1) is used, the respective effective potential is still unknown. This is because the actual interaction constant is dimensional, and the resulting quantum field theory is nonrenormalizable (the current status of this problem is reflected in [56]). However, in the case of the pseudoscalar Lagrangian density (2) describing the interaction of axionlike particles with fermions, the effective potential due to a two-axion exchange is spin-independent and takes the following simple form [43,57,58]:
where is the modified Bessel function of the second kind.
The effective potential (4) can be summed over all pairs of nucleons belonging to the test bodies and , leading to their total interaction energy
where and are the numbers of nucleons per unit volume of the first and second test bodies, respectively, and z is the closest separation distance between them. Finally, from (5), one arrives at the additional force acting between the test bodies due to the two-axion exchange
Equations (5) and (6) can be used to search for axionlike particles in experiments measuring the Casimir force and for constraining their parameters.
A similar situation takes place for the Yukawa-type corrections to Newton’s gravitational law, which arise due to an exchange of one scalar particle of mass between two pointlike particles (atoms or nucleons) with masses and separated by a distance r. It is conventional to notate the coupling constant of the Yukawa interaction as , where G is the Newtonian gravitational constant and is the proper dimensionless Yukawa strength. Then, the Yukawa-type correction to Newtonian gravity takes the form
where the interaction range represents the Compton wavelength of a scalar particle. As was mentioned in Section 1, the same correction to the Newton’s gravitational potential also arises in extra-dimensional physics with a low-energy compactification scale [44,45,46,47].
The Yukawa-type interaction energy between two macrobodies and arising due to the potential (7) is given by
where and are the mass densities of the first and second test bodies, respectively. In this case, the additional force acting between two test bodies is equal to
Both hypothetical forces (6) and (9) act on the background of the Casimir force measured at separations below a few micrometers. Note that the Newtonian gravitational force
calculated within the same range of separations is much less than the error in measuring the Casimir force and can be neglected (see below).
3. Measurements of the Casimir Force in the Micrometer Separation Range
All experiments measuring the Casimir force between two macrobodies used for obtaining constraints on axionlike particles [35,36,37,38,39,40,41] were performed at separations below a micrometer. A single direct measurement of the Casimir force between two macrobodies at separations up to m was reported quite recently and compared with theory with no fitting parameters [49]. Below, we briefly elucidate the main features of this experiment needed for obtaining new constraints on the axionlike particles and Yukawa-type corrections to Newtonian gravity.
In the experiment [49], the micromechanical torsional oscillator was used to measure the differential Casimir force between an Au-coated sapphire sphere of m radius and the top and bottom of Au-coated rectangular silicon trenches of m depth. Such a large depth of the trenches was chosen in order for the Casimir force between a sphere and a trench bottom (and all the more additional hypothetical forces) to be equal to zero. This means that the actually measured Casimir force acts between a sphere and a trench top. In so doing, however, the differential measurement scheme used allowed us to reach a rather low total experimental error equal to fN at the separation distance of m. Similar schemes of differential force measurements were previously used in [50,59,60,61].
The thicknesses of Au coatings on the sphere and the trench surfaces equal to nm and nm, respectively, were thick enough in order for Au-coated test bodies to be considered made from solid Au when calculating the Casimir force. For technological reasons, before depositing Au coatings, the sapphire sphere and silicon trench surfaces were also covered with Cr layers of thickness nm. These layers do not influence the Casimir force but should be accounted for in calculations of the additional forces due to two-axion exchange and the Yukawa-type potential in Section 4 and Section 5, respectively.
The Casimir force between an Au-coated sphere and an Au-coated trench top was measured over the separation region m and compared with an exact theory developed in the sphere-plate geometry using the scattering approach in the plane-wave representation [62,63,64] and the derivation expansion [65,66,67,68]. In doing so, the contribution of patch potentials to the measured signal was characterized by Kelvin probe microscopy. An impact of surface roughness was taken into account perturbatively [31,54,69,70] and was found to be negligible. It was shown [49] that the measurement data are in agreement with theory to within the total experimental error over the entire measurement range if the relaxation properties of conduction electrons are not included in computations. An inclusion of the relaxation of conduction electrons (i.e., using the dissipative Drude model at low frequencies) results in a strong contradiction between experiment and theory over the range of separations from 0.2 to m. These results are in line with previous precise experiments on measuring the Casimir interaction at shorter sphere-plate separations [61,71,72,73,74,75,76,77,78,79,80,81] and discussions of the so-called Casimir puzzle [82,83,84] (see also recent approaches to the resolution of this problem [85,86,87]).
It is necessary to stress that calculation of the Casimir force between the first test body (sphere) and the flat top of rectangular trenches in [49] was based on first principles of quantum electrodynamics at nonzero temperature and did not use any approximate methods, such as the proximity force approximation applied in the most of previously performed experiments [31,54] or fitting parameters. As for the total experimental errors , they were found in [49] at the 95% confidence level as a combination of both random and systematic errors.
Notice that, according to [88,89], the same experiment cannot be used to exclude an alternative model and to constrain the fundamental forces. This claim was made in 2011 when some of the background effects in the Casimir force (such as the role of patch potentials) and theoretical uncertainties (such as an error in the proximity force approximation) were not completely settled. As was, however, immediately objected in the literature [90,91], such a difference between the excluded and confirmed models of the Casimir force is of a form quite different from a correction to the fundamental force. This fact allows us to constrain the parameters of the latter. After the seminal experiment by R. S. Decca performed in 2016 [61], where the theoretical predictions of two models for the Casimir force differed by up to a factor of 1000 and one of them was conclusively rejected whereas another one was confirmed, it became amply clear that a comparison with the confirmed model can be reliably used for constraining the fundamental forces in all subsequent experiments.
When discussing the measure of agreement between experiment and theory, it is necessary also to take into account the contribution of differential Newtonian gravitational force between the sphere and the top and bottom of rectangular trenches. In [49] this force was assumed to be negligibly small. Taking into account that in Section 4 and Section 5 the measure of agreement between experiment and theory is used for constraining the parameters of axionlike particles and non-Newtonian gravity, below we estimate the role of Newton’s gravitational force more precisely.
The second test body, which is concentrically covered by the rectangular trenches, is a mm diameter Si disc (schematic of the experimental setup is shown in Figure 1 of [49]). As mentioned above, both of the test bodies are coated by layers of Cr and Au. In our estimation of the upper bound for the Newton’s gravitational force in this experiment, we assume that both the sphere and the disc of diameter D and thickness H, where H is the trench depth, are all-gold. By choosing the disc thickness equal to H, we disregard the Si substrate underlying trenches because it does not contribute to the differential gravitational force between the top and bottom of the trenches (unlike the Casimir and additional hypothetical forces, the more long-range gravitational force from the trench bottom cannot be considered equal to zero).
Taking into account that the disc radius is much larger that the sphere radius R, the gravitational force between them is given by [92]
where is the density of gold. Substituting the values of all parameters in (11), one obtains fN. It is seen that the upper bound for the gravitational force is much less than the experimental error in measuring the Casimir force, which is equal to fN at m (the variations in gravitational force depending on whether the sphere is above the top or bottom of the trenches are well below 0.11 fN). This confirms that the contribution of Newton’s gravitational force in this experiment is very small and can be neglected.
4. Constraints on Axionlike Particles
The results of the experiment [49] measuring the Casimir force in the micrometer seperation range allow us to obtain new constraints on the mass of axionlike particles and their coupling constants to nucleons. As explained in Section 2, measurements of the Casimir force between unpolarized test bodies can be used for constraining the parameters of axionlike particles in which interaction with fermions is described by the Lagrangian density (2). For this purpose, one should use the process of two-axion exchange between nucleons of the laboratory test bodies, which leads to the effective potential (4) and force (6). Thus, it is necessary to calculate this force in the experimental configuration of [49].
According to Section 3, this configuration reduces to a sapphire (AlO) sphere of radius R (the sapphire density is ) coated by the layers of Cr and Au of thicknesses and , respectively, interacting with a Si plate () in which the thickness exceeds H and can be considered infinitely large when calculating the hypothetical interactions rapidly decreasing with separation. The plate is also coated by the layer of Cr of thickness and by an external layer of Au of thickness indicated in Section 3.
The additional force arising in this configuration due to a two-axion exchange can be calculated by (5) and (6). The results of this calculation for a homogeneous sphere and plate are presented in [41]. The impact of two metallic layers is easily taken into account in perfect analogy to [38,40]. Finally, the additional force due to a two-axion exchange in the configuration of the experiment [49] takes the form
where is the mass of atomic hydrogen and the following expressions for the functions and are obtained:
where the function is defined as
The numerical coefficients C in (13) are specific for any material. They are calculated by the following equation:
where Z and N are the number of protons and the mean number of neutrons in an atomic nucleus of a given substance, and with M being the mean atomic or molecular mass.
The values of (15) for Au, Cr, Si and AlO, i.e., , , and , are proportional to with the factors found using the densities of Au, Si and AlO indicated above and . The values of for Au, Cr, Si and AlO are equal to 0.40422, 0.46518, 0.50238 and 0.49422, respectively, and those of are equal to 0.60378, 0.54379, 0.50628 and 0.51412 for the same respective materials [43].
Taking into consideration that, in the experiment [49], no additional interaction was observed within the total experimental error , the interaction (12) should satisfy the inequality
Using Equations (12)–(14), one can constrain the possible values of the axionlike particles mass and their coupling constant to nucleons g from (16).
The numerical analysis of (16) taking into account (12)–(14) and the values of at different z [49] shows that the strongest constraints on and g follow at m, where fN (see Section 4). These constraints are presented by the line labeled “new” in Figure 1. For comparison purposes, in the same figure, we show the constraints obtained earlier from the Cavendish-type experiment [93] (line “gr” [94]), from measuring the smallest gravitational forces using the torsional oscillator [95,96,97] (line “gr” [56]), from measuring the effective Casimir pressure [73,74] (line 1 [35] ), from the experiment using a beam of molecular hydrogen [98] (line “H” [99]) and from the differential measurement where the Casimir force was completely nullified [59] (the dashed line [38]). Note that the figure field above each line is excluded and that below each line is allowed by the results of respective experiment.
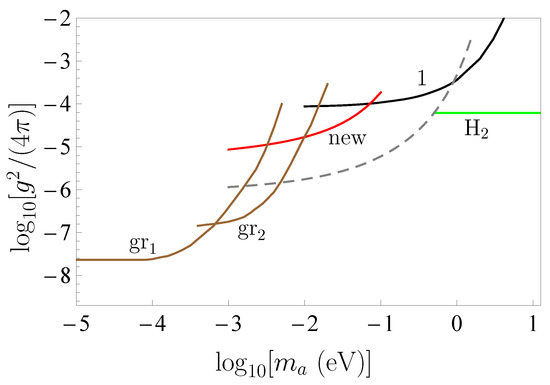
Figure 1.
The strongest constraints on the coupling constant of axionlike particles to nucleons obtained from different experiments. Lines labeled “gr” and “gr” are found from the Cavendish-type experiments and from measuring the minimum gravitational forces, respectively. Lines labeled “new” and “H” follow from the recent experiment on measuring the Casimir force in the micrometer separation range and from the experiment using a beam of molecular hydrogen. Line 1 and the dashed line are obtained from measuring the effective Casimir pressure and from the experiment nullifying the Casimir force. The regions above each line are excluded, and those below are allowed.
As is seen in Figure 1, in the region of axion masses from 10 to 74 meV the constraints on g obtained from the experiment [49] (line “new”) are stronger than those following from measuring the effective Casimir pressure (line 1) and the smallest gravitational forces (line “gr”). The maximum strengthening up to a factor of 4 is reached for the axion mass meV. Thus, in the region of axion masses indicated above, this experiment leads to stronger constraints than the previous experiments measuring the Casimir force [20,48]. The stronger constraints shown by the dashed line follow only from the experiment [59] where the Casimir force was completely nullified.
5. Constraints on Non-Newtonian Gravity
As mentioned in Section 1, the results of the experiment [49] measuring the Casimir force in the micrometer separation range can be also used for constraining the parameters of Yukawa-type corrections to Newtonian gravity. For this purpose, one should calculate the Yukawa-type force (8), (9) in the experimental configuration using its geometrical characteristics and densities of all constituting materials presented in Section 3 and Section 4.
The calculation results using (8) and (9) for a homogeneous sphere above a homogeneous plate are presented in [41]. Here, we modify them in perfect analogy to [38,40] to take into account the contributions of Cr and Au layers covering both a sphere and a trench in this experiment. The result is
where
and the function is defined as
By virtue of the fact that the Yukawa-type force (17) was not observed within the limits of the measurement error, it should satisfy the inequality
Similar to the case of an additional interaction due to a two-axion exchange between nucleons, the strongest constraints on the parameters of the Yukawa-type interaction and follow from (20) at m where fN.
The constraints obtained are shown by the line labeled “new” in Figure 2. For comparison purposes, in this figure we also show the constraints following from measuring of the effective Casimir pressure [73,74] (line 1), of the normal Casimir force between sinusoidally corrugated surfaces of a sphere and a plate at different orientation angles of corrugations [100,101] (line 2 [102]) and of the lateral Casimir force force between the sinusoidally corrugated surfaces of a sphere and a plate [103,104] (line 3 [105]). Note that somewhat stronger constraints than those shown by line 3 were obtained [106] from the experiment measuring the Casimir force between crossed cylinders [107] on an undefined confidence level [31,54]. However, the strongest constraints on the parameters of a Yukawa-type interaction in the region below m follow from the experiments on neutron scattering. They are shown by the line labeled “n” [108,109]. Similar to Figure 1, the regions above each line are excluded by the results of respective experiment, whereas the regions below each line are allowed.
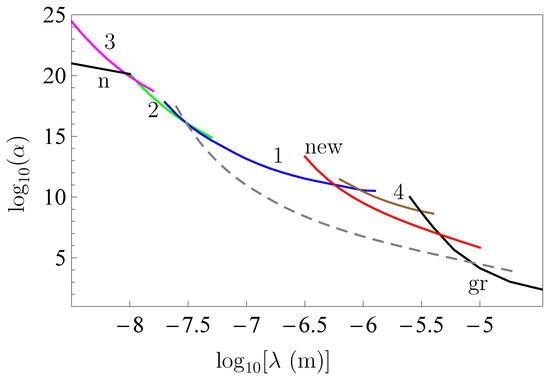
Figure 2.
The strongest constraints on the interaction constant and interaction range of the Yukawa-type interaction obtained from different experiments. Lines 1, 2 and 3 are found from measuring the effective Casimir pressure between two parallel plates, and normal and lateral Casimir forces between the sinusoidally corrugated surfaces of a sphere and a plate, respectively. The line labeled “n” is found from the experiments on neutron scattering. The lines labeled “new” and 4 follow from the experiment measuring the Casimir force in the micrometer separation range and from the experiment using a torsion pendulum. The line labeled “gr” and the dashed line are obtained from the Cavendish-type experiments and from the experiment nullifying the Casimir force. The regions above each line are excluded, and those below each line are allowed.
In the region of Figure 2 with a larger , the constraints shown by line 4 are obtained from measuring the Casimir force by means of the torsion pendulum [110]. The line labeled “gr” indicates the constraints on the Yukawa-type interaction following from the Cavendish-type experiments [93,94,111]. As for the dashed line, which covers the largest interaction range, it is obtained [59] from the differential force measurement where the Casimir force was completely nullified (compare with the dashed line in Figure 1 found from the same experiment).
As seen in Figure 2, the constraints labeled “new” are stronger than the constraints of lines 1 and “gr” following from measurements of the effective Casimir pressure and from the Cavendish-type experiments over the interaction range from 550 nm to m. The maximum strengthening by up to a factor of 24 is reached at m. The constraints obtained are weaker only as compared with those following from the experiment where the Casimir force was nullified [59].
6. Discussion
In this article, we considered the problems of dark matter axions, non-Newtonian gravity and the constraints on their parameters. As discussed in Section 1, axions and axionlike particles have gained much recognition as the most probable constituents of dark matter. An active search for axions using their interactions with photons, electrons, and nucleons is under way in many laboratories all over the world. A major contribution to the investigation of interactions between axions and photons in different astrophysical processes has been made by Prof. Yu. N. Gnedin, who suggested several prospective possibilities for the observation of axionlike particles and for constraining their parameters.
Here, we obtain new constraints on the coupling constant of axionlike particles to nucleons, which follow from the recently performed measurement of the differential Casimir force between Au-coated surfaces of the sphere and the top and bottom of rectangular trenches [49]. The differential character of this experiment allowed one to reach a very high precision and to obtain meaningful data up to a very large separation distance of m. The measure of agreement between the obtained data and the theoretical predictions based on first principles of quantum electrodynamics at nonzero temperature allowed us to find rather strong constraints on the axionlike particles and non-Newtonian gravity of Yukawa type.
The obtained constraints on the coupling constants of axionlike particles to nucleons are stronger by up to a factor of 4 than the previously known ones derived [56] from the gravitational experiments and from measuring the effective Casimir pressure [36,73,74]. This strengthening holds in the range of axion masses from 10 to 74 meV. We have also shown that the same experiment on measuring the differential Casimir force in the micrometer separation range [49] results in up to a factor of 24 stronger constraints on the interaction constant of Yukawa-type interactions compared with the ones found previously from measuring the effective Casimir pressure [73,74], an experiment using the torsion pendulum [110] and the Cavendish-type experiments [93,94,111]. In this case, the strengthening holds in the interaction range from nm to m.
Although the constraints obtained are not the strongest ones (the strongest constraints on both the axionlike particles and the Yukawa-type interaction in the interaction ranges indicated above were obtained from the experiment [59] where the Casimir force was nullified), they complement the results found from previous measurements of the Casimir interaction and can be considered as their additional confirmation.
The obtained results fall into intensive studies of axionlike particles, non-Newtonian gravity and constraints on their parameters. In addition to the literature already discussed in Section 1, it is pertinent to mention a haloscope search for dark matter axions that excludes some range of the axion–photon couplings in models of invisible axions [112] and another haloscope experiment for the search of galactic axions using a superconducting resonant cavity [113]. The first results of the promising experiment for searching the dark matter axions with masses below eV are reported in [114]. Two more haloscope experiments are performed for the search of dark matter axions using their interaction with electronic spins [115] and photons [116].
A few prospective experiments for constraining the parameters of axionlike particles and non-Newtonian gravity are suggested in the literature but have not yet been performed. Here, one should mention an experiment measuring the Casimir pressure between parallel plates at up to m separations (Cannex) [117,118,119,120]. An approach for searching for dark matter axions with eV using a superconducting radio frequency cavity was proposed in [121]. Several possibilities for probing the non-Newtonian gravity in a submillimeter interaction range by means of temporal lensing [122], molecular spectroscopy [123] and neutron interferometry [123,124] are also discussed. Finally, very recently, the possibility to detect the axion-nucleon interaction in the Casimir-less regime by means of levitated system was proposed [125]. According to the authors, their approach provides a possibility to strengthen the current constraints on g by several orders of magnitude in the wide region of axion masses from eV to 10 eV.
7. Conclusions
To conclude, the search for dark matter axions, non-Newtonian gravity and constraints on their parameters is a multidisciplinary problem of elementary particle physics, quantum field theory, gravitational theory, astrophysics and cosmology. At the moment, neither axions nor corrections to Newton’s gravitational law, other than that predicted by General Relativity theory, are observed, but more and more stringent constraints on them have been obtained. Keeping in mind that there are very serious reasons for creating axions at the very early stages of the evolution of the universe and for existence of deviations from Newton’s law of gravitation at very short separations, as predicted by the extended Standard Model, Supersymmetry, Supergravity and String theory, one may hope that these predictions will find experimental confirmation in the not too distant future.
Author Contributions
Investigation, both authors; writing, both authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Peter the Great Saint Petersburg Polytechnic University in the framework of the Russian state assignment for basic research (project N FSEG-2020-0024). V.M.M. was also partially funded by the Russian Foundation for Basic Research grant number 19-02-00453 A.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All necessary data are contained in this paper.
Acknowledgments
V.M.M. is grateful for partial support by the Russian Government Program of Competitive Growth of Kazan Federal University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bertone, G.; Hooper, D. Hystory of Dark Matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Oort, J.H. The force exerted by the stellar system in the direction perpendicular to the galactic plane and some related problems. Bull. Astron. Inst. Neth. 1932, 6, 249–287. [Google Scholar]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Overduin, J.M.; Wesson, P.S. Dark Matter and Background Light. Phys. Rep. 2004, 402, 267–406. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Sanders, R.H. The Dark Matter Problem: A Historical Perspective; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Matarrese, S.; Colpi, M.; Gorini, V.; Moshella, U. (Eds.) Dark Matter and Dark Energy; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Chadha-Day, F.; Ellis, J.; Marsh, D.J.E. Axion Dark Matter: What is it and Why Now? arXiv 2021, arXiv:2105.01406. [Google Scholar]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–283. [Google Scholar] [CrossRef]
- Kim, J.E. Light pseudoscalars, particle physics and cosmology. Phys. Rep. 1987, 150, 1–177. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Stubbs, C.W.; Rogers, W.F. Searches for new Macroscopic forces. Annu. Rev. Nucl. Part. Sci. 1991, 41, 269–320. [Google Scholar] [CrossRef]
- Rosenberg, L.J.; van Bibber, K.A. Searches for invisible axions. Phys. Rep. 2000, 325, 1–39. [Google Scholar] [CrossRef]
- Raffelt, G.G. Axions—Motivation, limits and searches. J. Phys. A Math. Theor. 2007, 40, 6607–6620. [Google Scholar] [CrossRef]
- Antoniadis, I.; Baessler, S.; Bücher, M.; Fedorov, V.V.; Hoedl, S.; Lambrecht, A.; Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V.; Reynaud, S.; et al. Short-range fundamental forces. C. R. Phys. 2011, 12, 755–778. [Google Scholar] [CrossRef]
- Kawasaki, M.; Nakayama, K. Axions: Theory and Cosmological Role. Annu. Rev. Nucl. Part. Sci. 2013, 63, 69–95. [Google Scholar] [CrossRef]
- Ivastorza, I.G.; Redondo, J. New experimental approaches in the search for axion-like particles. Progr. Part. Nucl. Phys. 2018, 102, 89–159. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Jackson Kimball, D.F.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics. Universe 2021, 7, 47. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Krasnikov, S.V. Polarimetric effects associated with the detection of Goldstone bosons in stars and galaxies. Sov. Phys. JETP 1992, 75, 933–937, Translated in Zh. Eksp. Teor. Fiz. 1992, 102, 1729–1738. [Google Scholar]
- Anselm, A.A.; Uraltsev, N.G. A second massless axion? Phys. Lett. B 1982, 114, 39–41. [Google Scholar] [CrossRef]
- Gnedin, Y.N. Magnetic Conversion of Photons into Massless Axions and Striking Feature in Quasar Polarized Light. Astrophys. Space Sci. 1997, 249, 125–129. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Dodonov, S.N.; Vlasyuk, V.V.; Spiridonova, O.I.; Shakhverdov, A.V. Astronomical searches for axions: Observation at the SAO 6-m telescope. Mon. Not. R. Astron. Soc. 1999, 306, 117–121. [Google Scholar] [CrossRef][Green Version]
- Gnedin, Y.N. Current status of modern dark matter problem. Int. J. Mod. Phys. A 2002, 17, 4251–4260. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Piotrovich, M.Y.; Natsvlishvili, T.M. PVLAS experiment: Some astrophysical consequences. Mon. Not. R. Astron. Soc. 2007, 374, 276–281. [Google Scholar] [CrossRef]
- PVLAS Collaboration. Experimental Observation of Optical Photons Generated in Vacuum by a Magnetic Field. Phys. Rev. Lett. 2007, 96, 110406. [Google Scholar]
- Piotrovich, M.Y.; Gnedin, Y.N.; Natsvlishvili, T.M. Coupling constants for axions and electromagnetic fields and cosmological observations. Astrophysics 2009, 52, 412–422. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Piotrovich, M.Y.; Natsvlishvili, T.M. New results in searching for axions by astronomical methods. Int. J. Mod. Phys. A 2016, 31, 1641019. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wet. 1948, 51, 793–795. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Derjaguin, B.V.; Abricosova, I.I.; Lifshitz, E.M. Direct measurement of molecular attraction between solids separated by a narrow gap. Quat. Rev. 1956, 10, 295–329. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Sokolov, I.Y. Casimir effect leads to new restrictions on long-rang force constant. Phys. Lett. A 1987, 125, 405–407. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on the parameters of an axion from measurements of the thermal Casimir-Polder force. Phys. Rev. D 2014, 89, 035010. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Stronger constraints on an axion from measuring the Casimir interaction by means of a dynamic atomic force microscope. Phys. Rev. D 2014, 89, 075002. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion-nucleon coupling constants from measurements of effective Casimir pressure by means of micromachined oscillator. Eur. Phys. J. C 2014, 74, 2859. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on axion-nucleon coupling constants from measuring the Casimir force between corrugated surfaces. Phys. Rev. D 2014, 90, 055013. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Improved constraints on the coupling constants of axion-like particles to nucleons from recent Casimir-less experiment. Eur. Phys. J. C 2015, 75, 164. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Constraints on axionlike particles and non-Newtonian gravity from measuring the difference of Casimir forces. Phys. Rev. D 2017, 95, 123013. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. Recent breakthrough and outlook in constraining the non-Newtonian gravity and axion-like particles from Casimir physics. Eur. Phys. J. C 2017, 77, 315. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Kuusk, P.; Mostepanenko, V.M. Constraints on non-Newtonian gravity and axionlike particles from measuring the Casimir force in nanometer separation range. Phys. Rev. D 2020, 101, 056013. [Google Scholar] [CrossRef]
- Kuzmin, V.A.; Tkachev, I.I.; Shaposhnikov, M.E. Restrictions imposed on light scalar particles by measurements of van der Waals forces. Pis’ma v Zh. Eksp. Teor. Fiz. 1982, 36, 49–52, Translated: JETP Lett. 1982, 36, 59–62. [Google Scholar]
- Fischbach, E.; Talmadge, C.L. The Search for Non-Newtonian Gravity; Springer: New York, NY, USA, 1999. [Google Scholar]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. New dimensions at a millimeter to a fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. Phenomenology, astrophysics, and cosmology of theories with millimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Floratos, E.G.; Leontaris, G.K. Low scale unification, Newton’s law and extra dimensions. Phys. Lett. B 1999, 465, 95–100. [Google Scholar] [CrossRef]
- Kehagias, A.; Sfetsos, K. Deviations from 1/r2 Newton law due to extra dimensions. Phys. Lett. B 2000, 472, 39–44. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Klimchitskaya, G.L. The State of the Art in Constraining Axion-to-Nucleon Coupling and Non-Newtonian Gravity from Laboratory Experiments. Universe 2020, 6, 147. [Google Scholar] [CrossRef]
- Bimonte, G.; Spreng, B.; Maia Neto, P.A.; Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Decca, R.S. Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe 2021, 7, 93. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30–8000 Nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Moody, J.E.; Wilczek, F. New macroscopic forces? Phys. Rev. D 1984, 30, 130–139. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure, Volume 1; Benjamin: New York, NY, USA, 1969. [Google Scholar]
- Adelberger, E.G.; Fischbach, E.; Krause, D.E.; Newman, R.D. Constraining the couplings of massive pseudoscalars using gravity and optical experiments. Phys. Rev. D 2003, 68, 062002. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion coupling constants from measuring the Casimir interaction between polarized test bodies. Phys. Rev. D 2016, 94, 035011. [Google Scholar] [CrossRef]
- Aldaihan, S.; Krause, D.E.; Long, J.C.; Snow, W.M. Calculations of the dominant long-range, spin-independent contributions to the interaction energy between two nonrelativistic Dirac fermions from double-boson exchange of spin-0 and spin-1 bosons with spin-dependent couplings. Phys. Rev. D 2017, 95, 096005. [Google Scholar] [CrossRef]
- Ferrer, F.; Nowakowski, M. Higg- and Goldstone-boson-mediated long range forces. Phys. Rev. D 1999, 59, 075009. [Google Scholar] [CrossRef]
- Drell, S.D.; Huang, K. Many-Body Forces and Nuclear Saturation. Phys. Rev. 1953, 91, 1527–1543. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Chan, H.B.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise measurements of the Casimir force and first realization of the “Casimir-less” experiment. J. Low Temp. Phys. 2004, 135, 63–74. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Chan, H.B.; Fischbach, E.; Krause, D.E.; Jamell, C.R. Constraining New Forces in the Casimir Regime Using the Isoelectronic Technique. Phys. Rev. Lett. 2005, 94, 240401. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Spreng, B.; Hartmann, M.; Henning, V.; Maia Neto, P.A.; Ingold, G.-L. Proximity force approximation and specular reflection: Application of the WKB limit of Mie scattering to the Casimir effect. Phys. Rev. A 2018, 97, 062504. [Google Scholar] [CrossRef]
- Henning, V.; Spreng, B.; Hartmann, M.; Ingold, G.-L.; Maia Neto, P.A. Role of diffraction in the Casimir effect beyond the proximity force approximation. J. Opt. Soc. Am. B 2019, 36, C77–C87. [Google Scholar] [CrossRef]
- Spreng, B.; Maia Neto, P.A.; Ingold, G.-L. Plane-wave approach to the exact van der Waals interaction between colloid particles. J. Chem. Phys. 2020, 153, 024115. [Google Scholar] [CrossRef] [PubMed]
- Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Proximity force approximation for the Casimir energy as a derivative expansion. Phys. Rev. D 2011, 84, 105031. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Kardar, M. Material dependence of Casimir force: Gradient expansion beyond proximity. Appl. Phys. Lett. 2012, 100, 074110. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Jaffe, R.L.; Kardar, M. Casimir forces beyond the proximity force approximation. Europhys. Lett. 2012, 97, 50001. [Google Scholar] [CrossRef]
- Bimonte, G. Going beyond PFA: A precise formula for the sphere-plate Casimir force. Europhys. Lett. 2017, 118, 20002. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir force between plates with small deviations from plane parallel geometry. Int. J. Mod. Phys. A 1995, 10, 2661–2681. [Google Scholar] [CrossRef]
- van Zwol, P.J.; Palasantzas, G.; De Hosson, J.T.M. Influence of random roughness on the Casimir force at small separations. Phys. Rev. B 2008, 77, 075412. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Improved tests of extra-dimensional physics and thermal quantum field theory from new Casimir force measurements. Phys. Rev. D 2003, 68, 116003. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. (N. Y.) 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Chang, C.-C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Banishev, A.A.; Chang, C.-C.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measurement of the gradient of the Casimir force between a nonmagnetic gold sphere and a magnetic nickel plate. Phys. Rev. B 2012, 85, 195422. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Casimir Force between Ferromagnetic Surfaces of a Ni-Coated Sphere and a Ni-Coated Plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef] [PubMed]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Casimir interaction between two magnetic metals in comparison with nonmagnetic test bodies. Phys. Rev. B 2013, 88, 155410. [Google Scholar] [CrossRef]
- Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Reducing detrimental electrostatic effects in Casimir-force measurements and Casimir-force-based microdevices. Phys. Rev. A 2018, 97, 032501. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Examining the Casimir puzzle with an upgraded AFM-based technique and advanced surface cleaning. Phys. Rev. B 2019, 100, 081406(R). [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Precision measurements of the gradient of the Casimir force between ultraclean metallic surfaces at larger separations. Phys. Rev. A 2019, 100, 052511. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Bezerra, V.B.; Decca, R.S.; Fischbach, E.; Geyer, B.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Romero, C. Present status of controversies regarding the thermal Casimir force. J. Phys. A Math. Gen. 2006, 39, 6589–6600. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Decca, R.S.; Fischbach, E.; Geyer, B.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M.; Romero, C. Comment on “Temperature dependence of the Casimir effect”. Phys. Rev. E 2006, 73, 028101. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Casimir Puzzle and Casimir Conundrum: Discovery and Search for Resolution. Universe 2021, 7, 84. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. An alternative response to the off-shell quantum fluctuations: A step forward in resolution of the Casimir puzzle. Eur. Phys. J. C 2020, 80, 900. [Google Scholar] [CrossRef]
- Hannemann, M.; Wegner, G.; Henkel, C. No-Slip Boundary Conditions for Electron Hydrodynamics and the Thermal Casimir Pressure. Universe 2021, 7, 108. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir entropy and nonlocal response function to the off-shell quantum fluctuations. Phys. Rev. D 2021, 103, 096007. [Google Scholar] [CrossRef]
- Lambrecht, A.; Reynaud, S. Casimir and short-range gravity tests. In Gravitational Waves and Experimental Gravity; Augé, E., Dumarchez, J., Vân, J.T.T., Eds.; Thê Gioi: Hanoi, Vietnam, 2011; pp. 199–206. [Google Scholar]
- Lambrecht, A.; Canaguier-Durand, A.; Guérout, R.; Reynaud, S. Casimir effect in the scattering approach: Correlations between material properties, temperature and geometry. In Casimir Physics; Dalvit, D.A.R., Milonni, P.W., Roberts, D.C., Rosa, F.S.S., Eds.; Springer: Heidelberg, Germany, 2011; pp. 97–127. [Google Scholar]
- Mostepanenko, V.M.; Bezerra, V.B.; Klimchitskaya, G.L.; Romero, C. New constraints on Yukawa-type interactions from the Casimir effect. Int. J. Mod. Phys. A 2012, 27, 1260015. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Constraints on non-Newtonian gravity and light elementary particles from measurements of the Casimir force by means of a dynamic atomic microscope. Phys. Rev. D 2012, 86, 065025. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Application of the proximity force approximation to gravitational and Yukawa-type forces. Phys. Rev. D 2009, 79, 124021. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Hoedl, S.; Hoyle, C.D.; Kapner, D.J.; Upadhye, A. Particle-Physics Implications of a Recent Test of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 2007, 98, 131104. [Google Scholar] [CrossRef]
- Long, J.C.; Chan, H.W.; Churnside, A.B.; Gulbis, E.A.; Varney, M.C.M.; Price, J.C. Upper limits to submillimetre-range forces from extra space-time dimensions. Nature 2003, 421, 922–925. [Google Scholar] [CrossRef]
- Yan, H.; Housworth, E.A.; Meyer, H.O.; Visser, G.; Weisman, E.; Long, J.C. Absolute measurement of thermal noise in a resonant short-range force experiment. Class. Quant. Grav. 2014, 31, 205007. [Google Scholar] [CrossRef]
- Long, J.C.; Kostelecký, V.A. Search for Lorentz violation in short-range gravity. Phys. Rev. D 2015, 91, 092003. [Google Scholar] [CrossRef]
- Ramsey, N.F. The tensor force between two protons at long range. Phys. A 1979, 96, 285–289. [Google Scholar] [CrossRef]
- Ledbetter, M.P.; Romalis, M.V.; Jackson Kimball, D.F. Constraints on Short-Range Spin-Dependent Interactions from Scalar Spin-Spin Coupling in Deuterated Molecular Hydrogen. Phys. Rev. Lett. 2013, 110, 040402. [Google Scholar] [CrossRef] [PubMed]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Demonstration of Angle-Dependent Casimir Force between Corrugations. Phys. Rev. Lett. 2013, 110, 250403. [Google Scholar] [CrossRef] [PubMed]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Experimental and theoretical investigation of the angular dependence of the Casimir force between sinusoidally corrugated surfaces. Phys. Rev. B 2014, 89, 235436. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Constraints on corrections to Newtonian gravity from two recent measurements of the Casimir interaction between metallic surfaces. Phys. Rev. D 2013, 87, 125031. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the asymmetric lateral Casimir force between corrugated surfaces in the nonadditive regime. Phys. Rev. B 2009, 80, 121402(R). [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Lateral Casimir force between sinusoidally corrugated surfaces: Asymmetric profiles, deviations from the proximity force approximation, and comparison with exact theory. Phys. Rev. B 2010, 81, 115417. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Advance and prospects in constraining the Yukawa-type corrections to Newtonian gravity from the Casimir effect. Phys. Rev. D 2010, 81, 055003. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Novello, M. Constraints on non-Newtonian gravity from the Casimir force measurements between two crossed cylinders. Phys. Rev. D 2001, 63, 115003. [Google Scholar] [CrossRef]
- Ederth, T. Template-stripped gold surfaces with 0.4-nm rms roughness suitable for force measurements: Application to the Casimir force in the 20–100-nm range. Phys. Rev. A 2000, 62, 062104. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V. Neutron scattering and extra short range interactions. Phys. Rev. D 2008, 77, 034020. [Google Scholar] [CrossRef]
- Kamiya, Y.; Itagami, K.; Tani, M.; Kim, G.N.; Komamiya, S. Constraints on New Gravitylike Forces in the Nanometer Range. Phys. Rev. Lett. 2015, 114, 161101. [Google Scholar] [CrossRef]
- Masuda, M.; Sasaki, M. Limits on Nonstandard Forces in the Submicrometer Range. Phys. Rev. Lett. 2009, 102, 171101. [Google Scholar] [CrossRef]
- Smullin, S.J.; Geraci, A.A.; Weld, D.M.; Chiaverini, J.; Holmes, S.; Kapitulnik, A. Constraints on Yukawa-type deviations from Newtonian gravity at 20 microns. Phys. Rev. D 2005, 72, 122001. [Google Scholar] [CrossRef]
- Du, N.; Force, N.; Khatiwada, R.; Lentz, E.; Ottens, R.; Rosenberg, L.J.; Rybka, G.; Carosi, G.; Woollett, N.; Bowring, D.; et al. Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment. Phys. Rev. Lett. 2018, 120, 151301. [Google Scholar] [CrossRef] [PubMed]
- Alesini, D.; Braggio, C.; Carugno, G.; Crescini, N.; D’Agostino, D.; Di Gioacchino, D.; Di Vora, R.; Falferi, P.; Gallo, S.; Gambardella, U.; et al. Galactic axions search with a superconducting resonant cavity. Phys. Rev. D 2019, 99, 101101. [Google Scholar] [CrossRef]
- Ouellet, J.L.; Salemi, C.P.; Foster, J.W.; Henning, R.; Bogorad, Z.; Conrad, J.M.; Formaggio, J.A.; Kahn, Y.; Minervini, J.; Radovinsky, A.; et al. First Results from ABRACADABRA-10 cm: A Search for Sub-μeV Axion Dark Matter. Phys. Rev. Lett. 2019, 122, 121802. [Google Scholar] [CrossRef]
- Crescini, N.; Alesini, D.; Braggio, C.; Carugno, G.; D’Agostino, D.; Di Gioacchino, D.; Falferi, P.; Gambardella, U.; Gatti, C.; Iannone, G.; et al. Axion Search with a Quantum-Limited Ferromagnetic Haloscope. Phys. Rev. Lett. 2020, 124, 171801. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Ahn, S.; Choi, J.; Ko, B.R.; Semertzidis, Y.K. Axion Dark Matter Search around 6.7 μeV. Phys. Rev. Lett. 2020, 124, 101802. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P.; Abele, H. Prospects for Searching Thermal Effects, Non-Newtonian Gravity and Axion-Like Particles: CANNEX Test of the Quantum Vacuum. Symmetry 2019, 11, 407. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P. Casimir pressure between metallic plates out of thermal equilibrium: Proposed test for the relaxation properties of free electrons. Phys. Rev. A 2019, 100, 022511. [Google Scholar] [CrossRef]
- Sedmik, R.I.P. Casimir and non-Newtonian force experiment (CANNEX): Review, status, and outlook. Int. J. Mod. Phys. A 2020, 35, 2040008. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Pitschmann, M. Next Generation Design and Prospects for Cannex. Universe 2021, 7, 234. [Google Scholar] [CrossRef]
- Berlin, A.; D’Agnolo, R.T.; Ellis, S.A.; Nantista, C.; Neilson, J.; Schuster, P.; Tantawi, S.; Toro, N.; Zhou, K. Axion dark matter detection by superconducting resonant frequency conversion. J. High Energy Phys. 2020, 2020, 88. [Google Scholar] [CrossRef]
- Faizal, M.; Patel, H. Probing Short Distance Gravity using Temporal Lensing. Int. J. Mod. Phys. A 2021, 36, 2150115. [Google Scholar] [CrossRef]
- Banks, H.; McCullough, M. Charting the fifth force landscape. Phys. Rev. D 2021, 103, 075018. [Google Scholar] [CrossRef]
- Rocha, J.M.; Dahia, F. Neutron interferometry and tests of short-range modifications of gravity. Phys. Rev. D 2021, 103, 124014. [Google Scholar] [CrossRef]
- Chen, L.; Liu, J.; Zhuy, K. Constraining Axion-to-Nucleon interaction via ultranarrow linewidth in the Casimir-less regime. arXiv 2021, arXiv:2107.08216. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).