Abstract
Based on the spectropolarimetric data of 33 Seyfert type 1 galaxies observed with the BTA-6m telescope of the Special Astrophysical Observatory, we estimated the magnetic field values at the event horizon of the supermassive black hole and the exponents of the power-law dependence s of the magnetic field on the radius. We used the model of optically thick geometrically thin Shakura–Sunyaev accretion disk. The average value of was found to be ∼4, which is in good agreement with the results obtained by other methods. The average value of s is , and its distribution maximum span is in the range od . This is a rather interesting result, since is usually adopted in calculations for Shakura–Sunyaev accretion disks. In addition, for two objects PG 1545+210 and 2MASX J06021107+2828382, the measured degree of polarization is greater than the maximum possible value at the angle between the line of sight and the axis of the accretion disk . It was concluded that for these objects the angle should be closer to .
1. Introduction
According to modern concepts, accretion disks of active galactic nuclei (AGNs) should have an intense magnetic field [1,2]. It is assumed that the magnetic field is formed as a result of the interaction of accreting matter with a rotating supermassive black hole (SMBH) [3,4,5,6,7,8]. The presence of a magnetic field should have a noticeable effect on the spectropolarimetric characteristics of the accretion disk radiation. The polarimetric observations demonstrate that AGNs have polarized radiation in different wavelength ranges, from ultraviolet to radio waves [9,10,11,12,13,14,15,16,17]. Several mechanisms for the origin of the observed polarization are discussed, for example, the light scattering in accretion disks or synchrotron radiation of charged particles. These mechanisms can act in different structures, such as the plane and warped accretion disks, toroidal rings near the accretion disks and relativistic jets. It happens that different models are proposed to explain the same source. There are several models of accretion disks (see for example Pariev et al. [18]). For objects of the type under study, the most popular and simple model is the optically thick geometrically thin Shakura–Sunyaev disk [19]. In this work, we assume that for our sample of objects (Seyfert type 1) accretion disk is the main source of polarized radiation in optical range and we use Shakura–Sunyaev disk model.
It should be noted that accurate determination of the dependence of the magnetic field on the radius in the disk is rather difficult task [16,18,20,21], consisting of intricate spectropolarimetric observations of distant and faint objects and complex and time consuming numerical simulations. Our goal was to estimate the magnitude of the magnetic field at the event horizon of the SMBH and probe the dependence of the magnetic field intensity on the radius in the AGN accretion disks using our spectropolarimetric observations with the BTA-6m telescope and our relatively simple model. The methodology described in Silant’ev et al. [22] was taken as a basis for this work.
2. Basic Equations
2.1. Stokes Parameters
When considering radiation from an axially symmetric accretion disk with a magnetic field, its integral Stokes parameters can be written in the following form [22]:
where , where i is the angle between the line of sight and the axis of the disk, is the value of the Stokes parameter without a magnetic field. The parameters a and b are expressed, in turn, as follows:
where is the wavelength, and are, respectively, the component of the magnetic field in the disk parallel and perpendicular to the disk axis (see Figure 1 from Silant’ev et al. [22]). Taking into account that in the Milne problem (multiple scattering of light in optically thick flattened atmospheres [23,24]) without a magnetic field, the Stokes parameter , we obtained the following value of the relative polarization and positional angle :
Note that depends only on the dimensionless parameters a and b and does not depend on .
The polarization value without a magnetic field was previously calculated by us numerically using the Sobolev–Chandrasekhar model [23,24] and is tabulated in Gnedin et al. [25]. In addition, we note that the polarization has a small effect on the radiation intensity [23]. Thus, we have the opportunity to accurately calculate the polarization value , using numerical integration for the parameter and tabular values for .
2.2. Magnetic Field
When considering the magnetic field in the accretion disk, it is usually assumed (see, for example, Pariev et al. [18]) that its dependence on the radius has a power-law form:
where is the value of the magnetic field intensity at the event horizon of SMBH in AGN, is the radius of the event horizon, is the mass of the SMBH, G is the gravitational constant, c is the speed of light, is the dimensionless spin of the SMBH, J is the angular momentum of the SMBH rotation. As for the s parameter, there are models with different values of this parameter [18], but for the Shakura–Sunyaev disk, the most often adopted value is [19]. In our work, we decided to investigate in more detail the influence of this parameter on the model and therefore we tried a number of values within .
2.3. Dependence of the Polarization Degree on the Wavelength
Since the polarization degree depends on the magnetic field, and the magnetic field depends on the radius, then in order to obtain the dependence of the polarization on the wavelength, we need the dependence of the radius on the wavelength. For the Shakura–Sunyaev accretion disk, we have [26]:
where is the distance in the accretion disk, which corresponds to wavelength , is the Eddington ratio, is the bolometric luminosity, is the Eddington luminosity, is the radiative efficiency, is the accretion rate.
3. Results of Theoretical Calculations
We estimated dependencies of radius , magnetic field strength B, polarization degree P and position angle on wavelength (in optical range) for , G, , , and various values of s. Results are presented in Table 1. In Inoue and Doi [27], the authors obtained 10 G at for AGNs with . These data are in good agreement with our model, in which, for G and , G.

Table 1.
Dependencies of radius , magnetic field strength B, polarization degree P and position angle on wavelength for , G, , , and various values of s.
We calculated the value of the polarization and the positional angle as a function of the value of the magnetic field intensity at the event horizon and the parameter s in the visible range. For this purpose we adopted the following parameter values characteristic of Seyfert type 1 AGN: , [17,28], radiative efficiency , Eddington ratio .
As for the angle i, since it is rather difficult to determine this angle from the observables, research usually adopts in the calculations. In our work, we used a more complex and arguably a more accurate method. Initially, the values were calculated for all angles from 0 to 90 degrees, and then the resulting data were convolved with a Gaussian centered at 45 degrees. If an angle other than 45 degrees was required for calculations, then a Gaussian with a center at this angle was taken.
Based on the generally assumed dipole nature of the magnetic field, and also based, for example, on the conclusions of Piotrovich et al. [29], the ratio between the components of the magnetic field parallel and perpendicular to the disk axis was taken as .
Figure 1 and Figure 2 show the results of these calculations in the form of three-dimensional graphs. In Figure 1, one can see that the average value of the polarization in the visible range depends rather strongly on the parameters and s. The rapid decrease in polarization with increasing field and decreasing s is due to Faraday depolarization (see Equation (2) from Silant’ev et al. [22]). It can be seen in Figure 2 that the gradient of the positional angle depends on the parameters in a rather complex way, which theoretically can make it possible to accurately determine the parameters from the observed gradient. However, the amplitude of this dependence, unfortunately, is rather small.
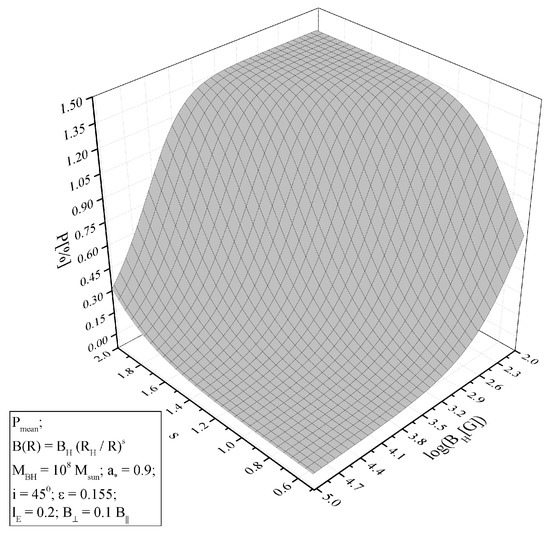
Figure 1.
Wavelength-averaged degree of polarization P depending on the value of the magnetic field intensity at the event horizon and the exponent of the power-law dependence s of the magnetic field on the radius in the disk.
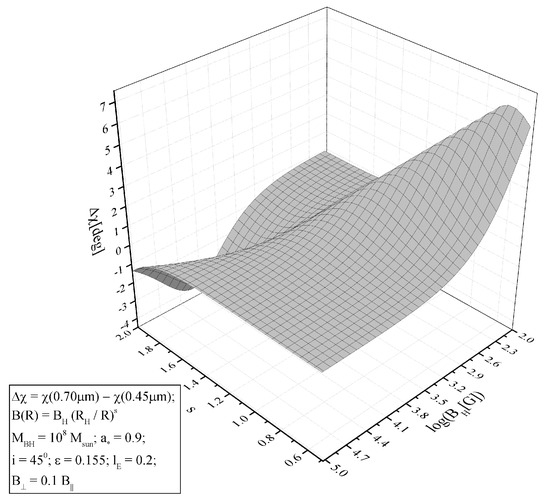
Figure 2.
The difference between the positional angles of polarized radiation at a wavelength of 0.70 μm and 0.45 μm depending on the value of the magnetic field intensity at the event horizon and the exponent of the power-law dependence s of the magnetic field on the radius in the disk.
In addition, we also plotted the dependencies of the degree of polarization and the positional angle on the wavelength for the above parameter values for different values of and s (see Figure 3, Figure 4, Figure 5 and Figure 6).
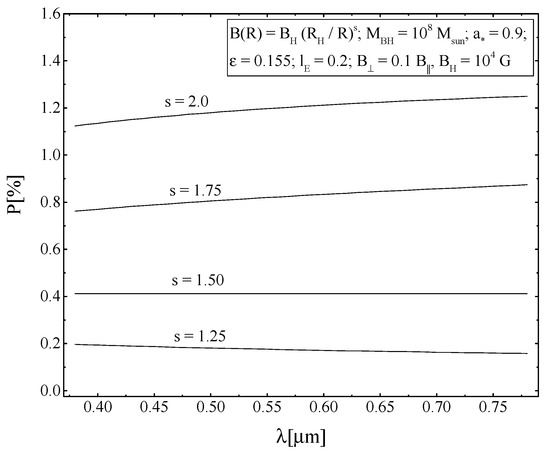
Figure 3.
Dependence of the degree of polarization P on the wavelength for different values of the parameter s.
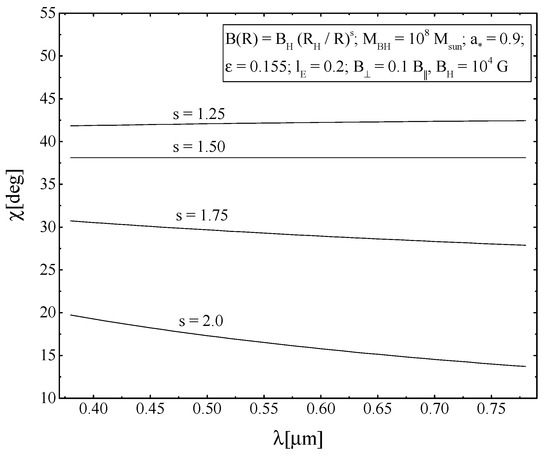
Figure 4.
Dependence of the positional angle on the wavelength for different values of the parameter s.
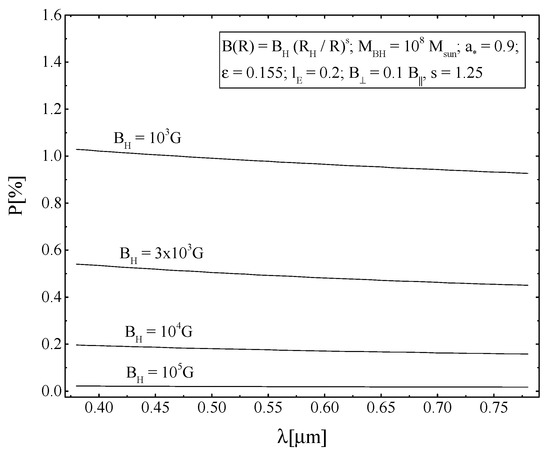
Figure 5.
Dependence of the degree of polarization P on the wavelength for different values of the parameter .
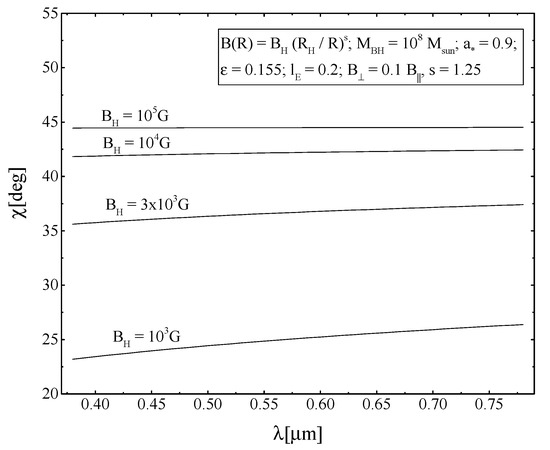
Figure 6.
Dependence of the positional angle on the wavelength for different values of the parameter .
It should be noted that the dependence of the degree of polarization and positional angle on the wavelength in our model was found to be relatively weak. It is practically impossible to reliably measure such a gradient of polarization and position angle in real astronomical observations with the existing signal-to-noise level. Therefore, in further calculations, we used the average value of the polarization, making sure that the dependence of the observed polarization on the wavelength was not too strong and had a monotonic form. As for the observed gradient of the position angle, it was evaluated only qualitatively; in particular, objects with a pronounced non-monotonic dependence of the position angle on the wavelength were discarded, for example, in the presence of the so-called ”S-shaped” feature, which appears to be due to other physical mechanisms (for example, scattering by a spherical optically thin envelope with a magnetic field [30]).
4. Estimations of and Based on Optical Spectropolarimetry of AGNs
In our work, we used the already published data of spectropolarimetric observations of a sample of 33 AGN in type 1 Seyfert galaxies, carried out on the BTA-6m telescope with the participation of the authors [16,17,31]. First round of observations were performed in 2008–2009. The observations were carried out with the SCORPIO focal reducer in the spectropolarimetric mode mounted at the prime focus. We used an EEV42-40 pixel CCD array with a pixel size of μm as the detector and a VPHG550g volume holographic phase grating from the SCORPIO kit operating in the range 3500–7200 Å as the dispersing element. The reciprocal linear dispersion in the detector plane was 1.8 Å/pixel. In the spectrograph, we used a set of five circular diaphragms 4”.5 in diameter arranged in the form of a pseudoslit with a step of 9.7-arcsec. A Savart plate placed behind the diaphragms was used as the polarization analyzer. We used the central diaphragm to take the spectra of an object in perpendicular polarization planes and the remaining diaphragms to take the night-sky spectra. The actual spectral resolution of our data was determined by the monochromatic image of the diaphragms and was 40–42 Å. The seeing in all sets of observations was at least 2”. The technique of polarization observations and calculations was described by Afanasiev and Moiseev [32]. To calibrate the wavelengths and the relative transmission of the diaphragms, we used an Ar–Ne–He filled line-spectrum lamp and a quartz lamp. To calibrate the spectropolarimetric channel of the spectrograph, we observed standards from Turnshek et al. [33]. Second round of observations were performed in 2012–2016. The observations were carried out with the SCORPIO-2 spectrograph [34]. The spectra were taken in two ranges: 4200–7500 Å for redshifts z < 0.1 (VPHG940 grating) and 5700–9500 Å for z > 0.1 (VPHG940 grating). The spectral resolution for a working 2” slit was 14 and 12 Å, respectively. For objects at Galactic latitudes we took into account the interstellar polarization that was determined from the observations of stars around the object. The technique of observations and data reduction is described in detail in Afanasiev and Amirkhanyan [35].
We have formed a sample of 33 sources with published mass estimates for their central SMBHs. Since our model assumes a geometrically thin, optically thick disk [19], we considered only objects with Eddington ratio in the range [36].
Note that in this work we used the average values of the parameters , and , neglecting the errors. This is explained by the following arguments. The parameters and themselves have little effect on the polarization value. The parameter has a more noticeable effect, but this effect can be neglected in comparison with the error of the observational spectropolarimetric data.
For each object, the dependence of the polarization and the gradient of the positional angle on and s was constructed as it was shown in Section 3. Then, this dependence was compared with observational data. The result is a set of values for and s that satisfies these conditions. After that, the values were additionally subject to the condition that they must fall within the limits obtained for these objects by independent methods [37,38]. In the paper Daly [38], errors in the determination of are not indicated, so we took them as in a logarithmic scale. For those objects for which the magnetic field strength was not previously estimated, we adopted the value , since the results of [37,38] estimates of the magnetic field for type 1 Seyfert nuclei give this characteristic range. The values of and s were averaged to obtain the average value and its associated dispersion.
For the objects PG 1545+210 and 2MASX J06021107+2828382, the measured polarization value was found to be greater than the maximum possible value with this calculation method. Since the polarization increases with the inclination angle, the angle value was used for these objects. It is believed that for objects of the type under study (Seyfert type 1 galaxies) this angle usually lies within (see, for example, Wu and Han [39]).
Our results are presented in Table 2.

Table 2.
Results of determination of the magnetic field intensity at the event horizon and parameter s for our objects. is the observed polarization. , a and are mass, spin and Eddington ratio of SMBH. is magnetic field at the event horizon estimated by the method described in Piotrovich et al. [37], except for objects Mkn 509, NGC 3227, NGC 5548 and Mkn 590 whose magnetic fields were estimated in Daly [38]. For objects for which the magnetic field was not previously estimated, we took the value .
5. Analysis of the Estimated Parameters of the Magnetic Field
As mentioned earlier, the value of the spin has a rather weak effect on the results, especially taking into account the fact that this value itself varies within rather narrow boundaries. Therefore, the dependence of and s on a is negligible.
Figure 7 shows the obtained values of the magnetic field at the event horizon and the exponent of the power-law dependence s in graphical form. No pronounced dependence among these parameters on each other is observed. However, one can notice that the values are concentrated in the right side of the graph. It should be noted that all the values of s we obtained are greater than the 5/4 value usually adopted for accretion disks in type 1 Seyfert nuclei [19]. Figure 8 presents the dependence of the magnetic field strength at the event horizon of the SMBH on its mass. There is a linear dependence of the form , which in a close agreement with a similar relation obtained by us in Piotrovich et al. [37]. Figure 9 depicts the dependence of the exponent of the power-law index s on the SMBH mass . We find a linear dependence . It should be noted here that the accuracy of this linear approximation is lower than that obtained for . Figure 10 displays the dependence of the magnetic field at the event horizon of the SMBH on its Eddington ratio . We derive a linear dependence of the form in agreement with the results obtained by Piotrovich et al. [37]. Figure 11 gives the dependence of the exponent of the power-law dependence of s on the Eddington ratio . A linear dependence of the form is visible, which, however, also has a lower accuracy than for .
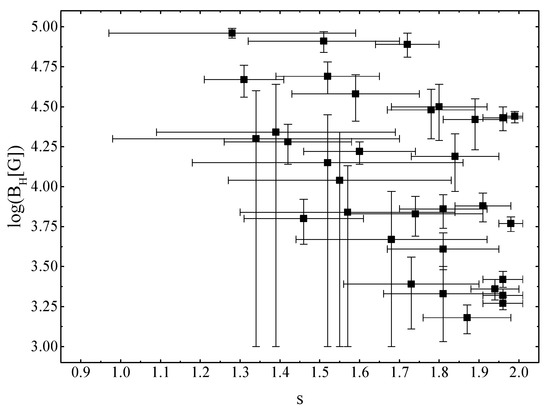
Figure 7.
The obtained values of the magnetic field intensity and the exponent of the power-law dependence s.
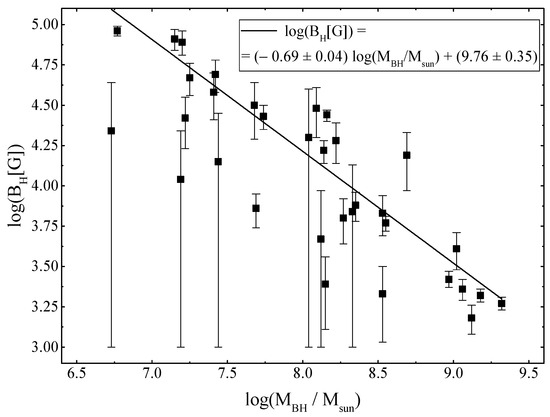
Figure 8.
Dependence of the magnetic field intensity on the mass of the SMBH .
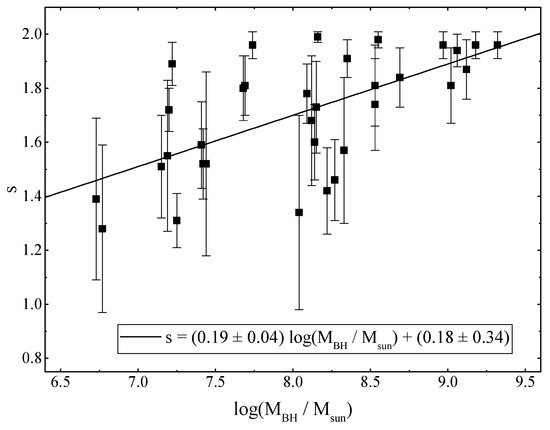
Figure 9.
Dependence of the exponent of the power-law dependence s on the SMBH mass .
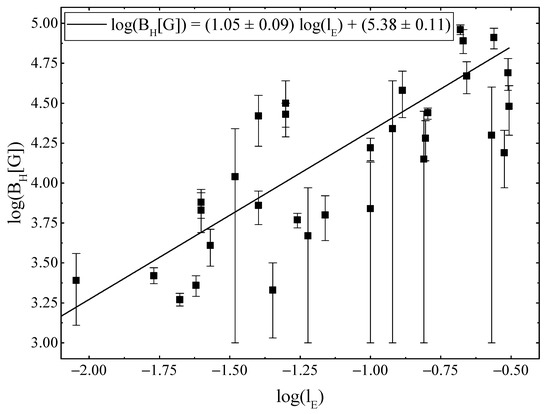
Figure 10.
Dependence of the magnetic field intensity on the Eddington ratio .
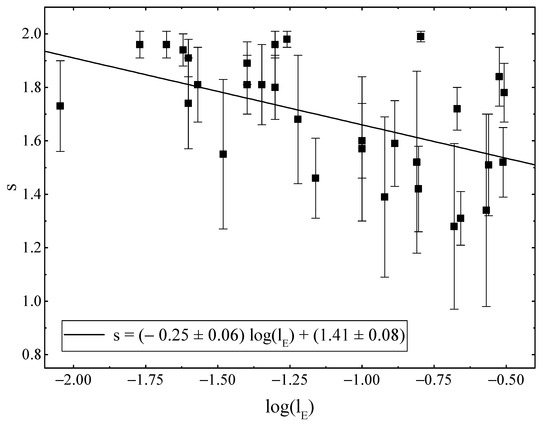
Figure 11.
Dependence of the exponent of the power-law dependence s on the Eddington ratio .
The histograms in Figure 12 and Figure 13 show the distributions of objects by the values and s. It should be noted that these histograms cannot be regarded as a source of completely accurate statistical data due to the limited number of objects. Our results are only estimates. It can be seen that, for the magnetic field, the peak of the distribution falls on the region . For comparison, we can mention that in our work Piotrovich et al. [37] the peak of the distribution was in the region of . This statistical difference is most likely due to the low statistics in current study. In general, these results are consistent with results from Daly [38].
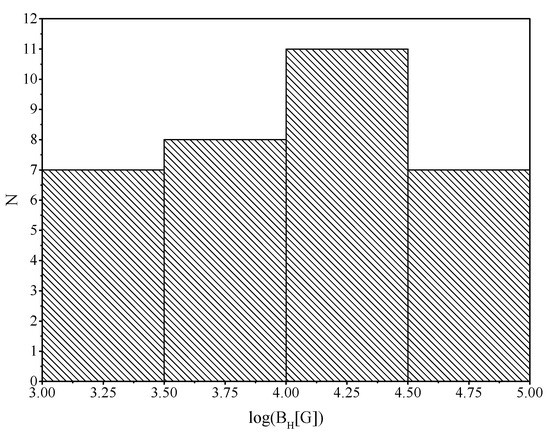
Figure 12.
A histogram showing the number of objects with a certain value.
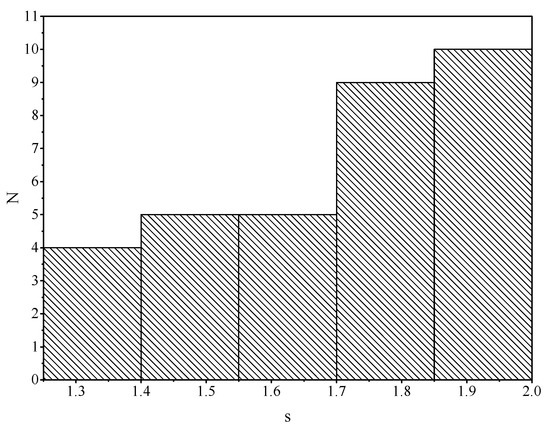
Figure 13.
A histogram showing the number of objects with a certain s value.
As for the parameter s, the peak of the distribution is in the region of , which is quite interesting, given that, as mentioned earlier, the standard value of s for accretion disks of the Shakura–Sunyaev type is usually considered to be 5/4 [19].
Table 3 presents the main statistical properties of the parameters of our model and the results of our calculations. The statistical properties of were found to be close to the values from Piotrovich et al. [37] and Daly [38].

Table 3.
Basic statistical properties of the parameters. “Mean” indicates the arithmetic mean, “Median” the median value, “SD” the standard deviation.
6. Conclusions
Based on the spectropolarimetric data of 33 Seyfert type 1 galaxies obtained with the BTA-6m telescope of the Special Astrophysical Observatory, estimates of the values of magnetic fields at the event horizon of the SMBHs and the values of the exponents of the power-law dependence s of the magnetic field on the radius , where is the radius of the event horizon.
The average value of was found to be ∼4, which is in good agreement with the results obtained by other methods [37,38], in which the magnetic field strength was estimated using the physical parameters of the relativistic jets. It was possible to reveal the dependence of the magnetic field on the SMBHs mass and the Eddington ratio of the form and , which agree well with the results of Piotrovich et al. [37].
The average value of s is , and the maximum distribution over s is within . This is a rather interesting result, since is usually taken in calculations for accretion disks in type 1 Seyfert nuclei. We also managed to estimate the dependence of s on the SMBHs mass and the Eddington ratio of the form and . In addition, although these approximations have a larger error than in the case of , they are still of interest. In particular, it may indicate that the more complex disk models are required than the Shakura–Sunyaev model. This problem undoubtedly requires further study.
In addition, for two objects PG 1545+210 and 2MASX J06021107+2828382, the measured polarization value was found to be greater than the maximum possible value at the inclination angle between the line of sight and the axis of the accretion disk . Since the polarization increases with the angle, it was concluded that for these objects the angle should be closer to .
Author Contributions
Conceptualization, M.P.; methodology, M.P.; validation, M.P.; formal analysis, M.P., S.B. and T.N.; investigation, S.B. and T.N.; resources, S.B. and T.N.; data curation, S.B. and T.N.; writing—original draft preparation, M.P.; writing—review and editing, M.P.; visualization, M.P.; supervision, M.P.; project administration, M.P.; funding acquisition, M.P. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the grant of Russian Science Foundation project number 20-12-00030 “Investigation of geometry and kinematics of ionized gas in active galactic nuclei by polarimetry methods”. Observations with the SAO RAS telescope are supported by the Ministry of Science and Higher Education of the Russian Federation (including agreement No.05.619.21.0016, project IDRFMEFI61919X0016).
Data Availability Statement
The data underlying this article are available in the article.
Acknowledgments
The authors are grateful to the employees of the Special Astrophysical Observatory V.L. Afanasiev (deceased 21 December 2020) and E.S. Shablovinskaya for help in carrying out observations and processing the results and the employee of the Central Astronomical Observatory at Pulkovo N.A. Silant’ev for useful comments and advice. The authors are also grateful to the reviewers for useful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blaes, O.M. Course 3: Physics Fundamentals of Luminous Accretion Disks around Black Holes. In Accretion Discs, Jets and High Energy Phenomena in Astrophysics; Beskin, V., Henri, G., Menard, F., Pelletier, G., Dalibard, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 78, pp. 137–185. [Google Scholar]
- Moran, J.M. The Black-Hole Accretion Disk in NGC 4258: One of Nature’s Most Beautiful Dynamical Systems. In Frontiers of Astrophysics: A Celebration of NRAO’s 50th Anniversary; Bridle, A.H., Condon, J.J., Hunt, G.C., Eds.; Astronomical Society of the Pacific Conference Series; National Radio Astronomy Observatory: Charlottesville, VA, USA, 2008; Volume 395, p. 87. [Google Scholar]
- Moderski, R.; Sikora, M.; Lasota, J.P. On Black Hole Spins and Dichotomy of Quasars. In Relativistic Jets in AGNs; Ostrowski, M., Sikora, M., Madejski, G., Begelman, M., Eds.; Jagiellonian University: Krakow, Poland, 1997; pp. 110–116. [Google Scholar]
- Li, L.X. Accretion Disk Torqued by a Black Hole. Astrophys. J. 2002, 567, 463–476. [Google Scholar] [CrossRef]
- Wang, D.X.; Xiao, K.; Lei, W.H. Evolution characteristics of the central black hole of a magnetized accretion disc. Mon. Not. R. Astron. Soc. 2002, 335, 655–664. [Google Scholar] [CrossRef]
- Wang, D.X.; Ma, R.Y.; Lei, W.H.; Yao, G.Z. Magnetic Coupling of a Rotating Black Hole with Its Surrounding Accretion Disk. Astrophys. J. 2003, 595, 109–119. [Google Scholar] [CrossRef]
- Zhang, W.M.; Lu, Y.; Zhang, S.N. The Black Hole Mass and Magnetic Field Correlation in Active Galactic Nuclei. Chin. J. Astron. Astrophys. Suppl. 2005, 5, 347–352. [Google Scholar] [CrossRef][Green Version]
- Ma, R.Y.; Yuan, F.; Wang, D.X. Influence of the Magnetic Coupling Process on Advection-dominated Accretion Flows around Black Holes. Astrophys. J. 2007, 671, 1981–1989. [Google Scholar] [CrossRef][Green Version]
- Martin, P.G.; Thompson, I.B.; Maza, J.; Angel, J.R.P. The polarization of Seyfert galaxies. Astrophys. J. 1983, 266, 470–478. [Google Scholar] [CrossRef]
- Webb, W.; Malkan, M.; Schmidt, G.; Impey, C. The Wavelength Dependence of Polarization of Active Galaxies and Quasars. Astrophys. J. 1993, 419, 494. [Google Scholar] [CrossRef]
- Impey, C.D.; Malkan, M.A.; Webb, W.; Petry, C.E. Ultraviolet Spectropolarimetry of High-Redshift Quasars with the Hubble Space Telescope. Astrophys. J. 1995, 440, 80. [Google Scholar] [CrossRef]
- Wilkes, B.J.; Schmidt, G.D.; Smith, P.S.; Mathur, S.; McLeod, K.K. Optical Detection of the Hidden Nuclear Engine in NGC 4258. Astrophys. J. Lett. 1995, 455, L13. [Google Scholar] [CrossRef][Green Version]
- Barth, A.J.; Tran, H.D.; Brotherton, M.S.; Filippenko, A.V.; Ho, L.C.; van Breugel, W.; Antonucci, R.; Goodrich, R.W. Polarized Narrow-Line Emission from the Nucleus of NGC 4258. Astron. J. 1999, 118, 1609–1617. [Google Scholar] [CrossRef]
- Smith, J.E.; Young, S.; Robinson, A.; Corbett, E.A.; Giannuzzo, M.E.; Axon, D.J.; Hough, J.H. A spectropolarimetric atlas of Seyfert 1 galaxies. Mon. Not. R. Astron. Soc. 2002, 335, 773–798. [Google Scholar] [CrossRef][Green Version]
- Modjaz, M.; Moran, J.M.; Kondratko, P.T.; Greenhill, L.J. Probing the Magnetic Field at Subparsec Radii in the Accretion Disk of NGC 4258. Astrophys. J. 2005, 626, 104–119. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Borisov, N.V.; Gnedin, Y.N.; Natsvlishvili, T.M.; Piotrovich, M.Y.; Buliga, S.D. Spectropolarimetric observations of active galactic nuclei with the 6-m BTA telescope. Astron. Lett. 2011, 37, 302–310. [Google Scholar] [CrossRef][Green Version]
- Afanasiev, V.L.; Gnedin, Y.N.; Piotrovich, M.Y.; Natsvlishvili, T.M.; Buliga, S.D. Determination of Supermassive Black Hole Spins Based on the Standard Shakura–Sunyaev Accretion Disk Model and Polarimetric Observations. Astron. Lett. 2018, 44, 362–369. [Google Scholar] [CrossRef]
- Pariev, V.I.; Blackman, E.G.; Boldyrev, S.A. Extending the Shakura–Sunyaev approach to a strongly magnetized accretion disc model. Astron. Astrophys. 2003, 407, 403–421. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Gnedin, Y.N.; Buliga, S.D.; Silant’ev, N.A.; Natsvlishvili, T.M.; Piotrovich, M.Y. Topology of magnetic field and polarization in accretion discs of AGN. Astrophys. Space Sci. 2012, 342, 137–145. [Google Scholar] [CrossRef]
- Baczko, A.K.; Schulz, R.; Kadler, M.; Ros, E.; Perucho, M.; Krichbaum, T.P.; Böck, M.; Bremer, M.; Grossberger, C.; Lindqvist, M.; et al. A highly magnetized twin-jet base pinpoints a supermassive black hole. Astron. Astrophys. 2016, 593, A47. [Google Scholar] [CrossRef]
- Silant’ev, N.A.; Piotrovich, M.Y.; Gnedin, Y.N.; Natsvlishvili, T.M. Magnetic fields of AGNs and standard accretion disk model: Testing by optical polarimetry. Astron. Astrophys. 2009, 507, 171–182. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Sobolev, V.V. A Treatise on Radiative Transfer; Van Nostrand: Princeton, NJ, USA, 1963. [Google Scholar]
- Gnedin, Y.N.; Piotrovich, M.Y.; Silant’ev, N.A.; Natsvlishvili, T.M.; Buliga, S.D. Polarization of Radiation and Basic Parameters of the Circumnuclear Region of Active Galactic Nuclei. Astrophysics 2015, 58, 443–452. [Google Scholar] [CrossRef]
- Poindexter, S.; Morgan, N.; Kochanek, C.S. The Spatial Structure of an Accretion Disk. Astrophys. J. 2008, 673, 34–38. [Google Scholar] [CrossRef]
- Inoue, Y.; Doi, A. Detection of Coronal Magnetic Activity in nearby Active Supermassive Black Holes. Astrophys. J. 2018, 869, 114. [Google Scholar] [CrossRef]
- Trakhtenbrot, B. The Most Massive Active Black Holes at z ~ 1.5–3.5 have High Spins and Radiative Efficiencies. Astrophys. J. Lett. 2014, 789, L9. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Silant’ev, N.A.; Gnedin, Y.N.; Natsvlishvili, T.M.; Buliga, S.D. The magnetic-field structure in a stationary accretion disk. Astron. Rep. 2016, 60, 486–497. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Silant’Ev, N.A.; Piotrovich, M.Y.; Pogodin, M.A. Polarization Effects in the Radiation of Magnetized Envelopes and Extended Accretion Structures. Astron. Rep. 2005, 49, 179–189. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Popović, L.Č.; Shapovalova, A.I. Spectropolarimetry of Seyfert 1 galaxies with equatorial scattering: Black hole masses and broad-line region characteristics. Mon. Not. R. Astron. Soc. 2019, 482, 4985–4999. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Moiseev, A.V. The SCORPIO Universal Focal Reducer of the 6-m Telescope. Astron. Lett. 2005, 31, 194–204. [Google Scholar] [CrossRef]
- Turnshek, D.A.; Bohlin, R.C.; Williamson, R.L.I.; Lupie, O.L.; Koornneef, J.; Morgan, D.H. An Atlas of Hubble Space Telescope Photometric, Spectrophotometric, and Polarimetric Calibration Objects. Astron. J. 1990, 99, 1243. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Moiseev, A.V. Scorpio on the 6 m Telescope: Current State and Perspectives for Spectroscopy of Galactic and Extragalactic Objects. Balt. Astron. 2011, 20, 363–370. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Amirkhanyan, V.R. Technique of polarimetric observations of faint objects at the 6-m BTA telescope. Astrophys. Bull. 2012, 67, 438–452. [Google Scholar] [CrossRef]
- Netzer, H.; Trakhtenbrot, B. Bolometric luminosity black hole growth time and slim accretion discs in active galactic nuclei. Mon. Not. R. Astron. Soc. 2014, 438, 672–679. [Google Scholar] [CrossRef][Green Version]
- Piotrovich, M.Y.; Mikhailov, A.G.; Buliga, S.D.; Natsvlishvili, T.M. Determination of magnetic field strength on the event horizon of supermassive black holes in active galactic nuclei. Mon. Not. R. Astron. Soc. 2020, 495, 614–620. [Google Scholar] [CrossRef]
- Daly, R.A. Black Hole Spin and Accretion Disk Magnetic Field Strength Estimates for More Than 750 Active Galactic Nuclei and Multiple Galactic Black Holes. Astrophys. J. 2019, 886, 37. [Google Scholar] [CrossRef]
- Wu, X.B.; Han, J.L. Inclinations and Black Hole Masses of Seyfert 1 Galaxies. Astrophys. J. Lett. 2001, 561, L59–L62. [Google Scholar] [CrossRef]
- Vestergaard, M.; Peterson, B.M. Determining Central Black Hole Masses in Distant Active Galaxies and Quasars. II. Improved Optical and UV Scaling Relationships. Astrophys. J. 2006, 641, 689–709. [Google Scholar] [CrossRef]
- Peterson, B.M.; Ferrarese, L.; Gilbert, K.M.; Kaspi, S.; Malkan, M.A.; Maoz, D.; Merritt, D.; Netzer, H.; Onken, C.A.; Pogge, R.W.; et al. Central Masses and Broad-Line Region Sizes of Active Galactic Nuclei. II. A Homogeneous Analysis of a Large Reverberation-Mapping Database. Astrophys. J. 2004, 613, 682–699. [Google Scholar] [CrossRef]
- Satyapal, S.; Dudik, R.P.; O’Halloran, B.; Gliozzi, M. The Link between Star Formation and Accretion in LINERs: A Comparison with Other Active Galactic Nucleus Subclasses. Astrophys. J. 2005, 633, 86–104. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Globina, V.N.; Piotrovich, M.Y.; Buliga, S.D.; Natsvlishvili, T.M. Spins of Supermassive Black Holes and the Magnetic Fields of Accretion Disks in Active Galactic Nuclei with Maser Emission. Astrophysics 2014, 57, 163–175. [Google Scholar] [CrossRef]
- Piotrovich, M.; Gnedin, Y.; Natsvlishvili, T.; Buliga, S. Estimates of supermassive black hole (SMBH) spins for the standard accretion disk model: Comparison with relativistic fitting of SMBH spectra. New Astron. 2018, 65, 25–28. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Gnedin, Y.N.; Natsvlishvili, T.M.; Buliga, S.D. Constraints on spin of a supermassive black hole in quasars with big blue bump. Astrophys. Space Sci. 2017, 362, 231. [Google Scholar] [CrossRef][Green Version]
- Marin, F. Are there reliable methods to estimate the nuclear orientation of Seyfert galaxies? Mon. Not. R. Astron. Soc. 2016, 460, 3679–3705. [Google Scholar] [CrossRef]
- Devereux, N. The dynamics of the broad-line region in NGC 3227. Mon. Not. R. Astron. Soc. 2021, 500, 786–794. [Google Scholar] [CrossRef]
- Savić, D.; Goosmann, R.; Popović, L.Č.; Marin, F.; Afanasiev, V.L. AGN black hole mass estimates using polarization in broad emission lines. Astron. Astrophys. 2018, 614, A120. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).