New Anisotropic Exact Solution in Multifield Cosmology
Abstract
:1. Introduction
2. Chiral Cosmology
Anisotropic Spacetime
3. Exact Solution
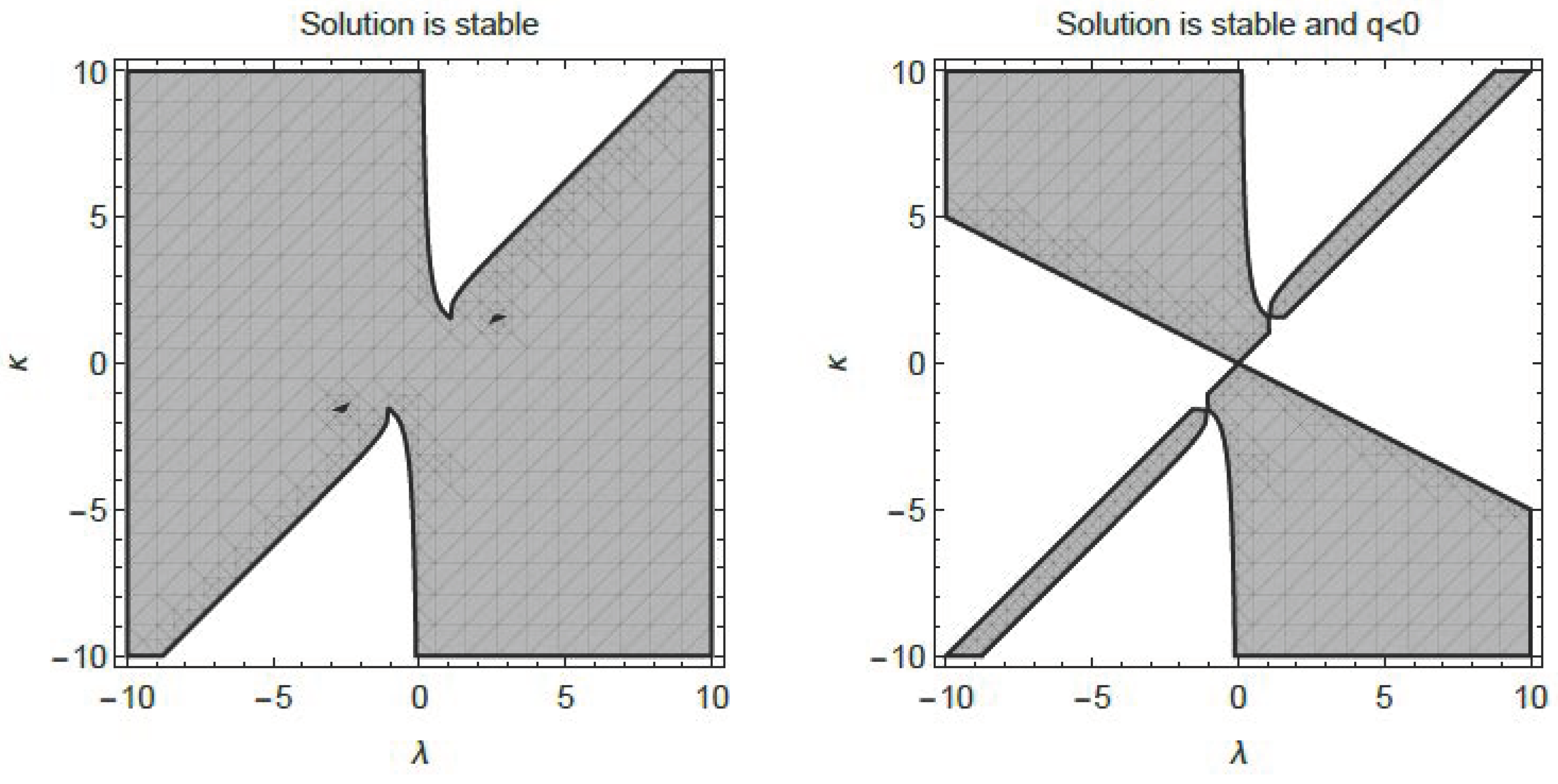
4. Stability Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guth, A. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef] [Green Version]
- Saadeh, D.; Feeney, S.; Pontzen, A.; Peiris, H.; McEwen, J.D. How isotropic is the Universe? Phys. Rev. Lett. 2016, 117, 131302. [Google Scholar] [CrossRef]
- Goldwirth, D.S. Inhomogeneous initial conditions for inflation. Phys. Rev. D 1991, 43, 3204–3213. [Google Scholar] [CrossRef]
- Clough, K.; Lim, E.A.; Di Nunno, B.S.; Fischler, W.; Flauger, R.; Paban, S. Robustness of Inflation to Inhomogeneous Initial Conditions. J. Cosmol. Astropart. Phys. 2017, 2017, 025. [Google Scholar] [CrossRef] [Green Version]
- Ellis, G.F.R.; Madsen, M.S. Exact scalar field cosmologies. Class. Quantum Gravity 1991, 8, 667–676. [Google Scholar] [CrossRef]
- Ram, B. Infinitely many solutions of Einstein cosmology in ’slow roll’. Phys. Lett. A 1993, 172, 404–406. [Google Scholar] [CrossRef]
- Barrow, J.D.; Saich, P. Scalar field cosmologies. Class. Quantum Gravity 1993, 10, 297. [Google Scholar] [CrossRef]
- Maartens, R.; Taylor, D.R.; Roussos, N. Exact inflationary cosmologies with exit. Phys. Rev. D 1995, 52, 3358. [Google Scholar] [CrossRef]
- Barrow, J.D.; Paliathanasis, A. Observational Constraints on New Exact Inflationary Scalar-field Solutions. Phys. Rev. D 2016, 94, 083518. [Google Scholar] [CrossRef] [Green Version]
- Chimento, L.P.; Jakubi, A.S. Scalar field cosmologies with perfect fluid in robertson-walker metric. Int. J. Mod. Phys. D 1996, 5, 71. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, N.; Sen, S. Power law inflation and scalar field cosmology with a causal viscous fluid. Phys. Rev. D 1998, 57, 4614–4619. [Google Scholar] [CrossRef]
- Chimento, L.P.; Mendez, V.; Zuccala, N. Cosmological models arising from generalized scalar field potentials. Class. Quantum Gravity 1999, 16, 3749–3763. [Google Scholar] [CrossRef]
- Kruger, A.T.; Norburry, J.W. Another exact inflationary solution. Phys. Rev. D 2000, 61, 087303. [Google Scholar] [CrossRef] [Green Version]
- Andrianov, A.A.; Cannata, F.; Kamenshchik, A.Y. General solution of scalar field cosmology with a (piecewise) exponential potential. J. Cosmol. Astropart. Phys. 2011, 10, 004. [Google Scholar] [CrossRef] [Green Version]
- Demianski, M.; de Ritis, R.; Rubano, C.; Scudellaro, P. Scalar fields and anisotropy in cosmological models. Phys. Rev. D 1992, 46, 1391–1398. [Google Scholar] [CrossRef]
- Chimento, L.P.; Cossarini, A.E.; Zuccala, N.A. Isotropic and anisotropic N-dimensional cosmologies with exponential potentials. Class. Quantum Gravity 1998, 15, 57–74. [Google Scholar] [CrossRef]
- Fadragas, C.R.; Leon, G.; Saridakis, E.N. Dynamical analysis of anisotropic scalar-field cosmologies for a wide range of potentials. Class. Quantum Gravity 2014, 31, 075018. [Google Scholar] [CrossRef] [Green Version]
- Tsamparlis, M.; Paliathanasis, A. The geometric nature of Lie and Noether symmetries. Gen. Relativ. Gravit. 2011, 43, 1861. [Google Scholar] [CrossRef]
- Christodoulakis, T.; Grammenos, T.; Helias, C.; Kevrekidis, P.G.; Spanou, A. Decoupling of the general scalar field mode and the solution space for Bianchi type I and V cosmologies coupled to perfect fluid sources. J. Math. Phys. 2006, 47, 042505. [Google Scholar] [CrossRef] [Green Version]
- Do, T.Q.; Kao, W.F. Anisotropic power-law inflation for a model of two scalar and two vector fields. Eur. Phys. J. C 2021, 81, 525. [Google Scholar] [CrossRef]
- Faraoni, V.; Jose, S.; Dussault, S. Multi-fluid cosmology in Einstein gravity: Analytical solutions. arXiv 2021, arXiv:2107.12488. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Saridakis, E.; Setare, M.R.; Xia, J.-Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef] [Green Version]
- Coley, A.A.; Hoogen, R.V.D. The Dynamics of Multi-Scalar Field Cosmological Models and Assisted Inflation. Phys. Rev. D 2000, 92, 023517. [Google Scholar] [CrossRef] [Green Version]
- Calcagni, G.; Liddle, A.R. Stability of multifield cosmological solutions. Phys. Rev. D 2008, 77, 023522. [Google Scholar] [CrossRef] [Green Version]
- Collinucci, A.; Nielsen, M.; Van Riet, T. Scalar cosmology with multi-exponential potentials. Class. Quantum Gravity 2005, 22, 1269–1287. [Google Scholar] [CrossRef]
- Paliathanasis, A. Dynamics of Chiral Cosmology. Class. Quantum Gravity 2020, 37, 195014. [Google Scholar] [CrossRef]
- Christodoulidis, P.; Paliathanasis, A. N-field cosmology in hyperbolic field space: Stability and general solutions. J. Cosmol. Astropart. Phys. 2021, 5, 038. [Google Scholar] [CrossRef]
- Christodoulidis, P. General solutions to N-field cosmology with exponential potentials. Eur. Phys. J. C 2021, 81, 471. [Google Scholar] [CrossRef]
- Socorro, J.; Pérez-Payán, S.; Hernández, R.; Espinoza-García, A.; Díaz-Barrón, L.R. Classical and quantum exact solutions for a FRW in chiral like cosmology. Class. Quantum Gravity 2021, 38, 135027. [Google Scholar] [CrossRef]
- Socorro, J.; Nuñez, O.E. Scalar potentials with multi-scalar fields from quantum cosmology and supersymmetric quantum mechanics. Eur. Phys. J. Plus 2017, 132, 168. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Barrón, L.R.; Espinoza-García, A.; Pérez-Payán, S.; Socorro, J. Anisotropic chiral cosmology: Exact solutions. Int. J. Mod. Phys. D. 2021, in press. [Google Scholar] [CrossRef]
- Ketov, S.V. Quantum Non-linear Sigma Models; Springer: Berlin, Germany, 2000. [Google Scholar]
- Chervon, S.V. Chiral Cosmological Models: Dark Sector Fields Description. Quantum Matter 2013, 2, 71–82. [Google Scholar] [CrossRef]
- Brown, A.R. Hyperbolic Inflation. Phys. Rev. Lett. 2018, 121, 251601. [Google Scholar] [CrossRef] [Green Version]
- Mizuno, S.; Mukohyama, S. Primordial perturbations from inflation with a hyperbolic field-space. Phys. Rev. D 2017, 96, 103533. [Google Scholar] [CrossRef] [Green Version]
- Lyth, D.H. A numerical study of non-gaussianity in the curvaton scenario. J. Cosmol. Astropart. Phys. 2006, 2006, 008. [Google Scholar]
- Langlois, D.; Renaux-Peterl, S. Perturbations in generalized multi-field inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 017. [Google Scholar] [CrossRef] [Green Version]
- Christodoulidis, P.; Roest, D.; Sfakianakis, E.I. Scaling attractors in multi-field inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 059. [Google Scholar] [CrossRef] [Green Version]
- Christodoulidis, P.; Roest, D.; Sfakianakis, E.I. Angular inflation in multi-field α-attractors. J. Cosmol. Astropart. Phys. 2019, 2019, 002. [Google Scholar] [CrossRef] [Green Version]
- Paliathanasis, A.; Tsamparlis, M. Two scalar field cosmology: Conservation laws and exact solutions. Phys. Rev. D 2014, 90, 103524. [Google Scholar] [CrossRef] [Green Version]
- Giacomini, A.; Gonzalez, E.; Leon, G.; Paliathanasis, A. Variational symmetries and superintegrability in multifield cosmology. arXiv 2021, arXiv:2104.13649. [Google Scholar]
- Paliathanasis, A.; Leon, G. Dynamics of a two scalar field cosmological model with phantom terms. Class. Quantum Gravity 2021, 38, 075013. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. Symmetries of Differential Equations in Cosmology. Symmetry 2018, 10, 233. [Google Scholar] [CrossRef] [Green Version]
- Mendes, L.E.; Henriques, A. Inflation in a simple Kantowski–Sachs model. Phys. Lett. B 1991, 254, 44–48. [Google Scholar] [CrossRef]
- Gron, O. Expansion isotropization during the inflationary era. Phys. Rev. D 1985, 32, 2522–2527. [Google Scholar] [CrossRef] [PubMed]
- Liddle, A.R.; Parson, P.; Barrow, J.D. Formalising the Slow-Roll Approximation in Inflation. Phys. Rev. D 1994, 50, 7222–7232. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paliathanasis, A. New Anisotropic Exact Solution in Multifield Cosmology. Universe 2021, 7, 323. https://doi.org/10.3390/universe7090323
Paliathanasis A. New Anisotropic Exact Solution in Multifield Cosmology. Universe. 2021; 7(9):323. https://doi.org/10.3390/universe7090323
Chicago/Turabian StylePaliathanasis, Andronikos. 2021. "New Anisotropic Exact Solution in Multifield Cosmology" Universe 7, no. 9: 323. https://doi.org/10.3390/universe7090323
APA StylePaliathanasis, A. (2021). New Anisotropic Exact Solution in Multifield Cosmology. Universe, 7(9), 323. https://doi.org/10.3390/universe7090323





