Advanced Virgo: Status of the Detector, Latest Results and Future Prospects
Abstract
1. Introduction
2. Astrophysical Sources
3. A Brief Historical Background of Italian GW Research Infrastructures
4. The Advanced Virgo Detector
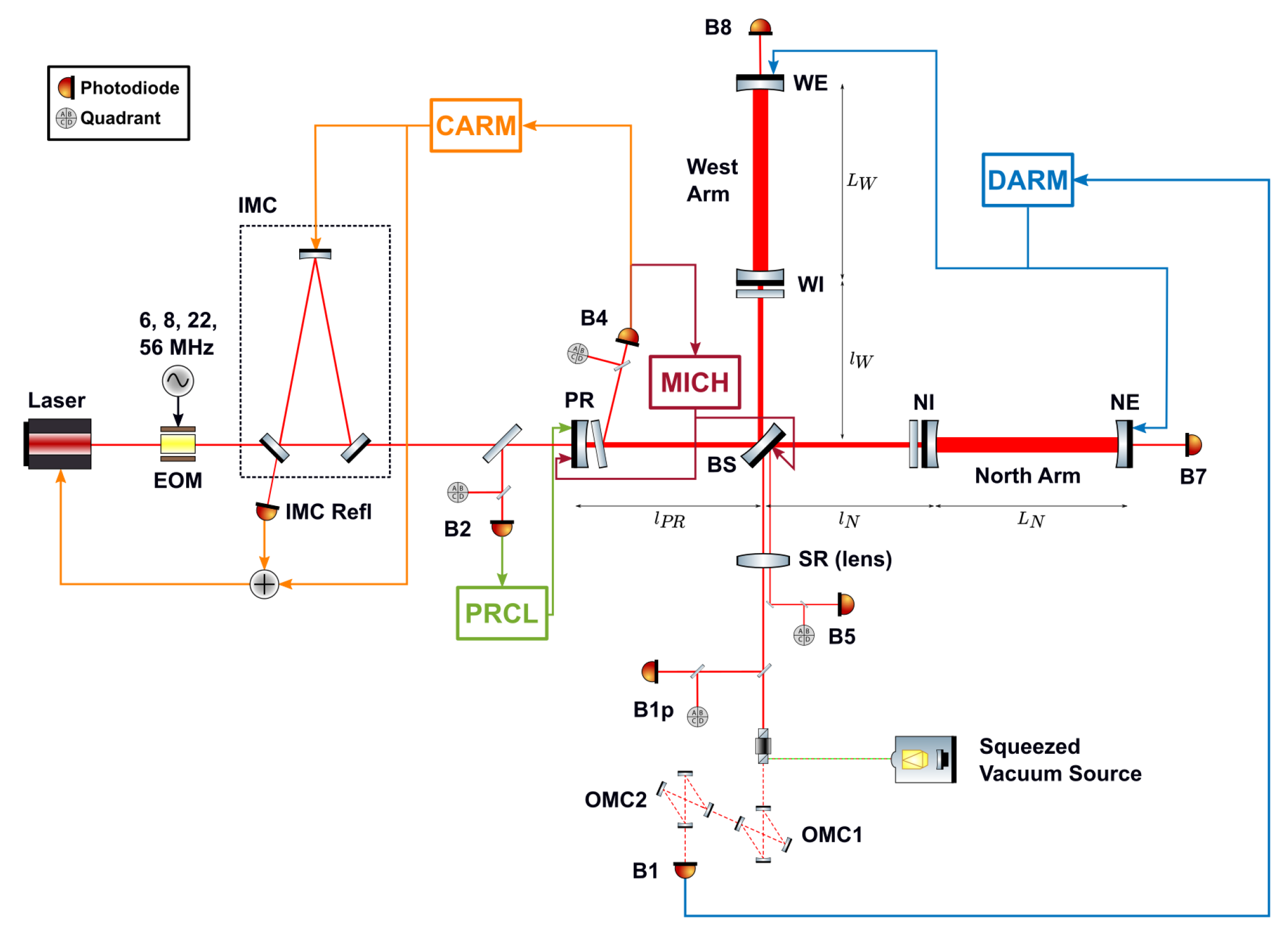
4.1. Optical Layout
- The Injection system (left part of Figure 2): here the main laser beam is generated, from a 1064 nm Nd:YAG laser source; such laser is pre-stabilized in both amplitude and frequency before actually being injected inside the interferometer, but other fundamental components are necessary at this stage. The main laser beam is passed through an Electro-Optical Modulator (EOM) which generates several radio-frequency sidebands for the carrier light, which are necessary for the Global Control of the interferometer (6 MHz, 8 MHz, and 56 MHz, cf. Section 4.3.1) or the control of the Injection system itself (22 MHz). Then, the laser beam (now carrier plus sidebands) is sent into a triangular resonant cavity, the Input Mode Cleaner (IMC), which serves the purpose of both cleaning the laser field from high order modes, in order to inject as much as possible in the interferometer only the TEM00 fundamental mode, and providing an additional stage of frequency stabilization. An additional short, rigid cavity (Reference Cavity, RFC) is used to control the IMC cavity length, such to provide an additional laser frequency stabilization also at low frequency. Then, the laser beam is injected in the main interferometer.
- The main interferometer (central and right part of Figure 2): it is composed by the seven main optics which form this enhanced Michelson configuration; in the middle, the Beam Splitter (BS) mirror equally splits the incoming light and sends it in the two arms of the interferometer. Differently from the standard Michelson interferometer, in Virgo the arms (North and West) are not composed by a single reflecting mirror at the end of each arm, but rather by a resonant Fabry-Pérot 3 km long cavity made by two highly reflective mirrors, with the reflecting sides facing one another. The use of Fabry-Pérot cavities makes so that the light can be trapped inside the arm for many round trips, before being reflected back or transmitted: this causes the big advantage that the effective arm length of the interferometer is amplified by a factor (where is the Finesse of the arm cavities), therefore increasing the detector sensitivity. Since the interferometer working point is dark fringe, this means that most of the light, once reflected by the arms and recombined by the BS mirror, is sent back toward the Injection system; therefore, a semi-reflective mirror is added between the Injection system and the Fabry-Pérot Michelson, in order to create with the latter another resonant cavity: this Power Recycling (PR) mirror reflects this rejected light back into the main interferometer, effectively increasing the circulating power of the laser field in the detector. With the same principle, but for a different outcome, a similar Signal Recycling (SR) mirror is added between the output port of the Fabry-Pérot Michelson and the main part of the Detection system: another resonant cavity is therefore present, with the purpose of recirculating the signal used for the detection, allowing shaping the sensitivity curve of the interferometer (see Section 7.1). However, this mirror has not been used in Advanced Virgo yet and it has been replaced by a simple lens; its full implementation is foreseen for the O4 Observing Run.
- The Detection system (bottom part of Figure 2 and outputs of the main resonant cavities): this is a more distributed system, but its main part is at the output of the main interferometer and deals with the collection, cleaning and the enhancement of the output beam after the recombination from the BS mirror, which is the signal used for the detection of gravitational waves. Such signal is passed through two Output Mode Cleaner (OMC) cavities: two monolithic, bow-tie shaped cavities, which provide the cleaning of the signal from any sideband field, as these are not necessary in the Advanced Virgo detection scheme [88]; the OMCs also provide an additional step of removal of high order modes. The beam is then collected by the main photodiode (B1). Several other photodiodes (PD) and quadrant photodiodes (QPD) are installed in the main output ports of the interferometer (B2 at the input port, B7 at North End, B8 at West End) or in the central area (B4 as a pick-off of the Power Recycling cavity, B1p as a pick-off of the output beam before the removal of the sidebands and B5 as a pick-off from the anti-reflective side of the BS mirror, sensitive mostly to the North Arm). All the PDs and QPDs (and the OMCs) are installed on under-vacuum, controlled Suspended Benches, in order to mitigate the effect of several sources of noise.
4.2. Technological Solutions for Advanced Virgo’s Sensitivity
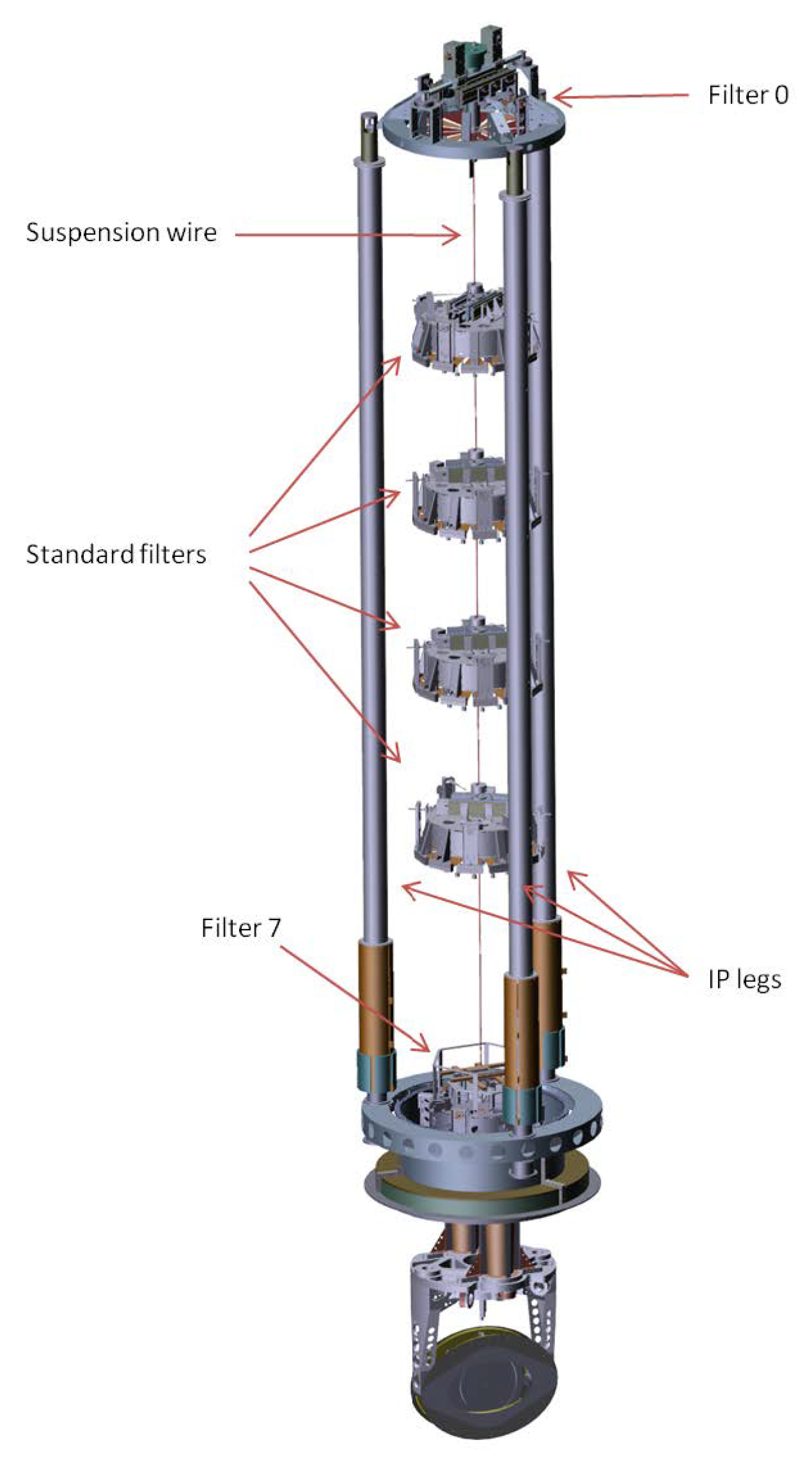
4.2.1. Low Frequency: Suspensions & Payloads
4.2.2. Mid-Frequency: Optics & Coatings
4.2.3. High Frequency: Laser & Squeezing
4.3. Interferometer Operation
4.3.1. Global Controls
- MICH = , it is the length difference of the short arms of the Michelson, and it defines the interference condition;
- PRCL = , it is the length of the Power Recycling cavity;
- CARM = , it is the average, common arm length of the long Fabry-Pérot cavities;
- DARM = , it is the differential arm length of the long Fabry-Pérot cavities; this degree of freedom is sensitive to the strain induced by the passage of a gravitational wave, so it is the most important of all and it ultimately determines the sensitivity of the interferometer.
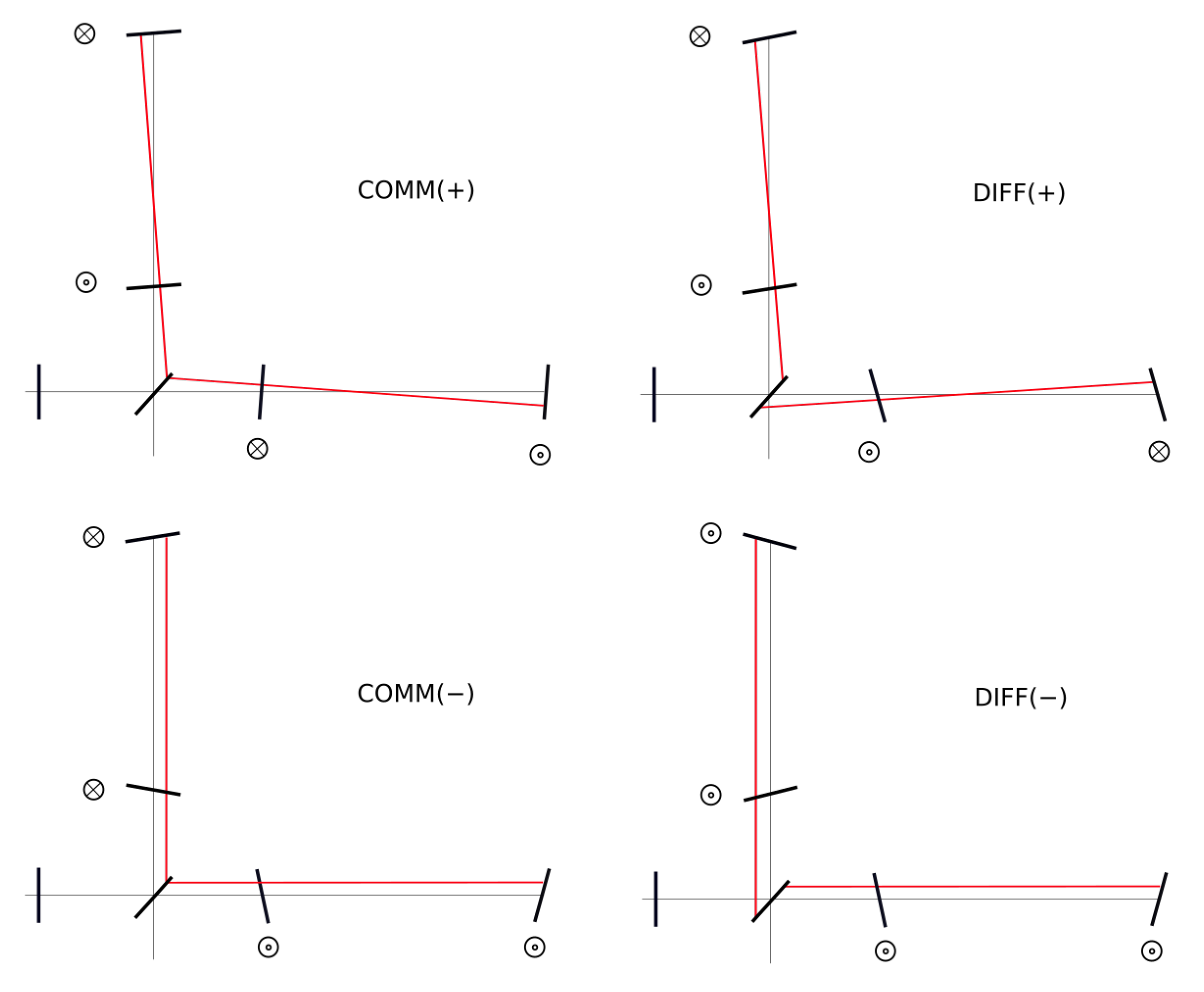
- COMM(+): common tilt of the arm cavities: the effect is two beams recombining in the same spot on the BS mirror;
- DIFF(+): differential tilt of the arm cavities: the effect is two spots recombining on the two opposite sides of the BS mirror;
- COMM(−): common shift of the arm cavities: the effect is two beams recombining in the same spot on the BS mirror;
- DIFF(−): differential shift of the arm cavities: the effect is two spots recombining on the two opposite sides of the BS mirror.
4.3.2. Thermal Compensation System
5. Performance of the Advanced Virgo Detector in the O3 Observing Run
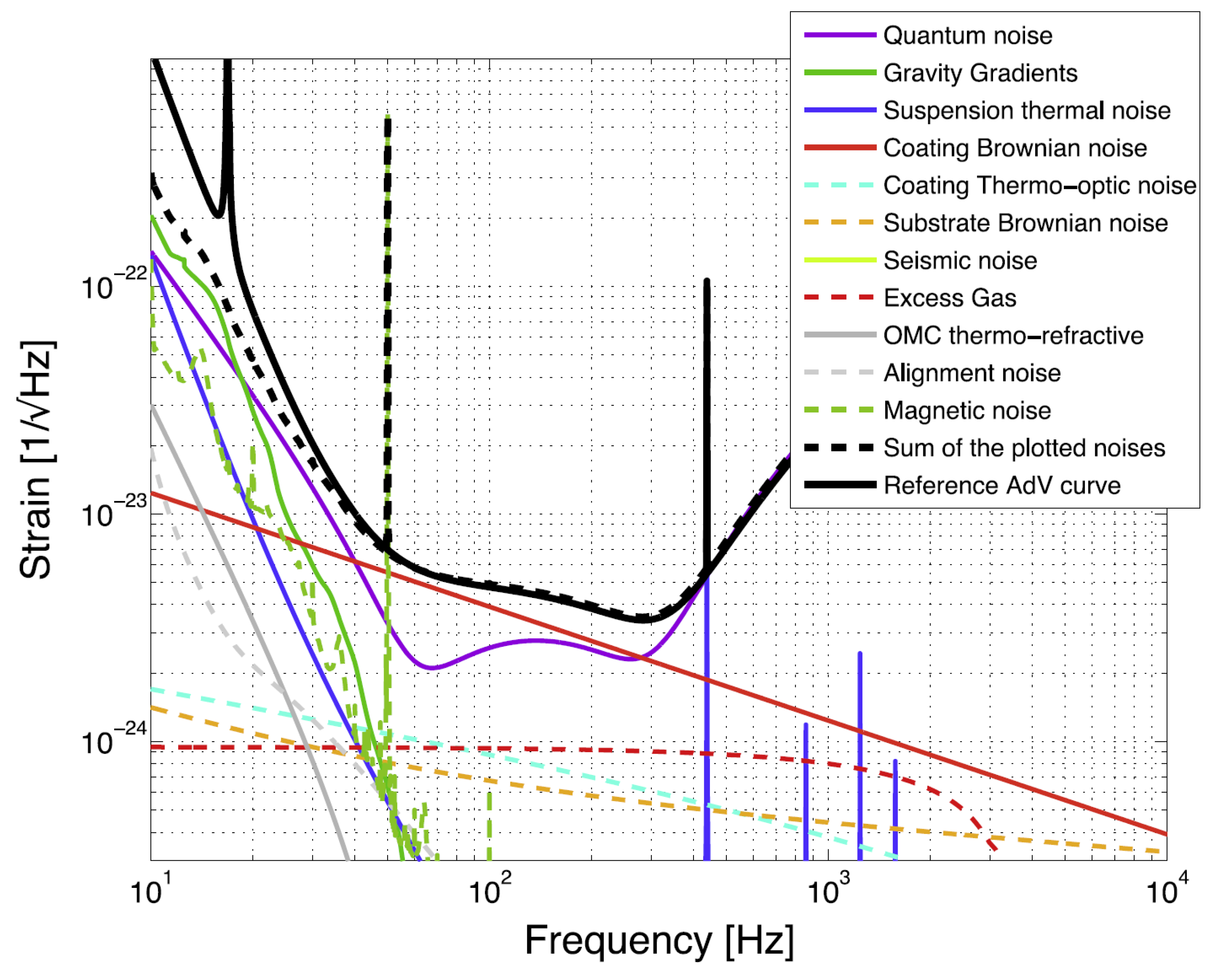
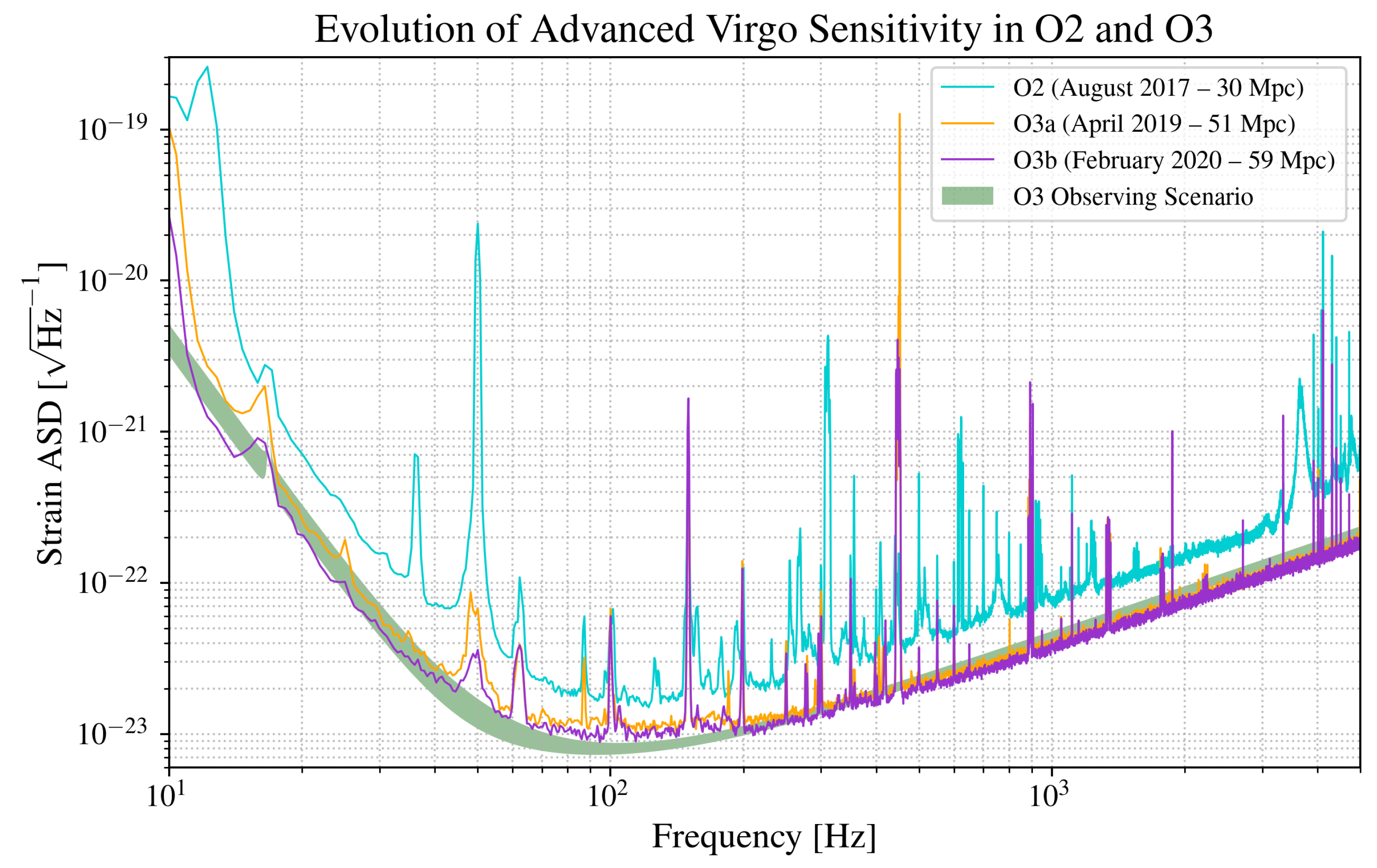
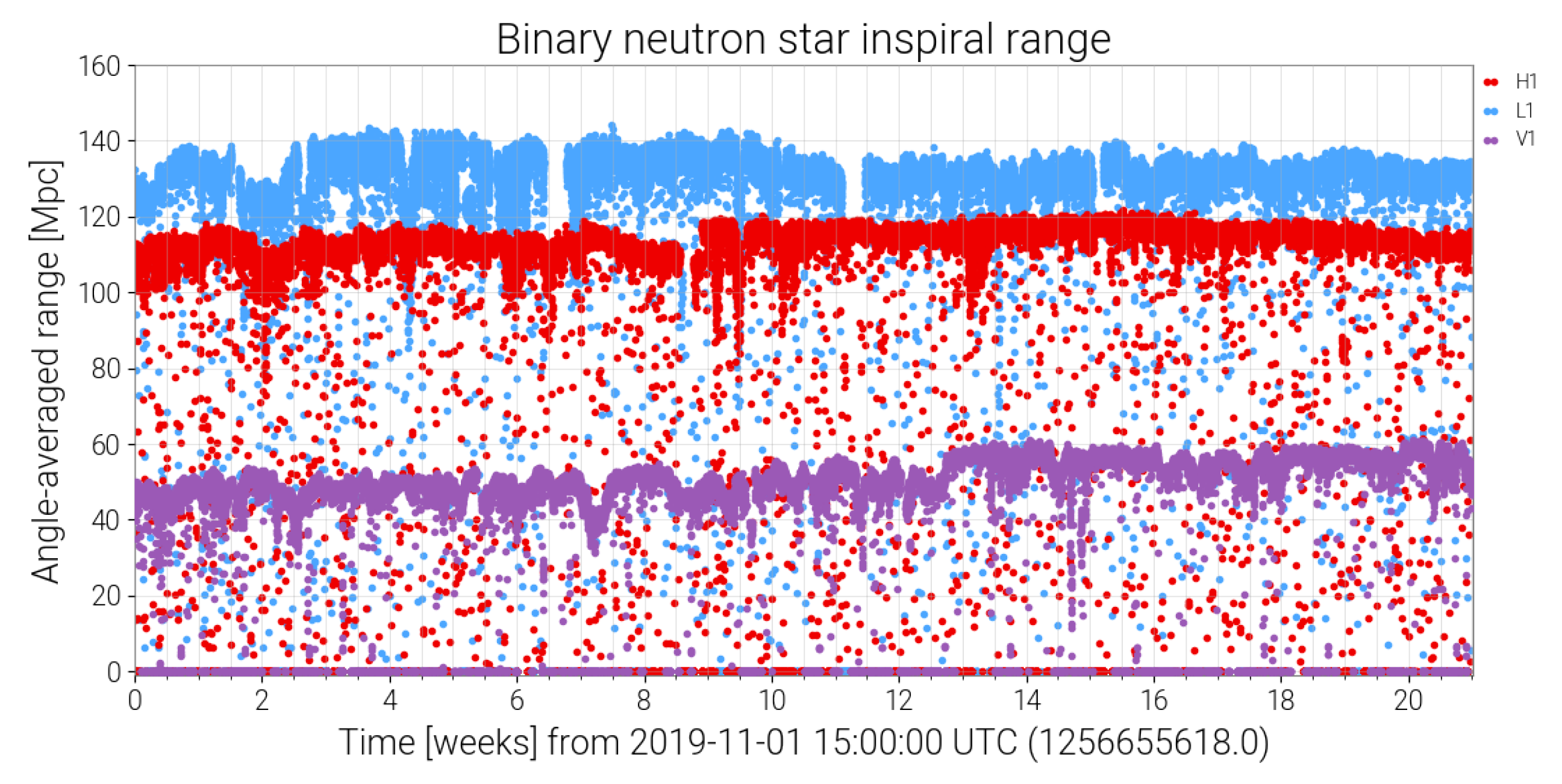
5.1. Noise and Performance in O3
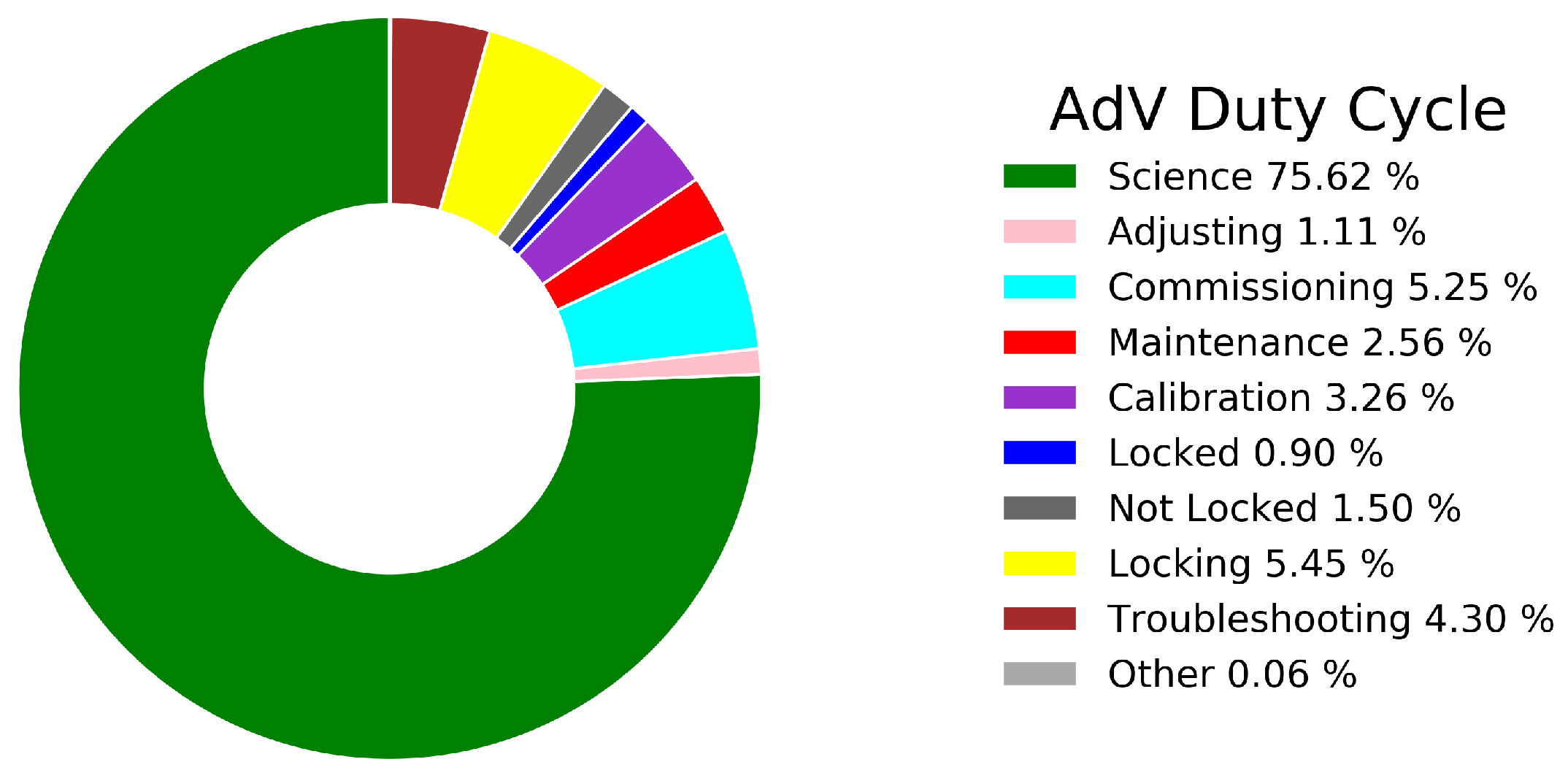
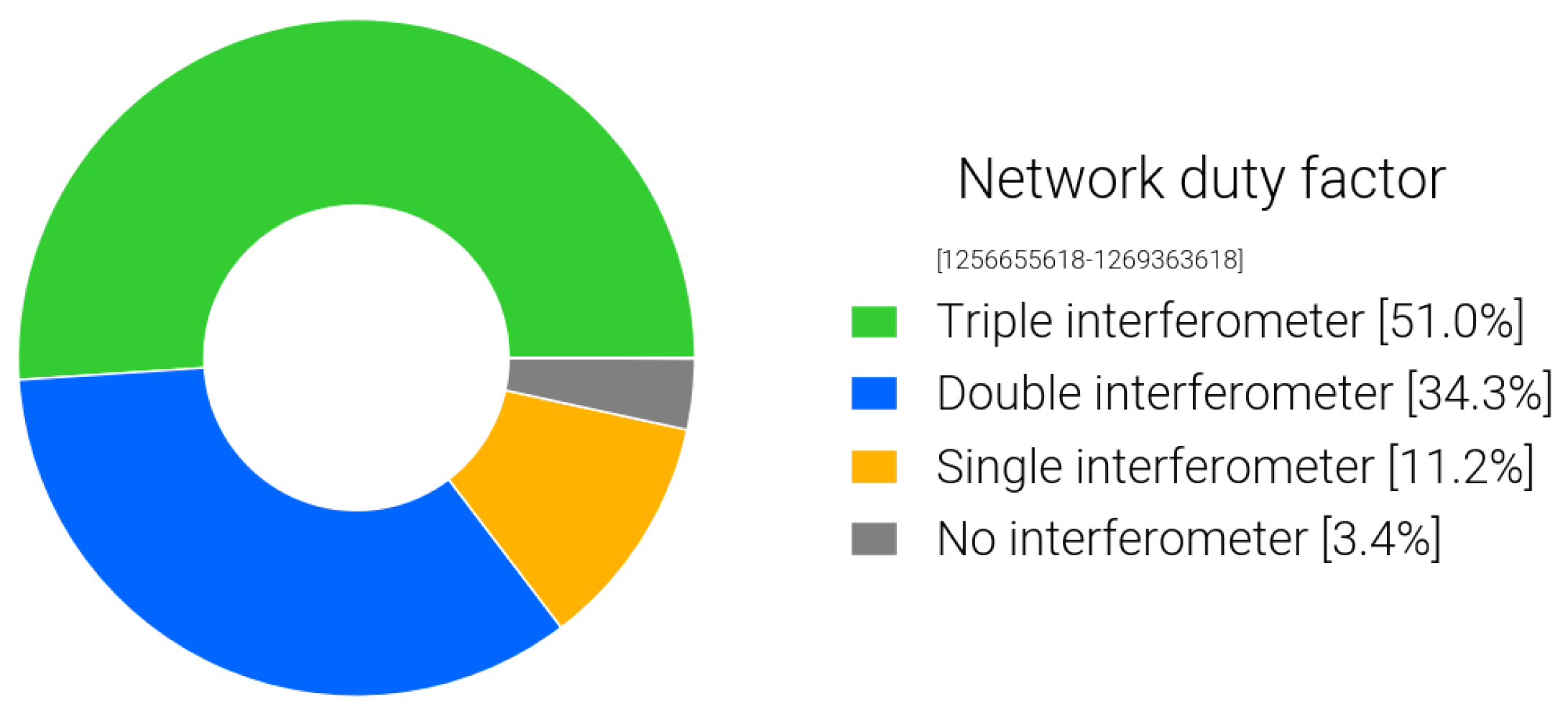
5.2. Data Quality
6. Data Analysis and Results
6.1. All-Sky GW Searches
6.2. Multi-Messenger Searches
6.3. Results
6.3.1. BH-BH/IMBH Detections
6.3.2. NS-BH Detections
6.3.3. NS-NS Detections and EM Counterparts
6.3.4. Tests of GR
6.3.5. Persistent Signals in O3
6.3.6. Dark Matter
6.3.7. Cosmic Strings
7. Future Prospects for Advanced Virgo Plus
7.1. AdV+ Phase I: The Upgrades for the Next Observing Run
- broadband configuration: the Signal Recycling Cavity has a detuning ; both the carrier and the sidebands are resonant in the SRC; the Reflectivity of the compound mirror is high, so the cavity Finesse is high and the cavity pole is moved to lower frequencies;
- tuned configuration: the Signal Recycling Cavity has a detuning ; the carrier is not resonant in the SRC, while the sidebands are; the Reflectivity of the compound mirror is low, so the cavity Finesse is low and the cavity pole is moved to higher frequencies;
- detuned configuration: the Signal Recycling Cavity is in an intermediate configuration, where ; here there is a single frequency where the detuning is equal to the round trip phase, resulting in a peaked response of the interferometer at a single frequency.
7.2. AdV+ Phase II: Towards the Limit of the 2nd Generation Detectors
- synthesis of new materials, new deposition techniques and new post deposition treatments
- optical, structural and mechanical characterization of the synthesized products
- modeling of the static and dynamic behavior.
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | A figure of merit to describe the sensitivity of a GW detector to a NS-NS source population. It is defined as the radius R of a Euclidean sphere with the volume equal to the space-time volume surveyed per unit detector time [146]. |
| 2 | https://gracedb.ligo.org/superevents/public/O3/ (accessed on 10 August 2021). |
| 3 | The T is an estimate of the duration of the GRB prompt emission. Specifically: T measures the duration of the time interval during which 90% of the total observed counts have been detected; the start of the T interval is defined by the time at which 5% of the total counts have been detected, and the end of the T interval is defined by the time at which 95% of the total counts have been detected. |
| 4 | https://snews.bnl.gov/ (accessed on 10 August 2021). |
| 5 | A third catalog release is currently in preparation. |
| 6 | The spin-down limit is the maximum GW amplitude the star can reach if only the gravitational wave emission mechanism is considered in the energy budget of the rotating star. |
References
- Maggiore, M. Gravitational Waves: Volume 2: Astrophysics and Cosmology, 1st ed.; Oxford University Press: Oxford, UK, 2018; p. 820. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. arXiv 2020, arXiv:2010.14527. [Google Scholar]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Properties of the Binary Black Hole Merger GW150914. Phys. Rev. D 2016, 116, 241102. [Google Scholar] [CrossRef]
- Metzger, B.D.; Berger, E. What is the Most Promising Electromagnetic Counterpart of a Neutron Star Binary Merger? Astrophys. J. 2012, 746, 48. [Google Scholar] [CrossRef]
- Perna, R.; Lazzati, D.; Giacomazzo, B. Short Gamma-Ray Bursts from the Merger of Two Black Holes. Astrophys. J. Lett. 2016, 821, L18. [Google Scholar] [CrossRef]
- Bartos, I.; Haiman, Z.; Marka, Z.; Metzger, B.D.; Stone, N.C.; Marka, S. Gravitational-wave localization alone can probe origin of stellar-mass black hole mergers. Nat. Commun. 2017, 8, 831. [Google Scholar] [CrossRef] [PubMed]
- Graham, M.J.; Ford, K.E.S.; McKernan, B.; Ross, N.P.; Stern, D.; Burdge, K.; Coughlin, M.; Djorgovski, S.G.; Drake, A.J.; Duev, D.; et al. Candidate Electromagnetic Counterpart to the Binary Black Hole Merger Gravitational-Wave Event S190521g*. Phys. Rev. D 2020, 124, 251102. [Google Scholar] [CrossRef] [PubMed]
- Kotake, K.; Sato, K.; Takahashi, K. Explosion mechanism, neutrino burst and gravitational wave in core-collapse supernovae. Rep. Prog. Phys. 2006, 69, 971–1143. [Google Scholar] [CrossRef]
- Ott, C.D. Topical Review: The gravitational-wave signature of core-collapse supernovae. Class. Quantum Gravity 2009, 26, 063001. [Google Scholar] [CrossRef]
- Gossan, S.E.; Sutton, P.; Stuver, A.; Zanolin, M.; Gill, K.; Ott, C.D. Observing gravitational waves from core-collapse supernovae in the advanced detector era. Phys. Rev. D 2016, 93, 042002. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Optically targeted search for gravitational waves emitted by core-collapse supernovae during the first and second observing runs of advanced LIGO and advanced Virgo. Phys. Rev. D 2020, 101, 084002. [Google Scholar] [CrossRef]
- Soderberg, A.M.; Berger, E.; Page, K.L.; Schady, P.; Parrent, J.; Pooley, D.; Wang, X.Y.; Ofek, E.O.; Cucchiara, A.; Rau, A.; et al. An extremely luminous X-ray outburst at the birth of a supernova. Nature 2008, 453, 469–474. [Google Scholar] [CrossRef]
- Garnavich, P.M.; Tucker, B.E.; Rest, A.; Shaya, E.J.; Olling, R.P.; Kasen, D.; Villar, A. Shock Breakout and Early Light Curves of Type II-P Supernovae Observed with Kepler. Astrophys. J. 2016, 820, 23. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847–850. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. Lett. 2003, 591, L17–L20. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. D 1987, 58, 1490–1493. [Google Scholar] [CrossRef] [PubMed]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud. Phys. Rev. D 1987, 58, 1494–1496. [Google Scholar] [CrossRef]
- Alexeyev, E.N.; Alexeyeva, L.N.; Krivosheina, I.V.; Volchenko, V.I. Detection of the neutrino signal from SN 1987A in the LMC using the INR Baksan underground scintillation telescope. Phys. Lett. B 1988, 205, 209–214. [Google Scholar] [CrossRef]
- Murase, K. New prospects for detecting high-energy neutrinos from nearby supernovae. Phys. Rev. D 2018, 97, 081301. [Google Scholar] [CrossRef]
- Lasky, P.D. Gravitational Waves from Neutron Stars: A Review. Publ. Astron. Soc. Aust. 2015, 32, e034. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Thompson, C. Corona of Magnetars. Astrophys. J. 2007, 657, 967–993. [Google Scholar] [CrossRef]
- Corsi, A.; Owen, B.J. Maximum gravitational-wave energy emissible in magnetar flares. Phys. Rev. D 2011, 83, 104014. [Google Scholar] [CrossRef]
- Mereghetti, S. The strongest cosmic magnets: Soft gamma-ray repeaters and anomalous X-ray pulsars. Astron. Astrophys. Rev. 2008, 15, 225–287. [Google Scholar] [CrossRef]
- Espinoza, C.M.; Lyne, A.G.; Stappers, B.W.; Kramer, M. A study of 315 glitches in the rotation of 102 pulsars. Mon. Not. R. Astron. Soc. 2011, 414, 1679–1704. [Google Scholar] [CrossRef]
- Haskell, B.; Schwenzer, K. Gravitational waves from isolated neutron stars. arXiv 2021, arXiv:2104.03137. [Google Scholar]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 673–736. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Adams, C.; Adams, T.; et al. Gravitational Waves from Known Pulsars: Results from the Initial Detector Era. Astrophys. J. 2014, 785, 119. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Constraints from LIGO O3 data on gravitational-wave emission due to r-modes in the glitching pulsar PSR J0537-6910. arXiv 2021, arXiv:2104.14417. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Gravitational-wave Constraints on the Equatorial Ellipticity of Millisecond Pulsars. Astrophys. J. Lett. 2020, 902, L21. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Diving below the Spin-down Limit: Constraints on Gravitational Waves from the Energetic Young Pulsar PSR J0537-6910. Astrophys. J. Lett. 2021, 913, L27. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for continuous gravitational waves from young supernova remnants in the early third observing run of Advanced LIGO and Virgo. arXiv 2021, arXiv:2105.11641. [Google Scholar]
- Lindblom, L.; Owen, B.J. Directed searches for continuous gravitational waves from twelve supernova remnants in data from Advanced LIGO’s second observing run. Phys. Rev. D 2020, 101. [Google Scholar] [CrossRef]
- Papa, M.A.; Ming, J.; Gotthelf, E.V.; Allen, B.; Prix, R.; Dergachev, V.; Eggenstein, H.B.; Singh, A.; Zhu, S.J. Search for Continuous Gravitational Waves from the Central Compact Objects in Supernova Remnants Cassiopeia A, Vela Jr., and G347.3–0.5. Astrophys. J. 2020, 897, 22. [Google Scholar] [CrossRef]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C. Directed search for continuous gravitational-wave signals from the Galactic Center in the Advanced LIGO second observing run. Phys. Rev. D 2020, 101. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data. Phys. Rev. D 2019, 100. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-sky search in early O3 LIGO data for continuous gravitational-wave signals from unknown neutron stars in binary systems. Phys. Rev. D 2021, 103, 064017. [Google Scholar] [CrossRef]
- Riles, K. Recent searches for continuous gravitational waves. Mod. Phys. Lett. A 2017, 32, 1730035. [Google Scholar] [CrossRef]
- Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Physics of Neutron Stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef]
- Buonanno, A.; Sigl, G.; Raffelt, G.G.; Janka, H.T.; Müller, E. Stochastic gravitational-wave background from cosmological supernovae. Phys. Rev. D 2005, 72, 084001. [Google Scholar] [CrossRef]
- Howell, E.; Coward, D.; Burman, R.; Blair, D.; Gilmore, J. The gravitational wave background from neutron star birth throughout the cosmos. Mon. Not. R. Astron. Soc. 2004, 351, 1237–1246. [Google Scholar] [CrossRef]
- Sandick, P.; Olive, K.A.; Daigne, F.; Vangioni, E. Gravitational waves from the first stars. Phys. Rev. D 2006, 73, 104024. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Allen, B. Cosmological constraints on cosmic-string gravitational radiation. Phys. Rev. D 1992, 45, 3447–3468. [Google Scholar] [CrossRef] [PubMed]
- Damour, T.; Vilenkin, A. Gravitational radiation from cosmic (super)strings: Bursts, stochastic background, and observational windows. Phys. Rev. D 2005, 71, 063510. [Google Scholar] [CrossRef]
- Ölmez, S.; Mandic, V.; Siemens, X. Gravitational-wave stochastic background from kinks and cusps on cosmic strings. Phys. Rev. D 2010, 81, 104028. [Google Scholar] [CrossRef]
- Grishchuk, L.P. Relic gravitational waves and limits on inflation. Phys. Rev. D 1993, 48, 3513–3516. [Google Scholar] [CrossRef]
- Easther, R.; Giblin, J.T., Jr.; Lim, E.A. Gravitational Wave Production at the End of Inflation. Phys. Rev. D 2007, 99, 221301. [Google Scholar] [CrossRef]
- Cook, J.L.; Sorbo, L. Particle production during inflation and gravitational waves detectable by ground-based interferometers. Phys. Rev. D 2012, 85, 023534. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Implications for the Stochastic Gravitational-Wave Background from Compact Binary Coalescences. Phys. Rev. D 2018, 120, 091101. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Bertone, G.; Croon, D.; Amin, M.; Boddy, K.K.; Kavanagh, B.; Mack, K.J.; Natarajan, P.; Opferkuch, T.; Schutz, K.; Takhistov, V.; et al. Gravitational wave probes of dark matter: Challenges and opportunities. SciPost Phys. Core 2020, 3. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance. Lect. Notes Phys. 2020. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive primordial black holes from hybrid inflation as dark matter and the seeds of galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef]
- Chapline, G.F. Cosmological effects of primordial black holes. Nature 1975, 253, 251–252. [Google Scholar] [CrossRef]
- Weber, J. Gravitational-Wave-Detector Events. Phys. Rev. Lett. 1968, 20, 1307–1308. [Google Scholar] [CrossRef]
- La Rana, A.; Milano, L. The Early History of Gravitational Wave Detection in Italy: From the First Resonant Bars to the Beginning of the Virgo Collaboration. 2017. Available online: https://www.paviauniversitypress.it/articolo/9788869520709-c17/539 (accessed on 10 August 2021).
- ROG Collaboration. Explorer Experiment Home Page. Available online: http://www.lnf.infn.it/esperimenti/rog/frame_explorer.htm (accessed on 19 June 2021).
- Astone, P.; Bassan, M.; Bonifazi, P.; Carelli, P.; Castellano, M.G.; Cavallari, G.; Coccia, E.; Cosmelli, C.; Fafone, V.; Frasca, S.; et al. Long-term operation of the Rome “Explorer” cryogenic gravitational wave detector. Phys. Rev. D 1993, 47, 362–375. [Google Scholar] [CrossRef]
- ROG Collaboration. Nautilus Experiment Home Page. Available online: http://www.lnf.infn.it/esperimenti/rog/frame_nautilus.htm (accessed on 19 June 2021).
- Astone, P.; Bassan, M.; Bonifazi, P.; Carelli, P.; Coccia, E.; Cosmelli, C.; Fafone, V.; Frasca, S.; Marini, A.; Mazzitelli, G.; et al. The gravitational wave detector NAUTILUS operating at T = 0.1 K. Astropart. Phys. 1997, 7, 231–243. [Google Scholar] [CrossRef]
- AURIGA Collaboration. AURIGA Experiment Home Page. Available online: http://www.auriga.lnl.infn.it/ (accessed on 19 June 2021).
- Zendri, J.P.; Baggio, L.; Bignotto, M.; Bonaldi, M.; Cerdonio, M.; Conti, L.; Rosa, M.D.; Falferi, P.; Fortini, P.L.; Inguscio, M.; et al. Status report and near future prospects for the gravitational wave detector AURIGA. Class. Quantum Gravity 2002, 19, 1925–1933. [Google Scholar] [CrossRef]
- Mauceli, E.; Geng, Z.K.; Hamilton, W.O.; Johnson, W.W.; Merkowitz, S.; Morse, A.; Price, B.; Solomonson, N. The Allegro gravitational wave detector: Data acquisition and analysis. Phys. Rev. D 1996, 54, 1264–1275. [Google Scholar] [CrossRef]
- Blair, D.G.; Ivanov, E.N.; Tobar, M.E.; Turner, P.J.; van Kann, F.; Heng, I.S. High Sensitivity Gravitational Wave Antenna with Parametric Transducer Readout. Phys. Rev. Lett. 1995, 74, 1908–1911. [Google Scholar] [CrossRef] [PubMed]
- IGEC Collaboration. The International Gravitational Event Collaboration Home Page. Available online: http://igec.lnl.infn.it/ (accessed on 19 June 2021).
- Astone, P.; Babusci, D.; Baggio, L.; Bassan, M.; Blair, D.G.; Bonaldi, M.; Bonifazi, P.; Busby, D.; Carelli, P.; Cerdonio, M.; et al. Methods and results of the IGEC search for burst gravitational waves in the years 1997–2000. Phys. Rev. D 2003, 68, 022001. [Google Scholar] [CrossRef]
- Astone, P.; Babusci, D.; Baggio, L.; Bassan, M.; Bignotto, M.; Bonaldi, M.; Camarda, M.; Carelli, P.; Cavallari, G.; Cerdonio, M.; et al. Results of the IGEC-2 search for gravitational wave bursts during 2005. Phys. Rev. D 2007, 76, 102001. [Google Scholar] [CrossRef]
- INFN. INFN Home Page. Frascati (RM). 2021. Available online: https://home.infn.it/en/ (accessed on 10 August 2021).
- Parigi Collaboration (Pisa, Napoli, Frascati, Orsay). Antenna Interferometrica a Grande Base per la Ricerca di Onde Gravitazionali. Technical Report VIR-0473B-15; INFN PI/AE 87/1; 1987. Available online: https://tds.virgo-gw.eu/ql/?c=11203 (accessed on 25 August 2021).
- CNRS. CNRS Home Page. Available online: http://www.cnrs.fr/en (accessed on 19 June 2021).
- Giazotto, A.; Campani, E.; Passuello, D.; Stefanini, A. Performance of an Active Pendulum with Interferometric Sensing 1986. In Proceedings of the Fourth Marcel Grossmann Meeting, Rome, Italy, 17–21 June 1985. [Google Scholar]
- Del Fabbro, R.; Di Virgilio, A.; Giazotto, A.; Kautzky, H.; Montelatici, V.; Passuello, D. Three-dimensional seismic super-attenuator for low frequency gravitational wave detection. Phys. Lett. A 1987, 124, 253–257. [Google Scholar] [CrossRef]
- Caron, B.; Dominjon, A.; Drezen, C.; Flaminio, R.; Grave, X.; Marion, F.; Massonnet, L.; Mehmel, C.; Morand, R.; Mours, B.; et al. Status of the VIRGO experiment. Nucl. Phys. B Proc. Suppl. 1996, 48, 107–109. [Google Scholar] [CrossRef]
- EGO. Virgo R&D and Interdisciplinarity. Available online: https://www.ego-gw.it/rd-interdisciplinarity/ (accessed on 13 June 2021).
- The Virgo Collaboration; The LIGO Scientific Collaboration. MOU between VIRGO and LIGO. Available online: https://tds.virgo-gw.eu/ql/?c=1632 (accessed on 1 July 2021).
- Accadia, T.; Acernese, F.; Alshourbagy, M.; Amico, P.; Antonucci, F.; Aoudia, S.; Giordano, G. Virgo: A laser interferometer to detect gravitational waves. J. Instrum. 2012, 7, P03012. [Google Scholar] [CrossRef]
- The Virgo Collaboration. Advanced Virgo Technical Design Report; Technical Report VIR-0128A-12; 2012. Available online: https://tds.virgo-gw.eu/ql/?c=8940 (accessed on 1 July 2021).
- The LIGO Scientific Collaboration; The Virgo Collaboration. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. D 2017, 119, 161101. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Nikhef. Nikhef Home Page. Available online: https://www.nikhef.nl/en/ (accessed on 21 June 2021).
- Hild, S.; Grote, H.; Degallaix, J.; Chelkowski, S.; Danzmann, K.; Freise, A.; Hewitson, M.; Hough, J.; Lück, H.; Prijatelj, M.; et al. DC-readout of a signal-recycled gravitational wave detector. Class. Quantum Gravity 2009, 26, 055012. [Google Scholar] [CrossRef]
- Acernese, F.; Alshourbagy, M.; Antonucci, F.; Aoudia, S.; Arun, K.G.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Bauer, T.S.; et al. Automatic Alignment for the first science run of the Virgo interferometer. Astropart. Phys. 2010, 33, 131–139. [Google Scholar] [CrossRef]
- Acernese, F.; Adams, T.; Agatsuma, K.; Aiello, L.; Allocca, A.; Amato, A.; Antier, S.; Arnaud, N.; Ascenzi, S.; Astone, P.; et al. Status of Advanced Virgo. EPJ Web Conf. 2018, 182, 02003. [Google Scholar] [CrossRef][Green Version]
- Beker, M.G.; van den Brand, J.F.J.; Hennes, E.; Rabeling, D.S. Newtonian noise and ambient ground motion for gravitational wave detectors. J. Phys. Conf. Ser. 2012, 363, 012004. [Google Scholar] [CrossRef]
- Harms, J. Terrestrial Gravity Fluctuations. Living Rev. Relativ. 2015, 18. [Google Scholar] [CrossRef] [PubMed]
- Harms, J.; Venkateswara, K. Newtonian-noise cancellation in large-scale interferometric GW detectors using seismic tiltmeters. Class. Quantum Gravity 2016, 33, 234001. [Google Scholar] [CrossRef]
- Tringali, M.C.; Bulik, T.; Harms, J.; Fiori, I.; Paoletti, F.; Singh, N.; Idzkowski, B.; Kutynia, A.; Nikliborc, K.; Suchiński, M.; et al. Seismic array measurements at Virgo’s west end building for the configuration of a Newtonian-noise cancellation system. Class. Quantum Gravity 2019, 37, 025005. [Google Scholar] [CrossRef]
- Singha, A.; Hild, S.; Harms, J. Newtonian-noise reassessment for the Virgo gravitational-wave observatory including local recess structures. Class. Quantum Gravity 2020, 37. [Google Scholar] [CrossRef]
- Badaracco, F.; Harms, J. Optimization of seismometer arrays for the cancellation of Newtonian noise from seismic body waves. Class. Quantum Gravity 2019, 36, 145006. [Google Scholar] [CrossRef]
- Ballardin, G.; Bracci, L.; Braccini, S.; Bradaschia, C.; Casciano, C.; Calamai, G.; Cavalieri, R.; Cecchi, R.; Cella, G.; Cuoco, E.; et al. Measurement of the VIRGO superattenuator performance for seismic noise suppression. Rev. Sci. Instruments 2001, 72. [Google Scholar] [CrossRef]
- Aisa, D.; Aisa, S.; Campeggi, C.; Colombini, M.; Conte, A.; Farnesini, L.; Vocca, H. The Advanced Virgo monolithic fused silica suspension. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 824, 644–645. [Google Scholar] [CrossRef]
- Naticchioni, L. The payloads of Advanced Virgo: Current status and upgrades. J. Phys. Conf. Ser. 2018, 957, 012002. [Google Scholar] [CrossRef]
- Acernese, F.; Antonucci, F.; Aoudia, S.; Arun, K.G.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Bauer, T.S.; Beker, M.G.; et al. Measurements of Superattenuator seismic isolation by Virgo interferometer. Astropart. Phys. 2010, 33, 182–189. [Google Scholar] [CrossRef]
- Callen, H.B.; Welton, T.A. Irreversibility and Generalized Noise. Phys. Rev. 1951, 83, 34–40. [Google Scholar] [CrossRef]
- Penn, S.D.; Harry, G.M.; Gretarsson, A.M.; Kittelberger, S.E.; Saulson, P.R.; Schiller, J.J.; Smith, J.R.; Swords, S.O. High quality factor measured in fused silica. Rev. Sci. Instrum. 2001, 72, 3670–3673. [Google Scholar] [CrossRef]
- Gretarsson, A.M.; Harry, G.M. Dissipation of mechanical energy in fused silica fibers. Rev. Sci. Instrum. 1999, 70, 4081–4087. [Google Scholar] [CrossRef]
- Heptonstall, A.; Barton, M.A.; Bell, A.S.; Bohn, A.; Cagnoli, G.; Cumming, A.; Grant, A.; Gustafson, E.; Hammond, G.D.; Hough, J.; et al. Enhanced characteristics of fused silica fibers using laser polishing. Class. Quantum Gravity 2014, 31, 105006. [Google Scholar] [CrossRef][Green Version]
- Rowan, S.; Twyford, S.; Hutchins, R.; Kovalik, J.; Logan, J.; McLaren, A.; Robertson, N.; Hough, J. Q factor measurements on prototype fused quartz pendulum suspensions for use in gravitational wave detectors. Phys. Lett. A 1997, 233, 303–308. [Google Scholar] [CrossRef]
- Gianpietro, C.; Gammaitoni, L.; Hough, J.; Kovalik, J.; McIntosh, S.; Punturo, M.; Rowan, S. Very High Q Measurements on a Fused Silica Monolithic Pendulum for Use in Enhanced Gravity Wave Detectors. Phys. Rev. Lett. 2000, 85, 2442–2445. [Google Scholar] [CrossRef]
- Amico, P.; Bosi, L.; Carbone, L.; Gammaitoni, L.; Punturo, M.; Travasso, F.; Vocca, H. Fused silica suspension for the VIRGO optics: Status and perspectives. Class. Quant. Grav. 2002, 19, 1669–1674. [Google Scholar] [CrossRef]
- Plissi, M.; Torrie, C.; Husman, M.; Robertson, N.; Strain, K.; Ward, H.; Lück, H.; Hough, J. GEO 600 triple pendulum suspension system: Seismic isolation and control. Rev. Sci. Instruments 2000, 71, 2539–2545. [Google Scholar] [CrossRef]
- Smith, J.; Gianpietro, C.; Crooks, D.; Fejer, M.; Gossler, S.; Lück, H.; Rowan, S.; Hough, J.; Danzmann, K. Mechanical quality factor measurements of monolithically-suspended fused silica test masses of the GEO600 gravitational wave detector. Class. Quantum Gravity 2004, 21. [Google Scholar] [CrossRef][Green Version]
- Lorenzini, M. The monolithic suspension for the Virgo interferometer. Class. Quant. Grav. 2010, 27, 084021. [Google Scholar] [CrossRef][Green Version]
- Cumming, A.V.; Bell, A.S.; Barsotti, L.; Barton, M.A.; Cagnoli, G.; Cook, D.; Cunningham, L.; Evans, M.; Hammond, G.D.; Harry, G.M.; et al. Design and development of the advanced LIGO monolithic fused silica suspension. Class. Quantum Gravity 2012, 29, 035003. [Google Scholar] [CrossRef]
- Heptonstall, A.; Barton, M.; Bell, A.; Cagnoli, G.; Cantley, C.; Crooks, D.; Cumming, A.; Grant, A.; Hammond, G.; Harry, G.; et al. Invited article: CO2 laser production of fused silica fibers for use in interferometric gravitational wave detector mirror suspensions. Rev. Sci. Instruments 2011, 82, 011301. [Google Scholar] [CrossRef]
- Montani, M.; on behalf of the Virgo Collaboration. Silica Fibers Production and Characterization for Future Gravitational Waves Detectors. In Proceedings of the GRAvitational-wave Science&technology Symposium 2019 (GRASS2019), Padova, Italy, 17–18 October 2019. [Google Scholar] [CrossRef]
- Piergiovanni, F.; Lorenzini, M.; Cagnoli, G.; Campagna, E.; Cesarini, E.; Losurdo, G.; Martelli, F.; Vetrano, F.; Viceré, A. The dynamics of monolithic suspensions for advanced detectors: A 3-segment model. J. Phys. Conf. Ser. 2010, 228, 012017. [Google Scholar] [CrossRef]
- Cagnoli, G.; Willems, P.A. Effects of nonlinear thermoelastic damping in highly stressed fibers. Phys. Rev. B 2002, 65, 174111. [Google Scholar] [CrossRef]
- Cagnoli, G.; Gammaitoni, L.; Kovalik, J.; Marchesoni, F.; Punturo, M. Full scale prototype of high Q pendulum for interferometric gravitational wave detectors. Rev. Sci. Instrum. 2000, 71, 2206–2210. [Google Scholar] [CrossRef]
- Dari, A.; Travasso, F.; Vocca, H.; Gammaitoni, L. Breaking strength tests on silicon and sapphire bondings for gravitational wave detectors. Class. Quantum Gravity 2010, 27, 045010. [Google Scholar] [CrossRef]
- Cimma, B.; Forest, D.; Ganau, P.; Lagrange, B.; Mackowski, J.M.; Michel, C.; Montorio, J.L.; Morgado, N.; Pignard, R.; Pinard, L.; et al. Ion beam sputtering coatings on large substrates: Toward an improvement of the mechanical and optical performances. Appl. Opt. 2006, 45, 1436–1439. [Google Scholar] [CrossRef]
- Pinard, L.; Michel, C.; Sassolas, B.; Balzarini, L.; Degallaix, J.; Dolique, V.; Flaminio, R.; Forest, D.; Granata, M.; Lagrange, B.; et al. Mirrors used in the LIGO interferometers for first detection of gravitational waves. Appl. Opt. 2017, 56, C11–C15. [Google Scholar] [CrossRef]
- Numata, K.; Yamamoto, K.; Ishimoto, H.; Otsuka, S.; Kawabe, K.; Ando, M.; Tsubono, K. Systematic measurement of the intrinsic losses in various kinds of bulk fused silica. Phys. Lett. A 2004, 327, 263–271. [Google Scholar] [CrossRef]
- Crooks, D.R.M.; Sneddon, P.; Cagnoli, G.; Hough, J.; Rowan, S.; Fejer, M.M.; Gustafson, E.; Route, R.; Nakagawa, N.; Coyne, D.; et al. Excess mechanical loss associated with dielectric mirror coatings on test masses in interferometric gravitational wave detectors. Class. Quantum Gravity 2002, 19, 4229. [Google Scholar] [CrossRef][Green Version]
- Granata, M.; Amato, A.; Cagnoli, G.; Coulon, M.; Degallaix, J.; Forest, D.; Mereni, L.; Michel, C.; Pinard, L.; Sassolas, B.; et al. Progress in the measurement and reduction of thermal noise in optical coatings for gravitational-wave detectors. Appl. Opt. 2020, 59, A229–A235. [Google Scholar] [CrossRef] [PubMed]
- Amato, A.; Cagnoli, G.; Canepa, M.; Coillet, E.; Degallaix, J.; Dolique, V.; Forest, D.; Granata, M.; Martinez, V.; Michel, C.; et al. High-Reflection Coatings for Gravitational-Wave Detectors:State of The Art and Future Developments. J. Phys. Conf. Ser. 2018, 957, 012006. [Google Scholar] [CrossRef]
- Gras, S.; Evans, M. Direct measurement of coating thermal noise in optical resonators. Phys. Rev. D 2018, 98, 122001. [Google Scholar] [CrossRef]
- Granata, M.; Amato, A.; Balzarini, L.; Canepa, M.; Degallaix, J.; Forest, D.; Dolique, V.; Mereni, L.; Michel, C.; Pinard, L.; et al. Amorphous optical coatings of present gravitational-wave interferometers. Class. Quantum Gravity 2020, 37, 095004. [Google Scholar] [CrossRef]
- Agresti, J.; Castaldi, G.; Desalvo, R.; Galdi, V.; Pierro, V.; Pinto, I. Optimized multilayer dielectric mirror coatings for gravitational wave interferometers. Proc. SPIE 2006, 6286, 628608. [Google Scholar] [CrossRef]
- Piergiovanni, F.; on behalf of the Virgo Collaboration. The research on amorphous coatings for future GW detectors. J. Phys. Conf. Ser. 2020, 1468, 012216. [Google Scholar] [CrossRef]
- Max Planck Institute for Gravitational Physics (Albert Einstein Institute). AEI Homepage. Available online: https://www.aei.mpg.de/ (accessed on 1 July 2021).
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Black, E.D. An introduction to Pound–Drever–Hall laser frequency stabilization. Am. J. Phys. 2001, 69, 79. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Chelkowski, S.; Hage, B.; Franzen, A.; Danzmann, K.; Schnabel, R. Coherent control of vacuum squeezing in the gravitational-wave detection band. Phys. Rev. Lett. 2006, 97, 011101. [Google Scholar] [CrossRef] [PubMed]
- Mehmet, M.; Vahlbruch, H. High-efficiency squeezed light generation for gravitational wave detectors. Class. Quantum Gravity 2018, 36, 015014. [Google Scholar] [CrossRef]
- Mehmet, M.; Vahlbruch, H. The Squeezed Light Source for the Advanced Virgo Detector in the Observation Run O3. Galaxies 2020, 8, 79. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Amato, A.; Ansoldi, S.; Antier, S.; Arène, M.; Arnaud, N.; Ascenzi, S.; et al. Increasing the astrophysical reach of the advanced Virgo detector via the application of squeezed vacuum states of light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar] [CrossRef]
- Mantovani, M.; Vajente, G. Alignment Accuracy Requirements for Advanced Virgo; Technical Report VIR-0247A-10; 2010. Available online: https://tds.virgo-gw.eu/ql/?c=7384 (accessed on 10 August 2021).
- Mantovani, M. Automatic Alignment Sensing and Control Scheme for Advanced Virgo MSRC Configuration; Technical Report VIR-0201A-11; 2011. Available online: https://tds.virgo-gw.eu/ql/?c=8255 (accessed on 10 August 2021).
- Bersanetti, D.; Casanueva Diaz, J.; Allocca, A.; Heitmann, H.; Hoak, D.; Mantovani, M.; Ruggi, P.; Swinkels, B. New algorithm for the Guided Lock technique for a high-Finesse optical cavity. Astropart. Phys. 2020, 117, 102405. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Aloy, M.A.; Amato, A.; Antier, S.; Arène, M.; Arnaud, N.; Ascenzi, S.; et al. The advanced Virgo longitudinal control system for the O2 observing run. Astropart. Phys. 2020, 116, 102386. [Google Scholar] [CrossRef]
- Allocca, A.; Bersanetti, D.; Casanueva Diaz, J.; De Rossi, C.; Mantovani, M.; Masserot, A.; Rolland, L.; Ruggi, P.; Swinkels, B.; Tapia San Martin, E.N.; et al. Interferometer Sensing and Control for the Advanced Virgo Experiment in the O3 Scientific Run. Galaxies 2020, 8, 85. [Google Scholar] [CrossRef]
- Lawrence, R.C. Active Wavefront Correction in Laser Interferometric Gravitational Wave Detectors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Brooks, A.F. Hartmann Wavefront Sensors for Advanced Gravitational Wave Interferometers. Ph.D. Thesis, School of Chemistry and Physics, University of Adelaide, Adelaide, Australia, 2007. [Google Scholar]
- Nardecchia, I. Control of Optical Aberrations in Advanced Interferometric Gravitational Wave Detectors. Ph.D. Thesis, Università degli Studi di Roma La Sapienza and Università degli Studi di Roma Tor Vergata, Roma, Italy, 2016. [Google Scholar]
- Aiello, L.; Cesarini, E.; Fafone, V.; Lorenzini, M.; Minenkov, Y.; Nardecchia, I.; Rocchi, A.; Sequino, V. Thermal compensation system in advanced and third generation gravitational wave interferometric detectors. J. Phys. Conf. Ser. 2019, 1226, 012019. [Google Scholar] [CrossRef]
- Aiello, L. Development of New Approaches for Optical Aberration Control in Gravitational Wave Interferometers. Ph.D. Thesis, Gran Sasso Science Institute, L’Aquila, Italy, 2019. [Google Scholar]
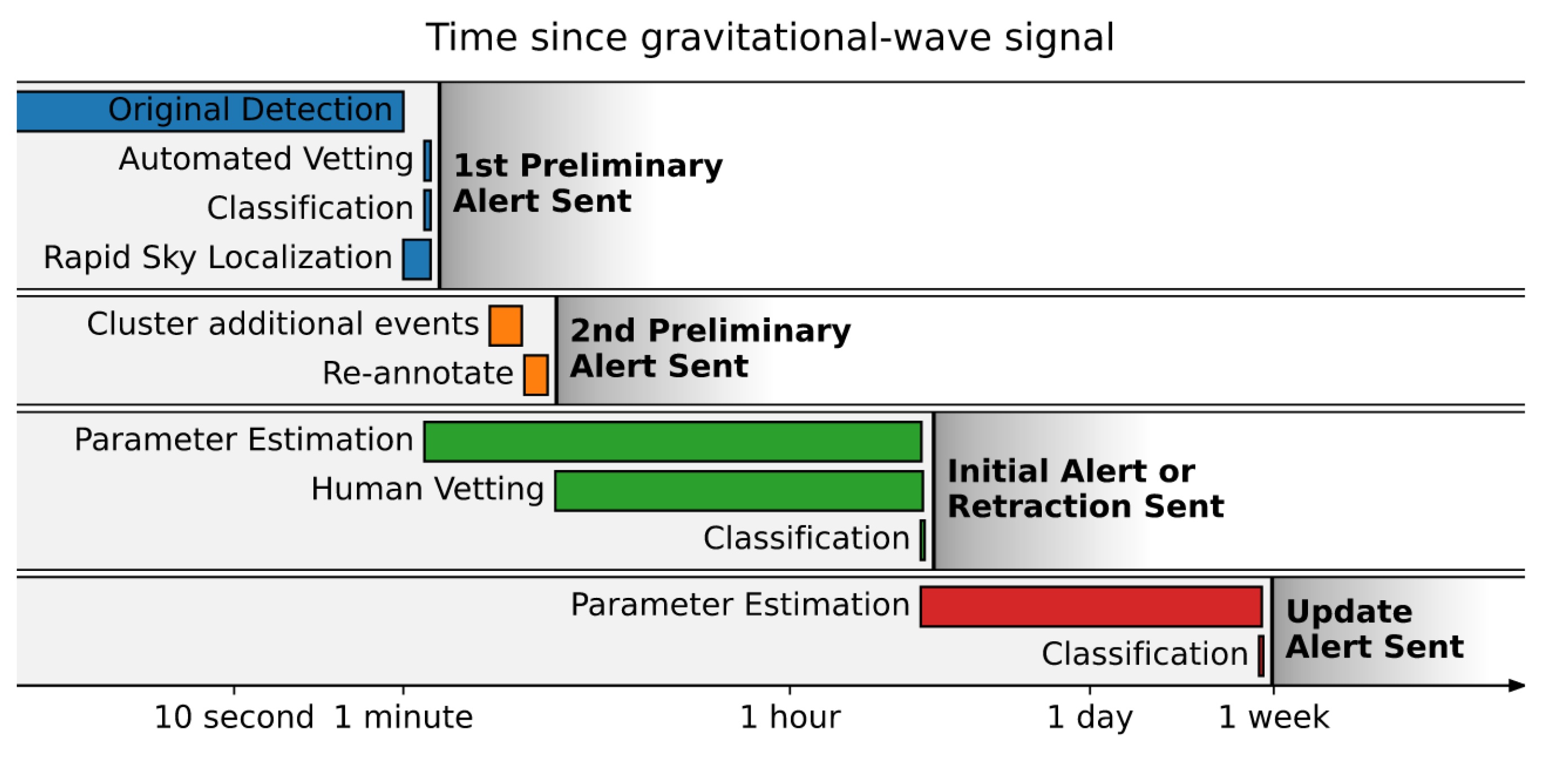
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef] [PubMed]
- LIGO/Virgo Collaborations. LIGO/Virgo Public Alerts User Guide. Available online: https://emfollow.docs.ligo.org/userguide/glossary.html (accessed on 2 August 2021).
- Gravitational Wave Open Science Center O3b Summary Page. Available online: https://www.gw-openscience.org/detector_status/O3b/ (accessed on 24 June 2021).
- LIGO. Instrument Science Sensitivity and performance of the Advanced LIGO detectors in the third observing run. Phys. Rev. D 2020, 102, 062003. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. A guide to LIGO–Virgo detector noise and extraction of transient gravitational-wave signals. Class. Quantum Gravity 2020, 37, 055002. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Characterization of transient noise in Advanced LIGO relevant to gravitational wave signal GW150914. Class. Quantum Gravity 2016, 33, 134001. [Google Scholar] [CrossRef]
- The Virgo Collaboration. Category 1 (CAT1) Data Quality Vetoes Applied to the Analysis of the O3 Run Virgo Data; Technical Report VIR-0560A-21; 2021. Available online: https://tds.virgo-gw.eu/ql/?c=16808 (accessed on 11 August 2021).
- LIGO-Virgo-KAGRA Collaboration. Gravitational-Wave Candidate Event Database. Available online: https://gracedb.ligo.org/ (accessed on 30 June 2021).
- Turin, G. An introduction to matched filters. IRE Trans. Inf. Theory 1960, 6, 311–329. [Google Scholar] [CrossRef]
- Messick, C.; Blackburn, K.; Brady, P.; Brockill, P.; Cannon, K.; Cariou, R.; Caudill, S.; Chamberlin, S.J.; Creighton, J.D.E.; Everett, R.; et al. Analysis framework for the prompt discovery of compact binary mergers in gravitational-wave data. Phys. Rev. D 2017, 95, 042001. [Google Scholar] [CrossRef]
- Nitz, A.; Harry, I.; Brown, D.; Biwer, C.M.; Willis, J.; Dal Canton, T.; Capano, C.; Pekowsky, L.; Dent, T.; Williamson, A.R.; et al. gwastro/pycbc: PyCBC release v1.16.11; 2020. [Google Scholar] [CrossRef]
- Aubin, F.; Brighenti, F.; Chierici, R.; Estevez, D.; Greco, G.; Guidi, G.M.; Juste, V.; Marion, F.; Mours, B.; Nitoglia, E.; et al. The MBTA pipeline for detecting compact binary coalescences in the third LIGO–Virgo observing run. Class. Quantum Gravity 2021, 38, 095004. [Google Scholar] [CrossRef]
- Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C. A method for detection of known sources of continuous gravitational wave signals in non-stationary data. Class. Quantum Gravity 2010, 27, 194016. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C. Coherent search of continuous gravitational wave signals: Extension of the 5-vectors method to a network of detectors. J. Phys. Conf. Ser. 2012, 363, 012038. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A. Searching for gravitational waves from known pulsars using the F and G statistics. Class. Quantum Gravity 2010, 27, 194015. [Google Scholar] [CrossRef]
- Dupuis, R.J.; Woan, G. Bayesian estimation of pulsar parameters from gravitational wave data. Phys. Rev. D 2005, 72, 102002. [Google Scholar] [CrossRef]
- Pitkin, M.; Isi, M.; Veitch, J.; Woan, G. A nested sampling code for targeted searches for continuous gravitational waves from pulsars. arXiv 2017, arXiv:1705.08978. [Google Scholar]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C.; Singhal, A. A new data analysis framework for the search of continuous gravitational wave signals. Class. Quantum Gravity 2018, 36, 015008. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C. Method for all-sky searches of continuous gravitational wave signals using the frequency-Hough transform. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef]
- Krishnan, B.; Sintes, A.M.; Papa, M.A.; Schutz, B.F.; Frasca, S.; Palomba, C. Hough transform search for continuous gravitational waves. Phys. Rev. D 2004, 70. [Google Scholar] [CrossRef]
- Wette, K.; Walsh, S.; Prix, R.; Papa, M. Implementing a semicoherent search for continuous gravitational waves using optimally constructed template banks. Phys. Rev. D 2018, 97. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T. Searching for periodic sources with LIGO. II. Hierarchical searches. Phys. Rev. D 2000, 61, 082001. [Google Scholar] [CrossRef]
- Goetz, E.; Riles, K. An all-sky search algorithm for continuous gravitational waves from spinning neutron stars in binary systems. Class. Quantum Gravity 2011, 28, 215006. [Google Scholar] [CrossRef]
- Anderson, W.G.; Brady, P.R.; Creighton, J.D.E.; Flanagan, E.E. Excess power statistic for detection of burst sources of gravitational radiation. Phys. Rev. D 2001, 63, 042003. [Google Scholar] [CrossRef]
- Klimenko, S.; Yakushin, I.; Mercer, A.; Mitselmakher, G. A coherent method for detection of gravitational wave bursts. Class. Quantum Gravity 2008, 25, 114029. [Google Scholar] [CrossRef]
- Salemi, F.; Milotti, E.; Prodi, G.A.; Vedovato, G.; Lazzaro, C.; Tiwari, S.; Vinciguerra, S.; Drago, M.; Klimenko, S. Wider look at the gravitational-wave transients from GWTC-1 using an unmodeled reconstruction method. Phys. Rev. D 2019, 100, 042003. [Google Scholar] [CrossRef]
- Klimenko, S.; Vedovato, G.; Drago, M.; Salemi, F.; Tiwari, V.; Prodi, G.A.; Lazzaro, C.; Ackley, K.; Tiwari, S.; Da Silva, C.F.; et al. Method for detection and reconstruction of gravitational wave transients with networks of advanced detectors. Phys. Rev. D 2016, 93, 042004. [Google Scholar] [CrossRef]
- Lynch, R.; Vitale, S.; Essick, R.; Katsavounidis, E.; Robinet, F. Information-theoretic approach to the gravitational-wave burst detection problem. Phys. Rev. D 2017, 95, 104046. [Google Scholar] [CrossRef]
- Sutton, P.J.; Jones, G.; Chatterji, S.; Kalmus, P.; Leonor, I.; Poprocki, S.; Rollins, J.; Searle, A.; Stein, L.; Tinto, M.; et al. X-Pipeline: An analysis package for autonomous gravitational-wave burst searches. New J. Phys. 2010, 12, 053034. [Google Scholar] [CrossRef]
- Suvorova, S.; Sun, L.; Melatos, A.; Moran, W.; Evans, R.J. Hidden Markov model tracking of continuous gravitational waves from a neutron star with wandering spin. Phys. Rev. D 2016, 93, 123009. [Google Scholar] [CrossRef]
- D’Antonio, S.; Palomba, C.; Frasca, S.; Astone, P.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Piccinni, O.J.; Pierini, L.; Rei, L. Sidereal filtering: A novel robust method to search for continuous gravitational waves. Phys. Rev. D 2021, 103, 063030. [Google Scholar] [CrossRef]
- Romano, J.D.; Cornish, N.J. Detection methods for stochastic gravitational-wave backgrounds: A unified treatment. Living Rev. Relativ. 2017, 20. [Google Scholar] [CrossRef]
- Thrane, E.; Kandhasamy, S.; Ott, C.D.; Anderson, W.G.; Christensen, N.L.; Coughlin, M.W.; Dorsher, S.; Giampanis, S.; Mandic, V.; Mytidis, A.; et al. Long gravitational-wave transients and associated detection strategies for a network of terrestrial interferometers. Phys. Rev. D 2011, 83, 083004. [Google Scholar] [CrossRef]
- Mitra, S.; Dhurandhar, S.; Souradeep, T.; Lazzarini, A.; Mandic, V.; Bose, S.; Ballmer, S. Gravitational wave radiometry: Mapping a stochastic gravitational wave background. Phys. Rev. D 2008, 77, 042002. [Google Scholar] [CrossRef]
- Zhang, Y.; Papa, M.A.; Krishnan, B.; Watts, A.L. Search for Continuous Gravitational Waves from Scorpius X-1 in LIGO O2 Data. Astrophys. J. 2021, 906, L14. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Search for gravitational waves from Scorpius X-1 in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2019, 100. [Google Scholar] [CrossRef]
- Middleton, H.; Clearwater, P.; Melatos, A.; Dunn, L. Search for gravitational waves from five low mass X-ray binaries in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2020, 102. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Skilling, J. Nested Sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar] [CrossRef]
- Veitch, J.; Raymond, V.; Farr, B.; Farr, W.; Graff, P.; Vitale, S.; Aylott, B.; Blackburn, K.; Christensen, N.; Coughlin, M.; et al. Parameter estimation for compact binaries with ground-based gravitational-wave observations using the LALInference software library. Phys. Rev. D 2015, 91, 042003. [Google Scholar] [CrossRef]
- Ashton, G.; Hübner, M.; Lasky, P.D.; Talbot, C.; Ackley, K.; Biscoveanu, S.; Chu, Q.; Divakarla, A.; Easter, P.J.; Goncharov, B.; et al. Bilby: A User-friendly Bayesian Inference Library for Gravitational-wave Astronomy. Astrophys. J. Suppl. Ser. 2019, 241, 27. [Google Scholar] [CrossRef]
- Biwer, C.M.; Capano, C.D.; De, S.; Cabero, M.; Brown, D.A.; Nitz, A.H.; Raymond, V. PyCBC Inference: A Python-based Parameter Estimation Toolkit for Compact Binary Coalescence Signals. Publ. Astron. Soc. Pac. 2019, 131, 024503. [Google Scholar] [CrossRef]
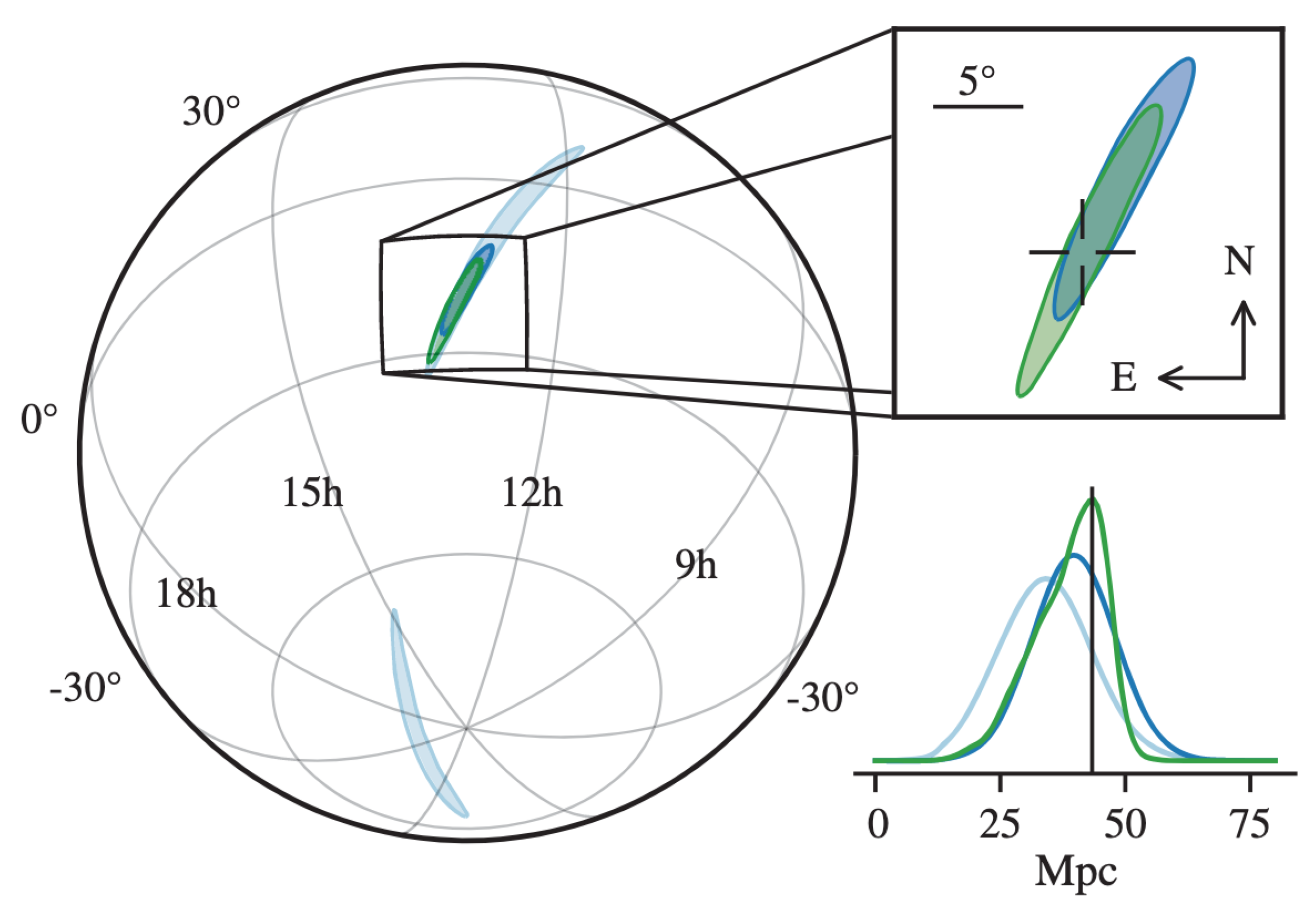
- Singer, L.P.; Price, L.R. Rapid Bayesian position reconstruction for gravitational-wave transients. Phys. Rev. D 2016, 93, 024013. [Google Scholar] [CrossRef]
- Klimenko, S.; Vedovato, G.; Drago, M.; Mazzolo, G.; Mitselmakher, G.; Pankow, C.; Prodi, G.; Re, V.; Salemi, F.; Yakushin, I. Localization of gravitational wave sources with networks of advanced detectors. Phys. Rev. D 2011, 83, 102001. [Google Scholar] [CrossRef]
- Cornish, N.J.; Littenberg, T.B. Bayeswave: Bayesian inference for gravitational wave bursts and instrument glitches. Class. Quantum Gravity 2015, 32, 135012. [Google Scholar] [CrossRef]
- Littenberg, T.B.; Cornish, N.J. Bayesian inference for spectral estimation of gravitational wave detector noise. Phys. Rev. D 2015, 91, 084034. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-Sky Search for Short Gravitational-Wave Bursts in the Second Advanced LIGO and Advanced Virgo Run. Phys. Rev. D 2019, 100, 024017. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-sky search for short gravitational-wave bursts in the first Advanced LIGO run. Phys. Rev. D 2017, 95, 042003. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-sky search for long-duration gravitational wave transients in the first Advanced LIGO observing run. Class. Quantum Gravity 2018, 35, 065009. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. All-sky search for long-duration gravitational-wave transients in the second Advanced LIGO observing run. Phys. Rev. D 2019, 99, 104033. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Low-latency Gravitational-wave Alerts for Multimessenger Astronomy during the Second Advanced LIGO and Virgo Observing Run. Astrophys. J. 2019, 875, 161. [Google Scholar] [CrossRef]
- Kelley, L.Z.; Mandel, I.; Ramirez-Ruiz, E. Electromagnetic transients as triggers in searches for gravitational waves from compact binary mergers. Phys. Rev. D 2013, 87, 123004. [Google Scholar] [CrossRef]
- Harry, I.W.; Fairhurst, S. Targeted coherent search for gravitational waves from compact binary coalescences. Phys. Rev. D 2011, 83, 084002. [Google Scholar] [CrossRef]
- Williamson, A.R.; Biwer, C.; Fairhurst, S.; Harry, I.W.; Macdonald, E.; Macleod, D.; Predoi, V. Improved methods for detecting gravitational waves associated with short gamma-ray bursts. Phys. Rev. D 2014, 90, 122004. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration. LIGO Algorithm Library—LALSuite; Free Software (GPL); LIGO Scientific Collaboration: Pasadena, CA, USA, 2018. [Google Scholar] [CrossRef]
- Wąs, M.; Sutton, P.J.; Jones, G.; Leonor, I. Performance of an externally triggered gravitational-wave burst search. Phys. Rev. D 2012, 86, 022003. [Google Scholar] [CrossRef]
- Urban, A. Monsters in the Dark: High Energy Signatures of Black Hole Formation with Multimessenger Astronomy. Ph.D. Thesis, University of Wisconsin, Milwaukee, WI, USA, 2016. [Google Scholar]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Countryman, S.; Keivani, A.; Bartos, I.; Marka, Z.; Kintscher, T.; Corley, R.; Blaufuss, E.; Finley, C.; Marka, S. Low-Latency Algorithm for Multi-messenger Astrophysics (LLAMA) with Gravitational-Wave and High-Energy Neutrino Candidates. arXiv 2019. [Google Scholar]
- Abdollahi, S.; Acero, F.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Fourth Source Catalog. Astrophys. J. Suppl. Ser. 2020, 247, 33. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Search for anisotropic gravitational-wave backgrounds using data from Advanced LIGO’s and Advanced Virgo’s first three observing runs. Phys. Rev. D 2021, 104, 022005. [Google Scholar] [CrossRef]
- Fermi-LAT Collaboration. Characterizing the population of pulsars in the inner Galaxy with the Fermi Large Area Telescope. arXiv 2017, arXiv:1705.00009. [Google Scholar]
- Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.O.; Backes, M.; Balzer, A.; Becherini, Y.; Tjus, J.B.; Berge, D.; et al. Acceleration of peta-electronvolt protons in the Galactic Centre. Nature 2016, 531, 476–479. [Google Scholar] [CrossRef]
- H.E.S.S. collaboration. collaboration The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW190412: Observation of a binary-black-hole coalescence with asymmetric masses. Phys. Rev. D 2020, 102, 043015. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW190521: A Binary Black Hole Merger with a Total Mass of 150 M⊙. Phys. Rev. D 2020, 125, 101102. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Search for lensing signatures in the gravitational-wave observations from the first half of LIGO-Virgo’s third observing run. arXiv 2021, arXiv:2105.06384. [Google Scholar]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Population Properties of Compact Objects from the Second LIGO-Virgo Gravitational-Wave Transient Catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Observation of Gravitational Waves from Two Neutron Star-Black Hole Coalescences. Astrophys. J. Lett. 2021, 915, L5. [Google Scholar] [CrossRef]
- Hosseinzadeh, G.; Cowperthwaite, P.S.; Gomez, S.; Villar, V.A.; Nicholl, M.; Margutti, R.; Berger, E.; Chornock, R.; Paterson, K.; Fong, W.; et al. Follow-up of the Neutron Star Bearing Gravitational-wave Candidate Events S190425z and S190426c with MMT and SOAR. Astrophys. J. Lett. 2019, 880, L4. [Google Scholar] [CrossRef]
- Andreoni, I.; Goldstein, D.A.; Kasliwal, M.M.; Nugent, P.E.; Zhou, R.; Newman, J.A.; Bulla, M.; Foucart, F.; Hotokezaka, K.; Nakar, E.; et al. GROWTH on S190814bv: Deep Synoptic Limits on the Optical/Near-infrared Counterpart to a Neutron Star-Black Hole Merger. Astrophys. J. 2020, 890, 131. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.J.L.; Diehl, R.; Domingo, A.; et al. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational-wave Event GW170817. Astrophys. J. Lett. 2017, 848, L15. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi Gamma-Ray Burst Monitor; INTEGRAL. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Coulter, D.A.; Kilpatrick, C.D.; Siebert, M.R.; Foley, R.J.; Shappee, B.J.; Drout, M.R.; Simon, J.S.; Piro, A.L.; Rest, A.; One-Meter Two-Hemisphere (1M2H) Collaboration. LIGO/Virgo G298048: Potential optical counterpart discovered by Swope telescope. GRB Coord. Netw. 2017, 21529, 1. [Google Scholar]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Smartt, S.J.; Chen, T.W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75–79. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef]
- Hallinan, G.; Corsi, A.; Mooley, K.P.; Hotokezaka, K.; Nakar, E.; Kasliwal, M.M.; Kaplan, D.L.; Frail, D.A.; Myers, S.T.; Murphy, T.; et al. A radio counterpart to a neutron star merger. Science 2017, 358, 1579–1583. [Google Scholar] [CrossRef] [PubMed]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Salafia, O.S.; Paragi, Z.; Giroletti, M.; Yang, J.; Marcote, B.; Blanchard, J.; Agudo, I.; An, T.; Bernardini, M.G.; et al. Compact radio emission indicates a structured jet was produced by a binary neutron star merger. Science 2019, 363, 968–971. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Gibson, B.K.; Ferrarese, L.; Kelson, D.D.; Sakai, S.; Mould, J.R.; Kennicutt, R.C.J.; Ford, H.C.; Graham, J.A.; et al. Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. Astrophys. J. 2001, 553, 47–72. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys. Rev. D 2021, 103. [Google Scholar] [CrossRef]
- Yunes, N.; Yagi, K.; Pretorius, F. Theoretical physics implications of the binary black-hole mergers GW150914 and GW151226. Phys. Rev. D 2016, 94, 084002. [Google Scholar] [CrossRef]
- Nair, R.; Perkins, S.; Silva, H.O.; Yunes, N. Fundamental Physics Implications for Higher-Curvature Theories from Binary Black Hole Signals in the LIGO-Virgo Catalog GWTC-1. Phys. Rev. Lett. 2019, 123, 191101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Tests of general relativity with the binary black hole signals from the LIGO-Virgo catalog GWTC-1. Phys. Rev. D 2019, 100. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Espinoza, C.M.; Arzoumanian, Z.; Enoto, T.; Tamba, T.; Antonopoulou, D.; Bejger, M.; Guillot, S.; Haskell, B.; Ray, P.S. Return of the Big Glitcher: NICER timing and glitches of PSR J0537-6910. Mon. Not. R. Astron. Soc. 2020, 498, 4605–4614. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. All-sky Search for Continuous Gravitational Waves from Isolated Neutron Stars in the Early O3 LIGO Data. Phys. Rev. D 2021, 103, 064017. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from the First All-Sky Search for Continuous Gravitational Waves from Small-Ellipticity Sources. Phys. Rev. Lett. 2020, 125, 171101. [Google Scholar] [CrossRef] [PubMed]
- Dergachev, V.; Papa, M.A. The search for continuous gravitational waves from small-ellipticity sources at low frequencies. arXiv 2021, arXiv:2104.09007. [Google Scholar]
- Steltner, B.; Papa, M.A.; Eggenstein, H.B.; Allen, B.; Dergachev, V.; Prix, R.; Machenschalk, B.; Walsh, S.; Zhu, S.J.; Behnke, O.; et al. Einstein@Home All-sky Search for Continuous Gravitational Waves in LIGO O2 Public Data. Astrophys. J. 2021, 909, 79. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from high-frequency all-sky search for continuous gravitational waves from small-ellipticity sources. Phys. Rev. D 2021, 103. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Upper Limits on the Isotropic Gravitational-Wave Background from Advanced LIGO’s and Advanced Virgo’s Third Observing Run. Phys. Rev. D 2021, 104, 022004. [Google Scholar] [CrossRef]
- Palomba, C.; D’Antonio, S.; Astone, P.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.L.; Muciaccia, F.; et al. Direct Constraints on the Ultralight Boson Mass from Searches of Continuous Gravitational Waves. Phys. Rev. Lett. 2019, 123, 171101. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.K.Y.; Vitale, S.; Hannuksela, O.A.; Li, T.G.F. Constraints on Ultralight Scalar Bosons within Black Hole Spin Measurements from the LIGO-Virgo GWTC-2. Phys. Rev. Lett. 2021, 126. [Google Scholar] [CrossRef]
- Bustillo, J.C.; Sanchis-Gual, N.; Torres-Forné, A.; Font, J.A.; Vajpeyi, A.; Smith, R.; Herdeiro, C.; Radu, E.; Leong, S.H.W. GW190521 as a Merger of Proca Stars: A Potential New Vector Boson of 8.7 × 10−13 eV. Phys. Rev. Lett. 2021, 126, 081101. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Constraints on dark photon dark matter using data from LIGO’s and Virgo’s third observing run. arXiv 2021, arXiv:2105.13085. [Google Scholar]
- Guo, H.K.; Riles, K.; Yang, F.W.; Zhao, Y. Searching for dark photon dark matter in LIGO O1 data. Commun. Phys. 2019, 2. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
- Jeannerot, R.; Rocher, J.; Sakellariadou, M. How generic is cosmic string formation in supersymmetric grand unified theories. Phys. Rev. D 2003, 68, 103514. [Google Scholar] [CrossRef]
- Sakellariadou, M. Gravitational waves emitted from infinite strings. Phys. Rev. D 1990, 42, 354–360. [Google Scholar] [CrossRef] [PubMed]
- Vachaspati, T.; Vilenkin, A. Gravitational radiation from cosmic strings. Phys. Rev. D 1985, 31, 3052–3058. [Google Scholar] [CrossRef]
- Vilenkin, A. Gravitational radiation from cosmic strings. Phys. Lett. B 1981, 107, 47–50. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Constraints on Cosmic Strings Using Data from the Third Advanced LIGO–Virgo Observing Run. Phys. Rev. Lett. 2021, 126, 241102. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Constraints on cosmic strings using data from the first Advanced LIGO observing run. Phys. Rev. D 2018, 97, 102002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F. Search for the isotropic stochastic background using data from Advanced LIGO’s second observing run. Phys. Rev. D 2019, 100, 061101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R. Upper Limits on the Stochastic Gravitational-Wave Background from Advanced LIGO’s First Observing Run. Phys. Rev. Lett. 2017, 118, 121101. [Google Scholar] [CrossRef] [PubMed]
- The Virgo Collaboration. Advanced Virgo Plus Phase I—Design Report; Technical Report VIR-0596A-19; 2019. Available online: https://tds.virgo-gw.eu/ql/?c=14430 (accessed on 11 August 2021).
- Chelkowski, S.; Vahlbruch, H.; Hage, B.; Franzen, A.; Lastzka, N.; Danzmann, K.; Schnabel, R. Experimental characterization of frequency-dependent squeezed light. Phys. Rev. A 2005, 71, 013806. [Google Scholar] [CrossRef]
- Oelker, E.; Isogai, T.; Miller, J.; Tse, M.; Barsotti, L.; Mavalvala, N.; Evans, M. Audio-band frequency-dependent squeezing for gravitational-wave detectors. Phys. Rev. Lett. 2016, 116, 041102. [Google Scholar] [CrossRef]
- Zhao, Y.; Aritomi, N.; Capocasa, E.; Leonardi, M.; Eisenmann, M.; Guo, Y.; Polini, E.; Tomura, A.; Arai, K.; Aso, Y.; et al. Frequency-Dependent Squeezed Vacuum Source for Broadband Quantum Noise Reduction in Advanced Gravitational-Wave Detectors. Phys. Rev. Lett. 2020, 124, 171101. [Google Scholar] [CrossRef] [PubMed]
- Capocasa, E.; Barsuglia, M.; Degallaix, J.; Pinard, L.; Straniero, N.; Schnabel, R.; Somiya, K.; Aso, Y.; Tatsumi, D.; Flaminio, R. Estimation of losses in a 300 m filter cavity and quantum noise reduction in the KAGRA gravitational-wave detector. Phys. Rev. D 2016, 93, 082004. [Google Scholar] [CrossRef]
- McCuller, L.; Whittle, C.; Ganapathy, D.; Komori, K.; Tse, M.; Fernandez-Galiana, A.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Matichard, F.; et al. Frequency-dependent squeezing for advanced LIGO. Phys. Rev. Lett. 2020, 124, 171102. [Google Scholar] [CrossRef] [PubMed]
- Sequino, V. Quantum noise reduction in Advanced Virgo. Phys. Scr. 2021, 96, 104014. [Google Scholar] [CrossRef]
- Mullavey, A.J.; Slagmolen, B.J.J.; Miller, J.; Evans, M.; Fritschel, P.; Sigg, D.; Waldman, S.J.; Shaddock, D.A.; McClelland, D.E. Arm-length stabilisation for interferometric gravitational-wave detectors using frequency-doubled auxiliary lasers. Opt. Express 2012, 20, 81–89. [Google Scholar] [CrossRef]
- Izumi, K.; Arai, K.; Barr, B.; Betzwieser, J.; Brooks, A.; Dahl, K.; Doravari, S.; Driggers, J.C.; Korth, W.Z.; Miao, H.; et al. Multicolor cavity metrology. J. Opt. Soc. Am. A 2012, 29, 2092–2103. [Google Scholar] [CrossRef]
- Staley, A.; Martynov, D.; Abbott, R.; Adhikari, R.X.; Arai, K.; Ballmer, S.; Barsotti, L.; Brooks, A.F.; DeRosa, R.T.; Dwyer, S.; et al. Achieving resonance in the Advanced LIGO gravitational-wave interferometer. Class. Quantum Gravity 2014, 31, 245010. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Aso, Y.; Bae, S.; et al. An arm length stabilization system for KAGRA and future gravitational-wave detectors. Class. Quantum Gravity 2020, 37, 035004. [Google Scholar] [CrossRef]
- De Rossi, C.; Brooks, J.; Casanueva Diaz, J.; Chiummo, A.; Genin, E.; Gosselin, M.; Leroy, N.; Mantovani, M.; Montanari, B.; Nocera, F.; et al. Development of a Frequency Tunable Green Laser Source for Advanced Virgo+ Gravitational Waves Detector. Galaxies 2020, 8, 87. [Google Scholar] [CrossRef]
- Cesarini, E.; Lorenzini, M.; Amato, A.; Cagnoli, G.; Cassar, Q.; Dickmann, J.; Granata, M.; Fafone, V.; Heinert, D.; Kroker, S.; et al. The Virgo Coating Collaboration: A detailed study on thermoelasticity in crystalline materials and other research lines. PoS. In Proceedings of the GRAvitational-wave Science&technology Symposium 2018 (GRASS2018), Padova, Italy, 1–2 March 2018. [Google Scholar] [CrossRef]
- Harry, G.M.; Gretarsson, A.M.; Saulson, P.R.; Kittelberger, S.E.; Penn, S.D.; Startin, W.J.; Rowan, S.; Fejer, M.M.; Crooks, D.R.M.; Cagnoli, G.; et al. Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings. Class. Quantum Gravity 2002, 19, 897–917. [Google Scholar] [CrossRef]
- Granata, M.; Coillet, E.; Martinez, V.; Dolique, V.; Amato, A.; Canepa, M.; Margueritat, J.; Martinet, C.; Mermet, A.; Michel, C.; et al. Correlated evolution of structure and mechanical loss of a sputtered silica film. Phys. Rev. Mater. 2018, 2, 053607. [Google Scholar] [CrossRef]
- Puosi, F.; Fidecaro, F.; Capaccioli, S.; Pisignano, D.; Leporini, D. In silico broadband mechanical spectroscopy of amorphous tantala. Phys. Rev. Res. 2019, 1, 033121. [Google Scholar] [CrossRef]
- Amato, A.; Terreni, S.; Granata, M.; Michel, C.; Sassolas, B.; Pinard, L.; Canepa, M.; Cagnoli, G. Observation of a Correlation Between Internal friction and Urbach Energy in Amorphous Oxides Thin Films. Sci. Rep. 2020, 10, 1670. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bersanetti, D.; Patricelli, B.; Piccinni, O.J.; Piergiovanni, F.; Salemi, F.; Sequino, V. Advanced Virgo: Status of the Detector, Latest Results and Future Prospects. Universe 2021, 7, 322. https://doi.org/10.3390/universe7090322
Bersanetti D, Patricelli B, Piccinni OJ, Piergiovanni F, Salemi F, Sequino V. Advanced Virgo: Status of the Detector, Latest Results and Future Prospects. Universe. 2021; 7(9):322. https://doi.org/10.3390/universe7090322
Chicago/Turabian StyleBersanetti, Diego, Barbara Patricelli, Ornella Juliana Piccinni, Francesco Piergiovanni, Francesco Salemi, and Valeria Sequino. 2021. "Advanced Virgo: Status of the Detector, Latest Results and Future Prospects" Universe 7, no. 9: 322. https://doi.org/10.3390/universe7090322
APA StyleBersanetti, D., Patricelli, B., Piccinni, O. J., Piergiovanni, F., Salemi, F., & Sequino, V. (2021). Advanced Virgo: Status of the Detector, Latest Results and Future Prospects. Universe, 7(9), 322. https://doi.org/10.3390/universe7090322






