Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State
Abstract
| 1. Introduction | 2 |
| 2. The Equation of State | 3 |
| 3. Nuclear Physics Input into the Dense Matter EoS | 6 |
| 3.1. Macroscopic Approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 6 |
| 3.1.1. Semi-Empirical Mass Formula and Nuclear Matter . . . . . . . . . | 6 |
| 3.1.2. Liquid Drop Based Models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 7 |
| 3.2. Microscopic Approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 10 |
| 3.2.1. NN Interactions in Free Space . . . . . . . . . . . . . . . . . . . . . . . . . . . | 10 |
| Realistic Potentials . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . | 10 |
| Chiral Effective Field Theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 11 |
| 3.2.2. Density-Dependent NN Interactions . . . . . . . . . . . . . . . . . . . . . | 14 |
| Skyrme Interaction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 14 |
| Relativistic Mean-Field Models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 16 |
| Quark–Meson Coupling Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 17 |
| 4. Astrophysical and Terrestrial Data | 18 |
| 4.1. Neutron Stars: Masses and Radii . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 18 |
| 4.2. GravitationalWaves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 20 |
| 4.2.1. Observation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 20 |
| 4.2.2. Extraction of Information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 21 |
| 4.3. Heavy Ion Collisions at Low and Medium Energies . . . . . . . . . . . . | 21 |
| 4.4. High-Energy Heavy Ion Collisions . . . . . . . . . . . . . . . . . . . . . . . . . . | 23 |
| 5. Concluding Remarks | 24 |
| References | 25 |
1. Introduction
It can be said at once that this approximation will not be as successful in nuclear theory as in the theory of atoms. The main reason for this is the saturation type of the nuclear forces: Any given nuclear particle interacts essentially only with two particles of other kind. Therefore the force between a given pair of particles will be of the same order of magnitude as the force exerted by the whole nucleus on one particle. This is contrary to the assumptions of the Hartree theory. These are that in first approximation the total action of the nucleus on one particle may be represented by an average field, corresponding to the average distribution of all other particles over the nucleus. The correlations between the different particles, i.e., the fact that the motion of one particle is influenced by the instantaneous position of the others, is supposed to cause only small perturbations in the Hartree theory. These assumptions of the Hartree theory are well satisfied in the atomic problem because the force due to the nucleus, and the force corresponding to the average charge distribution of the electrons are very much stronger than the fluctuations of the force caused by, say, a close approach of one other electron to the electron considered. In nuclear physics, the force on one neutron changes by 100 percent or more according to whether a proton happens to be near the neutron or not. Therefore the correlations between the nuclear particles will be of extreme importance for any satisfactory calculation of nuclear energies, and the Hartree method will afford only a poor approximation. In spite of these serious objections against the Hartree method, we are forced to use it because no better method seems practicable at the moment.
2. The Equation of State
3. Nuclear Physics Input into the Dense Matter EoS
3.1. Macroscopic Approach
3.1.1. Semi-Empirical Mass Formula and Nuclear Matter
3.1.2. Liquid Drop Based Models
3.2. Microscopic Approach
3.2.1. NN Interactions in Free Space
Realistic Potentials
Chiral Effective Field Theory
3.2.2. Density-Dependent NN Interactions
Skyrme Interaction
Relativistic Mean-Field Models
Quark–Meson Coupling Model
4. Astrophysical and Terrestrial Data
4.1. Neutron Stars: Masses and Radii
4.2. Gravitational Waves
4.2.1. Observation
4.2.2. Extraction of Information
4.3. Heavy Ion Collisions at Low and Medium Energies
4.4. High-Energy Heavy Ion Collisions
5. Concluding Remarks
In the past quarter of the century physicists have devoted a huge amount of experimentation and mental labor to this problem–probably more man-hours than have been given to any other scientific question in the history of mankind.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bethe, H.A.; Bacher, R.F. Nuclear physics: A stationary states of nuclei. Rev. Mod. Phys. 1936, 8, 82. [Google Scholar] [CrossRef]
- Gamow, G. Mass defect curve and nuclear constitution. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1930, 126, 632–644. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Llanes-Estrada, F.J.; Lope-Oter, E. Hadron matter in neutron stars in view of gravitational wave observations. Prog. Part. Nucl. Phys. 2019, 109, 103715. [Google Scholar] [CrossRef]
- Burgio, G.F.; Vidana, I.; Schulze, H.J.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 103879. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Balberg, S.; Lichtenstadt, I.; Cook, G.B. Roles of hyperons in neutron stars. Astrophys. J. Suppl. 1999, 121, 515–531. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Stone, J.R.; Reinhard, P.G. The Skyrme interaction in finite nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2007, 58, 587–657. [Google Scholar] [CrossRef]
- Stone, J.R.; Dexheimer, V.; Guichon, P.A.M.; Thomas, A.W.; Typel, S. Equation of state of hot dense hyperonic matter in the quark-meson-coupling (QMC-a) model. MNRAS 2021, 502, 3476–3490. [Google Scholar] [CrossRef]
- Fortin, M.; Raduta, A.R.; Avancini, S.; Providência, C. Relativistic hypernuclear compact stars with calibrated equations of state. Phys. Rev. D 2020, 101, 034017. [Google Scholar] [CrossRef]
- Vidaña, I. Hyperons: The strange ingredients of the nuclear equation of state. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180145. [Google Scholar] [CrossRef] [PubMed]
- Weber, F. Quark matter in neutron stars. J. Phys. G Nucl. Part. Phys. 1999, 25, R195–R229. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Alford, M.G. Quark matter in neutron stars. Nucl. Phys. A 2009, 830, 385c–392c. [Google Scholar] [CrossRef]
- Lastowiecki, R.; Blaschke, D.; Fischer, T.; Klähn, T. Quark matter in high-mass neutron stars? Phys. Part. Nucl. 2015, 46, 843–845. [Google Scholar] [CrossRef]
- Weber, F.; Farrell, D.; Spinella, W.M.; Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Maloney, I. Phases of hadron-quark matter in (proto) neutron stars. Universe 2019, 5, 169. [Google Scholar] [CrossRef]
- Baym, G.; Furusawa, S.; Hatsuda, T.; Kojo, T.; Togashi, H. New neutron star equation of state with quark-hadron crossover. Astrophys. J. 2019, 885, 42. [Google Scholar] [CrossRef]
- Spinella, W.M.; Weber, F.; Contrera, G.A.; Orsaria, M.G. Quark matter in neutron stars. In Discoveries at the Frontiers of Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 95–106. [Google Scholar] [CrossRef]
- Li, A.; Miao, Z.; Han, S.; Zhang, B. Constraints on the maximum mass of neutron stars with a quark core from GW170817 and NICER PSR J0030+0451 data. Astrophys. J. 2021, 913, 27. [Google Scholar] [CrossRef]
- Backes, B.C.T.; Marquez, K.D.; Menezes, D.P. Effects of Strong Magnetic Fields on the Hadron-Quark Deconfinement Transition. arXiv 2021, arXiv:2103.14733. [Google Scholar]
- Kapusta, J.I.; Welle, T. Neutron stars with a crossover equation of state. arXiv 2021, arXiv:2103.16633. [Google Scholar]
- Roark, J.; Dexheimer, V. Deconfinement phase transition in proto-neutron-star matter. Phys. Rev. C 2018, 98. [Google Scholar] [CrossRef]
- Roark, J.; Du, X.; Constantinou, C.; Dexheimer, V.; Steiner, A.W.; Stone, J.R. Hyperons and quarks in proto-neutron stars. MNRAS 2019, 486, 5441–5447. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907. [Google Scholar] [CrossRef]
- Pasechnik, R.; Šumbera, M. Phenomenological review on quark-gluon plasma: Concepts vs. observations. Universe 2017, 3, 7. [Google Scholar] [CrossRef]
- Richards, C.B.; Baumgarte, T.W.; Shapiro, S.L. Accretion onto a small black hole at the center of a neutron star. Phys. Rev. D 2021, 103, 104009. [Google Scholar] [CrossRef]
- Suzuki, A. Pion Condensation in Neutron Star Matter. Prog. Theor. Phys. 1976, 55, 1477–1487. [Google Scholar] [CrossRef]
- Hansel, P.; Proszynski, M. Pion condensation in cold dense matter and neutron stars. Astrophys. J. 1982, 258, 306. [Google Scholar] [CrossRef]
- Ellis, P.J.; Knorren, R.; Prakash, M. Kaon condensation in neutron star matter with hyperons. Phys. Lett. B 1995, 349, 11–17. [Google Scholar] [CrossRef]
- Ramos, A.; Schaffner-Bielich, J.; Wambach, J. Kaon condensation in neutron stars. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2001; pp. 175–202. [Google Scholar] [CrossRef]
- Lim, Y.; Kwak, K.; Hyun, C.H.; Lee, C.H. Kaon condensation in neutron stars with skyrme-hartree-fock models. Phys. Rev. C 2014, 89. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Charged ρ-meson condensation in neutron stars. Nucl. Phys. A 2018, 970, 291–315. [Google Scholar] [CrossRef]
- Chamel, N. Superfluidity and superconductivity in neutron stars. J. Astrophys. Astron. 2017, 38, 43. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and superconductivity in neutron stars. In The Physics and Astrophysics of Neutron Stars; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 401–454. [Google Scholar] [CrossRef]
- von Weizsäcker, C.F. Zur theorie der kernmassen. Z. Fuer Phys. 1935, 96, 431–458. [Google Scholar] [CrossRef]
- Kirson, M.W. Mutual influence of terms in a semi-empirical mass formula. Nucl. Phys. A 2008, 798, 29–60. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.H.; Thibault, C. The Ame2003 atomic mass evaluation. Nucl. Phys. A 2003, 729, 337–676. [Google Scholar] [CrossRef]
- Bethe, H.A. Theory of nuclear matter. Annu. Revs. Nucl. Sci. 1971, 21, 93–244. [Google Scholar] [CrossRef]
- Hofstadter, R. Electron scattering and nuclear structure. Rev. Mod. Phys. 1956, 28, 214–254. [Google Scholar] [CrossRef]
- Hofstadter, R.; BumilIer, F.; Yearian, M.R. Electromagnetic structure of the proton and neutron. Rev. Mod. Phys. 1958, 30, 482. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Gayoso, C.A.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; et al. An accurate determination of the neutron skin thickness of 208Pb through parity-violation in electron scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Myers, W.D.; Swiatecki, W.J. Nuclear masses and deformations. Nucl. Phys. 1966, 81, 1. [Google Scholar] [CrossRef]
- Myers, W.D.; Swiatecki, W.J. Average nuclear properties. Ann. Phys. 1969, 55, 395–505. [Google Scholar] [CrossRef]
- Myers, W.D.; Switecki, W.J. The nuclear droplet model for arbitrary shapes. Ann. Phys. 1974, 84, 186. [Google Scholar] [CrossRef]
- Moller, P.; Nix, J.R.; Myers, W.D.; Swiatecki, W.J. Nuclear ground-state masses and deformations. At. Data Nucl. Data Tables 1995, 59, 185–381. [Google Scholar] [CrossRef]
- Möller, P.; Myers, W.D.; Sagawa, H.; Yoshida, S. New finite-range droplet mass model and equation-of-state parameters. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109–110, 1–204. [Google Scholar] [CrossRef]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.; Lee, J.; Lynch, W.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: Experiment, theory, and observation. J. Phys. G Nucl. Part. Phys. 2014, 41, 093001. [Google Scholar] [CrossRef]
- Stone, J.R.; Miller, J.C.; Koncewicz, R.; Stevenson, P.D.; Strayer, M.R. Nuclear matter and neutron-star properties calculated with the Skyrme interaction. Phys. Rev. C 2003, 68. [Google Scholar] [CrossRef]
- Li, B.A.; Ramos, À.; Verde, G.; Vidaña, I. Topical issue on nuclear symmetry energy. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
- Li, B.A.; Krastev, P.G.; Wen, D.H.; Zhang, N.B. Towards understanding astrophysical effects of nuclear symmetry energy. Eur. Phys. J. A 2019, 55. [Google Scholar] [CrossRef]
- Fattoyev, F.; Piekarewicz, J.; Horowitz, C. Neutron skins and neutron stars in the multimessenger era. Phys. Rev. Lett. 2018, 120. [Google Scholar] [CrossRef] [PubMed]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-II on the equation of state of neutron-rich matter. arXiv 2021, arXiv:2101.03193. [Google Scholar]
- Essick, R.; Tews, I.; Landry, P.; Schwenk, A. Astrophysical constraints on the symmetry energy and the neutron skin of 208Pb with minimal modeling assumptions. arXiv 2021, arXiv:2102.10074. [Google Scholar]
- Landry, P.; Essick, R. Nonparametric inference of the neutron star equation of state from gravitational wave observations. Phys. Rev. D 2019, 99, 084049. [Google Scholar] [CrossRef]
- Yue, T.G.; Chen, L.W.; Zhang, Z.; Zhou, Y. Constraints on the Symmetry Energy from PREX-II in the Multimessenger Era. arXiv 2021, arXiv:2102.05267. [Google Scholar]
- Blaizot, J.P. Nuclear compressibilities. Phys. Rep. 1980, 64, 171–248. [Google Scholar] [CrossRef]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55–95. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Gogny, D.; Grammaticos, B. Nuclear compressibility and monopole resonances. Nucl. Phys. A 1976, 265, 315–336. [Google Scholar] [CrossRef]
- Stone, J.R.; Danielewicz, P.; Iwata, Y. Proton and neutron density distributions at supranormal density in low- and medium-energy heavy-ion collisions. Phys. Rev. C 2017, C96, 014612. [Google Scholar] [CrossRef]
- Reid, R.V. Local phenomenological nucleon-nucleon potentials. Ann. Phys. 1968, 50, 411–448. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high-quality N-Npotential models. Phys. Rev. C 1994, 49, 2950. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995, 51, 38–51. [Google Scholar] [CrossRef]
- Aghbolaghi, Z.A.; Bigdeli, M. Argonne family potentials and neutron star matter equation of state. Eur. Phys. J. Plus 2019, 134. [Google Scholar] [CrossRef]
- Machleidt, R. The meson theory of nuclear forces and nuclear structure. In Advances in Nuclear Physics; Negele, J.W., Vogt, E., Eds.; Springer US: Boston, MA, USA, 1989; Volume 19, pp. 189–376. [Google Scholar] [CrossRef]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001, 63. [Google Scholar] [CrossRef]
- Coester, F.; Cohen, S.; Day, B.; Vincent, C.M. Variation in nuclear-matter binding energies with phase-shift-equivalent two-body potentials. Phys. Rev. C 1970, 1, 769. [Google Scholar] [CrossRef]
- Coester, F.; Day, B.; Goodman, A. Variation of nuclear-matter binding energies with phase-shift-equivalent two-body potentials. Phys. Rev. C 1972, 5, 1135. [Google Scholar] [CrossRef]
- Li, Z.H.; Lombardo, U.; Schulze, H.J.; Zuo, W.; Chen, L.W.; Ma, H.R. Nuclear matter saturation point and symmetry energy with modern nucleon-nucleon potentials. Phys. Rev. C 2006, 74. [Google Scholar] [CrossRef]
- Brueckner, K.A.; Levinson, C.A.; Mahmoud, H.M. Two-body forces and nuclear saturation. I. Central forces. Phys. Rev. 1954, 95, 217. [Google Scholar] [CrossRef]
- Davies, K.T.R.; Baranger, M.; Tarbutton, R.M.; Kuo, T.T.S. Brueckner-Hartree-Fock Calculations of Spherical Nuclei in an Harmonic-Oscillator Basis. Phys. Rev. 1969, 177, 1519–1526. [Google Scholar] [CrossRef]
- Davies, K.T.R.; McCarthy, R.J. Brueckner-Hartree-Fock calculations of spherical nuclei in a harmonic-oscillator basis. III. Renormalized calculations using the Reid potential. Phys. Rev. C 1971, 4, 81–97. [Google Scholar] [CrossRef]
- McCarthy, R.J.; Davies, K.T.R. Self-Consistent Occupation Probabilities in Brueckner-Hartree-Fock Calculations. Phys. Rev. C 1970, 1, 1644–1647. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F. Properties of the nuclear medium. Rep. Prog. Phys. 2012, 75, 026301. [Google Scholar] [CrossRef] [PubMed]
- Li, G.Q.; Machleidt, R.; Brockmann, R. Properties of dense nuclear and neutron matter with relativistic nucleon-nucleon interactions. Phys. Rev. C 1992, 45, 2782. [Google Scholar] [CrossRef] [PubMed]
- Pandharipande, V.R.; Wiringa, R.B. Variations on a theme of nuclear matter. Rev. Mod. Phys. 1979, 51, 821–861. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Pandharipande, V.R. Variational calculations of asymmetric nuclear matter. Nucl. Phys. A 1981, 369, 470–482. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Ramanan, S.; Schwenk, A. Convergence of the Born series with low-momentum interactions. Nucl. Phys. A 2006, 773, 203–220. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Ramanan, S.; Schwenk, A. Low-momentum interactions with smooth cutoffs. Nucl. Phys. A 2007, 784, 79–103. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Platter, L. Density matrix expansion for low-momentum interactions. Eur. Phys. J. A 2009, 39, 219–241. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys. 2010, 65, 94–147. [Google Scholar] [CrossRef]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288–292. [Google Scholar] [CrossRef]
- Weinberg, S. Three-body interactions among nucleons and pions. Phys. Lett. B 1992, 295, 114–121. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1–75. [Google Scholar] [CrossRef]
- Sammarruca, F.; Chen, B.; Coraggio, L.; Itaco, N.; Machleidt, R. Dirac-Brueckner-Hartree-Fock versus chiral effective field theory. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R.; Nosyk, Y. Nucleon-nucleon scattering up to N5LO in chiral effective field theory. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Drischler, C.; Furnstahl, R.; Melendez, J.; Phillips, D. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A Bayesian approach with correlated uncertainties. Phys. Rev. Lett. 2020, 125. [Google Scholar] [CrossRef] [PubMed]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral effective field theory and the high-density nuclear equation of state. arXiv 2021. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R.; Nosyk, Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys. Rev. C 2017, 96. [Google Scholar] [CrossRef]
- Hoppe, J.; Drischler, C.; Hebeler, K.; Schwenk, A.; Simonis, J. Probing chiral interactions up to next-to-next-to-next-to-leading order in medium-mass nuclei. Phys. Rev. C 2019, 100. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Chiral interactions up to N3LO and nuclear saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef]
- Carbone, A.; Polls, A.; Rios, A. Microscopic predictions of the nuclear matter liquid-gas phase transition. Phys. Rev. C 2018, 98. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J.W. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef]
- Lonardoni, D.; Tews, I.; Gandolfi, S.; Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Res. 2020, 2. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Baldo, M.; Bombaci, I.; Burgio, G.F. Microscopic nuclear equation of state with three-body forces and neutron star structure. Astron. Astrophys. 1997, 328, 274. [Google Scholar]
- Muether, H.; Prakash, M.; Ainsworth, T.L. Nuclear symmetry energy in relativistic Brueckner-Hartree-Fock calculations. Phys. Lett. B 1987, 199, 469. [Google Scholar] [CrossRef]
- Gogny, D.; Padjen, R. The propagation and damping of the collective modes in nuclear matter. Nucl. Phys. A 1977, 293, 365–378. [Google Scholar] [CrossRef]
- Decharge, J.; Gogny, D. Hartree-Fock-Bogolyubov calculation with D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [Google Scholar] [CrossRef]
- Moszkowski, S.A. Nuclear surface properties with a simple effective interaction. Phys. Rev. C 1970, 2, 402. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. CVII. The nuclear surface. Philos. Mag. 1956, 1, 1043–1054. [Google Scholar] [CrossRef]
- Bell, J.S.; Skyrme, T.H.R. CVIII. The nuclear spin-orbit coupling. Philos. Mag. 1956, 1, 1055–1068. [Google Scholar] [CrossRef]
- Skyrme, T. The spin-orbit interaction in nuclei. Nucl. Phys. 1958–1959, 9, 635–640. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The effective nuclear potential. Nucl. Phys. 1959, 9, 615. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities part II. Nuclei far from stability. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Klupfel, P.; Reinhard, P.G.; Burvenich, T.J.; Maruhn, J.A. Variations on a theme by Skyrme: A systematic study of adjustments of model parameters. Phys. Rev. 2009, C79, 034310. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Colò, G.; Sagawa, H. New Skyrme interaction with improved spin-isospin properties. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Margueron, J.; Grasso, M.; Goriely, S.; Colò, G.; Sagawa, H. Extended Skyrme Interaction in the spin channel. Prog. Theor. Phys. Suppl. 2012, 196, 172–175. [Google Scholar] [CrossRef][Green Version]
- Li, A.; Zhou, X.R.; Sagawa, H. Tensor force and shape evolution of Si isotopes in the Skyrme–Hartree–Fock model. Prog. Theor. Exp. Phys. 2013, 2013. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Hartree-Fock-Bogoliubov nuclear mass model with 0.50 MeV accuracy based on standard forms of Skyrme and pairing functionals. Phys. Rev. C 2013, 88. [Google Scholar] [CrossRef]
- Goriely, S. Further explorations of Skyrme–Hartree–Fock–Bogoliubov mass formulas. XV: The spin–orbit coupling. Nucl. Phys. A 2015, 933, 68–81. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XVI. Inclusion of self-energy effects in pairing. Phys. Rev. C 2016, 93, 034337. [Google Scholar] [CrossRef]
- Reinhard, P.G. Estimating the relevance of predictions from the Skyrme-Hartree-Fock model. Phys. Scr. 2015, 91, 023002. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Tondeur, F.; Brack, M.; Farine, M.; Pearson, J.M. Static nuclear properties and the parametrisation of Skyrme forces. Nucl. Phys. A 1984, 420, 297–319. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Sá Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Carlsson, B.G.; Dobaczewski, J.; Kortelainen, M. Local nuclear energy density functional at next-to-next-to-next-to-leading order. Phys. Rev. C 2008, 78. [Google Scholar] [CrossRef]
- Raimondi, F.; Carlsson, B.G.; Dobaczewski, J. Effective pseudopotential for energy density functionals with higher-order derivatives. Phys. Rev. C 2011, 83. [Google Scholar] [CrossRef]
- Carlsson, B.G.; Toivanen, J.; von Barth, U. Fluctuating parts of nuclear ground-state correlation energies. Phys. Rev. C 2013, 87. [Google Scholar] [CrossRef]
- Davesne, D.; Becker, P.; Pastore, A.; Navarro, J. Infinite matter properties and zero-range limit of non-relativistic finite-range interactions. Ann. Phys. 2016, 375, 288–312. [Google Scholar] [CrossRef]
- Walecka, J.D. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Chin, S.A. A relativistic many-body theory of high density matter. Ann. Phys. 1977, 108, 301–367. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. relativistic calculation of nuclear matter and nuclear surface. Nucl. Phys. A 1977, 292, 413. [Google Scholar] [CrossRef]
- Serot, B.D. A relativistic nuclear field theory with π and ρ mesons. Phys. Lett. B 1979, 86, 146–150. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. Relativistic nuclear many-body theory. In Recent Progress in Many-Body Theories; Springer US: Boston, MA, USA, 1992; Volume 16, pp. 49–92. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Toki, H. Relativistic equation of state of nuclear matter for the supernova explosion and the birth of neutron stars. Astrophys. J. 1994, 422, 700. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Finelli, P.; Ring, P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys. Rev. C 2002, 66. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71. [Google Scholar] [CrossRef]
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I-Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Hirata, D.; Toki, H.; Sagawa, H. Comparison of the relativistic mean-field theory and the Skyrme Hartree-Fock theory for properties of nuclei and nuclear matter. Nucl. Phys. A 1993, 552, 437–450. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.H.; Reinhard, P.G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121–180. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193–263. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A possible quark mechanism for the saturation of nuclear matter. Phys. Lett. B 1988, 200, 235. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Saito, K.; Rodionov, E.N.; Thomas, A.W. The role of nucleon structure in finite nuclei. Nucl. Phys. A 1996, 601, 349. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Quark–Meson-Coupling (QMC) model for finite nuclei, nuclear matter and beyond. Prog. Part. Nucl. Phys. 2018, 100, 262–297. [Google Scholar] [CrossRef]
- Rikovska-Stone, J.; Guichon, P.A.M.; Matevosyan, H.H.; Thomas, A.W. Cold uniform matter and neutron stars in the quark-mesons-coupling model. Nucl. Phys. A 2007, 792, 341–369. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOgrav nine-year data set: Mass and geometric measurements of binary millisecond pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year data set: High-precision timing of 45 millisecond pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Panda, P.K.; Menezes, D.P.; Providência, C. Hybrid stars in the quark-meson coupling model with superconducting quark matter. Phys. Rev. C 2004, 69, 025207. [Google Scholar] [CrossRef]
- Menezes, D.P.; Panda, P.K.; Providência, C. Kaon condensation in the quark-meson coupling model and compact stars. Phys. Rev. C 2005, 72, 035802. [Google Scholar] [CrossRef]
- Panda, P.K.; Providência, C.; Menezes, D.P. Warm stellar matter within the quark-meson-coupling model. Phys. Rev. C 2010, 82, 045801. [Google Scholar] [CrossRef]
- Panda, P.K.; Santos, A.M.S.; Menezes, D.P.; Providência, C. Compact stars within a soft symmetry energy quark-meson-coupling model. Phys. Rev. C 2012, 85, 055802. [Google Scholar] [CrossRef]
- Miyatsu, T.; Katayama, T.; Saito, K. Effects of Fock term, tensor coupling and baryon structure variation on a neutron star. Phys. Lett. 2012, B709, 242–246. [Google Scholar] [CrossRef]
- Miyatsu, T.; Yamamuro, S.; Nakazato, K. A new equation of state for neutron star matter with nuclei in the crust and hyperons in the core. Astrophys. J. 2013, 777, 4. [Google Scholar] [CrossRef]
- Panda, P.K.; Menezes, D.P.; Providência, C. Effects of the symmetry energy on the kaon condensates in the quark-meson coupling model. Phys. Rev. C 2014, 89, 045803. [Google Scholar] [CrossRef]
- Bohr, H.; Moszkowski, S.A.; Panda, P.K.; Providência, C.; da Providência, J. QMC approach based on the Bogoliubov independent quark model of the nucleon. Int. J. Mod. Phys. 2016, E25, 1650007. [Google Scholar] [CrossRef]
- Lourenço, O.; Lenzi, C.H.; Dutra, M.; Frederico, T.; Bhuyan, M.; Negreiros, R.; Flores, C.V.; Grams, G.; Menezes, D.P. Neutron star cooling and GW170817 constraint within quark-meson coupling models. Chin. Phys. C 2021, 45, 025101. [Google Scholar] [CrossRef]
- Stone, J.R. Neutron stars interiors: Theory and reality. Eur. Phys. J. A 2016, 52, 66. [Google Scholar] [CrossRef]
- Martinez, K.L.; Thomas, A.W.; Stone, J.R.; Guichon, P.A.M. Parameter optimization for the latest quark-meson coupling energy-density functional. Phys. Rev. C 2019, 100, 024333. [Google Scholar] [CrossRef]
- Stone, J.R.; Morita, K.; Guichon, P.A.M.; Thomas, A.W. Physics of even-even superheavy nuclei with 96 < Z < 110 in the quark-meson-coupling model. Phys. Rev. C 2019, 100. [Google Scholar] [CrossRef]
- Martinez, K.L.; Thomas, A.W.; Guichon, P.A.M.; Stone, J.R. Tensor and pairing interactions within the quark-meson coupling energy-density functional. Phys. Rev. C 2020, 102, 034304. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined mass and geometric measurements of the high-mass PSR J0740+6620. arXiv 2021, arXiv:2104.00880. [Google Scholar]
- Özel, F.; Freire, P. Masses, radii, and the equation of state of neutron stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter equation of state. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Raithel, C.A. Constraints on the Neutron Star Equation of State from GW170817. Eur. Phys. J. A 2019, 55, 80. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Wei, J.B. Nuclear physics aspects of the GW170817 neutron star merger event. Nucl. Part. Phys. Proc. 2019, 306–308, 61. [Google Scholar] [CrossRef]
- Weih, L.R.; Most, E.R.; Rezzolla, L. Optimal neutron-star mass ranges to constrain the equation of state of nuclear matter with electromagnetic and gravitational-wave observations. Astrophys. J. 2019, 881, 73. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625. [Google Scholar] [CrossRef]
- Al-Mamun, M.; Steiner, A.W.; Nättilä, J.; Lange, J.; O’Shaughnessy, R.; Tews, I.; Gandolfi, S.; Heinke, C.; Han, S. Combining electromagnetic and gravitational-wave constraints on neutron-star masses and radii. Phys. Rev. Lett. 2021, 126. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Landry, P. Inferring neutron star properties from GW170817 with universal relations. Phys. Rev. D 2019, 99. [Google Scholar] [CrossRef]
- Essick, R.; Tews, I.; Landry, P.; Reddy, S.; Holz, D.E. Direct astrophysical tests of chiral effective field theory at supranuclear densities. Phys. Rev. C 2020, 102. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef]
- Radice, D.; Dai, L. Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 2019, 55. [Google Scholar] [CrossRef]
- d’Etivaux, N.B.; Guillot, S.; Margueron, J.; Webb, N.; Catelan, M.; Reisenegger, A. New constraints on the nuclear equation of state from the thermal emission of neutron stars in quiescent low-mass X-ray binaries. Astrophys. J. 2019, 887, 48. [Google Scholar] [CrossRef]
- Jiang, J.L.; Tang, S.P.; Shao, D.S.; Han, M.Z.; Li, Y.J.; Wang, Y.Z.; Jin, Z.P.; Fan, Y.Z.; Wei, D.M. The equation of state and some key parameters of neutron stars: Constraints from GW170817, the nuclear data, and the low-mass X-ray binary data. Astrophys. J. 2019, 885, 39. [Google Scholar] [CrossRef]
- Jiang, J.L.; Tang, S.P.; Wang, Y.Z.; Fan, Y.Z.; Wei, D.M. PSR J0030-0451, GW170817, and the nuclear data: Joint constraints on equation of state and bulk properties of neutron stars. Astrophys. J. 2020, 892, 55. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef]
- Landry, P.; Essick, R.; Chatziioannou, K. Nonparametric constraints on neutron star matter with existing and upcoming gravitational wave and pulsar observations. Phys. Rev. D 2020, 101. [Google Scholar] [CrossRef]
- Raithel, C.; Ozel, F.; Psaltis, D. Optimized statistical approach for comparing multi-messenger neutron star data. Astrophys. J. 2021, 908, 103. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR j0030-0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER view of PSR j0030-0451: Millisecond pulsar parameter estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Watts, A.L.; Andersson, N.; Chakrabarty, D.; Feroci, M.; Hebeler, K.; Israel, G.; Lamb, F.K.; Miller, C.; Morsink, S.; Ozel, F.; et al. Colloquium: Measuring the neutron star equation of state using X-ray timing. Rev. Mod. Phys. 2016, 88. [Google Scholar] [CrossRef]
- Reardon, D.J.; Hobbs, G.; Coles, W.; Levin, Y.; Keith, M.J.; Bailes, M.; Bhat, N.D.R.; Burke-Spolaor, S.; Dai, S.; Kerr, M.; et al. Timing analysis for 20 millisecond pulsars in the Parkes Pulsar Timing Array. MNRAS 2015, 455, 1751–1769. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics and General Relativity, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Rosswog, S.; Liebendörfer, M. High-resolution calculations of merging neutron stars—II. Neutrino emission. MNRAS 2003, 342, 673–689. [Google Scholar] [CrossRef]
- Rosswog, S.; Price, D. MAGMA: A three-dimensional, Lagrangian magnetohydrodynamics code for merger applications. Mon. Not. R. Astron. Soc. 2007, 379, 915–931. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Gravitational waves and neutrino emission from the merger of binary neutron stars. Phys. Rev. Lett. 2011, 107, 051102. [Google Scholar] [CrossRef] [PubMed]
- Paschalidis, V.; Etienne, Z.B.; Shapiro, S.L. Importance of cooling in triggering the collapse of hypermassive neutron stars. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- Endrizzi, A.; Ciolfi, R.; Giacomazzo, B.; Kastaun, W.; Kawamura, T. General relativistic magnetohydrodynamic simulations of binary neutron star mergers with the APR4 equation of state. Class. Quantum Gravity 2016, 33, 164001. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint constraint on the neutron star equation of state from multimessenger observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef]
- Perego, A.; Bernuzzi, S.; Radice, D. Thermodynamics conditions of matter in neutron star mergers. Eur. Phys. J. A 2019, 55. [Google Scholar] [CrossRef]
- Bernuzzi, S. Neutron star merger remnants. Gen. Relativ. Gravit. 2020, 52, 108. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A. The dynamics of binary neutron star mergers and GW170917. Annu. Rev. Nucl. Part. Sci. 2020, 70, 95. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Cowperthwaite, P.S.; Berger, E.; Villar, V.A.; Metzger, B.D.; Nicholl, M.; Chornock, R.; Blanchard, P.K.; Fong, W.; Margutti, R.; Soares-Santos, M.; et al. The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. Astrophys. J. 2017, 848, L17. [Google Scholar] [CrossRef]
- Breschi, M.; Bernuzzi, S.; Zappa, F.; Agathos, M.; Perego, A.; Radice, D.; Nagar, A. Kilohertz gravitational waves from binary neutron star remnants: Time-domain model and constraints on extreme matter. Phys. Rev. D 2019, 100. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a compact binary coalescence with total mass ∼ 3.4 M ⊙. Astrophys. J. 2020, 892, L3. [Google Scholar] [CrossRef]
- Dexheimer, V.; Gomes, R.O.; Klähn, T.; Han, S.; Salinas, M. GW190814 as a massive rapidly-rotating neutron star with exotic degrees of freedom. Phys. Rev. C 2020, 103, 025808. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. GW190814 secondary component with mass 2.50–2.67 M⊙ as a superfast pulsar. Astrophys. J. 2020, 902, 38. [Google Scholar] [CrossRef]
- Biswas, B.; Nandi, R.; Char, P.; Bose, S.; Stergioulas, N. GW190814: On the properties of the secondary component of the binary. Mon. Not. R. Astron. Soc. 2021, 505, 1600–1606. [Google Scholar] [CrossRef]
- Demircik, T.; Ecker, C.; Järvinen, M. Rapidly spinning compact stars with deconfinement phase transition. Astrophys. J. Lett. 2021, 907, L37. [Google Scholar] [CrossRef]
- Roupas, Z. Secondary component of gravitational-wave signal GW190814 as an anisotropic neutron star. Astrophys. Space Sci. 2021, 366, 1–5. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Loeb, A. Formation of mass gap objects in highly asymmetric mergers. Astrophys. J. 2020, 899, L15. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Reed, B. GW190814: Impact of a 2.6 solar mass neutron star on nucleonic equations of state. arXiv 2020, arXiv:2007.03799. [Google Scholar]
- Lim, Y.; Bhattacharya, A.; Holt, J.W.; Pati, D. Revisiting constraints on the maximum neutron star mass in light of GW190814. arXiv 2020, arXiv:2007.06526. [Google Scholar]
- Godzieba, D.A.; Radice, D.; Bernuzzi, S. On the maximum mass of neutron stars and GW190814. Astrophys. J. 2021, 908, 122. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.; et al. Search for post-merger gravitational waves from the remnant of the binary neutron star merger GW170817. Astrophys. J. 2017, 851, L16. [Google Scholar] [CrossRef]
- Lindblom, L. Causal representations of neutron-star equations of state. Phys. Rev. D 2018, 97, 123019. [Google Scholar] [CrossRef]
- Martinon, G.; Maselli, A.; Gualtieri, L.; Ferrari, V. Rotating protoneutron stars: Spin evolution, maximum mass, and I-Love-Q relations. Phys. Rev. D 2014, 90, 064026. [Google Scholar] [CrossRef]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. MNRAS 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate universal relations for neutron stars and quark stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Wei, J.B.; Figura, A.; Burgio, G.F.; Chen, H.; Schulze, H.J. Neutron star universal relations with microscopic equations of state. J. Phys. G Nucl. Part. Phys. 2019, 46, 034001. [Google Scholar] [CrossRef]
- Lenka, S.S.; Char, P.; Banik, S. Properties of massive rotating protoneutron stars with hyperons: Structure and universality. J. Phys. G Nucl. Part. Phys. 2019, 46, 105201. [Google Scholar] [CrossRef]
- Raduta, A.R.; Oertel, M.; Sedrakian, A. Proto-neutron stars with heavy baryons and universal relations. MNRAS 2020, 499, 914–931. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Stone, J.R.; Danielewicz, P.; Iwata, Y. Coulomb effects in low- and medium-energy heavy-ion collisions. in press.
- Zhang, Z.; Ko, C.M. Pion production in a transport model based on mean fields from chiral effective field theory. Phys. Rev. C 2018, 98. [Google Scholar] [CrossRef]
- Zhang, Z.; Lim, Y.; Holt, J.W.; Ko, C.M. Nuclear dipole polarizability from mean-field modeling constrained by chiral effective field theory. Phys. Lett. B 2018, 777, 73–78. [Google Scholar] [CrossRef]
- Aichelin, J.; Ko, C.M. Subthreshold Kaon Production as a Probe of the Nuclear Equation of State. Phys. Rev. Lett. 1985, 55, 2661–2663. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.M. Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 1974–1977. [Google Scholar] [CrossRef] [PubMed]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Estee, J.; Lynch, W.; Tsang, C.; Barney, J.; Jhang, G.; Tsang, M.; Wang, R.; Kaneko, M.; Lee, J.; Isobe, T.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126. [Google Scholar] [CrossRef]
- Haensel, P. Non-equilibrium neutrino emissivities and opacities of neutron star matter. Astron. Astrophys. 1992, 262, 131. [Google Scholar]
- Gourgoulhon, E.; Haensel, P. Upper bounds on the neutrono burst from collapse of a neutron star into a black hole. Astron. Astrophys. 1993, 271, 187. [Google Scholar]
- Stephanov, M. QCD Phase Diagram and the Critical Point. Prog. Theor. Phys. Suppl. 2004, 153, 139–156. [Google Scholar] [CrossRef]
- Begun, V.V.; Gaździcki, M.; Gorenstein, M.I. Hadron-resonance gas at freeze-out: Reminder on the importance of repulsive interactions. Phys. Rev. C 2013, 88. [Google Scholar] [CrossRef]
- Xu, J.; Ko, C.M. Chemical freeze-out in relativistic heavy-ion collisions. Phys. Lett. B 2017, 772, 290–293. [Google Scholar] [CrossRef]
- Sagun, V.V.; Bugaev, K.A.; Ivanytskyi, A.I.; Yakimenko, I.P.; Nikonov, E.G.; Taranenko, A.V.; Greiner, C.; Blaschke, D.B.; Zinovjev, G.M. Hadron resonance gas model with induced surface tension. Eur. Phys. J. A 2018, 54. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Hadron yields in central nucleus-nucleus collisions, the statistical hadronization model and the QCD phase diagram. arXiv 2021, arXiv:2101.05747. [Google Scholar]
- Reichert, T.; Inghirami, G.; Bleicher, M. Probing chemical freeze-out criteria in relativistic nuclear collisions with coarse grained transport simulations. Eur. Phys. J. A 2020, 56. [Google Scholar] [CrossRef]
- Sun, X.; Masui, H.; Poskanzer, A.M.; Schmah, A. Blast wave fits to elliptic flow data atsNN=7.7–2760GeV. Phys. Rev. C 2015, 91. [Google Scholar] [CrossRef]
- Hanauske, M.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Bovard, L.; Most, E.R.; Papenfort, L.J.; Schramm, S.; Stöcker, H. Neutron star mergers: Probing the EoS of hot, dense matter by gravitational waves. Particles 2019, 2, 4. [Google Scholar] [CrossRef]
- Sagun, V.V.; Lopes, I.; Ivanytskyi, A.I. The Induced Surface Tension Contribution for the Equation of State of Neutron Stars. Astrophys. J. 2019, 871, 157. [Google Scholar] [CrossRef]
- Bethe, H.A. What holds the nucleus together. Sci. Am. 1953, 189, 58. [Google Scholar] [CrossRef]
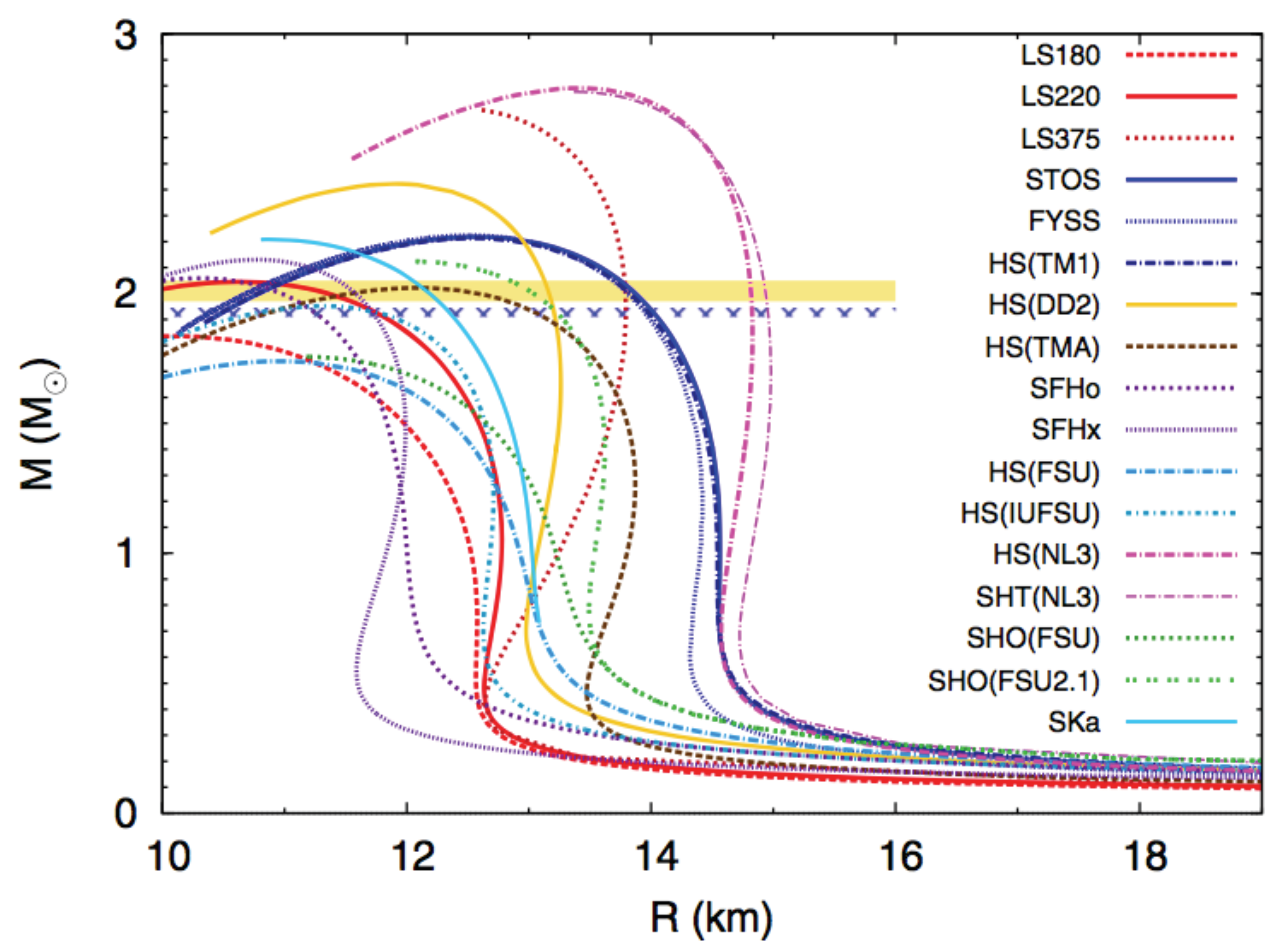
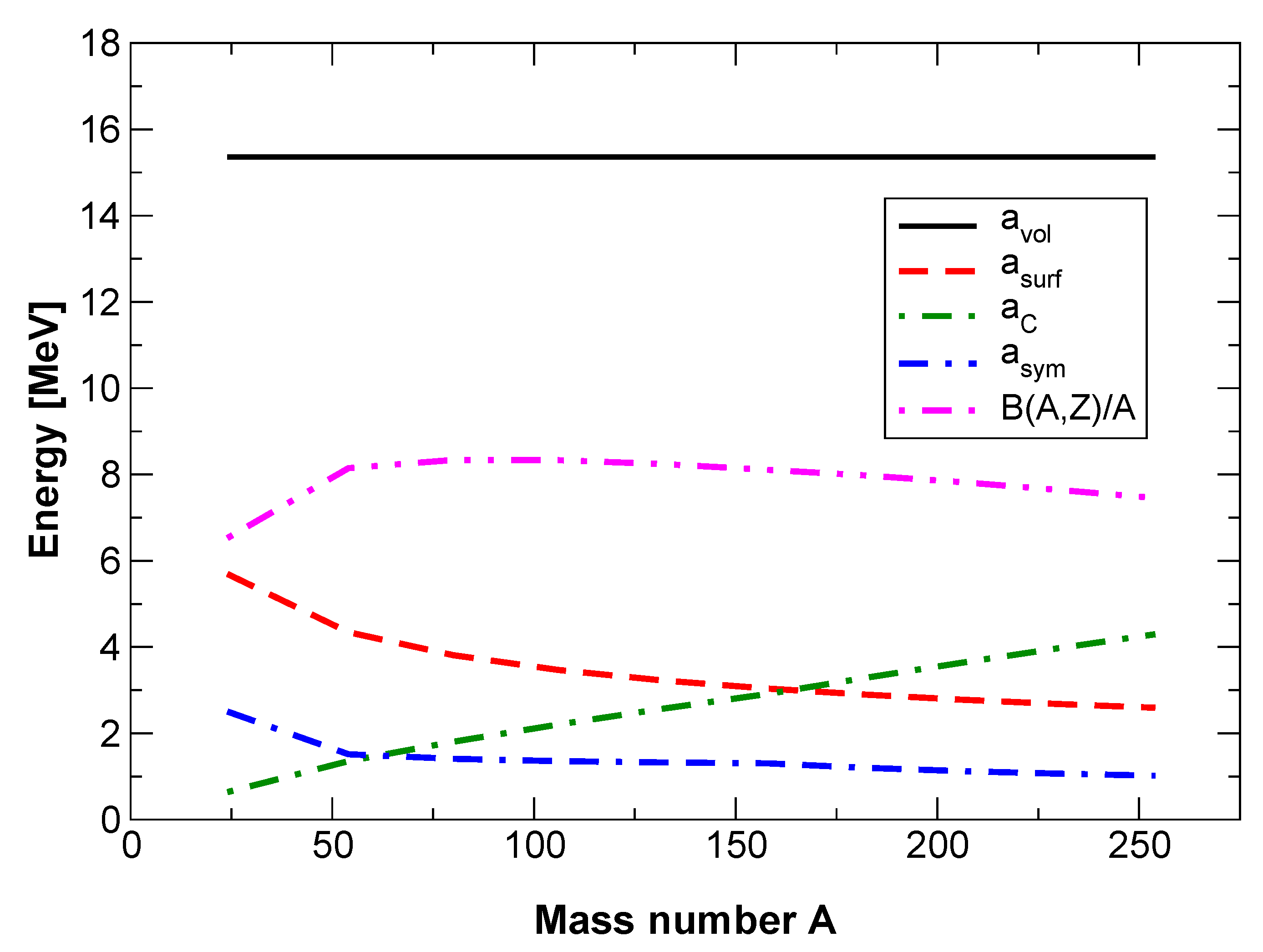
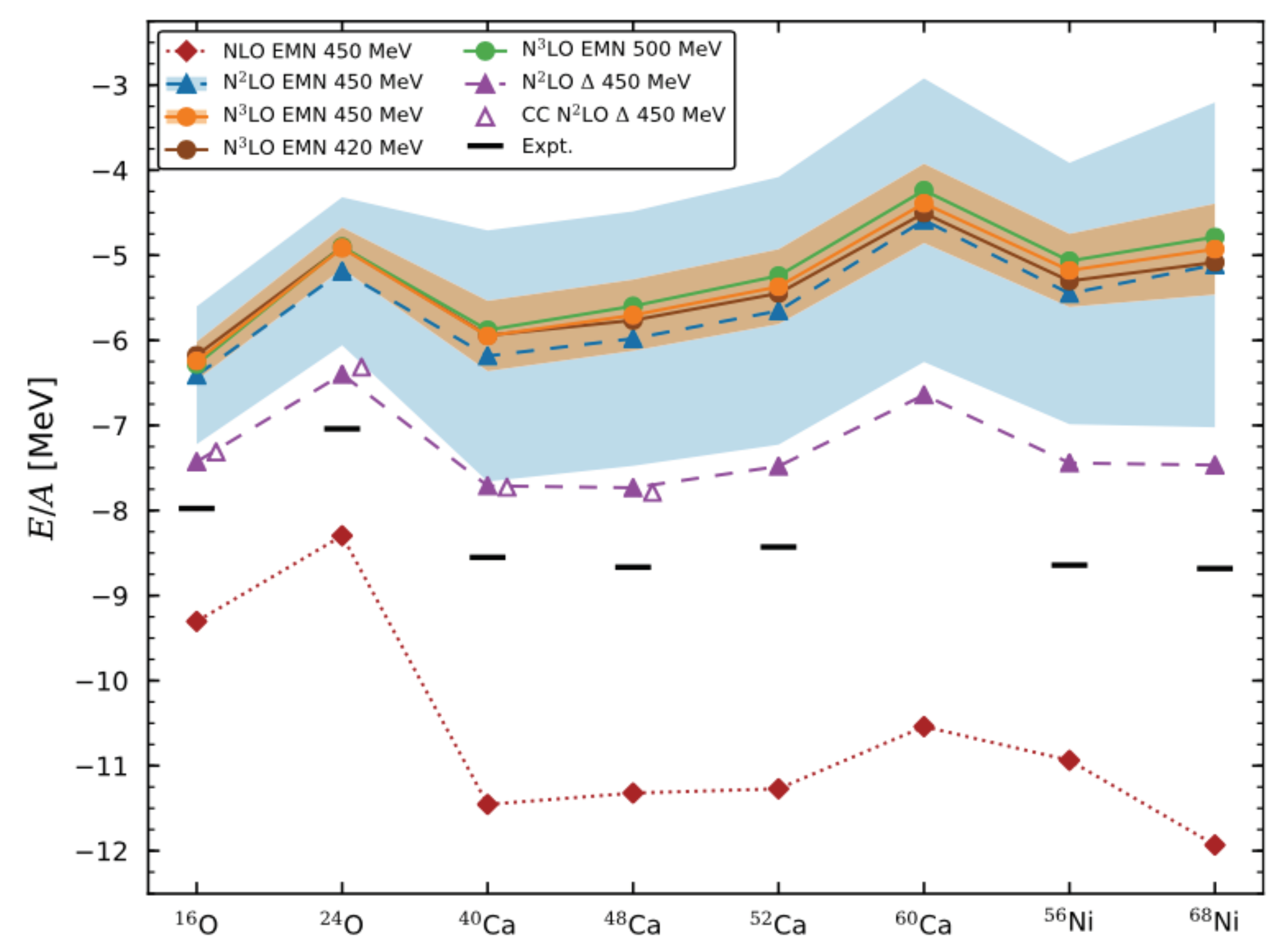
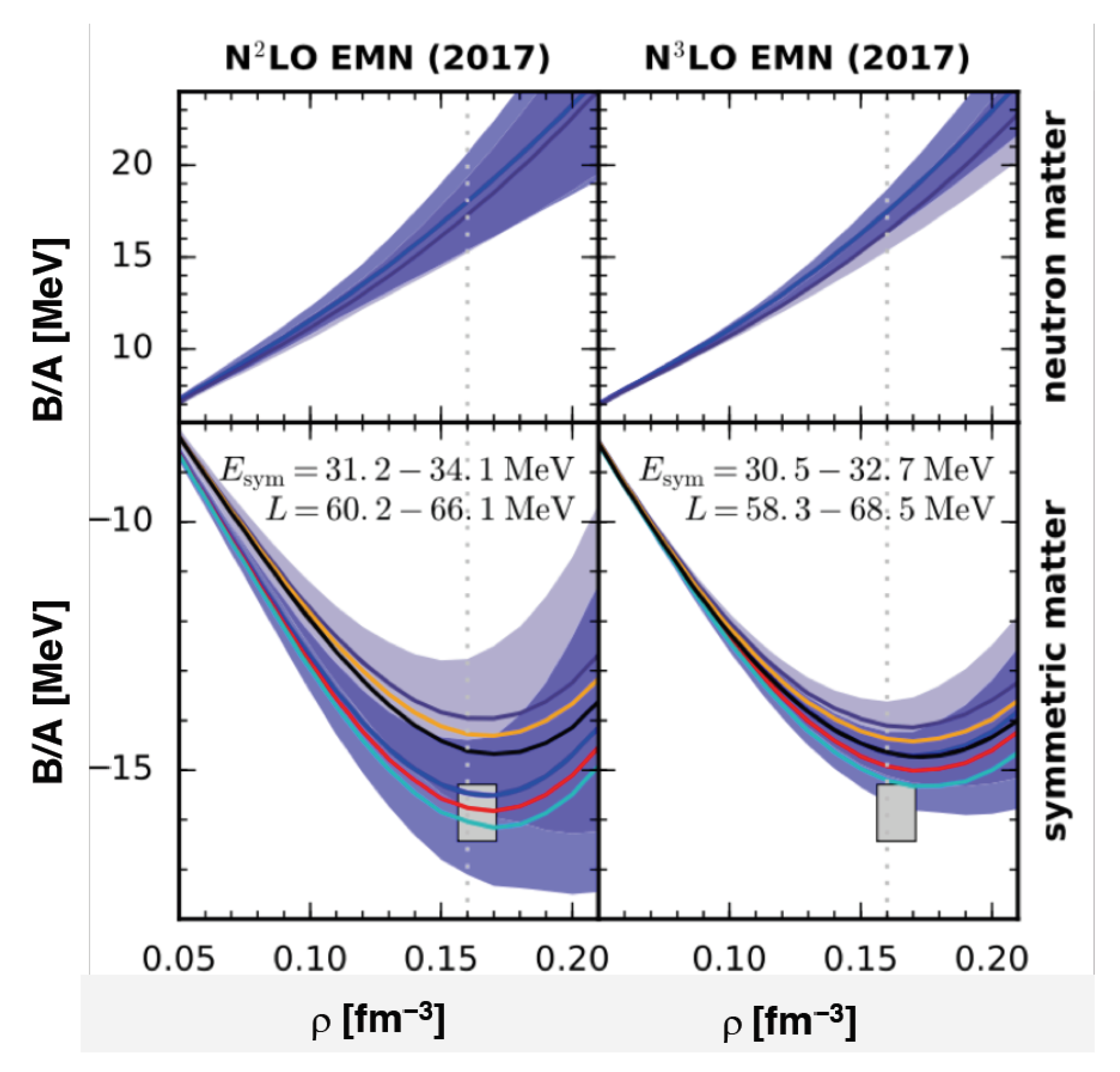
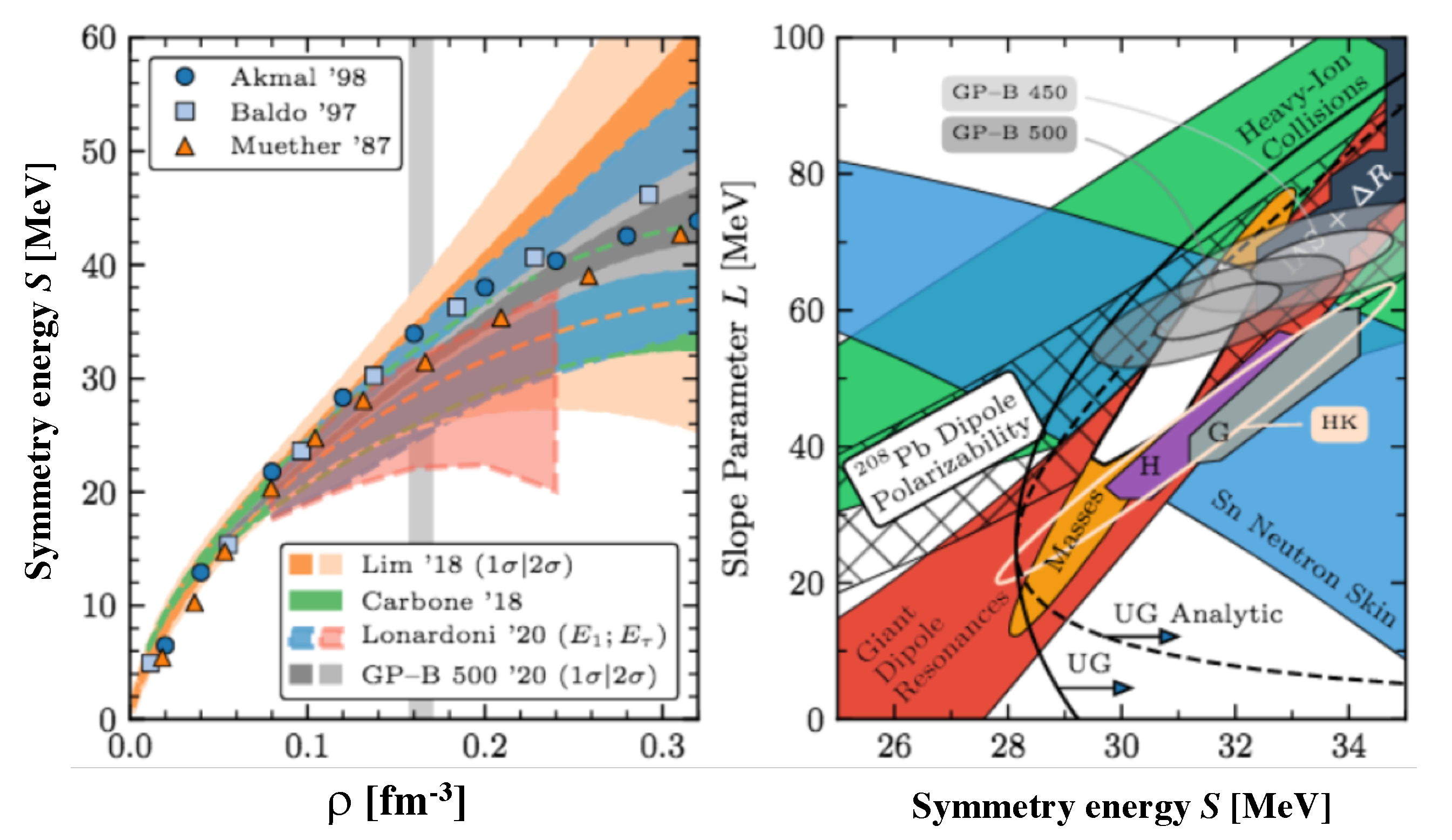
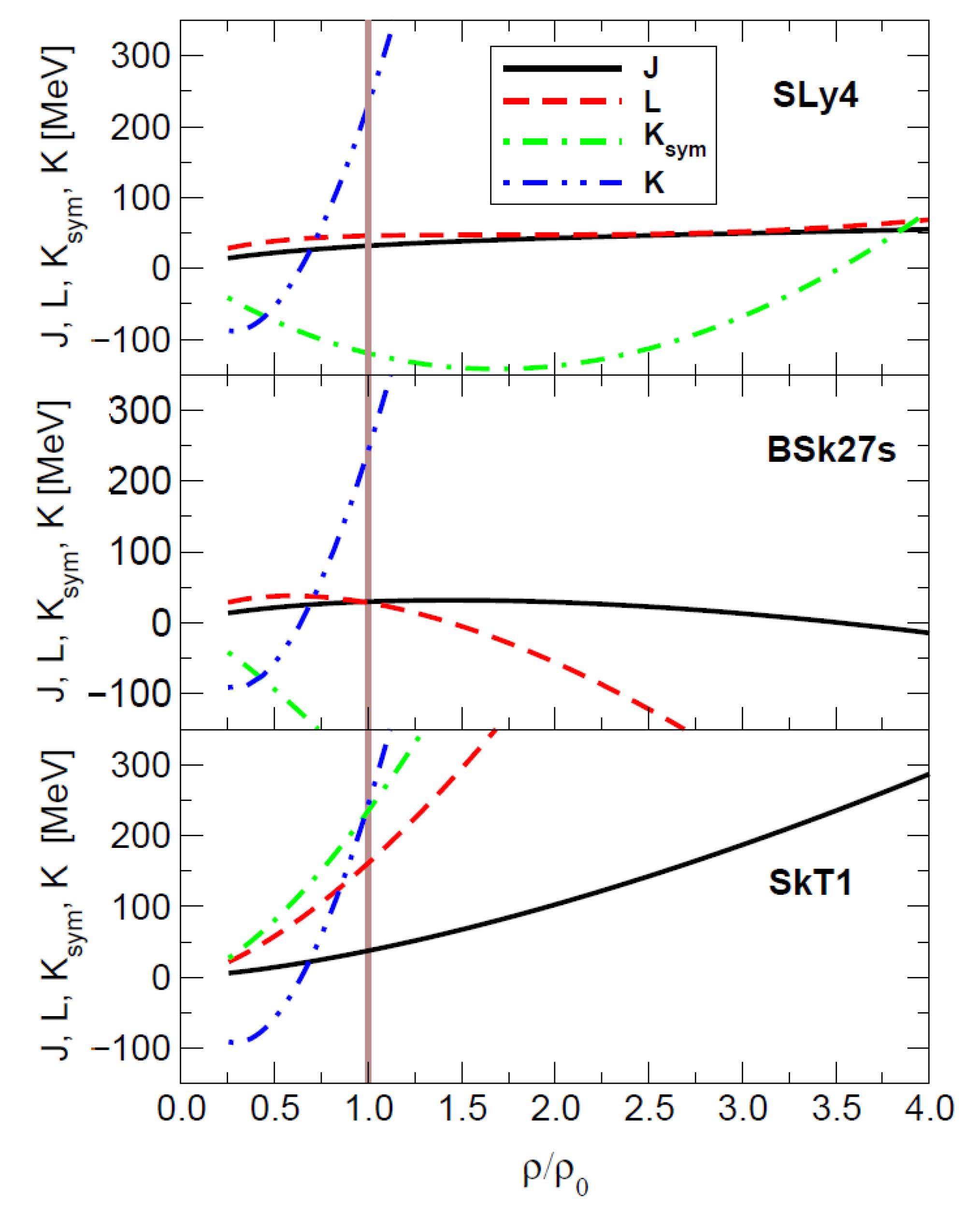
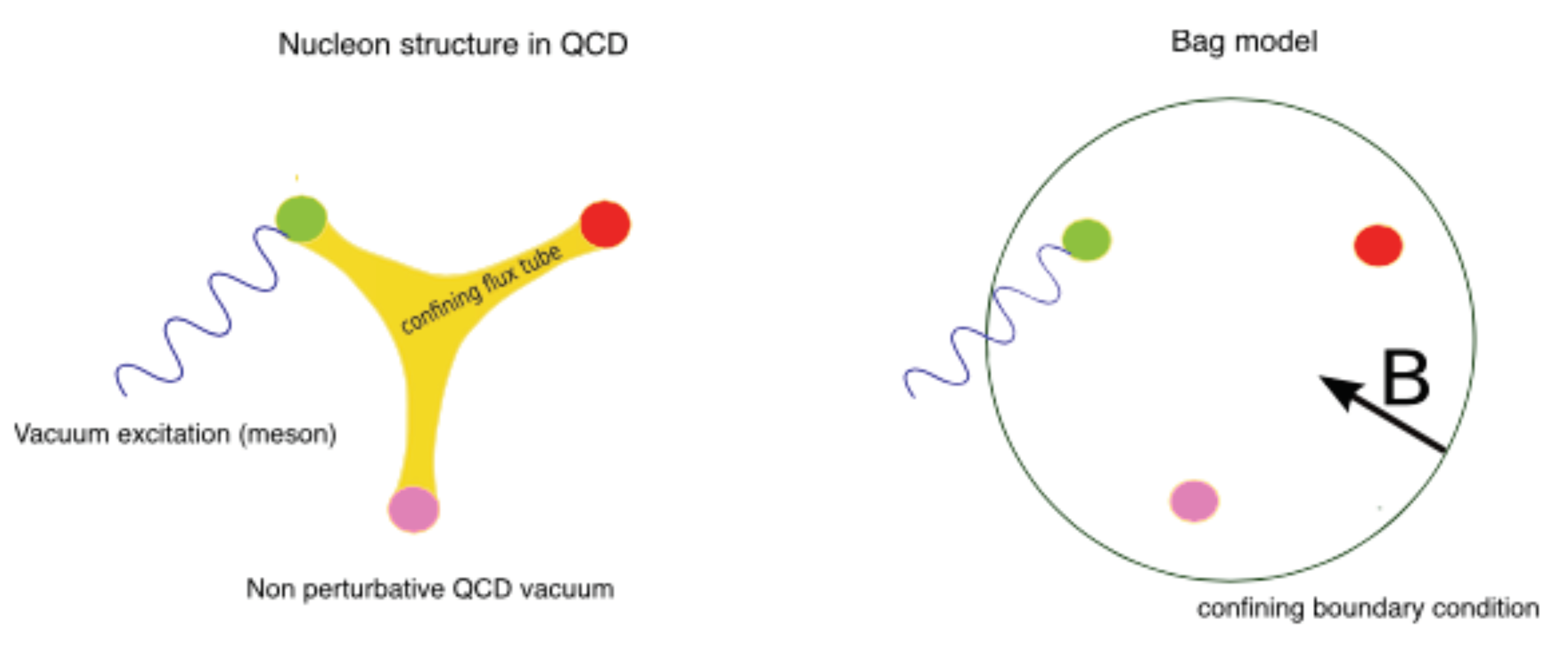
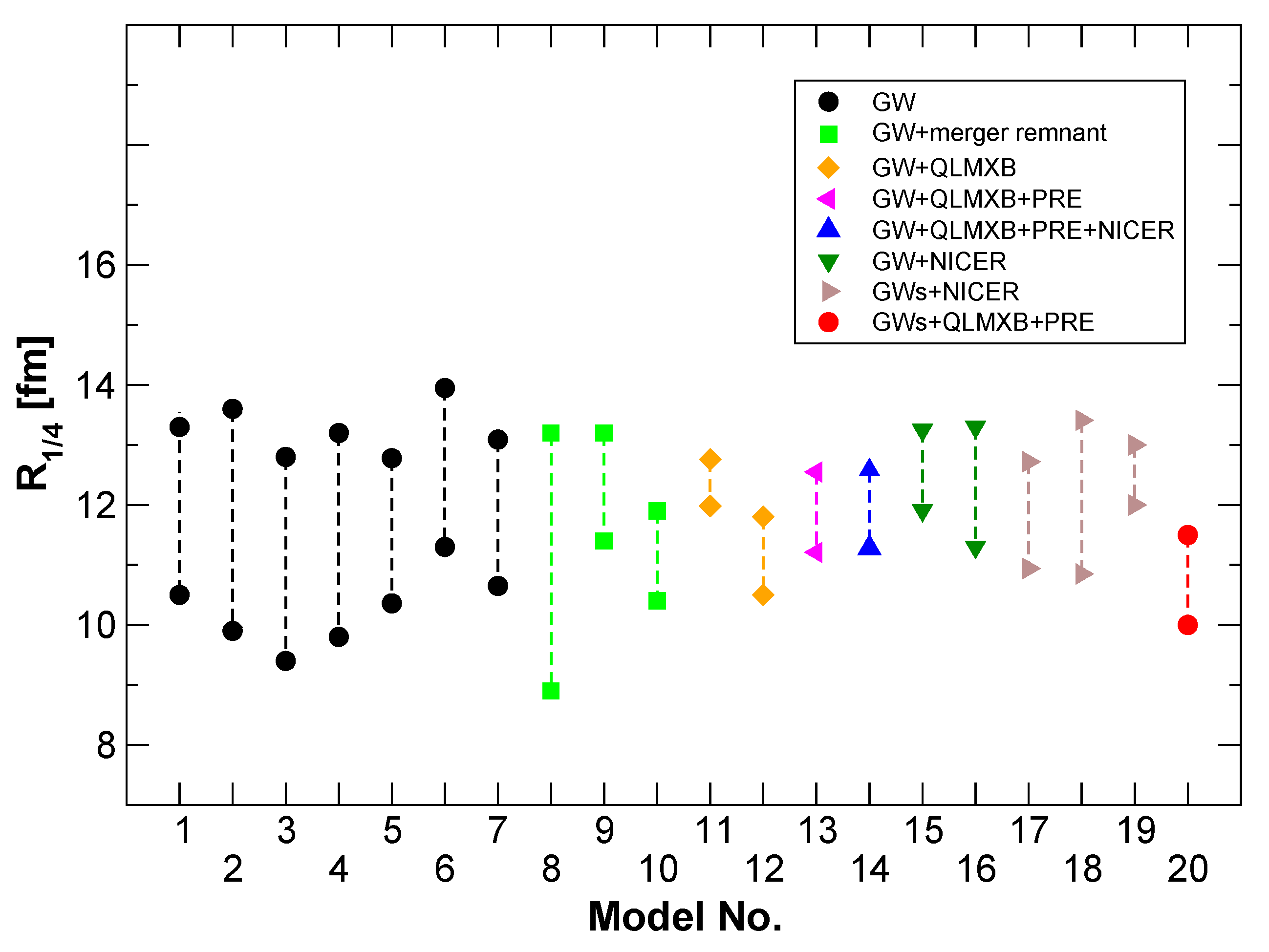
| Property | HIC | NS |
|---|---|---|
| Time scale | 10 s | 10 s |
| Interactions | strong | strong |
| weak | ||
| Gravity | no | yes |
| Coulomb | yes | no |
| Strangeness | conserved | not conserved in weak |
| Nucleons | yes | yes |
| Hyperons | no | yes |
| Pions/Kaons | yes | condensate possible |
| Leptons | no | yes |
| p/n ratio | ∼1 | ∼0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stone, J.R. Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State. Universe 2021, 7, 257. https://doi.org/10.3390/universe7080257
Stone JR. Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State. Universe. 2021; 7(8):257. https://doi.org/10.3390/universe7080257
Chicago/Turabian StyleStone, Jirina R. 2021. "Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State" Universe 7, no. 8: 257. https://doi.org/10.3390/universe7080257
APA StyleStone, J. R. (2021). Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State. Universe, 7(8), 257. https://doi.org/10.3390/universe7080257





