1. Introduction
Many real solids possess a spin structure. For example, ferromagnets are characterized by the distribution of magnetic moments described by the unit vector field (
n-field) in the continuum approximation. This unit vector field may have defects (singularities) that are called disclinations. Disclinations define many important properties of media and attract much interest in physics (see, e.g., [
1,
2]). Real solids may have many disclinations, and it is highly likely to have the continuous description for their distribution. The approach based on the
n-field is applicable for single disclinations when we can write down equations for the
n-field with suitable boundary conditions on the corresponding cuts in media. However this approach is not applicable for the continuous distribution of disclinations because, in this case, the
n-field has singularities at each point and therefore does not exist at all.
The promising approach to this problem is the geometric theory of defects [
3,
4] which describes defects in elastic media within the Riemann–Cartan geometry. To avoid the problem with singularities of the
n-filed we introduce new variable–the
(3) connection–which is smooth even for continuous distribution of disclinations. The curvature tensor for this connection acquires the physical interpretation as the surface density of the Frank vector characterizing disclinations. The Frank vector for a single straight linear disclination equals, by definition, to the total rotational angle of the
n-field when it goes around the disclination axis which is a multiple of
. If defects are absent in some domain of media, then the
(3) connection is a pure gauge, and the
n field can be reconstructed in this domain in full agreement with standard models.
We note that the geometric theory of defects is a more general model also describing the distribution of dislocations that are defects in elastic media itself. These defects correspond to nontrivial torsion, the latter having physical interpretation as the surface density of the Burgers vector of dislocations. The Burgers vector for a single straight linear dislocation is equal, by definition, to the jump of the displacement vector when it goes around the dislocation axis. In the present paper, we deal only with disclinations assuming that the metric is Euclidean which corresponds to the absence of elastic stresses but the connection is nontrivial.
There is some interest in describing effects of dislocations on physical properties of solids within the geometric theory of defects (see, e.g., [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]). In the present paper, we deal only with another defects–disclinations. As far as we know, the first application of the geometric theory of defects to disclinations was given in [
15,
16,
17] where straight linear disclinations were described in full agreement with the classical theory [
1]. Several examples of point disclinations were given in [
18]. A short review of disclinations in the geometric theory of defects can be found in [
19].
Since the Lie algebras
and
are isomorphic, then the static solutions of
gauge models can be considered as describing some distribution of disclinations and, possibly, dislocations. In particular, it was noted that the ’t Hooft–Polyakov monopole has straightforward physical interpretation in the geometric theory of defects describing media with continuous distribution of disclinations and dislocations [
20]. It means that the ’t Hooft–Polyakov monopole can, in principle, be observed in solids. There arises a problem. On the one hand, the solution describes the continuous distribution of disclinations, and the
n-field does not exist in a strict sense. On the other hand, there is a spin in each site of the crystal lattice. The problem relates to what is the corresponding spin distribution for a given nontrivial
(3) connection? The answer to this question relies on the definition of the presumable paths of parallel transport of spins and requires additional physical assumptions which are not known at present. In the present paper, we consider one of the possible and simplest way to compute spin distribution for the ’t Hooft–Polyakov monopoles. As an example, we consider the Bogomolny–Prasad–Sommerfield solution.
2. The ’t Hooft–Polyakov Monopole
The famous ’t Hooft–Polyakov monopoles [
21,
22] are the exact solutions of the field equations in the
(2) gauge theory interacting with the triplet of scalar fields in the adjoint representation and
-type interaction (for review, see, e.g., [
23,
24,
25]). The solutions are static and spherically symmetric. Therefore, the problem is reduced to minimization of the three-dimensional Euclidean energy functional which can be regarded as the free energy expression in solid state physics. We consider the
(2) connection components as the
(3) connection because their Lie algebras coincide, the triplet of scalar fields being the source of defects. Moreover, we assume that the
(3) group acts not only in the isotopic space but also in the tangent space to the space manifold
, the metric of the space being Euclidean. So the ’t Hooft–Polyakov monopoles correspond to Euclidean metric (and triad) and nontrivial
(3) connection which give rise to nontrivial Riemann–Cartan geometry of space.
Let us consider three-dimensional Euclidean space
with Cartesian coordinates
and Euclidean metric
,
. The spherically symmetric
(2) gauge fields
,
interacting with the triplet of scalar fields
in the adjoint representation minimize the three-dimensional energy [
23,
24,
25]:
where indices are raised and lowered by Euclidean metrics
and
,
− are the curvature tensor components for (2)-connection and the covariant derivative of scalar fields; – are coupling constants, is the totally antisymmetric tensor, , and .
The spherically symmetric ansatz is:
where
and
are some dimensionless functions on radius
,
.
We assume that the (3) group acts simultaneously in the isotopic space and base manifold. Therefore the difference between Greek and Latin indices disappear, but we shall distinguish them as long as possible.
The Euler–Lagrange equations for functional (
1) in the spherically symmetric case reduce to:
At present we know only a few exact analytic solutions to this system of equations for
[
26,
27,
28] (see also [
29,
30,
31,
32]). In the following, we consider the Bogomol’nyi–Prasad–Sommerfield solution [
26,
27]:
It is easily checked that this solution has finite energy (
1).
Solutions of Equation (
4) describe ’t Hooft–Polyakov monopoles in the
gauge model. In the geometric theory of defects, we consider functional (
1) as the expression for the free energy describing static distribution of disclinations and dislocations in elastic media with defects, the triplet of scalar fields being the source of defects. This is possible because the Lie algebra
is isomorphic to
, and scalar fields are real (in the fundamental representation of
group).
The Euclidean metric means that elastic stresses are absent in media. The Cartan variables (triad and
(3) connection) for monopole solutions are:
where we use the spherically symmetric
-connection (
3). In the considered case, simple calculations yield the following expressions for curvature and torsion:
In the geometric theory of defects, curvature (
7) and torsion (
8) have physical meaning of surface densities of Frank and Burgers vectors, respectively. That is they are equal to
k-th components of respective vectors on surface element
. If
is normal to the surface element, then there are the following densities of Frank and Burgers vectors:
where
and tensor
is decomposed into irreducible components.
We see that ’t Hooft–Polyakov monopoles describe a continuous distribution of disclinations and dislocations in media. The problem lies in what is seen in real crystals. We do not observe directly the distribution of the Frank and Burgers vectors, but we observe instead the distribution of spins on lattice sites of a crystal. So, we have to compute it for a given (3) connection. In what follows, we concentrate our attention only on the distribution of disclinations as the first step in the analysis.
3. Distributions of Spins
To compute the distributions of spins, we follow the idealogy adopted in lattice gauge models [
33] (for review, see, e.g., [
34]). For simplicity, we consider the cubic lattice. There is a spin at each lattice site. We ascribe the rotational
(3) matrix to each link of the lattice. This is possible because we know the connection, and the rotational matrix is given by the path-ordered integral of the connection along the link which corresponds to the parallel transport of spins. Thus we obtain the unique rotational matrix at each link. The problem is that curvature of the connection is nontrivial, and the parallel transport of spins depends on the path. In particular, we must avoid closed paths because a spin cannot take different directions at a given site. Thus we fix the spin at one site, say, at the origin of the coordinate system, and parallelly transport it to the whole lattice. The paths have to reach all sites but without closed loops. It is clear that there are many possibilities. To choose the unique one, we must engage additional physical assumptions. At the moment, we do not know how to do this uniquely and therefore consider one of the simplest possibilities, because it is interesting to see how the ’t Hooft–Polyakov monopole may look in a crystal.
The following calculations are performed in the continuous approximation.
Let the spin (unit vector)
at the origin be directed along the
axis. We parallelly transport it to a point
along a path
,
,
,
. A path is assumed to have no intersection points. In our notation, we use the covector
,
, instead of vector components (sure, they coincide in the Cartesian coordinates). Then the result of parallel transport is given by the path-ordered exponent (see, e.g., [
35], Section 14.5).
where
is the rotational matrix and the dot denotes differentiation with respect to the path parameter
t.
First, we consider the parallel transport from the origin to a point
along the ray
. Then
and the integrand for connection (
6) is zero:
Because is proportional to along a ray, and the parallel transport does not change the vector.
We see that parallel transport along rays from the origin in produces no effect on spins for the ’t Hooft–Polyakov connection independently of function .
Let us consider another possibility for the parallel transport. First, we transport the vector
from the origin along the
axis. Previous calculations tell us that it is not changed. Then we parallelly transport it along the rays in the perpendicular planes
. Thus the path is
and
, where
is the final point (now we write the coordinate indices of
y at the bottom to distinguish them from exponents). The integrand in Equation (
11) for connection (
6) becomes:
where
Now one can easily check that the integrands commute:
Therefore the ordered exponent (
11) coincides with the usual one and can be easily calculated:
where
and
For the Bogomol’nyi–Prasad–Sommerfield solution (
5), the integral can be easily taken:
where we rescaled the constant
for simplicity. The rotational matrix for the Bogomol’nyi–Prasad–Sommerfield solution is:
where
For the Bogomol’nyi–Prasad–Sommerfield solution, the rotational matrix is:
One can easily check that
for
or
. In addition, the asymptotics at infinities are the same:
Now we can easily calculate spins components:
where
We see, that the spin distribution is invariant with respect to rotations around the
z axis, as expected. Therefore, without loss of generality, we may put
to visualize the distribution. Then:
where
It implies that spins are rotated on the same plane
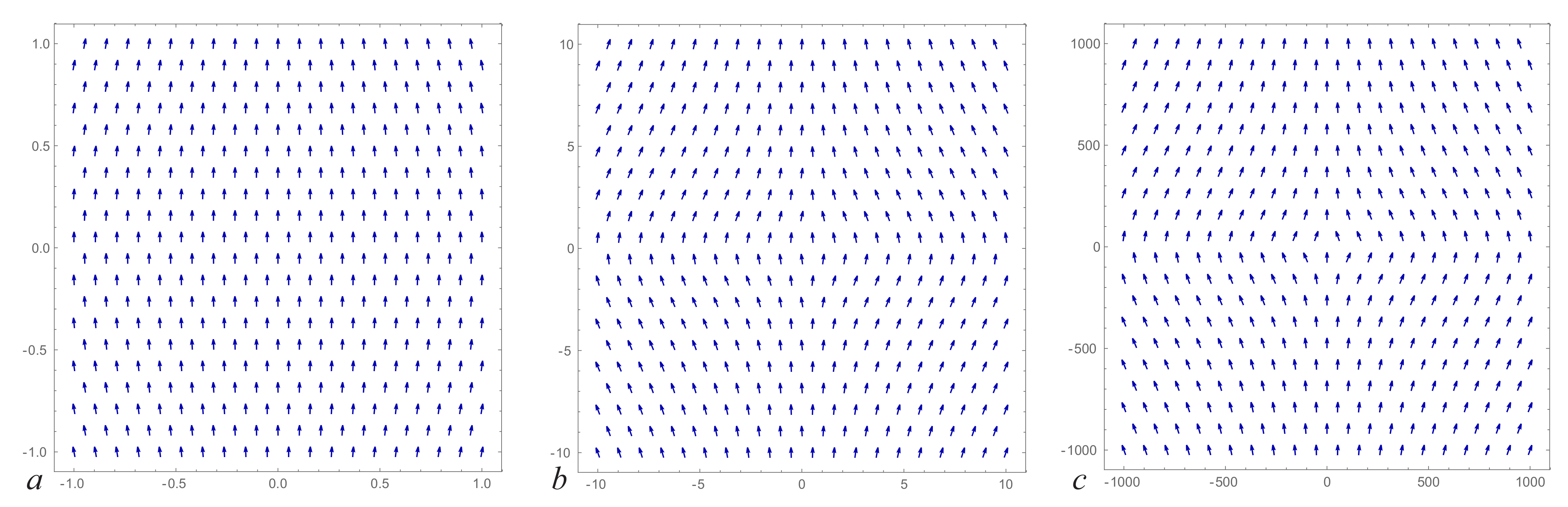
. The corresponding spin distributions are shown in
Figure 1 for a different range of coordinates.
Notice that for large coordinate values, the function tanh goes exponentially to unity and:
This function is homogeneous, and the spin distribution is self-similar. Therefore the
Figure 1b,c are almost the same though the range of coordinates differs one hundred times. The difference appears only near the origin, as shown in
Figure 1a.
4. Conclusions
The geometric theory of defects describes dislocations and disclinations in elastic media and crystals in the continuous approximation. It is well suited for the description of single defects as well as their continuous approximation. In the present paper, we consider media with Euclidean metric but nontrivial (3)-connection. This assumption corresponds to the absence of elastic forces.
The famous ’t Hooft–Polyakov monopoles are static spherically symmetric solutions of Yang–Mills theory. The isomorphism of and Lie algebras implies that the ’t Hooft–Polyakov monopoles have new physical interpretation in solid state physics. In contrast to the original model, the (3) group acts now not in the isotopic space but in the tangent space, giving rise to nontrivial torsion and curvature. These geometrical notions have physical interpretation as surface densities of Burgers and Frank vectors in the geometric theory of defects, respectively. To visualize these solutions in media, we have to compute the corresponding spin distributions. This is done in the present paper. We follow the prescription from lattice gauge theory. Spins are assumed to be located at sites of simple cubic lattice. Afterwards the rotational matrix for a given (3) connection is attributed to each link connecting neighboring sites. The spin is fixed at the origin and parallelly transported along links to all other sites along non-intersecting paths. There are many ways to do this, but we do not know the right prescription at present. Therefore we choose one of the simplest ways. First, we parallelly transport the spin along the z axis and then by radial rays in perpendicular planes. In this case, everything is computed analytically in the continuous approximation. The Bogomol’nyi–Prasad–Sommerfield solution is considered as an example for which we computed the spins distribution. The particular feature of the obtained distribution is its self-similarity at large scales. This is proved for the Bogomol’nyi–Prasad–Sommerfield solution, but seems to have place for other monopole solutions.
We leave interesting questions, such as what kind of media have to be chosen for experimental observation of monopoles and what is the right prescription for parallel transport of spins for reconciliation of the theory and practice, for future investigations. The present paper is a small step in this direction but it shows that this is possible.