Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State

Abstract

(1) This review has been written in memory of Steven Moszkowski who unexpectedly passed away in December 2020. It has been inspired by our many years of discussions. Steven’s enthusiasm, drive and determination to understand atomic nuclei in simple terms of basic laws of physics was infectious. He sought the fundamental origin of nuclear forces in free space, and their saturation and modification in nuclear medium. His untimely departure left our job unfinished but his legacy lives on. (2) Focusing on the nuclear force acting in nuclear matter of astrophysical interest and its equation of state (EoS), we take several typical snapshots of evolution of the theory of nuclear forces. We start from original ideas in the 1930s moving through to its overwhelming diversity today. The development is supported by modern observational and terrestrial data and their inference in the multimessenger era, as well as by novel mathematical techniques and computer power. (3) We find that, despite the admirable effort both in theory and measurement, we are facing multiple models dependent on a large number of variable correlated parameters which cannot be constrained by data, which are not yet accurate, nor sensitive enough, to identify the theory closest to reality. The role of microphysics in the theories is severely limited or neglected, mostly deemed to be too difficult to tackle. (4) Taking the EoS of high-density matter as an example, we propose to develop models, based, as much as currently possible, on the microphysics of the nuclear force, with a minimal set of parameters, chosen under clear physical guidance. Still somewhat phenomenological, such models could pave the way to realistic predictions, not tracing the measurement, but leading it.

Contents

1. Introduction	2
2. The Equation of State	3
3. Nuclear Physics Input into the Dense Matter EoS	6
3.1. Macroscopic Approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	6
3.1.1. Semi-Empirical Mass Formula and Nuclear Matter . . . . . . . . .	6
3.1.2. Liquid Drop Based Models . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
3.2. Microscopic Approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	10
3.2.1. NN Interactions in Free Space . . . . . . . . . . . . . . . . . . . . . . . . . . .	10
Realistic Potentials . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . .	10
Chiral Effective Field Theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	11
3.2.2. Density-Dependent NN Interactions . . . . . . . . . . . . . . . . . . . . .	14
Skyrme Interaction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	14
Relativistic Mean-Field Models . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	16
Quark–Meson Coupling Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	17
4. Astrophysical and Terrestrial Data	18
4.1. Neutron Stars: Masses and Radii . . . . . . . . . . . . . . . . . . . . . . . . . . . .	18
4.2. GravitationalWaves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
4.2.1. Observation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
4.2.2. Extraction of Information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	21
4.3. Heavy Ion Collisions at Low and Medium Energies . . . . . . . . . . . .	21
4.4. High-Energy Heavy Ion Collisions . . . . . . . . . . . . . . . . . . . . . . . . . .	23
5. Concluding Remarks	24
References	25

1. Introduction

In 1936, Bethe and Bacher [1] reviewed rather extensive data, subject to experimental techniques of the day, available on the charge, weight, binding energy, size, spin, statistics and electromagnetic moments of nuclei and outlined the then current state of knowledge of nuclear physics. Radioactive decay had been extensively studied and experiments with scattering of neutrons and protons by protons yielded fundamental cross-section and angular distribution information. Data on the photo-disintegration of the deuteron and the capture of neutrons by protons were also available. Analysis of the data required model input about the force acting between nucleons bound in nuclei and in free space. Qualitative features of the force, deduced from the data, relied heavily on analogy with atoms and chemistry and are remarkably similar to what we know today. The linear dependence of the nuclear mass on the number of nucleons in the nucleus, and particularly, the comparison of properties of the deuteron, triton and alpha particle led to deduction of fundamental properties of nuclear forces–the saturation, short range, exchange character and the charge, spin and isospin dependence. Their attempts to find an analytic expression for the nuclear force in order to calculate properties of the lightest nuclei failed. The three most prominent models, the Heisenberg, Wigner and Majorana forces did not cover all the aspects of the nuclear interaction. One of the problems was that determination of the parameters of the forces relied on a combined data from finite nuclei and free nucleon scattering, which we now know are not directly compatible.

The effort to compute nuclear binding energies precisely led to development in two different directions: the single-particle “statistical model” [1] and the liquid drop model of Gamow (1930) [2]. Neither model required a quantitative analytical form for the nuclear force, derived from first principles. Thus started the trend of phenomenology, lasting to this day. This trend has had two consequences: it requires experimental data to calibrate any theory, thus theory always trails experiment. It diverted the attention of the field from seeking the true nature of the nuclear force.

The “statistical” model assumed, in the first approximation, each particle moving independently of the others. It had been applied to atoms, using the Hartree method, with great success. It is educational to recall a comment about application of this method in nuclear physics, made by Bethe and Bacher in 1936 [1]:

It can be said at once that this approximation will not be as successful in nuclear theory as in the theory of atoms. The main reason for this is the saturation type of the nuclear forces: Any given nuclear particle interacts essentially only with two particles of other kind. Therefore the force between a given pair of particles will be of the same order of magnitude as the force exerted by the whole nucleus on one particle. This is contrary to the assumptions of the Hartree theory. These are that in first approximation the total action of the nucleus on one particle may be represented by an average field, corresponding to the average distribution of all other particles over the nucleus. The correlations between the different particles, i.e., the fact that the motion of one particle is influenced by the instantaneous position of the others, is supposed to cause only small perturbations in the Hartree theory. These assumptions of the Hartree theory are well satisfied in the atomic problem because the force due to the nucleus, and the force corresponding to the average charge distribution of the electrons are very much stronger than the fluctuations of the force caused by, say, a close approach of one other electron to the electron considered. In nuclear physics, the force on one neutron changes by 100 percent or more according to whether a proton happens to be near the neutron or not. Therefore the correlations between the nuclear particles will be of extreme importance for any satisfactory calculation of nuclear energies, and the Hartree method will afford only a poor approximation. In spite of these serious objections against the Hartree method, we are forced to use it because no better method seems practicable at the moment.

In 2021, although refined in some ways, no better method is available. However, Bethe’s warning comment has been forgotten.

The original liquid drop model treated the nucleus as a drop of incompressible liquid made of protons and neutrons and focused only on classical macroscopic characteristics of nuclei. The liquid drop approach had, among other things, the advantage of allowing extrapolation beyond finite nuclei to infinite matter, essential for modeling of astrophysical objects. We will discuss this model in some detail in Section 3.1.

Free nucleon–nucleon scattering experiments in the 1950s and later stimulated more elaborate modeling of the bare nucleon–nucleon (NN) potentials (coined the “realistic” potentials) and of the structure of the deuteron (see Section 3.2.1). However, it has become clear that these potentials do not work in finite nuclei and that the fundamental question is: why and how are forces between free nucleons modified in nuclear medium?

This problem has been addressed in many hundreds of papers over the years, but a satisfactory solution is yet to be found. A frequent argument is that the exact solution of the nuclear many-body problem, which is beyond the current computer resources, will be obtained when quantum computers become available. This would of course imply that the free nucleon interaction is fully understood. There is, however, another way of thinking about it. Rather than improvement in computing power, the physics of the nuclear force may require new insight, both in theory and in identification of experimental/observational data exhibiting adequate sensitivity to its impact. Spelling out the problem and illustrating some of its consequences may encourage a fresh way forward.

It is well beyond the scope of this paper to cover even a small fraction of all the theoretical models in the literature, related directly or indirectly to the problem of the nuclear force. Here, we focus only on dense baryonic matter, believed to exist in cold and hot compact objects and present selected snapshots which, in our mind, illustrate well the message we wish to convey to the reader. Finite nuclei and their interactions will be mentioned only when a broader context is helpful to the discussion. However, it is clear that any success in describing the nuclear force must equally well describe both dense baryonic matter and finite nuclei.

This paper is divided into the following sections: in Section 2, the concept of the equation of state (EoS) is introduced in the context of compact objects; the nuclear physics input to the EoS is highlighted in Section 3, presenting the basic ideas of macroscopic (Section 3.1) and microscopic (Section 3.2) models, followed by a short survey of reliable observational and terrestrial data available for constraining the EoS in Section 4, including neutron stars in Section 4.1, gravitational waves in Section 4.2 and heavy-ion collisions in Section 4.3 and Section 4.4; Section 5 contains concluding remarks.

2. The Equation of State

In a general form, the EoS is a relation between any thermodynamical state variables of a system which fully specify the state of the system under a given physical condition. In the context of compact objects, the EoS is usually defined as a relation between the pressure, energy density and temperature. It is important to emphasize that the EoS also depends on the composition of the system, which is crucial for modeling astrophysical objects in various situations. In other words, the nuclear and particle physics input into models of compact objects is contained in their EoS. Oertel et al. [3] reviewed comprehensively the status of our knowledge about the EoS of neutron stars (NSs) and core-collapse supernovae (CCSN) before the observation of gravitational waves (GW), detailing many theoretical methods and astrophysical and terrestrial data needed for constructing an EoS model and constraining its parameters. A more recent review [4], focussed on a wide range of aspects of the GW observation, and related them to a hybrid EoS, built on the chiral effective field theory ($\chi$EFT) at low density and the perturbative QCD (pQCD) at high densities. The recent status of the research of the EoS of neutron stars can be found in [5].

The NS EoS forms the principal input into the Tolman–Oppenheimer–Volkov (TOV) equation [6], yielding the gravitational mass of the star as a function of its radius. Despite all the constraints available, the predictions for the maximum gravitational mass and the related radius of a cold NS with only proton, neutrons and leptons in the interior differ substantially, as illustrated in Figure 1.

There is no general consensus on the composition of the NS core. The common understanding is that at densities at and below approximately three times nuclear saturation density (${\rho }_0\sim$ 0.16 fm${}^{-3}$; see Section 3.1) the matter in a cold NS consists of nucleons and leptons in chemical equilibrium. At higher densities in cold stars, hyperons appear naturally (due to Pauli blocking), when their chemical potentials exceed their effective masses and the strangeness non-conserving weak processes become possible [7,8,9,10,11]. Different models vary in predictions of the threshold densities for appearance of hyperons, which depend on hyperon couplings and the consequent hyperon binding energies [12]. At higher temperatures, hyperons exist at all densities [11], and have to be accounted for in EoS models.

Hyperons add additional degrees of freedom to the system, which inevitably lower the pressure with increasing energy density and hyperon content (softening of the EoS). As a consequence, the maximum gravitational mass of cold NSs with hyperons is lower than that of nucleon-only stars, in some models below the observation limits (the “hyperon puzzle”). This is a model-dependent effect related to the choice of hyperon couplings which are still not well known, although some estimates can be obtained from data on hypernuclei. Thus, unambiguous observational fingerprints of hyperon presence in NS interiors have not been established, despite the extensive literature on the subject. A most informative recent review of hyperon physics in high-density matter can be found in [13].

Another frequently discussed component of NS interiors is matter consisting of (partially) deconfined quarks. The idea started in the 1970s and has been developing since (see, e.g., [14,15,16,17,18,19,20,21,22,23]). Many forms and phases of the quark matter and of the hadron-quark transition as well as studies of the interplay between hyperonic and quark matter [24,25] have been suggested but, again as in the case of hyperons, no observational fingerprints have yet been found. Annalla et al. [26] suggested that the hadron-quark matter can be mapped by a discontinuity (jump) in the square of the speed of sound as a function of particle number density in a NS. However, Stone et al. [11] demonstrated that the predicted jumps are most likely related to generic instabilities, caused by changes in composition of the hadronic matter, for example the appearance of hyperons, and cannot be taken as a specific signature of a hadron-quark phase transition. Such instabilities could be understood in a classical analogy with the effect of induced vibration in a medium, causing impedance through its refracting index on propagation of a sound wave.

The microscopy of quark deconfinement and its nature in NS cores poses unanswered questions. It is not clear to what extent the conditions inside NSs compare to those in heavy-ion collisions where the quark-gluon plasma was detected by the STAR and PHENIX experiments at the RHIC collider at the Brookhaven National Laboratory in early 2020s. The results were recently confirmed at ALICE, ATLAS and CMS experiments at the LHC at CERN collider (https://home.cern/science/physics/heavy-ions-and-quark-gluon-plasma (accessed on 7 June 2021)) [27]. However, the quark-gluon plasma produced in these experiments is essentially baryon free, which is very different to conditions in NS star cores. The current beam scan for the critical point in the QCD diagram (see Section 4.3 by the STAR collaboration is designed to produce baryon-rich quark-gluon plasma to see whether its phase transition changes to a first-order one once the baryon chemical potential is larger than a critical value. This effort is expected to continue also on the planned new facilities FAIR and NICA. Such information will be important for putting the question of existence of the quark matter on firmer ground.

Very recently, the possibility of accretion of non-spinning mini-black holes in the center of a non-rotating NS was revisited [28]. The concept of endoparasitic black holes in NSs is not new, but cannot be rejected outright, although again a definitive observational fingerprint has not been identified.

Boson condensates, pions [29,30], kaons [31,32,33] and $\rho$-mesons [34] have been also considered to be present in the NSs interiors. To add to the complexity, proton superconductivity and neutron superfluidity in the NS cores have been extensively studied [35,36].

The extreme environment in NS interiors, to the limited extent we understand it, allows the existence of the above possibilites (and more), in accord with known physical laws. However, presently available observational data are very unlikely to provide sufficient sensitivity to all the individual scenarios and their relationships as encoded in the EoS.

3. Nuclear Physics Input into the Dense Matter EoS

3.1. Macroscopic Approach

In this section, we review the basic ideas and assumptions which were used to build the first macroscopic models of nuclei. These models are still used today, with only some technical modifications, despite their very simple (semi) classical origin.

3.1.1. Semi-Empirical Mass Formula and Nuclear Matter

One of the early models of the atomic nucleus employed the analogy with a drop of incompressible liquid. Gamow [2] formulated the first liquid drop model and Weizsäcker [37] and Bethe and Bacher [1] used this model to express the total binding energy $B(A,Z)$ and the binding energy per particle $B(A,Z)/A$ of an even–even nucleus with N neutrons, Z protons and the mass number $A=N+Z$ with uniform matter and charge density, in the form, known as the semi-empirical mass formula (SMF)

$$B(A,Z)=a_{\mathrm{vol}}A+a_{\mathrm{surf}}{A}^{2/3}+a_{\mathrm{C}}{Z}^2{A}^{-1/3}+a_{\mathrm{sym}}{(N-Z)}^2{A}^{-1}$$

(1)

where $a_{\mathrm{vol}}$, $a_{\mathrm{surf}}$, $a_{\mathrm{C}}$ and $a_{\mathrm{sym}}$ are coefficients of the volume, surface, Coulomb and symmetry terms. The A dependence of the individual terms is based on the assumption that the nucleus is a sphere with radius R, containing closely packed spherical nucleons with radii $r_0$ [1]. The symmetry term arises because the protons and neutrons, as different particles, are treated separately as non-interacting Fermi gases obeying the Pauli principle. For different numbers of protons and neutrons there will be a difference between the energy levels occupied by protons and neutrons which will contribute to the total energy of the nucleus and decrease its binding energy. To obtain the coefficients in Equation (1), the binding energy is fitted to experimental nuclear masses, $M(A,Z)=(Zm{(}^{1}H)+N{m}_{\mathrm{n}}-B(A,Z))/c^2$.

It is instructive to review the relative magnitude and the mass number dependence of different terms in the SMF using the binding energy per particle as given in Equation (2).

$$B(A,Z)/A=a_{\mathrm{vol}}+a_{\mathrm{surf}}{A}^{-1/3}+a_{\mathrm{C}}{Z}^2{A}^{-4/3}+a_{\mathrm{sym}}{(N-Z)}^2{A}^{-2}$$

(2)

We calculate individual terms in Equation (2) as a function of $A=N+Z$ of selected nuclei between ${}^{16}$O and ${}^{254}$Fm. The coefficients $a_{\mathrm{vol}}$, $a_{\mathrm{surf}}$, $a_{\mathrm{C}}$ and $a_{\mathrm{sym}}$ are taken as 15.36, 16.42, 0.691 and 22.53 MeV, respectively. These values were determined by Kirson [38] from a fit of the basic Equation (1) to the 2003 mass table [39]. As shown in Figure 2, the major contribution comes from the volume term which is independent of A. The total is reduced by the surface term, dominant in light nuclei, competing with the Coulomb term which, as expected, becomes more important in heavy nuclei. The symmetry term plays the least important role, except for very light nuclei, and decreases with increasing A in finite nuclei. However, this term plays an important role in highly isospin asymmetric systems such as NS.

The mass number independence of the volume term in Equation (2) was one of the reasons for introducing the concept of infinite nuclear matter (INM) ([1,40] and refs. therein), a hypothetical medium made up of infinite number of uniformly distributed protons and neutrons, with a given proton/neutron ratio, and no Coulomb field. INM has only two properties that can be calculated, the binding energy per particle and the particle number density.

The binding energy per particle of INM with $N=Z$, the symmetric nuclear matter (SNM), $E_0$, is given by the coefficient $a_{\mathrm{v}}$ in Equation (2) as all the other terms tend to zero for A $\to \infty$ and N = Z. However, it is important to remember that the value of $a_{\mathrm{v}}$ has been obtained by fitting the full SMF formula to experimental masses. Thus, by approximating $E_0$ by $a_{\mathrm{v}}$ we assume that the terms in the SMF are independent (not correlated) and the volume term, strictly speaking, describes matter consisting of nucleons interacting without a distinction between protons and neutrons. Effects of correlations and refining terms in SMF were studied, for example, by Kirson [38]. There are many fits available in the literature but they all converge to $a_{\mathrm{v}}$ between 14 and 17 MeV [38].

To calculate the particle number density of the SNM, an assumption has to be made concerning the relation between R, $r_0$ and A. Taking there are A nucleons in the sphere with the radius R, containing A smaller spheres with equal radii $r_0$, the volume of the sphere is $V=4/3\pi R^3$, which is equal to 4/3$\pi r_{{}_0}^{3}fA$, with f being the packing factor. This relation leads to the standard expression for the mass number dependence of nuclear radius $R=R_0{A}^{1/3}$, with $R_0=f{r}_0$ and the A-independent particle number density ${\rho }_0$ = $A/V=3/\left(4\pi {R_0}^3\right)$.

The value of $R_0$ was determined from electron scattering experiments on heavy nuclei and on hydrogen and the deuteron, which confirmed the finite size of the nucleon [41,42]. These experiments confirmed that, on average, the central density of heavy nuclei is rather independent of the mass number A, that the nuclear radius is indeed proportional to $A^{1/3}$. The results were, however, not quite model independent as the analysis required empirical input of the proton charge distribution (12 different function were used in [41]). The value of $R_0$ = 1.12 fm led to ${\rho }_0$ = 0.17 fm${}^{-3}$ [40]. We note that it is quite remarkable that approximately sixty years later and with more sophisticated experiments and theory available, the value of ${\rho }_0$ obtained from parity-violating electron scattering measurement (PREXII) on ${}^{208}$Pb is reported as 0.1480 ± 0.0036 (exp) ± 0.0013 (theo) fm${}^{-3}$ [43].

The assumed constancy of the binding energy per particle and of the particle number density of SNM has a fundamental meaning. The constant density implies that there must be a balance between attractive and repulsive components of the nuclear force which are equilibrated at that density–the saturation density. At this density, the number of surrounding nucleons for each nucleon in the matter is the same, regardless of the position in space. If the nuclear force is of a short range comparable with the inter-nucleon distance, each nucleon will interact only with a few nucleons in its vicinity, resulting, on average, in the same contribution to the total binding energy per particle –the saturation energy.

3.1.2. Liquid Drop Based Models

The interest in modeling nuclear masses led to further development of the liquid drop-based model of finite nuclei and nuclear matter. Shell effects and a small deformation (but still taking constant bulk particle distribution) were added in the 1966 liquid drop model (LDM) of Myers and Swiatecki [44]. Variable proton and neutron density distribution throughout the nuclear volume, decreasing smoothly to zero in the surface region, nuclear surface diffusines and thickness were included in the droplet model (DLM) for spherical (1969) [45] and arbitrary shapes (1974) [46]. The volume, surface and Coulomb terms were expanded in a Taylor series around the LDM values in terms of the proton–neutron asymmetry $\delta$ = $({\rho }_{\mathrm{n}}-{\rho }_{\mathrm{p}})/\rho$ ($\rho ={\rho }_{\mathrm{n}}+{\rho }_{\mathrm{p}}$) and deviation of the density $\rho$ from its nuclear matter value ${\rho }_0$$ϵ=({\rho }_0-\rho )/\left(3{\rho }_0\right)$. Using these expansions, the energy per particle in nuclear matter can be expressed as [45]

$$B(\rho ,\delta ,ϵ)/A=-a_{\mathrm{vol}}+J{\delta }^2+1/2(K{ϵ}^2-2Lϵ{\delta }^2+\dots )$$

(3)

where $J,L$, and K are the symmetry energy coefficients, L gives the density dependence of the symmetry energy and K is the nuclear compressibility coefficient. (Note that we take the sign $a_{\mathrm{vol}}$ as negative in compliance of the general usage of a bound system having negative energy.) For symmetric nuclear matter $\delta =0$ and the minimum value of the binding energy per particle $B(\delta =0,ϵ=0)/A$ equals $E_0$ and occurs at $\rho ={\rho }_0$. In asymmetric nuclear matter (ANM), at $\rho ={\rho }_0$, the energy per particle is dependent on the proton–neutron asymmetry as $-E_0+J{\delta }^2$ and is always higher than $-E_0$.

A more recent development of liquid drop-based physics is the finite range droplet model (FRDM) of Moller and collaborators ([47,48,49] and ref. therein). The macroscopic part of the latest FRDM (2016) [49] involves further refinement as compared to the DLM, and has 38 adjustable constants. The FRDM is currently seen as one of the most reliable models not only of nuclear masses, but also shapes and related quantities, such as fission barriers and $\alpha$ and $\beta$ decay rates.

We move on to consider what is known concerning the values of the macroscopic parameters $J,L$ and K. Although there is a general consensus about the most likely values of the saturation properties of infinite nuclear matter based on nuclear masses, mass modeling is less sensitive to the $J,L$ and K values, important for the EoS of nuclear matter (some sensitivity to L has been explored in [49]). There has been a consolidated effort to find other experimental and theoretical constraints for these parameters without reaching agreement. Values obtained from different relevant experiments are dependent on models used for their analysis, and the data themselves often suffer from large uncertainties (see e.g., [50,51]).

The value of the symmetry energy coefficient J in Equation (3) at ${\rho }_0$ is reasonably well constrained between approximately 28 and 34 MeV, but its density dependence, the parameter L, is still unclear. It was first investigated in connection with the EoS of cold NSs in 2003 [52] and later examined in numerous scenarios. Bao-An Li et al. [53] comprehensively reviewed papers up to 2014, including open theoretical issues, constraints from terrestrial laboratory experiments and imprints and extraction of the symmetry energy from astrophysical observations. Future perspectives in the research were outlined, but no positive conclusion was drawn. A recent progress reports on the subject was published by Bao-An Li and collaborators in 2019 [21,54], including current and future data from GW, but again, no definitive conclusion was reached. The current limits on the value of L at ${\rho }_0$ range between approximately 30 and 100 MeV and its density dependence is not constrained.

Very recently, the results of the second PREX-II experiment yielding the neutron skin thickness of ${}^{208}$Pb through parity violating asymmetry in elastic scattering of longitudinally polarized electrons [43]. The skin thickness, 0.283 ± 0.071 fm, is larger than predicted by most of the current theoretical models. This value would constrain the density dependence of the symmetry energy in nuclear matter around the saturation density and have implication on radii and composition of NSs [55]. The result has been used, with a certain class of relativistic mean-field (RMF) models (see Section 3.2.2) to extract model-dependent values of J, L to be 38.1 ± 4.7 MeV and 107 ± 37 MeV, respectively [56] at a density of approximately 0.15 fm${}^{-3}$. These values differ considerably from the canonical values produced by most of the currently established models; see, e.g., [3] for a review. It would be helpful to show that the RMF models, as adjusted to reproduce the thick neutron skin of ${}^{208}$Pb, are performing equally well on other observables of finite nuclei across the nuclear chart. It would be also interesting to know what saturation energy at saturation density they predict. Some steps towards investigation of the consequences of the results in [56] have been already taken. For example, Essick et al. [57] used a non-parametric EoS representation [58] to constrain the J, L, and ${}^{208}$Pb neutron skin directly from observations of NSs with minimal modeling assumptions and obtained J = 35${}_{-0.09}^{+12}$ MeV, L = 57${}_{-0.53}^{+66}$ MeV and ${}^{208}$Pb skin thickness to be 0.18${}_{-0.09}^{+10}$ fm. If additional constraint on the EoS at densities below ${\rho }_0$, obtained from the $\chi$EFT is imposed in their Bayesian framework, the errors decrease and the final result is J = 34 ± 3 MeV, L = 58 ± 19 MeV and ${}^{208}$Pb skin thickness to be 0.19${}_{-0.04}^{+3}$ fm, close to predictions of more traditional models. Yue et al. [59] tested the new result obtained by the PREXII collaboration in their analysis including a complex set of data on ground states of finite nuclei and giant monopole resonances, the constraints on the equation of state of symmetric nuclear matter at suprasaturation densities from flow data in heavy-ion collisions, the largest neutron star (NS) mass reported so far for PSR J0740+6620, the NS tidal deformability extracted from gravitational wave signal GW170817 and the mass–radius of PSR J0030+045 measured simultaneously by NICER. They set limits on the nuclear matter parameters at saturation density J = 34.5 ± 1.5 MeV, L = 85.5 ± 22.3 MeV and ${}^{208}$Pb skin thickness to be between 0.22 and 0.27 fm. As a minor point, we note that the symmetry energy coefficient J in Equation (3) and the symmetry energy $S(\rho ,\delta ,ϵ)$, frequently defined as

$$S(\rho ,\delta ,ϵ)=B(\rho ,\delta =1,ϵ)/A-B(\rho ,\delta =0,ϵ)/A,$$

(4)

the difference between the energy per particle of the maximally asymmetric matter [pure neutron matter (PNM)] and that of the SMN are not equal, except at the saturation density. To the first order in $ϵ,S(\rho ,\delta ,ϵ)=J-Lϵ$ at any other density, illustrating the inherent correlation between J and L. Higher-order corrections also contribute to the difference (not shown here).

The compressibility coefficient, K, is another fundamental property of nuclear matter which has received a lot of attention with no definitive result. It quantifies the monopole vibration (breathing mode) of the nuclear surface, which is best studied via measurement of the monopole giant resonance (GMR) energies $E_{\mathrm{GMR}}$. The compressibility of a nucleus with the mass number A, $K_{\mathrm{A}}$, can be related to $E_{\mathrm{GMR}}$ as $K_{\mathrm{A}}$ = $(M/{\hslash }^2)<r^2>E_{\mathrm{GMR}}^2$ with M being the mass of the nucleon and r the rms matter radius of the nucleus [60,61]. In the macroscopic approach, $K_{\mathrm{A}}$ can be parameterized, in analogy with the SMF, in terms of $A^{-1/3}$ and the asymmetry $\beta =(N-Z)/A$ as [62]

$$K_{\mathrm{A}}=K_{\mathrm{vol}}+K_{\mathrm{surf}}{A}^{-1/3}+K_{\mathrm{Coul}}{Z}^2{A}^{-4/3}+K_{sym}{\beta }^2$$

(5)

where the coefficients can be seen as the second derivatives of $a_{\mathrm{vol}}$, $a_{\mathrm{surf}}$, $a_{\mathrm{C}}$ and $a_{\mathrm{sym}}$ in the SMF (1) with respect to r, with the number of protons and neutrons kept constant. The coefficients in Equation (5) are then obtained from fits to experimental $E_{\mathrm{GMR}}$ and the value of K is deduced by identifying it with $K_{\mathrm{vol}}$.

Stone, Stone and Moszkowski [63] reviewed in detail the methods of analysis of GMR data as well as values of K obtained using different techniques and theories between 1961 and 2016. 37 different results, covering a range of K from 100 to 380 MeV were found, with a trend to higher values K in relativistic than in non-relativistic mean-field models. They further analysed the data on $E_{\mathrm{GMR}}$ available in 2016 using a simplified expression for $K_{\mathrm{A}}$

$$K_{\mathrm{A}}-K_{\mathrm{Coul}}{Z}^2{A}^{-4/3}=K_{\mathrm{vol}}(1+c{A}^{-1/3})+K_{sym}{\beta }^2$$

(6)

where c is the ratio of $K_{\mathrm{surf}}$ and $K_{\mathrm{vol}}$. Taking fixed $K_{\mathrm{Coul}}$ from theory and sampling the values of c in the range −2.4 and −1.6, the best fit to the A dependence of $E_{\mathrm{GMR}}$ in the region from Ni to Pb was found for the ratio c closely distributed at approximately −2. This procedure yielded the value of K between 250 and 315 MeV. Neglecting the difference between $K_{\mathrm{surf}}$ and $K_{\mathrm{vol}}$, (c = −1) yielded somewhat lower results, K between 220 and 260 MeV, but the fit to E${}_{\mathrm{GMR}}$ was significantly worse. This outcome reflects the role of the diffuse nuclear surface, more compressible than the stiffer bulk inside, in determination of $K_{\mathrm{A}}$, which should not be ignored.

As a final comment in this section, we reiterate that the (semi) classical models of nuclear matter do not require quantitative explicit knowledge of the nuclear force. Yet, the saturation energy and density of the SNM, obtained using rather simple classical assumptions, are directly related to the fundamental features of nuclear force, the short range and saturation. To constrain parameters of mass formula-based models, only gross nuclear data are needed; ground-state experimental masses, charge and matter radii and energies of low amplitude vibrational modes. Nevertheless, the ability to reproduce the saturation properties of SNM is accepted as a necessary requirement for low-energy nuclear structure theories which then calculate further quantities, such as the symmetry energy and its derivatives.

3.2. Microscopic Approach

3.2.1. NN Interactions in Free Space

As discussed in Section 3.1, macroscopic models are not explicitly dependent on details of nuclear forces. The early experiments with free neutron–proton and proton–proton scattering (see Section 1) and problems with their interpretation were followed by more elaborate attempts to improve understanding of the nuclear force.

Realistic Potentials

Since the late 1950s, a vast amount of data on partial waves, their phase shifts and related properties from free nucleon scattering with energies up to 350 MeV were accumulated (for current status see http://nn-online.org (accessed on 7 June 2021)). This stimulated more sophisticated versions of the realistic free NN phenomenological potential, e.g., the non-relativistic Reid soft-core, Reid93 and Argonne families [64,65,66,67] and the relativistic Nijmegen and Bonn families [65,68,69], the latter based on meson-exchange models of the nuclear interaction. Each of these potentials depended on many parameters (∼10–40), which allowed a close-to-perfect fit to data.

There were two major consequences of this development. First, it turned out that most of the two-body potentials were phase-shift-equivalent, meaning that they worked equally well in reproduction of the data, but a unique identification of the nuclear force remained illusive. Second, as already mentioned in the Introduction, when applied to nuclear matter and/or finite nuclei, they did not work. The bare NN interactions were not additive in a many-body environment as, for example, in the way that Coulomb interactions are. The predicted saturation energy and density of SNM were in disagreement with the values extracted from macroscopic models [70,71,72]. Brueckner–Hartree–Fock (BHF) [73] theory with two-body potentials, such as the Reid-soft core, applied to finite nuclei, produced only poor agreement with experimental ground-state binding energy and rms radii [74,75,76]. Higher-order corrections were added and parameterized to improve the results (for details, see comments in [77]).

The medium effect on the bare NN interaction was further studied in later years (for an excellent review, see [78]). Brueckner G-matrix theory was applied in both, the non-relativistic BHF [72] and relativistic Dirac–Brueckner–Hartree–Fock (DBHF) [68,79] frameworks. Variational [80,81] and V${}_{lowk}$ methods [82,83,84,85] studied the medium effect by means of perturbation theory. Various techniques were applied to ensure convergence of the perturbation series, including limitation of high momentum components in the scattering amplitudes and renormalization schemes. As a general outcome of these efforts, it has become clear three-body, and possibly higher order, forces play an essential role in the NN interaction in medium and must be added to two-body models to overcome the first hurdle–to predict correctly the fundamental properties of nuclear matter, the saturation density and energy. As a negative side of this varied effort it has been impossible to establish the best approach.

Chiral Effective Field Theory

Another, increasingly popular, tool providing interactions for modeling high-density matter up to approximately twice nuclear saturation density is the chiral effective field theory $\chi$EFT, originally proposed by Weinberg [86,87]. In the absence of the possibility of deriving nuclear forces directly from QCD, which is not perturbative at low densities, the $\chi$EFT model has been formulated in terms of nucleons, their excitations, and pions, instead of quarks and gluons [88]. The theory provides a systematic low-momentum expansion of long- and medium-range forces between nucleons and pions, consistent with the spontaneously broken QCD chiral symmetry. The short-range physics is parameterized by contact terms constrained by parity, time-reversal and the usual conservation laws, but not by chiral symmetry. These terms have to be fitted to data. The contributions to the $\chi$EFT expansions are regulated by a cutoff parameter that has to determined from a comparison with experiment. The positive aspect of the theory is that it provides a systematic hierarchy of nuclear interactions by including the three-body and higher-order forces naturally on the same footing. However, again, it has not yet provided a unique solution to the problem of the nuclear force.

An interesting early exploration of the impact of the $\chi$EFT approach was reported by Sammarruca et al. [89]. The authors compared two very different methods of calculating properties of PNM and SNM, the symmetry energy and the mass–radius curve of a cold NS. In the first scenario, the realistic meson-theoretic two-body Bonn-B potential was used in the DBHF approximation. The second employed a high-precision NN chiral potential and chiral effective three-nucleon forces at the N2LO order. The authors found the results very close and concluded that the two approaches, formally different, are complementary and contain the important features of nuclear forces but are not sensitive to the exact way nucleons act in nuclear matter.

There has been an increasing number of $\chi$EFT applications reported in recent years (for reviews, see [90,91,92]). High-quality two-body NN potentials, ranging from leading order (LO) to next-to-next-to-next-to-next-LO were constructed. EMN2017, the highest-order potential (N4LO), reproduced the world data on NN scattering below the pion threshold available up to 2016 with ${\chi }^2$/datum 1.15, the best result obtained with $\chi$EFT [90,93]. Chiral EMN2017 potentials at NLO, N2LO and N3LO orders, with the three-body interaction at N2LO and N3LO, fitted to saturation properties of SNM and the binding energy of the triton, have been used recently to study ground-state energies and charge radii of closed-shell medium-mass nuclei [94]. We show in Figure 3 results of the binding energy per particle in oxygen, calcium and nickel nuclei. The reader is referred to the original reference for details of this figure. On the whole, the nuclei are over-bound at the NLO level and converge to under-binding with the increasing orders. The final results have still several tens of MeV to be accounted for. The radii (not shown here) are systematically too large.

To illustrate typical EoS of PNM and SNM calculated with EMN2017 chiral potentials [93], we show results of Drischler et al. using ENM2017 [95] in Figure 4. We observe that although the error bands are reduced in N3LO as compared to N2LO, they diverge significantly above the saturation density. Very recently, Drischler et al. [92] reported results on the density dependence of the symmetry energy S from various chiral potentials [96,97,98] and of the $S-L$ correlation. The results, demonstrated in Figure 5, are compared with those of selected phenomenological models [99,100,101] (left panel) and the latest constraints from various experimental and empirical sources (right panel).

Figure 4 and Figure 5 demonstrate that, at best, the models with $\chi$EFT potentials, combined with many-body perturbation methods and/or Bayesian schemes show agreement with predictions of phenomenological models, but do not discriminate among them. The errors are still too large, even at the nuclear saturation density and certainly above. Thus,the models cannot not be meaningfully applied to high-density hadronic matter in compact objects. In addition, the proliferation of $\chi$EFTmodels, using various orders and cutoff values, and employing different methods of many-body approaches detracts from the value of individual results. This reduces the chance of understanding the fundamentals of the nuclear force in medium by this approach.

3.2.2. Density-Dependent NN Interactions

The difficulty with adapting realistic potentials to a dense environment led to construction of nuclear interactions directly parameterized as a function of density. Such interactions were seen as less fundamental, but promised more flexibility, wider application range and easier handling in mean-field approximations. The non-relativistic Skyrme [77], Gogny [102,103] and the Moszkowski [104] models were constructed. These models have been used successfully for both, nuclear matter and finite nuclei.

Skyrme Interaction

The Skyrme potential was developed by Skyrme and collaborators [105,106,107,108] in 1956–1959. This mean-field potential had a two-body part, closely related to scattering of particles in free space and a three-body part, representing many-body effects. To simplify the calculation, short-range expansion of matrix elements of the two-body potential was used, up to second power of relative momenta of the two particles. The matrix elements depended on three familiar parameters $t_0,t_1$, and $t_2$, the measures of the mean central potential, with exchange character, controlled by the parameters $x_0,x_1$, and $x_2$. A tensor potential in even (odd) states, of strength T (U), and a short range spin-orbit two-body potential, were included. This formulation of the Skyrme potential allowed only scattering in S and P states, implying its validity only for low relative momenta.

The three-body part of the potential was expressed as a contact term dependent on one constant $t_3$. This term gave a contribution to the two-body term, proportional to the local density. Skyrme also explored four-body forces and D-wave states but detailed implementation was beyond the scope of his paper. Specifically, to include D-wave scattering would have required the expansion to the fourth power of the relative momenta (see below).

Vautherin and Brink [77] revisited the Skyrme potential in 1972. They adopted the two- and three-body parts of the potential in momentum space and transformed it to coordinate space. They confirmed that the two-body matrix elements of the potential correspond only to S- and P-wave interactions. Furthermore, they also found an equivalent form of the original three-body potential as a two-body density-dependent interaction. With improved fitting technique, two sets of values of the five model parameters (only $x_0$ was considered), SI and SII, which achieved considerably improved agreement with experimental data as compared with [108]. However, they pointed out that, due to their correlations, a multiplicity of choices of the parameters was possible.

Owing to the relative ease in its implementation in Hartree–Fock calculations, the Skyrme model enjoyed immediate success. However, this success has had a negative effect on the development of the field. After Vautherin and Brink, the Skyrme model was applied to a ever wider ranges of experimental data on finite nuclei. Good fits were achieved by increasing the number of variable parameters and refining the Skyrme Hamiltonian [10,109,110,111,112,113,114,115,116]. However, the quadratic limit on the expansion was never changed. In its current most general form, the Skyrme energy density functional contains all conceivable bilinear couplings of densities and currents up to second order in derivatives. This approach introduces 23 coupling constants which are, in principle, density dependent. In a more manageable minimalist approach, the number of the constants can be reduced to ∼10 [10,117].

The parameters of the Skyrme model in the Hartree–Fock approximation (SHF) are adjusted using least-squares fitting techniques to a large sample of current ground-state and low-energy excitation data. The saturation properties of the SNM are either fixed and included in the fits or systematically varied within the accepted empirical range (see Section 3.1) in order to study their effects on properties of finite nuclei. In particular, the density dependence $J,L,K_{\mathrm{sym}}$ and K (with $K_{\mathrm{sym}}$ being the curvature, second derivative, of J with respect to particle number density) all show rather dramatic differences in different versions of the model. Figure 6 shows prediction of the widely used versions SLy4 [118], BSk27s [114] and SkT1 [119]. Fit is required to the values of $J,L,K$ at the saturation density. Note, however, the different predicted variation of the quantity L, the density dependence of the symmetry energy, which, with increasing density, is more or less constant, decreases and increases in the three models, respectively. There is no consensus as to how L should vary. $K_{\mathrm{sym}}$ has even uncertain sign. Both $K_{\mathrm{sym}}$ and L seriously influence the EoS of NSs.

In 2012, Dutra et al. [120] tested 240 different Skyrme parameter using then accepted constraints on nuclear matter properties. Dutra et al. considered the macroscopic quantities derived from liquid drop-type models, from heavy-ion collisions (but see Section 4.3) and from giant resonances. In addition they employed a range of microscopic data, including neutron and proton effective mass, $\beta$-equilibrium matter, Landau parameters of SNM and PNM, and observational data on high- and low-mass cold NSs. Only 16 sets were found to satisfy the macroscopic constraints. This 16 reduced to 5 when microscopic constraints were included. However, it was not possible to justify the success of these five on physical grounds. They did not show the way forward.

The low relative momentum limit of the Skyrme interaction imposes a fundamental constraint on its proper application which has been widely ignored. As stated above, the two-body term of the Skyrme potential is dependent only on the relative momenta of the two particles to the second power meaning that it accommodates only to S- and P-wave interactions. In dense matter, the kinetic energy of particles with momentum $k_{\mathrm{F}}$, at the Fermi surface, ${\hslash }^2{k}_{\mathrm{F}}^2/2m$ is approximately 37, 77 and 122 MeV at densities ${\rho }_0$, 3${\rho }_0$ and 6${\rho }_0$, respectively ($k_{\mathrm{F}}$ = ${(3{\pi }^2\rho /2)}^{1/3}$), taking the rest mass of the nucleon in free space. The mean energy is 60% lower than these values, but the lower effective mass in matter rises them again. Scattering experiments show that at energies approximately 100 MeV the contribution of D-waves not included in the Skyrme potential as commonly used cannot be neglected. Skyrme [108] emphasized that including D-wave interactions would require the addition of a term dependent on the fourth power of the relative momenta. He discussed its effect only in finite nuclei, i.e., up to saturation density. Thus, although the Skyrme EoS is frequently numerically applied up to high density expected in the interior of heavy NSs, all such applications are inconsistent with the limit on physical validity of the model. In other words, a Skyrme-based EoS is only correctly used in NSs with central particle number density below approximately 3${\rho }_0$. The author recalls a comment by David Brink after she and colleagues published the first paper in which the Skyrme model was applied to NSs [52] pointing out this problem. This paper and most subsequent standard Skyrme model NS calculations suffer from this defect.

More general phenomenological energy density functionals (EDF) than those built on the standard Skyrme interaction discussed here have been explored [121,122,123,124]. They include terms dependent on the relative momenta k and k${}^{\prime }$ up to the sixth order. The number of the additional terms and related variable parameters is high as compared to the standard EDF, which makes use of these extensions impractical.

Relativistic Mean-Field Models

Relativistic mean-field models (RMF) use nuclear interactions based on meson exchange between point-like nucleons (without internal structure) and have been seen as a more fundamental, but still phenomenological, approach to the nuclear many-body problem. These models have several aspects not present in their non-relativistic counterparts. These included intrinsic Lorentz covariance, automatic inclusion of spin, appropriate saturation mechanism for nuclear matter, causality. They do not have problems related to the superluminal speed of sound in medium. Furthermore, RMF models are naturally applicable to high-density matter whereas the non-relativistic low-momentum Skyrme model is not.

Among the first were models of the (non-linear) Walecka type, since the 1970s [125,126,127,128] and later [129,130]. These models used density-independent nucleon–meson coupling constants which kept the number of adjustable parameters to approximately eight, similar to the early Skyrme interactions. Density dependence of the couplings, introduced by Typel and Wolter in 1999 [131] and developed later, e.g., [132,133,134], increased this number to approximately 15, again on a par with modern Skyrme parameterizations.

There have been several reviews and studies of the differences in predictive power of RMF and SHF models [10,135,136]. The level of success in modelling of finite nuclei is comparable in both models [110,133,137]. RMF models do not suffer from the applicability limit on SHF models discussed above. The proliferation of RMF and SHF variants is very similar. Dutra et al. [138] examined the performance of 263 RMF models used for nuclear matter and found that only 4 of them satisfied all the constraints. When the constraint on the volume part of the isospin incompressibility was eliminated, this number increased to 35.

Quark–Meson Coupling Model

A special class of relativistic models, the quark–meson coupling (QMC) model was developed by Guichon and collaborators [139,140,141]. It is an effective relativistic mean-field model in which the forces between individual baryons are self-consistently mediated by exchange of virtual mesons between the valence quarks in the baryons. The effect of the medium surrounding the baryons in dense matter, such as in NS cores and nuclei, modifies dynamics of the valence quarks in the individual baryons. In other words, in the nuclear medium, the quark–meson couplings acquire an effective density dependence, which is determined by the response of the quark structure of the baryons to the meson fields.

In the QMC model, the baryons are represented as non-overlapping MIT bags (but other models of confinement can be used without a loss of generality). In a literal interpretation of the bag model, where only quarks and gluons can live inside the cavity, this coupling would be unnatural. However, in a more realistic underlying picture, the quarks are attached to a string (see Figure 7) but otherwise move in the non-perturbative QCD vacuum. There, nothing prevents them from feeling the vacuum fluctuations, which are described by meson fields. This feature allows the QMC model to be used up to approximately 7–8 ${\rho }_0$ without concerns about the bag overlap.

The model has five adjustable parameters to be fitted to data, all having clear physics meaning, three coupling constants of the $\sigma$, $\omega$ and $\rho$ meson fields to the quarks, the mass of the $\sigma$ meson (not well known experimentally) and the radius of the bag model representing the baryons. All other fixed parameters of the model are either taken at their experimental value or calculated within the model. Once fixed, the adjustable parameters form a set which is so constrained that any variation would disturb the internal integrity of the model. Should a serious discrepancy between the model prediction and new observational and experimental data occur, physics missing in the model must be sought.

This unique concept has several fundamental consequences. As shown already in [139], the model offers a natural explanation for the saturation of the nuclear force, automatically includes many-body forces and there is no need to change the number of parameters when the baryonic composition in the matter changes. Thus, matter consisting only from nucleons and matter containing the full baryon octet (nucleons and hyperons) is described by the same parameter set and the hyperon-nucleon and hyperon-hyperon couplings are fixed by the quark structure within the model. The often discussed “hyperon puzzle” does not occur in the QMC model.

The QMC model was first applied to NSs ([142] in 2007 and predicted the existence of a cold NS, with $\mathsf{\Lambda }$ and ${\mathrm{\Xi }}^0$ hyperons in their cores and a maximum mass of 1.97 M${}_{\odot }$, three years before such a star was observed by [143,144,145]. Very recently, the model was extended to finite temperature [11] and yielded EoS tables suitable for use in modeling proto-neutron stars (PNSs), CCSN, and remnants of binary neutron star mergers (BNSM).

Some variants of the QMC model of dense matter in compact objects, using simplified expressions for the bag representing the nucleon, the effective mass of the nucleon and the treatment of meson fields were reported [146,147,148,149,150,151,152,153,154,154]. The authors of these QMC versions allow some flexibility in their parameters not permitted in the fully self-consistent version above.

Application of a non-relativistic version of the QMC model to finite nuclei yielded predictions of ground-state properties of finite nuclei in excellent agreement with experimental data over a wide range including superheavy nuclei far beyond the parameter fitting range [155,156,157,158]. Interestingly, the QMC model is, to our knowledge, the only non-relativistic mean-field model in which the spin-orbit coupling appears naturally.

To summarize this section, the examples shown here of various attempts used to understand the effect of nuclear medium on the bare NN interaction have not reached the “the holy grail’ as yet to a satisfactory conclusion. The models do not have enough sensitivity to interpret their differences in relation to the physics they are based on.

4. Astrophysical and Terrestrial Data

4.1. Neutron Stars: Masses and Radii

In this section, we select data extracted with no (or minimal) nuclear model dependence. These constitute major serious constraints for NS models and the EoS of baryonic matter. The TOV equation yields only the gravitational mass as a function of its radius and yields a maximum mass for a given EoS. Thus ideally the mass and radius of the same object are needed from observation. However, this has proved difficult. The only other constraint on a proposed EoS is the maximum observed mass. Thus, the maximum observed mass serves to eliminate many models.

The gravitational mass of NSs can only be measured in binaries. Masses have been extracted from observation for decades using different methods (see, e.g., https://www3.mpifr-bonn.mpg.de/staff/pfreire/NS-masses.html (accessed on 7 June 2021)). The most precisely measured mass (1.441 M${}_{\odot }$) is that of the Hulse-Taylor Pulsar PSR B1913+16, observed in 1974 [159]. This mass was taken as the canonical mass of cold NSs for a long time.

The situation changed when, in 2010, Demorest et al. [143] announced the mass of the binary millisecond pulsar 1.97 ± 0.04 M${}_{\odot }$ PSR J1614-2230 (further updated [144,145]). Since then two stars, PSR J0348+0432 and the millisecond pulsar J0740+6620, were reported with mass approximately 2 M${}_{\odot }$ [160,161,162]), with the highest mass 2.08 ± 0.07 M${}_{\odot }$ [162],

Extraction of NS radii from observation, mainly from radio and X-ray signals but also from surface thermal emission, is rather complicated. Many assumptions about the origin of the signal, the surface temperature, the stellar atmosphere and its distance from the observer have to be made.

Oezel and Freire in 2016 [163] summarized observational methods and their analysis to yield NS radii and placed a constraint on radii between 10 and 11.5 km. Ironically, the mass of the star is a required assumption and many take it to be 1.4 M${}_{\odot }$. Further investigations [164,165,166,167,168,169,170,171] broadened these model-dependent limits to between 10 and 15 km.

There have been several recent attempts to use data from BNSM events to extract limits on radii and masses of the merging stars and find constraints on their EoS. Various techniques were used, mainly based on Bayesian schemes, but also nuclear models such as, for example, (D)BHF [168] (for a review, see [167]). In Figure 8, we illustrate Bayesian inference for the radius of a 1.4 M${}_{\odot }$ NS, presented by Al-Mamun et al. in 2021 [171] in their Table I. The results were obtained combining GW and electromagnetic data (see caption of Figure 8 for details). The spread of the values does not indicate preference for a particular result which would provide the desired constraint.

The latest step towards determination of the mass and radius of the same object is found in a report of the NICER mission. Bayesian inference of the energy-dependent thermal X-ray waveform of the isolated pulsar PSR J0030+0451 yielded its estimated mass 1.44${}_{-0.14}^{+0.15}$ M${}_{\odot }$ and equatorial circumferential radius 13.02${}_{-1.06}^{+1.24}$ km [182]. This result is consistent with the outcome of an independent analysis of the same data by [183] who obtained 1.34${}_{-0.16}^{+0.15}$ M${}_{\odot }$ and radius 12.71${}_{-1.19}^{+1.14}$ km. Although the Bayesian inference method yields, in principle, both mass and radius, it is still subject to the choice of the prior. Fully independent mass and radius data would be preferable. To our knowledge there is no more data available from the NICER primary target, the bright pulsar PSR J0437-4715 [184]. The mass of this star 1.44 ± 0.07 has been measured independently with uncertainty ∼5% [185] but its radus remains unknown.

We illustrate the maximum mass (black rectangle) and mass/radius (elipse) constraints [182,183] in Figure 9, superimposed on predictions from EoS of the QMC-A, CMF and DD2 models (for details, see [11]). Predictions of the old, well established, APR [99] and GLENHYB [186] EoS are also shown. To conclude this section, it is clear that the presently available mass/radius data are not yet precise enough to select between these EoS which are based on very different underlying physics.

4.2. Gravitational Waves

4.2.1. Observation

Observation of gravitational waves (GW) and their counterparts from BNSM has added a potential new dimension to the search for constraints on the NS EoS. The dynamics of the BNSM have frequently been modeled in the past to guide observation [187,188,189,190,191]. Modern general relativity (GR)-based hydrodynamic simulations have been reported [192,193] since the observation (for reviews, see [194,195]).

There are three GW events involving NS reported to date. The first, GW170817 [196] is compatible with a collisison of a binary NS system with chirp mass 1.186(1) M${}_{\odot }$, mass ratio q ∈ [1,1.34], and reduced tidal parameter $\tilde{\mathsf{\Lambda }}\simeq$ 300 and smaller than ∼800. Two electromagnetic counterparts were observed, a gamma ray burst GRB170817, 1.7 s after the coalescence, and an optical signal AT2017gfo (kilonova) [197,198], observed 0.47–18.5 days after the event.

The second, GW19025 [199] was, with 90% probability, the coalesce of two objects with masses ranging from 1.12 to 2.52 M${}_{\odot }$ (dependent on the component spin magnitude) which is consistent with the individual binary components being neutron stars. Both the chirp mass and the total mass of this system are larger than any previously known binary NS system. Thus, a possibility that one or both components are light black holes cannot be ruled out from GW observation. No confirmed electromagnetic or neutrino emissions related to this event were identified.

The third, also possibly involving a NS, GW190814 [200], is compatible with a coalesce of a 22–24.3 M${}_{\odot }$ black hole (primary) and a 2.50–2.67 M${}_{\odot }$ compact object (secondary). No electromagnetic counterparts have been observed. This event represents a new class of binary coalescence sources with highly unequal mass and low primary spin [200]. The secondary component is either the lightest black hole or the heaviest NS ever discovered. However, this is still a question of debate [201,202,203,204,205,206,207,208,209].

The post-merger GW signal, which is expected to have the largest luminosity and is essential for determination of the remnant’s fate, has not been observed in any of these events. It is most likely emitted at frequencies above the main sensitivity band of current detectors [210].

4.2.2. Extraction of Information

Obtaining specific information from the GW wave form (the frequency range, peak amplitude and luminosity), supplemented by the additional spectroscopic evidence, is far from straightforward and depends on extensive, detailed modelling. The only realistic approach at present involves statistical likelihood-based Bayesian schemes of simulation.

To make these simulations computationally viable, two major diversions from state-of-the-art NS modeling using microscopic EoS must be made. The EoS is greatly simplified to allow a minimum number of parameters to be determined by sampling [58,171,173,180,211]. In addition, quasi-universal relations between selected pairs of suitably normalized NS properties are built in to the simulations in the form of simple functions, e.g., polynomials, determined by only a few parameters [11,134,212,213,214,215,216,217].

The price to pay for these simplifications and the whole statistical approach is the loss of all connection to the microscopy of NS matter. Future improved and more complete GW observations are likely to offer much enhanced sensitivity to model content. Thus, although these observations contain new physics of great interest, extraction of meaningful information on the EoS and the nucleon–nucleon interaction in medium from existing data is not possible.

4.3. Heavy Ion Collisions at Low and Medium Energies

Heavy ion collisions (HIC) with a beam energy below approximately 10 GeV/nucleon have long been seen as the only terrestrial experiments which could offer constraints upon the EoS of dense matter. Properties of the EoS such as the incompressibility at saturation density and density dependence of the symmetry energy are reflected in the output of the collision, the elliptic and transverse flows, as a function of the projectile and target nuclide combinations and the incident beam energy. The dynamics of the collision changes with the incident beam energy as different physical aspects play dominant roles, and naturally requires sophisticated modelling. Relevant to this this work, we discuss the Boltzmann–Uhlenbeck–Uehling (BUU) approach, used primarily for medium-to-high beam energies.

Danielewicz et al. [218] in 2002 used a model based on the pBUU to explore the density dependence of pressure and hence of the EoS in zero-temperature SNM and PNM in the range of baryon number density up to 4.6 ${\rho }_0$, consistent with experimental data on the particle flow. The uncertainty in the input EoS governing the collision was reflected in spread of pressure vs. density plots. Over the years these diagrams have been used as one of the powerful constraints of the EoS of high-density matter. However, recently, this analysis has been seriously questioned.

Stone, Danielewicz and Iwata [63] revisited the model in 2017, with the aim of exploring the maximum density that can be achieved in Ca and Sn collisions at beam energies below 800 MeV/particle and the density dependence of the symmetry energy. They concluded that the highest total particle densities were of the order of 2.5 ${\rho }_0$, only weakly dependent on initial conditions, far lower than earlier indications suggested. The maximum proton–neutron asymmetry $\delta$ was found ∼0.17 in all investigated systems and at all beam energies, scarcely rising above its value in the coliding nuclei. This weakened the argument that such studies could assist with the physics of neutron stars.

Recently this study was extended including Pb collisions as a representation of the heaviest system accesible HIC experiments. The still unpublished results [219] revealed that there no increase in the highest achieved density and furthermore that there is a significant contribution of Coulomb interaction to both the maximum total density and the isospin asymmetry at that density, which reduces the nuclear interaction effects.

The BUU transport model has also been used by Zhang and Ko [220] using a variant of the Skyrme interaction Sk$\chi$m* obtained by fitting the nuclear equation of state and nucleon effective masses in asymmetric nuclear matter predicted by the two- and three-body chiral interactions as well as the binding energies of finite nuclei [221]. They studied the effect of baryon mean-field potentials on the kinematics of scattering and decay processes in the Au and Sn collisions and the equilibrium properties of a hot $N+\Delta +\pi$ system. This approach allows control of the isovector mass, not available in the pBUU transport, which may lead to more realistic momentum dependence in the isoscalar sector. However, there are some concerns about the new interaction itself. The Sk$\chi$m* force predicts rather low isovector effective mass, very soft symmetry energy (low value of the slope L at saturation density) and too small neutron skin in ${}^{208}$Pb, in disagreement with the latest PREXII result. The Skyrme interaction (Equation (6) in [221]), utilizes a short-range expansion up the two-body matrix element of the potential up to second power of relative momenta of the two particles (for discussion, see Section 3.2.2. It is not clear how this basic property of the Skyrme model was taken into account in derivation of the Sk$\chi$m* force and in its application to HIC at beam energies of several hundreds of MeV/A.

Aichelin et al. [222] used the BUU transport model in 1985 to the first study of sensitivity of kaon production at sub-threshold energies in central collisions of heavy nuclei at beam energies approximately 700 MeV/A. Using empirical EoSs, a significant sensitivity was found to their stiffness. In 2001, Fuchs et al. [223] investigated the dependence of the K${}^{+}$ production on the nuclear EoS. The observed increase in the excitation function of K${}^{+}$ multiplicities in heavy (Au+Au) over light (C+C) systems, when going far below threshold, strongly favored a soft equation of state.

A comprehensive summary of the search for a connection between results of HIC experiments, available before 2008, and the isospin dependence of in-medium nuclear effective interactions and the equation of state of neutron-rich nuclear matter can be found in the review by Bao-An Li and collaborators [224]. The particular focus of the review, the density dependence of the symmetry energy and its effect on nuclear and astrophysical phenomena has been a topic of interest to these days [225], still waiting for the final solution.

However, the main problem with seeking to use HIC data at low and medium beam energies to constrain the NS and CCSN EoS concerns a particular feature of the EoS which is often overlooked (see Section 2). The EoS of any system is dependent on its composition. We compare the physical nature of matter created in the HIC and existing in cold NS cores in

Table 1. Physical properties of matter in HIC at beam energies considered in [218] and in the interior of a cold NS. No phase transitions to quark matter are included.

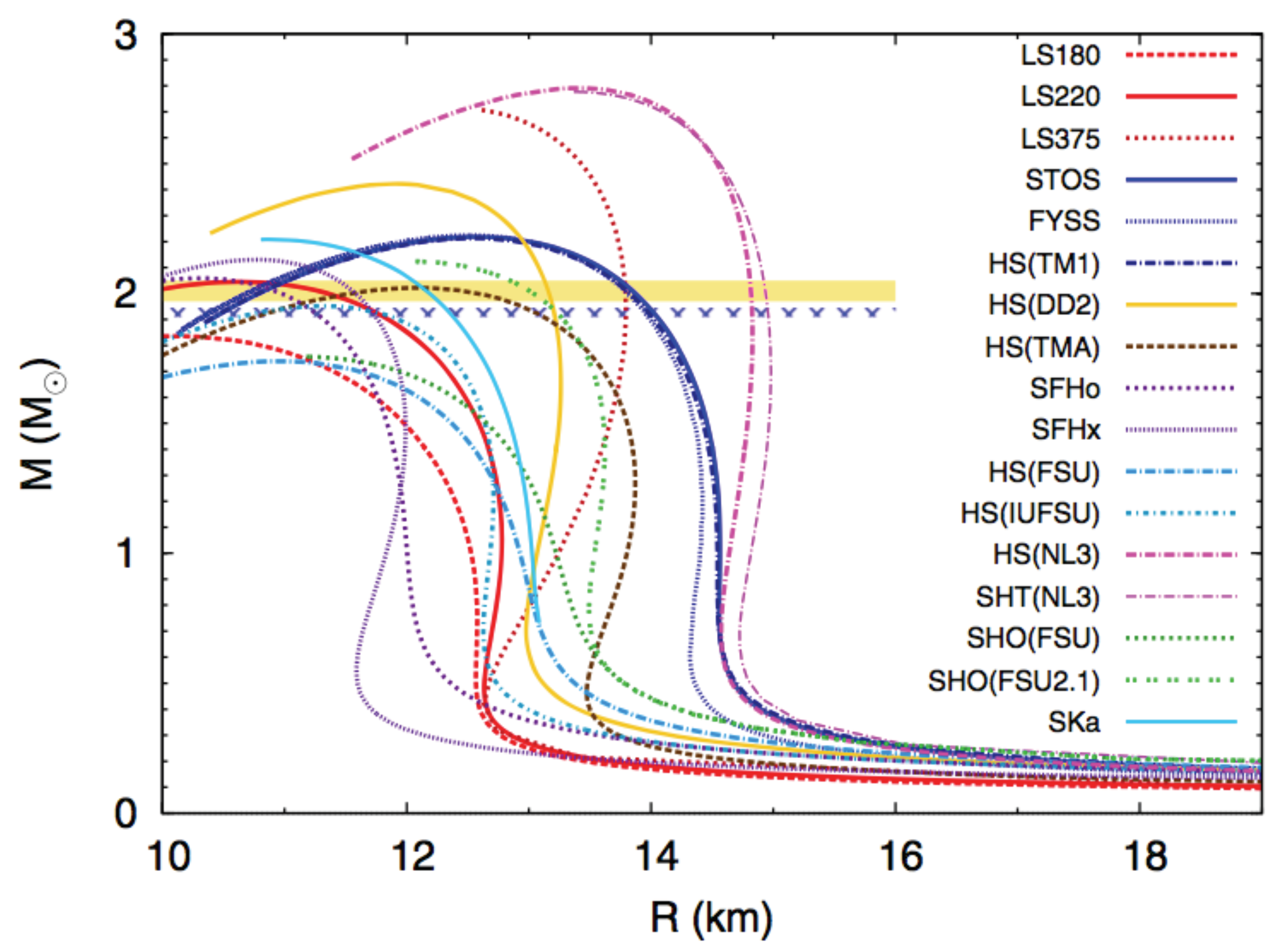
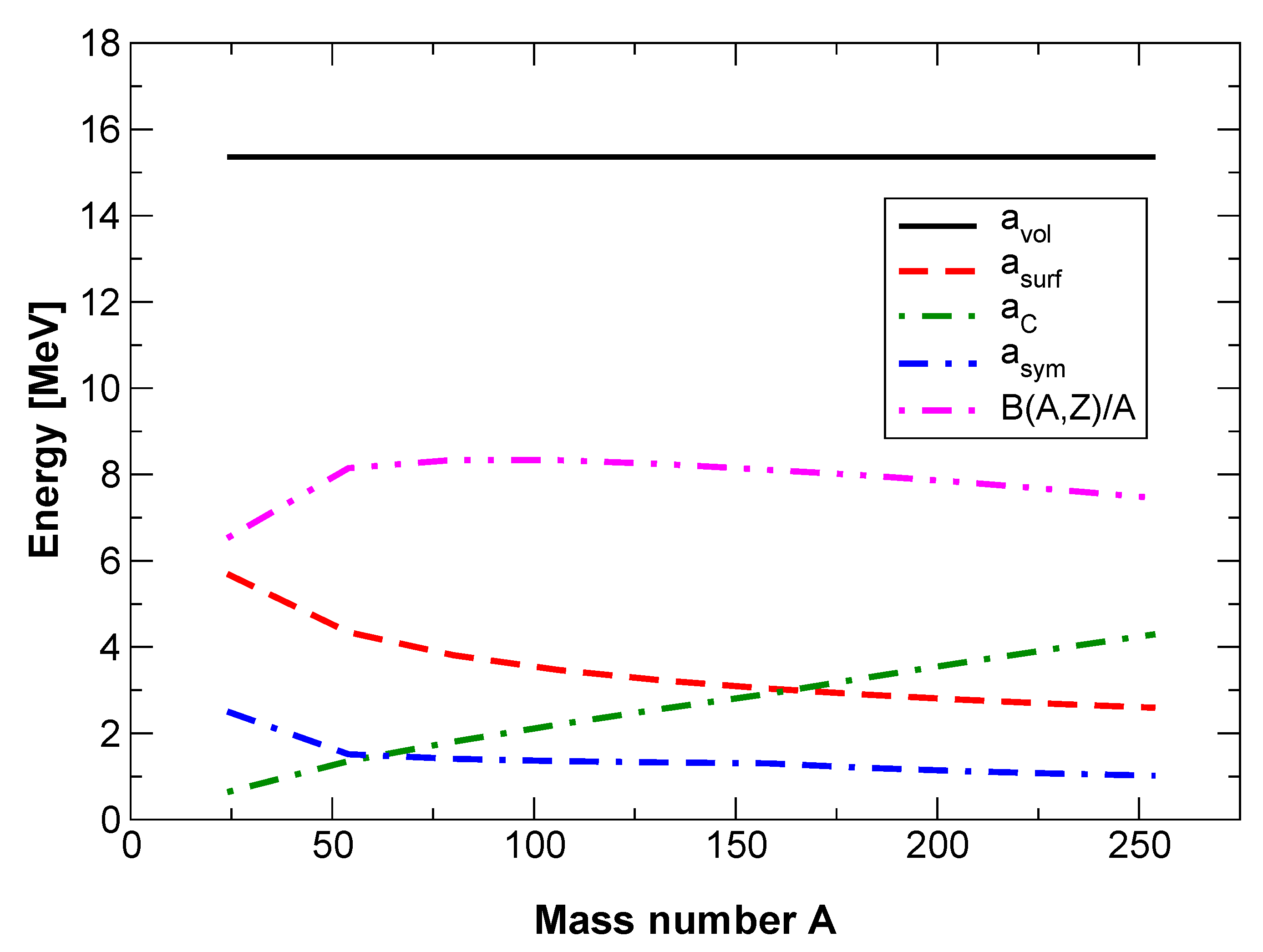
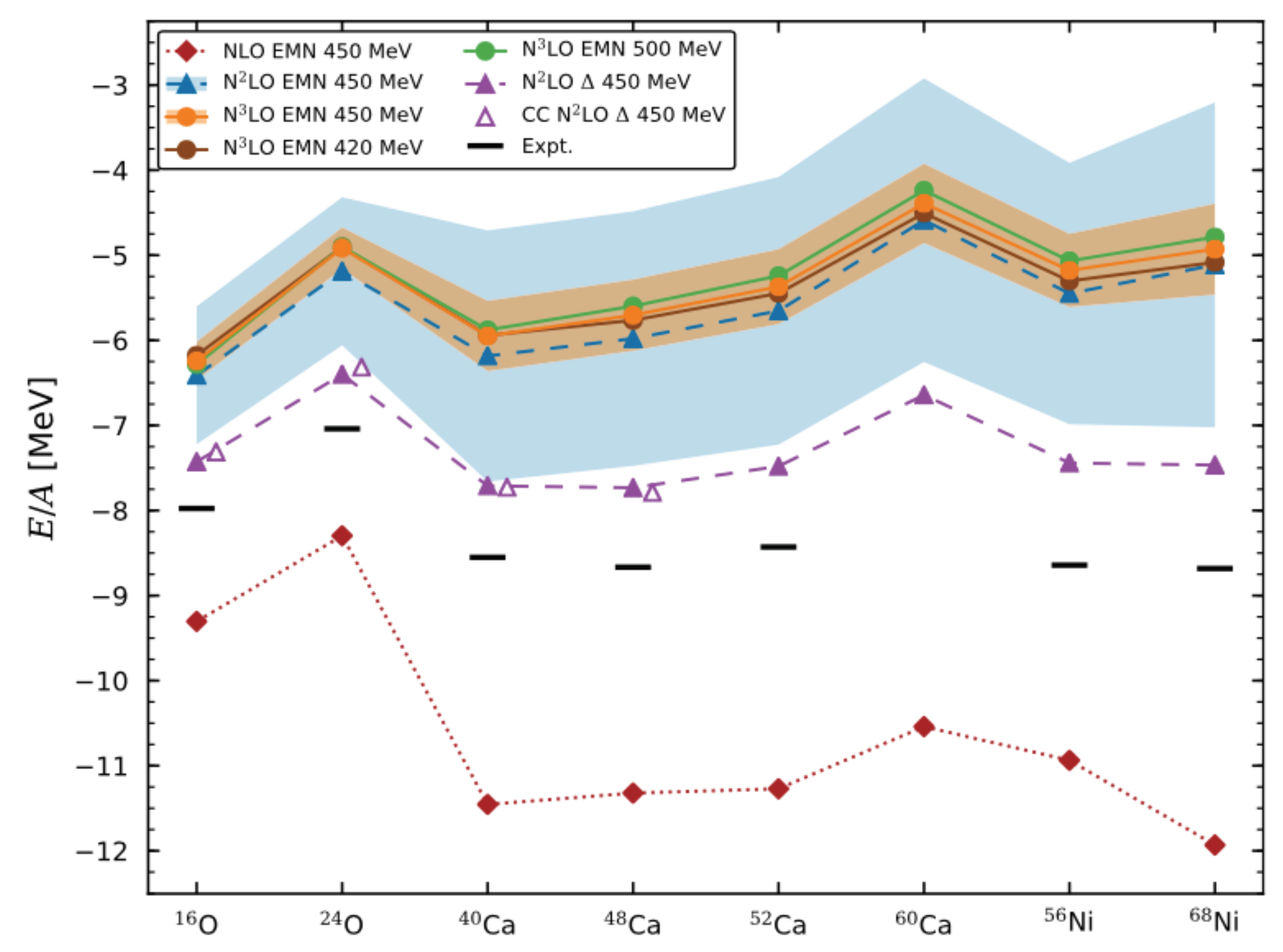
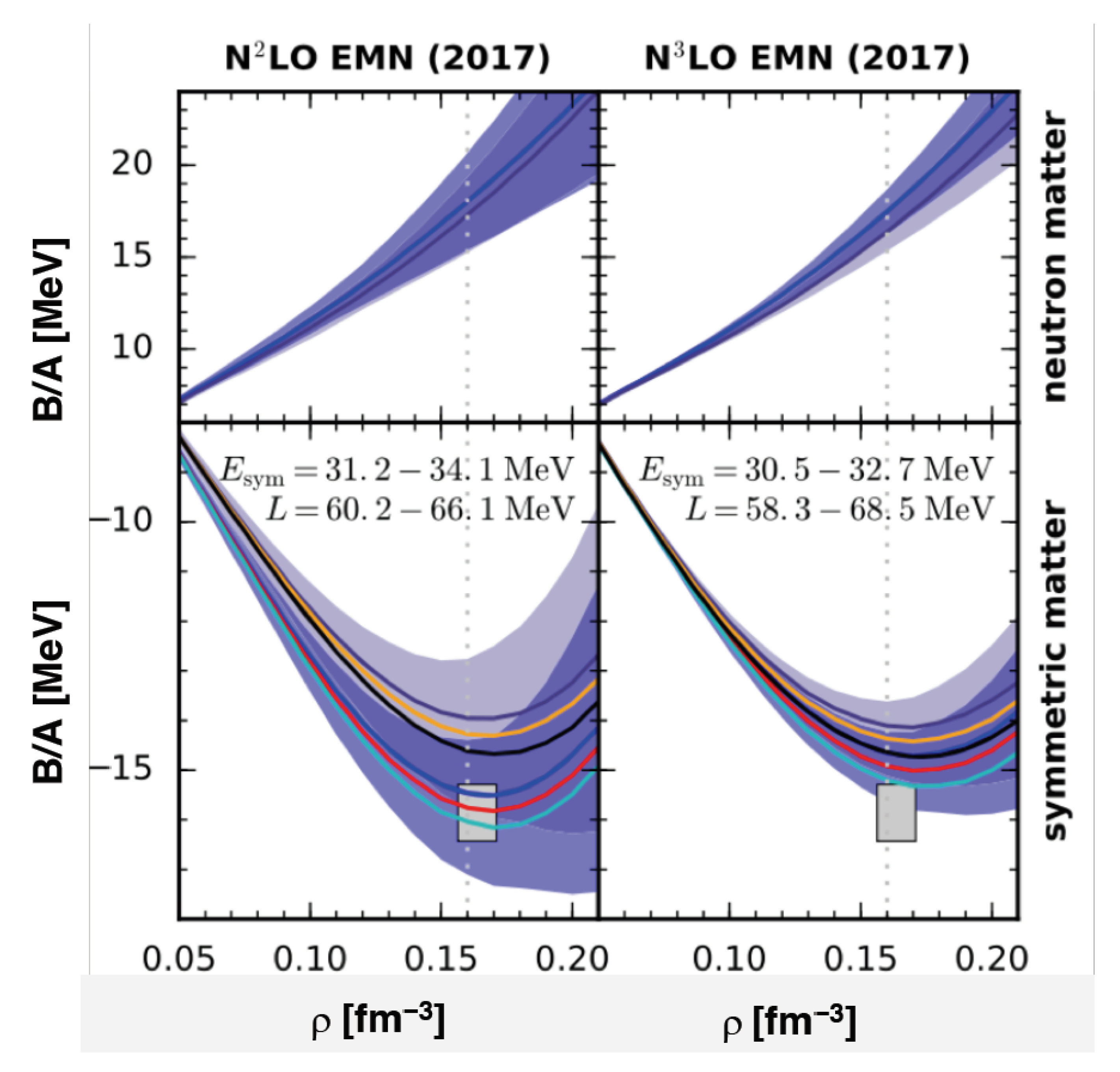
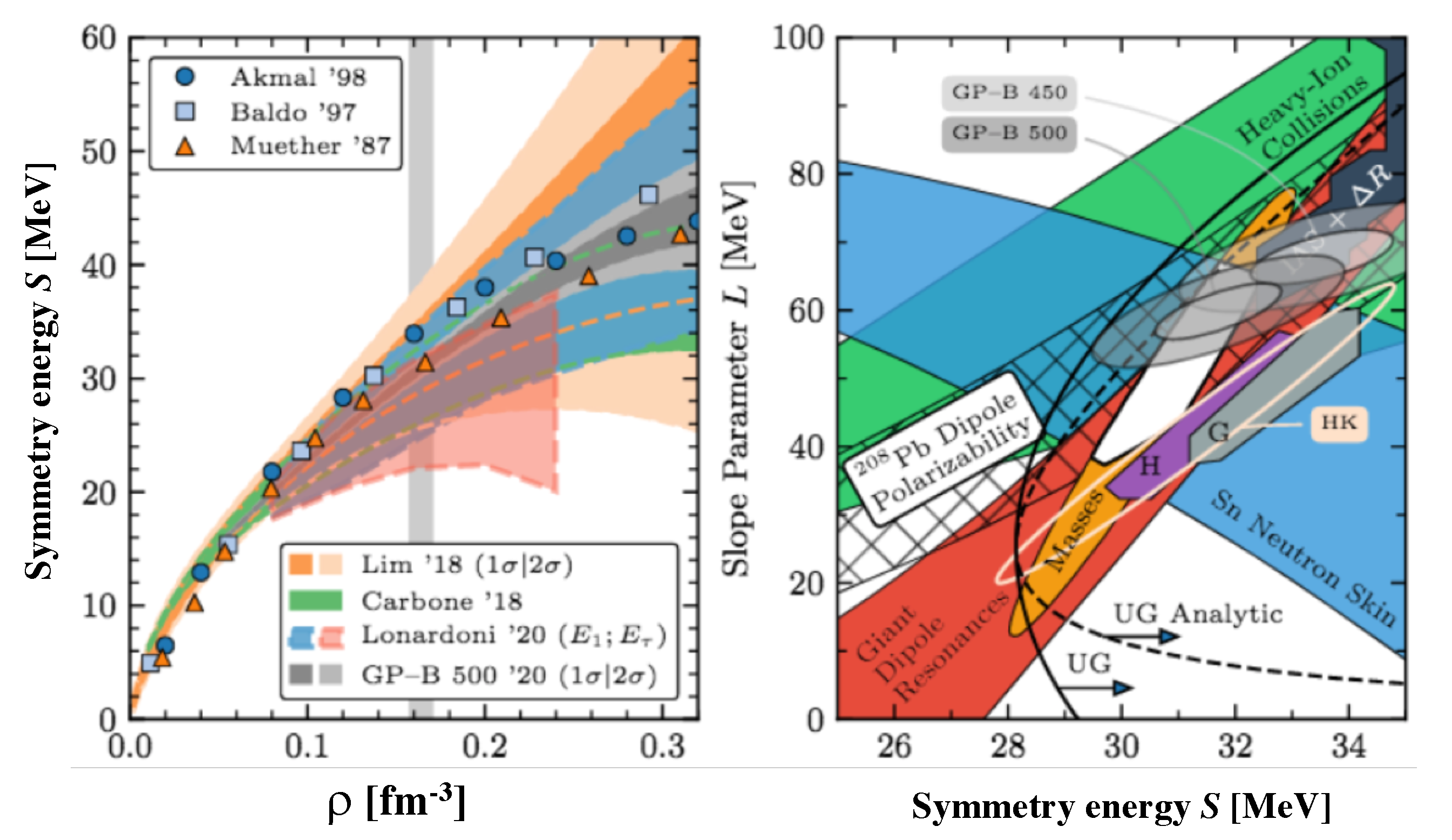
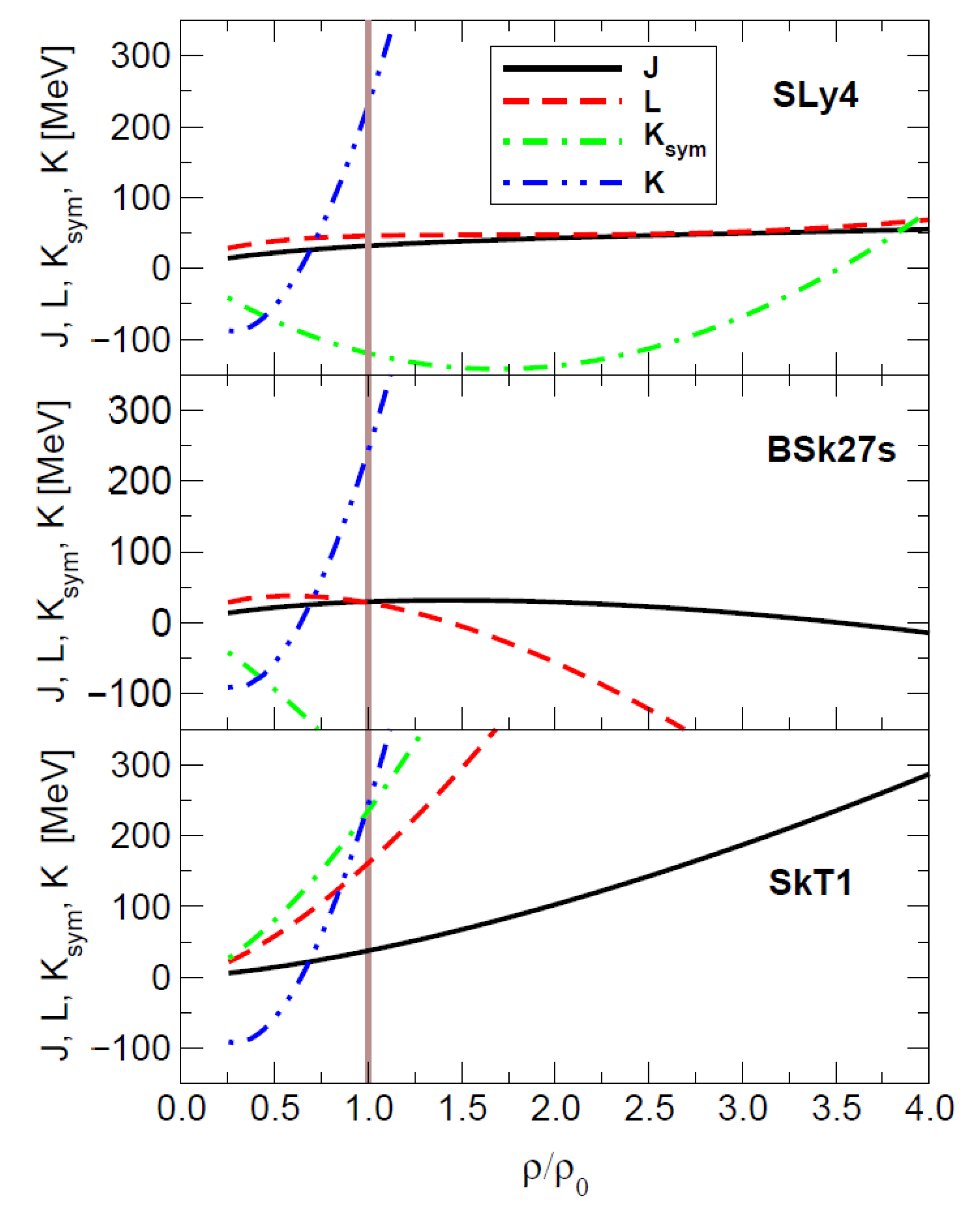
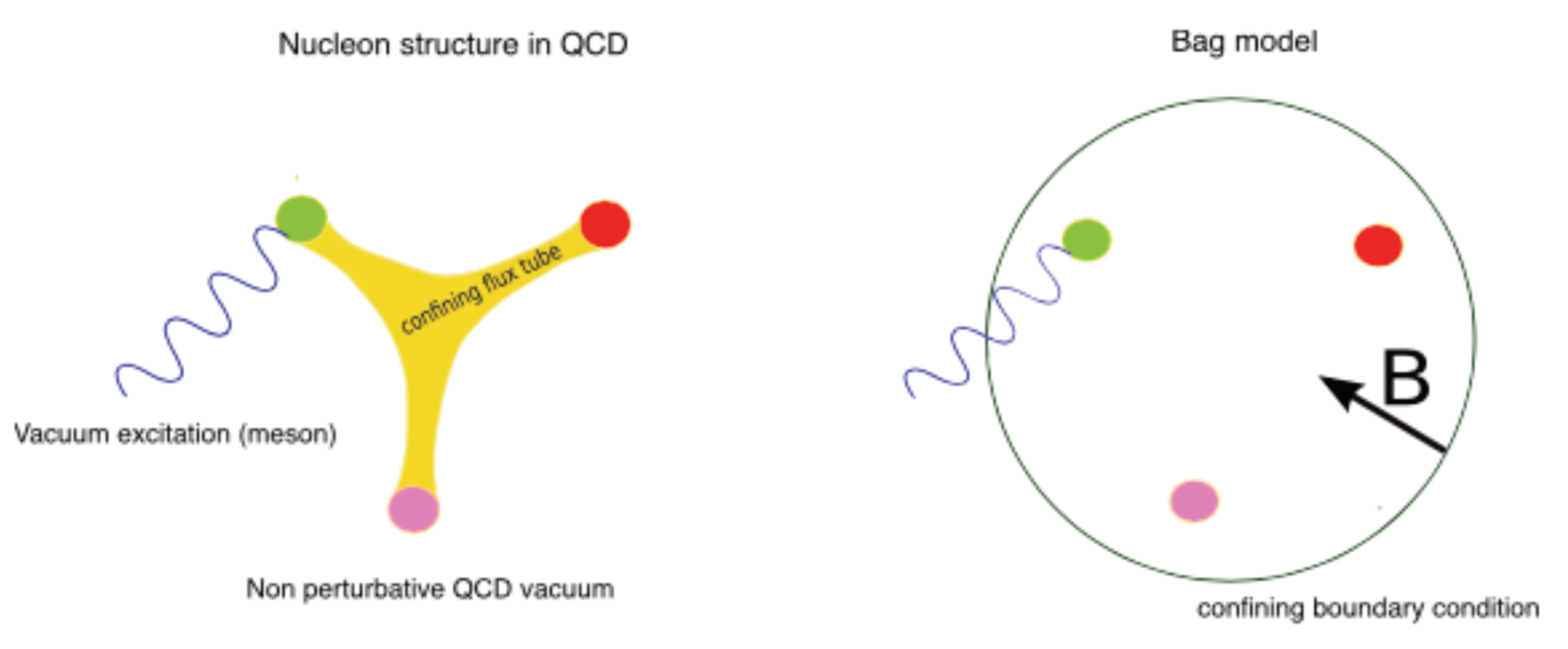
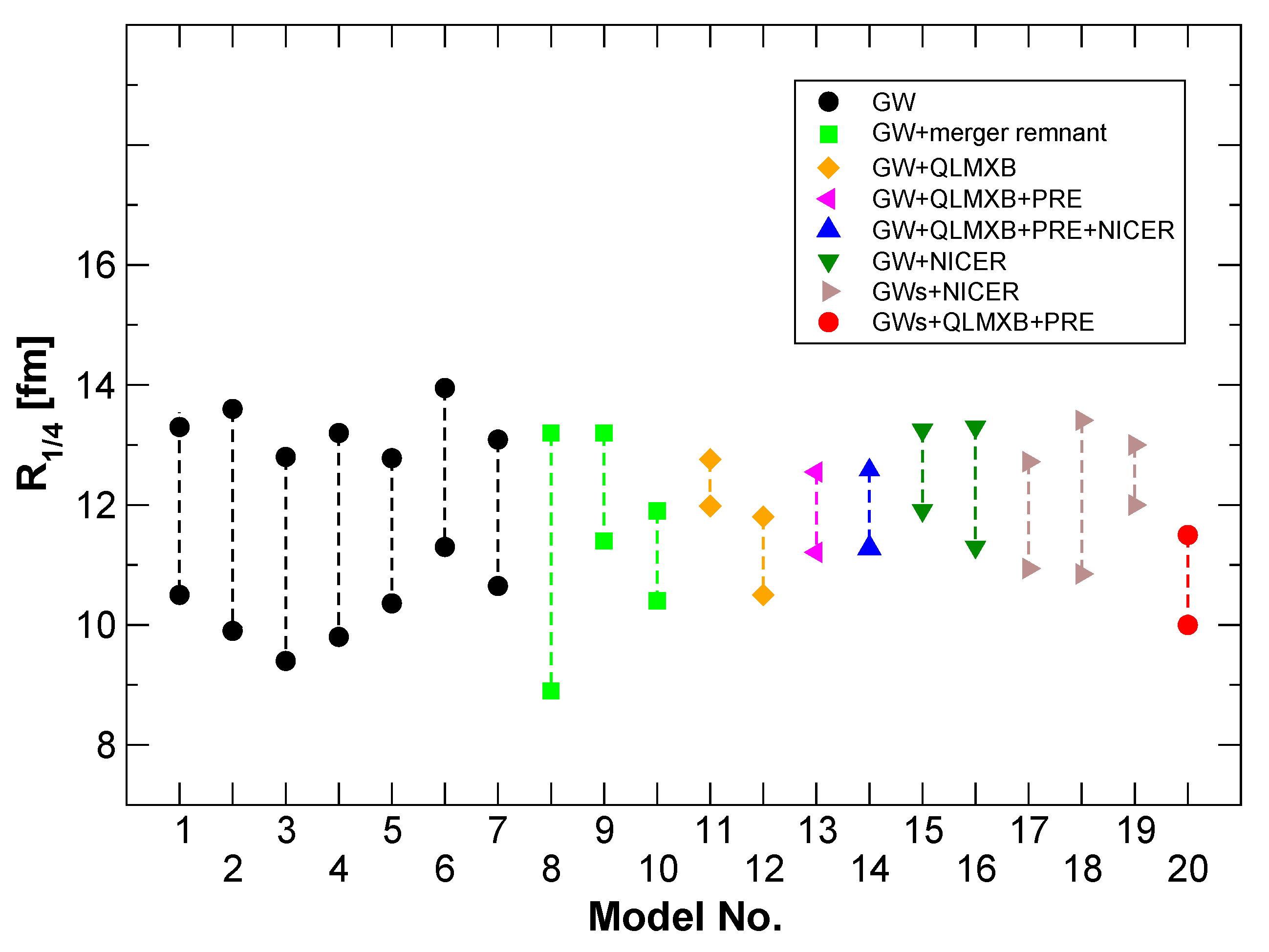
Property	HIC	NS
Time scale	10${}^{-24}$ s	10${}^{-13}$ s
Interactions	strong	strong
		weak
Gravity	no	yes
Coulomb	yes	no
Strangeness	conserved	not conserved in weak
Nucleons	yes	yes
Hyperons	no	yes
Pions/Kaons	yes	condensate possible
Leptons	no	yes
p/n ratio	∼1	∼0.1

to highlight the fundamental incompatibility of the two systems. The main difference springs from the duration of the collision and of the formation of a NS. The time-scale of HIC is that of the strong interaction, ∼10${}^{-24}$ s. Thus, only products of the strong interaction can appear, nucleons in ground and excited states and free pions, possibly kaons. In a NS, the situation is much more complex. As discussed in more detail in Section 4.1, the star develops since its birth on time scales allowing not only the strong, but most importantly, weak interactions to act, which fundamentally changes the high-density matter makeup in NS cores. The time scale of weak interaction in free space is approximately 10${}^{-13}$ s but can be longer in dense matter, up to ∼1 year [226,227]. This allows appearance of weak interacton products throughout the life of a NS. Furthermore the proton–neutron asymmetry in cold NS matter is remote from that reached in HIC. Another important difference between HIC and NSs, of course, is the role of gravity in the NS, which, together with the nuclear force, determines the pressure and density distribution of the matter.

Considering CCSN matter, it is closer to matter in HIC in one respect. The proton–neutron ratio is close to one half at the birth of the PNS. However, leptons, not present in the HIC, play an essential role in CCSN physics and the evolution of its remnant. Also, questions concerning the existence (or not) of equilibrium in HIC, which would allow estimation of the temperature reached in the collision and its comparison with temperatures expected in CCSN events are not yet fully resolved.

The recent object of great interest is the remnant of BNSM. As already mentioned in Section 4.2, there is a considerable theoretical effort to model its properties. However, the vital piece of information needed to put these models on a more solid ground, the post-merger GW signal, has not been observed as yet. It is therefore not clear, for example, which part of the remnant is heated up to temperatures, supposedly comparable its those achieved in HIC, the baryonic core or the surrounding neutrino mantel ([194] and ref. therein). Thus, any constraints derived from modeling of the remnant should be taken as tentative.

We therefore conclude that data from heavy-ion collisions in this regime cannot directly infer constraints on properties of compact objects. Although technically possible, such process cannot be justified at the fundamental level.

4.4. High-Energy Heavy Ion Collisions

The hadron production in nuclear collisions at ultra-relativistic beam energies has been studied at different facilities, such as (now historical) CERN SPS, RHIC and currently at highest beam energy at LHC for a long time. The main objective has been to create conditions close to those at the Early Universe when quarks were not confined in hadrons but were able to move freely over distances larger than the size of the hadrons. The mechanism of hadronization of the quark soup as a function of temperature T and the baryonic chemical potential ${\mu }_{\mathrm{B}}$ is extremely complex and is in the heart of understanding of the so called QCD phase diagram of a strong interacting matter in chemical and thermal equilibrium which includes information of phase boundaries and transitions between hadronic and quark matter. The diagram includes the first-order transition line between the hadronic (ordered) and quark (disordered) matter which ends with the critical point where the transition is of second order [228]. The high T and low ${\mu }_{\mathrm{B}}$ region of the diagram is readily probed in heavy-ion collision experiments, while the low T and high ${\mu }_{\mathrm{B}}$ region is the domain of nuclear matter and neutron stars.

Theoretical tools developed to make predictions and interpret high-energy experiments include a variety of approaches. Thermal statistical models, such as hadron-resonance gas model [229,230,231], and statistical hadronization model [232,233], as well as ultra-relativistic quantum molecular dynamics models [234] and the blast-wave model [235] are used. One of the main objectives of these studies is to obtain information on particle production. The various criteria for the chemical freeze-out (inelastic reactions cease) and the kinematic (thermal) freeze-out, when the elastic reactions also cease, and the composition of the hadronic matter is fixed in time [230,233,234] are investigated. The hierarchy of particles produced in the range of temperatures from ∼160 to 50 MeV and ${\mu }_{\mathrm{B}}$ from ∼20 to approximately 800 MeV starts with pions and kaons and carried on particle and antiparticle pairs of protons, $\mathsf{\Lambda }$, $\mathrm{\Xi }$ and $\mathsf{\Omega }$ hyperons, followed by light He and H clusters [232,233]. Typical baryon number density is below the saturation density fo nuclear matter. All these species are produced in reactions governed by the strong interaction, conserving strangeness, because the typical time of the reactions is not longer than 10${}^{-23}$ s. The new facilities being currently built, FAIR at GSI and NICA in JINR [236], designed to probe the medium T and ${\mu }_{\mathrm{B}}$ of the QCD diagram, will face the same problem, already discussed in Section 4.3. The longer life-time of compact objects (see Section 4) allows for the weak interactions to develop, which changes not only the hadron make-up but also brings in leptons, essential for the physical processes in these objects to proceed. Therefore attempts to derive constraints on properties of compact objects from high-energy heavy-ion collisions, (see, e.g., [236,237]) suffer from the same fundamental problem as outlined in Section 4.3.

5. Concluding Remarks

The baryon–baryon interaction in free space and its modification by the surrounding medium is far from being understood. The current proliferation of models with many correlated not-well-constrained parameters does not help in its solution. The more complex the current models are, the more difficult it becomes to interpret the results on a fundamental level. Hans Bethe in his 1953 paper [238] “What holds the nucleus together” said that

In the past quarter of the century physicists have devoted a huge amount of experimentation and mental labor to this problem–probably more man-hours than have been given to any other scientific question in the history of mankind.

In 2021, we have scarcely advanced. This paper deliberately took a step back into the history of the field of high-density matter in search for some important clues or assumptions, which might have been made way back and forgotten over time. Some of the basic concepts of models we use today, such as the macroscopic drop-type models, are based on a very classical picture of the nucleus and are almost 90 years old. SNM, introduced decades ago as a testing ground for nuclear models, is an idealized approximation of reality. We still take its basic properties, saturation density and energy, as essential constraints of our models today. Relativistic meson-theoretical and non-relativistic potential models are used side by side in free nucleon–nucleon scattering analysis and found phase-shift equivalent. The $\chi$EFT was first introduced in the 1970s, almost at the same time as the density-dependent effective interactions for mean-field approximation to both nuclear matter and finite nuclei.

All these concepts and techniques are in full use today. Many papers employing EoS based on different physics make predictions on observables of interest and compare the results between themselves and with experiment. However, no strongly preferred EoS model has emerged.

We should realize that with enough parameters, one can fit almost anything. The current observational and terrestrial constraints are not sufficiently model sensitive enough. There is, in principle, an infinite number of EoS of high-density matter that can be constructed on totally different physical backgrounds which all satisfy the data. The same data are reflected in parameters of different models in different ways. A specifically tailored model, with a larger number of parameters, is apparently better, if only a fit to a limited class of data is sought. However, such models gibe description rather than understanding.

The ideal goal of understanding the nuclear force in the same fundamental way as the gravitational, electromagnetic, strong forces is probably out of our reach at present. A positive way forward may be to focus on theories with a minimal number of variable parameters constrained by physics. One example of such effort is the QMC model discussed in Section 3.2.2. As a phenomenological mean-field model, it does not provide information on the baryon–baryon interaction in free space, so the concept of the interaction between hadrons being propagating between their constituent quarks is not universal. However, with a set of five well-constrained parameters, its reproduction of experimental data, both on compact objects and finite nuclei, is impressive, and its predictive power is still being explored. The model is developing by refining the physics content, not varying or adding parameters. Thus, there is only one parameter set per version of the model, in stark contrast with other mean-field models.

Finally, there is the fundamental question of the sensitivity of available data to the microscopy of our models. We are faced with a range of predictions of a particular phenomenon from various models, based on different physics, and do not seem to have means to distinguish among them. A question can be asked as to what we actually learn from the models except that they are consistent with the data.

Only a limited selection of examples are presented here. Many topics were omitted, including the dynamic properties of pulsars, NS cooling, the effect of magnetic fields, the role of superfluidity and superconductivity in the star cores and their crusts, the mechanism of core-collapse supernovae, and the lattice and perturbative QCD. The story that repeats itself in these areas only strengthens the need for new ideas. This is much more difficult than mere detailed modifications of old theories but it is the only way to move the field forward.