A Precessing Jet Scenario for the Multi-Wavelength Long-Term Modulation of LS I +61°303
Abstract
1. Introduction
2. Observations of the LTM at Multiple Wavelengths
2.1. Radio
2.2. Optical
2.3. X-rays
2.4. GeV
2.5. TeV
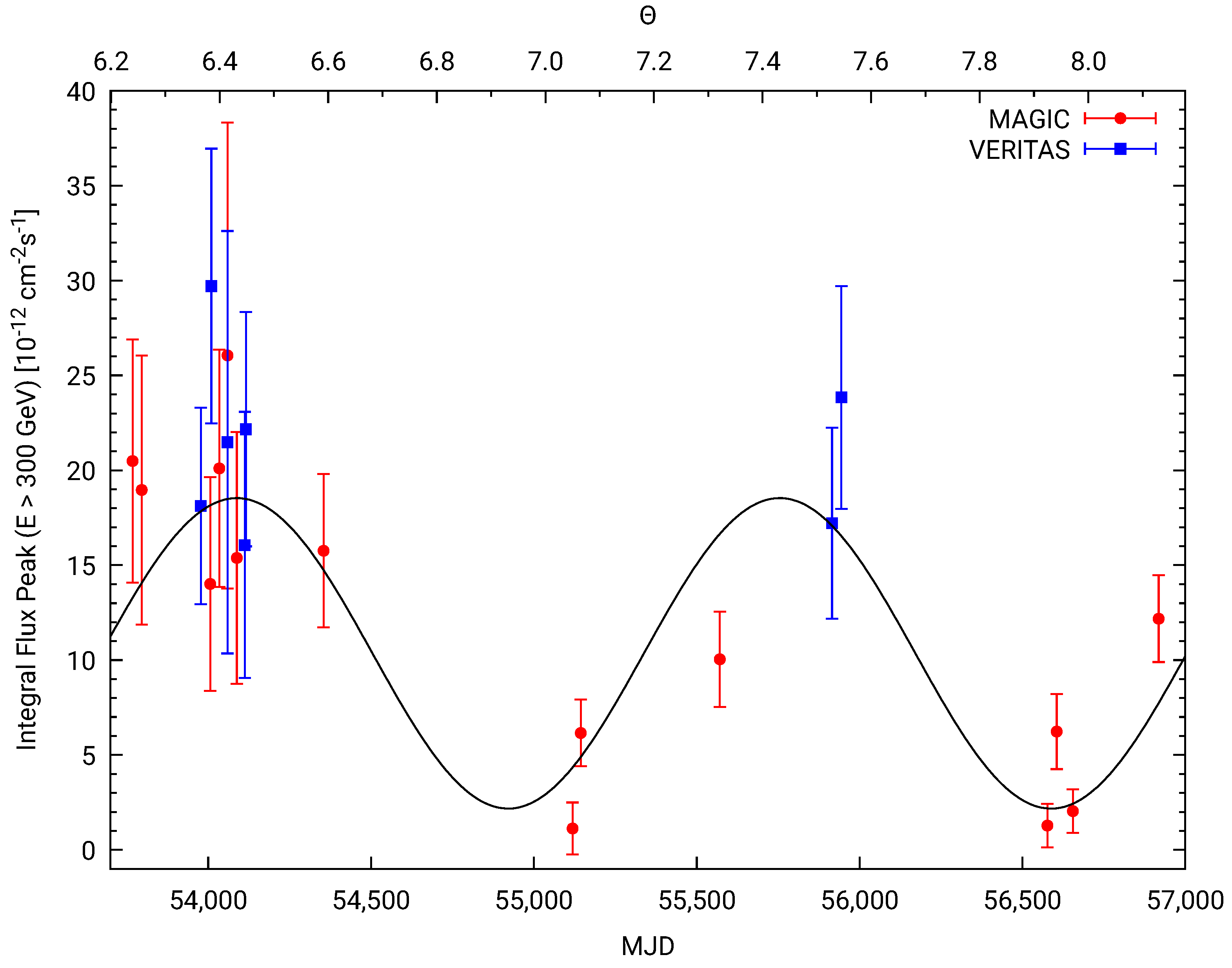
2.5.1. Observational History
2.5.2. Determination of the LTM Phase-Offset
3. Phase-Offsets across Wavelengths
4. Discussion
4.1. Plasma Cooling and Opaticity in a Precessing Jet
- The distance between the location of the TeV and GeV emission is considerably larger than between the other wavelengths.
- It takes the plasma longer to travel from the TeV region to the GeV region than in between the other regions because the velocity is smaller closer to the base of the jet.
- It takes the plasma longer to lose its energy from TeV down to GeV than from that point onwards.
4.2. Are the TeV Photons Produced by a Different Mechanism?
4.3. What Is the Origin of Optical Emission in LS I +61°303?
5. Conclusions
- By re-analyzing archived TeV data [14] we determined that LTM pattern at TeV is offset from the pattern at radio by . We point out that, while this value fits into the monotonically incrasing trend with the other wavelengths, this also means perfect anti-correlation with the radio emission in terms of the LTM pattern.
- The LTM of LS I +61°303 is established at radio, X-ray, GeV, and TeV wavelengths by long-term monitoring of the source. There is a systematic trend of the modulation pattern being increasingly offset from the radio pattern as the energy increases. Emission at higher energy is lagging emission at lower energy in a strictly monotonically increasing manner (Figure 2).
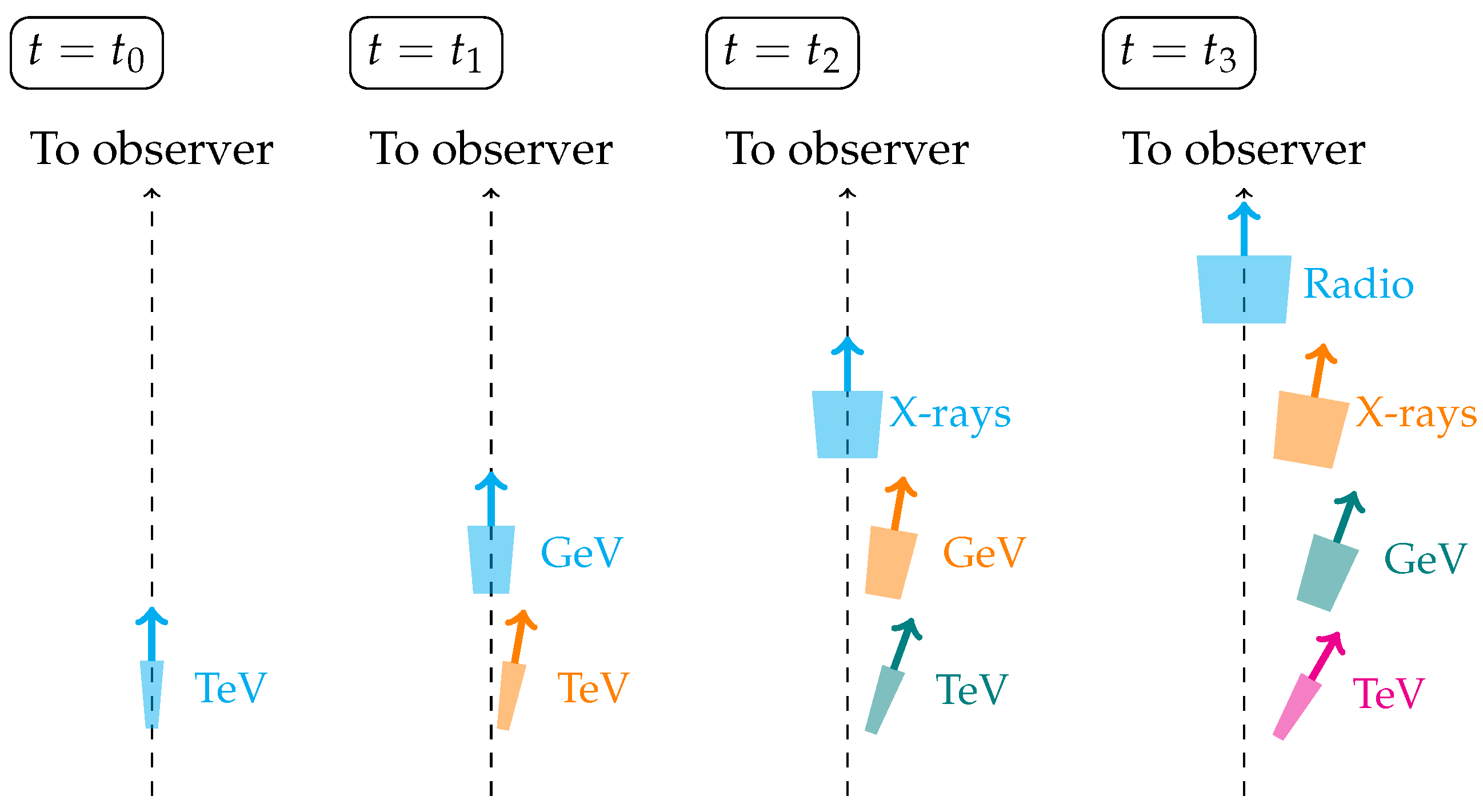
- We extended the physical scenario first introduced by Jaron et al. [9] to X-rays and TeV. In this scenario, the emission regions are located closer to the base of the jet as the energy increases (Figure 3). Because the LTM is the result of interference between orbit and precession, an earlier peak in the precession profile propagates to a later peak in the LTM pattern with increasing energy, as observed. We also note that while the radio, X-ray, and GeV emissions are fitted by a very simple trend, the TeV emission appears to be significantly offset from that. This is a challenge for this scenario at TeV energies.
- We consider an alternative scenario in which the TeV photons are produced in shocks resulting from the injection of plasmoids during magnetic reconnection events. It is interesting to note that this would imply a connection between the large phase-offset of the LTM at TeV energies and the hour time-scale phenomenon of quasi periodic oscillations at radio and X-rays. This would explain two phenomena, occurring at different energy bands and on time-scales of different orders of magnitude (hours vs. years) in the same coherent picture. This should be subject of future investigations.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BAT | Burst Alert Telescope |
| EW | Equivalent Width |
| INTEGRAL | INTErnational Gamma-Ray Astrophysics Laboratory |
| LAT | Large Area Telescope |
| LTM | Long-Term Modulation |
| MAGIC | Major Atmospheric Gamma Imaging Cherenkov Telescopes |
| MFF | Modulated Flux Fraction |
| OVRO | Owens Valley Radio Observatory |
| PCA | Proportional Counter Array |
| RXTE | Rossi X-ray Timing Explorer |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VHE | Very High Energy |
| VLBA | Very Long Baseline Array |
| VLBI | Very Long Baseline Interferometry |
| 1 | |
| 2 | There is an inconsistency within the numbers reported in Zamanov & Martí [42]. Namely, the values of the phases of the fitted cosine functions in their Table 1 do not correspond to this reported LTM phase-shift of 0.25. During the review process for this article it was clarified that the value for the phase of EW(H) is in fact (and not ). Hence, the LTM phase-shift quoted in the abstract of Zamanov & Martí [42] remains correct. |
| 3 | In their original publication, Jaron et al. [9] determine the phase-offset between the LTM pattern at radio relative to the GeV emission. This is why their value has the opposite sign. In this present work, we express all LTM phase-offsets with respect to the radio emission. Since all higher energy emissions lag the radio in term of the LTM pattern, this results in positive signs for the phase-offsets reported here. |
| 4 | In reality it is not necessarily the case that the jet is perfectly aligned with the line of sight at any time. However, there is certainly a moment when the jet encloses the smallest angle with respect to the line of sight. For the sake of clarity, in Figure 3 this smallest angle is chosen to be zero. |
| 5 | Please note that we denote this time-origin with a capital , not to be confused with the used in Figure 3 and the explanation above. |
References
- Casares, J.; Ribas, I.; Paredes, J.M.; Martí, J.; Allende Prieto, C. Orbital parameters of the microquasar LS I +61°303. Mon. Not. R. Astron. Soc. 2005, 360, 3. [Google Scholar] [CrossRef][Green Version]
- Massi, M.; Migliari, S.; Chernyakova, M. The black hole candidate LS I +61°303. Mon. Not. R. Astron. Soc. 2017, 468, 3. [Google Scholar] [CrossRef]
- Gregory, P.C.; Taylor, A.R. New highly variable radio source, possible counterpart of γ-ray source CG135+1. Nature 1978, 272, 704–706. [Google Scholar] [CrossRef]
- Peracaula, M.; Marti, J.; Paredes, J.M. Short term radio variability and polarization properties of LS I +61°303. Astron. Astrophys. 1997, 328, 283–289. [Google Scholar]
- Jaron, F.; Sharma, R.; Massi, M.; Fuhrmann, L.; Angelakis, E.; Myserlis, I.; Li, G.-X.; Shi, X. Radio QPO in the γ-ray-loud X-ray binary LS I +61°303. MOnthly Not. R. Astron. Soc. Lett. 2017, 471, L110–L114. [Google Scholar] [CrossRef]
- Nösel, S.; Sharma, R.; Massi, M.; Cimò, G.; Chernyakova, M. Hour time-scale QPOs in the X-ray and radio emission of LS I +61°303. Mon. Not. R. Astron. Soc. 2018, 476, 2516–2521. [Google Scholar] [CrossRef]
- Sharma, R.; Massi, M.; Chernyakova, M.; Malyshev, D.; Perrott, Y.C.; Kraus, A.; Dzib, S.A.; Jaron, F.; Cantwell, T.M. Radio/X-ray correlations and variability in the X-ray binary LS I +61°303. Mon. Not. R. Astron. Soc. 2021, 500, 4166–4172. [Google Scholar] [CrossRef]
- Gregory, P.C. Bayesian Analysis of Radio Observations of the Be X-Ray Binary LS I +61°303. Astrophys. J. 2002, 575, 1–10. [Google Scholar] [CrossRef]
- Jaron, F.; Massi, M.; Kiehlmann, S.; Hovatta, T. Simultaneous long-term monitoring of LS I +61°303 by OVRO and Fermi-LAT. Mon. Not. R. Astron. Soc. 2018, 478, 1–10. [Google Scholar] [CrossRef]
- Massi, M.; Torricelli-Ciamponi, G. Origin of the long-term modulation of radio emission of LS I +61°303. Astron. Astrophys. 2016, 585, A123. [Google Scholar] [CrossRef]
- Jaron, F.; Massi, M. Prediction of the radio outbursts of LS I +61°303. Astron. Astrophys. 2013, 559, A129. [Google Scholar] [CrossRef][Green Version]
- Li, J.; Torres, D.F.; Zhang, S.; Hadasch, D.; Rea, N.; Caliandro, G.A.; Chen, Y.; Wang, J. Unveiling the Super-orbital Modulation of LS I +61°303 in X-Rays. Astrophys. J. Lett. 2012, 744, L13. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bonamente, E.; Brandt, T.J.; Bregeon, J.; Brigida, M.; et al. Associating Long-term γ-ray Variability with the Superorbital Period of LS I +61°303. Astrophys. J. Lett. 2013, 773, L35. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Super-orbital variability of LS I +61°303 at TeV energies. Astron. Astrophys. 2016, 591, A76. [Google Scholar] [CrossRef]
- Dubus, G. Gamma-ray binaries: Pulsars in disguise? Astron. Astrophys. 2006, 456, 801–817. [Google Scholar] [CrossRef]
- Johnston, S.; Manchester, R.N.; Lyne, A.G.; Bailes, M.; Kaspi, V.M.; Qiao, G.; D’Amico, N. PSR 1259-63: A Binary Radio Pulsar with a Be Star Companion. Astrophys. J. Lett. 1992, 387, L37. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D.; Mc Keague, S.; van Soelen, B.; Marais, J.P.; Martin-Carrillo, A.; Murphy, D. New insight into the origin of the GeV flare in the binary system PSR B1259-63/LS 2883 from the 2017 periastron passage. Mon. Not. R. Astron. Soc. 2020, 497, 1–10. [Google Scholar] [CrossRef]
- Dubus, G.; Guillard, N.; Petrucci, P.; Martin, P. Sizing up the population of gamma-ray binaries. Astron. Astrophys. 2017, 608, A59. [Google Scholar] [CrossRef]
- Zimmermann, L.; Fuhrmann, L.; Massi, M. The broad-band radio spectrum of LS I +61°303 in outburst. Astron. Astrophys. 2015, 580, L2. [Google Scholar] [CrossRef]
- Massi, M.; Kaufman Bernadó, M. Radio Spectral Index Analysis and Classes of Ejection in LS I +61°303. Astrophys. J. 2009, 702, 2–10. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodríguez, L.F. Microquasars in our Galaxy. Nature 1998, 392, 6677. [Google Scholar] [CrossRef]
- Massi, M.; Chernyakova, M.; Kraus, A.; Malyshev, D.; Jaron, F.; Kiehlmann, S.; Dzib, S.A.; Sharma, R.; Migliari, S.; Readhead, A.C.S. Evidence for periodic accretion-ejection in LS I +61°303. Mon. Not. R. Astron. Soc. 2020, 498, 3592–3600. [Google Scholar] [CrossRef]
- Massi, M.; Ros, E.; Zimmermann, L. VLBA images of the precessing jet of LS I +61°303. Astron. Astrophys. 2012, 540, A142. [Google Scholar] [CrossRef]
- Massi, M.; Jaron, F. Long-term periodicity in LS I +61°303 as beat frequency between orbital and precessional rate. Astron. Astrophys. 2013, 554, A105. [Google Scholar] [CrossRef][Green Version]
- D’Aì, A.; Cusumano, G.; La Parola, V.; Segreto, A.; Mineo, T. Temporal features of LS I +61°303 in hard X-rays from the Swift/BAT survey data. Mon. Not. R. Astron. Soc. 2016, 456, 2. [Google Scholar] [CrossRef][Green Version]
- Jaron, F.; Massi, M. Discovery of a periodical apoastron GeV peak in LS I +61°303. Astron. Astrophys. 2014, 572, A105. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.W.; Torricelli-Ciamponi, G.; Massi, M.; Reid, M.J.; Zhang, B.; Shao, L.; Zheng, X.W. Revisiting LS I +61°303 with VLBI astrometry. Mon. Not. R. Astron. Soc. 2018, 474, 3. [Google Scholar] [CrossRef]
- Martí, J.; Paredes, J.M. Modelling of LS I +61°303 from near infrared data. Astron. Astrophys. 1995, 298, 151. [Google Scholar]
- Taylor, A.R.; Kenny, H.T.; Spencer, R.E.; Tzioumis, A. VLBI Observations of the X-Ray Binary LS I +61°303. Astrophys. J. 1992, 395, 268. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Paredes, J.M.; Romero, G.E.; Ribó, M. The radio to TeV orbital variability of the microquasar LS I +61°303. Astron. Astrophys. 2006, 459, L25–L28. [Google Scholar] [CrossRef]
- Romero, G.E.; Okazaki, A.T.; Orellana, M.; Owocki, S.P. Accretion vs. colliding wind models for the gamma-ray binary LS I +61°303: An assessment. Astron. Astrophys. 2007, 474, 15–22. [Google Scholar] [CrossRef]
- Massi, M.; Torricelli-Ciamponi, G. Intrinsic physical properties and Doppler boosting effects in LS I +61°303. Astron. Astrophys. 2014, 564, A23. [Google Scholar] [CrossRef]
- Jaron, F.; Torricelli-Ciamponi, G.; Massi, M. Understanding the periodicities in radio and GeV emission from LS I +61°303. Astron. Astrophys. 2016, 595, A92. [Google Scholar] [CrossRef][Green Version]
- Lisakov, M.M.; Kovalev, Y.Y.; Savolainen, T.; Hovatta, T.; Kutkin, A.M. A connection between γ-ray and parsec-scale radio flares in the blazar 3C 273. Mon. Not. R. Astron. Soc. 2017, 468, 4. [Google Scholar] [CrossRef]
- Lobanov, A.P. Ultracompact jets in active galactic nuclei. Astron. Astrophys. 1998, 330, 79–89. [Google Scholar]
- Pushkarev, A.B.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Lobanov, A.P.; Savolainen, T.; Zensus, J.A. MOJAVE: Monitoring of Jets in Active galactic nuclei with VLBA Experiments. IX. Nuclear opacity. Astron. Astrophys. 2021, 545, A113. [Google Scholar] [CrossRef]
- Paredes, J.M. Observació Radiomeètrica de Radioestralles. Ph.D. Thesis, Universitat de Barcelona, Departament d’Astronomia i Meteorologia, Barcelona, Spain, 9 January 1987. [Google Scholar]
- Gregory, P.C.; Xu, H.-J.; Backhouse, C.J.; Reid, A. Four Year Modulation of Periodic Radio Outbursts from LS I +61°303. Astrophys. J. 1989, 339, 1054. [Google Scholar] [CrossRef]
- Taylor, A.R.; Gregory, P.C. Periodic radio emission from LS I +61°303. Astrophys. J. 1982, 255, 210–216. [Google Scholar] [CrossRef]
- Rivinius, T.; Carciofi, A.C.; Martayan, C. Classical Be stars. Rapidly rotating B stars with viscous Keplerian decretion disks. Astron. Astrophys. Rev. 2013, 21, 69. [Google Scholar] [CrossRef]
- Zamanov, R.K.; Martí, J.; Paredes, J.M.; Fabregat, J.; Ribó, M.; Tarasov, A.E. Evidence of Hα periodicities in LS I +61°303. Astron. Astrophys. 1999, 351, 543–550. [Google Scholar]
- Zamanov, R.; Martí, J. First correlation between compact object and circumstellar disk in the Be/X-ray binaries. Astron. Astrophys. 2000, 358, L55–L58. [Google Scholar]
- Paredes-Fortuny, X.; Ribó, M.; Bosch-Ramon, V.; Casares, J.; Fors, O.; Núñez, J. Evidence of coupling between the thermal and nonthermal emission in the gamma-ray binary LS I +61°303. Astron. Astrophys. 2015, 575, L6. [Google Scholar] [CrossRef]
- Bignami, G.F.; Caraveo, P.A.; Lamb, R.C.; Markert, T.H.; Paul, J.A. Einstein X-ray identification of the variable radio star LS I +61°303. Astrophys. J. 1981, 247, L85–L88. [Google Scholar] [CrossRef]
- Li, J.; Torres, D.F.; Zhang, S. Spectral Analysis in Orbital/Superorbital Phase Space and Hints of Superorbital Variability in the Hard X-Rays of LS I +61°303. Astrophys. J. Lett. 2014, 785, L19. [Google Scholar] [CrossRef]
- Gregory, P.C.; Taylor, A.R.; Crampton, D.; Hutchings, J.B.; Hjellming, R.M.; Hogg, D.; Hvatum, H.; Gottlieb, E.W.; Feldman, P.A.; Kwok, S. The radio, optical, X-ray, gamma-ray star LS I +61°303. Astron. J. 1979, 84, 1030–1036. [Google Scholar] [CrossRef]
- Hermsen, W.; Swanenburg, B.N.; Bignami, G.F.; Boella, G.; Buccheri, R.; Scarsi, L.; Kanbach, G.; Mayer-Hasselwander, H.A.; Masnou, J.L.; Paul, J.A.; et al. New high energy gamma-ray sources observed by COS B. Nature 1977, 269, 494–495. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Baughman, B.M.; et al. Fermi LAT Observations of LS I +61°303: First Detection of an Orbital Modulation in GeV Gamma Rays. Astrophys. J. Lett. 2009, 701, L123–L128. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartelt, M.; Bartko, H.; et al. Variable Very-High-Energy Gamma-Ray Emission from the Microquasar LS I +61°303. Science 2006, 312, 5781. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195. [Google Scholar] [CrossRef]
- Yuan, F.; Lin, J.; Wu, K.; Ho, L.C. A magnetohydrodynamical model for the formation of episodic jets. Mon. Not. R. Astron. Soc. 2009, 395, 4. [Google Scholar] [CrossRef]
- Petropoulou, M.; Giannios, D.; Sironi, L. Blazar flares powered by plasmoids in relativistic reconnection. Mon. Not. R. Astron. Soc. 2016, 462, 3. [Google Scholar] [CrossRef]
- Sironi, L.; Giannios, D.; Petropoulou, M. Plasmoids in relativistic reconnection, from birth to adulthood: First they grow, then they go. Mon. Not. R. Astron. Soc. 2016, 462, 1. [Google Scholar] [CrossRef]
- Fender, R.P.; Russell, D.M.; Knigge, C.; Soria, R.; Hynes, R.I.; Goad, M. An anticorrelation between X-ray luminosity and Hα equivalent width in X-ray binaries. Mon. Not. R. Astron. Soc. 2009, 393, 4. [Google Scholar] [CrossRef][Green Version]
- Russell, D.M.; Fender, R.P.; Hynes, R.I.; Brocksopp, C.; Homan, J.; Jonker, P.G.; Buxton, M.M. Global optical/infrared-X-ray correlations in X-ray binaries: Quantifying disc and jet contributions. Mon. Not. R. Astron. Soc. 2006, 371, 3. [Google Scholar] [CrossRef]
- Massi, M.; Zimmermann, L. Feasibility study of Lense-Thirring precession in LS I +61°303. Astron. Astrophys. 2010, 515, A82. [Google Scholar] [CrossRef][Green Version]

| Parameter | Value |
|---|---|
| a | |
| b | |
| Name | Energy Range [eV] | Phase-Offset | Reference |
|---|---|---|---|
| Radio | (5.0–7.4) | Jaron et al. [9] | |
| X-rays (soft) | (3–30) | Li et al. [12] | |
| X-rays (hard) | (18–60) | ∼0.2 | Li et al. [45] (not used here) |
| GeV | (0.1–3.0) | Jaron et al. [9] | |
| TeV | (0.3–10) | This work, based on [14] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaron, F. A Precessing Jet Scenario for the Multi-Wavelength Long-Term Modulation of LS I +61°303. Universe 2021, 7, 245. https://doi.org/10.3390/universe7070245
Jaron F. A Precessing Jet Scenario for the Multi-Wavelength Long-Term Modulation of LS I +61°303. Universe. 2021; 7(7):245. https://doi.org/10.3390/universe7070245
Chicago/Turabian StyleJaron, Frédéric. 2021. "A Precessing Jet Scenario for the Multi-Wavelength Long-Term Modulation of LS I +61°303" Universe 7, no. 7: 245. https://doi.org/10.3390/universe7070245
APA StyleJaron, F. (2021). A Precessing Jet Scenario for the Multi-Wavelength Long-Term Modulation of LS I +61°303. Universe, 7(7), 245. https://doi.org/10.3390/universe7070245






