Abstract
Superinsulators (SI) are a new topological state of matter, predicted by our collaboration and experimentally observed in the critical vicinity of the superconductor-insulator transition (SIT). SI are dual to superconductors and realise electric-magnetic (S)-duality. The effective field theory that describes this topological phase of matter is governed by a compact Chern-Simons in (2+1) dimensions and a compact BF term in (3+1) dimensions. While in a superconductor the condensate of Cooper pairs generates the Meissner effect, which constricts the magnetic field lines penetrating a type II superconductor into Abrikosov vortices, in superinsulators Cooper pairs are linearly bound by electric fields squeezed into strings (dual Meissner effect) by a monopole condensate. Magnetic monopoles, while elusive as elementary particles, exist in certain materials in the form of emergent quasiparticle excitations. We demonstrate that at low temperatures magnetic monopoles can form a quantum Bose condensate (plasma in (2+1) dimensions) dual to the charge condensate in superconductors. The monopole Bose condensate manifests as a superinsulating state with infinite resistance, dual to superconductivity. The monopole supercurrents result in the electric analogue of the Meissner effect and lead to linear confinement of the Cooper pairs by Polyakov electric strings in analogy to quarks in hadrons. Superinsulators realise thus one of the mechanism proposed to explain confinement in QCD. Moreover, the string mechanism of confinement implies asymptotic freedom at the IR fixed point. We predict thus for superinsulators a metallic-like low temperature behaviour when samples are smaller than the string scale. This has been experimentally confirmed. We predict that an oblique version of SI is realised as the pseudogap state of high- superconductors.
1. Introduction
Although extremely successful in describing many aspects of particle physics, the standard model does not explain the mechanism of confinement that binds quarks into hadrons. In 1978, in a Gedanken experiment for quark confinement [1] ’t Hooft introduced the idea of a dual superconductor in which, in analogy to the Meissner effect, chromo-electric fields would be squeezed into thin flux tubes with quarks at their ends in a condensate of magnetic monopoles. When quarks are pulled apart, it is energetically favourable to pull out of the vacuum additional quark-antiquark pairs and to form several short strings instead of a long string. As a consequence, colour charge can never be observed at distances above a fundamental length scale, and quarks are confined. Only colour-neutral hadron jets can be observed in collider events. In this phase, that he called the “extreme opposite” of a superconductor, there is zero quark mobility and, thus, an infinite chromo-electric resistance. He, hence, called this phase a “superinsulator”.
In condensed matter, superinsulation emerges in materials that have Cooper pairs and vortices as relevant degrees of freedom. It was originally predicted for Josephson junction arrays (JJA) [2] and then experimentally found in InO superconducting films [3], in Tin films [4,5] and NbTiN films [6]. Superinsulations emerge in all these systems at the insulating side of the superconductor-insulator transition (SIT). The SIT and the nature of the phases that it harbours is determined by the competition between two quantum orders embodied in the topological interactions between charges and vortices (Aharonov-Bohm/Aharonov-Casher (ABC)) and is, thus, a realisation of the field-theoretical Mandelstam’t Hooft S-duality [1,7] in a material. A local formulation of such topological interactions requires the introduction of two emergent gauge fields and (a tensor field in (3+1) dimensions) coupled to the conserved charge and vortex currents, respectively. The effective field theory that describes this topological phase of matter is a mixed Chern-Simons (CS) field theory in (2+1) dimensions and a BF theory in (3+1) dimensions.
Superinsulators are characterised by an infinite resistance that persists at finite temperatures: charges cannot move even if a voltage (below a critical threshold) is applied. This infinite resistance is due to linear confinement of charges [8] in a condensate of magnetic monopoles (instanton plasma in (2+1) dimensions). This confining mechanism is exactly the mechanism that is realised in compact QED, [9,10], the simplest example of a strongly coupled gauge theory with a massive photon and linear confinement of charges: the vortex Bose condensate constricts electric fields into electric flux tubes that bind Cooper pairs and anti-Copper pairs (Figure 1). The superinsulating state is nothing else than a plasma of magnetic monopoles (instantons) since, in a condensate, vortex number is not conserved. In (3+1), dimensions vortices can be viewed as magnetic filaments connecting magnetic monopoles at their ends [10]. In this one-color version of quantum chromodynamics (QCD) Cooper pairs play the role of quarks.

Figure 1.
Dual Mandelstam’t Hooft–Polyakov confinement. From top to bottom: quark confinement by chromo-electric strings; magnetic tube (Abrikosov vortex) that forms in a superconductor between two magnetic monopoles; electric string that forms in a superinsulator between the Cooper pair and anti-Cooper pair. The lines are the force lines for magnetic and electric fields respectively. In all cases the energy of the string (the binding energy) is proportional to the distance between either the monopoles or the charges.
Although the search of magnetic monopoles has been the object of years of efforts [11], they are elusive as elementary particles. In the materials that exhibit superinsulations, instead, magnetic monopoles are present in the form of emergent quasiparticle excitations realising the electric–magnetic symmetry. They behave as quantum particles and at low temperatures, they form a quantum Bose condensate dual to the charge condensate in superconductors. Their supercurrents cause the electric analogue of the Meissner effect and lead to linear confinement of the Cooper pairs [8,12,13,14]. Magnetic monopoles play, thus, a crucial role in the formation and properties of the superinsulating state. As we will show below, this phase is a phase in which vortex strings with magnetic monopoles at their the endpoints become loose and confine charges. On the contrary, appreciable vortex tension implies that vortices are short and confines monopoles in small dipoles, as shown in Figure 2. Charges are thus liberated.
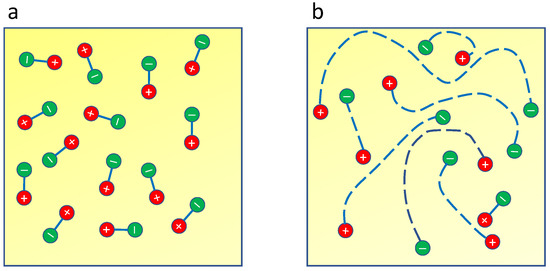
Figure 2.
Magnetic monopole states at low temperatures. (a) Monopoles are confined into small dipoles by the tension of vortices connecting them. (b) As the tension vanishes, vortices become loose and magnetic monopoles at their endpoints condense.
A salient feature of QCD is asymptotic freedom, the weakening of the interaction coupling strength at short distances (ultraviolet (UV) limit). At large distances (infrared (IR) limit), the quarks are thought to be confined within hadrons, which are physical observable excitations, by the QCD strings. Quarks themselves cannot be extracted from hadrons and be seen in isolation. The mechanism for the transition from weak quark interactions in the UV regime to confinement and strings in the IR regime remains an open issue. Confinement by strong interactions prevents a direct view on quarks despite that they move nearly free at the small scales. As we will show below, superinsulators, instead, allow for a direct observation of the interior of electric mesons made of Cooper pairs by standard transport measurements. We reveal the transition from the confined to the asymptotic free Cooper pair motion upon decreasing the distance between electrodes, modelling the observation scale.
Pure gauge compact QED in 2D, with only closed string excitations [15] is not re-normalisable. However, coupling the action to dynamical matter results in a non-trivial fixed point [16]. The same occurs in our case: deep non-relativistic compact QED is induced by an underlying matter dynamics from which it inherits the corresponding Berezinskii-Kosterlitz-Thouless (BKT) [17,18,19] fixed point separating an integer topological phase, [20,21,22] from a confined phase. The CS mass sets the gap for the topological phase, [20,21,22], that corresponds to a functional first Landau level and consists of an intertwined incompressible fluid of charges and vortices. The confined phase, instead, is a highly entangled vortex condensate in which charges are linearly bound. As we will show below, the effective coupling of the theory will thus flows to small values in the UV limit, and the induced compact QED2 becomes asymptotically free (the theory is actually asymptotically safe, since the critical point is at a finite value of the coupling different from zero but we will use the more familiar term for simplicity’s sake here), the BKT transition representing the infrared (IR) confining fixed point.
The review is organised like this. In Section 1, we present the effective gauge theories description of the SIT in (2+1) dimensions and show how the BKT transition arises. We then derive the phase diagram. In Section 2, we will discuss the characteristics of the superinsulating phase, computing the string tensions for the electric strings that bind the Cooper pairs and show how the asymptotic free regime arises. We then generalised the model of the SIT to the (3+1)-dimensional case in Section 3 and compute the phase diagram that essentially coincides with the one in one dimension less. In Section 4, we discuss the characteristic of the superinsulating phase and show that also in (3+1) dimensions this is a confinement phase in which Cooper pairs are bounded by electric flux tubes in a condensate of magnetic monopole. Section 5 is devoted to conclusions.
2. 2+1 Dimensions
We will use natural units , but restore physical units when necessary. The infinite-range ABC interaction, embodying the quantum phase acquired either by a charge encircling a vortex or by a vortex encircling a charge, dominates the structure of the critical vicinity of the SIT. The world-lines of elementary charges and vortices are described by:
where the index labels the elementary charges and vortices, parametrized by the coordinates and , respectively, n is the dimensionless charge ( in our case to describes Cooper pairs), and Greek subscripts run over the Euclidean three dimensional space encompassing the 2D space coordinates and the Wick rotated time coordinate. ABC phases are encoded in the Gauss linking number between the two curves (1):
where is the completely antisymmetric tensor. To ensure a local formulation of the action (2), one introduces two emergent gauge fields, and mediating ABC interactions and the topological part of the action takes the form
Equation (3) defines the mixed Chern-Simons (CS) action [23,24,25] and represents the local formulation of the topological interactions between charges and vortices. Since it contains only one field derivative, it is the dominant contribution to the action at long distances and it is invariant under the gauge transformations and , reflecting the conservation of the charge and vortex numbers. In this representation and are the continuous charge and vortex number current fluctuations, while and stand for integer point charges and vortices.
The CS kernel has a zero mode [23,24,25] and needs a regularisation. To this end we will use the next-order terms in the effective action of the SIT that contain two field derivatives and that are gauge invariant. Introducing the dual field strengths and and setting for Cooper pairs, we obtain the action -4.6cm0cm
where and are the magnetic fields, and the electric fields and is the magnetic permeability and is the electric permittivity which define the speed of light in the material. The two coupling constants and have canonical dimension [1/length] so, naively the two kinetic terms are infrared-irrelevant. However they are necessary to correctly define the pure CS limit in which the topological mass [26,27], where is the London penetration depth in the bulk material. With the two energy scales and we can define a dimensionless coupling constant , where d is the thickness of the film and is the fine structure constant. g plays the role of the conductance in materials. The electric-magnetic duality (charge–vortex symmetry) is given by the action symmetry with respect to the transformation . Thus, g is a tuning parameter driving the system across the SIT, and the SIT itself corresponds to .
To describe the linking number the two compact emergent gauge fields must be compact. To formulate U(1) symmetries we will use a lattice regularisation introducing a lattice of spacing ℓ. This is not entirely trivial, however, since particular care has to be exercised in the definition of the lattice CS term so that discrete gauge invariance is maintained [2]. To this end we introduce the forward and backward derivatives and shift operators
We also introduce forward and backward finite differences:
Summation by parts on the lattice interchanges both the two derivatives (with a minus sign) and the two shift operators. Gauge transformations are defined by using the forward lattice derivative. In terms of these operators one can then define two lattice Chern-Simons terms
where no summation is implied over equal indices. Summation by parts on the lattice interchanges also these two operators (without any minus sign). Gauge invariance is then guaranteed by the relations
Note that the product of the two Chern-Simons terms gives the lattice Maxwell operator
where is the 3D Laplace operator.
Integrating out the fictitious gauge fields we obtain an action for the topological excitations alone:
where is the 2D spatial Laplacian. The third term in this action describes the lattice version of the topological linking of electric and magnetic strings of width and, due to the Dirac quantization condition, at large distances, it reduces to an integer. We will thus drop this term.
The phase diagram is determined by the condensation (or lack thereof) of topological defects. The conditions for the condensation are derived using the standard free energy arguments [28]: the action of the Euclidean field theory model plays the same role as the energy and quantum corrections to the classical action play the same role as the entropy in an equivalent statistical mechanics model in one additional spatial dimension. The ground state of the quantum model corresponds to the minimum of its free energy. Following the standard lattice gauge field theory arguments of [29] we retain only the self-interaction terms in (10)
where is proportional to the diagonal element of the lattice kernel representing the inverse of the operator and we consider strings made of N bonds with integer electric and magnetic quantum numbers Q and M. We assign to strings an entropy proportional to their length, being given by with since, at each step, the non-backtracking strings can choose among 5 possible directions on how to continue. The main contribution to the free energy is thus:
with the dimensionless parameter given by:
which, together with the ratio fully determines the quantum phase structure.
When the energy term in (12) dominates, the free energy is positive and minimized by short closed loop configurations while, when the entropy dominates, the free energy is negative and minimised by large strings and long closed loops giving the following condensation conditions for long strings with integer quantum numbers Q and M:
If two or more condensations are allowed, one has to choose the one with the lowest free energy. This condition describes the interior of an ellipse with semi-axes
on a square lattice of integer electric and magnetic charges. The ratio determines the ratio of the semi-axes while the parameter sets the overall scale of the ellipse. The quantum phase diagram is found by noting which integer charges lie within the ellipse when the semi-axes and the overall scale are varied:
The phase structure is shown in Figure 3.
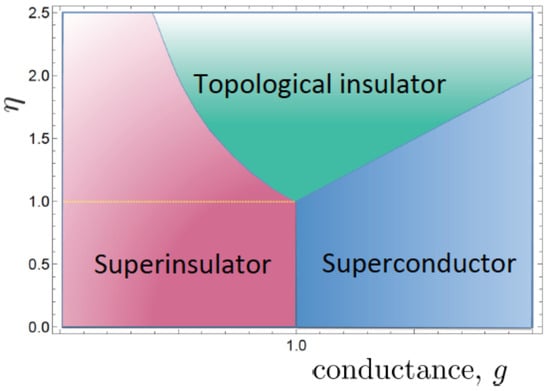
Figure 3.
The quantum phase diagram of the SIT as a function of the coupling constant g. The point , is a tricritical point dominating the phase structure.
A detailed description of all these possible phases can be found in [8,30]. In what follows we will concentrate on the superinsulating phase.
3. Superinsulating Phase
To understand the nature of the superinsulating state, we couple the charge current to the physical electromagnetic gauge field by adding to the action the minimal coupling term and set , since charges are dilute, in (4). The effective action , which gives the electromagnetic response of an ensemble of charges in a superinsulator, is obtained by integrating out the gauge fields and , and summing over the condensed vortices . The action we obtain is the deep non-relativistic version of Polyakov’s compact QED action [10] in which only the electric fields survive
where is the effective coupling constant
The partition function that we obtain is:
where is the spatial Laplacian instead of the full Laplacian in 3D Euclidean space-time present in the relativistic version of the model. As we will see, this difference has important consequences on the model since the interaction of the monopoles near the SIT, in this case, is logarithmic, , instead of an inverse linear power of the relativistic model.
The deep non-relativistic limit does not affect, however, the main consequence of Polyakov’s original idea [10]: the physics of a superinsulator is governed by the spontaneous proliferation of instantons , corresponding to magnetic monopoles, so that the vortex number is not conserved in the condensate. These instantons represent quantum tunnelling events by which vortex fluctuations appear and disappear in the condensate. Then, in a mirror analogue to the monopole confinement, i.e., formation of Abrikosov vortices as a result of the Meissner effect in a Cooper pair condensate, the magnetic monopole condensation leads to a dual phenomenon, the emergence of the electric strings [10] mediating confinement of Cooper pairs in superinsulators.
The deep non-relativistic limit plays a crucial role in the shape of the monopoles. The gauge invariance of the fields force the constraint that is satisfied by choosing and consequently . m represents instanton quantum tunnelling events in which vortices on the film appear and disappear and their magnetic flux flows in and out isotropically in the four available spatial directions, as it is shown in Figure 4. Another important effects of instantons is that they disorder the system and generate a mass for the photon given by [10]
rendering thus the Coulomb potential screened with a a screening length .
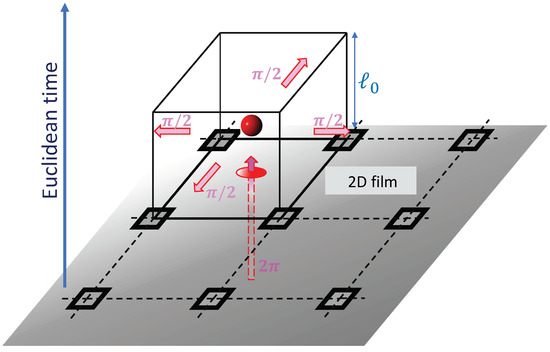
Figure 4.
A non-relativistic magnetic monopole instanton representing a quantum tunnelling event in which a fundamental vortex of flux at time t is divided up into four fluxes that flow out isotropically in the spatial directions. At the next instant there is no vortex on the film anymore. For simplicity the condensate islands are represented schematically as in a regular array.
To probe Cooper pair confinement we compute the expectation value of the Wilson loop operator , where C is a closed loop in 3D Euclidean space-time (a factor ℓ is absorbed into the gauge field to make it dimensionless),
When the loop C is restricted to the plane formed by the Euclidean time and one of the space coordinates, measures the potential between two external probe charges . A perimeter law indicates a short-range potential, while an area-law is tantamount to a linear interaction between the probe charges [10] with a new emergent scale represented by the string tension that gives the strength of the linear potential. We now multiply the Wilson loop operator by 1 in the form on the plaquettes forming the surface S encircled by the loop C and we introduce a unit vector perpendicular to the plaquettes forming the surface S.
We then decompose into transverse and longitudinal components, with , , where are integers and . The two sets of integers are thus traded for one set of integers and one set of integers representing the magnetic monopoles. The integers are used to shift the integration domain for the gauge field to . The real variables are then also absorbed into the gauge field. The integral over this non-compact gauge field gives then the Gaussian fluctuations around the instantons m, representing the saddle points of the action. Gaussian fluctuations do not contribute to confinement and, thus, can be neglected. Only the summation over instantons, , remains:
For , i.e., Cooper pair probes, the sum over instantons gives rise to an area law for the expectation value of the Wilson loop (21) with a string tension given by [31]
where is now the infrared-regularized 2D lattice Coulomb potential at coinciding points. This linear potential is due to a flux tube (string) of electric field connecting Cooper pairs and Cooper holes. This string, with a Cooper pair and a Cooper hole at its endpoints, has a typical width [15] and typical length and is the electric equivalent of a strong interaction pion. When one pulls this string by, say, an external voltage, Cooper pairs and Cooper holes start moving apart but there comes a moment where it becomes energetically favourable for the system to pop out a Cooper pair-Cooper hole pair in some intermediate island and to form two short strings. Only neutral states exist asymptotically in this phase of the system and the resistance becomes infinite since charges cannot move anymore. There is, however, a crucial difference with the relativistic case, in which monopoles are always in a plasma phase due to their weak inverse linear interaction. In the deep non-relativistic limit, the interactions between monopoles is logarithmic, as we already pointed out, so, near the SIT they can undergo a confining quantum BKT transition [17,18,19] for sufficiently strong coupling constants g. In fact plays the role of the temperature and, from (17), we see that g plays the role of an inverse temperature, so we have the usual XY model: for low values of g instantons are free and charges are confined, while instants undergo a confining transition and become logarithmically confined at . This quantum BKT transition represents the SIT itself with a transition between the superinsulating phase and the intermediate Bose metal, the bosoic topological insulator phase.
The BKT transition is an infinite-order transition and follows from the observation that the dual formulation of the 2D Coulomb gas is the well known sine-Gordon model. To obtain the Coulomb gas formulation we start from from (18) and rewrite the Gaussian term in the action for the topological excitations in terms on an auxiliary field as:
where
is the instanton fugacity and we have adopted the dilute gas approximation in which we consider only . is the infrared-regularised value of the lattice Coulomb kernel at coinciding points. The sums can be now computed, with the result
which is nothing else than the partition function of the sine-Gordon model (for a review see [32]) which describes the physics of the planar XY model. Following the results for the XY model [32] we find thus a critical coupling which plays the role of the critical temperature in this quantum BKT transitions. Monopoles and linear confinement of charges can exist only for , in excellent agreement with the estimate obtained from the crude free energy argument for strings which would correspond to the string entropy value .
For the XY model described by (25) re-normalisation group flow (varying the temperature) is expressed best in terms of the two variables
The half line , is an half line of infrared fixed points all corresponding to states with bound vortices and differing by a constant representing the initial conditions of the flow equations. In our case, g flows to large values in the IR limit, and the line , is a line of confining IR fixed points for the charges. The magnetic monopole instantons cause linear confinement of charges in the superinsulating phase and the granularity scale ℓ (lattice spacing) determines the string tension of this linear potential and sets thus also the scale of linearly bound pairs of charges, see (22). The SIT corresponds to an IR Berezinskii-Kosterlitz-Thouless [17,18,19] fixed point . The BKT re-normalisation flow toward short UV scales implies a decreasing g and an increasing z. The confining interaction decreases when flowing towards short scales and, we reach the scale O(ℓ) as we will show, charges essentially do not feel any potential anymore, showing what is called asymptotic freedom. This phenomenon is typically associated with non-Abelian gauge theories, where it characterises their UV fixed point [33], here it is associated with the sine-Gordon model (and not the compact QED) and describes an IR fixed point so it should be called asymptotic safety but here will use the more familiar term asymptotic freedom.
The only evidence for quarks inside hadrons is indirect, through high-energy collision that smash them and create hadron jets in colliders such as LHC. In such experiments, it is impossible to “look inside hadrons” to study the UV to IR confining transition. Here we show that this is, instead, possible in condensed matter superinsulators since the electric interaction is much weaker than the strong interaction and, therefore, the size an electric pion larger than the size of real pion. In superinsulators if the string length scale is large enough so that the regime is realized, one can probe the interior of “superinsulating mesons” by measuring the dependencies on samples with linear dimensions . In this case the “interior” interaction at intermediate scales is a screened Coulomb potential. This should result in a strong size-dependence of the response, such that the superinsulating hyperactivated behaviour of the resistance observed in sufficiently large samples changes to a metal-like behaviour in sufficiently small systems with . This size-dependence corresponds exactly to the transition from the confinement regime at large scale to the asymptotic free regime inside the “electric mesons”.
To gain more insight about this transition, let us focus on the interaction energy between charges separated by a distance r, derived from the compact QED model of superinsulation (we henceforth restore physical units) is
where the second term is the so-called Lüscher term [34] and the third term, containing the MacDonald function , is the screened 2D Coulomb potential, reducing to for while decaying exponentially at , with ≈ the superconducting coherence length. For , the Lüscher term is negligible, so that . Near the SIT, the strength of the Coulomb potential becomes [8]
The exact form of is given in [8] and is not relevant here.
When samples are very big, with their dimension L such that , charges are confined and we expect the usual hyperactivated behaviour of the resistance as a function of temperature of superinsulators. However, for samples with dimensions in the range Cooper pairs sufficiently far apart feel neither the string tension, since the string is loose on these scales, nor the Coulomb interaction, which is screened on the scale . We expect thus to observe a transition from hyperactivated resistance behaviour to a metallic saturation at the lowest temperatures when the sample size is decreased. This is exactly what has been observed in a NbTiN superinsulating film by varying the bridge length on which the external voltage is applied [12], as shown in Figure 5. For large bridge lengths the film displays hyperactivated resistances, for the smallest bridge length 0.2 mm, however, we see metallic saturated behaviour at low temperatures. The crossover from hyperactivation to metallic behaviour should take place around a bridge length . The typical string size can be estimated from experimental data as follows. The energy is the energy necessary to break up the string by raising the temperature. So it is a measure of and, therefore,
where we have reinstated physical units with . Using the experimentally determined deconfinement temperature and the known dielectric constant of NbTiN near the SIT [6], , one can obtain an estimate mm in excellent quantitative agreement with the observation of the metallic crossover. This is the first direct experimental evidence of asymptotic freedom.
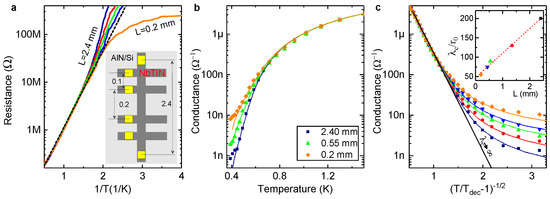
Figure 5.
Sheet resistance of a NbTiN superinsulating film as a function of the effective sample size (bridge length) (a) Logarithmic plot of sheet resistance vs. inverse temperature for bridges of various length L. The dashed straight line shows the Arrhenius behaviour . Inset: experimental setup. The Si substrate with AlN buffer layer is shown with light gray and the Hall bridge of NbTiN is dark grey. The square gold contacts are given in yellow. All lateral sizes are given in millimetres. (b) Same data as in (a) but replotted in terms of the conductance vs. T in log-line scale. The dotted lines are fits using a two dimensional Coulomb gas model that generalises the Berezinskii-Kosterlitz-Thouless (BKT) formula for the conductance by incorporating a self-consistent solution of the effects of electrostatic screening, where the screening length and enter as fitting parameters. For all bridges the deconfinement temperature is mK. (c) Same data as in (b) but for temperature renormalized as . The solid line corresponds to the case of an infinite electrostatic screening length .
4. (3+1) Dimensions
In this section, we will generalise our theory to the (3+1)-dimensional case. We will use in what follow a relativistic notation. The relevant degrees of freedom, Cooper pairs, and Josephson vortices, can acquire topological ABC phases when one is encircling the other. However, vortices are now one-dimensional extended objects and their world-surfaces are described by the two-index antisymmetric tensor (we will use for the moment a continuous notation). Due to this the generalisation of the Chern-Simons representations of the linking number will include a Kalb-Ramond antisymmetric tensor fields [35] which couples to the vortex current giving the BF action, generalising (3):
where and are the charge and vortex currents, respectively. Although the field strength associated to is, as usual, , in (3+1) dimensions its the dual field strength is a 2-tensor,
The field strength associated with the tensor field is a 3-tensor
and its dual field strength is, thus, a vector:
These field strengths and can be used to add dynamics to the purely topological BF term (30),
where f is a dimensionless coupling and has canonical dimension [1/length]. This action was introduced as a field theory for a condensed matter system in [2]. The BF model is topological, since it is metric-independent. In addition to the usual gauge transformations , (34), is also invariant under gauge transformations of the second kind,
When using the BF term to model the emergent behaviour of condensed matter systems, one identifies the topologically conserved charge current and vortex current as
with Cooper pairs measured in integer units of and vortices in integer units of .
To formulate the gauge-invariant lattice -term, we follow [2] and introduce the lattice operators
The two lattice operators are interchanged (no minus sign) upon summation by parts on the lattice and are gauge invariant so that:
and satisfy the equations
where is the lattice Laplacian. We use the notation and for the forward and backwards finite difference operators.
As in the (2+1)-dimensional case, in the Euclidean lattice formulation, and becomes integer link and plaquette variables and . In 4 Euclidean dimensions they describes the Euclidean world-lines of point charges and Euclidean world-surfaces of vortices. In materials, the velocity of light will be by defining the Euclidean time lattice spacing as , where is the electric permittivity and is the magnetic permeability we incorporate this velocity by rescaling all time derivatives, currents, and zero-components of gauge fields by the factor . As a consequence, both gauge fields acquire a dispersion relation with the topological mass given by , and we thus obtain the lattice action:
The dimensionless parameter encodes the effective Coulomb interaction strength in the material, is the magnetic scale, , where is the London penetration depth of the superconducting granules.
To find the topological action for monopoles, we start from Equation (40) and integrate out fictitious gauge fields and
The last term can be neglected since it represents the Aharonov-Bohm phases of charged particles around vortices of width . In fact we consider scales much larger than , the denominator in (41) reduces to and this last term becomes , reflecting the absence of Aharonov-Bohm phases between charges and magnetic fluxes .
Gauge invariance requires closed vortex loops. The presence of magnetic monopoles at the endpoints of open vortices will break the gauge symmetry of the second kind (35) and the longitudinal components of the tensor gauge field will become usual vector gauge fields for the magnetic monopoles. What is the effect of this gauge breaking term? Monopoles will experience the same type of Coulomb interaction experienced by charges, but this interaction is subdominant with respect to the linear tension created by the vortices between a monopole–antimonopole pair. We can thus neglect it for the determination of the phase structure and admit open vortices with magnetic monopoles at the endpoints.
The important consequence of the topological interactions is that they induce self-energies in form of the mass of Cooper pairs and tension for vortices between magnetic monopoles. These self-energies are encoded in the short-range kernels in the action (41), which we approximate by a constant. World-lines and world-surfaces are thus assigned energies, that are nothing else that their Euclidean actions in the present statistical field theory setting, proportional to their length N and area A which we measure in numbers of links and plaquettes,
Here Q and M are the integer quantum numbers carried by the two kinds of topological excitations and , where is the diagonal element of the lattice kernel representing the inverse of the operator . As in the (2+1)-dimensional case, to construct the free energy, we need to estimate the entropy of link strings and plaquette surfaces. The entropy is, for string, proportional to their length , and for surfaces proportional to their area [36]. Both coefficients are non-universal: for strings since at each step the non-backtracking string can choose among 7 possible directions on how to continue, while, for surfaces, does not have such a simple interpretation but can be estimated numerically. The total free energy that we obtain is:
where we have defined
When the self-energy dominates, large string and surface configurations are suppressed in the partition function and Cooper pairs or vortices are gapped excitations, suppressed by their large action. On the contrary, when the entropy dominates large string and surface configurations are favoured in the “free energy” (effective action) and they condense. The phase in which long world-lines of Cooper pairs condense is a superconducting phase characterised by a charge Bose condensate. The phase in which a Bose condensate of magnetic monopoles forms, instead, is a superinsulator.
The formation of larger world-surface implies that the strings binding monopoles and antimonopoles into neutral pairs become loose on distance scales . This implies that magnetic monopoles at the endpoints of the loose vortices become deconfined and Bose condense.
The combined energy-entropy balance equations are best viewed as defining the interior of an ellipse on a 2D integer lattice of electric and magnetic quantum numbers,
where the semi-axes are given by
with
In (3+1)-dimensional case, however, only configurations with or have to be considered, and configurations with and must be excluded since the two types of excitations are different. The phase diagram is found by establishing which integer charges lie within the ellipse when the semi-axes are varied. We thus obtain a phase diagram that is essentially as in (2+1) dimensions:
with the tuning parameter g given in this case by:
5. (3+1) Dimensions Superinsulating Phase
To derive the effective action for a superinsulator in (3+1) dimensions we follow exactly the same steps as in the (2+1)-dimensional case and we add the minimal coupling of the charge current to the electromagnetic field:
and we compute its effective action by integrating over the fictitious gauge fields and . Using summation by parts, however, the above coupling amounts only to a shift
in (40). The electromagnetic response is then obtained by integrating over the fictitious gauge fields and setting :
Equation (51) is the action of Polyakov’s compact QED in (3+1) dimensions.
To prove linear confinement of charges we introduce two external probe charges and compute the expectation value for the corresponding Wilson loop operator W(C), where C is a closed loop, now in 4D Euclidean space-time:
where on the links forming the closed loop C and everywhere else. We can now use the lattice Stoke’s theorem and, for small values of the coupling f, the saddle-point approximation to rewrite Equation (52) as:
where the quantities are unit surface elements perpendicular (in 4D) to the plaquettes forming the surface S encircled by the loop C and vanish on all other plaquettes. We have also multiplied the Wilson loop operator by 1 in the form .
At this point, we can simply repeat the computation of Polyakov [10] which shows an area law behaviour for the expectation value of the Wilson loop:
where A is the area of the surface S enclosed by the loop C and the string tension is given by
where is the value of the 4D lattice Coulomb potential at coinciding points. The monopole condensate, thus, generates a string binding together charges and preventing charge transport in systems of a sufficient size. A magnetic monopole condensate is a 3D superinsulator, characterized by an infinite resistance at finite temperatures [2,8,14]. The critical value of the effective Coulomb interaction strength for the transition to the superinsulating phase is .
These results shows that the string confinement mechanism of superinsulation allows to generalise the concept of a superinsulator to (3+1) dimensions. The SIT has, however, been experimentally found only in (2+1) dimensions. What will be the experimental hallmark of superinsulation in (3+1) dimensions and, at the same time, unequivocally discriminate between the 3d and 2d superinsulators, exposing the linear nature of the underlying confinement? We can gain insight on this problem by looking at the finite temperature behaviour and the deconfinement transition at which string confinement of Cooper pairs ceases to exist. At a critical temperature the linear tension of the string turns to zero and the superinsulator transforms into a conventional insulator. In [37], we have shown that the confining string theory description of superinsulation leads to a deconfinement criticality that depends on the space dimension. In fact the critical behaviour is embodied by the behaviour of the (dimensionless) correlation length that is proportional to the inverse of the square root of the string tension near the critical temperature. In (2+1) dimensions when approaching the deconfinement transition from below the correlation length at the transition diverges according to the law
reproducing thus the BKT [17,18,19] criticality, typical of the 2D XY model, criticality that was predicted for compact QED in (2+1) dimensions by Svetitsky and Yaffe [38].This behaviour has been experimentally observed in [6]. In (3+1) dimensions, instead, we predicted in [37] that the finite-temperature confinement–deconfinement transition is in the Vogel-Fulcher-Tamman class [39], a quasi-2D behaviour in which the correlation length at the transition diverges according to the law
This criticality differs from the one of the 2D XY model only by the power in the exponent. This critical behaviour has been detected in InO films [40], in which the thickness is much larger than the superconducting coherence length. While it seems premature to view this result as a conclusive evidence, yet one can view it as a possible indication of linear confinement in 3d superinsulators.
6. Conclusions
Even after decades of intense research the problem of quark confinement has not yet been completely understood. One of the most promising ways to explain confinement is that confinement of colour is produced by dual superconductivity [1,7,10]: the chromoelectric field produced by quark–antiquark pairs is constrained by the dual Meissner effect into Abrikosov flux tubes in the same way as magnetic field is confined in usual superconductors of type II. This produces an energy proportional to the distance of the pairs, , with the string tension, leading to confinement. Magnetic monopoles, however, have never been observed as elementary particles. In this review, we have shown that they exist as emergent excitations in superconducting films exhibiting the SIT as instantons, where they can form a plasma, and as particles in 3D materials, where they can form a Bose condensate. Monopoles give thus rise to a new state of matter, the superinsulator, in which electric fields are squeezed into flux tubes by the dual Meissner effect leading to linear confinement of charges. Superinsulators realize thus a single-colour version of quantum chromodynamics (QCD) with Cooper pairs playing the role of quarks. Due to the Abelian nature of QED, although in strong coupling, for superinsulators it is possible to derive analytically the linear confinement by electric strings. In QCD, instead, this is possible only through numerical computations. Superinsulators are, thus, a toy model for exploring and testing the fundamental implications of confinement by monopoles and asymptotic safety via desktop experiments on superconductors.
Author Contributions
M.C.D. and C.A.T. the authors equally contributed to this work. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hooft, G.T. On the phase transition towards permanent quark confinement. Nucl. Phys. 1978, B138, 1–25. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Sodano, P.; Trugenberger, C.A. Gauge theories of Josephson junction arrays. Nucl. Phys. B 1996, 474, 641–677. [Google Scholar] [CrossRef]
- Sambandamurthy, G.; Engels, L.W.; Johansson, A.; Peled, E.; Shahar, D. Experimental Evidence for a Collective Insulating State in Two-Dimensional Superconductors. Phys. Rev. Lett. 2005, 94, 017003. [Google Scholar] [CrossRef]
- Vinokur, V.M.; Baturina, T.I.; Fistul, M.V.; Mironov, A.Y.; Baklanov, M.R.; Strunk, C. Superinsulator and quantum synchronization. Nature 2008, 452, 613–615. [Google Scholar] [CrossRef] [PubMed]
- Baturina, T.I.; Vinokur, V.M. Superinsulator–Superconductor duality in two dimensions. Ann. Phys. 2013, 331, 236–257. [Google Scholar] [CrossRef]
- Mironov, A.Y.; Silevitch, D.M.; Proslier, T.; Postolova, S.V.; Burdastyh, M.V.; Gutakovskii, A.K.; Rosenbaum, T.F.; Vinokur, V.M.; Baturina, T.I. Charge Berezinskii-Kosterlitz-Thouless transition in superconducting NbTiN films. Sci. Rep. 2018, 8, 4082. [Google Scholar] [CrossRef]
- Mandelstam, S. Vortices and quark confinement in non-Abelian gauge theories. Phys. Rep. 1976, 23, 245–249. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Confinement and asymptotic freedom with Cooper pairs. Commun. Phys. 2018, 1, 1–7. [Google Scholar] [CrossRef]
- Polyakov, A.M. Compact gauge fields and the infrared catastrophe. Phys. Lett. 1975, 59, 82–84. [Google Scholar] [CrossRef]
- Polyakov, A.M. Gauge Fields and Strings; Harwood Academic Publisher: Chur, Switzerland, 1987. [Google Scholar]
- Milton, K.A. Theoretical and experimental status of magnetic monopoles. Rep. Prog. Phys. 2006, 69, 1637–1712. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Gammaitoni, L.; Strunk, C.; Postolova, S.V.; Mironov, A.Y.; Trugenberger, C.A.; Vinokur, V.M. Direct probe of the interior of an electric pion in a Cooper pair superinsulator. Nat. Commun. Phys. 2020, 3, 142. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Gammaitoni, L.; Trugenberger, C.A.; Vinokur, V.M. The superconductor-superinsulator transition: S-duality and the QCD on the desktop. J. Supercond. Novel Magn. 2019, 51, 32–47. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Quantum magnetic monopole condensate. Nature Commun. Phys. 2021, 4, 25. [Google Scholar]
- Caselle, M.; Panero, M.; Vadacchino, D. Width of the flux tube in compact U(1) gauge theory in three dimensions. J. High Energy Phys. 2016, 2, 180. [Google Scholar] [CrossRef]
- Kleinert, H.; Nogueira, F.S.; Sudbo, A. Kosterlitz-Thouless-like deconfinement mechanism in the (2+1)-dimensional Abelian Higgs model. Nucl. Phys. 2003, B666, 361–395. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group I. Classical systems. Sov. Phys. JETP 1970, 32, 493–500. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J. Phys. C Solid State Phys. 1972, 5, L124. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensioal systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Lu, Y.-M.; Vishwanath, A. Theory and Classification of interacting integer topological phases in two dimensions: A Chern-Simons approach. Phys. Rev. B 2012, 86, 125119. [Google Scholar] [CrossRef]
- Wang, C.; Senthil, T. Boson topological insulators: A window into highly entangled quantum phases. Phys. Rev. B 2013, 87, 235122. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Z.-C.; Liu, Z.-X.; Wen, X.-G. Symmetry protected topological orders and the group cohomology of their symmetry group. Phys. Rev. B 2013, 87, 155114. [Google Scholar] [CrossRef]
- Jackiw, R.; Templeton, S. How super-renormalizable interactions cure infrared divergences. Phys. Rev. 1981, D23, 2291. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R.; Templeton, S. Three-dimensional massive gauge theories. Phys. Rev. Lett. 1982, 48, 975. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R.; Templeton, S. Topologically massive gauge theories. Ann. Phys. (N. Y.) 1982, 140, 372–411. [Google Scholar] [CrossRef]
- Dunne, G.; Jackiw, R.; Trugenberger, C.A. Topological (Chern-Simons) quantum mechanics. Phys. Rev. 1990, D41, 661–666. [Google Scholar] [CrossRef]
- Dunne, G.; Jackiw, R.; Trugenberger, C.A. Chern-Simons theory in the Schrödinger representation. Ann. Phys. 1989, 194, 197–223. [Google Scholar] [CrossRef]
- Cardy, J.L.; Rabinovici, E. Phase structure of Z(p) models in presence of the theta parameter. Nucl. Phys. 1982, B205, 1–16. [Google Scholar] [CrossRef]
- Banks, T.; Myerson, R.; Kogut, J. Phase Transitions in Abelian Lattice Gauge Theories. Nucl. Phys. 1977, B129, 493–510. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Mironov, A.Y.; Postolova, S.V.; Liu, X.; Hao, Z.; Silevitch, D.M.; Kopelevich, Y.; Kim, P.; Trugenberger, C.A.; Vinokur, V.M. Bosonic topological intermediate state in the superconductor-insulator transition. Phys. Lett. 2020, A384, 126570. [Google Scholar] [CrossRef]
- Trugenberger, C.A.; Diamantini, M.C.; Poccia, N.; Nogueira, F.S.; Vinokur, V.M. Magnetic monopoles and superinsulation in Josephson junction arrays. Quantum Rep. 2020, 2, 388–399. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Greensite, J. An Introduction to the Confinement Problem; Springer: Berlin, Germany, 2011. [Google Scholar]
- Lüscher, M. Symmetry-breaking aspects of the roughening transition in gauge theories. Nucl. Phys. B 1981, 180, 317–329. [Google Scholar] [CrossRef]
- Kalb, M.; Ramond, P. Classical direct interstring action. Phys. Rev. 1974, D9, 2273–2284. [Google Scholar] [CrossRef]
- Nelson, D.; Piran, T.; Weinberg, S. Statistical Mechanics of Membranes and Surfaces; World Scientific: Singapore, 2004. [Google Scholar]
- Diamantini, M.C.; Gammaitoni, L.; Trugenberger, C.A.; Vinokur, V.M. Vogel-Fulcher-Tamman criticality of 3D superinsulators. Sci. Rep. 2018, 8, 15718. [Google Scholar] [CrossRef] [PubMed]
- Svetitsky, B.; Yaffe, L.G. Critical behavior at finite temperature confinement transitions. Nucl. Phys. 1982, B210, 423–447. [Google Scholar] [CrossRef]
- Anderson, P.W. Lectures on Amorphous Systems. In Les Houches, Session XXXI; Balian, R., Maynard, R., Toulouse, G., Eds.; World Scientific, North Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Ovadia, M.; Kalok, D.; Tamir, I.; Mitra, S.; Sacépé, B.; Shahar, D. Evidence for a finite-temperature insulator. Sci. Rep. 2015, 5, 13503. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).