First Results of the 140Ce(n,γ)141Ce Cross-Section Measurement at n_TOF
Abstract
1. Introduction
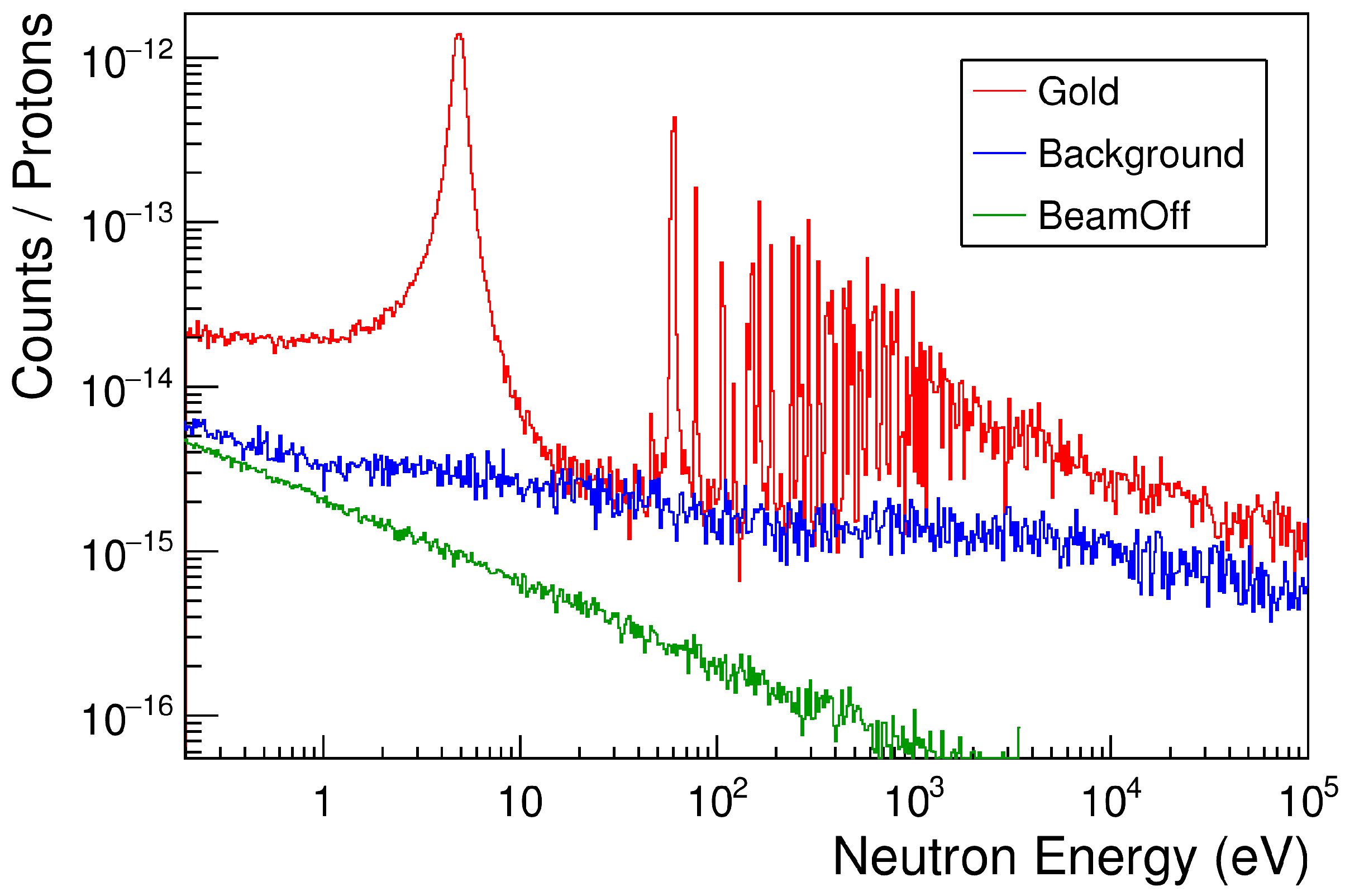
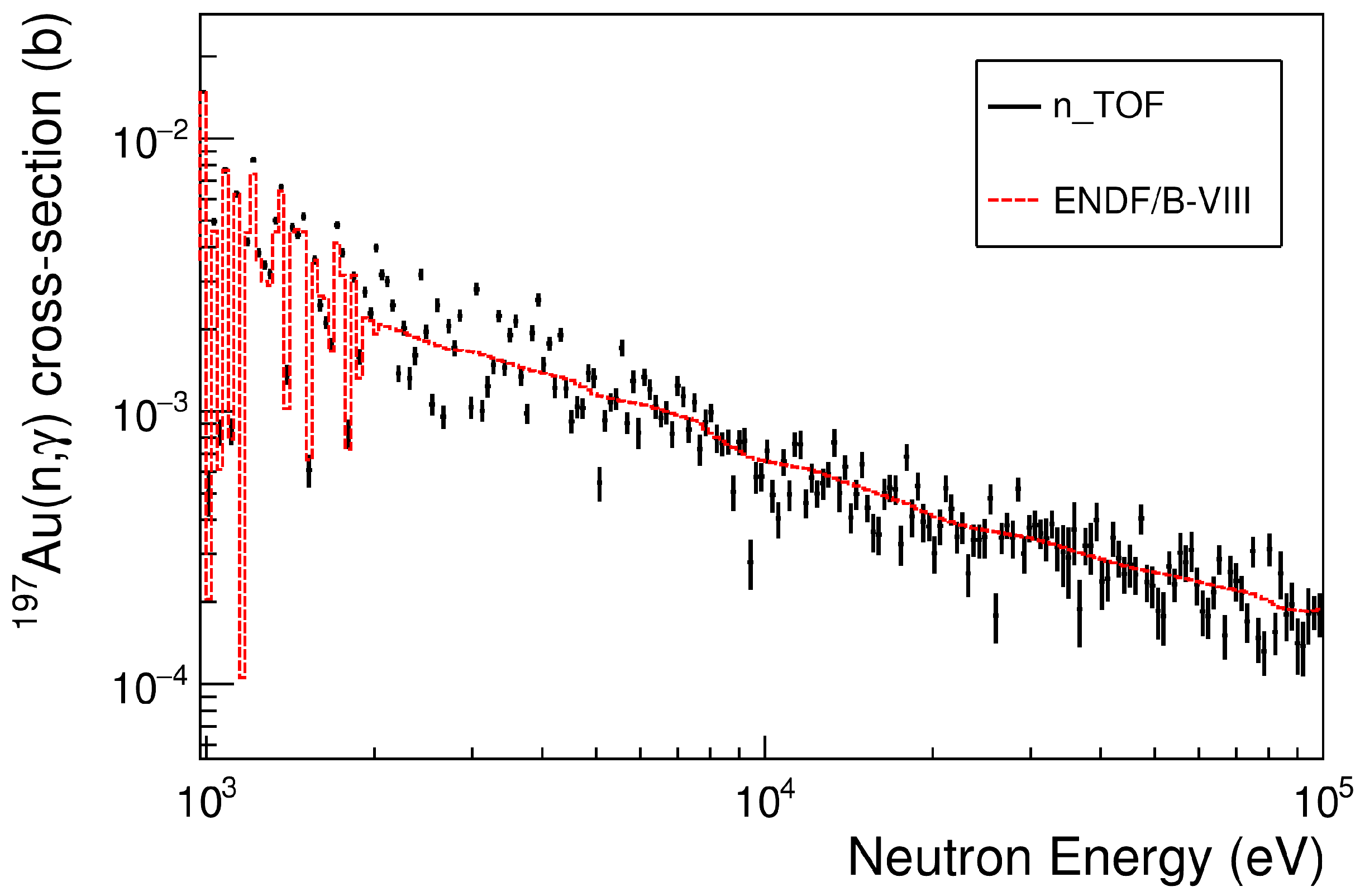
2. Experimental Apparatus and Data Analysis
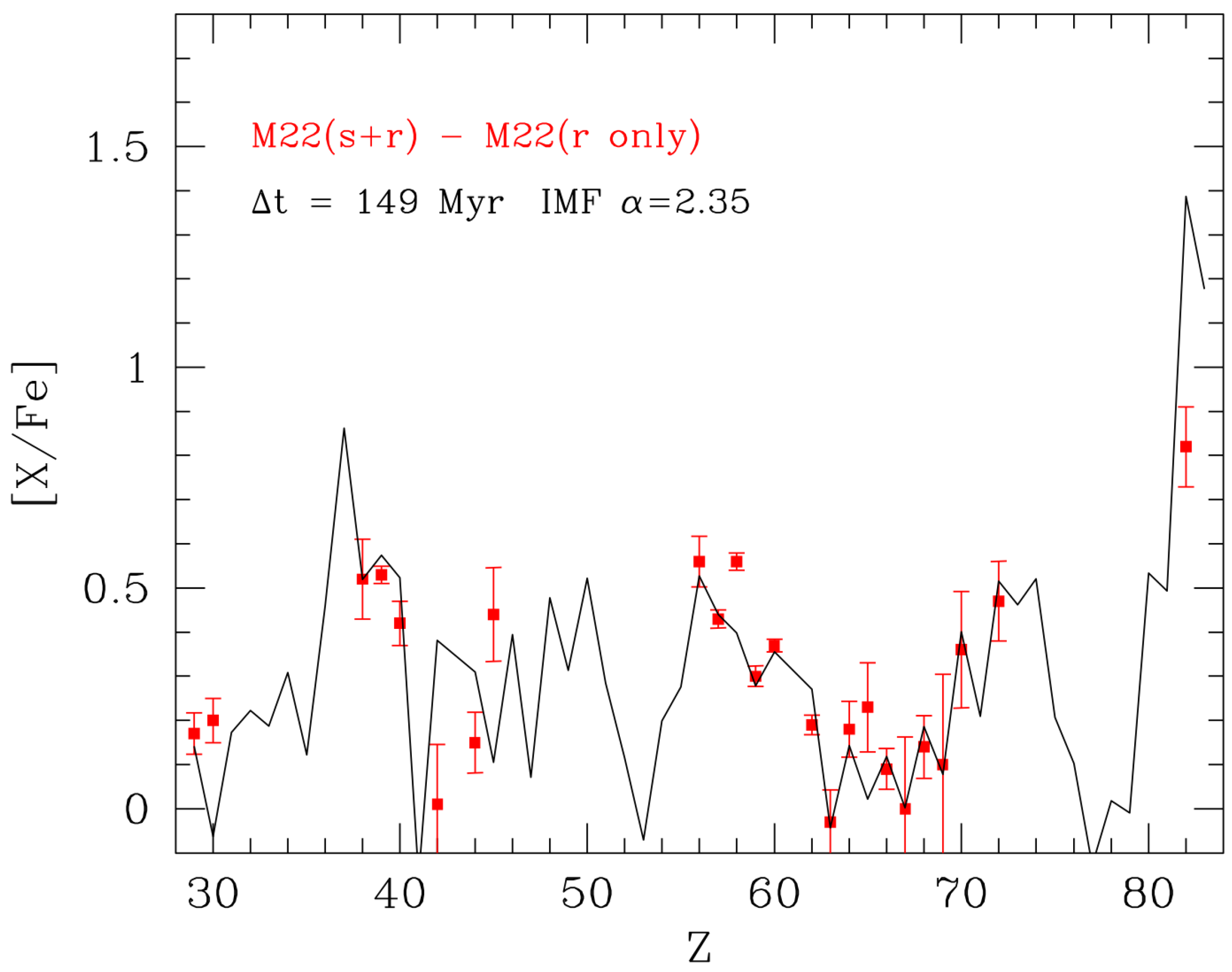
3. Discussion and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| 1. | [El/Fe] = log(N(El)/N(Fe)) − log(N(El)/N(Fe)). |
| 2. | Area of a resonance, defined as g. |
References
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–654. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Stellar evolution, nuclear astrophysics, and nucleogenesis; PAtomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1957. [Google Scholar]
- Busso, M.; Gallino, R.; Wassergurg, G. Nucleosynthesis in Asymptotic Giant Branch Stars: Relevance for Galactic Enrichment and Solar System Formation. ARA&A 1999, 37, 239. [Google Scholar]
- Cristallo, S.; La Cognata, M.; Massimi, C.; Best, A.; Palmerini, S.; Straniero, O.; Trippella, O.; Busso, M.; Ciani, G.F.; Mingrone, F.; et al. The Importance of the 13C(α,n)16O Reaction in Asymptotic Giant Branch Stars. ApJ 2018, 859, 105. [Google Scholar] [CrossRef]
- Straniero, O.; Gallino, R.; Cristallo, S. S process in low-mass asymptotic giant branch stars. Nucl. Phys. A 2006, 777, 311. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Gallino, R.; Piersanti, L.; Dominguez, I.; Ledered, M.T. Evolution, Nucleosynthesis, and Yields of Low-mass Asymptotic Giant Branch Stars at Different Metallicities. ApJ 2011, 696, 797. [Google Scholar] [CrossRef]
- Cristallo, S.; Piersanti, L.; Straniero, O.; Gallino, R.; Domínguez, I.; Abia, C.; Di Rico, G.; Quintini, M.; Bisterzo, S. Evolution, Nucleosynthesis, and Yields of Low-mass Asymptotic Giant Branch Stars at Different Metallicities. II. The FRUITY Database. ApJS 2011, 197, 17. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Piersanti, L.; Gobrecht, D. Evolution, Nucleosynthesis, and Yields of AGB Stars at Different Metallicities. III. Intermediate-mass Models, Revised Low-mass Models, and the ph-FRUITY Interface. ApJS 2015, 219, 40. [Google Scholar] [CrossRef]
- Straniero, O.; Cristallo, S.; Piersanti, L. Heavy elements in globular clusters: the role of asymptotic giant branch stars. ApJ 2014, 785, 77. [Google Scholar] [CrossRef]
- Young, P.A. Stellar Hydrodynamics in Radiative Regions. ApJ 2003, 595, 1114. [Google Scholar] [CrossRef][Green Version]
- Roederer, I.U. Characterizing the heavy elements in globular cluster M22 and an empirical s-process abundance distribution derived from the two stella groups. ApJ 2011, 742, 37. [Google Scholar] [CrossRef]
- Terlizzi, R.; Abbondanno, U.; Aerts, G.; Alvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; Audouin, L.; Badurek, G.; et al. The 139La(n,γ) cross-section: Key for the onset of the s-process. Phys. Rev. C 2007, 75, 035807. [Google Scholar] [CrossRef]
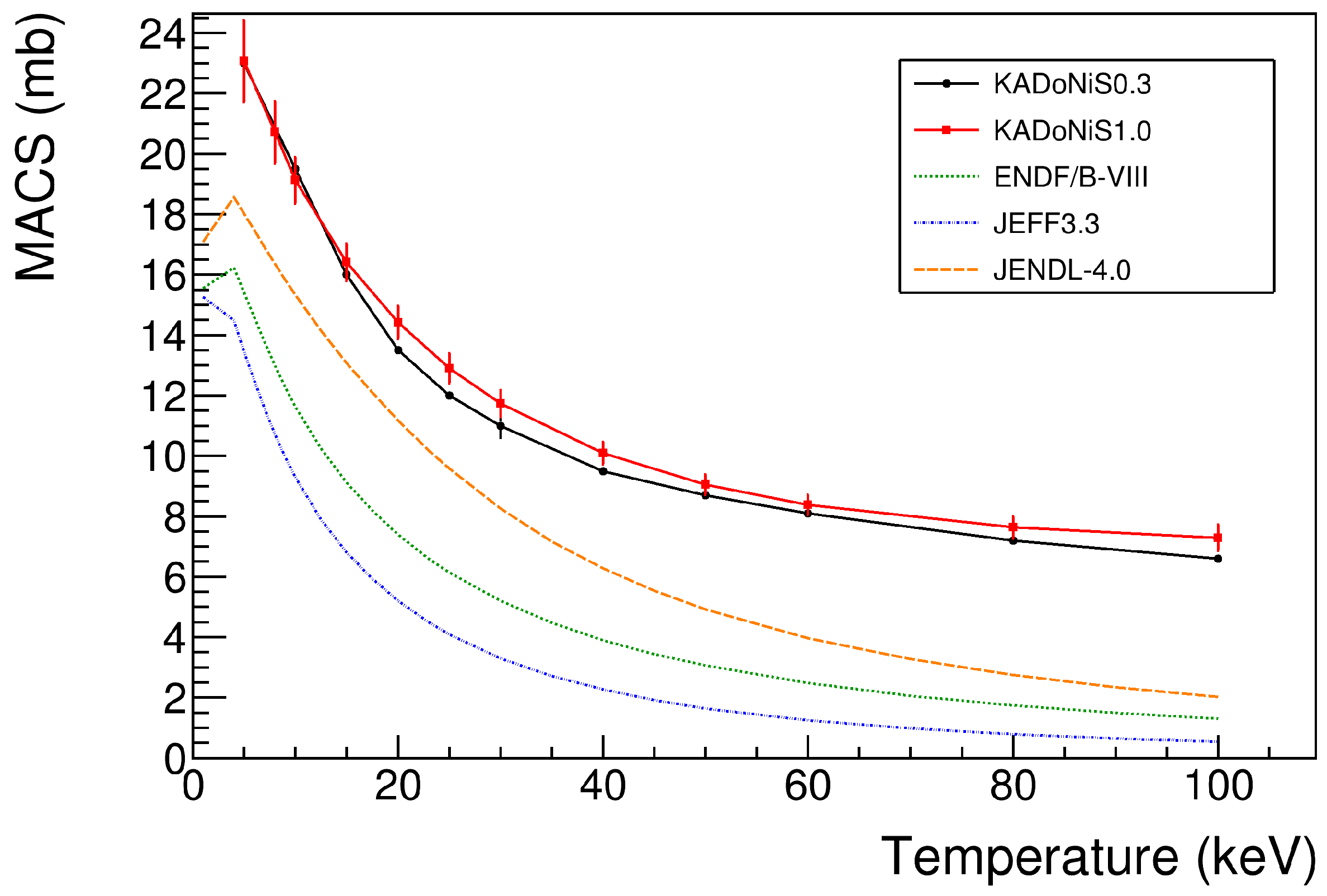
- Dillmann, I.; Plag, R.; Käppeler, F.; Rauscher, T. KADoNiS v0.3—The third update of the “Karlsruhe Astrophysical Database of Nucleosynthesis in Stars”. In Proceedings of the Workshop “EFNUDAT Fast Neutrons—Scientific Workshop on Neutron Measurements, Theory & Applications”, Geel, Belgium, 28–30 April 2009. [Google Scholar]
- Käppeler, F.; Toukan, K.A.; Schumann, M.; Mengoni, A. Neutron capture cross-sections of the cerium isotopes for s- and p-process studies. Phys. Rev. C 1996, 53, 1397–1408. [Google Scholar] [CrossRef]
- de L. Musgrove, A.R. Resonance Neutron Capture in 138Ba and 140Ce and the Prompt Neutron Correction to γ-ray Detectors. Aust. J. Phys. 1979, 32, 213–221. [Google Scholar]
- Koehler, P.E.; Winters, R.R.; Guber, K.H.; Rauscher, T.; Harvey, J.A.; Raman, S.; Spencer, R.R.; Blackmon, J.C.; Larson, D.C.; Bardayan, D.W.; et al. High-resolution neutron capture and transmission measurements, and the stellar neutron-capture cross-section of 88Sr. Phys. Rev. C 2000, 62, 055803. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. J. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Shibata, K.; Iwamoto, O.; Nakagawa, T.; Iwamoto, N.; Ichihara, A.; Kunieda, S.; Chiba, S.; Furutaka, K.; Otuka, N.; Ohsawa, T.; et al. JENDL-4.0: A New Library for Nuclear Science and Engineering. J. Nucl. Sci. Technol. 2011, 48, 0022–3131. [Google Scholar] [CrossRef]
- Plompen, A.J.M.; Cabellos, O.; De Saint, J.C.; Fleming, M.; Algora, A.; Angelone, M.; Archier, P.; Bauge, E.; Bersillon, O.; Blokhin, A.; et al. The joint evaluated fission and fusion nuclear data library, JEFF-3.3. Eur. Phys. J. A 2020, 56, 181. [Google Scholar] [CrossRef]
- Dillmann, I.; Heil, M.; Käppeler, F.; Plag, R.; Rauscher, T.; Thielemann, F.K. The Karlsruhe Astrophysical Database of Nucleosynthesis in Stars 1.0 (test version). Am. Inst. Phys. Conf. Ser. 2006, 819, 123. [Google Scholar]
- n_TOF Collaboration Website. Available online: https://ntof-exp.web.cern.ch/ (accessed on 15 February 2021).
- Mazzone, A.; Cristallo, S.; Aberle, O.; Alaerts, G.; Alcayne, V.; Amaducci, S.; Andrzejewski, J.; Audouin, L.; Babiano-Suarez, V.; Bacak, M.; et al. Measurement of the 154Gd(n,γ) cross-section and its astrophysical implications. Phys. Lett. B 2020, 804, 135405. [Google Scholar] [CrossRef]
- Rukelj, Z.; Homes, C.C.; Orlita, M.; Akrap, A. Neutron Capture on the s-Process Branching Point 171Tm via Time-of-Flight and Activation. Phys. Rev. Lett. 2020, 125, 142701. [Google Scholar]
- Guerrero, C.; Tsinganis, A.; Berthoumieux, E.; Barbagallo, M.; Belloni, F.; Gunsing, F.; Weiß, C.; Chiaveri, E.; Calviani, M.; Vlachoudis, V.; et al. Performance of the neutron time-of-flight facility n_TOF at CERN. Eur. Phys. J. A 2013, 49, 27. [Google Scholar] [CrossRef]
- Plag, R.; Heil, M.; Käppeler, F.; Pavlopoulos, P.; Reifarth, R.; Wisshak, K.; n_TOF Collaboration. An optimized C6D6 detector for studies of resonance-dominated (n,γ) cross-sections. Nucl. Instrum. Methods Phys. Res. A 2003, 496, 425–436. [Google Scholar] [CrossRef]
- Marrone, S.; Mastinu, P.F.; Abbondanno, U.; Baccomi, R.; Marchi, E.B.; Bustreo, N.; Colonna, N.; Gramegna, F.; Loriggiola, M.; Marigo, S.; et al. A low background neutron flux monitor for the n_TOF facility at CERN. Nucl. Instrum. Methods Phys. Res. A 2004, 517, 389–398. [Google Scholar] [CrossRef]
- Macklin, R.L.; Gibbons, J.H. Capture-Cross-section Studies for 30-220-keV Neutrons Using a New Technique. Phys. Rev. 1967, 159, 1007–1012. [Google Scholar] [CrossRef]
- Schillebeeckx, P.; Becker, B.; Danon, Y.; Guber, K.; Harada, H.; Heyse, J.; Junghans, A.R.; Kopecky, S.; Massimi, C.; Moxon, M.C.; et al. Determination of Resonance Parameters and their Covariances from Neutron Induced Reaction Cross Section Data. Nucl. Data Sheets 2012, 113, 3054–3100. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4–a simulation toolkit. Nucl. Instrum. Methods Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Barbagallo, M.; Guerrero, C.; Tsinganis, A.; Tarrio, D.; Altstadt, S.; Andriamonje, S.; Andrzejewski, J.; Audouin, L.; Bécares, V.; Bečvář, F.; et al. High-accuracy determination of the neutron flux at n_TOF. Eur. Phys. J. A 2013, 49, 156. [Google Scholar] [CrossRef]
- Macklin, R.L.; Halperin, J.; Winters, R.R. Absolute neutron capture yield calibration. Nucl. Instrum. Methods Phys. Res. A 1979, 164, 213–214. [Google Scholar] [CrossRef]
- Larson, N. Updated Users’ Guide for SAMMY Multilevel R-Matrix Fits to Neutron Data Using Bayes’ Equation; Tech. Rep. ORNL/TM-9179/R4; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1998. [Google Scholar]
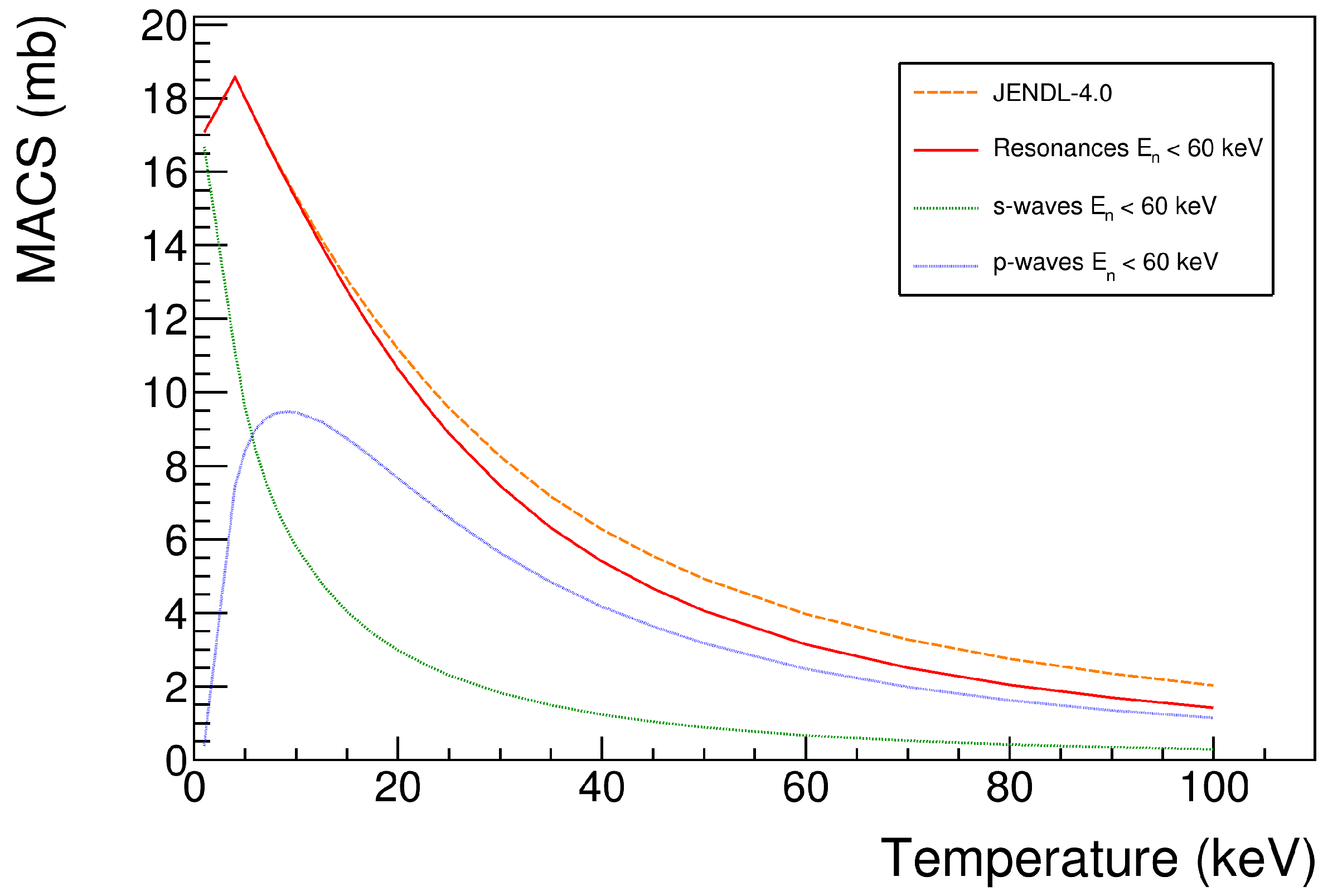
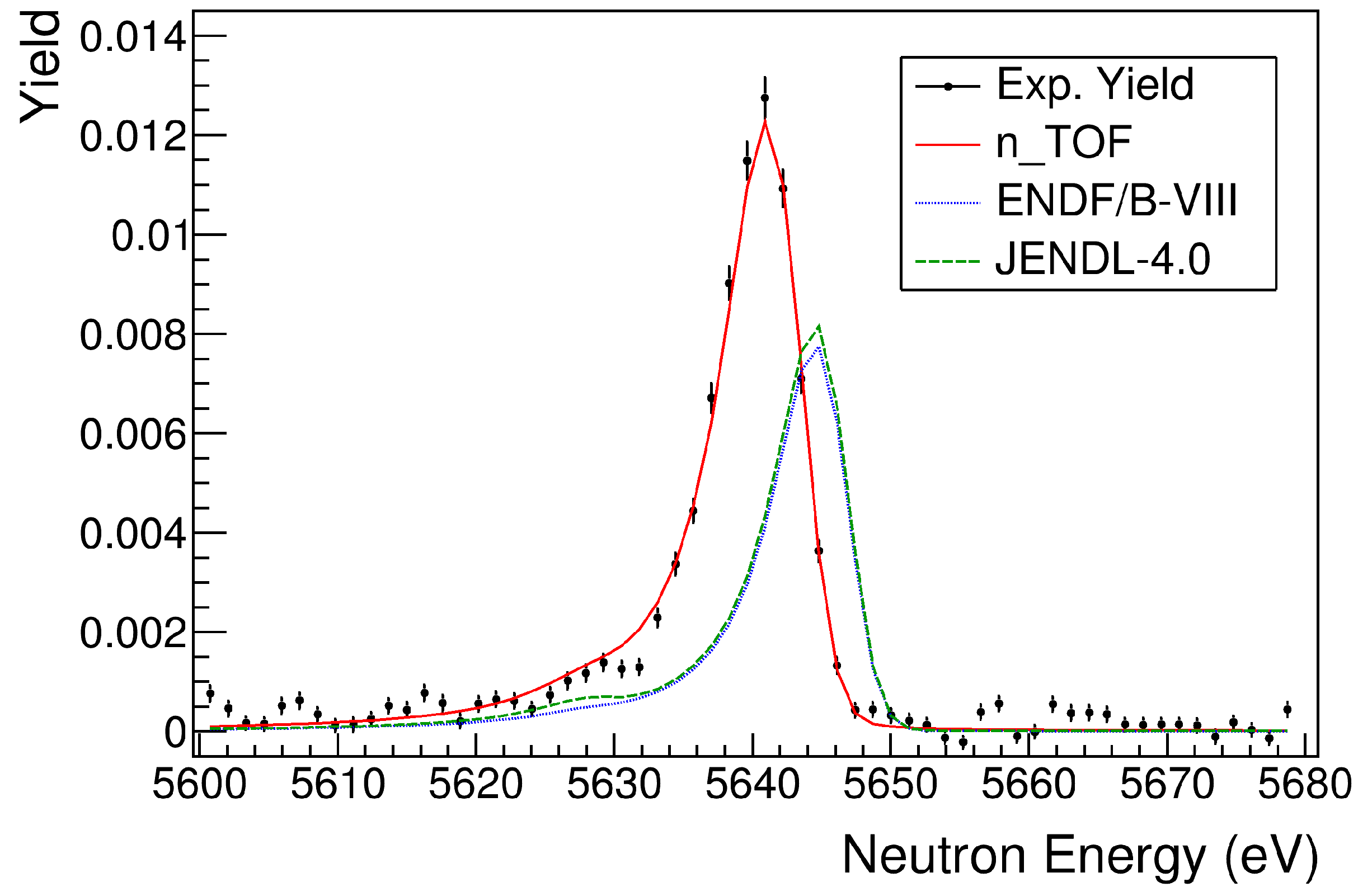
| Source | Energy (eV) | g (meV) |
|---|---|---|
| n_TOF | 5636.56 ± 0.05 | 21.6 ± 1.2 |
| JENDL-4.0 | 5640 | 11.0 |
| ENDF/B-VIII | 5640 | 10.5 |
| Musgrove et al. | 5640 ± 5 | 10 ± 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaducci, S.; Colonna, N.; Cosentino, L.; Cristallo, S.; Finocchiaro, P.; Krtička, M.; Massimi, C.; Mastromarco, M.; Mazzone, A.; Mengoni, A.; et al. First Results of the 140Ce(n,γ)141Ce Cross-Section Measurement at n_TOF. Universe 2021, 7, 200. https://doi.org/10.3390/universe7060200
Amaducci S, Colonna N, Cosentino L, Cristallo S, Finocchiaro P, Krtička M, Massimi C, Mastromarco M, Mazzone A, Mengoni A, et al. First Results of the 140Ce(n,γ)141Ce Cross-Section Measurement at n_TOF. Universe. 2021; 7(6):200. https://doi.org/10.3390/universe7060200
Chicago/Turabian StyleAmaducci, Simone, Nicola Colonna, Luigi Cosentino, Sergio Cristallo, Paolo Finocchiaro, Milan Krtička, Cristian Massimi, Mario Mastromarco, Annamaria Mazzone, Alberto Mengoni, and et al. 2021. "First Results of the 140Ce(n,γ)141Ce Cross-Section Measurement at n_TOF" Universe 7, no. 6: 200. https://doi.org/10.3390/universe7060200
APA StyleAmaducci, S., Colonna, N., Cosentino, L., Cristallo, S., Finocchiaro, P., Krtička, M., Massimi, C., Mastromarco, M., Mazzone, A., Mengoni, A., Valenta, S., Aberle, O., Alcayne, V., Andrzejewski, J., Audouin, L., Babiano-Suarez, V., Bacak, M., Barbagallo, M., Bennett, S., ... Žugec, P., on behalf of the n_TOF Collaboration. (2021). First Results of the 140Ce(n,γ)141Ce Cross-Section Measurement at n_TOF. Universe, 7(6), 200. https://doi.org/10.3390/universe7060200






