Taxonomy of Dark Energy Models

Abstract

The accelerated expansion of the Universe is one of the main discoveries of the past decades, indicating the presence of an unknown component: the dark energy. Evidence of its presence is being gathered by a succession of observational experiments with increasing precision in its measurements. However, the most accepted model for explaining the dynamic of our Universe, the so-called Lambda cold dark matter, faces several problems related to the nature of such energy component. This has led to a growing exploration of alternative models attempting to solve those drawbacks. In this review, we briefly summarize the characteristics of a (non-exhaustive) list of dark energy models as well as some of the most used cosmological samples. Next, we discuss how to constrain each model’s parameters using observational data. Finally, we summarize the status of dark energy modeling.

1. Introduction

One of the most important discoveries in modern cosmology since the observation of the Universe expansion by George Lemaître [1] and Edwin Hubble [2] and the detection of the cosmic microwave background (CMB) [3,4] is the accelerated expansion at late times. This cosmic acceleration was detected at the end of the 1990s, when two independent collaborations were observing high redshift type Ia supernovae (SNIa) to measure the curvature and deceleration parameter of the Universe [5,6]; both groups established a cosmological constant model of the Universe, with ${\Omega }_m\approx$ 0.3, and  ${\Omega }_{\Lambda }\approx$ 0.7. Later, this result was confirmed by different cosmological probes, for example the CMB [7,8], baryon acoustic oscillations (e.g., [9,10]), and gravitational lensing, both strong (e.g., [11]) and weak (e.g., [12]).

In recent decades, substantial effort has been made to understand the nature of Dark Energy (DE)  (e.g., see [13] for a recent review) with the $\Lambda$ Cold Dark Matter model ($\Lambda$CDM) being the cornerstone of modern cosmology and the simplest one, composed of two dominant components, known as cold dark matter (DM) and cosmological constant, and three subdominant components identified as baryons, photons, and neutrinos. The $\Lambda$CDM model is not only effective at background level (isotropic and homogeneous Universe), but also robust at linear perturbations, having accurate predictions for the matter power spectrum and the small differences for photons temperature observed in the CMB [14,15]. As mentioned previously, the $\Lambda$CDM model is composed of ∼32% cold dark matter, which is essential for the structure formation, being the most suitable explanation for the rotation curves of galaxies (see for instance [16,17,18]). It is assumed that dark matter is a non-relativistic particle and the preferred candidates are the particles emerging from the Supersymmetric theory [19,20]. However, the lack of evidence of these particles strengthens the proposition of other candidates such as Axions, Ultra light scalar field dark matter, and others [21,22,23]. Despite the remarkable achievements of the $\Lambda$CDMmodel, it has important afflictions when describing the nature of the cosmological constant (CC) through the idea of a quantum vacuum fluctuations [24,25]. This idea generates, from the theoretical point of view, an error of ∼${10}^{120}$ orders of magnitude, and it is known as the fine tuning problem [26]. In addition, the CC has the coincidence problem [26], i.e., why did the Universe accelerate at late epochs and not before of after? On top of that, recent observations from Planck and Supernovae Type Ia differ in their values for $H_0$ (see also [27,28] for recent values measured using gravitational lens systems), introducing tension between different observations at different redshifts [29,30,31,32,33]. The community attributes the problem to the $\Lambda$CDM model and in particular to the CC; therefore, new approaches are proposed to alleviate the discrepancy among observations (see also [34,35,36]).

In the context of these tensions and the problems with CC, a plethora of alternative dark energy models have been explored. Our aim is to review a set of those models consisting of fluids that can be described by a variety of formulations. Some of them can be described by different fluids and their particles that compose them, like scalar fields, while others that do not need extra fluids but require modifications to general theory of relativity (GTR, [37,38,39,40,41,42,43,44,45,46,47,48,49,50]) (for recent overviews of GTR, see, e.g., [51,52,53] and references therein). Specifically, the first category contains models avoiding the idea of associating the Universe acceleration with quantum vacuum fluctuations (like in CC) and thus assume a fluid expression manageable by the quantum field theory. The second one consist of models introducing extensions to GTR, generating a Universe acceleration without the addition of extra fluids. However, the current overabundance of models is overwhelming, posing difficulties to decide which is the best candidate to compete against the $\Lambda$CDM model.

Recent years have also witnessed the increase in observational surveys designed to obtain precise measurements aimed to probe DE’s nature. With this improvement in the instrument sensitivity came the mechanism to discriminate between models of DE; i.e., tensions between different probes could lead to ruling out some of them. In this context, we consider widely used samples (such as SNIa [5], CMB [15], baryon acoustic oscillations) as well as other recent compilations (strong gravitational lens systems [54,55,56], starburst galaxies [57,58,59,60,61,62], and observational Hubble parameters [56,63].

The outline of the review is as follows: Section 2 summarizes the basic equations, Section 3 presents the cosmological samples that we use to constraint the different theoretical models, and  Section 4 describes the DE models, together with the constraints of the free parameters of each model. Finally, in  Section 5, we give a discussion and conclusion of the models mentioned, discussing the promising models and what the contribution is to the understanding of the Universe acceleration.

2. Basic Equations for the Background Cosmology

Modern cosmology is based on the general theory of relativity, whose master equation is the field equation given by

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu },$$

(1)

where $G_{\mu \nu }\equiv R_{\mu \nu }-g_{\mu \nu }R/2$ is known as the Einstein tensor, composed of the Ricci tensor ($R_{\mu \nu }$), the Ricci scalar (R), and the metric tensor ($g_{\mu \nu }$). The right side of Equation (1) shows the Newton gravitational constant (G) and the energy momentum tensor. Hereafter we will use natural units ($c=\hslash =1$), unless we explicitly mention the opposite.

Hereafter, we focus our attention on the background cosmology considering a homogeneous and isotropic Universe. In this vein, we use the standard line element of Friedmann–Lemaitre–Robertson–Walker (FLRW) with flat geometry $k=0$, as 

$$d{s}^2=-d{t}^2+a{\left(t\right)}^2(d{r}^2+r^{2}d{\Omega }^2),$$

(2)

where $d{\Omega }^2\equiv d{\theta }^2+{sin}^2\theta d{\phi }^2$ and $a\left(t\right)$ is the scale factor. The energy-momentum tensor is written, as always, as

$$T_{\mu \nu }=p{g}_{\mu \nu }+(\rho +p)u_{\mu }{u}_{\nu },$$

(3)

where p, $\rho$, $u_{\mu }$, and $g_{\mu \nu }$ are the pressure, density, four-velocity of the fluid, and the metric tensor, respectively. The covariant derivative of the energy momentum tensor ${\nabla }^{\mu }{T}_{\mu \nu }=0$ generates the continuity equation, given by

$$\sum _i\left[{\dot{\rho }}_i+3\frac{\dot{a}}{a}({\rho }_i+p_i)\right]=0,$$

(4)

where the sum is over all the species, and dots stand for derivatives with respect to time.

Through the Einstein field equations, we arrive at the Friedmann equation, which is a first-order non-linear differential equation composed of the scale factor and the densities of the species. Therefore, the equation takes the form

$$H^2\equiv {\left(\frac{\dot{a}}{a}\right)}^2=\frac{8\pi G}{3}\sum _i{\rho }_i,$$

(5)

where H is known as the Hubble parameter, which indicates the Universe expansion rate. Hence, it is possible to define the dimensionless Friedmann equation in the form

$$E{\left(z\right)}^2\equiv {\left(\frac{H}{H_0}\right)}^2=\sum _i\Omega {\left(z\right)}_i,$$

(6)

where $\Omega \left(z\right)\equiv 8\pi G\rho \left(z\right)/3H_0^2$ is known as the density parameter, a function of the redshift (z), and the sum runs for the components of the Universe used in the model (${\Omega }_b$, ${\Omega }_{dm}$, ${\Omega }_r$, ${\Omega }_{de}$ represent baryons, dark matter, radiation, and dark energy, respectively), $H_0$ is the Hubble constant (this is the Hubble parameter evaluated at $z=0$). With the previous equations, it is possible to define the flat condition as

$$1=\sum _i{\Omega }_i;$$

(7)

notice that the density parameters are evaluated at $z=0$ and they are denoted with the label 0. The comoving distance from the observer to redshift z is given by (units of c are recovered in the following equations)

$$r\left(z\right)=\frac{c}{H_0}{\int }_0^z\frac{d{z}^{\prime }}{E\left(z^{\prime }\right)}.$$

(8)

Therefore, we define the luminosity distance, denoted as $d_L\left(z\right)$, as 

$$d_L\left(z\right)=\frac{c}{H_0}(1+z){\int }_0^z\frac{d{z}^{\prime }}{E\left(z^{\prime }\right)},$$

(9)

where c is the speed of light. The angular diameter distance is related to the comoving distance as

$$D_A=d_L\left(z\right)/{(1+z)}^2,$$

(10)

In addition, the angular diameter distance between two objects at redshifts $z_1$ and $z_2$ ($z_1<z_2$) is given by

$$D_{12}\left(z\right)=\frac{c}{H_0(1+z)}{\int }_{z_1}^{z_2}\frac{d{z}^{\prime }}{E\left(z^{\prime }\right)},$$

(11)

3. Cosmological Samples

Observational samples are required not only to investigate the consistency of any theoretical model prediction but also to discern between different models. In this section, we review the most common samples used as “standard candles” to probe those models. Given a cosmological model, the astronomical distance to an object is generally measured using the redshift to the object and the distance–redshift relationship provided by the model (see Equation (9)). However, when the goal is to infer the cosmological model, an independent distance measurement is needed. The methods to obtain these independent measurements are based on empirical relationships, and thus, the astronomical objects following those relations are called standard candles.

Knowing the intrinsic flux of a standard candle(recall the relation between the flux (f), intrinsic luminosity (L), and the luminosity distance ($d_L$): $f=L/\left(4\pi d_L^2\right)$), we can obtain a relation between the apparent magnitude (m, observed) and the absolute magnitude (M, acquired from an empirical relation)

$$m=M+5{log}_{10}\left(\frac{d_L}{10pc}\right).$$

(12)

In the following sections, we include a general description of some of the most used cosmological samples with emphasis on the quantification of the goodness-of-fit (or figure-of-merit) by defining a function (${\chi }^2$) associated with the sample errors or covariances, which is applied to investigate the cosmological models presented in Section 4.

3.1. Type Ia Supernovae

Type Ia supernova is believed to originate from a white dwarf accreting matter from a companion star. When the white dwarf exceeds the Chandrasekhar mass limit (∼$1.4M_{\odot }$, where $M_{\odot }$ is 1 solar mass), there is a collapse and subsequent explosion. As all the SNIa have roughly the same luminosity (SNIa peak luminosities could have a scatter of ∼0.3 mag, but, after applying a correction related to the correlation between the peak luminosity and the light-curve decline time (the so-called “stretch”), the scatter is reduced to ≤0.15 mag), and they can be used as standard candles.

Samples of SNIa (e.g., [31,47,64,65,66]) provide distance modulus measurements (see Equation (12)). As the measurements in this kind of sample are correlated, it is convenient to build the chi square function as

$${\chi }_{\mathrm{SNIa}}^2=a+log\left(\frac{e}{2\pi }\right)- \frac{b^2}{e},$$

(13)

where

$$\begin{array}{ccc}\hfill a& =& \Delta {\tilde{\mathit{\mu }}}^T·{\mathbf{Cov}}_{\mathbf{P}}^{-\mathbf{1}}·\Delta \tilde{\mathit{\mu }},\hfill \\ \hfill b& =& \Delta {\tilde{\mathit{\mu }}}^T·{\mathbf{Cov}}_{\mathbf{P}}^{-\mathbf{1}}·\Delta \mathbf{1},\hfill \\ \hfill e& =& \Delta {\mathbf{1}}^T·{\mathbf{Cov}}_{\mathbf{P}}^{-\mathbf{1}}·\Delta \mathbf{1},\hfill \end{array}$$

(14)

and $\Delta \tilde{\mathit{\mu }}$ is the vector of residuals between the theoretical distance modulus and the observed one, $\Delta \mathbf{1}={(1,1,\cdots ,1)}^T$, and ${\mathbf{Cov}}_{\mathbf{P}}$ is the covariance matrix formed by adding the systematic and statistic uncertainties, i.e.,  ${\mathbf{Cov}}_{\mathbf{P}}={\mathbf{Cov}}_{\mathbf{P},\mathbf{sys}}+{\mathbf{Cov}}_{\mathbf{P},\mathbf{stat}}$. The super-index T on the above expressions denotes the transpose of the vectors.

The theoretical distance modulus is estimated by

$$m_{th}=\mathcal{M}+5{log}_{10}[d_L\left(z\right)/10pc],$$

(15)

where $\mathcal{M}$ is a nuisance parameter that has been marginalized in (13).

3.2. Baryon Acoustic Oscillations

Another way to establish a constraint of model parameters is through the standard rules known as Baryon Acoustic Oscillations (BAO). These are primordial signatures in the matter power spectrum produced by the interaction between baryons and photons in a hot plasma in the pre-recombination epoch.

The theoretical BAO angular scale (${\theta }_{th}$) is estimated as

$${\theta }_{th}\left(z\right)=\frac{r_{drag}}{(1+z)D_A\left(z\right)},$$

(16)

where $d_L$ and $D_A$ are written in Equations (9) and (10), respectively. The parameter $r_{drag}$ indicates the sound horizon at baryon drag epoch. The comoving sound horizon, $r_s\left(z\right)$, is defined as

$$r_s\left(z\right)=\frac{c}{H_0}{\int }_z^{\infty }\frac{c_s\left(z^{\prime }\right)}{E\left(z^{\prime }\right)}d{z}^{\prime },$$

(17)

where the sound speed $c_s\left(z\right)=1/\sqrt{3\left(1+{\overline{R}}_b/\left(1+z\right)\right)}$, with ${\overline{R}}_b=\mathrm{31,500}{\Omega }_b{h}^2$($T_{CMB}$/2.7K)${}^{-4}$, and $T_{CMB}$ is the CMB temperature. The redshift $z_{drag}$ at the baryon drag epoch is well fitted with the formula proposed by Eisenstein and Hu [67]

$$z_{drag}=\frac{1291{\left({\Omega }_{m0}{h}^2\right)}^{0.251}}{1+0.659{\left({\Omega }_{m0}{h}^2\right)}^{0.828}}[1+b_1{\left({\Omega }_{b0}{h}^2\right)}^{b_2}],$$

(18)

where

$$\begin{array}{ccc}{b}_1\hfill & =& 0.313{\left({\Omega }_{m0}{h}^2\right)}^{-0.419}\left[1+0.607{\left({\Omega }_{m0}{h}^2\right)}^{0.674}\right],\hfill \end{array}$$

(19)

$$\begin{array}{ccc}{b}_2\hfill & =& 0.238{\left({\Omega }_{m0}{h}^2\right)}^{0.223}.\hfill \end{array}$$

(20)

where ${\Omega }_{m0}$ and ${\Omega }_{b0}$ are the matter component (dark matter plus baryons) and baryon component at $z=0$, respectively. For this work, we set the $r_{drag}=147.21\pm 0.23$, obtained by Planck collaboration [15]. Notice that, as BAO data points are estimated using $r_{drag}$, which depends on the cosmological model, they could be considered as biased.

The most recent compilation of transversal BAO measurements ${\theta }_{BAO}\left(z\right)$ is presented in [68]. A total of 15 measurements [69,70,71,72,73] were obtained using the data releases (DR), DR7, DR10, DR11, DR12, DR12Q (quasars), of Sloan Digital Sky Survey (SDSS) [74]. As transversal angular BAO points are considered uncorrelated, the chi square function is built as

$${\chi }_{\mathrm{BAO}}^2=\sum _{i=1}^N{\left(\frac{{\theta }_{\mathrm{BAO}}^i-{\theta }_{th}\left(z_i\right)}{{\sigma }_{{\theta }_{\mathrm{BAO}}^i}}\right)}^2,$$

(21)

where ${\theta }_{\mathrm{BAO}}^i\pm {\sigma }_{{\theta }_{\mathrm{BAO}}^i}$ is the BAO angular scale, N is the number of data and their uncertainty at $68\%$ measured at $z_i$. It is worth mentioning that there is a sample of six correlated data points, with their associated covariance matrix, collected in [75] and measured by [76,77,78]. In this case, the chi square function is

$${\chi }_{cBAO}^2={\overrightarrow{X}}^T{\mathrm{Cov}}^{-1}\tilde{\mathrm{X}}$$

(22)

where $\overrightarrow{X}$ is the difference between the theoretical and observational quantities of $d_A\left(z_{drag}\right)/D_V\left(z_i\right)$ measured at the redshift $z_i$,   ${\mathrm{Cov}}^{-1}$ is the inverse covariance matrix (see [75] for details), and the dilation scale ($D_V$) is defined as [79]

$$D_V={\left[\frac{d_A^2\left(z\right)cz}{H_{0}E\left(z\right)}\right]}^{1/3}$$

(23)

where $d_A\left(z\right)=(1+z)D_A\left(z\right)$ is the comoving angular–diameter distance.

3.3. Cosmic Microwave Background Radiation

In the early Universe, baryons and photons were coupled, leading to coherent oscillations that are observed in the power spectrumof the CMB (e.g., WMAP [8,80], Planck [15,81]) (the power spectrum is the statistical description of the temperature anisotropies observed in the CMB map). This is a powerful probe due to its ability to estimate the cosmological parameters with high precision [82]. The information of the CMB acoustic peaks can be condensed in three quantities, with the following distance posteriors: the acoustic scale ($l_A$), the shift parameter (R), and the decoupling redshift ($z_{\ast }$). Several authors have proved that these quantities are almost independent of the DE model considered, and thus they can be used to test the parameters of alternative cosmologies [83,84,85]. The acoustic scale is defined as

$$l_A=\frac{\pi r\left(z_{\ast }\right)}{r_s\left(z_{\ast }\right)},$$

(24)

where $r_s$ is the sound horizon (Equation (17)) at the redshift of decoupling $z_{\ast }$ given by Hu and Sugiyama [86],

$$z_{\ast }=1048[1+0.00124{\left({\Omega }_{b}0h^2\right)}^{-0.738}][1+g_1{\left({\Omega }_{m0}{h}^2\right)}^{g_2}],$$

(25)

where

$$g_1=\frac{0.0783{\left({\Omega }_b{h}^2\right)}^{-0.238}}{1+39.5{\left({\Omega }_{b}0h^2\right)}^{0.763}},g_2=\frac{0.560}{1+21.1{\left({\Omega }_{b}0h^2\right)}^{1.81}}.$$

(26)

The shift parameter is defined as [87]

$$R=\frac{\sqrt{{\Omega }_{m0}{H}_0^2}}{c}r\left(z_{\ast }\right).$$

(27)

where ${\Omega }_{m0}$ includes the baryon and DM components.

Thus, the ${\chi }^2$ for the CMB data is constructed as

$${\chi }_{\mathrm{CMB}}^2=X^T{\mathrm{Cov}}_{\mathrm{CMB}}^{-1}X,$$

(28)

where ${\mathrm{Cov}}_{\mathrm{CMB}}^{-1}$ is the inverse covariance matrix of the distance posteriors and

$$X=\left(\begin{array}{c}{l}_A^{th}-l_A^{obs}\\ R^{th}-R^{obs}\\ z_{\ast }^{th}-z_{\ast }^{obs}\end{array}\right),$$

(29)

the superscripts $th$ and $obs$ refer to the theoretical and observational estimations, respectively.

To infer the parameters of the alternative cosmologies, we employ the distance posteriors of WMAP [80] and Planck [88].

3.4. Observational Hubble Parameter

The Hubble parameter is estimated mostly by using the differential age (DA, [63]) methodology and from BAO measurements. The former method consists of measuring the age between pairs of passive evolving galaxies (dubbed cosmic chronometers) with similar metallicity and separated by a small redshift interval with redshift $z\lesssim 2.0$ (for example, the authors of [89] measure $dz\sim 0.04$ at $z<0.4$ and $dz\sim 0.3$ at $z>0.4$). Thus, the expansion rate is written as

$$H\left(z\right)=-\frac{1}{1+z}\frac{dz}{dt},$$

(30)

where $dz$ is measured with high accuracy (reference [89] indicates that spectroscopic redshifts of galaxies have typical uncertainties ${\sigma }_z<0.001$). The OHD from the DA method are considered cosmological independent measurements. On the other hand, the OHD from BAO surveys are non-homogeneous, since they depend on the cosmological model selected. By taking a unique value for $r_{drg}$ in these data, an OHD homogeneous sample can be obtained (see [66] for further details).

The observational Hubble parameter data (OHD) represents the most direct way to constrain the parameter space to mimic the observational expansion rate; the chi square function can be expressed as

$${\chi }_{\mathrm{OHD}}^2=\sum _{i=1}^N{\left(\frac{H_{th}\left(z_i\right)-H_{obs}\left(z_i\right)}{{\sigma }_{obs}^i}\right)}^2,$$

(31)

where $H_{th}\left(z_i\right)$ is the theoretical estimate using (6) or a generalization, $H_{obs}\left(z_i\right)\pm {\sigma }_{obs}^i$ is the observational Hubble parameter (from DA, (non)-homogeneous BAO points, or the joint of them) with its uncertainty at the redshift $z_i$, and N is the number of points used.

3.5. Strong Gravitational Lens Systems

A strong gravitational lens systems (SLS) offers a unique opportunity to study the ${\Omega }_m-w$ plane because their confidence regions are almost orthogonal to those of standard rulers (like BAO and CMB). Different groups of SLS have been used to constrain cosmological parameters with different methods [54,55,56,90,91,92,93]. These systems have lenses in the region $0\lesssim z\lesssim 1$ with their respective sources in the range $0.2\lesssim z\lesssim 3.5$. The chi square function for SLS takes the form

$${\chi }_{\mathrm{SLS}}^2=\sum _i^{204}\frac{{[D^{th}(z_L,z_S)-D^{obs}({\theta }_E,{\sigma }^2)]}^2}{{\left(\delta D^{obs}\right)}^2},$$

(32)

where the observable to confront is $D^{obs}=c^2{\theta }_E/4\pi {\sigma }^2$, where ${\theta }_E$ is the Einstein radius of the lens obtained by assuming the gravitational lens potential is modeled by a Singular Isothermal Sphere (SIS), defined by

$${\theta }_E=4\pi \frac{{\sigma }_{SIS}^2{D}_{LS}}{c^2{D}_S}.$$

(33)

In the above expression, ${\sigma }_{SIS}$ is the 3D velocity dispersion of the lens galaxy, $D_S$ is the angular diameter distance to the source, and $D_{LS}$ is the angular diameter distance from the lens to the source defined by Equation (11), where $1\to L$ and $2\to S$. Note that, as SLS data assumes a lens model for ${\theta }_E$ and ${\sigma }_{SIS}$ comes from spectroscopy, the sample is independent of h and, as consequence, the parameter constraints do not depend on h. The uncertainty of $D^{obs}$ is estimated by

$$\delta D^{obs}=D^{obs}{\left[{\left(\frac{\delta {\theta }_E}{{\theta }_E}\right)}^2+4{\left(\frac{\delta \sigma }{\sigma }\right)}^2\right]}^{1/2},$$

(34)

where $\delta {\theta }_E$ and $\delta \sigma$ are the uncertainties of the Einstein radius and the observed line-of-sight (1D) velocity dispersion, respectively.

The theoretical counterpart is estimated by the ratio

$$D^{th}\equiv D_{LS}/D_S.$$

(35)

A corrective parameter f is often introduced in Equation (32) to take into account possible systematic differences among systems (e.g., elliptical instead of spherical profile for the lens halo, line-of-sight stellar velocity dispersion as opposed to the dark matter halo velocity dispersion, and steeper mass distribution profile; see, for example [54,94]).

3.6. Ionized Gas in Starburst Galaxies

Authors ([57,58,59,60,61], and references therein) have argued that the correlation between the measured luminosity L and the inferred velocity dispersion $\sigma$ of the ionized gas (e.g., $H\beta$, $H\alpha$, $\left[OIII\right]$ emission lines) in extreme starburst galaxies (i.e., containing a population of O and/or B stars) may be used as a cosmological tracer to constrain cosmological model parameters. Compilations provide apparent magnitude, emission line luminosity, and velocity dispersion (e.g., [61,62]), and the chi square function is estimated as

$${\chi }_{\mathrm{HIIG}}^2=A-B^2/C,$$

(36)

where

$$\begin{array}{ccc}A\hfill & =& \sum _{i=1}^{153}{\left(\frac{{\mu }_{th}\left(z_i\right)-{\mu }_{obs}^i}{{\sigma }_{{\mu }_{obs}^i}}\right)}^2,\hfill \end{array}$$

(37)

$$\begin{array}{ccc}B\hfill & =& \sum _{i=1}^{153}\frac{{\mu }_{th}\left(z_i\right)-{\mu }_{obs}^i}{{\sigma }_{{\mu }_{obs}^i}},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}C\hfill & =& \sum _{i=1}^{153}\frac{1}{{\left({\sigma }_{{\mu }_{obs}^i}\right)}^2}.\hfill \end{array}$$

(39)

In the above expressions, ${\mu }_{obs}^i\pm {\sigma }_{obs}^i$ is the observed distance modulus with its uncertainty at redshift $z_i$. The theoretical estimate at the redshift z is obtained by using (9) and

$${\mu }_{th}\left(z\right)={\mu }_0+5log\left[d_L\left(z\right)\right],$$

(40)

where ${\mu }_0$ is a nuisance parameter that has been marginalized.

3.7. Joint Analysis

Testing the consistency of a given cosmological model requires a range of observational samples with complementary sensitivity to the cosmological parameters. The constraint on those parameters is usually achieved by combining several samples also known as joint analysis.

For instance, a Bayesian Markov Chain Monte Carlo (MCMC) analysis is able to constrain the phase-space parameter $\Theta$ of a cosmological model given a number of cosmological samples. In general, the procedure consists of using emcee Python package [95] for two phases: the burn-in and the MCMC. The first is performed with a certain number of steps to achieve the convergence of the chains according to the Gelman–Rubin criterion [96]. The second phase is performed with an appropriate number of steps for sampling the confidence regions. Additionally, for each model, the  priors (flat or Gaussian) of the parameters are chosen according to values provided in the literature. For the joint analysis, the figure-of-merit to be optimized is given by

$${\chi }_{\mathrm{Joint}}^2=\sum {\chi }_{\mathrm{data}},$$

(41)

where the ${\chi }_{\mathrm{data}}$ represents the name of the different samples. In general, the joint analysis is calculated using the combination of at least three data samples, but ideally it should contain all of them.

4. Taxonomy of Dark Energy Models

This section is dedicated to describing the different constrictions through the samples mentioned previously for the different DE models studied in the literature. We divide our study into DE models linked to a fluid with the capability of accelerating the Universe and models in which the Einstein field equations of General Theory of Relativity are modified.

Among the featured models, the first category includes the following: constant DE equation of state, Parameterizations of DE, Chaplygin fluid, Viscous models, and Phenomenological (Generalized) emergent DE (PEDE and GEDE) [37,38,39]. The second category includes the following: Brane models (with constant and variable tension), Unimodular Gravity, Einstein–Gauss–Bonet and Cardassian models [40,41,42,43,44,45,46,47,48,49,97].

4.1. Accelerating Universe Fluids

In this subsection we summarize all those models that involve a fluid enabling a late acceleration without modifications to GTR.

4.1.1. The $\Lambda$CDM Model

The $\Lambda$CDM is the consensus model dominated by a cold dark matter and a cosmological constant component with subdominant species of baryons and relativistic particles (photons and neutrinos), which not only the most favoured by diverse observations but also the simplest. The dimensionless Friedmann function is given by Equation (6), which reads

$$E{\left(z\right)}^2={\Omega }_{m0}{(z+1)}^3+{\Omega }_{r0}{(z+1)}^4+{\Omega }_{\Lambda 0}.$$

(42)

The flatness condition is satisfied and written in the form

$$1={\Omega }_{m0}+{\Omega }_{r0}+{\Omega }_{\Lambda 0}.$$

(43)

Therefore, the CC density parameter can be written in terms of matter, while radiation takes the form

$${\Omega }_{r0}=2.469\times {10}^{-5}{h}^{-2}(1+0.2271N_{eff}),$$

(44)

where $N_{eff}=3.04$ is the standard number of relativistic species [83] and $h=H_0/100$km s${}^{-1}$ Mpc${}^{-1}$, where $H_0=67.66\pm 0.42$ km s${}^{-1}$Mpc${}^{-1}$ with Planck [15], while $H_0=73.2\pm 1.3$ km s${}^{-1}$Mpc${}^{-1}$ with Riess [98], presenting a tension between the observations and known as $H_0$ tension. Regarding the matter density parameter, the value is constrained as ${\Omega }_{m0}=0.3111\pm 0.0056$, using Planck satellite [15], which is a combination of baryonic and dark matter. Despite the model achievements, $\Lambda$CDM is afflicted with several problems, like the nature of CC [24,25], the ${\sigma }_8$ tension [29,30], and the $H_0$ tension [31,32,33].

4.1.2. The $\omega$CDM Model

This model is the simplest extension of the CC. The dark energy has a constant equation of state (EoS), but it deviates from $w=-1$ and should satisfy $\omega <-1/3$ to obtain an accelerated Universe. The equation $E\left(z\right)$ can be written as:

$$\begin{array}{c}\hfill E{\left(z\right)}_{\omega }^2={\Omega }_{m0}{(1+z)}^3+{\Omega }_{r0}{(1+z)}^4+(1-{\Omega }_{m0}-{\Omega }_{r0}){(1+z)}^{3(1+\omega )},\end{array}$$

(45)

The $\omega$CDM constraints are obtained assuming flat priors on the parameters. Table 1 presents the mean values for the $\omega$CDM parameters using using independently OHD (31 data from cosmic chronometers), CMB (Planck), and SNIa (Pantheon) and the joint of them. Figure 1 shows the mean value curve of the $H\left(z\right)$ function (top panel) for the wCDM model using these data. The bottom panel shows the constraint contours at $1\sigma ,2\sigma$, and $3\sigma$ confidence levels. Notice that, although SNIa data are not able to constrain the h parameter, the three different samples provide consistent constraints on the ${\Omega }_{m0}-\omega$ space. Indeed, the joint analysis provides stringent constraints, which are consistent with those of the $\Lambda$CDM model.

Table 1. Mean values for the $\omega$CDM parameters using the samples OHD, SNIa, CMB (Planck), and the joint of them.

$\mathit{\omega }\mathit{CDM}$
Data	${\mathbf{\chi }}_{\mathit{min}}^{\mathbf{2}}$	${\mathbf{\Omega }}_{\mathit{m}}$	${\mathit{w}}_{\mathbf{0}}$	$\mathit{h}$
OHD	$15.24$	${0.30}_{-0.06}^{+0.06}$	$-{1.19}_{-0.49}^{+0.51}$	${0.69}_{-0.05}^{+0.06}$
SNIa	$1035.92$	${0.32}_{-0.08}^{+0.06}$	$-{1.06}_{-0.23}^{+0.20}$	${0.60}_{-0.27}^{+0.26}$
CMB	$0.05$	${0.29}_{-0.05}^{+0.06}$	$-{1.06}_{-0.22}^{+0.21}$	${0.69}_{-0.06}^{+0.06}$
Joint	$1050.59$	${0.30}_{-0.01}^{+0.01}$	$-{1.02}_{-0.03}^{+0.03}$	${0.68}_{-0.01}^{+0.01}$

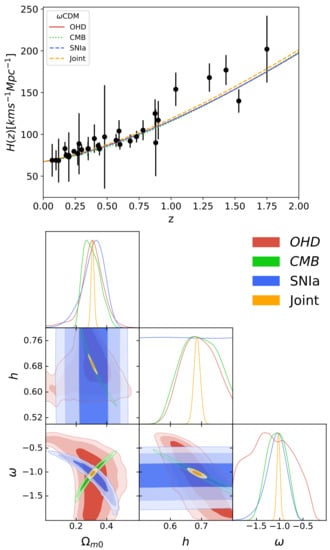
Figure 1. Top panel: Best fit curve of the $H\left(z\right)$ function for the $\omega$CDM model using observational Hubble parameter data (OHD) (cosmic chronometers), cosmic microwave background (CMB) (Planck), and SNIa (Pantheon) data and the joint analysis of them. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) confidence levels.

4.1.3. Dark Energy Parameterizations

The natural alternatives to the $\omega$CDM is to consider DE to vary with redshift through a parameterization $w\left(z\right)$. These functions are proposed phenomenologically to mimic the behavior of the CC at late times. In the following, we present some of these models for a Universe containing dark and baryonic matter, radiation, and dark energy.

• The Chevallier–Polarski–Linder parametrization (CPL) [99,100]. An approach to study dynamical DE models is through a parametrization of its EoS. The dimensionless Hubble parameter $E\left(z\right)$ for this Universe is given by

  $$E^2\left(z\right)={\Omega }_{m0}{(1+z)}^3+{\Omega }_{r0}{(1+z)}^4+{\Omega }_{de}{f}_{de}\left(z\right),$$

  (46)
  We compute ${\Omega }_{r0}$ in the same form as is given by Equation (44).
  The density parameter for DE is written as ${\Omega }_{de}=1-{\Omega }_{m0}-{\Omega }_{r0}$, and the function $f_{de}\left(z\right)$ depends on $w\left(z\right)$ as

  $$f_{de}\left(z\right)\equiv \frac{{\rho }_{de}\left(z\right)}{{\rho }_{de}\left(0\right)}=\exp \left(3{\int }_0^z\frac{1+w\left(z\right)}{1+z}\mathrm{dz}\right),$$

  (47)

  where ${\rho }_{de}\left(z\right)$ is the energy density of DE at redshift z, and ${\rho }_{de}\left(0\right)$ is its present value. One of the most popular parameterizations is proposed by [99,101], and reads as

  $$\omega \left(z\right)={\omega }_0+{\omega }_1\frac{z}{(1+z)},$$

  (48)

  where ${\omega }_0$ is the EoS at redshift $z=0$ and ${\omega }_1{=\mathrm{d}w/\mathrm{d}z|}_{z=0}$. Although this function is widely used, it has a divergence problem when $z=-1$. The function $f_{de}\left(z\right)$ for the CPL parametrization is

  $$f_{de}{\left(z\right)}_{CPL}^2={(1+z)}^{3(1+{\omega }_0+{\omega }_1)}exp\left(\frac{-3{\omega }_{1}z}{1+z}\right),$$

  (49)
  The h, ${\Omega }_{m0}$, ${\omega }_0$, and ${\omega }_1$ parameters are constrained using the OHD from cosmic chronometers [66]. Figure 2 shows the reconstruction of $H\left(z\right)$ using the best fit of the MCMC analysis: $h={0.73}_{-0.08}^{+0.10}$, ${\Omega }_{m0}={0.29}_{-0.08}^{+0.09}$, ${\omega }_0=-{1.51}_{-0.91}^{+0.80}$, and ${\omega }_1=-{0.20}_{-2.53}^{+2.38}$. The confidence contours of the parameters at $1\sigma ,2\sigma$, and $3\sigma$ are also shown.
  

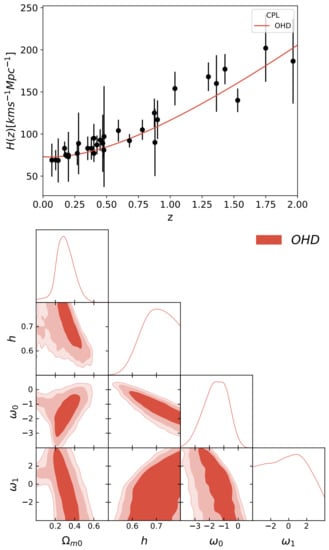  Figure 2. Top panel: Best fit curve of the $H\left(z\right)$ function for the Chevallier–Polarski–Linder (CPL) parameterization using OHD (cosmic chronometers). Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) confidence levels for OHD data.
• The Jassal-Bagla-Padmanabhan (JBP) parametrization. Jassal et al. [102] proposed the following ansatz to parametrize the dark energy EoS,

  $$\omega \left(z\right)={\omega }_0+{\omega }_1\frac{z}{{(1+z)}^2},$$

  (50)

  where ${\omega }_0$ is the EoS at redshift $z=0$ and ${\omega }_1{=(\mathrm{d}w/\mathrm{d}z)|}_{z=0}$. The function $f_{de}\left(z\right)$ is

  $$f_{de}{\left(z\right)}_{JBP}={(1+z)}^{3(1+{\omega }_0)}exp\left(\frac{3{\omega }_1{z}^2}{2{(1+z)}^2}\right),$$

  (51)
• The Barbosa–Alcaniz (BA) parametrization. Barboza and Alcaniz [103] considered a EoS given by:

  $$w\left(z\right)=w_0+w_1\frac{z(1+z)}{1+z^2}.$$

  (52)
  This ansatz behaves linearly at low redshifts as $w_0+w_1$, and $w\to w_0+w_{1}z$ when $z\to \infty$. In addition, $w\left(z\right)$ is well-behaved for all epochs of the Universe. For instance, the DE dynamics in the future, at $z=-1$, can be investigated without dealing with a divergence. Solving the integral in Equation (47) and using Equation (52) results in:

  $$f_{de}{\left(z\right)}_{BA}={(1+z)}^{3(1+w_0)}{(1+z^2)}^{\frac{3}{2}{w}_1}.$$

  (53)
• Feng–Shen–Li–Li (FSLL, [104]) parametrizations.- The authors suggested two dark energy EoS given by:

  $$w\left(z\right)=w_0+w_1\frac{z}{1+z^2},\mathrm{FSLLI}$$

  (54)

  $$w\left(z\right)=w_0+w_1\frac{z^2}{1+z^2}\mathrm{FSLLII}.$$

  (55)
  Both functions have the advantage of being divergence-free throughout the entire cosmic evolution, even at $z=-1$. At low redshifts, $w\left(z\right)$ behaves as $w_0+w_{1}z$ and $w_0+w_1{z}^2$ for FSLLI and FSLLII, respectively. In addition, when $z\to \infty$, the EoS has the same value ($w_0$) as the present epoch for FSLLI and $w_0+w_1$ for FSLLII. Using Equations (54) and (55) to solve Equation (47) leads to:

  $$f_{de\pm }\left(z\right)={(1+z)}^{3(1+w_0)}\exp \left[\pm \frac{3w_1}{2}\arctan \left(\mathrm{z}\right)\right]{\left(1+z^2\right)}^{\frac{3}{4}{w}_1}{\left(1+z\right)}^{\mp \frac{3}{2}{w}_1},$$

  (56)

  where $f_{+}$ and $f_{-}$ correspond to FSLLI and FSLLII, respectively.
• Sendra–Lazkoz (SL, [105]) introduced new polynomial parameterizations to reduce the parameter correlation, so they can be better constrained by the observations at low redshifts. One of these parameterizations is given by:

  $$w\left(z\right)=-1+c_1\left(\frac{1+2z}{1+z}\right)+c_2{\left(\frac{1+2z}{1+z}\right)}^2,$$

  (57)

  where the constants are defined as $c_1=(16w_0-9w_{0.5}+7)/4$, and $c_2=-3w_0+(9w_{0.5}-3)/4$, and $w_{0.5}$ is the value of the EoS at $z=0.5$. This $w\left(z\right)$ function is well-behaved at higher redshifts as $(-1-8w_0+9w_{0.5})/2$. The substitution of Equation (57) into Equation (47) results in the following:

  $$f_{de}{\left(z\right)}_{SL}={(1+z)}^{\frac{3}{2}(1-8w_0+9w_{0.5})}\exp \left[\frac{3z\left\{w_0(52z+40)-9w_{0.5}(5z+4)+7z+4\right\}}{8{(1+z)}^2}\right].$$

  (58)
  Notice that, although DE parameterizations are common and they could solve the coincidence problem, there is not a unique way to choose the form of the function. Furthermore, in many cases, there are not strong arguments to justify the functional form by an association with a first-principles theory of quantum fields or gravity. A different approach, which is model-independent, consists of, for example investigating the cosmographic parameters that characterize the kinematics of the cosmic expansion (e.g., [106,107,108,109,110]). Some authors have used the Hubble parameter, the deceleration parameter ($q\left(a\right)=-\ddot{a}a/{\dot{a}}^2$), or even higher-order derivatives of the scale factor a, such as Jerk and Snap (e.g., [111,112]). By estimating these cosmographic parameters using cosmological data, it is possible to associate its features to a given DE model (see [111,113,114,115,116,117]).
  The cosmological constraints for the aforementioned models are obtained assuming flat priors on the DE parameters and a Gaussian prior on h. Table 2 provides the mean values for the ${\Omega }_m$, $w_0$, and $w_1$ ($w_{0.5}$) parameters of the JBP, BA, FSLLI, FSLLII, and SL DE parameterizations using the joint of the OHD sample (34 data points from DA and BAO measurements) in the redshift range $0.07<z<2.3$ [118], distance posteriors from Planck [119], and different BAO measurements (see details in [120]). Figure 3 shows the reconstruction of $H\left(z\right)$ for these parametrizations using the parameter mean values (top panel) and the $1\sigma$ and $3\sigma$ confidence contour of the cosmological constraints (bottom panel). Notice that the DE parameterizations are consistent for ${\Omega }_{m0}$ and ${\omega }_0$.
  Table 2. Mean values for the ${\Omega }_m$, $w_0$, and $w_1\left(w_{0.5}\right)$ parameters using the joint analysis of OHD, CMB, and BAO data for the JBP, BA, FSLLI, FSLLII, and SL DE parameterizations (see [120]).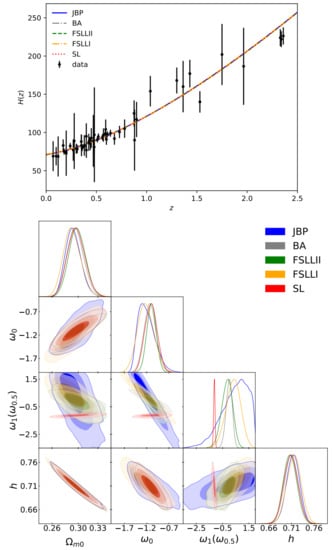

  DE Parametrizations
  Model	${\mathbf{\chi }}_{\mathit{min}}^{\mathbf{2}}$	${\Omega }_{\mathit{m}}$	${\mathit{w}}_{\mathbf{0}}$	${\mathit{w}}_{\mathbf{1}}\left({\mathit{w}}_{\mathbf{0.5}}\right)$	$\mathit{h}$
  JBP	$67.22$	${0.29}_{-0.01}^{+0.01}$	$-{1.22}_{-0.16}^{+0.21}$	${0.55}_{-1.18}^{+0.91}$	${0.71}_{-0.014}^{+0.014}$
  BA	$67.46$	${0.29}_{-0.01}^{+0.01}$	$-{1.12}_{-0.13}^{+0.13}$	${0.007}_{-0.24}^{+0.22}$	${0.71}_{-0.015}^{+0.015}$
  FSLLI	$67.01$	${0.29}_{-0.01}^{+0.01}$	$-{1.22}_{-0.17}^{+0.18}$	${0.32}_{-0.57}^{+0.54}$	${0.71}_{-0.015}^{+0.015}$
  FSLLII	$67.61$	${0.29}_{-0.01}^{+0.01}$	$-{1.09}_{-0.10}^{+0.10}$	$-{0.13}_{-0.44}^{+0.39}$	${0.70}_{-0.014}^{+0.014}$
  SL	$68.52$	${0.29}_{-0.01}^{+0.01}$	$-{1.10}_{-0.13}^{+0.13}$	$-{1.13}_{-0.05}^{+0.05}$	${0.70}_{-0.015}^{+0.015}$

  

  Figure 3. Top panel: Best fit curve of $H\left(z\right)$ for the DE parameterization functions from the joint analysis of OHD, CMB, and BAO measurements. Bottom panel: 2D contours of the free model parameters at $1\sigma$, and $3\sigma$ (from darker to lighter color bands) confidence levels using this joint analysis.

4.1.4. Chaplygin-Like Fluid

One point of view for studying the DE and DM problems is through the unified dark fluids approach, which is known as Chaplygin gas (see, for instance, [121,122,123,124,125]). An example of this is the well-known generalized Chaplygin gas [126,127] described by the EoS $p=-A{\rho }^{-\alpha }$, where A and $\alpha$ are constants (the case $\alpha =1$ is the original model proposed by S. Chaplygin [128]). This fluid behaves as DM at early epoch and DE at late times and may have its origin from the Nambu–Goto d-brane action. Although this interesting formulation reproduces the accelerated expansion of the Universe, it presents flaws to describe the CMB anisotropies [129]. In this context, an alternative to Chaplygin gas was proposed by Hova and Yang [130], dubbed generalized Chaplygin gas-like, with EoS

$$p_{df}=-{\rho }_{df}+{\rho }_{df}\mathrm{sinc}(\mu \pi {\rho }_{df0}/{\rho }_{df}),$$

(59)

where $\mathrm{sinc}\left(x\right)\equiv sin\left(x\right)/x$ and ${\rho }_{df}$ is the dark fluid density, which plays the role of the mixture of DE and DM densities. In this case, $\mu$ is a dimensionless parameter constrained as $\mu \gtrsim 0.688$ to be consistent with the stellar age bound (Hova and Yang Hova and Yang [130] adopt $\mu \approx 0.876$ to obtain a Universe age of $t\approx 13.7$ Gyrs) and ${\rho }_{df0}$ is the present energy density of this fluid, constrained in terms of the density parameter as ${\Omega }_{df0}\sim 0.96$ in Hova and Yang [130]. It behaves as a CC in the late stage of the universe and as DM at the matter domination epoch. The evolution of the EoS of the dark fluid is given by

$${\omega }_{df}\left(z\right)\equiv -1+\frac{{(z+1)}^{3}tan\left(\lambda \right)}{[{(z+1)}^6+{tan}^2\lambda ]\xi \left(z\right)},$$

(60)

where $\xi \left(z\right)\equiv \arctan [{(z+1)}^{-3}tan\lambda ]$ and $\lambda \equiv \mu \pi /2$. To explore the universe dynamics in this context, we consider a general FLRW metric including baryonic and radiation components; hence, we write the Friedmann and acceleration equations as

$$\begin{array}{ccc}{H}^2\hfill & =& \frac{8\pi G}{3}\left({\rho }_{df}+\sum _i{\rho }_i\right)-\frac{k}{a^2},\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\frac{\ddot{a}}{a}\hfill & =& -\frac{4\pi G}{3}\left\{\left[3\mathrm{sinc}\left(\frac{2\lambda {\rho }_{df0}}{{\rho }_{df}}\right)-2\right]{\rho }_{df}+\sum _i(1+3{\omega }_i){\rho }_i\right\},\hfill \end{array}$$

(62)

From Equation (6) we have [130,131]

$$E{\left(z\right)}^2=\frac{\lambda {\Omega }_{df0}}{\xi \left(z\right)}+\sum _i{\Omega }_{i0}{(z+1)}^{3(1+{\omega }_i)}+{\Omega }_k{(z+1)}^2,$$

(63)

where ${\Omega }_{df0}\equiv 8\pi G{\rho }_{df0}/3H_0^2$ is the density parameter associated with the Chaplygin gas-like fluid, ${\Omega }_{i0}$ and ${\omega }_i$ are the density parameters and the EoS for baryonic matter and radiation (according to Equation (44)), and ${\Omega }_k\equiv -k/H_0^2$ is the curvature density parameter and $H_0=h\times 100\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$. In addition, from (7), we have the constraint ${\Omega }_{df0}+{\Omega }_{b0}+{\Omega }_{r0}=1-{\Omega }_k$.

Figure 4 shows the best fit curve (top panel) for the Chaplygin-like gas when the curvature term is neglected using the OHD, SNIa and OHD+SNIa (Joint) samples. Additionally, 2D contours at $1\sigma$, $2\sigma$, and $3\sigma$ confidence level (CL) and 1D posterior distribution of the free parameters are displayed for each sample. Table 3 presents the best fit values and their uncertainties at $1\sigma$ for the model free parameters.

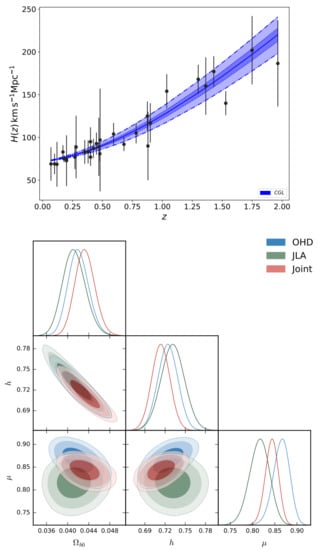
Figure 4. Top panel: Best fit curve of Chaplygin-like gas and its uncertainty at $1\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using DA OHD, SNIa (JLA), and OHD+SNIa (Joint) data. Adapted from [131].

Table 3. Mean values for the model parameters (${\Omega }_{b0}$, h, $\mu$) derived from OHD and SNIa measurements for a flat universe (see [131]).

Data Set	OHD	JLA	Joint
${\chi }_{min}^2$	$14.9$	$690.8$	$706.7$
${\Omega }_{b0}$	${0.042}_{-0.002}^{+0.002}$	${0.041}_{-0.002}^{+0.002}$	${0.043}_{-0.002}^{+0.002}$
h	${0.724}_{-0.015}^{+0.015}$	${0.724}_{-0.017}^{+0.018}$	${0.714}_{-0.014}^{+0.014}$
$\mu$	${0.865}_{-0.019}^{+0.018}$	${0.816}_{-0.023}^{+0.021}$	${0.843}_{-0.015}^{+0.014}$
a	-	${0.141}_{-0.007}^{+0.007}$	${0.142}_{-0.007}^{+0.007}$
b	-	${3.11}_{-0.08}^{+0.08}$	${3.12}_{-0.08}^{+0.08}$
$M_b^1$	-	$-{19.00}_{-0.06}^{+0.06}$	$-{19.01}_{-0.04}^{+0.04}$
${\delta }_M$	-	${0.07}_{-0.02}^{+0.02}$	${0.07}_{-0.02}^{+0.02}$

4.1.5. Viscous Model

The accelerated expansion of the Universe may be also described by considering dissipative effects in the Universe components, mainly in the matter component. The bulk viscosity coefficient, which satisfies the cosmological principle, is introduced in the energy-momentum tensor, Equation (3), as an effective pressure as $p\to \tilde{p}=p+\Pi$ where $\Pi =-3\xi H$ based on the Eckart formalism. Under this argument, several models for $\xi$ have been addressed, such as:

• $\xi ={\xi }_0{\rho }_m^s$. This model, where ${\rho }_m$ is the energy density of dust matter and ${\xi }_0,s$ are constants, is probably the simplest one that successfully reproduces the late accelerated stage of the Universe. Some studies that consider a single fluid in the Universe are presented in [132] (see, for example [133], for a case in a causal theory). Additionally, there are other works that include several components such as radiation and DE [65].
• $\xi =\xi \left(z\right)$. In spite of the success of the previous model at late epochs of the Universe, it has problems in early epochs because $\xi$ diverges. This motivates the use of alternative viscosity models such as those proposed by [134], in particular polynomial forms of the redshift.
• $\xi =Acosh\left(b{E}^{-n}\right)$ and $\xi =Atanh\left(b{E}^{-n}\right)$. Alternatively, more complex models are investigated in [134] by proposing the viscosity as a hyperbolic function of the dimensionless Hubble parameter E.

When a single dust matter fluid is contained in the Universe, the dimensionless Hubble parameter is obtained using Equation (6). Then, we obtain the following system to be solved

$$-2(1+z)\frac{dE\left(z\right)}{dz}+3E\left(z\right)=9\lambda \left(z\right),$$

(64)

where $\lambda \left(z\right)=\xi \left(z\right){\kappa }^2/3H_0^2$. For $\lambda \left(z\right)={\lambda }_0+{\lambda }_1{(1+z)}^n$, we obtain,

$$E\left(z\right)={\lambda }_2{(1+z)}^{3/2}-\frac{{\lambda }_1}{2n-3}{(1+z)}^n+\frac{{\lambda }_0}{3},$$

(65)

where

$${\lambda }_2=1+\frac{{\lambda }_1}{2n-3}-\frac{{\lambda }_0}{3}.$$

(66)

Figure 5 shows the best fit curve of $H\left(z\right)$ (top panel) using non-homogeneous OHD+SNIa data. Two-dimensional contours at at $1\sigma$, $2\sigma$, and $3\sigma$ CL of the free model parameters are also displayed at the bottom panel for OHD, SNIa, OHD+SNIa data. Additionally, we include the best fit curves and 2D contours when $\lambda \left(z\right)=1/3tanh\left(b{E}^{-n}\right)$ and $\lambda \left(z\right)=1/3cosh\left(b{E}^{-n}\right)$. Table 4 and Table 5 show the best fit values and their uncertainties at $1\sigma$ of the single fluid models.

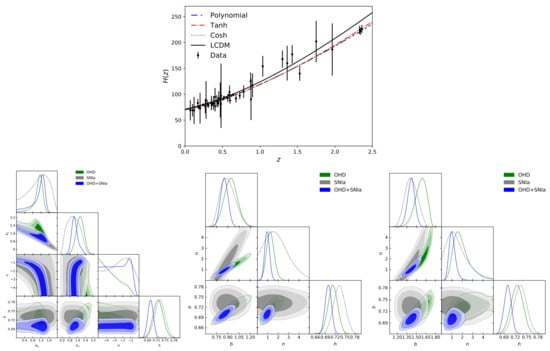
Figure 5. Top panel: Best fit curves of $H\left(z\right)$ in the single viscous fluid model for different bulk viscosity coefficient and its uncertainty at $1\sigma$ and $3\sigma$. Bottom panel: 2D contours of the free model parameters for the polynomial (left), tanh (middle), cosh (right) models, respectively, at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL and 1D posterior distributions of the model parameters using nonhomogeneous OHD, SNIa, OHD+SNIa data. Figure adapted from [134].

Table 4. Best fitting parameters of the polynomial model (see [134] for details).

Data	${\mathit{\chi }}^2$	${\mathit{\lambda }}_0$	${\mathit{\lambda }}_1$	n	h	$\mathcal{M}$
OHD	$15.1$	${1.112}_{-0.256}^{+0.154}$	${1.844}_{-0.408}^{+0.399}$	$-{3.628}_{-0.990}^{+1.534}$	${0.726}_{-0.017}^{+0.017}$	-
SNIa	$1027.9$	${1.129}_{-0.618}^{+0.459}$	${1.159}_{-0.668}^{+0.702}$	$-{2.351}_{-1.712}^{+1.374}$	${0.732}_{-0.017}^{+0.017}$	${5.741}_{-0.055}^{+0.053}$
OHD+SNIa	$1053.2$	${1.183}_{-0.487}^{+0.177}$	${1.273}_{-0.281}^{+0.363}$	$-{2.656}_{-1.596}^{+1.494}$	${0.700}_{-0.009}^{+0.009}$	${5.634}_{-0.023}^{+0.023}$

Table 5. Best fitting parameters of the hyperbolic models (see [134] for details).

Tanh Model
Data	${\chi }^2$	b	n	h	$\mathcal{M}$
OHD	$28.8$	${0.937}_{-0.087}^{+0.088}$	${1.230}_{-0.350}^{+0.376}$	${0.713}_{-0.015}^{+0.014}$	-
SNIa	$1026.3$	${0.894}_{-0.094}^{+0.109}$	${1.727}_{-1.005}^{+1.271}$	${0.733}_{-0.018}^{+0.018}$	${5.747}_{-0.056}^{+0.054}$
OHD+SNIa	$1055.7$	${0.853}_{-0.050}^{+0.050}$	${0.933}_{-0.222}^{+0.236}$	${0.699}_{-0.009}^{+0.009}$	${5.644}_{-0.023}^{+0.023}$
Cosh Model
Data	${\chi }^2$	b	n	h	$\mathcal{M}$
OHD	$26.7$	${1.580}_{-0.098}^{+0.084}$	${1.790}_{-0.605}^{+0.939}$	${0.724}_{-0.016}^{+0.016}$	-
SNIa	$1041.5$	${1.417}_{-0.096}^{+0.106}$	${1.348}_{-0.782}^{+1.225}$	${0.733}_{-0.017}^{+0.017}$	${5.747}_{-0.053}^{+0.051}$
OHD+SNIa	$1054.7$	${1.420}_{-0.059}^{+0.056}$	${1.014}_{-0.273}^{+0.339}$	${0.700}_{-0.010}^{+0.009}$	${5.640}_{-0.024}^{+0.023}$

A generalized form of the previous model (Equation (65)) considers one additional fluid to the dust matter component. The authors of [135] analyze the case that includes a DE component with EoS $w=-1$ to describe the late time stage of the Universe. Notice that the radiation component at this time can be considered negligible. In this case, the Hubble parameter is given by

$$\begin{array}{ccc}\hfill E\left(z\right)& =& \sqrt{\Omega \left(z\right)}\left[1+\frac{{\lambda }_0}{3\sqrt{{\Omega }_{de0}}}{sinh}^{-1}\left(\sqrt{\frac{{\Omega }_{de0}}{{\Omega }_{m0}{(1+z)}^3}}\right)\right.\hfill \\ & & \left.-\frac{{\lambda }_0}{3\sqrt{{\Omega }_{de0}}}{sinh}^{-1}\left(\sqrt{\frac{{\Omega }_{de0}}{{\Omega }_{m0}}}\right)\right]\hfill \\ & & +\sqrt{\Omega \left(z\right)}\left[\frac{{\lambda }_1}{2n\sqrt{{\Omega }_{de0}}}{(1+z)}^n\times \right.\hfill \\ & & \left.{}_2{F}_1\left(\frac{1}{2},\frac{n}{3},1+\frac{n}{3},-\frac{{\Omega }_{m0}{(1+z)}^3}{{\Omega }_{de0}}\right.\right)\hfill \\ & & \left.-\frac{{\lambda }_1}{2n\sqrt{{\Omega }_{de0}}}{}_2{F}_1\left(\frac{1}{2},\frac{n}{3},1+\frac{n}{3},-\frac{{\Omega }_{m0}}{{\Omega }_{de0}}\right)\right],\hfill \end{array}$$

(67)

where $E\left(0\right)=\Omega \left(0\right)=1$, $\Omega \left(z\right)={\Omega }_{m0}{(1+z)}^3+{\Omega }_{de0}$, and ${}_2{F}_1$ is the hypergeometric function. Based on the results obtained in [134], Equation (67) is obtained assuming $n=-2$. It is straightforward that the case for a constant viscosity coefficient is obtained when ${\lambda }_1=0$. Figure 6 displays the best fit curves (top panel) of Equation (67) over OHD data, obtained by confronting to OHD+SNIa+SLS data, and 2D contours at $1\sigma$, $2\sigma$, and $3\sigma$ CL of the free model parameters are presented at the bottom panel for OHD, SNIa, SLS, and OHD+SNIa+SLS data. Table 6 shows the best fit values and their uncertainties at $1\sigma$ of the free model parameters.

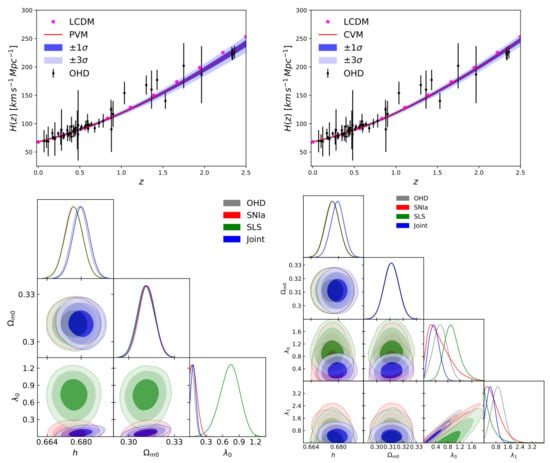
Figure 6. Top panel: Best fit curve of viscous fluid model and its uncertainty at $1\sigma$ and $3\sigma$ and $\Lambda$CDM. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL and 1D posterior distribution of the model parameters using nonhomogeneous OHD, SNIa, SLS and OHD+SNIa+SLS (Joint) data. Figure adapted from [135].

Table 6. Best fitting values of the free model parameters (see [135] for details).

Sample	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{m}0}$	${\mathit{\lambda }}_0$	${\mathit{\lambda }}_1$	$\mathcal{M}$
${\xi }_0=\mathrm{Constant}$
OHD	$25.9$	${0.679}_{-0.004}^{+0.004}$	${0.312}_{-0.005}^{+0.005}$	${0.053}_{-0.035}^{+0.047}$	–	–
SNIa	$1027.1$	${0.676}_{-0.004}^{+0.004}$	${0.312}_{-0.005}^{+0.005}$	${0.080}_{-0.072}^{+0.071}$	–	$-{19.400}_{-0.016}^{+0.016}$
SLS	$602.3$	${0.677}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.737}_{-0.188}^{+0.175}$	–	–
Joint	$1684.1$	${0.680}_{-0.004}^{+0.004}$	${0.311}_{-0.005}^{+0.006}$	${0.071}_{-0.040}^{+0.047}$	–	$-{19.400}_{-0.012}^{+0.012}$
${\xi }_0=\mathrm{Polynomial}$
OHD	$20.9$	${0.676}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.551}_{-0.228}^{+0.237}$	${0.929}_{-0.401}^{+0.412}$	–
SNIa	$1044.5$	${0.676}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.461}_{-0.280}^{+0.441}$	${0.580}_{-0.395}^{+0.620}$	$-{19.400}_{-0.019}^{+0.019}$
SLS	$603.6$	${0.676}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.927}_{-0.235}^{+0.284}$	${0.312}_{-0.231}^{+0.484}$	–
Joint	$1668.8$	${0.679}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.347}_{-0.164}^{+0.183}$	${0.465}_{-0.263}^{+0.301}$	$-{19.400}_{-0.014}^{+0.014}$

4.1.6. Interacting Viscous Models

A generalized case of the viscous models presented in the previous section is to consider a flat FLRW Universe that contains a non-perfect fluid as dust matter (dm) component that interacts with a perfect fluid as the DE component, together with the radiation fluid. Similarly, through the energy-momentum tensor, Equation (3), the viscous term is included in the field equations by changing $p\to \tilde{p}=p+\Pi$ as the sum of the total barotropic pressure of the fluids (p) and the bulk viscosity coefficient ($\Pi$), where $\rho$ is the energy density of the fluid and $u_{\mu }$ is the associated four-velocity. Inspired by the viscosity behavior in fluid mechanics that is proportional to the speed, we assume $\Pi =-3\zeta H$. Furthermore, the matter component and DE interact through an energy exchange term Q and a viscosity effect encoded in the terms containing the bulk viscosity coefficient $\zeta$. In this approach, the Friedmann, continuity, and acceleration equations are [65]

$$\begin{array}{ccc}& & H^2=\frac{8\pi G}{3}\left({\rho }_r+{\rho }_{dm}+{\rho }_{de}\right),\hfill \end{array}$$

(68)

$$\begin{array}{ccc}& & {\dot{\rho }}_r+4H{\rho }_r=0,\hfill \end{array}$$

(69)

$$\begin{array}{ccc}& & {\dot{\rho }}_{dm}+3H{\rho }_{dm}=9H^2\zeta +Q,\hfill \end{array}$$

(70)

$$\begin{array}{ccc}& & {\dot{\rho }}_{de}+3{\gamma }_{de}H{\rho }_{de}=-Q,\hfill \end{array}$$

(71)

$$\begin{array}{ccc}& & 2\dot{H}-24\pi GH\zeta =-8\pi G\left({\rho }_{dm}+\frac{4}{3}{\rho }_r+{\gamma }_{de}{\rho }_{de}\right),\hfill \end{array}$$

(72)

where ${\rho }_r$, ${\rho }_{dm}$, and ${\rho }_{de}$ are the relativistic species, dust matter, and dark energy densities, respectively. Note that the DE component behaves as CC when ${\gamma }_{de}=0$. In particular, the typical ansatz for the viscosity coefficient is considered and given by

$$\zeta =\frac{\xi }{{\kappa }^2}{\left(\frac{{\rho }_{dm}}{{\rho }_{dm0}}\right)}^{1/2},$$

(73)

where ${\rho }_{dm0}$ is the dm density at present epoch and $\xi$ is a free parameter with units of $\left[\xi \right]=$[eV]. It is convenient to use the dimensionless parameter of $\xi$ defined as ${\xi }_0=\sqrt{3}\xi /\kappa {\rho }_{dm0}$. Additionally, the interacting term Q is considered to be [136]

$$Q=\beta H\frac{{\rho }_{de}{\rho }_{dm}}{{\rho }_{de}+{\rho }_{dm}},$$

(74)

where $\beta$ is a free parameter. It is straightforward that a Universe with only viscosity effects is obtained when $\beta =0$. Figure 7 shows the best fit curve (top panel) to OHD data for interacting viscous model (${\xi }_0\ne 0,\beta \ne 0$), viscous model ($\beta =0$), interacting model (${\xi }_0=0$) and $\Lambda$CDM, respectively. 2D contours at $1\sigma$, $2\sigma$, and $3\sigma$ CL and 1D posterior distributions of the free model parameters are presented at the bottom panel. Authors in [65] found that the energy density dynamics of the mentioned models are similar to the evolution of $\Lambda$CDM. Table 7 reports the best fit values and their uncertainties at $1\sigma$ for the free parameters of IVM, IM, VM, and LCDM models.

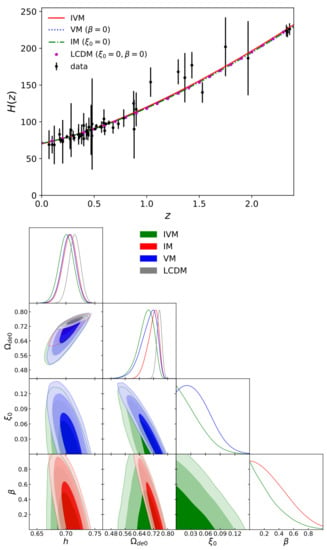
Figure 7. Top panel: Best fit curve of IVM and $\Lambda$CDM. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using nonhomogeneous OHD data. Figure adapted from [65].

Table 7. Best fit values for the free parameters of IVM, IM, VM, and LCDM models using the OHD sample. The uncertainties are at $1\sigma$ (see [65] for details).

Model	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{de}0}$	${\mathit{\xi }}_0$	$\mathit{\beta }$
IVM	$30.5$	${0.701}_{-0.013}^{+0.012}$	${0.682}_{-0.040}^{+0.040}$	${0.028}_{-0.020}^{+0.033}$	${0.200}_{-0.145}^{+0.260}$
IM	$29.2$	${0.707}_{-0.012}^{+0.011}$	${0.721}_{-0.037}^{+0.026}$	0	${0.283}_{-0.197}^{+0.290}$
VM	$29.1$	${0.705}_{-0.012}^{+0.011}$	${0.698}_{-0.054}^{+0.038}$	${0.040}_{-0.026}^{+0.035}$	0
LCDM	$28.9$	${0.715}_{-0.010}^{+0.010}$	${0.753}_{-0.015}^{+0.014}$	0	0

4.1.7. Phenomenological Emergent Dark Energy Model

The phenomenological emergent dark energy model (PEDE) was proposed by [37] and assumes that the DE is negligible at early times, emerging at late times. These kind of models are known as emergent and contribute to elucidate a solution to the $H_0$ tension. The idea consists in proposing a function that mimics the evolution of DE density parameter from a phenomenological point of view. The PEDE model has the same degrees of freedom as the $\Lambda$CDM model.

We consider a FLRW metric that contains matter (m, dark matter plus baryons), radiation (r), and PEDE. The dynamics of this Universe are described by the Friedmann Equation (5) and the continuity equation for each component as follows:

$$\begin{array}{ccc}& & {\dot{\rho }}_{DE}+3H(1+w_{DE}){\rho }_{DE}=0,\hfill \end{array}$$

(75a)

$$\begin{array}{ccc}& & {\dot{\rho }}_{\mathrm{m}}+3H(1+w_m){\rho }_{\mathrm{m}}=0,\hfill \end{array}$$

(75b)

$$\begin{array}{ccc}& & {\dot{\rho }}_r+3H(1+w_r){\rho }_r=0,\hfill \end{array}$$

(75c)

By solving Equations (75a)–(75c) we can rewrite Equation (6) in terms of the density parameters and redshift, as

$$H{\left(z\right)}^2=H_0^2\left[{\Omega }_{m0}{\left(1+z\right)}^3+{\Omega }_{r0}{\left(1+z\right)}^4+{\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)\right],$$

(76)

where ${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)={\Omega }_{\mathrm{DE}0}f\left(z\right)$, where ${\Omega }_{\mathrm{DE}}$ follows Equation (7). Notice that the authors of [37] propose a phenomenological functional form for $f\left(z\right)$, described by Equation (47) and hence ${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)$ as (where it is defined that ${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)\equiv {\rho }_{DE}/{\rho }_c^{\left(0\right)}$.)

$${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)={\Omega }_{\mathrm{DE}}^{\left(0\right)}\left[1-\tanh \left({log}_{10}(1+z)\right)\right],$$

(77)

where ${\tilde{\Omega }}_{\mathrm{DE}}\to 0$ at $z\to \infty$ and ${\tilde{\Omega }}_{\mathrm{DE}}\to 1.4$ at $z\to -1$, (where it is defined that ${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)\equiv {\rho }_{DE}/{\rho }_c^{\left(0\right)}$). Notice that

$$\begin{array}{cc}& {\Omega }_{DE}\left(z\right)=\frac{H_0^2}{H{\left(z\right)}^2}{\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)=\frac{H_0^2}{H{\left(z\right)}^2}{\Omega }_{\mathrm{DE}}^{\left(0\right)}\left[1-\tanh \left({log}_{10}(1+z)\right)\right],\end{array}$$

(78)

Therefore, the dimensionless Friedmann equation results as

$$\begin{array}{c}\hfill E{\left(z\right)}^2={\Omega }_{m0}{(1+z)}^3+{\Omega }_{r0}{(1+z)}^4+{\Omega }_{\mathrm{DE}0}[1-\tanh \left({log}_{10}(1+\mathrm{z})\right)],\end{array}$$

(79)

where the radiation density parameter at current epoch is calculated with Equation (44). To constrain the PEDE parameters, different OHD are employed: those from the DA technique (i.e., cosmic chronometers), and a full sample (homogeneous and non-homogeneous) of BAO measurements. Results of the constrictions are presented in Figure 8; the top panel illustrates the $H\left(z\right)$ reconstruction and the bottom panel the confidence contours for the case ${\Omega }_m\left(z_t\right)={\Omega }_{de}\left(z_t\right)$. Table 8 presents the constraints for the model free parameters together with the associated ${\chi }^2$ (see [39] for details).

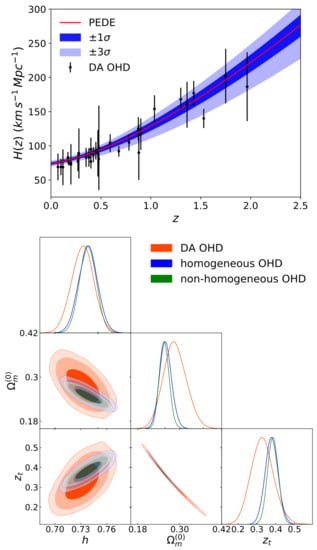
Figure 8. Top panel: Best fit curve of PEDE model and its uncertainty at $1\sigma$ and $3\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using DA, homogeneous, and non-homogeneous OHD data. Figure adapted from [39].

Table 8. Mean values of the free parameters for the PEDE model using homogeneous, non-homogeneous and DA OHD and a Gaussian prior on $h=0.7403\pm 0.0142$ [32]. The last column shows the estimated redsfhit $z_t$ using the condition ${\Omega }_m\left(z_t\right)={\Omega }_{DE}\left(z_t\right)$ (see [39], for details). The uncertainties reported correspond to $1\sigma$ confidence level. In parenthesis are the best fit values when a flat prior on h is considered in the region $[0,1]$.

Sample	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{m}}^{\left(0\right)}$	$\mathbf{\Delta }$	${\mathit{z}}_{\mathit{t}}$
PEDE
homogeneous OHD	$24.5$ ($24.5$)	${0.740}_{-0.011}^{+0.011}$ (${0.738}_{-0.018}^{+0.018}$)	${0.252}_{-0.015}^{+0.016}$ (${0.254}_{-0.022}^{+0.024}$)	$1.0$	0
non-homogeneous OHD	$32.1$ ($32.1$)	${0.740}_{-0.010}^{+0.010}$ (${0.740}_{-0.014}^{+0.014}$)	${0.249}_{-0.013}^{+0.013}$ (${0.249}_{-0.016}^{+0.018}$)	$1.0$	0
DA OHD	$14.7$ ($14.6$)	${0.739}_{-0.014}^{+0.014}$ (${0.723}_{-0.044}^{+0.049}$)	${0.319}_{-0.039}^{+0.035}$ (${0.329}_{-0.045}^{+0.057}$)	$1.0$	0

4.1.8. Generalized Emergent Dark Energy

Recently, the authors of [38] proposed a generalization for the PEDE model, also known as Generalized Emergent Dark Energy Model (GEDE) model, by introducing

$${\tilde{\Omega }}_{\mathrm{DE}}\left(z\right)={\Omega }_{\mathrm{DE}}^{\left(0\right)}\frac{1-\tanh \left({\Delta log}_{10}\left(\frac{1+z}{1+z_t}\right)\right)}{1+\tanh \left(\Delta {log}_{10}(1+z_t)\right)},$$

(80)

where $z_t$ is a transition redshift, ${\Omega }_{DE}\left(z_t\right)={\Omega }_{m0}{(1+z_t)}^3$, $\Delta$ is an appropriate dimensionless non-negative free parameter with the characteristic that if $\Delta =0$ the $\Lambda$CDM model is recovered, and when $\Delta =1$ and $z_t=0$ the previously PEDE model is obtained. As $z_t$ can be related to ${\Omega }_{m0}$ and $\Delta$, then $z_t$ is not a free parameter. Notice that the DE density parameter is given by

$$\begin{array}{cc}& {\Omega }_{\mathrm{DE}}=\frac{H_0^2}{H^2}(1-{\Omega }_{m0}-{\Omega }_{r0})\frac{1-\tanh \left({\Delta log}_{10}\left(\frac{1+z}{1+z_t}\right)\right)}{1+\tanh \left(\Delta {log}_{10}(1+z_t)\right)}.\end{array}$$

(81)

The GEDE Friedmann Equation is written as

$$\begin{array}{ccc}& & E\left(z\right)={\left[{\Omega }_{m0}{\left(1+z\right)}^3+{\Omega }_{r0}{\left(1+z\right)}^4+{\Omega }_{\mathrm{DE}}^{\left(0\right)}\frac{1-\tanh \left({\Delta log}_{10}\left(\frac{1+z}{1+z_t}\right)\right)}{1+\tanh \left(\Delta {log}_{10}(1+z_t)\right)}\right]}^{1/2}.\hfill \end{array}$$

(82)

The results obtained from the MCMC analysis using the same data as PEDE model are shown in Figure 9, presenting the best fit curve for $H\left(z\right)$ confronting with the OHD data and the constraints for ${\Omega }_m^{\left(0\right)}$ and $\Delta$, which is the free parameter for GEDE. Table 9 presents the constraints for all the free parameters together with their respective ${\chi }^2$ (see [39] for details).

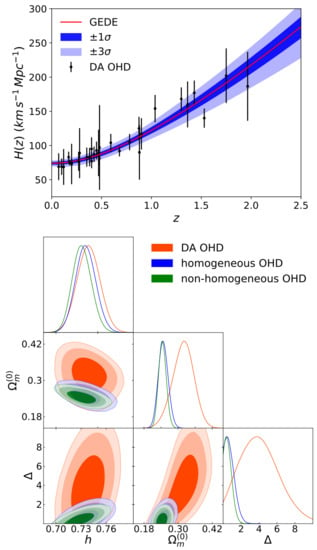
Figure 9. Top panel: Best fit curve of GEDE model and its uncertainty at $1\sigma$ and $3\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using DA, homogeneous and non-homogeneous OHD data. Figure adapted from [39].

Table 9. Mean values of the free parameters for GEDE model using homogeneous, non-homogeneous and DA OHD and a Gaussian prior on $h=0.7403\pm 0.0142$ [32]. The last column shows the estimated redsfhit $z_t$ using the condition ${\Omega }_m\left(z_t\right)={\Omega }_{DE}\left(z_t\right)$ (see [39] for details). The uncertainties reported correspond to $1\sigma$ confidence level. In parenthesis are the best fit values when a flat prior on h is considered in the region $[0,1]$.

Sample	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{m}}^{\left(0\right)}$	$\mathbf{\Delta }$	${\mathit{z}}_{\mathit{t}}$
GEDE
homogeneous OHD	$23.7$ ($23.0$)	${0.735}_{-0.012}^{+0.012}$ (${0.725}_{-0.020}^{+0.023}$)	${0.247}_{-0.017}^{+0.018}$ (${0.256}_{-0.022}^{+0.025}$)	${0.690}_{-0.457}^{+0.624}$ (${0.533}_{-0.390}^{+0.712}$)	${0.403}_{-0.057}^{+0.058}$ (${0.385}_{-0.056}^{+0.058}$)
non-homogeneous OHD	$30.2$ ($28.6$)	${0.731}_{-0.011}^{+0.012}$ (${0.718}_{-0.015}^{+0.017}$)	${0.245}_{-0.013}^{+0.014}$ (${0.255}_{-0.017}^{+0.018}$)	${0.539}_{-0.352}^{+0.470}$ (${0.332}_{-0.244}^{+0.472}$)	${0.417}_{-0.043}^{+0.044}$ (${0.403}_{-0.043}^{+0.043}$)
DA OHD	$14.7$ ($14.6$)	${0.739}_{-0.014}^{+0.014}$ (${0.723}_{-0.044}^{+0.048}$)	${0.319}_{-0.039}^{+0.036}$ (${0.329}_{-0.046}^{+0.057}$)	${3.930}_{-2.083}^{+2.304}$ (${3.264}_{-2.230}^{+3.258}$)	${0.183}_{-0.057}^{+0.094}$ (${0.174}_{-0.064}^{+0.083}$)

4.2. Modifications to General Theory of Relativity

In this subsection, we present models that modify the GTR in order to obtain a late Universe acceleration.

4.2.1. Constant Brane Tension

Brane world models are inspired by the seminal papers of [137,138] in which they assume a four-dimensional manifold called the brane immersed in a five dimensional Anti-d’Sitter space time called the bulk. The mentioned configuration is a way to understand the hierarchy problem but could alsobe extended to describe the cosmology. The main parameter of the theory is called the brane tension, which differentiates between the high- and low-energy physics involved and becomes a free parameter that needs to be constrained by different cosmological samples. For this model in particular, the brane tension is constant; hence, we call it a Constant Brane Tension (CBT) model.

First of all, we introduce the Einstein’s field equation projected onto the brane

$$G_{\mu \nu }+{\xi }_{\mu \nu }={\kappa }_{\left(4\right)}^2{T}_{\mu \nu }+{\kappa }_{\left(5\right)}^4{\Pi }_{\mu \nu }+{\kappa }_{\left(5\right)}^2{F}_{\mu \nu },$$

(83)

where $T_{\mu \nu }$ is defined in Equation (3) as the matter trapped in the brane, $G_{\mu \nu }$ is the classical Einstein’s tensor described by (1), and the rest of the terms in the right and left sides of this equation are explicitly given by:

$$\begin{array}{ccc}{\kappa }_{\left(4\right)}^2\hfill & =& 8\pi G_N=\frac{{\kappa }_{\left(5\right)}^4}{6}\lambda ,\hfill \end{array}$$

(84a)

$$\begin{array}{ccc}{\Pi }_{\mu \nu }\hfill & =& -\frac{1}{4}{T}_{\mu \alpha }{T}_{\nu }^{\alpha }+\frac{T{T}_{\mu \nu }}{12}+\frac{g_{\mu \nu }}{24}(3T_{\alpha \beta }{T}^{\alpha \beta }-T^2),\hfill \end{array}$$

(84b)

$$\begin{array}{ccc}{F}_{\mu \nu }\hfill & =& \frac{2T_{AB}{g}_{\mu }^A{g}_{\nu }^B}{3}+\frac{2g_{\mu \nu }}{3}\left(T_{AB}{n}^A{n}^B-\frac{{}^{\left(5\right)}T}{4}\right),\hfill \end{array}$$

(84c)

$$\begin{array}{ccc}{\xi }_{\mu \nu }\hfill & =& {}^{\left(5\right)}{C}_{AFB}^E{n}_E{n}^F{g}_{\mu }^A{g}_{\nu }^B.\hfill \end{array}$$

(84d)

Here $G_N$ is the Newton’s gravitational constant, $\lambda$ is the previously mentioned brane tension, and ${\kappa }_{\left(4\right)}$ and ${\kappa }_{\left(5\right)}$ are the four- and five-dimensional coupling constants of gravity, respectively. The tensor ${\Pi }_{\mu \nu }$ represents the quadratic corrections on the brane generated by the energy-momentum tensor, $F_{\mu \nu }$ gives the contributions of the energy-momentum tensor in the bulk, which is projected onto the brane through the unit normal vector $n_A$. The tensor ${\xi }_{\mu \nu }$ provides the contribution of the five-dimensional Weyl’s tensor projected onto the brane manifold [139]. Notice that the latin letters take the values $0,1,2,3,4$. It is worth noting that non-local corrections are negligible in cosmological cases [40], under the assumption of a AdS${}_{\left(5\right)}$ bulk.

To derive the Friedmann equations under the modified field equations, we consider an homogeneous and isotropic Universe in which a line element is given by Equation (2). We consider radiation and dark matter components as perfect fluids in the brane. We assume that the bulk has no matter component. Using Equation (61), we obtain the modified Friedmann Equation:

$$H^2=\frac{8\pi G}{3}\sum _i{\rho }_i\left(1+\frac{{\rho }_i}{2\lambda }\right).$$

(85)

Note that ${\rho }_i$ is the energy density for the radiation, dark matter, and DE. It is worth noting that the low energy regime, i.e., the canonical Friedmann equation, is recovered when ${\rho }_i/2\lambda \to 0$. Crossed terms were not used in the Friedmann equation; i.e., there is no interaction between different species. In addition, if we consider, for instance, that the bulk black hole mass vanishes, the bulk geometry reduces to ${\mathrm{AdS}}_5$ and ${\rho }_{ϵ}=0$ [40]. Thus, the Friedmann equation can be written as:

$$\begin{array}{c}\hfill H^2=\frac{8\pi G}{3}\left[\frac{{\rho }_{0m}}{a^3}\left(1+\frac{{\rho }_{0m}}{2\lambda a^3}\right)+\frac{{\rho }_{0r}}{a^4}\left(1+\frac{{\rho }_{0r}}{2\lambda a^4}\right)+\frac{{\rho }_{0de}}{a^{3(1+{\omega }_{de})}}\left(1+\frac{{\rho }_{0de}}{2\lambda a^{3(1+{\omega }_{de})}}\right)\right].\end{array}$$

(86)

The above equation can be expressed in terms of the density parameters through the dimensionless Friedmann equation

$$\begin{array}{ccc}& & E{\left(z\right)}^2={\Omega }_{0m}{(1+z)}^3+{\Omega }_{0r}{(1+z)}^4+{\Omega }_{0de}{(1+z)}^{3(1+{\omega }_{de})}\hfill \\ & & +\mathcal{M}\left[{\Omega }_{0m}^2{(1+z)}^6+{\Omega }_{0r}^2{(1+z)}^8+{\Omega }_{0de}^2{(1+z)}^{6(1+{\omega }_{de})}\right],\hfill \end{array}$$

(87)

where

$$\mathcal{M}\equiv \frac{H_0^2}{2{\kappa }^2\lambda },$$

(88)

where ${\rho }_{crit}$ is the Universe critical density. Notice that when $\mathcal{M}\to 0$, the canonical Friedmann equation with $w_{de}$ is recovered. If $w_{de}={\omega }_{\Lambda }=-1$, i.e., the DE is the CC, we obtain the traditional $\Lambda$CDM dynamics.

At early times, the brane dynamics dominate over other terms in the Universe, but is negligible at late times. Indeed, given a value for the brane tension, we can infer the limits of high and low energies in terms of the redshift: $z+1\gg {\sum }_i{(\lambda /{\rho }_{0i})}^{1/3(1+{\omega }_i)}$ and $z+1\ll {\sum }_i{(\lambda /{\rho }_{0i})}^{1/3(1+{\omega }_i)}$, respectively. For example, in the matter domination epoch, the previous expressions can be rewritten as: $z\gg {(\lambda /{\rho }_{0m})}^{1/3}-1$ and $z\ll {(\lambda /{\rho }_{0m})}^{1/3}-1$, for high and low energy limits, respectively.

Table 10 shows the bestfit for the different free parameters together with the estimated ${\chi }^2$. Figure 10 shows the severe tension between the different cosmological samples (OHD, SNIa, SLS, HIIG, BAO), hence concluding that the model is not viable to replace the $\Lambda$CDM model unless an additional DE component is included, which defeats the purpose of choosing this model.

Table 10. Best fitting values of the free parameters for the constant brane tension model with the different samples used in this paper.

Sample	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{m}0}$	${\mathit{w}}_{\mathit{de}}$	${log}_{10}\mathcal{M}$
OHD	$18.19$	${0.72}_{-0.01}^{+0.01}$	${0.21}_{-0.03}^{+0.02}$	$-{1.00}_{-0.12}^{+0.11}$	<−0.88
BAO	$5.46$	${0.73}_{-0.01}^{+0.01}$	${0.20}_{-0.07}^{+0.04}$	$-{0.53}_{-0.19}^{+0.13}$	<−9.52
SNIa	$574.73$	${0.72}_{-0.01}^{+0.01}$	${0.13}_{-0.07}^{+0.06}$	$-{0.81}_{-0.10}^{+0.07}$	<−0.31
CMB	$10.87$	${0.73}_{-0.01}^{+0.01}$	${0.29}_{-0.01}^{+0.01}$	$-{1.12}_{-0.06}^{+0.06}$	<−15.0
Joint	$636.70$	${0.71}_{-0.01}^{+0.01}$	${0.30}_{-0.01}^{+0.01}$	$-{1.12}_{-0.03}^{+0.03}$	<−16.2

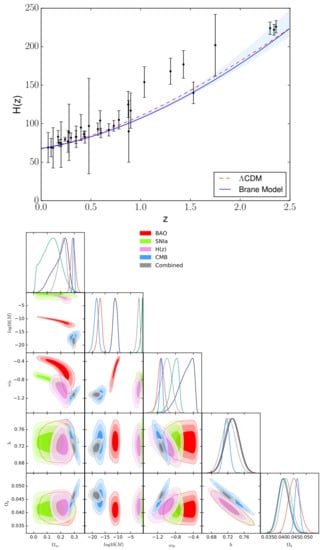
Figure 10. Top panel: Best fit curve of constant brane tension model and its uncertainty at $1\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using OHD, SNIa (Pantheon), SLS, HIIG, BAO, and Joint data.

4.2.2. Variable Brane Tension

A natural extension to the previous model is the one called variable brane tension (BVT). The framework is the same as the one in Section 4.2.1, but now an extra degree of freedom is assumed, and a brane tension emerges as a function of the redshift. Naturally, the model resolves the problems associated with the presence of the brane tension at early epochs but also generates a CC with five-dimensional origins. We briefly discuss the theoretical framework of a BVT model, which was previously studied in [42]. We start from the BVT field equation as

$$G_{\mu \nu }-8\pi G{T}_{\mu \nu }=\frac{1}{\lambda }\left[48\pi G{\Pi }_{\mu \nu }+\frac{3}{4\pi G}{\xi }_{\mu \nu }\right],$$

(89)

where

$$\begin{array}{ccc}& & {\xi }_{\mu \nu }=\mathcal{U}\left(u_{\mu }{u}_{\nu }+\frac{1}{3}{ϵ}_{\mu \nu }\right)+{\mathcal{P}}_{\mu \nu },\hfill \end{array}$$

(90)

$$\begin{array}{ccc}& & {\Pi }_{\mu \nu }=-\frac{1}{4}{T}_{\mu \alpha }{T}_{\nu }^{\alpha }+\frac{1}{12}{T}_{\alpha }^{\alpha }{T}_{\mu \nu }+\frac{1}{24}{g}_{\mu \nu }[3T_{\alpha \beta }{T}^{\alpha \beta }-{\left(T_{\alpha }^{\alpha }\right)}^2].\hfill \end{array}$$

(91)

where $G_{\mu \nu }$ is described in (1), and ${\xi }_{\mu \nu }$ as a non-local Weyl tensor decomposed in its irreducibility form, which also contains $\mathcal{U}$ is the non-local energy density, ${\mathcal{P}}_{\mu \nu }$ as the non-local anisotropic stress tensor, $u_{\alpha }$ as the four-velocity, and ${ϵ}_{\mu \nu }\equiv g_{\mu \nu }+u_{\mu }{u}_{\nu }$. In addition $T_{\mu \nu }$ is the standard energy-momentum tensor and ${\Pi }_{\mu \nu }$ contains a quadratic form of the energy–momentum tensor. Notice that the corrective terms that comes from brane world is contingent to the brane tension defined by $\lambda$, which in this model is not a constant. Therefore, the low energy limit is considered when $\lambda \to \infty$ recovers the traditional field equation of GR, while in the other limit $\lambda \to 0$, extra terms play a preponderant role. Finally, note that in this case we do not consider extra fields onto the bulk, neglecting the terms that come from $F_{\mu \nu }$ and only considering those fields in the brane.

Therefore, if we introduce the previously line element in Equation (89) together with the perfect fluid energy-momentum tensor (Equation (3)), we have the following Friedmann Equation [42]:

$$E{\left(z\right)}^2={\Omega }_{0m}{(z+1)}^3+{\Omega }_{0r}{(z+1)}^4+\frac{\mathcal{M}}{\widehat{\lambda }\left(z\right)}[{\Omega }_{0m}^2{(z+1)}^6+{\Omega }_{0r}^2{(z+1)}^8],$$

(92)

where we have already considered matter and radiation components, where their evolution comes from the conservation of the energy-momentum tensor (${\nabla }^{\mu }{T}_{\mu \nu }=0$) and their separability from the quadratic part of the field equation. The brane tension evolves homogeneously and isotropically because it is only on the temporal function and can be chosen using other physical assumptions. In addition, the brane tension is not directly coupled with the continuity equation of the fluids, and it is defined as $\widehat{\lambda }\left(z\right)\equiv {\lambda }_0\lambda \left(z\right)$, where $\widehat{\lambda }\left(z\right)$ is a dimensionless function that can be selected appropriately. Moreover, $\mathcal{M}\equiv 3H_0^2/16\pi G{\lambda }_0$ and, under the flatness condition, we have the constriction

$$\mathcal{M}=\frac{1-{\Omega }_{0m}-{\Omega }_{0r}}{{\Omega }_{0m}^2+{\Omega }_{0r}^2}\widehat{\lambda }(z=0).$$

(93)

Regarding the choice of the $\widehat{\lambda }\left(z\right)$ function, we pick a polynomial form as $\widehat{\lambda }\left(z\right)={(z+1)}^n$, where n is a free parameter and $n\in \mathbb{R}$. Garcia-Aspeitia et al. [42] discuss the inspiration for this function, arguing that it could be a generalization of the Eötvös law, similar functions can be found in tracker behavior for scalar fields.

Using a joint analysis that contains OHD, CMB, BAO and SNIa observations (see Figure 11 and Table 11), the authors of [42] found out $n=6.19\pm 0.12$. Notice that the result is consistent with predictions because if we use Equation (92), neglecting ${(z+1)}^8$, the term $\mathcal{M}$ will behave as a CC at late times but with extra dimensions origin.

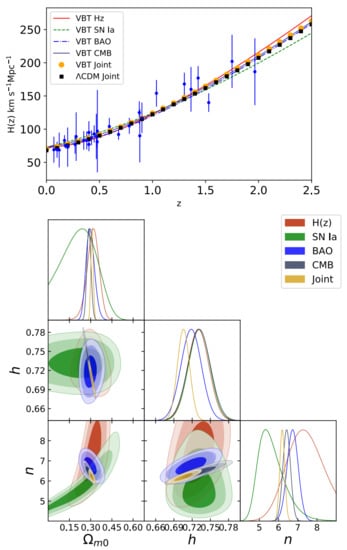
Figure 11. Top panel: Best fit curve for the variable brane tension model and its uncertainty at $1\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using OHD, SNIa, BAO, CMB, and Joint data.

Table 11. Best fitting values of the free parameters for the Variable Brane Tension model with the different samples used in this paper.

Sample	${\mathit{\chi }}_{\mathit{min}}^2$	h	${\mathbf{\Omega }}_{\mathit{m}0}$	n	${\mathit{\lambda }}_0({10}^{-12}$ eV${}^4)$
OHD	$14.46$	${0.730}_{-0.017}^{+0.017}$	${0.318}_{-0.042}^{+0.039}$	${7.400}_{-0.926}^{+1.100}$	${3.20}_{-0.95}^{+1.05}$
BAO	$9.49$	${0.718}_{-0.016}^{+0.016}$	${0.297}_{-0.028}^{+0.031}$	${6.730}_{-0.289}^{+0.287}$	${2.62}_{-0.57}^{+0.77}$
SNIa	$691.10$	${0.731}_{-0.017}^{+0.017}$	${0.231}_{-0.120}^{+0.114}$	${5.580}_{-0.568}^{+0.815}$	${1.48}_{-1.16}^{+2.40}$
CMB	$3.64$	${0.732}_{-0.017}^{+0.017}$	${0.288}_{-0.013}^{+0.014}$	${6.420}_{-0.185}^{+0.185}$	${2.52}_{-0.17}^{+0.19}$
Joint	$716.43$	${0.706}_{-0.009}^{+0.009}$	${0.31}_{-0.008}^{+0.008}$	${6.190}_{-0.120}^{+0.121}$	${2.81}_{-0.11}^{+0.12}$

4.2.3. Unimodular Gravity

Unimodular Gravity (UG) is a remarkable proposition to tackle the problem of the CC by limiting the metric in the following way $\sqrt{-g}=\xi$, where $\xi$ is a constant, restricting the field equations at only nine linear independent equations and the field equation is trace-free [43]. The possibility to integrate the line element of FLRW gives us the opportunity to obtain clues about the nature of CC, tracing its presence at epochs of reionization [45].

UG can be described by the following field equation:

$$R_{\mu \nu }-\frac{1}{4}{g}_{\mu \nu }R=8\pi G\left(T_{\mu \nu }-\frac{1}{4}{g}_{\mu \nu }T\right),$$

(94)

where all the tensors are the standards of GR and G is the Newton’s gravitational constant.

In order to study the background cosmology, we consider an isotropic, homogeneous FLRW metric (2), the perfect fluid energy momentum tensor is written as shown Equation (3). Hence, we have [43,44]

$$\dot{H}=\frac{\ddot{a}}{a}-H^2=-4\pi G\sum _i({\rho }_i+p_i),$$

(95)

where the dots stands for time derivative. In addition, a general conservation for UG theory is now written in the form

$${\nabla }^{\mu }[32\pi G{T}_{\mu \nu }-(R+8\pi GT)g_{\mu \nu }]=0.$$

(96)

Without independently assuming the energy momentum conservation (${\nabla }^{\mu }{T}_{\mu \nu }=0$), Equation (96) introduces new Friedmann, acceleration and fluid equations coupled with third-order derivatives in the scale factor. Hence, in the case of non traditional conservation of the energy-momentum tensor, Equation (96) must be solved to obtain the characteristic fluid equation. Solving for (96) under a FLRW metric and perfect fluid, we have

$$\sum _i\left[\frac{d}{dt}({\rho }_i+p_i)+3H({\rho }_i+p_i)\right]=\frac{H^3}{4\pi G}(1-j),$$

(97)

where the sum is over all the species in the Universe and $j\equiv \stackrel{⃛}{a}/a{H}^3$ is the Jerk Parameter (JP) [110,140], well known in cosmography and proposed by [45] for the study of UG.

On the other hand, the integral-transcendent-Friedmann equation can be computed with the help of Equations (5) and (97), obtaining the Friedmann equation as

$$H^2=\frac{8\pi G}{3}\sum _i{\rho }_i+H_{corr}^2.$$

(98)

where the non-canonical extra term in Equation (98), i.e., the UG correction to the Friedmann and acceleration equations, is defined in the form

$$H_{corr}^2\equiv \frac{8\pi G}{3}\sum _i{p}_i+\frac{2}{3}{\int }_{a_{ini}}^{a\left(t\right)}H{\left(a^{\prime }\right)}^2[j\left(a^{\prime }\right)-1]\frac{d{a}^{\prime }}{a^{\prime }},$$

(99)

where the sum runs over the different species in the Universe and $a_{ini}$ is some constant initial value.

According to [45], it is plausible to consider an ansatz for the JP in terms of the redshift with the following characteristics

$$j\left(z\right)=\frac{9(1+w)w}{2E{\left(z\right)}^2}{\Omega }_{0i}{(z+1)}^{3(w+1)}+1,$$

(100)

where w is the EoS for any fluid. If we choose ${\Omega }_{0i}\to {\Omega }_{0r}$ as the radiation density parameter (matter emerges naturally from Equation (97), so the other expected fluid should be radiation to avoid introducing an exotic fluid) and $w\to w_r=1/3$ as the EoS of radiation, then the functional form reproduces the $\Lambda$CDM jerk parameter in all eras [45].

From the previous equation and Equation (98), it is possible to deduce

$$\begin{array}{c}\hfill E{\left(z\right)}^2={\Omega }_{0m}{(z+1)}^3+{\Omega }_{0r}{(z+1)}^4+{\Omega }_{0exs}{(z_{ini}+1)}^4,\end{array}$$

(101)

where ${\Omega }_{0exs}\equiv w_r{\Omega }_{0r}$.

Note that the source of the Universe acceleration is the constant term in the previous Equation (101), where we can naturally relate ${\Omega }_{0\Lambda }\to {\Omega }_{0exs}{(z_{ini}+1)}^4$. Since our choice in Equation (100) depends on the EoS and the energy density parameter of the radiation, the constant inherits those terms.

Figure 12 shows the constraints for $z_{ini}$ and h considering the SNIa, BAO, OHD, CMB and a joint data, with the best-fit values in Table 12 (see [45,97], for details). The results suggest a $z_{ini}=11.47$, which is in the reionization era. The interpretation of the result is that UG is an emergent DE theory, with DE arising during the reionization period.

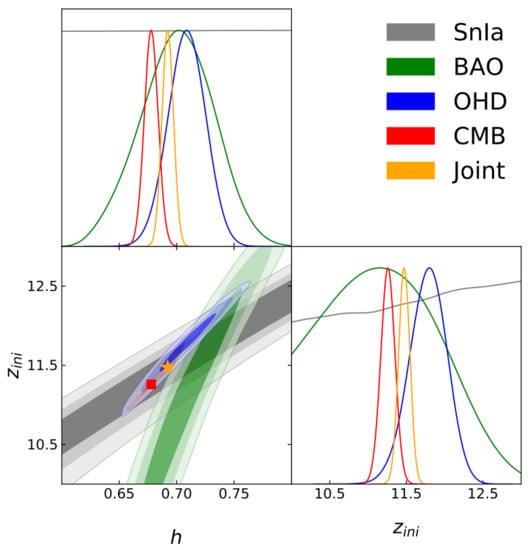
Figure 12. 1D marginalized posterior distributions and the 2D $68\%$, $95\%$, and $99.7\%$ of CL for the h, and $z_{ini}$ parameters of the UG model. The star (square) marker represents the best fit value of Joint (CMB) data.

Table 12. Mean values for the UG model parameters (h, $z_{ini}$) and ${\chi }_{min}^2$, derived from each data set and the joint analysis (see [97]).

Sample	${\mathit{\chi }}_{\mathit{min}}^2$	h	${\mathit{z}}_{\mathit{ini}}$
OHD	$22.0$	${0.709}_{-0.016}^{+0.016}$	${11.788}_{-0.250}^{+0.237}$
SnIa	$1036.0$	${0.602}_{-0.272}^{+0.270}$	${10.623}_{-3.021}^{+2.366}$
CMB	$0.0001$	${0.678}_{-0.006}^{+0.006}$	${11.259}_{-0.092}^{+0.091}$
BAO	$12.9$	${0.701}_{-0.033}^{+0.031}$	${10.847}_{-1.383}^{+0.979}$
Joint	$1097.6$	${0.692}_{-0.005}^{+0.005}$	${11.473}_{-0.073}^{+0.074}$

4.2.4. Einstein–Gauss–Bonet

Einstein–Gauss–Bonet (EGB) is a recent proposition that modifies the geometrical part of the field equations [46], maintaining the continuity equation in its original form. In [47], they constrained the free parameter through diverse observations finding results compatible with the cosmological standard model. However, the authors also found that specific values of the free parameter could generate an eternal acceleration, even in epochs in which is not expected (reionization, nucleosynthesis, etc). Other mathematical flaws of the EGB model have recently been found [141,142,143,144,145].

The action of the EGB gravity can be written in the form [46]

$$\begin{array}{c}\hfill S_{EGB}\left[g_{\mu \nu }\right]=\int d^{d+1}x\sqrt{-g}\left[\frac{1}{16\pi G}(R-2\Lambda )+{\mathcal{L}}_m+\frac{\alpha }{d-3}\mathcal{G}\right],\end{array}$$

(102)

where $\Lambda$ is an effective cosmological constant, R is the Ricci scalar, ${\mathcal{L}}_m$ is the matter Lagrangian, $\alpha$ is an appropriate free parameter, $\mathcal{G}=6R_{[\mu \nu }^{\mu \nu }{R}_{\rho \sigma ]}^{\rho \sigma }$ is the Gauss–Bonnet contribution to the Einstein–Hilbert action and $d+1$ is considered in the limit when ${lim}_{d\to 3}d+1$ as presented in [46]. Minimizing the action, the field equation can be written as

$$\begin{array}{ccc}& & G_{\mu \nu }+\Lambda g_{\mu \nu }+\frac{\alpha }{(d-3)}(4R{R}_{\mu \nu }-8R_{\mu \alpha }{R}_{\nu }^{\alpha }-8R_{\mu \alpha \nu \beta }{R}^{\alpha \beta }+4R_{\mu \alpha \beta \sigma }{R}_{\nu }^{\alpha \beta \sigma }\hfill \\ & & -g_{\mu \nu }\mathcal{G})=8\pi G{T}_{\mu \nu }.\hfill \end{array}$$

(103)

Note that when $\alpha =0$, the standard Einstein field equation with a CC is recovered.

In order to study the background cosmology, we assume a flat FLRW given by Equation (2), the energy–momentum tensor is the usual given by (3). After some manipulations of the previous expressions, the Friedmann equation for EGB reads

$$H^2+3\alpha H^4=\frac{8\pi G}{3}\sum _i{\rho }_i+\frac{\Lambda }{3}.$$

(104)

Moreover, the continuity equation takes its traditional form as (4). In terms of the dimensionless variables, Equation (104) is rewritten as

$$E{\left(z\right)}^2+\overline{\alpha }E{\left(z\right)}^4={\Omega }_{m0}{(z+1)}^3+{\Omega }_{r0}{(z+1)}^4+{\Omega }_{\Lambda 0},$$

(105)

where $\overline{\alpha }\equiv 3\alpha H_0^2$, ${\Omega }_{i0}\equiv {\kappa }^2{\rho }_i/3H_0^2$ and ${\Omega }_{\Lambda 0}\equiv \Lambda /3H_0^2$, composed of matter (baryons and dark matter) and relativistic particles (photons and neutrinos). Another important consideration is that $\overline{\alpha }$ is a positive value as inflation demands (see Reference [146] for details).

In order to constrain the $\overline{\alpha }$ parameter, we divide the problem in two branches through Equation (105). Therefore, if we only consider the branch where we have a real value of $E\left(z\right)$, then we have [47]

$$\begin{array}{c}\hfill E{\left(z\right)}^2=\frac{1}{2\overline{\alpha }}\left[\sqrt{1+4\overline{\alpha }\Omega {\left(z\right)}_{std}}-1\right],\end{array}$$

(106)

where

$$\Omega {\left(z\right)}_{std}\equiv {\Omega }_{m0}{(z+1)}^3+{\Omega }_{r0}{(z+1)}^4+{\Omega }_{\Lambda 0},$$

(107)

is the standard cosmological model. Equation (106) is constrained to the condition $E\left(0\right)=1$, which has the following relation [47]

$${\Omega }_{\Lambda 0}=\frac{{(2\overline{\alpha }+1)}^2-1}{4\overline{\alpha }}-{\Omega }_{m0}-{\Omega }_{r0}.$$

(108)

Notice that when $\overline{\alpha }\to 0$, in (106), the standard Friedmann equation is recovered.

Figure 13 shows the MCMC analysis implemented using OHD, SNIa, SLS, HIIG, and BAO samples. The upper panel shows the reconstruction of $H\left(z\right)$ and the bottom panel presents the CL contours for the free parameter of the theory $\overline{\alpha }$. In addition, best-fits for the free parameters if the model are presented in Table 13 in conjunction with the ${\chi }^2$ parameter (see details in [47]).

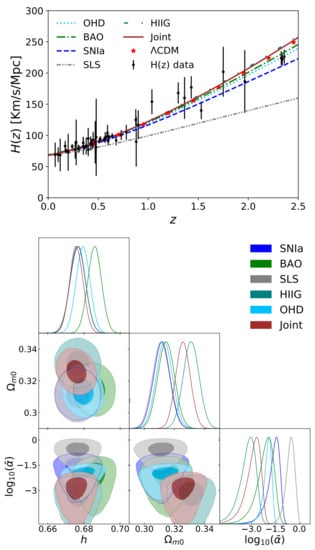
Figure 13. Top panel: Best fit curve of Einstein–Gauss–Bonnet model and its uncertainty at $1\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using OHD, SNIa (Pantheon), SLS, HIIG, BAO and Joint data. Figure adapted from [47].

Table 13. Best fitting values of the free parameters for the EGB model with the different samples used in this paper (see [47] for details).

Sample	${\mathit{\chi }}^2$	h	${\mathbf{\Omega }}_{\mathit{m}0}$	$\overline{\mathit{\alpha }}$	$\mathcal{M}$
OHD	$25.8$	${0.677}_{-0.004}^{+0.004}$	${0.312}_{-0.005}^{+0.005}$	${0.011}_{-0.005}^{+0.007}$	–
BAO	$40.7$	${0.686}_{-0.004}^{+0.004}$	${0.315}_{-0.006}^{+0.006}$	${0.008}_{-0.006}^{+0.014}$	–
SNIa	$39.8$	${0.677}_{-0.004}^{+0.004}$	${0.312}_{-0.005}^{+0.005}$	${0.028}_{-0.018}^{+0.028}$	$-{19.400}_{-0.016}^{+0.016}$
SLS	$577.8$	${0.676}_{-0.004}^{+0.004}$	${0.311}_{-0.006}^{+0.006}$	${0.281}_{-0.143}^{+0.218}$	–
HIIG	$2269.5$	${0.677}_{-0.004}^{+0.004}$	${0.331}_{-0.005}^{+0.005}$	${0.0006}_{-0.0005}^{+0.0011}$	–
Joint	$6181.9$	${0.676}_{-0.004}^{+0.004}$	${0.326}_{-0.005}^{+0.005}$	${0.001}_{-0.001}^{+0.002}$	$-{19.400}_{-0.012}^{+0.012}$

4.2.5. Cardassian Models

Cardassian models (the name Cardassian comes from alien creatures shown in the television series Star Trek) are a phenomenological form to describe the late time acceleration of the Universe that could be theoretically sustained under the assumption of extra dimensions. The models assume an extra function in the Friedmann equations whose form is related to those of the polytropic fluids. Therefore, just the presence of matter and radiation in this functional form automatically produce a late time Universe acceleration without the need for a CC. The main disadvantage is the apparition of additional terms that must be constrained with observations and the difficulties to describe the model from theoretical arguments. It is important to mention that the Cardassian models are divided into the Original Cardassian (OC) and the Modified Polytropic Cardassian (MPC).

The theoretical details of OC model, introduced by Reference [48], is given by the following Friedmann equation:

$$\begin{array}{ccc}& & E{\left(z\right)}^2={\Omega }_{m0}{(1+z)}^3+{\Omega }_{r0}{(1+z)}^4+(1-{\Omega }_{m0}-{\Omega }_{r0})\hfill \\ & & \times {\left(\frac{{\Omega }_{m0}{(1+z)}^3+{\Omega }_{r0}{(1+z)}^4}{{\Omega }_{m0}+{\Omega }_{r0}}\right)}^n,\hfill \end{array}$$

(109)

where n is a free parameter. Despite OC model arising from a phenomenological assumption in order to obtain an accelerated Universe, it is important to notice that the mathematical structure can be strictly obtained from brane world models with n-branes immersed in a five dimensional bulk.

In addition, the MPC model [49] takes the form

$$\begin{array}{c}\hfill E{\left(z\right)}^2={\Omega }_{r0}{(1+z)}^4+{\Omega }_{m0}{(1+z)}^3\beta {\left(z\right)}^{1/l},\end{array}$$

(110)

where

$$\begin{array}{c}\hfill \beta \left(z\right)\equiv 1+\left[{\left(\frac{1-{\Omega }_{r0}}{{\Omega }_{m0}}\right)}^l-1\right]{(1+z)}^{3/(n-1)},\end{array}$$

(111)

here l and n are free parameters.

Table 14 gives the minimum chi-square and mean values for the OC and MPC parameters using the samples OHD (DA), SNIa (compressed JLA), and the joint analysis of these data sets. Figure 14 shows the best fit of $H\left(z\right)$ for the original (left panel) and modified polytropic Cardassian models (right), respectively. The figures also show the confidence contours (bottom panels) for both Cardassian models using SNIa (cJLA, compressed JLA), OHD uniformed with the sound horizon estimation from Planck data, and the Joint analysis of both data (denoted J3). It is worth noting that both models can reproduce the dynamics of the Hubble measurements.

Table 14. Mean values for the OC and MPC parameters using the samples OHD (DA), SNIa (compressed JLA), and the joint analysis of these data sets. (see [66], for details).

Orignal Cardassian
Data	${\chi }_{min}^2$	${\Omega }_m$	n	l	h
OHD (DA)	$15.22$	${0.30}_{-0.06}^{+0.06}$	$-{0.19}_{-0.50}^{+0.51}$	$--$	${0.69}_{-0.05}^{+0.06}$
SNIa	$32.95$	${0.22}_{-0.12}^{+0.11}$	${0.16}_{-0.26}^{+0.17}$	$--$	${0.72}_{-0.19}^{+0.19}$
Joint	$54.28$	${0.25}_{-0.02}^{+0.02}$	${0.11}_{-0.07}^{+0.07}$	$--$	${0.69}_{-0.01}^{+0.01}$
Modified polytropic Cardassian
OHD (DA)	$17.95$	${0.32}_{-0.07}^{+0.06}$	${0.10}_{-0.60}^{+0.38}$	${2.13}_{-1.33}^{+2.34}$	${0.68}_{-0.05}^{+0.07}$
SNIa	$33.76$	${0.22}_{-0.13}^{+0.12}$	${0.36}_{-0.33}^{+0.07}$	${2.61}_{-1.83}^{+2.27}$	${0.72}_{-0.19}^{+0.18}$
Joint	$54.23$	${0.25}_{-0.03}^{+0.03}$	${0.06}_{-0.58}^{+0.29}$	${0.89}_{-0.47}^{+1.29}$	${0.68}_{-0.01}^{+0.01}$

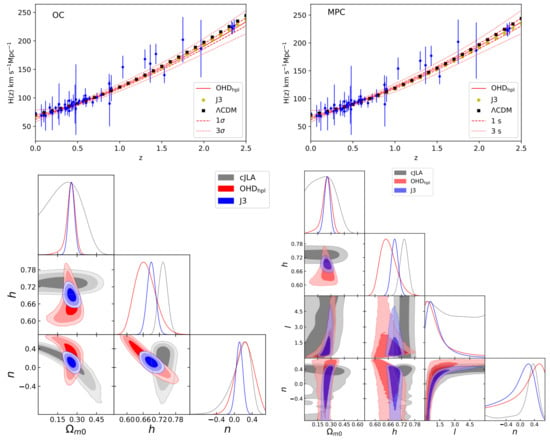
Figure 14. Top panel: Best fit curve of $H\left(z\right)$ for the original and modified polytropic Cardassian models and uncertainties at $1\sigma$ and $1\sigma$. Bottom panel: 2D contours of the free model parameters at $1\sigma ,2\sigma$, and $3\sigma$ (from darker to lighter color bands) CL using SNIa (cJLA, compressed JLA), OHD, and the Joint analysis of both data (denoted J3).

5. Discussion and Conclusions

In this review, we presented a brief and non-exhaustive review on DE models that, however, summarizes some important scientific results, settling the ground for the ideas exposed in this work.

Our motivation to explore alternatives to $\Lambda$CDM lies in the problems that afflict the cosmological constant and the recently observed tension in the ${\sigma }_8$ and $H_0$ parameters estimated from different samples. Notice how the CC is directly related to the problem of the Universe acceleration, and therefore, a competitive model should be implemented. However, regarding the $H_0$ tension, it is not clear whether it is related to dark energy or not (see, for example, [147]), although some authors assume that this is the case [33].

For each type of dark energy presented in this review, we have summarized its main characteristics, its theoretical structure and in its capabilities to fit the data provided by modern observations. Parameterizations are always the standard form to tackle the problem of Universe acceleration, but there is not a unique way of choosing the form of the function. Furthermore, in many cases, there are not solid arguments to justify the chosen form, and it is anfractuous to associate the parameterization with some quantum field or with a model that modifies the GR. Models like Chaplygin and Viscous encompass the dark energy and dark matter contribution in just one theoretical framework through a diffusion function in the continuity equations. The theoretical background is robust, with its equations deduced from a quantum field theory in which a scalar field is involved. In addition, the diverse data samples tend to prefer the mentioned models over others with extra complexities.

We also described models with a late apparition of the dark energy (CC always exist in the Universe evolution). The PEDE, GEDE, and UG models allow us to estimate the birth of DE at the reionization epoch. These kind of models are valuable because their mathematical expression is able to resolve the tension between Planck and SNIa data. Observational constraints also favor them over other models. Furthermore, extra-dimensional models contain a theoretical complexity that undermines their recognition; for instance, the RS model has severe faults when it is contrasted with observations. However, the addition of extra degrees of freedom to obtain a variable brane tension reduces the disagreement with observations and shed light on the nature of CC; i.e., it comes from the existence of extra dimensions. The disadvantage is that the CC problem is now dragged into the extra dimensions scenario, introducing difficulties to calculate the expected value in our four-dimensional Universe. EGB model surge as a curiosity in recent literature, but after a more rigorous mathematical exam, there are several notorious flaws in its theoretical arguments. In addition, from a cosmological point of view, it is based on an spurious early acceleration that could cause severe problems with the well-known characteristics of the Universe in epochs such as the nucleosynthesis. Constraints on EGB obtained with the SLS data sample and applied to dynamical systems point out that the early acceleration never ends. Finally, Cardassian models are phenomenological models that could be justified by the assumption of extra dimensions. Although this complicate the equations, they have the advantage of avoiding tensions when contrasted with observations. Note that, as expected, Cardassian models tend to reproduce the CC, not showing a dynamical DE.

As a final remark, we would like to reflect on the $H_0$ tension considering the different models discussed in this review. In Table 15, we present the compilation of the dimensionless Hubble parameter (h) for all the models with their respective selected samples and priors. We have used a Gaussian prior in most of the cases using Riess or Planck data [15,31], while only in four models do we consider a flat prior. For the purpose of the following discussion, we compare only those models with flat priors, which are CPL, UG, and both Cardassian models. Only those models using joint samples that include CMB are able to constrain $H_0$, and thus, the best-fit value is in agreement with Planck’s result. However this is not the final word about the $H_0$ tension; Reference [147] has recently suggested that this might be related to a misunderstanding of the distance ladder measurements (i.e., a need for a better agreement between the SNIa absolute magnitude and the Cepheid-based distance ladder) instead of an “exotic late-time physics”.

Table 15. Best fitting values of the h parameter for all the models presented.

Model	h	Sample	Prior
wCDM	${0.68}_{-0.01}^{+0.01}$	OHD, SNIa, CMB	Gaussian (${0.6766}_{-0.0042}^{+0.0042})$
CPL	${0.73}_{-0.08}^{+0.10}$	OHD	Flat [0.2,1.0]
JBP	${0.71}_{-0.014}^{+0.014}$	OHD, CMB, BAO	Gaussian (${0.73}_{-0.0175}^{+0.0175}$)
BA	${0.71}_{-0.015}^{+0.015}$	OHD, CMB, BAO	Gaussian (${0.73}_{-0.0175}^{+0.0175}$)
FSLLI	${0.71}_{-0.015}^{+0.015}$	OHD, CMB, BAO	Gaussian (${0.73}_{-0.0175}^{+0.0175}$)
FSLLII	${0.70}_{-0.014}^{+0.014}$	OHD, CMB, BAO	Gaussian (${0.73}_{-0.0175}^{+0.0175}$)
SL	${0.70}_{-0.015}^{+0.015}$	OHD, CMB, BAO	Gaussian (${0.73}_{-0.0175}^{+0.0175}$)
Chaplygin-Like Fluid	${0.71}_{-0.014}^{+0.014}$	OHD, SNIa	Gaussian (${0.723}_{-0.017}^{+0.017}$)
Viscous (Polynomial)	${0.70}_{-0.009}^{+0.009}$	OHD, SNIa	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
Viscous (Hyperbolic tanh)	${0.69}_{-0.009}^{+0.009}$	OHD, SNIa	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
Viscous (Hyperbolic cosh)	${0.70}_{-0.010}^{+0.009}$	OHD, SNIa	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
Viscous (${\xi }_0=$ Constant)	${0.68}_{-0.004}^{+0.004}$	OHD, SNIa, SLS	Gaussian (${0.6766}_{-0.0042}^{+0.0042}$)
Viscous (${\xi }_0=$ Polynomial)	${0.67}_{-0.004}^{+0.004}$	OHD, SNIa, SLS	Gaussian (${0.6766}_{-0.0042}^{+0.0042}$)
Interacting Viscous	${0.70}_{-0.013}^{+0.012}$	OHD	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
PEDE	${0.74}_{-0.011}^{+0.011}$	Homogeneous OHD	Gaussian (${0.7403}_{-0.0142}^{+0.0142}$)
GEDE	${0.73}_{-0.012}^{+0.012}$	Homogeneous OHD	Gaussian (${0.7403}_{-0.0142}^{+0.0142}$)
CBT	${0.71}_{-0.01}^{+0.01}$	BAO, SNIa, OHD, CMB	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
VBT	${0.70}_{-0.009}^{+0.009}$	OHD, SNIa, BAO, BAO	Gaussian (${0.7324}_{-0.0174}^{+0.0174}$)
UG	${0.69}_{-0.005}^{+0.005}$	OHD, SNIa, CMB, BAO	Flat [0.2,1.0]
EGB	${0.67}_{-0.004}^{+0.004}$	SNIa, BAO, OHD, SLS, HIIG	Gaussian (${0.6766}_{-0.0042}^{+0.0042}$)
Original Cardassian	${0.69}_{-0.01}^{+0.01}$	SNIa, OHD	Flat [0,1]
Modified Polytropic Cardassian	${0.68}_{-0.01}^{+0.01}$	SNIa, OHD	Flat [0,1]

Finally, we summarize our results in the following way. The Brane model with constant tension deduced from the RS paradigm and the EGB have several failures, which may call into question the viability of both models. Variable brane tension, Cardassian, and viscous models can be considered as promising, having problems with the complexity of their theoretical background. Parameterizations, Chaplygin, UG, PEDE, and GEDE are excellent competitors against the standard paradigm, with a strong possibility of resolving the $H_0$ tension and contributing to elucidating the nature of the dark energy component, the Universe acceleration, and its possible consequences in the fate of our Universe.