Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics
Abstract
1. Introduction
2. The Hypothetical Interactions of Power Type
3. The Yukawa-Type Interactions
4. Other Spin-Independent Hypothetical Interactions
5. Constraints on the Spin-Dependent Interactions
6. Constraints on Some Exotic Particles
7. Implications for the Quantum Vacuum, Dark Energy, and the Cosmological Constant
8. Discussion
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Adler, R.J.; Casey, B.; Jacob, O.C. Vacuum catastrophe: An elementary exposition of the cosmological constant problem. Am. J. Phys. 1995, 63, 620–626. [Google Scholar] [CrossRef]
- Peccei, R.D. The Strong CP Problem and Axions. Lect. Notes Phys. 2008, 741, 3–17. [Google Scholar]
- Matarrese, S.; Colpi, M.; Gorini, V.; Moshella, U. (Eds.) Dark Matter and Dark Energy; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Anselm, A.A.; Uraltsev, N.G. A second massless axion? Phys. Lett. B 1982, 114, 39–41. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–283. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Ferrara, S.; Scherk, J.; Zumino, B. Algebraic properties of extended supergravity theories. Nucl. Phys. B 1977, 121, 393–402. [Google Scholar] [CrossRef]
- Fujii, Y. The theoretical background of the fifth force. Int. J. Mod. Phys. A 1991, 6, 3505–3557. [Google Scholar] [CrossRef]
- Salam, A.; Strathdee, J. On goldstone fermions. Phys. Lett. B 1974, 49, 465–467. [Google Scholar] [CrossRef]
- Deser, S.; Zumino, B. Broken Supersymmetry and Supergravity. Phys. Rev. Lett. 1977, 38, 1433–1436. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Olive, K.A.; Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 2008, 77, 043524. [Google Scholar] [CrossRef]
- Fischbach, E.; Talmadge, C.L. The Search for Non-Newtonian Gravity; Springer: New York, NY, USA, 1999. [Google Scholar]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure, Vol. 1; Benjamin: New York, NY, USA, 1969. [Google Scholar]
- Ferrer, F.; Nowakowski, M. Higg- and Goldstone-boson-mediated long range forces. Phys. Rev. D 1999, 59, 075009. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Fischbach, E.; Krause, D.E.; Newman, R.D. Constraining the couplings of massive pseudoscalars using gravity and optical experiments. Phys. Rev. D 2003, 68, 062002. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. New dimensions at a millimeter to a fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. Phenomenology, astrophysics, and cosmology of theories with millimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Floratos, E.G.; Leontaris, G.K. Low scale unification, Newton’s law and extra dimensions. Phys. Lett. B 1999, 465, 95–100. [Google Scholar] [CrossRef]
- Kehagias, A.; Sfetsos, K. Deviations from 1/r2 Newton law due to extra dimensions. Phys. Lett. B 2000, 472, 39–44. [Google Scholar] [CrossRef]
- Aldaihan, S.; Krause, D.E.; Long, J.C.; Snow, W.M. Calculations of the dominant long-range, spin-independent contributions to the interaction energy between two nonrelativistic Dirac fermions from double-boson exchange of spin-0 and spin-1 bosons with spin-dependent couplings. Phys. Rev. D 2017, 95, 096005. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Stubbs, C.W.; Rogers, W.F. Searches for new Macroscopic forces. Annu. Rev. Nucl. Part. Sci. 1991, 41, 269–320. [Google Scholar] [CrossRef]
- Rosenberg, L.J.; van Bibber, K.A. Searches for invisible axions. Phys. Rep. 2000, 325, 1–39. [Google Scholar] [CrossRef]
- Antoniadis, I.; Baessler, S.; Bücher, M.; Fedorov, V.V.; Hoedl, S.; Lambrecht, A.; Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V.; Reynaud, S.; et al. Short-range fundamental forces. Compt. Rend. 2011, 12, 755–778. [Google Scholar] [CrossRef]
- Ivastorza, I.G.; Redondo, J. New experimental approaches in the search for axion-like particles. Progr. Part. Nucl. Phys. 2018, 102, 89–159. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Jackson Kimball, D.F.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Kuzmin, V.A.; Tkachev, I.I.; Shaposhnikov, M.E. Restrictions imposed on light scalar particles by measurements of van der Waals forces. Zhetf Pisma Redaktsiiu 1982, 36, 49–52, Translated: JETP Lett. 1982, 36, 59–62. [Google Scholar]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L.; Scardigli, F. Heuristic derivation of the Casimir effect in minimal length theories. Int. J. Mod. Phys. D 2020, 29, 2050011. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Petruzziello, L.; Stabile, A. Casimir effect in Post-Newtonian gravity with Lorentz-violation. Eur. Phys. J. C 2018, 78, 976. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Sokolov, I.Y. Restrictions on long-range forces folllowing from the Casimir effect. Yadern. Fiz. 1987, 46, 1174–1180, Translated: Sov. J. Nucl. Phys. 1987, 46, 685–688. [Google Scholar]
- Feinberg, G.; Sucher, J. Long-Range Forces from Neutrino-Pair Exchange. Phys. Rev. 1968, 166, 1638–1644. [Google Scholar] [CrossRef]
- Fischbach, E. Long-range forces and neutrino mass. Ann. Phys. 1996, 247, 213–291. [Google Scholar] [CrossRef]
- Gundlach, J.H.; Smith, G.L.; Adelberger, E.G.; Heckel, B.R.; Swanson, H.E. Short-Range Test of the Equivalence Principle. Phys. Rev. Lett. 1997, 78, 2523–2526. [Google Scholar] [CrossRef]
- Smith, G.L.; Hoyle, C.D.; Gundlach, J.H.; Adelberger, E.G.; Heckel, B.R.; Swanson, H.E. Short-range tests of the equivalence principle. Phys. Rev. D 2000, 61, 022001. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Hoedl, S.; Hoyle, C.D.; Kapner, D.J.; Upadhye, A. Particle-Physics Implications of a Recent Test of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 2007, 98, 131104. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Sokolov, I.Y. The Casimir effect leads to new restrictions on long-range force constants. Phys. Lett. A 1987, 125, 405–408. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Abrikosova, I.I.; Lifshitz, E.M. Direct measurement of molecular attraction between solids separated by a narrow gap. Quat. Rev. 1956, 10, 295–329. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Sokolov, I.Y. Stronger restrictions on the constants of long-range forces decreasing as r−n. Phys. Lett. A 1990, 146, 373–374. [Google Scholar] [CrossRef]
- Fischbach, E.; Krause, D.E. Constraints on Light Pseudoscalars Implied by Tests of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 1999, 83, 3593–3597. [Google Scholar] [CrossRef]
- Tan, W.-H.; Du, A.-B.; Dong, W.-C.; Yang, S.-Q.; Shao, C.-G.; Guan, S.-G.; Wang, Q.-L.; Zhan, B.-F.; Luo, P.-S.; Tu, L.-C.; et al. Improvement for Testing the Gravitational Inverse-Square Law at the Submillimeter Range. Phys. Rev. Lett. 2020, 124, 051301. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, K.-D. Detecting large extra dimensions with optomechanical levitated sensors. Eur. Phys. J. C 2019, 79, 18. [Google Scholar] [CrossRef]
- Brax, P.; Fichet, S.; Pignol, G. Bounding quantum dark forces. Phys. Rev. D 2018, 97, 115034. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Tabor, D.; Winterton, R.H.S. Surface Forces: Direct Measurement of Normal and Retarded van der Waals Forces. Nature 1968, 219, 1120–1121. [Google Scholar] [CrossRef] [PubMed]
- Mostepanenko, V.M.; Novello, M. Constraints on non-Newtonian gravity from the Casimir force measurements between two crossed cylinders. Phys. Rev. D 2001, 63, 115003. [Google Scholar] [CrossRef]
- Ederth, T. Template-stripped gold surfaces with 0.4-nm rms roughness suitable for force measurements: Application to the Casimir force in the 20–100-nm range. Phys. Rev. A 2000, 62, 062104. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Advance and prospects in constraining the Yukawa-type corrections to Newtonian gravity from the Casimir effect. Phys. Rev. D 2010, 81, 055003. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Constraints on corrections to Newtonian gravity from two recent measurements of the Casimir interaction between metallic surfaces. Phys. Rev. D 2013, 87, 125031. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Kuusk, P.; Mostepanenko, V.M. Constraints on non-Newtonian gravity and axionlike particles from measuring the Casimir force in nanometer separation range. Phys. Rev. D 2020, 101, 056013. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the asymmetric lateral Casimir force between corrugated surfaces in the nonadditive regime. Phys. Rev. B 2009, 80, 121402(R). [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Lateral Casimir force between sinusoidally corrugated surfaces: Asymmetric profiles, deviations from the proximity force approximation, and comparison with exact theory. Phys. Rev. B 2010, 81, 115417. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Demonstration of Angle-Dependent Casimir Force between Corrugations. Phys. Rev. Lett. 2013, 110, 250403. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Experimental and theoretical investigation of the angular dependence of the Casimir force between sinusoidally corrugated surfaces. Phys. Rev. B 2014, 89, 235436. [Google Scholar] [CrossRef]
- Sedighi, M.; Svetovoy, V.B.; Broer, W.H.; Palasantzas, G. Casimir forces from conductive silicon carbide surfaces. Phys. Rev. B 2014, 89, 195440. [Google Scholar] [CrossRef]
- Sedighi, M.; Svetovoy, V.B.; Palasantzas, G. Casimir force measurements from silicon carbide surfaces. Phys. Rev. B 2016, 93, 085434. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Improved tests of extra-dimensional physics and thermal quantum field theory from new Casimir force measurements. Phys. Rev. D 2003, 68, 116003. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. (N. Y.) 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Constraints on axionlike particles and non-Newtonian gravity from measuring the difference of Casimir forces. Phys. Rev. D 2017, 95, 123013. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Chan, H.B.; Fischbach, E.; Krause, D.E.; Jamell, C.R. Constraining New Forces in the Casimir Regime Using the Isoelectronic Technique. Phys. Rev. Lett. 2005, 94, 240401. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30–8000 Nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Masuda, M.; Sasaki, M. Limits on Nonstandard Forces in the Submicrometer Range. Phys. Rev. Lett. 2009, 102, 171101. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Guan, S.; Chen, K.; Wu, W.; Tian, Z.; Luo, P.; Jin, A.; Yang, S.; Shao, C.; Luo, J. Test of non-Newtonian gravitational forces at micrometer range with two-dimensional force mapping. Phys. Rev. D 2016, 94, 122005. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Klimchitskaya, G.L. The State of the Art in Constraining Axion-to-Nucleon Coupling and Non-Newtonian Gravity from Laboratory Experiments. Universe 2020, 6, 147. [Google Scholar] [CrossRef]
- Smullin, S.J.; Geraci, A.A.; Weld, D.M.; Chiaverini, J.; Holmes, S.; Kapitulnik, A. Constraints on Yukawa-type deviations from Newtonian gravity at 20 microns. Phys. Rev. D 2005, 72, 122001. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef]
- Hoskins, J.K.; Newman, R.D.; Spero, R.; Schultz, J. Experimental tests of the gravitational inverse-square law for mass separations from 2 to 105 cm. Phys. Rev. D 1985, 32, 3084–3095. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.-J.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Karshenboim, S.G. Constraints on a long-range spin-independent interaction from precision atomic physics. Phys. Rev. D 2010, 82, 073003. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Pignol, G.; Protasov, K.V. Neutron scattering and extra short range interactions. Phys. Rev. D 2008, 77, 034020. [Google Scholar] [CrossRef]
- Kamiya, Y.; Itagami, K.; Tani, M.; Kim, G.N.; Komamiya, S. Constraints on New Gravitylike Forces in the Nanometer Range. Phys. Rev. Lett. 2015, 114, 161101. [Google Scholar] [CrossRef] [PubMed]
- Haddock, C.C.; Oi, N.; Hirota, K.; Ino, T.; Kitaguchi, M.; Matsumoto, S.; Mishima, K.; Shima, T.; Shimizu, H.M.; Snow, W.M.; et al. Search for deviations from the inverse square law of gravity at nm range using a pulsed neutron beam. Phys. Rev. D 2018, 97, 062002. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. Recent breakthrough and outlook in constraining the non-Newtonian gravity and axion-like particles from Casimir physics. Eur. Phys. J. C 2017, 77, 315. [Google Scholar] [CrossRef]
- Hebestreit, E.; Frimmer, M.; Reimann, R.; Novotny, L. Sensing Static Forces with Free-Falling Nanoparticles. Phys. Rev. Lett. 2018, 121, 063602. [Google Scholar] [CrossRef] [PubMed]
- Borkowski, M.; Buchachenko, A.A.; Ciuryło, R.; Julienne, P.S.; Yamada, H.; Kikuchi, Y.; Takasu, Y.; Takahashi, Y. Weakly bound molecules as sensors of new gravitylike forces. Sci. Rep. 2019, 9, 14807. [Google Scholar] [CrossRef]
- Bennett, R.; O’Dell, D.H.J. Revealing short-range non-Newtonian gravity through Casimir–Polder shielding. New J. Phys. 2019, 21, 033032. [Google Scholar] [CrossRef]
- Sedmik, R.; Brax, P. Status Report and first Light from Cannex: Casimir Force Measurements between flat parallel Plates. J. Phys. Conf. Ser. 2018, 1138, 012014. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P.; Abele, H. Prospects for Searching Thermal Effects, Non-Newtonian Gravity and Axion-Like Particles: CANNEX Test of the Quantum Vacuum. Symmetry 2019, 11, 407. [Google Scholar] [CrossRef]
- Yang, S.-H.; Pi, C.-M.; Zheng, X.-P.; Weber, F. Non-Newtonian Gravity in Strange Quark Stars and Constraints from the Observations of PSR J0740+6620 and GW170817. Astrophys. J. 2020, 902, 32. [Google Scholar] [CrossRef]
- Moody, J.E.; Wilczek, F. New macroscopic forces? Phys. Rev. D 1984, 30, 130–139. [Google Scholar] [CrossRef]
- Kim, J.E. Light pseudoscalars, particle physics and cosmology. Phys. Rep. 1987, 150, 1–177. [Google Scholar] [CrossRef]
- Raffelt, G.G. Axions–motivation, limits and searches. J. Phys. A Math. Theor. 2007, 40, 6607–6620. [Google Scholar] [CrossRef]
- Drell, S.D.; Huang, K. Many-Body Forces and Nuclear Saturation. Phys. Rev. 1953, 91, 1527–1543. [Google Scholar] [CrossRef]
- Raffelt, G. Limits on a CP-violating scalar axion-nucleon interaction. Phys. Rev. D 2012, 86, 015001. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on the parameters of an axion from measurements of the thermal Casimir–Polder force. Phys. Rev. D 2014, 89, 035010. [Google Scholar] [CrossRef]
- Obrecht, J.M.; Wild, R.J.; Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Cornell, E.A. Measurement of the Temperature Dependence of the Casimir–Polder Force. Phys. Rev. Lett. 2007, 98, 063201. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Stronger constraints on an axion from measuring the Casimir interaction by means of a dynamic atomic force microscope. Phys. Rev. D 2014, 89, 075002. [Google Scholar] [CrossRef]
- Chang, C.C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion-nucleon coupling constants from measurements of effective Casimir pressure by means of micromachined oscillator. Eur. Phys. J. C 2014, 74, 2859. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on axion-nucleon coupling constants from measuring the Casimir force between corrugated surfaces. Phys. Rev. D 2014, 90, 055013. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Improved constraints on the coupling constants of axion-like particles to nucleons from recent Casimir-less experiment. Eur. Phys. J. C 2015, 75, 164. [Google Scholar] [CrossRef]
- Spero, R.; Hoskins, J.K.; Newman, R.; Pellam, J.; Schultz, J. Test of the Gravitational Inverse-Square Law at Laboratory Distances. Phys. Rev. Lett. 1980, 44, 1645–1648. [Google Scholar] [CrossRef]
- Long, J.C.; Chan, H.W.; Churnside, A.B.; Gulbis, E.A.; Varney, M.C.M.; Price, J.C. Upper limits to submillimetre-range forces from extra space-time dimensions. Nature 2003, 421, 922–925. [Google Scholar] [CrossRef]
- Yan, H.; Housworth, E.A.; Meyer, H.O.; Visser, G.; Weisman, E.; Long, J.C. Absolute measurement of thermal noise in a resonant short-range force experiment. Class. Quant. Grav. 2014, 31, 205007. [Google Scholar] [CrossRef]
- Long, J.C.; Kostelecký, V.A. Search for Lorentz violation in short-range gravity. Phys. Rev. D 2015, 91, 092003. [Google Scholar] [CrossRef]
- Grifols, J.A.; Massó, E.; Toldrà, R. Majorana neutrinos and long range forces. Phys. Lett. B 1996, 389, 563–565. [Google Scholar] [CrossRef]
- Hollik, W.G.; Linster, M.; Tabet, T. A study of New Physics searches with tritium and similar molecules. Eur. Phys. J. C 2020, 80, 661. [Google Scholar] [CrossRef]
- Daido, R.; Takahashi, F. The sign of the dipole-dipole potential by axion exchange. Phys. Lett. B 2017, 772, 127–129. [Google Scholar] [CrossRef]
- Vasilakis, G.; Brown, J.M.; Kornak, T.R.; Romalis, M.V. Limits on New Long Range Nuclear Spin-Dependent Forces Set with a K-3He Comagnetometer. Phys. Rev. Lett. 2009, 103, 261801. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, N.F. The tensor force between two protons at long range. Physica A 1979, 96, 285–289. [Google Scholar] [CrossRef]
- Ledbetter, M.P.; Romalis, M.V.; Jackson Kimball, D.F. Constraints on Short-Range Spin-Dependent Interactions from Scalar Spin-Spin Coupling in Deuterated Molecular Hydrogen. Phys. Rev. Lett. 2013, 110, 040402. [Google Scholar] [CrossRef]
- Almasi, A.; Lee, J.; Winarto, H.; Smiciklas, M.; Romalis, M.V. New Limits on Anomalous Spin-Spin Interactions. Phys. Rev. Lett. 2020, 125, 201802. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Ding, J.; Wang, J.; Ren, X. Constraints on spin-dependent exotic interactions between electrons at the nanometer scale. Phys. Rev. D 2017, 96, 055028. [Google Scholar] [CrossRef]
- Choi, T.; Paul, W.; Rolf-Pissarczyk, S.; Macdonald, A.J.; Natterer, F.D.; Yang, K.; Willke, P.; Lutz, C.P.; Heinrich, A.J. Atomic-scale sensing of the magnetic dipolar field from single atoms. Nat. Nanotech. 2017, 12, 420. [Google Scholar] [CrossRef]
- Baumann, S.; Paul, W.; Choi, T.; Lutz, C.P.; Ardavan, A.; Heinrich, A.J. Electron paramagnetic resonance of individual atoms on a surface. Science 2015, 350, 417. [Google Scholar] [CrossRef]
- Kotler, S.; Ozeri, R.; Jackson Kimball, D.F. Constraints on Exotic Dipole-Dipole Couplings between Electrons at the Micrometer Scale. Phys. Rev. Lett. 2015, 115, 081801. [Google Scholar] [CrossRef] [PubMed]
- Kotler, S.; Akerman, N.; Navon, N.; Glickman, Y.; Ozeri, R. Measurement of the magnetic interaction between two bound electrons of two separate ions. Nature 2014, 510, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Karshenboim, S.G. Constraints on a long-range spin-dependent interaction from precision atomic physics. Phys. Rev. D 2010, 82, 113013. [Google Scholar] [CrossRef]
- Ji, W.; Chen, Y.; Fu, C.; Ding, M.; Fang, J.; Xiao, Z.; Wei, K.; Yan, H. New Experimental Limits on Exotic Spin-Spin-Velocity-Dependent Interactions by Using SmCo5 Spin Sources. Phys. Rev. Lett. 2018, 121, 261803. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Chu, P.-H.; Savukov, I.; Newman, S. Experimental limit on an exotic parity-odd spin- and velocity-dependent interaction using an optically polarized vapor. Nat. Commun. 2019, 10, 2245. [Google Scholar] [CrossRef] [PubMed]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraining axion coupling constants from measuring the Casimir interaction between polarized test bodies. Phys. Rev. D 2016, 94, 035011. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Casimir Force between Ferromagnetic Surfaces of a Ni-Coated Sphere and a Ni-Coated Plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Casimir interaction between two magnetic metals in comparison with nonmagnetic test bodies. Phys. Rev. B 2013, 88, 155410. [Google Scholar] [CrossRef]
- Derbin, A.V.; Kayunov, A.S.; Muratova, V.V.; Semenov, D.A.; Unzhakov, E.V. Constraints on the axion-electron coupling for solar axions produced by a Compton process and bremsstrahlung. Phys. Rev. D 2011, 83, 023505. [Google Scholar] [CrossRef]
- Falk, A.L.; Klimov, P.V.; Ivády, V.; Szász, K.; Christle, D.J.; Koehl, W.F.; Gali, A.; Awschalom, D.D. Optical Polarization of Nuclear Spins in Silicon Carbide. Phys. Rev. Lett. 2015, 114, 247603. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.-C.; Mota, D.F.; Shaw, D. Detecting chameleons through Casimir force measurements. Phys. Rev. D 2007, 76, 124034. [Google Scholar] [CrossRef]
- Almasi, A.; Brax, P.; Iannuzzi, D.; Sedmik, R.I.P. Force sensor for chameleon and Casimir force experiments with parallel-plate configuration. Phys. Rev. D 2015, 91, 102002. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P. Casimir pressure between metallic plates out of thermal equilibrium: Proposed test for the relaxation properties of free electrons. Phys. Rev. A 2019, 100, 022511. [Google Scholar] [CrossRef]
- Sedmik, R.I.P. Casimir and non-Newtonian force experiment (CANNEX): Review, status, and outlook. Int. J. Mod. Phys. A 2020, 35, 2040008. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Screening Long-Range Forces through Local Symmetry Restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J.; Levy, A.; Matas, A. Symmetron cosmology. Phys. Rev. D 2011, 84, 103521. [Google Scholar] [CrossRef]
- Elder, B.; Vardanyan, V.; Arkami, Y.; Brax, P.; Davis, A.-C.; Decca, R.S. Classical symmetron force in Casimir experiments. Phys. Rev. D 2020, 101, 064065. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.-C.; Shaw, D. Dilaton and modified gravity. Phys. Rev. D 2010, 82, 063519. [Google Scholar] [CrossRef]
- Ryutov, D.D.; Budker, D.; Flambaum, V.V. A Hypothetical Effect of the Maxwell-Proca Electromagnetic Stresses on Galaxy Rotation Curve. Astrophys. J. 2019, 871, 218. [Google Scholar] [CrossRef]
- Mattioli, L.; Frassino, A.M.; Panella, O. Casimir–Polder interactions with massive photons: Implications for BSM physics. Phys. Rev. D 2019, 100, 116023. [Google Scholar] [CrossRef]
- Kroff, D.; Malta, P.C. Constraining hidden photons via atomic force microscope measurements and the Plimpton-Lawton experiment. Phys. Rev. D 2020, 102, 095015. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. The cosmological constant and the theory of elementary particles. Uspekhi Fiz. Nauk 1968, 95, 209–230, Translated: Sov. Phys. Usp. 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110, Translated: Sov. Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Usp. Fiz. Nauk 1961, 73, 381–422, Translated: Adv. Phys. 1961, 10, 165–209. [Google Scholar] [CrossRef]
- Leonhardt, U. Lifshitz theory of the cosmological constant. Ann. Phys. 2019, 411, 167973. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Klimchitskaya, G.L. Whether an Enormously Large Energy Density of the Quantum Vacuum Is Catastrophic. Symmetry 2019, 11, 314. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Some remarks on axion dark matter, dark energy and energy of the quantum vacuum. Int. J. Mod. Phys. A 2020, 35, 2040036. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.-C. Atomic interferometry test of dark energy. Phys. Rev. D 2016, 94, 104069. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.-C. Casimir, gravitational, and neutron tests of dark energy. Phys. Rev. D 2015, 91, 063503. [Google Scholar] [CrossRef]
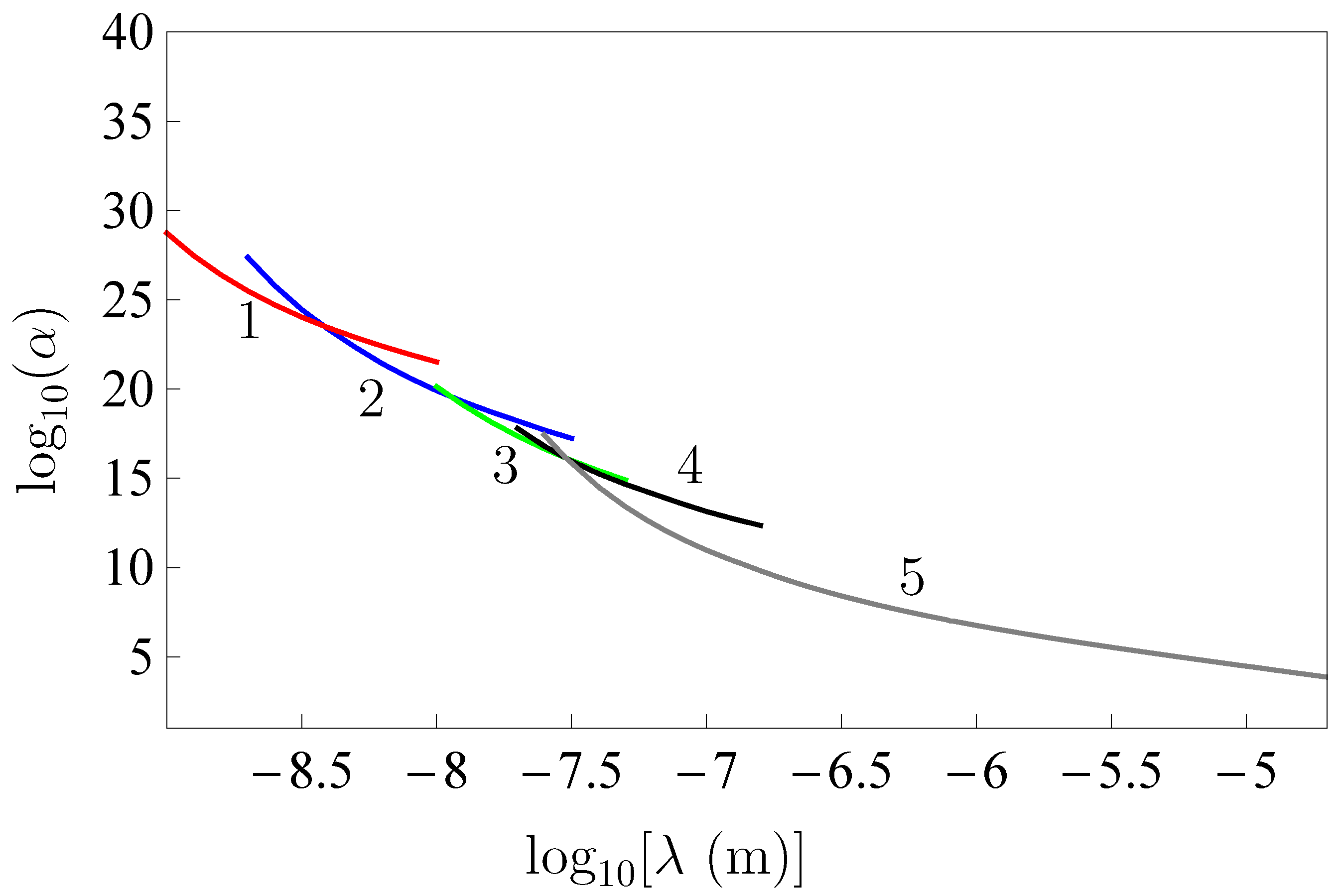
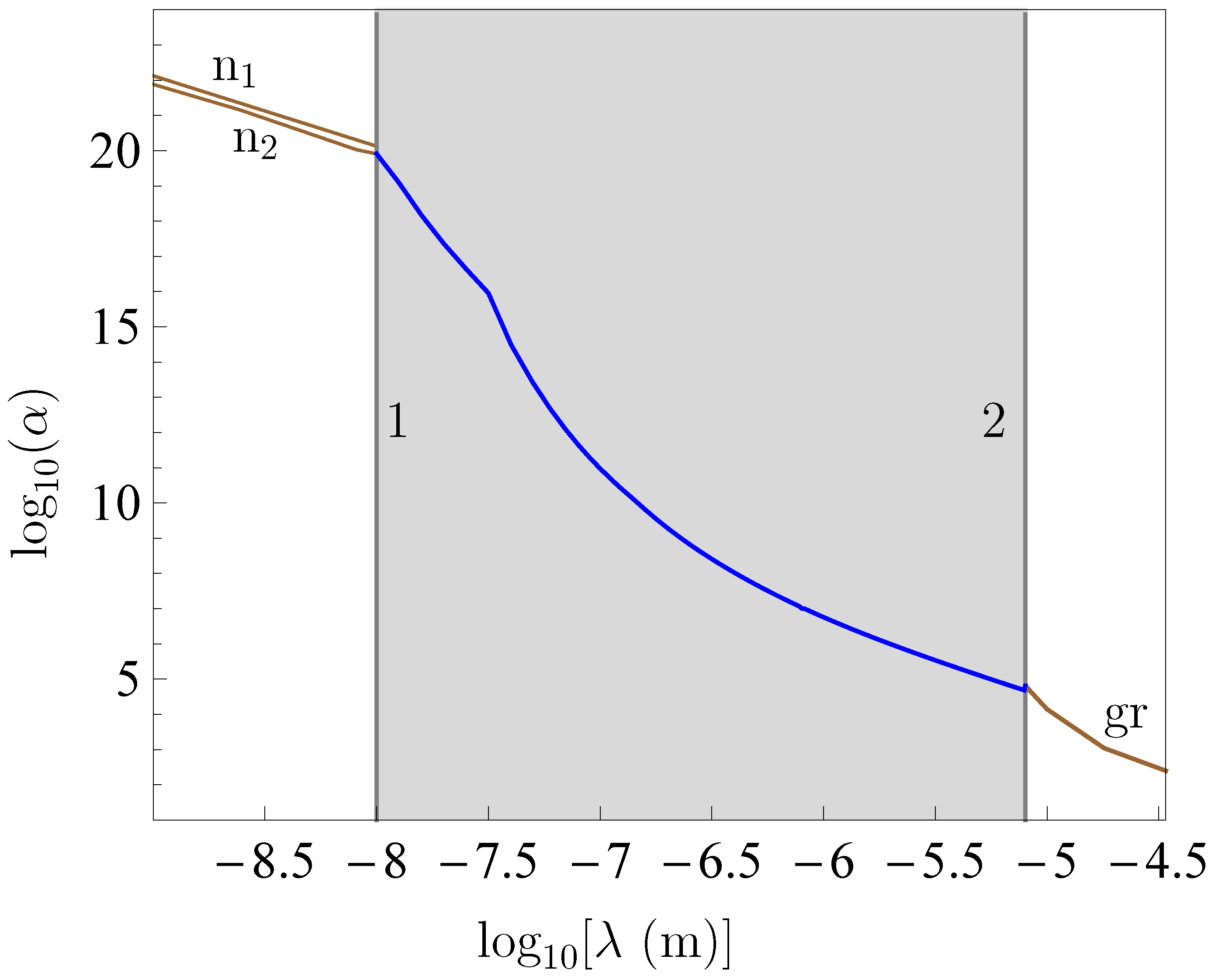

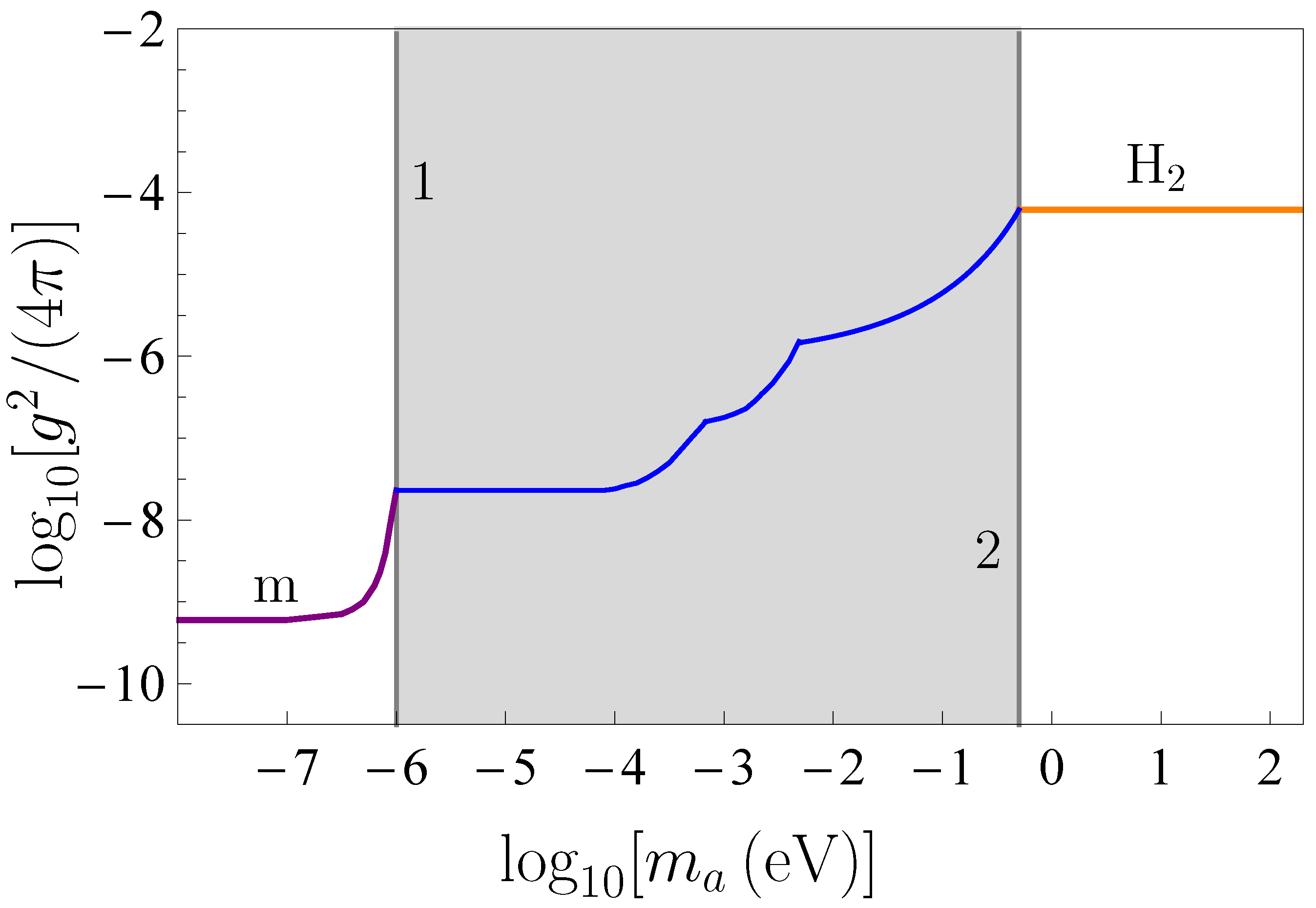
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimchitskaya, G.L. Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics. Universe 2021, 7, 47. https://doi.org/10.3390/universe7030047
Klimchitskaya GL. Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics. Universe. 2021; 7(3):47. https://doi.org/10.3390/universe7030047
Chicago/Turabian StyleKlimchitskaya, Galina L. 2021. "Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics" Universe 7, no. 3: 47. https://doi.org/10.3390/universe7030047
APA StyleKlimchitskaya, G. L. (2021). Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics. Universe, 7(3), 47. https://doi.org/10.3390/universe7030047






