Zeta Functions and the Cosmos—A Basic Brief Review
Abstract
1. Introduction
2. Basics on Zeta Functions
3. On Divergent Series and Zeta Regularization
- If , then .
- If , and , then.
- If , then .
- From axiom 3, for the series , we obtain , and from there . This seems reasonable, because the partial sums of this series oscillate between 0 and 1, and 1/2 is the middle value.
- From axiom 2, we see that for , when we subtract it, term by term, from the series in the preceding example: . Thus, it turns out that . This value is not so easy to understand, logically. The same will occur with many other of the divergent series we will encounter.
3.1. Zeta Regularization in a Nutshell
3.2. The Zeta Function as a Summation Method
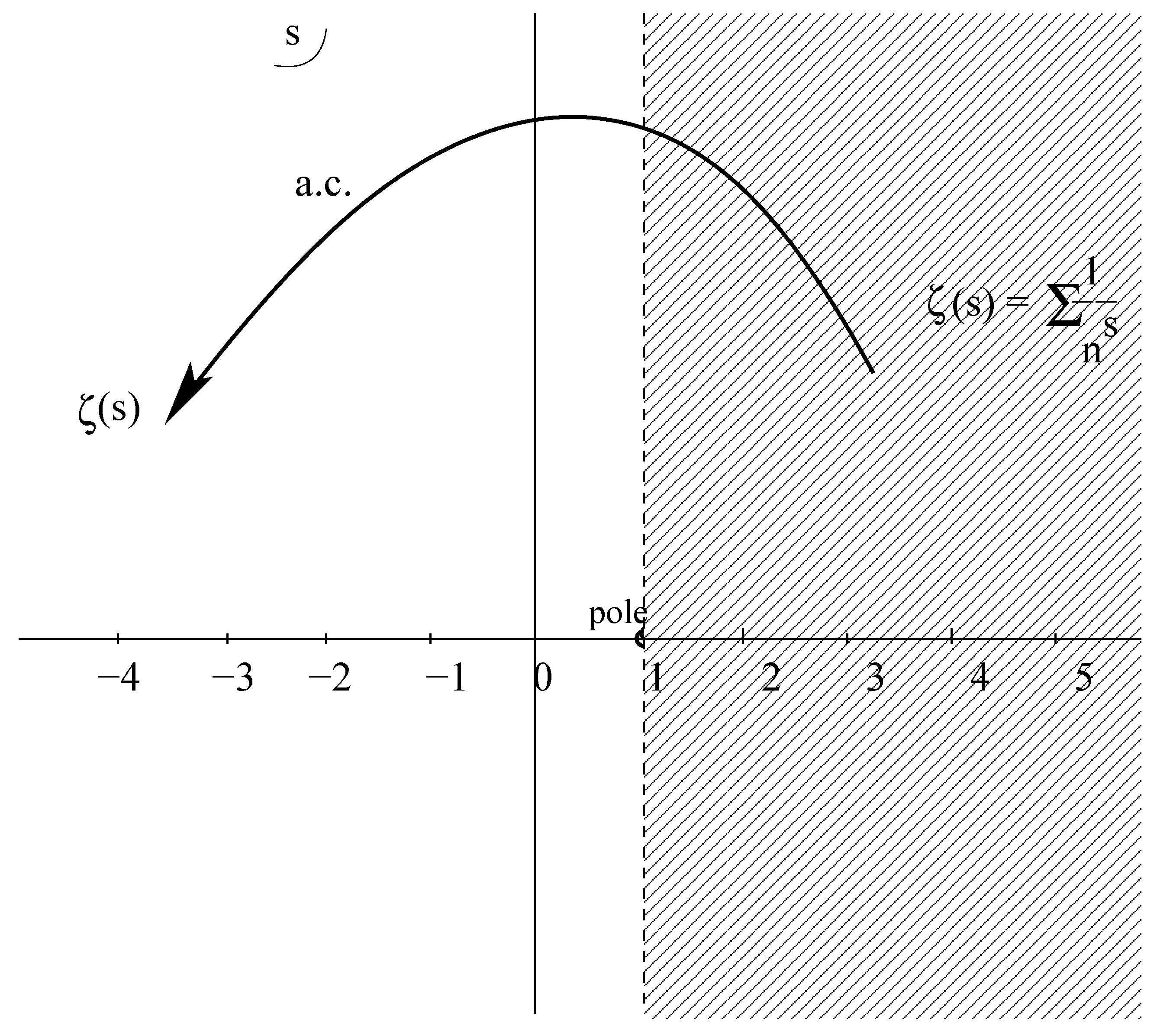
- In view of the zeta function definition, we envisage the seriesas a particular value of the Riemann zeta, namely when . But this point is on the left half of the complex plane, as divided in two by the abscissa of convergence (Figure 1). There, the series as such diverges; but it is not the series, which gives the value of the zeta function there, not on that side of the plane. There, we must use its analytic continuation, which is nicely defined and yields a perfectly finite number, namely . ThusThis is therefore the sum of the series , when we view it as a particular value of the zeta function.
- Next, let us considerWithout more ado, we immediately recognize that this is the zeta function when the exponent is set to . We look at the value of the Riemann zeta there, and it turns out to be . Therefore,
4. The Friedmann-Lemaître-Robertson-Walker (FLRW) Model and the Cosmological Constant
4.1. Towards the Observational Justification of the FLRW Model
4.2. The Universe Is Indeed Homogeneous and Isotropic
4.3. On the Topology and Curvature of Space
4.3.1. On the Curvature of the Universe
4.3.2. On the Topology of the Universe
4.4. The Cosmological Constant and Quantum Vacuum Energy
4.5. From General Relativity to Cosmology: On the Meaning of Einstein’s Equations
- In partial fulfillment of Mach’s principle, he established in his theory that the following ingredients were on the same footing: the space-time geometry (curvature), radiation energy, matter, and the cc.
- The geometric term, , would consist of a linear combination of the metric, , and of its first and second order derivatives, only.
- The energy-momentum tensor, would contain all possible forms of matter and energies in the universe, other than the gravitational one.
5. Zeta-Function Regularization in Curved Spacetime
- Many of the topologies for the space-time manifold are actually not product topologies, of the form , to allow such procedure.
- Some of these non-product topologies are actually quite interesting and worth of study exactly as they are, without unjustified simplifications.
- In view of the Heisenberg uncertainty principle, in quantum mechanical setups the meaning of ‘equal time’ looses precise sense and one is bound to look for alternatives.
5.1. Some Words on the Calculation of the Determinants
5.2. An Update of the Most Influential Contributions on Zeta Function Regularization
6. Quantum Fluctuations of the Cosmological Vacuum Energy
6.1. Two Examples of the Use of the Zeta Function Method
6.2. A Brief Update on the Dynamical Casimir Effect
6.3. An Update of the Impact of Papers on Zeta Functions and Cosmology
7. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wigner, E. The unreasonable effectiveness of mathematics in the natural sciences, Richard courant lecture in mathematical sciences delivered at New York University, May 11, 1959. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Acad. Wet. 1948, 51, 793–795. [Google Scholar]
- Turnbull, H.W. The Great Mathematicians; New York University Press: New York, NY, USA, 1961. [Google Scholar]
- Alton, E.J. Encyclopedia of World Biography; McGraw-Hill: New York, NY, USA, 1973; Volume 4, pp. 30–31. [Google Scholar]
- Maor, E. To Infinity and Beyond: A Cultural History of the Infinite; Princeton University Press: Princeton, NJ, USA, 1991. [Google Scholar]
- Hardy, G.H. Divergent Series; Oxford University Press: Oxford, UK, 1949. [Google Scholar]
- Cao, T.Y.; Schweber, S.S. The conceptual foundations and the philosophical aspects of renormalization theory. Synthese 1993, 97, 33–108. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. Regularization and renormalization of gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Pauli, W.; Villars, F. On the Invariant Regularization in Relativistic Quantum Theory. Rev. Mod. Phys. 1949, 21, 434–444. [Google Scholar] [CrossRef]
- Creutz, M. Quarks, Gluons and Lattices; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Asymptotically Free Gauge Theories I. Phys. Rev. D 1973, 8, 3633–3652. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J.B. The renormalization group and the ϵ expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Scharf, G. Finite Quantum Electrodynamics: The Causal Approach; Springer: Berlin, Germany, 1995. [Google Scholar]
- Blanchet, L.; Faye, G. Hadamard regularization. J. Math. Phys. 2000, 41, 7675–7714. [Google Scholar] [CrossRef]
- Hadamard, J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations; Dover Publications: New York, NY, USA, 1923. [Google Scholar]
- Atiyah, M.F.; Singer, I.M. The Index of Elliptic Operators on Compact Manifolds. Bull. Am. Math. Soc. 1963, 69, 422–433. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Singer, I.M. The Index of Elliptic Operators I. Ann. Math. 1968, 87, 484–530. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Segal, G.B. The Index of Elliptic Operators: II. Ann. Math. 1968, 87, 531–545. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Singer, I.M. The Index of Elliptic Operators III. Ann. Math. 1968, 87, 546–604. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Singer, I.M. The Index of Elliptic Operators IV. Ann. Math. 1971, 93, 119–138. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Singer, I.M. The Index of Elliptic Operators V. Ann. Math. 1971, 93, 139–149. [Google Scholar] [CrossRef]
- Wu, Z.C. The Cosmological Constant is Probably Zero, and a Proof is Possibly Right. Phys. Lett. B 2008, 659, 891–893. [Google Scholar] [CrossRef]
- Stack Overflow Network—What If Cosmological Constant Was Zero? Available online: https://physics.stackexchange.com/questions/373659/what-if-cosmological-constant-was-zero (accessed on 29 December 2020).
- Hawking, S.W. Why is the apparent cosmological constant zero? In Unified Theories of Elementary Particles; Lecture Notes in Physics; Springer: Berlin, Germany, 2005; Volume 160, pp. 167–175. [Google Scholar]
- Steinhardt, P.J.; Turok, N. Why the Cosmological Constant Is Small and Positive. Science 2006, 312, 1180–1183. [Google Scholar] [CrossRef]
- Ramond, P. Field Theory: A Modern Primer; Addison-Wesley: Redwood City, CA, USA, 1989. [Google Scholar]
- Elizalde, E. Multiple zeta-functions with arbitrary exponents. J. Phys. A Gen. Phys. 1989, 22, 931–942. [Google Scholar] [CrossRef]
- Elizalde, E.; Romeo, A. Rigorous extension of the proof of zeta-function regularization. Phys. Rev. D Part. Fields 1989, 40, 436–443. [Google Scholar] [CrossRef]
- Elizalde, E. On the zeta-function regularization of a two-dimensional series of Epstein-Hurwitz type. J. Math. Phys. 1990, 31, 170. [Google Scholar] [CrossRef][Green Version]
- Elizalde, E. Analysis of an inhomogeneous generalized Epstein-Hurwitz zeta function with physical applications. J. Math. Phys. 1994, 35, 6100. [Google Scholar] [CrossRef]
- Elizalde, E. The vacuum energy density for spherical and cylindrical universes. J. Math. Phys. 1994, 35, 3308. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Romeo, A.; Bytsenko, A.A.; Zerbini, S. Zeta Regularization Techniques with Applications; World Scientific: Singapore, 1994. [Google Scholar]
- Elizalde, E. Ten Physical Applications of Spectral Zeta Functions, 2nd ed.; Lecture Notes in Physics; Springer: Berlin, Germany, 2012; Volume 855. [Google Scholar]
- Bytsenko, A.A.; Cognola, G.; Vanzo, L.; Zerbini, S. Quantum Fields and Extended Objects in Space-Times with Constant Curvature Spatial Section. Phys. Rep. 1996, 266, 1–126. [Google Scholar] [CrossRef]
- Bender, C.B.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Chowla, S.; Selberg, A. On Epstein’s zeta function (I). Proc. Natl. Acad. Sci. USA 1949, 35, 317–374. [Google Scholar] [CrossRef] [PubMed]
- Elizalde, E. An extension of the Chowla-Selberg formula useful in quantizing with the Wheeler-De Witt equation. J. Phys. A 1994, 27, 3775–3786. [Google Scholar] [CrossRef][Green Version]
- Elizalde, E. Zeta function regularization is uniquely defined and well. J. Phys. A Math. Gen. 1994, 27, L299–L304. [Google Scholar] [CrossRef]
- Iyanaga, S.; Kawada, Y. (Eds.) Encyclopedic Dictionary of Mathematics; The MIT Press: Cambridge, UK, 1977; Volume II, p. 1372. [Google Scholar]
- Elizalde, E. Multidimensional extension of the generalized Chowla-Selberg formula. Commun. Math. Phys. 1998, 198, 83–95. [Google Scholar] [CrossRef]
- Elizalde, E. Zeta functions: Formulas and applications. J. Comput. Appl. Math. 2000, 118, 125–142. [Google Scholar] [CrossRef]
- Elizalde, E. Explicit zeta functions for bosonic and fermionic fields on a non-commutative toroidal spacetime. J. Phys. A 2001, 34, 3025–3036. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Collins, J. Renormalization: An Introduction to Renormalization, the Renormalization Group and the Operator-Product Expansion; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- McComb, W.D. Renormalization Methods: A Guide for Beginners; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Elizalde, E. On the concept of determinant for the differential operators of Quantum Physics. J. High Energy Phys. 1999, 9907, 015. [Google Scholar] [CrossRef]
- Bernhard, R. Über die Anzahl der Primzahlen unter einer gegebenen Grösse, Monatsberichte der Berliner Akademie. In Gesammelte Werke; Teubner: Leipzig, Germany, 1892; Reprinted by Dover: New York, NY, USA, 1953. [Google Scholar]
- Bombieri, E. The Riemann Hypothesis—Official Problem Description. Clay Mathematics Institute. Available online: https://www.claymath.org/sites/default/files/official_problem_description.pdf (accessed on 29 December 2020).
- Burton, D.M. Elementary Number Theory; Tata McGraw-Hill Publishing Company Limited: Noida, India, 2006. [Google Scholar]
- Knauf, A. Number theory, dynamical systems and statistical mechanics. Rev. Math. Phys. 1999, 11, 1027–1060. [Google Scholar] [CrossRef]
- Wiles, A. Twenty years of number theory. In Mathematics: Frontiers and Perspectives, Providence; American Mathematical Society: Providence, RI, USA, 2000; pp. 32–342. [Google Scholar]
- Gelbart, S.S.; Miller, S.D. Riemann’s zeta function and beyond. Bull. Am. Math. Soc. (NS) 2004, 41, 59–112. [Google Scholar] [CrossRef]
- Bytsenko, A.A.; Cognola, G.; Elizalde, E.; Moretti, V.; Zerbini, S. Analytic Aspects of Quantum Fields; World Scientific: Singapore, 2004. [Google Scholar]
- Van Dyck, R.S., Jr. Anomalous Magnetic Moment of Single Electrons and Positrons: Experiment. In Quantum Electrodynamics; Kinoshita, T., Ed.; World Scientific: Singapore, 1990; pp. 322–388. [Google Scholar]
- Kinoshita, T. The Fine structure constant. Rep. Prog. Phys. 1996, 59, 1459. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Demonstration of the Casimir Force in the 0.6 to 6 m Range. Phys. Rev. Lett. 1997, 78, 5–9. [Google Scholar] [CrossRef]
- Mohideen, U.; Roy, A. Precision Measurement of the Casimir Force from 0.1 to 0.9 m. Phys. Rev. Lett. 1998, 81, 4549. [Google Scholar] [CrossRef]
- Harris, B.W.; Chen, F.; Mohideen, U. Precision measurement of the Casimir force using gold surfaces. Phys. Rev. A 2000, 62, 052109. [Google Scholar] [CrossRef]
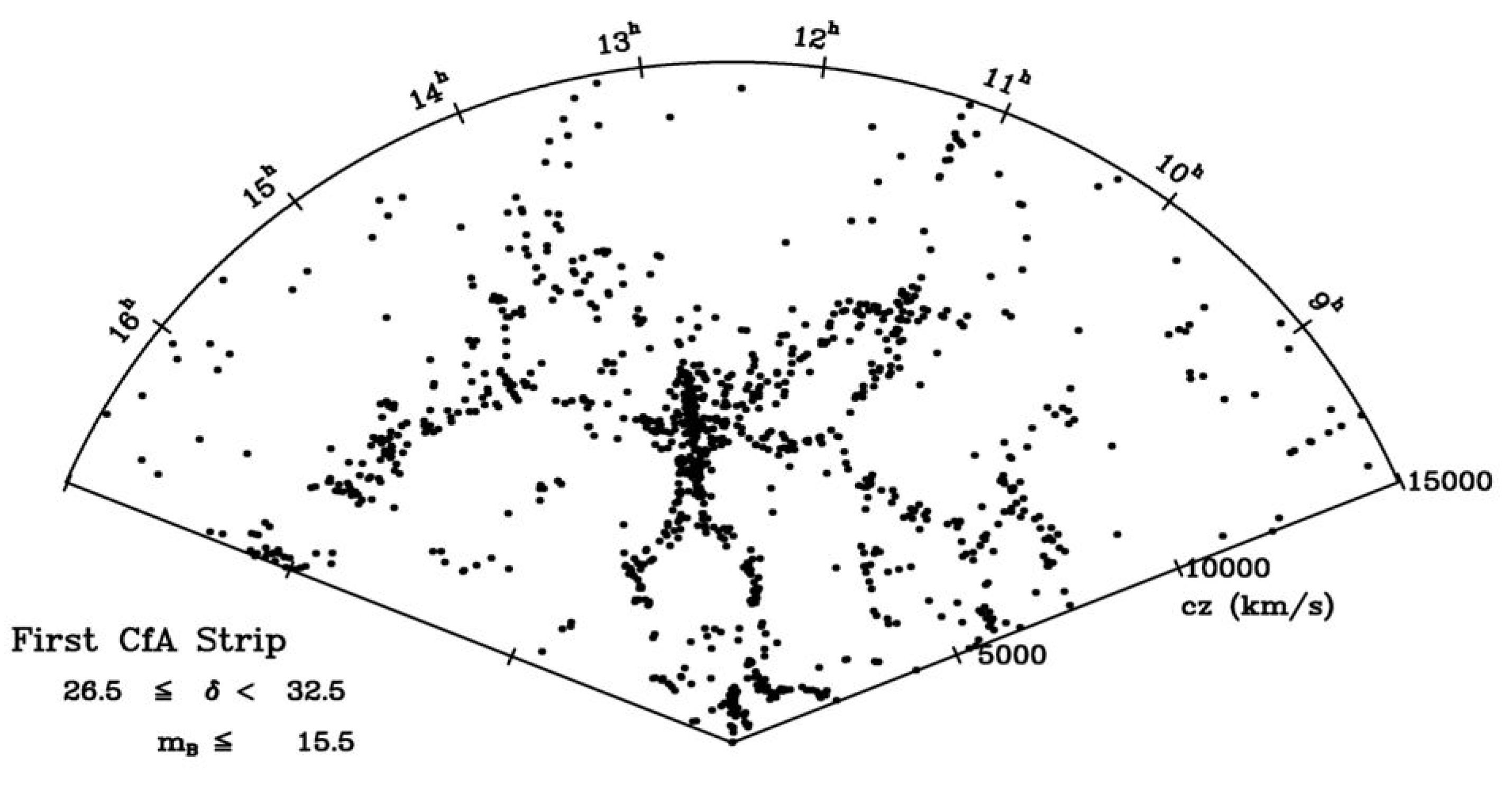
- de Lapparent, V.; Geller, M.J.; Huchra, J. A slice of the universe. Astrophys. J. Lett. 1986, 302, L1–L5. [Google Scholar] [CrossRef]
- de Lapparent, V.; Geller, M.J.; Huchra, J. The mean density and two-point correlation function for the CfA redshift survey slices. Astrophys. J. 1988, 332, 44–56. [Google Scholar] [CrossRef]
- da Costa, L.N.; Pellegrini, P.S.; Sargent, W.L.W.; Tonry, J.; Davis, M.; Meiksin, A.; Latham, D.W.; Menzies, J.W.; Coulson, I.A. The southern sky redshift survey. Astrophys. J. 1988, 327, 544. [Google Scholar] [CrossRef]
- Jones, B.J.T. The Large Scale Structure of the Universe. In Observational and Physical Cosmology; Sánchez, F., Collados, M., Rebolo, R., Eds.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Ostriker, J.P.; Thompson, C.; Witten, E. Cosmological effects of superconducting strings. Phys. Lett. B 1986, 180, 231–239. [Google Scholar] [CrossRef]
- Geller, M.J.; Huchra, J. Mapping the universe. Science 1989, 246, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of galaxies and large-scale structure with cold dark matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- Planck Project. Available online: http://www.rssd.esa.int/index.php?project=Planck (accessed on 27 December 2020).
- European Space Agency. Available online: http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=34730 (accessed on 27 December 2020).
- Sloan Digital Sky Survey. Available online: http://www.sdss.org (accessed on 27 December 2020).
- APM Survey, Oxford. Available online: http://www-astro.physics.ox.ac.uk/~wjs/apm_survey.html (accessed on 27 December 2020).
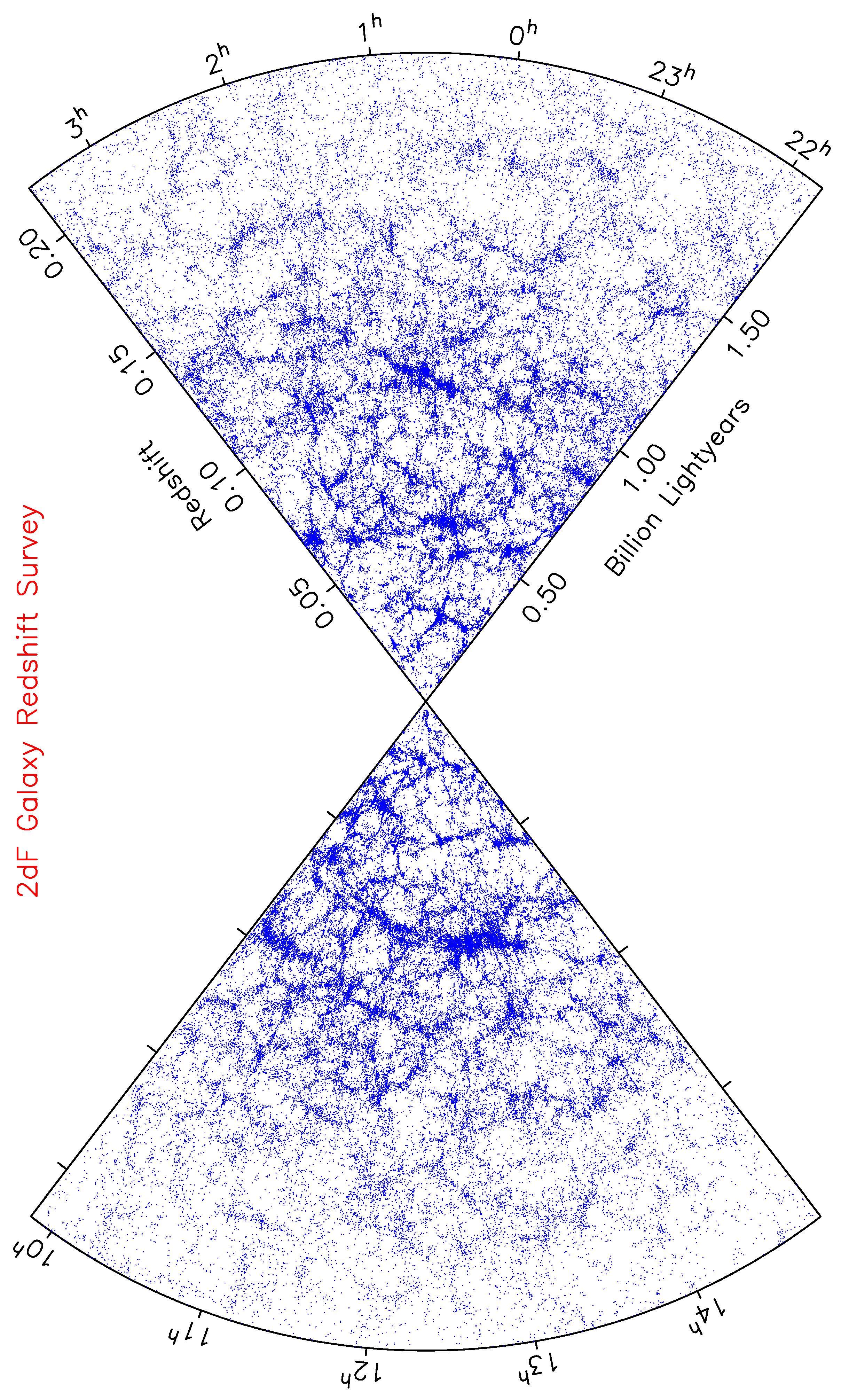
- The 2dF Galaxy Redshift Survey. Available online: http://www.aao.gov.au/2df/ (accessed on 27 December 2020).
- Wilkinson Microwave Anisotropy Probe. Available online: http://map.gsfc.nasa.gov/ (accessed on 27 December 2020).
- Saslaw, W.C. The Distribution of the Galaxies: Gravitational Clustering in Cosmology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Totsuji, H.; Kihara, T. The correlation function for the distribution of galaxies. Publ. Astron. Soc. Jpn. 1969, 21, 221. [Google Scholar]
- Saadeh, D.; Feeney, S.M.; Pontzen, A.; Peiris, H.V.; McEwen, J.D. How Isotropic is the Universe? Phys. Rev. Lett. 2016, 117, 131302. [Google Scholar] [CrossRef] [PubMed]
- Tegmark, M. Measuring spacetime: From Big Bang to Black Holes. Science 2002, 296, 1427–1433. [Google Scholar] [CrossRef] [PubMed]
- Handley, W. Curvature tension: Evidence for a closed universe. arXiv 2019, arXiv:1908.09139. [Google Scholar]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters. arXiv 2020, arXiv:2007.07288. [Google Scholar]
- Cornish, N.J.; Spergel, D.N.; Starkman, G.D.; Komatsu, E. Constraining the Topology of the Universe. Phys. Rev. Lett. 2004, 92, 201302. [Google Scholar] [CrossRef]
- Luminet, J.-P.; Weeks, J.R.; Riazuelo, A.; Lehoucq, R.; Uzan, J.-P. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature 2003, 425, 593–595. [Google Scholar] [CrossRef]
- Luminet, J.-P. Cosmic Topology. Scholarpedia 2015, 10, 31544. [Google Scholar] [CrossRef]
- Bjørken, J.D. Cosmology and the standard model. Phys. Rev. D 2003, 67, 043508. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Fischler, W.; Klebanov, I.; Polchinski, J.; Susskind, L. Quantum mechanics of the googolplexus. Nucl. Phys. B 1989, 237, 157–177. [Google Scholar] [CrossRef]
- Coleman, S. Why there is nothing rather than something: A theory of the cosmological constant. Nucl. Phys. B 1988, 310, 643–668. [Google Scholar] [CrossRef]
- Coleman, S. Black holes as red herrings: Topological fluctuations and the loss of quantum coherence. Nucl. Phys. B 1988, 307, 867–882. [Google Scholar] [CrossRef]
- Weinberg, S. Anthropic bound on the cosmological constant. Phys. Rev. Lett. 1987, 59, 2607. [Google Scholar] [CrossRef] [PubMed]
- Baum, E. Zero cosmological constant from minimum action. Phys. Lett. B 1984, 133, 185–186. [Google Scholar] [CrossRef]
- Hawking, S.W. The cosmological constant is probably zero. Phys. Lett. B 1984, 134, 403–404. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Elizalde, E. Some issues on the foundations of Modern Cosmology, Gravitation and Quantum Physics. Universe 2020, 6, 189. [Google Scholar] [CrossRef]
- Wilczek, F. Total Relativity: Mach 2004. Phys. Today 2004, 57, 10–12. [Google Scholar] [CrossRef]
- Peebles, P.J. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Peebles, P.J. Large-Scale Structure of the Universe; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Structure Formation in the Universe; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hawking, S.W. Zeta function regularization of path integrals in curved spacetime. Commun. Math. Phys. 1977, 55, 133–148. [Google Scholar] [CrossRef]
- Hawking, S.W.; Israel, W. (Eds.) General Relativity, an Einstein Centenary Survey; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Ramond, P. Field Theory, a Modern Primer; The Benjamin/Cummings Publishing: San Francisco, CA, USA, 1981. [Google Scholar]
- Birrell, N.; Davies, P.C.W. Quantum Fields in Curved Spaces; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP Publishing: Bristol, UK, 1992. [Google Scholar]
- Kirsten, K.; Elizalde, E. Casimir energy of a massive field in a genus-1 surface. Phys. Lett. B 1996, 365, 72–78. [Google Scholar] [CrossRef]
- Calderón, A.P.; Zygmund, A. Singular integral operators and differential equations. Am. J. Math. 1957, 79, 901–921. [Google Scholar] [CrossRef]
- Calderón, A.P.; Zygmund, A. Local properties of solutions of elliptic partial differential equations. Stud. Math. 1961, 20, 181–225. [Google Scholar] [CrossRef]
- Calderón, A.P.; Vaillancourt, R. A class of bounded pseudo-differential operators. Proc. Natl. Acad. Sci. USA 1972, 69, 1185–1187. [Google Scholar] [CrossRef]
- Hörmander, L. The Analysis of Partial Differential Operators; Springer: Berlin, Germany, 1983–1985; Volumes I–IV. [Google Scholar]
- Treves, F. Introduction to Pseudodifferential and Fourier Integral Operators; Plenum: New York, NY, USA, 1980; Volumes I and II. [Google Scholar]
- Taylor, M.E. Pseudodifferential Operators; Princeton University Press: Princeton, NJ, USA, 1981. [Google Scholar]
- Lawson, H.; Michelsohn, M.L. Spin Geometry; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin, Germany, 1980. [Google Scholar]
- Dowker, J.S.; Critchley, R. Effective Lagrangian and energy-momentum tensor in de Sitter space. Phys. Rev. D 1976, 13, 3224. [Google Scholar] [CrossRef]
- Kirsten, K. Spectral Functions in Mathematics and Physics; Chapman & Hall: London, UK, 2001. [Google Scholar]
- Blau, S.K.; Visser, M.; Wipf, A. Analytic results for the effective action. Int. J. Mod. Phys. A 1991, 6, 5409–5433. [Google Scholar] [CrossRef]
- Bordag, M.; Elizalde, E.; Kirsten, K. Heat kernel coefficients of the Laplace operator on the D-dimensional ball. J. Math. Phys. 1996, 37, 895–916. [Google Scholar] [CrossRef]
- Vassilevich, D.V. Heat kernel expansion: User’s manual. Phys. Rep. 2003, 388, 279–360. [Google Scholar] [CrossRef]
- Perlmutter, S.; et al. [Supernova Cosmology Project Collaboration] Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; et al. [Hi-Z Supernova Team Collaboration] Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Tonry, J.L.; Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Coil, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C. Cosmological results from high-z supernovae. Astrophys. J. 2003, 594, 1–24. [Google Scholar] [CrossRef]
- Knop, R.A.; Aldering, G.; Amanullah, R.; Astier, P.; Blanc, G.; Burns, M.S.; Conley, A.; Deustua, S.E.; Doi, M.; Ellis, R.; et al. New Constraints on ΩM, ΩΛ, and w from an Independent Set of 11 High-Redshift Supernovae Observed with the Hubble Space Telescope. Astrophys. J. 2003, 598, 102–137. [Google Scholar] [CrossRef]
- Garavini, G.; Folatelli, G.; Goobar, A.; Nobili, S.; Aldering, G.; Amadon, A.; Amanullah, R.; Astier, P.; Balland, C.; Blanc, G.; et al. Spectroscopic observations and analysis of the peculiar SN 1999aa. Astron. J. 2004, 128, 387–404. [Google Scholar] [CrossRef]
- Riess, A.G. The case for an accelerating universe from supernovae. Publ. Astron. Soc. Pac. 2000, 112, 1284. [Google Scholar] [CrossRef]
- Carroll, S.M. Why is the Universe Accelerating? In Measuring and Modeling the Universe; Freedman, W.L., Ed.; Carnegie Observatories Astrophysics Series; Cambridge University Press: Cambridge, UK, 2004; Volume 2. [Google Scholar]
- de Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; Gasperis, G.D.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef]
- Hanany, S.; Ade, P.; Balbi, A.; Bock, J.; Borrill, J.; Boscaleri, A.; de Bernardis, P.; Ferreira, P.G.; Hristov, V.V.; Jaffe, A.H.; et al. MAXIMA-1: A Measurement of the cosmic microwave background anisotropy on angular scales of 10 arcminutes to 5 degrees. Astrophys. J. Lett. 2000, 545, L5. [Google Scholar] [CrossRef]
- Balbi, A.; Ade, P.; Bock, J.; Borrill, J.; Boscaleri, A.; de Bernardis, P.; Ferreira, P.G.; Hanany, S.; Hristov, V.V.; Jaffe, A.H.; et al. Constraints on cosmological parameters from MAXIMA-1. Astrophys. J. Lett. 2000, 545, L1–L4. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astroph. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Heath Jones, D.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2011, 418, 1707–1724. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Bizyaev, D.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; Cuesta, A.J.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Release 9 spectroscopic galaxy sample. Mon. Not. R. Astron. Soc. 2012, 427, 3435–3467. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; et al. [DES collaboration] Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing. Phys. Rev. D 2019, 99, 123505. [Google Scholar] [CrossRef]
- Pain, R.; Astier, P. Observational evidence of the accelerated expansion of the Universe. C. R. Phys. 2012, 13, 521–538. [Google Scholar]
- Sahni, V.; Starobinsky, A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Solà, J. On the scaling behavior of the cosmological constant and the possible existence of new forces and new light degrees of freedom. Phys. Lett. B 2000, 475, 236–246. [Google Scholar] [CrossRef]
- Mongan, T.R. A Simple Quantum Cosmology. Gen. Relativ. Gravit. 2001, 33, 1415–1424. [Google Scholar] [CrossRef]
- Weinberg, S. A Priori Probability Distribution of the Cosmological Constant. Phys. Rev. D 2000, 61, 103505. [Google Scholar] [CrossRef]
- Blanloeil, V.; Roukema, B.F. (Eds.) Cosmological Topology in Paris 1998. arXiv 1998, arXiv:astro-ph/0010170. [Google Scholar]
- Sokolov, I.Y. Topologically nontrivial nature of the universe in connection with the anisotropy of the background radiation. JETP Lett. 1993, 57, 617–621. [Google Scholar]
- Cornish, N.J.; Spergel, D.; Starkman, G. Circles in the Sky: Finding Topology with the Microwave Background Radiation. Class. Quant. Gravity 1998, 15, 2657–2670. [Google Scholar] [CrossRef]
- Cornish, N.J.; Spergel, D.; Starkman, G. Does Chaotic Mixing Facilitate Ω<1 Inflation? Phys. Rev. Lett. 1996, 77, 215–218. [Google Scholar]
- Müller, D.; Fagundes, H.V.; Opher, R. Casimir energy in a small volume multiply connected static hyperbolic pre-inflationary Universe. Phys. Rev. D 2001, 63, 123508. [Google Scholar] [CrossRef]
- Banks, T.; Dine, M.; Nelson, A.E. Constraints on theories with large extra dimensions. J. High Energy Phys. 1999, 06, 014. [Google Scholar] [CrossRef]
- Elizalde, E. Complete determination of the singularity structure of zeta functions. J. Phys. A 1997, 30, 2735–2744. [Google Scholar] [CrossRef]
- Elizalde, E. A very simple computation of the Casimir effect. II Nuovo Cim. B 1989, 104, 685–700. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Repulsive Casimir effect from extra dimensions and Robin boundary conditions: From branes to pistons. Phys. Rev. D 2009, 79, 065023. [Google Scholar] [CrossRef]
- Elizalde, E.; Saharian, A.A.; Vardanyan, T.A. Casimir effect for parallel plates in de Sitter spacetime. Phys. Rev. D 2010, 81, 124003. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Fermionic condensate and Casimir densities in the presence of compact dimensions with applications to nanotubes. Phys. Rev. D 2011, 83, 105023. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Fermionic Casimir densities in anti-de Sitter spacetime. Phys. Rev. D 2013, 87, 084003. [Google Scholar] [CrossRef]
- Sahni, V.; Habib, S. Does Inflationary Particle Production suggest Ωm<1? Phys. Rev. Lett. 1998, 81, 1766–1769. [Google Scholar]
- Parker, L.; Raval, A. Nonperturbative effects of vacuum energy on the recent expansion of the universe. Phys. Rev. D 1999, 60, 063512. [Google Scholar] [CrossRef]
- Parker, L.; Raval, A. Vacuum effects of ultra-low mass particle account for Recent Acceleration of Universe. Phys. Rev. D 1999, 60, 123502. [Google Scholar] [CrossRef]
- Parker, L.; Raval, A. New quantum aspects of a vacuum-dominated universe. Phys. Rev. D 2000, 62, 083503, Erratum in Phys. Rev. D 2003, 67, 029903. [Google Scholar] [CrossRef]
- Dodonov, V. Fifty Years of the Dynamical Casimir Effect. Physics 2020, 2, 67–104. [Google Scholar] [CrossRef]
- Moore, G.T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 1970, 11, 2679–2691. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum field theory in curved spacetime. Phys. Rep. 1975, 19, 295–357. [Google Scholar] [CrossRef]
- Fulling, S.A.; Davies, P.C.W. Radiation from a moving mirror in two-dimensional space-time: Conformal anomaly. Proc. R. Soc. Lond. A 1976, 348, 393–414. [Google Scholar]
- Ford, L.H.; Vilenkin, A. Quantum radiation by moving mirrors. Phys. Rev. D 1982, 25, 2569–2575. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Klimov, A.B.; Man’ko, V.I. Nonstationary Casimir effect and oscillator energy level shift. Phys. Lett. A 1989, 142, 511–513. [Google Scholar] [CrossRef]
- Golestanian, R.; Kardar, M. Path integral approach to the dynamic Casimir effect with fluctuating boundaries. Phys. Rev. A 1998, 58, 1713–1722. [Google Scholar] [CrossRef]
- Haro, J.; Elizalde, E. Hamiltonian approach to the dynamical Casimir effect. Phys. Rev. Lett. 2006, 97, 130401. [Google Scholar] [CrossRef]
- Haro, J.; Elizalde, E. Physically sound Hamiltonian formulation of the dynamical Casimir effect. Phys. Rev. D 2007, 76, 065001. [Google Scholar] [CrossRef]
- Elizalde, E. Dynamical Casimir effect with semi-transparent mirrors, and cosmology. J. Phys. A Math. Theor. 2008, 41, 164061. [Google Scholar] [CrossRef][Green Version]
- Haro, J.; Elizalde, E. Black hole collapse simulated by vacuum fluctuations with a moving semitransparent mirror. Phys. Rev. D 2008, 77, 045011. [Google Scholar] [CrossRef]
- Kim, W.-J.; Brownell, J.H.; Onofrio, R. Detectability of dissipative motion in quantum vacuum via superradiance. Phys. Rev. Lett. 2006, 96, 200402. [Google Scholar] [CrossRef]
- Brevik, I.; Milton, K.A.; Odintsov, S.D.; Osetrin, K.E. Dynamical Casimir effect and quantum cosmology. Phys. Rev. D 2000, 62, 064005. [Google Scholar] [CrossRef]
- Christensen, S.M.; Duff, M.J. Quantizing gravity with a cosmological constant. Nucl. Phys. B 1980, 170, 480–506. [Google Scholar] [CrossRef]
- Elizalde, E. Uses of zeta regularization in QFT with boundary conditions: A cosmo-topological Casimir effect. J. Phys. A Math. Gen. 2006, 39, 6299–6307. [Google Scholar] [CrossRef]
- Aref’eva, I.Y.; Volovich, I.V. Quantization of the Riemann zeta-function and cosmology. Int. J. Geom. Methods Mod. Phys. 2007, 4, 881–895. [Google Scholar] [CrossRef]
- Elizalde, E. Matching the observational value of the cosmological constant. Phys. Lett. B 2001, 516, 143–150. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—The weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Wetterich, C. The cosmon model for an asymptotically vanishing time-dependent cosmological “constant”. Astron. Astrophys. 1995, 301, 321–328. [Google Scholar]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D. Late-time cosmology in (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. D 2004, 70, 043539. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Wang, Q.; Unruh, W.G. Comment on “Hiding the Cosmological Constant”. Phys. Rev. Lett. 2020, 125, 089001. [Google Scholar] [CrossRef]
- Gurzadyan, V.G.; Stepanian, A. Cosmological constant as a fundamental constant. Eur. Phys. J. Plus 2019, 134, 98. [Google Scholar] [CrossRef]
- Leonhardt, U. Lifshitz theory of the cosmological constant. Ann. Phys. 2019, 411, 167973. [Google Scholar] [CrossRef]
- Carlip, S. Hiding the cosmological constant. Phys. Rev. Lett. 2019, 123, 131302. [Google Scholar] [CrossRef] [PubMed]
- Santos, E. The cosmological constant problem or how the quantum vacuum drives the slow accelerating expansion of the universe. arXiv 2018, arXiv:1805.03018. [Google Scholar]
| 1. | Einstein was so successful that he is now generally considered to be the author of this statement. |
| 2. | For completeness, we should add Padé approximates to the list [45]. |
| 3. | The trace is very non-linear. But many people seem to forget this basic fact and numerous errors have been committed because of this—and published sometimes in very good journals. Often, the erroneous conclusion has been reached that the zeta function method was not working, when the mistake was due to an illegal application of the same [48]. |
| 4. | This theorem says that the amount of prime numbers less than or equal to a given positive integer, x, goes as , when . The theorem was actually proven, making use of Riemann’s work, by Hadamard and De la Vallé-Poussin. |
| 5. | At this very point one recovers the original harmonic series and this divergence remains. |
| 6. | |
| 7. | Namely, one or two extra dimensions, with possible compactification radii of the order of the Planck length. |


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elizalde, E. Zeta Functions and the Cosmos—A Basic Brief Review. Universe 2021, 7, 5. https://doi.org/10.3390/universe7010005
Elizalde E. Zeta Functions and the Cosmos—A Basic Brief Review. Universe. 2021; 7(1):5. https://doi.org/10.3390/universe7010005
Chicago/Turabian StyleElizalde, Emilio. 2021. "Zeta Functions and the Cosmos—A Basic Brief Review" Universe 7, no. 1: 5. https://doi.org/10.3390/universe7010005
APA StyleElizalde, E. (2021). Zeta Functions and the Cosmos—A Basic Brief Review. Universe, 7(1), 5. https://doi.org/10.3390/universe7010005




