Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral
Abstract
1. Introduction
2. Singular and Regular Black-Hole Spacetimes and Their Curvature Invariants
2.1. Singular Black-Hole Spacetimes
2.2. Regular Black-Hole Spacetimes
3. Singularity-Resolving Dynamics
3.1. Einstein–Hilbert Dynamics
3.2. Curvature-Squared Dynamics
3.3. Beyond Four-Derivative Dynamics
4. Conclusions and Outlook
- (i)
- To dynamically suppress singular black-hole spacetimes that are vacuum solutions of Einstein equations, a local action constructed from higher powers of R or alone is insufficient and invariants built out of the Riemann tensor are required. In turn, a local action containing these further invariants may feature ghosts These could be avoided by including appropriate functions of the curvature invariants [83,84] or might be present, but not result in a physical inconsistency of the theory [18,19]. which would be absent if one would restrict to higher powers in R, only. The latter could be taken as a motivation to focus on -type of actions for gravity. Here, we provide evidence that actions, while potentially providing physically interesting effective descriptions of gravity, fail at a key requirement of quantum gravity, namely dynamical singularity-resolution. In some sense, therefore, the challenge of potential ghosts and the dynamical resolution of singularities appear to be two sides of the same coin.
- (ii)
- The contribution of black-hole spacetimes to the gravitational path integral has been used to argue that quantum gravity should result in the violation of global symmetries [85,86,87]. The argument hinges on the presence of black-hole spacetimes in the gravitational path integral. As we have argued, this depends on the choice of dynamics. The latter is also key to understand the final state of black-hole evaporation. Our study motivates that under certain circumstances, at least the contribution of certain singular black-hole spacetimes to the gravitational path integral could vanish. This could in turn imply that quantum-gravity approaches which feature such higher-order terms in the action might not generically violate global symmetries. This might for instance include asymptotically safe gravity, where indeed results in Euclidean studies of truncated dynamics for gravity-matter systems do not provide any indications for the violation of global symmetries [88,89].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. Astrophys. J. 2008, 689, 1044–1062. [Google Scholar] [CrossRef]
- Collaboration, E.H.T. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Lehners, J.L.; Stelle, K. A Safe Beginning for the Universe? Phys. Rev. D 2019, 100, 083540. [Google Scholar] [CrossRef]
- Calmet, X.; Hsu, S.D.; Reeb, D. Quantum gravity at a TeV and the renormalization of Newton’s constant. Phys. Rev. D 2008, 77, 125015. [Google Scholar] [CrossRef]
- Hoyle, C.; Kapner, D.; Heckel, B.R.; Adelberger, E.; Gundlach, J.; Schmidt, U.; Swanson, H. Sub-millimeter tests of the gravitational inverse-square law. Phys. Rev. D 2004, 70, 042004. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M.J.G. One loop divergencies in the theory of gravitation. Ann. Inst. H. Poincare Phys. Theor. 1974, A20, 69–94. [Google Scholar]
- Goroff, M.H.; Sagnotti, A. Quantum Gravity at two Loops. Phys. Lett. 1985, 160B, 81–86. [Google Scholar] [CrossRef]
- van de Ven, A.E.M. Two loop quantum gravity. Nucl. Phys. 1992, B378, 309–366. [Google Scholar] [CrossRef]
- Donoghue, J.F. Leading quantum correction to the Newtonian potential. Phys. Rev. Lett. 1994, 72, 2996–2999. [Google Scholar] [CrossRef]
- Donoghue, J.F. Introduction to the effective field theory description of gravity. In Advanced School on Effective Theories; Almunecar: Granada, Spain, 1995. [Google Scholar]
- Hartle, J.; Hawking, S. Wave Function of the Universe. Adv. Ser. Astrophys. Cosmol. 1987, 3, 174–189. [Google Scholar] [CrossRef]
- Feldbrugge, J.; Lehners, J.L.; Turok, N. No smooth beginning for spacetime. Phys. Rev. Lett. 2017, 119, 171301. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hartle, J.B.; Hertog, T. What is the No-Boundary Wave Function of the Universe? Phys. Rev. D 2019, 99, 043526. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of Higher Derivative Quantum Gravity. Phys. Rev. 1977, D16, 953–969. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Renormalizable asymptotically free quantum theory of gravity. Nucl. Phys. B 1982, 201, 469–491. [Google Scholar] [CrossRef]
- Salvio, A. Quadratic Gravity. Front. Phys. 2018, 6, 77. [Google Scholar] [CrossRef]
- Anselmi, D.; Piva, M. The Ultraviolet Behavior of Quantum Gravity. JHEP 2018, 5, 027. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Menezes, G. Arrow of Causality and Quantum Gravity. Phys. Rev. Lett. 2019, 123, 171601. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Ultraviolet divergencies in quantum theories of gravitation. In General Relativity: An Einstein Centenary Survey; IAEA: Vienna, Austria, 1979; pp. 790–831. [Google Scholar]
- Reuter, M. Nonperturbative Evolution Equation for Quantum Gravity. Phys. Rev. 1998, D57, 971–985. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Flow equation of quantum Einstein gravity in a higher derivative truncation. Phys. Rev. D 2002, 66, 025026. [Google Scholar] [CrossRef]
- Machado, P.F.; Saueressig, F. On the renormalization group flow of f(R)-gravity. Phys. Rev. D 2008, 77, 124045. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R.; Rahmede, C. Investigating the Ultraviolet Properties of Gravity with a Wilsonian Renormalization Group Equation. Ann. Phys. 2009, 324, 414–469. [Google Scholar] [CrossRef]
- Benedetti, D.; Machado, P.F.; Saueressig, F. Asymptotic safety in higher-derivative gravity. Mod. Phys. Lett. 2009, A24, 2233–2241. [Google Scholar] [CrossRef]
- Dietz, J.A.; Morris, T.R. Asymptotic safety in the f(R) approximation. JHEP 2013, 1, 108. [Google Scholar] [CrossRef]
- Benedetti, D.; Caravelli, F. The Local potential approximation in quantum gravity. JHEP 2012, 6, 017. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. A bootstrap towards asymptotic safety. arXiv 2013, arXiv:1301.4191. [Google Scholar]
- Ohta, N.; Percacci, R.; Vacca, G.P. Renormalization Group Equation and scaling solutions for f(R) gravity in exponential parametrization. Eur. Phys. J. C 2016, 76, 46. [Google Scholar] [CrossRef]
- Demmel, M.; Saueressig, F.; Zanusso, O. A proper fixed functional for four-dimensional Quantum Einstein Gravity. JHEP 2015, 8, 113. [Google Scholar] [CrossRef]
- Christiansen, N.; Falls, K.; Pawlowski, J.M.; Reichert, M. Curvature dependence of quantum gravity. Phys. Rev. 2018, D97, 046007. [Google Scholar] [CrossRef]
- Gonzalez-Martin, S.; Morris, T.R.; Slade, Z.H. Asymptotic solutions in asymptotic safety. Phys. Rev. D 2017, 95, 106010. [Google Scholar] [CrossRef]
- Falls, K.; King, C.R.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. Asymptotic safety of quantum gravity beyond Ricci scalars. Phys. Rev. D 2018, 97, 086006. [Google Scholar] [CrossRef]
- De Brito, G.P.; Ohta, N.; Pereira, A.D.; Tomaz, A.A.; Yamada, M. Asymptotic safety and field parametrization dependence in the f(R) truncation. Phys. Rev. D 2018, 98, 026027. [Google Scholar] [CrossRef]
- Falls, K.; Ohta, N.; Percacci, R. Towards the determination of the dimension of the critical surface in asymptotically safe gravity. Phys. Lett. B 2020, 810, 135773. [Google Scholar] [CrossRef]
- Eichhorn, A. The Renormalization Group flow of unimodular f(R) gravity. JHEP 2015, 4, 096. [Google Scholar] [CrossRef]
- Percacci, R. An Introduction to Covariant Quantum Gravity and Asymptotic Safety; 100 Years of General Relativity; World Scientific: Singapore, 2017; Volume 3. [Google Scholar] [CrossRef]
- Eichhorn, A. An asymptotically safe guide to quantum gravity and matter. Front. Astron. Space Sci. 2019, 5, 47. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Quantum Gravity and the Functional Renormalization Group: The Road towards Asymptotic Safety; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Manrique, E.; Rechenberger, S.; Saueressig, F. Asymptotically Safe Lorentzian Gravity. Phys. Rev. Lett. 2011, 106, 251302. [Google Scholar] [CrossRef]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. arXiv 2020, arXiv:2004.06810. [Google Scholar] [CrossRef]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. arXiv 2020, arXiv:2006.04853. [Google Scholar]
- Manrique, E.; Reuter, M. Bare Action and Regularized Functional Integral of Asymptotically Safe Quantum Gravity. Phys. Rev. D 2009, 79, 025008. [Google Scholar] [CrossRef]
- Manrique, E.; Reuter, M. Bare versus Effective Fixed Point Action in Asymptotic Safety: The Reconstruction Problem. Available online: https://pos.sissa.it/079/001/pdf (accessed on 22 January 2021).
- Morris, T.R.; Slade, Z.H. Solutions to the reconstruction problem in asymptotic safety. JHEP 2015, 11, 094. [Google Scholar] [CrossRef][Green Version]
- Narlikar, V.V.; Karmarkar, K.R. The scalar invariants of a general gravitational metric. Proc. Indian Acad. Sci. Math. Sci. 1949, 29, 92. [Google Scholar] [CrossRef]
- Overduin, J.; Coplan, M.; Wilcomb, K.; Henry, R.C. Curvature Invariants for Charged and RotatingBlack Holes. Universe 2020, 6, 22. [Google Scholar] [CrossRef]
- Fulling, S.A.; King, R.C.; Wybourne, B.G.; Cummins, C.J. Normal forms for tensor polynomials 1: The Riemann tensor. Class. Quant. Grav. 1992, 9, 1151–1197. [Google Scholar] [CrossRef]
- Lu, H.; Perkins, A.; Pope, C.N.; Stelle, K.S. Black Holes in Higher-Derivative Gravity. Phys. Rev. Lett. 2015, 114, 171601. [Google Scholar] [CrossRef] [PubMed]
- Lü, H.; Perkins, A.; Pope, C.N.; Stelle, K.S. Spherically Symmetric Solutions in Higher-Derivative Gravity. Phys. Rev. 2015, D92, 124019. [Google Scholar] [CrossRef]
- Abdelqader, M.; Lake, K. Invariant characterization of the Kerr spacetime: Locating the horizon and measuring the mass and spin of rotating black holes using curvature invariants. Phys. Rev. D 2015, 91, 084017. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A Brief introduction. Kerr Fest: Black Holes in Astrophysics, General Relativity and Quantum Gravity. arXiv 2007, arXiv:0706.0622. [Google Scholar]
- Vaidya, P.C. Nonstatic Solutions of Einstein’s Field Equations for Spheres of Fluids Radiating Energy. Phys. Rev. 1951, 83, 10–17. [Google Scholar] [CrossRef]
- Vaidya, P.C. Newtonian Time in General Relativity. Nature 1953, 171, 260–261. [Google Scholar] [CrossRef]
- Vaidya, P.C. An Analytical Solution for Gravitational Collapse with Radiation. Astrophys. J. 1966, 144, 943. [Google Scholar] [CrossRef]
- Kuroda, Y. Naked Singularities in the Vaidya Spacetime. Prog. Theor. Phys. 1984, 72, 63–72. [Google Scholar] [CrossRef][Green Version]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole space-times. Phys. Rev. 2000, D62, 043008. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum geometry and the Schwarzschild singularity. Class. Quant. Grav. 2006, 23, 391–411. [Google Scholar] [CrossRef]
- Modesto, L. Loop quantum black hole. Class. Quant. Grav. 2006, 23, 5587–5602. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F.; Raghuraman, A. Black Holes and Asymptotically Safe Gravity. Int. J. Mod. Phys. 2012, A27, 1250019. [Google Scholar] [CrossRef]
- Held, A.; Gold, R.; Eichhorn, A. Asymptotic safety casts its shadow. JCAP 2019, 1906, 029. [Google Scholar] [CrossRef]
- Platania, A. Dynamical renormalization of black-hole spacetimes. Eur. Phys. J. C 2019, 79, 470. [Google Scholar] [CrossRef]
- Faraoni, V.; Giusti, A. Unsettling physics in the quantum-corrected Schwarzschild black hole. Symmetry 2020, 12, 1264. [Google Scholar] [CrossRef]
- Bardeen, J. Non-singular general-relativistic gravitational collapse. arXiv 1968, arXiv:1305.4790. [Google Scholar]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Relat. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef]
- Frolov, V.P. Notes on nonsingular models of black holes. Phys. Rev. D 2016, 94, 104056. [Google Scholar] [CrossRef]
- Collaboration, E.H.T. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar] [CrossRef]
- Giddings, S.B. Searching for quantum black hole structure with the Event Horizon Telescope. Universe 2019, 5, 201. [Google Scholar] [CrossRef]
- Carballo-Rubio, R.; Di Filippo, F.; Liberati, S.; Visser, M. Opening the Pandora’s box at the core of black holes. Class. Quant. Grav. 2020, 37, 145005. [Google Scholar] [CrossRef]
- Bonanno, A.; Khosravi, A.P.; Saueressig, F. Regular black holes have stable cores. arXiv 2020, arXiv:2010.04226. [Google Scholar]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. 2006, B632, 547–551. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Planck stars. Int. J. Mod. Phys. 2014, D23, 1442026. [Google Scholar] [CrossRef]
- Saueressig, F.; Alkofer, N.; D’Odorico, G.; Vidotto, F. Black holes in Asymptotically Safe Gravity. arXiv 2016, arXiv:1503.06472. [Google Scholar]
- Litim, D.F.; Nikolakopoulos, K. Quantum gravity effects in Myers-Perry space-times. JHEP 2014, 4, 21. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Stock, D. Quantum-improved Schwarzschild-(A)dS and Kerr-(A)dS spacetimes. Phys. Rev. 2018, D98, 106008. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.I. Note on the Kerr spinning particle metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Drake, S.; Szekeres, P. Uniqueness of the Newman-Janis algorithm in generating the Kerr-Newman metric. Gen. Relat. Grav. 2000, 32, 445–458. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S.; Saueressig, F. Gravitational Two-Loop Counterterm Is Asymptotically Safe. Phys. Rev. Lett. 2016, 116, 211302. [Google Scholar] [CrossRef]
- Kluth, Y.; Litim, D. Fixed Points of Quantum Gravity and the Dimensionality of the UV Critical Surface. arXiv 2020, arXiv:2008.09181. [Google Scholar]
- Draper, T.; Knorr, B.; Ripken, C.; Saueressig, F. Finite Quantum Gravity Amplitudes: No Strings Attached. Phys. Rev. Lett. 2020, 125, 181301. [Google Scholar] [CrossRef]
- Platania, A.; Wetterich, C. Non-perturbative unitarity and fictitious ghosts in quantum gravity. Phys. Lett. B 2020, 811, 135911. [Google Scholar] [CrossRef]
- Kamionkowski, M.; March-Russell, J. Planck scale physics and the Peccei-Quinn mechanism. Phys. Lett. B 1992, 282, 137–141. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.D.; Linde, D.A.; Susskind, L. Gravity and global symmetries. Phys. Rev. D 1995, 52, 912–935. [Google Scholar] [CrossRef]
- Banks, T.; Seiberg, N. Symmetries and Strings in Field Theory and Gravity. Phys. Rev. D 2011, 83, 084019. [Google Scholar] [CrossRef]
- Eichhorn, A.; Held, A. Viability of quantum-gravity induced ultraviolet completions for matter. Phys. Rev. D 2017, 96, 086025. [Google Scholar] [CrossRef]
- Eichhorn, A.; Pauly, M. Constraining power of asymptotic safety for scalar fields. arXiv 2020, arXiv:2009.13543. [Google Scholar]
- Feldbrugge, J.; Lehners, J.L.; Turok, N. Lorentzian Quantum Cosmology. Phys. Rev. D 2017, 95, 103508. [Google Scholar] [CrossRef]
- Horava, P. Quantum Gravity at a Lifshitz Point. Phys. Rev. D 2009, 79, 084008. [Google Scholar] [CrossRef]
- Steinwachs, C.F. Towards a unitary, renormalizable and ultraviolet-complete quantum theory of gravity. arXiv 2020, arXiv:2004.07842. [Google Scholar] [CrossRef]
- Daum, J.; Reuter, M. Einstein-Cartan gravity, Asymptotic Safety, and the running Immirzi parameter. Ann. Phys. 2013, 334, 351–419. [Google Scholar] [CrossRef]
- Harst, U.; Reuter, M. The ’Tetrad only’ theory space: Nonperturbative renormalization flow and Asymptotic Safety. JHEP 2012, 5, 005. [Google Scholar] [CrossRef]
- Knorr, B.; Ripken, C. Scattering amplitudes in affine gravity. arXiv 2020, arXiv:2012.05144. [Google Scholar]
- De Brito, G.P.; Pereira, A.D. Unimodular quantum gravity: Steps beyond perturbation theory. JHEP 2020, 9, 196. [Google Scholar] [CrossRef]
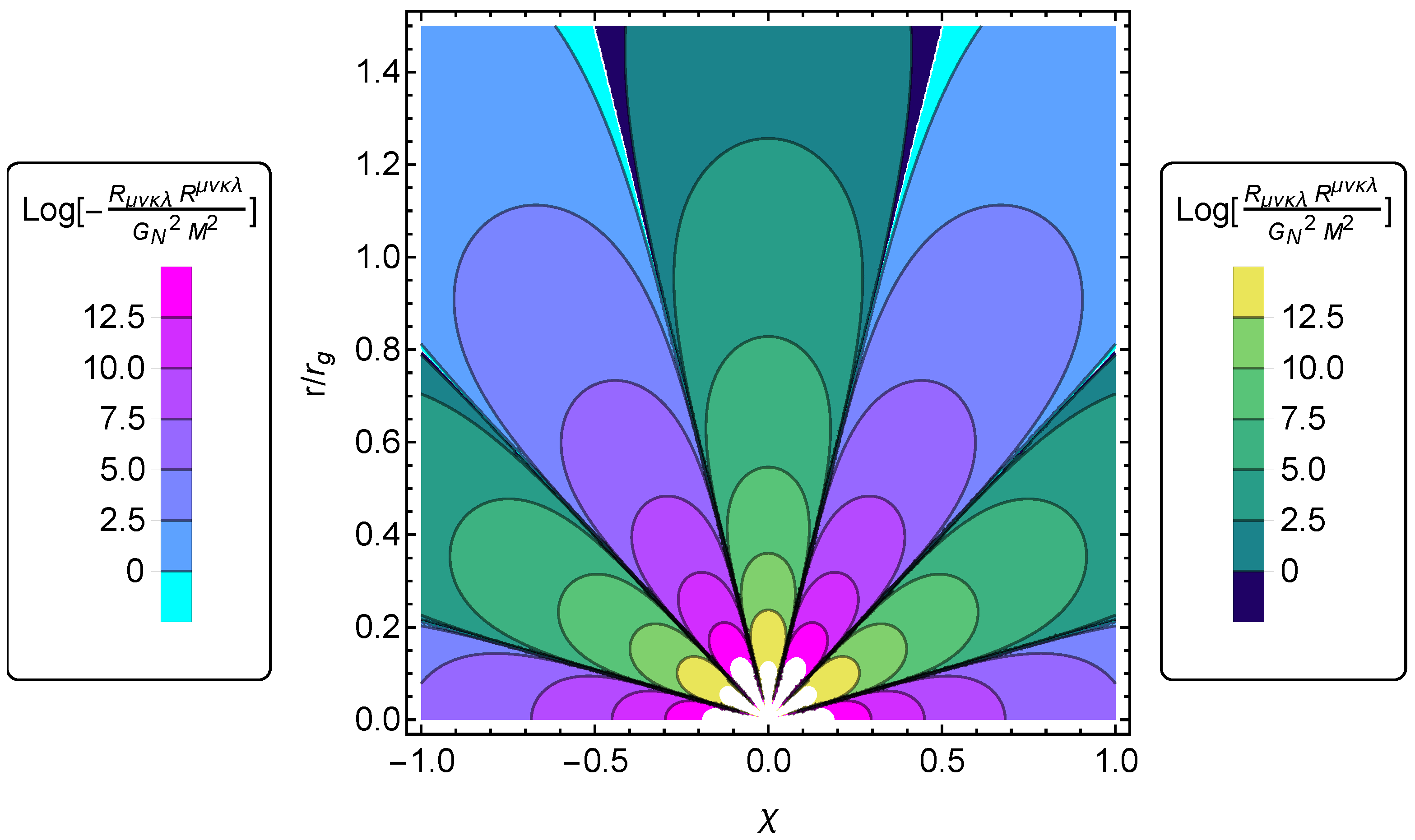
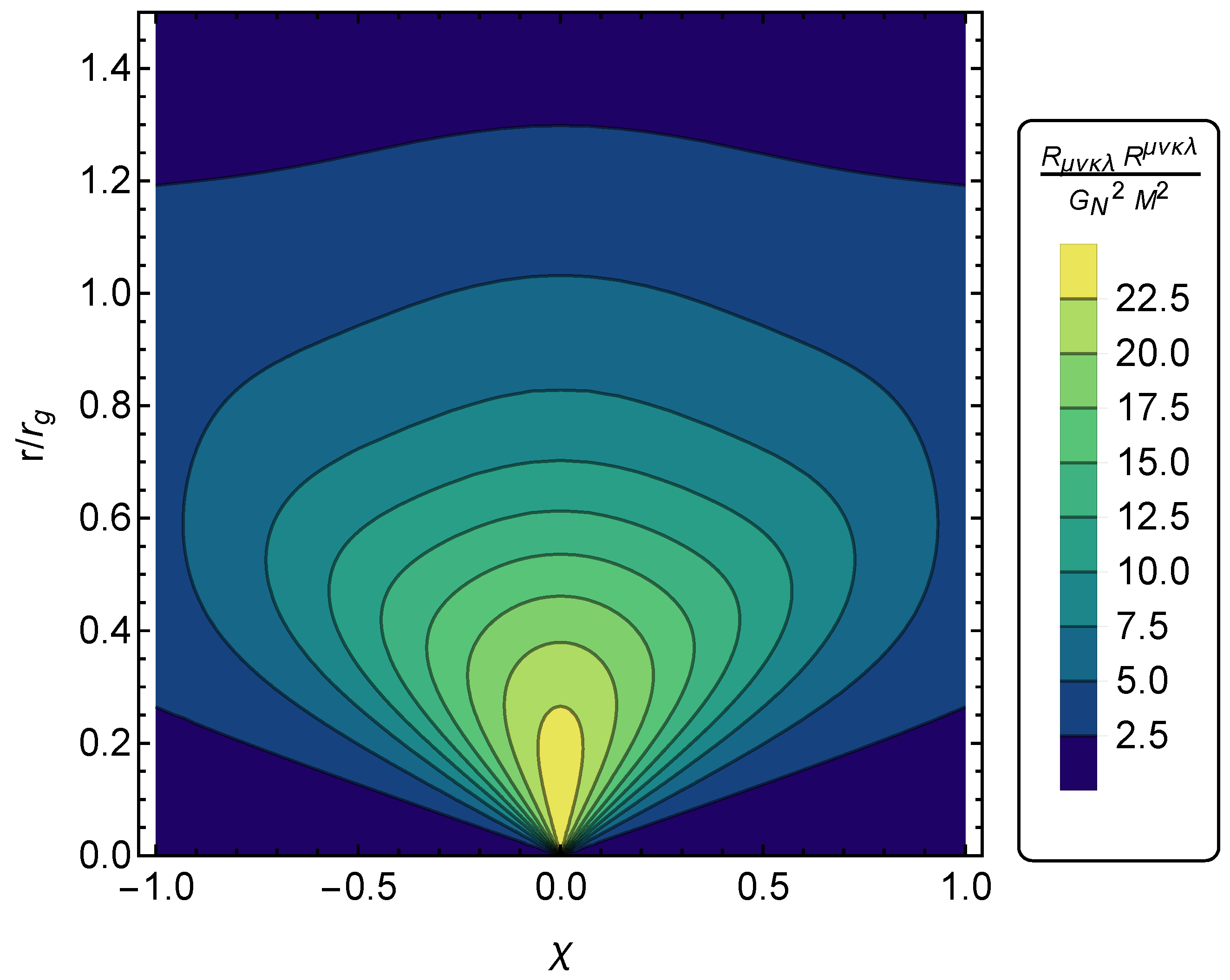
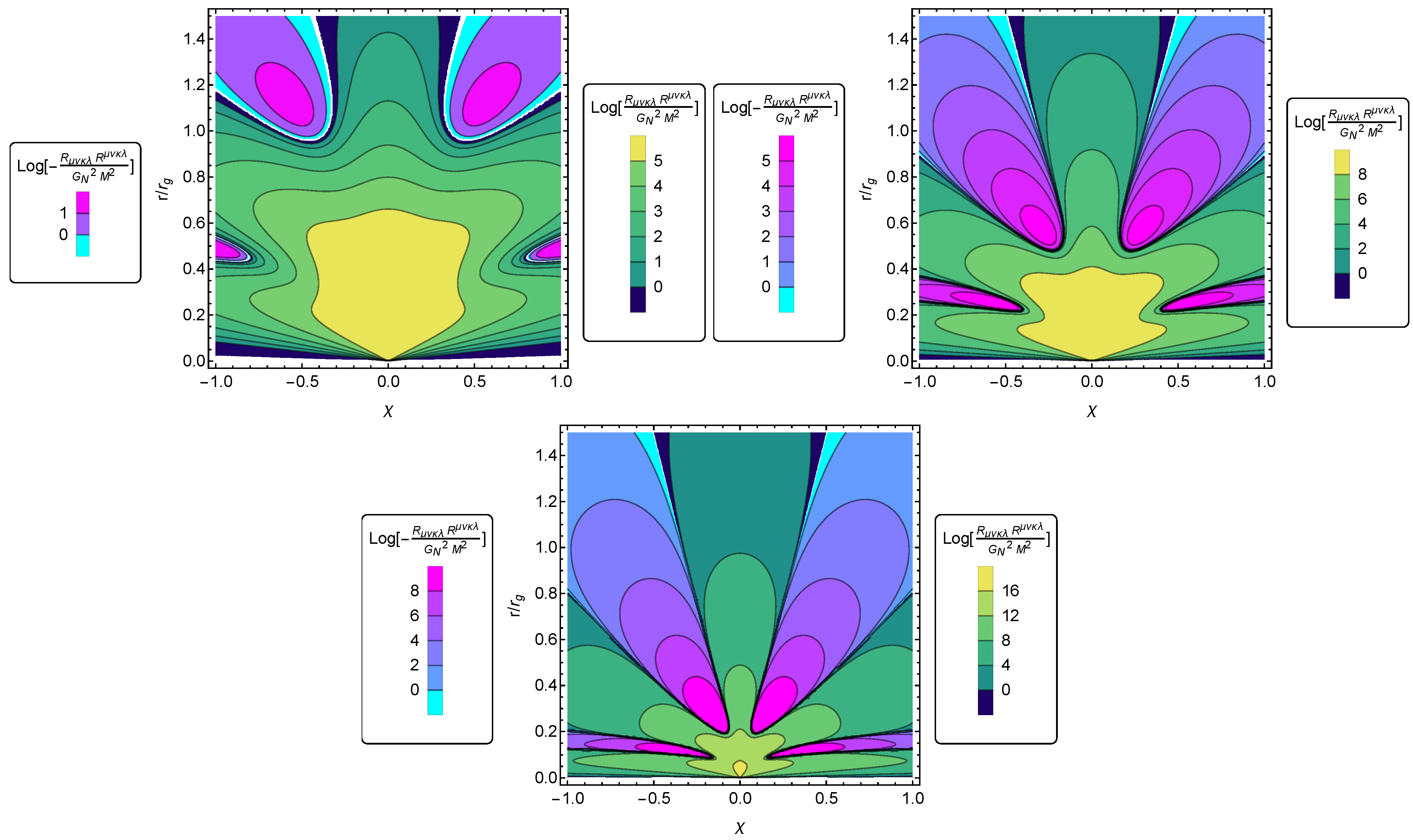
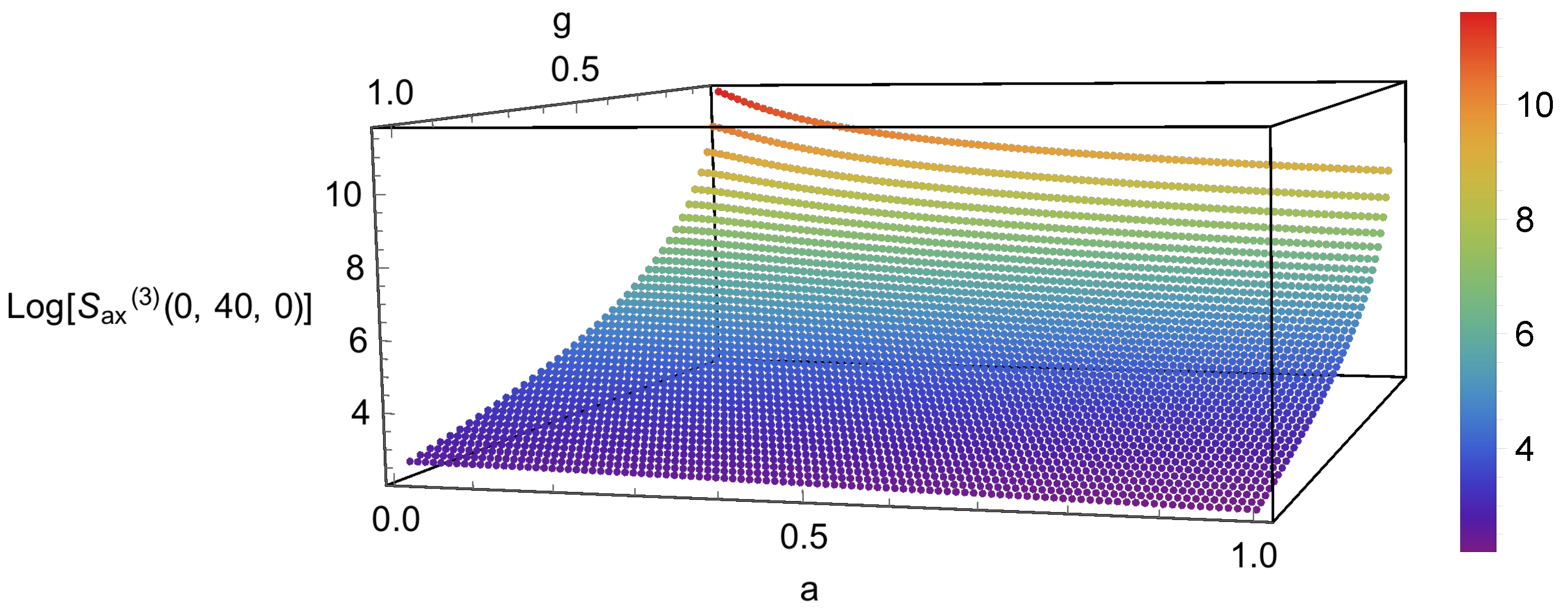
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borissova, J.N.; Eichhorn, A. Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral. Universe 2021, 7, 48. https://doi.org/10.3390/universe7030048
Borissova JN, Eichhorn A. Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral. Universe. 2021; 7(3):48. https://doi.org/10.3390/universe7030048
Chicago/Turabian StyleBorissova, Johanna N., and Astrid Eichhorn. 2021. "Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral" Universe 7, no. 3: 48. https://doi.org/10.3390/universe7030048
APA StyleBorissova, J. N., & Eichhorn, A. (2021). Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral. Universe, 7(3), 48. https://doi.org/10.3390/universe7030048






