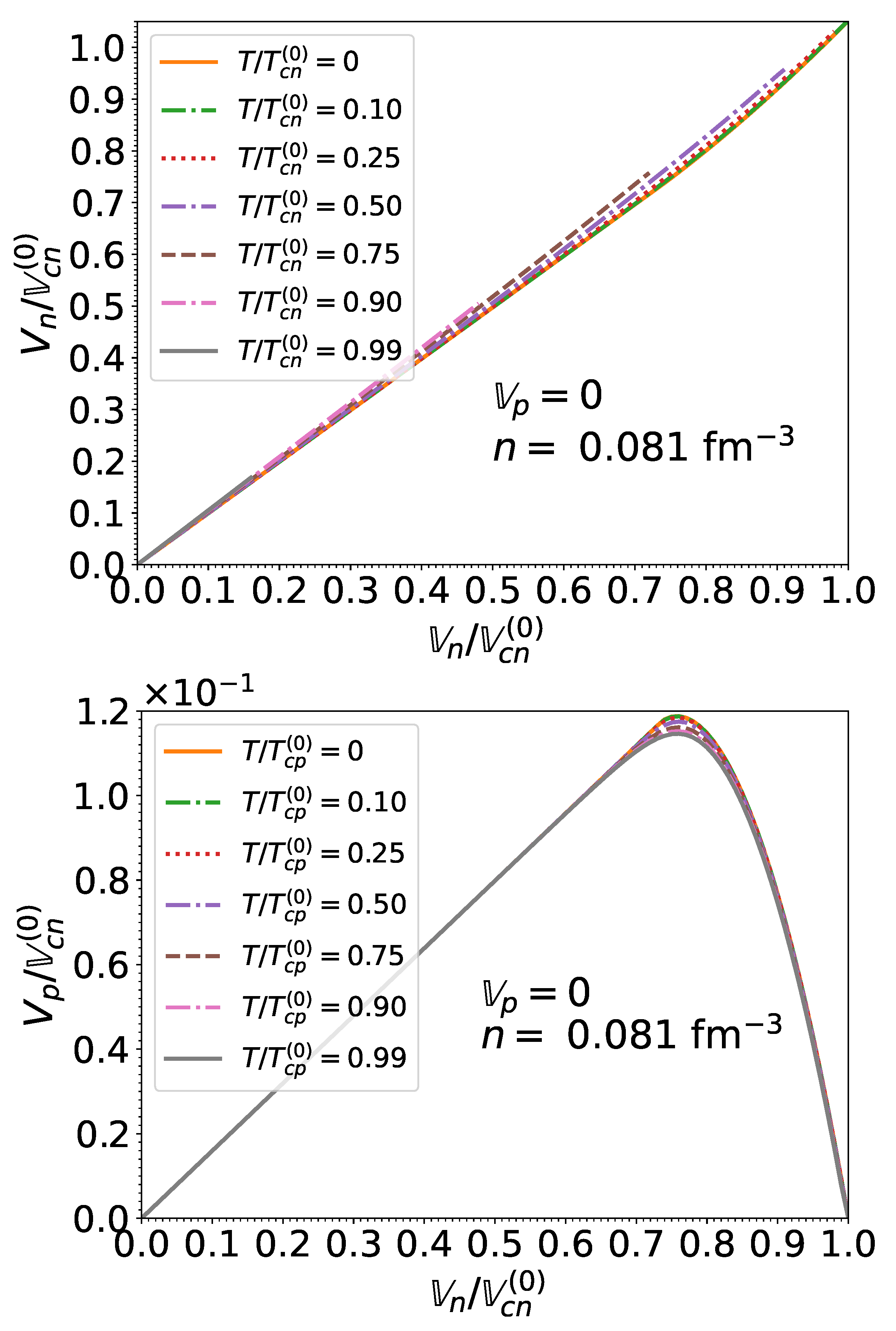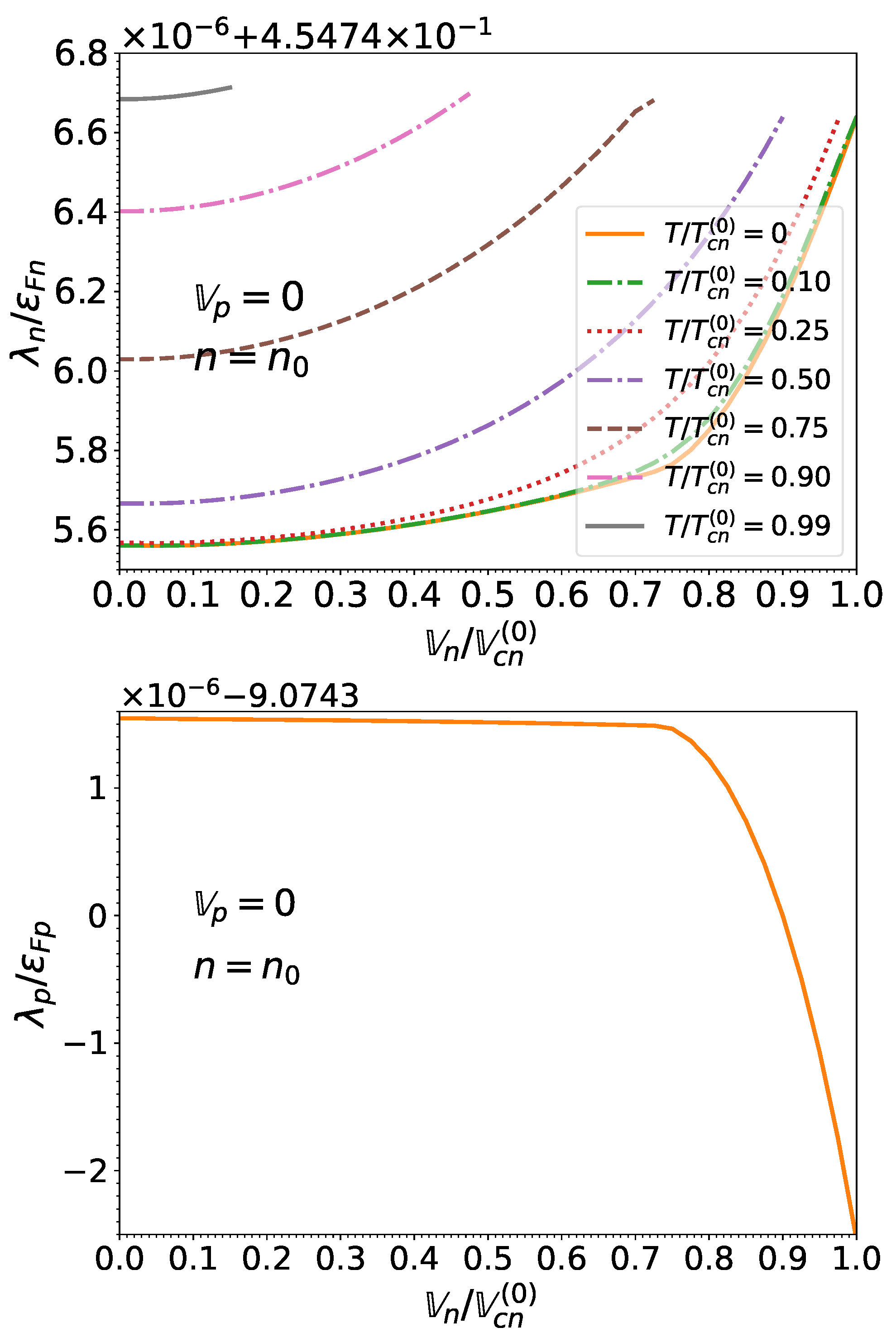Abstract
Temperature and velocity-dependent S pairing gaps, chemical potentials and entrainment matrix in dense homogeneous neutron–proton superfluid mixtures constituting the outer core of neutron stars, are determined fully self-consistently by solving numerically the time-dependent Hartree–Fock–Bogoliubov equations over the whole range of temperatures and flow velocities for which superfluidity can exist. Calculations have been made for in beta-equilibrium using the Brussels–Montreal functional BSk24. The accuracy of various approximations is assessed and the physical meaning of the different velocities and momentum densities appearing in the theory is clarified. Together with the unified equation of state published earlier, the present results provide consistent microscopic inputs for modeling superfluid neutron-star cores.
1. Introduction
Different superfluid and superconducting phases are predicted to exist in neutron stars (see, e.g., [1] for a review). In particular, the (electrically charge neutral) outer core is expected to be made of a neutron–proton superfluid mixture in beta-equilibrium with a normal gas of leptons. More speculative superfluid phases involving other particles such as hyperons or quarks might occur in the innermost region of the core of a neutron star but will not be considered here. Although the interior of the star is highly degenerate, thermal effects may still play an important role in the rotational evolution of the star [2,3,4]. This stems from the fact that the critical temperatures above which superfluidity is destroyed ( for neutrons and protons respectively) are much smaller than the Fermi temperatures , and may thus be comparable to the actual temperature T of the star. Superfluidity leads to a very complicated dynamics, characterized by the coexistence of different flows (see, e.g., [5] for a recent review). The core of a neutron star involves at least three distinct fluids: the neutron and proton superfluids, as well as a normal fluid made of leptons and excitations. Due to nuclear interactions, the neutron and proton superfluids in the core do not flow freely. They are mutually coupled by entrainment effects of the same kind as the ones discussed by Andreev and Bashkin [6] in the context of superfluid He-He mixtures: the mass currents are expressible as linear combinations of the velocity of the normal fluid and of the so-called “superfluid velocities” as
where is the mass density of nucleon of charge type q with associated nucleon number density (ignoring the small difference between neutron and proton masses, which is denoted simply by m). As shown by Carter and Khalatnikov in the context of Landau’s canonical two-fluid model of superfluid He [7] (see also [8]), are not true velocities but physically represent average nucleon momenta per unit mass. Indeed, it can be easily seen that the true velocities should be defined in terms of the mass currents as and in general these velocities do not coincide with . To avoid any misinterpretation, the superfluid “velocities” are thus written with a capital letter. Please note that is a true velocity. The importance of entrainment effects is measured by the (symmetric) matrix , which is a key microscopic input for modeling the dynamics of neutron stars, see, e.g., [5] and references therein. The entrainment matrix is expected to depend not only on the composition and the baryon density , but also on the superfluid velocities as well as the temperature, and this may have an impact on neutron-star oscillations [9,10,11,12]. The influence of temperature and velocity on entrainment effects has been previously studied within Landau’s theory [13,14,15]. However, the Landau parameters, the critical temperatures, and the composition had to be given. Recently, we have derived the entrainment matrix self-consistently for arbitrary superfluid velocities and temperatures within the nuclear-energy-density functional theory by solving exactly the time-dependent Hartree–Fock–Bogoliubov (TDHFB) equations [16,17]. The expressions we have obtained are quite general and applicable to a wide variety of functionals.
In this paper, we have calculated various properties of homogeneous neutron–proton superfluid mixtures in the outer core of neutron stars by solving numerically the self-consistent TDHFB equations using the Brussels–Montreal functional BSk24 [18] for which unified equations of state are already available [19,20,21,22] as well as gravitoelectric and gravitomagnetic tidal Love numbers up to [23,24]. More importantly, unlike most available functionals, BSk24 has been accurately calibrated to realistic microscopic calculations of S pairing gaps in infinite homogeneous nuclear matter (at zero temperature and in the absence of currents). We have determined within the same microscopic framework not only the entrainment matrix but also the S pairing gaps and chemical potentials of the superfluid mixture without any approximation, varying the superfluid velocities, the temperature and the baryon density. In this way, we have also been able to assess the accuracy of various approximations. We have focused on S nuclear superfluid phases, which are reliably predicted to exist in the outer core of neutron stars (see, e.g., [25] and references therein). We have not considered PF neutron superfluidity. As a matter of fact, it has been recently shown that in regions where both types of pairing can potentially exist, the PF superfluid phase is completely excluded by the S phase unless strong magnetic fields are present [26].
The formalism to describe nuclear superfluidity is presented in Section 2. After briefly recapitulating the general principles of the TDHFB theory in Section 2.1 and the functionals in Section 2.2, the exact solution in homogeneous nuclear matter is given in Section 2.3, where explicit expressions for various quantities entering the calculations of superfluid properties are derived. The physical interpretation of the different velocities and momentum densities are clarified in Section 2.4. In Section 2.5, it is shown how the TDHFB theory can be recast into Landau’s theory after introducing a series of approximations. Applications to neutron stars are presented in Section 3. The main features of the Brussels–Montreal functionals are recapitulated in Section 3.1. After describing our numerical implementation of the TDHFB equations in Section 3.2, detailed numerical results for various properties of the superfluid mixture are presented and analyzed in Section 3.3, Section 3.4, Section 3.5, Section 3.6, Section 3.7 and Section 3.8. The accuracy of various approximations and interpolations are also discussed. Our conclusions are given in Section 4.
2. Nuclear Superfluidity within the Time-Dependent Hartree–Fock–Bogoliubov Theory
2.1. General Principles
The TDHFB theory [27] provides a unified microscopic framework for studying the dynamics of various nuclear systems, ranging from atomic nuclei to the dense nuclear matter present in neutron stars—the main focus of this work.
Introducing the one-body density matrix and pairing tensor defined in terms of thermal averages of products of creation () and destruction () operators for nucleons of charge type q in a quantum state i (using the symbol † for Hermitian conjugation and ∗ for complex conjugation), and assuming that the energy E of a nucleon-matter element of volume V is a function of , and lead to the following equations of motion [27]:
where denote the chemical potentials. The matrices and , defined by
generally depend themselves on , and and must therefore be determined self-consistently.
2.2. Functionals of Local Densities and Currents
The class of energy functionals that we consider here depend on the density matrices and pair tensors only through the following local densities and currents:
- (i)
- the nucleon densities at position at time t ( distinguishing the two spin states),
- (ii)
- the kinetic-energy densities (in units of at position and time t,
- (iii)
- the momentum densities (in units of ℏ) at position and time t,
- (iv)
- the abnormal densities at position and time t
where
are the so-called normal and abnormal density matrices respectively [28], and is the single-particle wavefunction associated with the state i. The abnormal densities are the local order parameters of the neutron and proton superfluid phases [17]. These densities are complex and the gradient of their respective phase defines the superfluid velocities as follows:
2.3. Application to Homogeneous Systems
Considering a homogeneous neutron–proton superfluid mixture with stationary flows in the normal-fluid rest frame where , the TDHFB equations can be solved exactly [17]. In particular, the entrainment matrix reads ( denotes the Kronecker symbol and is the total mass density)
with
Here represents the nuclear-energy terms contributing to the mass currents. Galilean invariance requires that these terms depend on the following combinations:
The subscripts 0 and 1 denote isoscalar and isovector quantities, respectively, namely sums over neutrons and protons for the former (e.g., ) and differences between neutrons and protons for the latter (e.g., ). The temperature and velocity-dependent functions are defined by ( being the Boltzmann constant)
where we have introduced the effective superfluid velocities
and represent the energies of quasiparticle excitations, given by
with
In turn, the vector is expressible in terms of the superfluid velocities as follows
The pairing gaps (as defined as the nonvanishing matrix elements of the pair potential, see [17] ) are obtained from the self-consistent equations
where it is understood that the summation must be regularized to remove ultraviolet divergences, as will be discussed below. The gap equations must be solved together with the particle number conservation conditions
As can be seen from Equation (31), Equations (28), (33) and (34) all depend on the reduced chemical potentials defined by
so that neither the pairing gaps nor the entrainment matrix require the explicit form of the potentials .
From now on, we will take the continuum limit, i.e., we will replace discrete summations over wave vectors by integrations as follows:
with the solid angle in -space and the density of single-particle states per one spin state given by
is the dilogarithm function, and we have introduced the dimensionless ratios
The Fermi temperature is defined by with the Fermi energy
and Fermi wave number ; the Fermi velocity is given by
Similarly, the gap Equation (33) and the particle number conservation Equation (34) become, respectively
and is a cutoff above the Fermi level to regularize the ultraviolet divergences (see Section 3.1). Expressing the hyperbolic functions in terms of the exponential function, we can alternatively rewrite (43) and (44) as
We have made use of the identity .
It is worth remarking that although the pairing gaps and the entrainment matrix depend in general on the directions of the superfluid velocities , this dependence is entirely contained in the norm of the effective superfluid velocities . Using Equations (29) and (32), it can be seen that the two kinds of velocities are related by
It is important to realize that this relation is highly non-linear because the matrix elements , defined by Equations (21)–(25), depend themselves on the effective superfluid velocities through the functions . For this reason, the mapping between , and is quite complicated. It is, therefore, much more convenient to express the results in terms of instead of . In particular, it can be seen that the neutron (proton) pairing gaps depend only the norms of neutron (proton) effective superfluid velocity. It is only when the chemical potentials are needed rather than the reduced ones that the directions of the superflows become important since are obtained from Equation (35) using Equation (32), namely
The potentials are functions of the nucleon densities , the momentum densities and the kinetic densities . The momentum density can be expressed as [17]
Using Equation (8), we find for the kinetic-energy density:
In the regime , , and , the second term in the right-hand side of Equation (51) becomes negligible and the integral reduces to the Thomas-Fermi expression . The kinetic-energy density can be equivalently expressed in terms of the exponential function as
2.4. Physical Interpretation of the Different Velocities and Momentum Densities
Using Equation (66) of [17], it can be immediately seen that the true velocities associated with the transport of nucleons (mass) are related to the effective superfluid velocities (29) through the relation
Let us recall that these velocities are measured relative to the normal-fluid rest frame. At zero temperature and subcritical superflow of nucleons of type q, the functions will be shown to vanish in Section 3.5: in this case, the effective superfluid velocity thus actually represents the true velocity . At finite temperatures, the excitation of quasiparticles entails a finite fraction : nucleons thus move with a lower speed at than at . If nucleons of type q are nonsuperfluid, as we will see in Section 3.5, therefore their true velocity vanishes : nucleons move with the normal fluid (however, the other nucleon species can flow with a different velocity if it is superfluid). The function thus measures the relative importance of quasiparticle excitations for the transport of nucleons of type q.
As already mentioned earlier, the superfluid “velocity” defined by the gradient of the phase of the condensate through Equation (13) represents the momentum per unit mass of the superfluid. The superfluid momentum density of the nucleon species q, given by , does not coincide with the momentum density introduced in Equation (54). This stems from the fact that the latter not only accounts for the superfluid momentum density but also includes the contribution from quasiparticles. This can be directly seen from Equation (50), which can be equivalently written as
The second term can be interpreted as the momentum density of quasiparticles. Indeed, this contribution vanishes if , i.e., in the absence of quasiparticle excitations. It is only in this limiting case that the total momentum density coincides with the superfluid momentum density . In general, it can be shown using the self-consistent solutions of the TDHFB equations presented in the previous section that the total mass current is equal to the total momentum density
as required by Galilean invariance (this identity can be more easily demonstrated using the general expression of the mass currents [16]).
The distinction between the different velocities and momentum densities becomes irrelevant if both nucleon species are nonsuperfluid since implies that , , and all vanish in the fluid rest frame, i.e., all nucleons move with the normal fluid, as expected. Likewise, in the limiting case of a single superfluid constituent at zero temperature and subcritical superflow, we have .
2.5. Landau’s Approximations
The neutron–proton superfluid mixture can be alternatively described using Landau’s theory [13,14,15]. The TDHFB theory can be reduced to a similar form after introducing a series of approximations. Specifically, assuming that the critical temperatures and the critical superfluid velocities are small compared to their Fermi counterpart,
- the single-particle energies (31) are calculated at zero temperature, in the absence of currents ignoring any dependence on the pairing gaps, and expanding linearly around the Fermi surface (denoting by the approximate expression for a quantity Q)
- the quasiparticle energies (30) are similarly expanded as
- the density of single-particle states in -space integrations (36) is approximated by its value on the Fermi surface, with
In previous studies [13,14,15], the pairing gaps were obtained in the weak-coupling approximation at zeroth order from the following approximate equation (see Appendix A)
or in terms of the exponential function
where denotes the pairing gaps at in the absence of currents. The latter were determined using the BCS relation [29] (introducing the Euler–Mascheroni constant )
by fixing arbitrarily the associated critical temperatures .
Moreover, the functions were replaced by the functions of [15], which can be expressed as
where
Introducing the critical effective superfluid velocities [30]
the approximate pairing gap Equation (59) and the functions (62) can be equivalently expressed in terms of the reduced temperature and the reduced effective superfluid velocity as follows:
or using Equation (60)
and
with
These alternative formulations show that and are universal functions of suitably rescaled temperature and effective superfluid velocity, independently of the nucleon species under consideration, the composition, and the details of the adopted nuclear-energy-density functional.
3. Application to Neutron Stars
Although the entrainment matrix can be written in the deceptively simple analytical form (19), its dependencies on the temperature and on the superfluid velocities remain implicit and highly nontrivial. To obtain actual values, numerical solutions of Equations (43) and (44) are needed. In this work, we have considered the Brussels–Montreal functionals, whose main features are described in Section 3.1. Results are presented in the subsequent sections.
3.1. Brussels–Montreal Functionals
The Brussels–Montreal functionals from BSk16 and beyond (see [31,32] for a brief overview) were constructed from extended Skyrme effective nucleon-nucleon interactions, whose parameters were precision-fitted to essentially all experimental nuclear data on atomic masses and charge radii while ensuring realistic properties of homogeneous nuclear matter (neutron-matter equation of state, effective masses, symmetry energy, incompressibility coefficient, pairing gaps).
The functional derivatives of the energy with respect to and appearing in the effective masses, the matrix and the entrainment matrix are expressible in terms of the parameters of the effective interaction as [16]
The potentials in homogeneous matter read (recalling the shorthand notations , and )
The functional derivative of the energy E with respect to the square modulus of the abnormal density is related to the strength of the effective pairing interaction as
In most existing functionals, is expressed [33] as the sum of a constant “volume” term and a “surface term” proportional to the density n to some power with parameters adjusted empirically to reproduce the average pairing gaps in some finite nuclei [34]. Such functionals may thus lead to unreliable predictions when applied to homogeneous nuclear matter [35]. On the contrary, the pairing strengths of the Brussels–Montreal functionals were determined so as to reproduce the pairing gaps in infinite homogeneous neutron matter and in symmetric nuclear matter at and in the absence of currents (these reference gaps will be denoted by and respectively), as obtained from many-body calculations using realistic potentials (see [35,36,37] for details). Very accurate analytical expressions for the pairing strengths were obtained in [38]:
The parameters are used here to distinguish Brussels–Montreal functionals BSk17-29 [18,36,39,40,41] which neglect self-energy corrections () from the most recent series BSk30-32 [32] which include them (). Since reference pairing gaps for arbitrary composition are needed, the following interpolation ansatz was adopted in [36] for BSk17 and subsequent functionals:
where and the upper (lower) sign is to be taken for . Because this parametrization is empirical, we have found that may become negative depending on the composition and density n. In such cases, we merely set . As for the nucleon mass, it is defined as .
For numerical calculations, we will adopt the Brussels–Montreal functional BSk24 [18]. The reference pairing gaps were taken from the extended Brueckner–Hartree–Fock calculations of [42]. The associated parameters are indicated in Table 1 and Table 2. The reference gaps can be conveniently represented as
where , H is the Heaviside unit-step function, and , , and are fitted parameters. The functional BSk24 has been recently employed for determining the composition and the equation of state of dense matter throughout all regions of a neutron star [19,20] including the pasta mantle [21] and allowing for strong magnetic fields [22]. More importantly, as shown in [23,43,44], this functional turns out to be in very good agreement with existing astrophysical observations including those from the binary neutron-star merger GW170817 [45] as well as from PSR J0740+6620 and PSR J0030+0451 by the Neutron star Interior Composition Explorer (NICER) [46,47,48,49]. Results for the entrainment matrix at finite temperatures but in the absence of superflows have been recently published in [11] within Landau’s theory using values for the Landau parameters calculated for the Brussels–Montreal functionals including BSk24 and setting arbitrarily the critical temperatures. We will present here consistent numerical results for the pairing gaps, chemical potentials and entrainment matrix for arbitrary temperatures and superfluid velocities in different regions of neutron-star cores.

Table 1.
Parameters of the functional BSk24 [18]. The unit of length is femtometer and the unit of energy is megaelectronvolt.

Table 2.
Parameters of the reference gaps from [37]. The unit of length is femtometer and the unit of energy is megaelectronvolt. With kind permission of The European Physical Journal (EPJ).
3.2. Numerical Implementation
The TDHFB equations are solved as follows. We first compute the pairing gaps at zero temperature and in the absence of currents by solving Equations (43) and (44) for and via a root-finding method with a precision of , searching around the approximate solutions and the following expression given by Equation (14) in [38]:
In a second stage, we use this solution to determine iteratively the pairing gaps and the reduced chemical potentials at finite temperature and for given effective superfluid velocities and . An initial guess for is obtained by solving Equation (59) using for the gap obtained previously. With this first estimate of the gap, Equation (44) is solved using the Newton-Raphson method and as the initial guess. Substituting these first estimates for and in the right-hand side of Equation (43) leads to a new estimate for the pairing gap , which is injected in Equation (44) to refine the chemical potential . The process is repeated until the difference in the pairing gaps between two successive iterations lies below . Having found and , the functions are calculated from Equation (38). The entrainment matrix can be easily inferred from Equations (19)–(25) together with Equations (69) and (70).
3.3. S Pairing Gaps
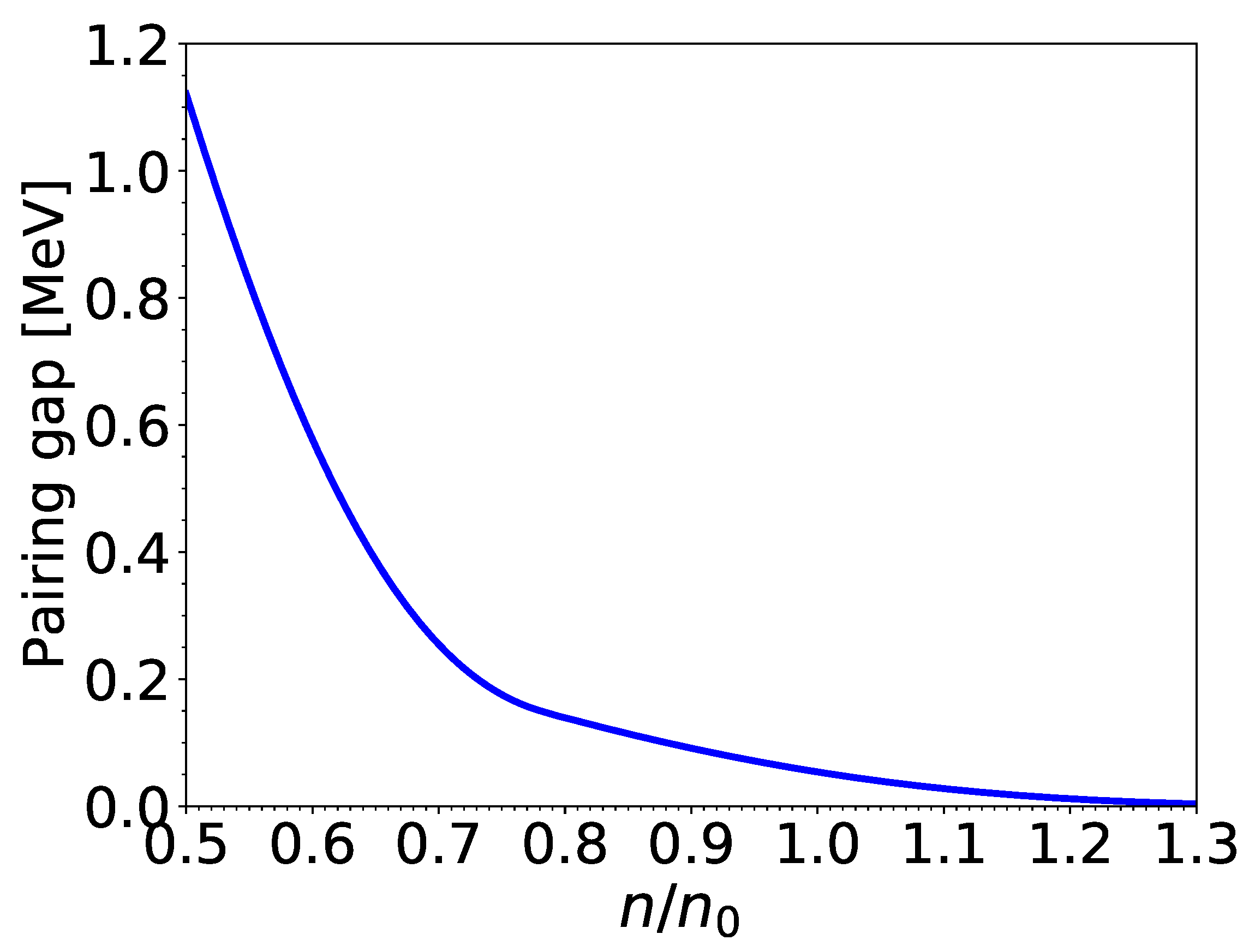
The S neutron and proton pairing gaps for matter in beta-equilibrium at and are displayed in Figure 1 and Figure 2 at densities relevant for the outer core of neutron stars above the crust-core transition at density fm, where fm is the nuclear saturation density with the corresponding mass density g cm. We have made use of the composition calculated in [19].
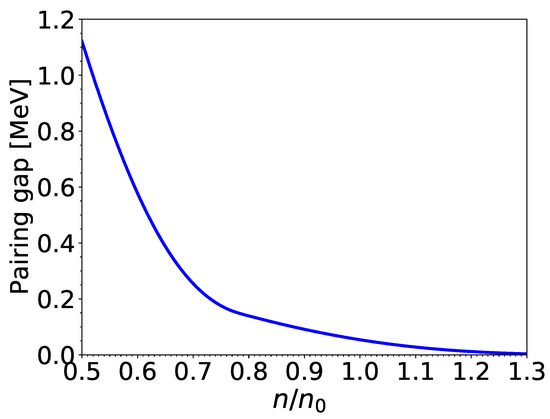
Figure 1.
neutron pairing gaps (in MeV) at zero temperature and in the absence of currents for matter in beta-equilibrium as a function of the baryon density n in units of saturation density . The pairing gaps obtained from (77) are indistinguishable from the exact ones.
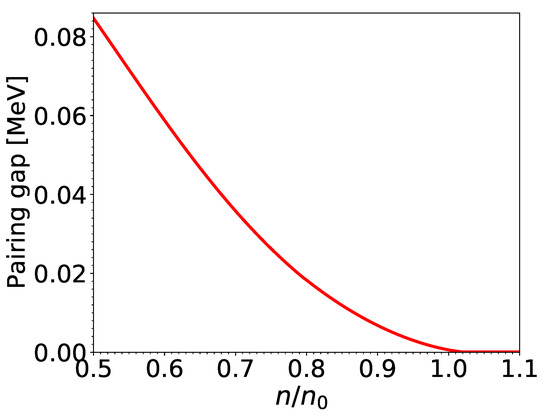
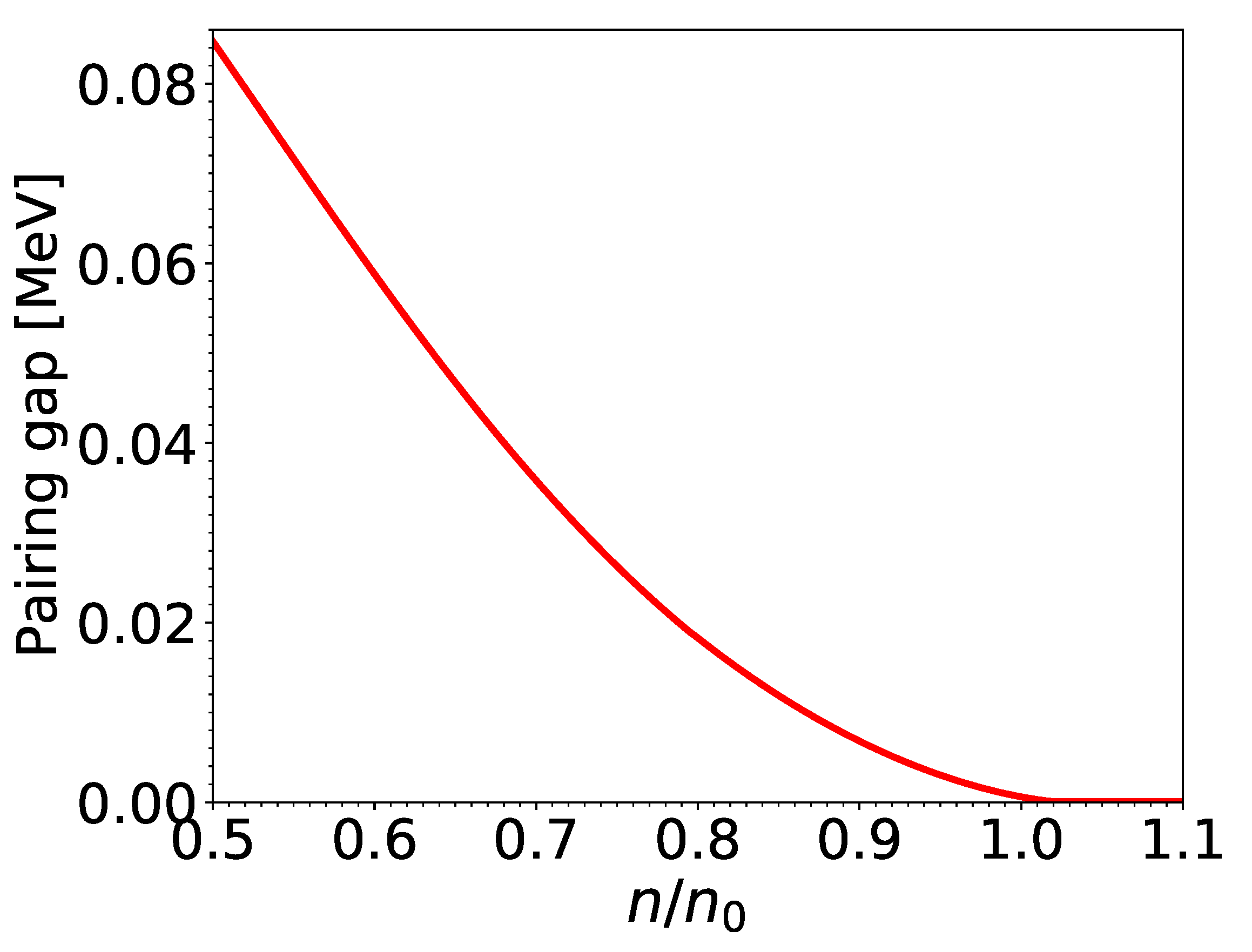
Figure 2.
Same as Figure 1 for proton pairing gaps.
The approximate formula (77) is found to be in excellent agreement with the exact results, the deviations being contained within the thickness of the solid lines. With neutron-star matter containing only a few percents of protons, the reference pairing gaps for neutrons (74) are approximately given by that in pure neutron matter , as obtained from the many-body calculations of [42] using realistic potentials. On the contrary, the reference pairing gaps for protons are mainly determined by the interpolation . This explains why the proton gaps are significantly smaller than the neutron ones unlike those usually employed in neutron-star studies, as e.g., in [4]. This result could reveal a deficiency of the interpolation (74). On the other hand, the proton pairing gaps remain highly uncertain (see, e.g., [25,50,51]). Recent many-body calculations [52] taking into account medium-polarization effects through self-energy and vertex corrections lead to very small proton pairing gaps in neutron-star matter of comparable magnitudes to those plotted in Figure 2. This study also shows that the three-body interactions, especially those between two protons and one neutron, reduce considerably the domain of temperatures and densities over which protons are superfluid (see also [53,54]).
The variations of the neutron and proton pairing gaps with temperature and effective superfluid velocity are found to be essentially independent of density when considering the dimensionless ratios , and , with
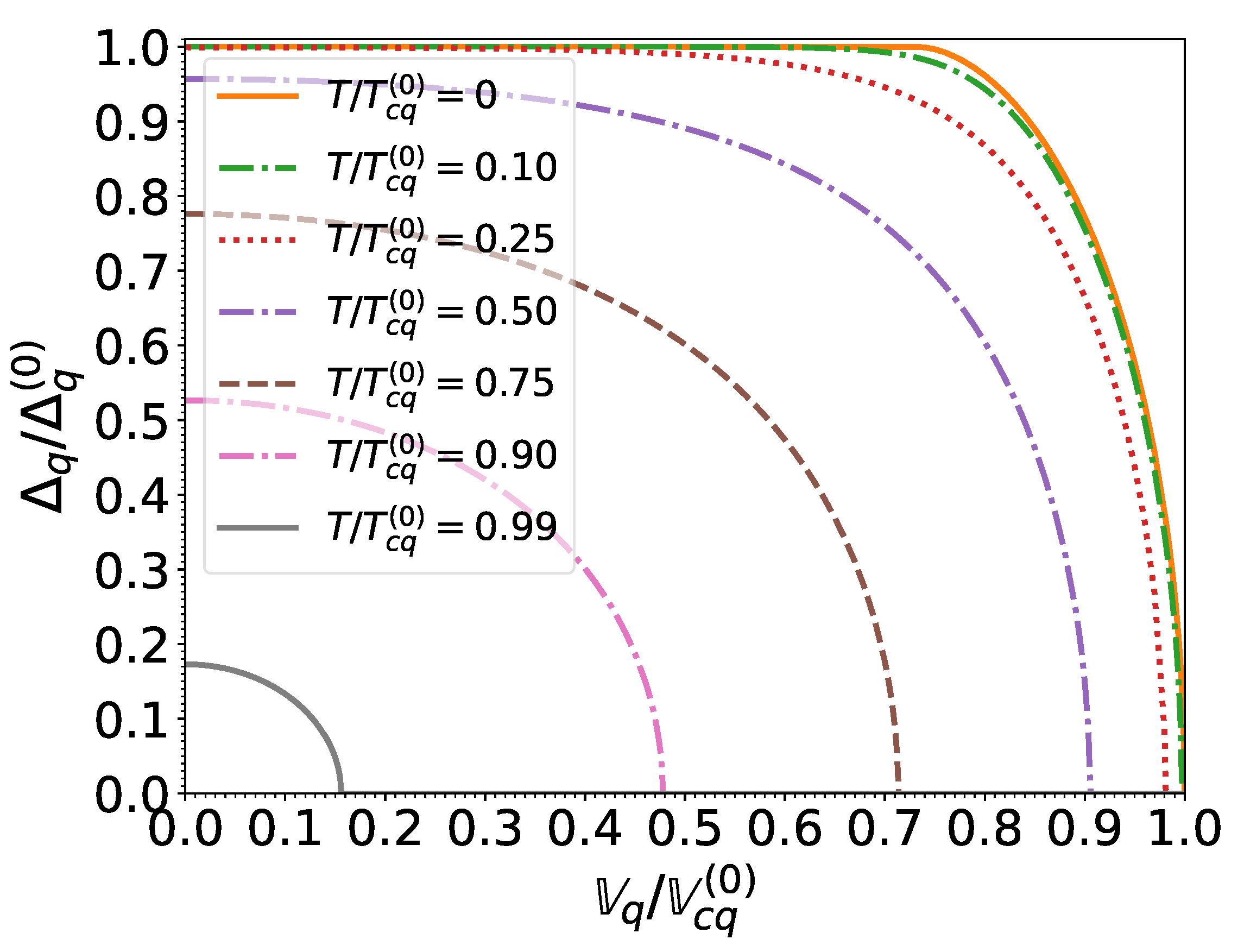
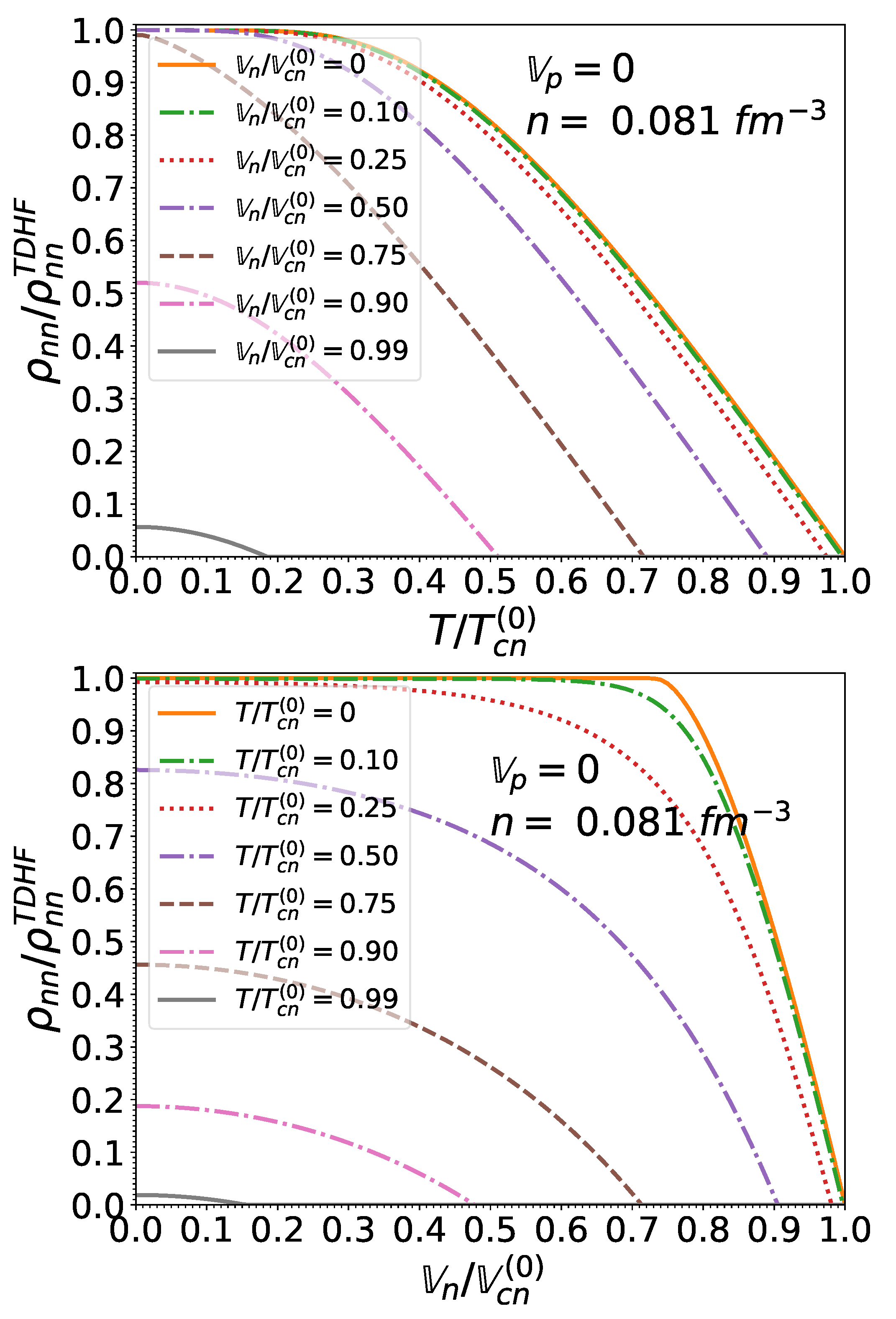
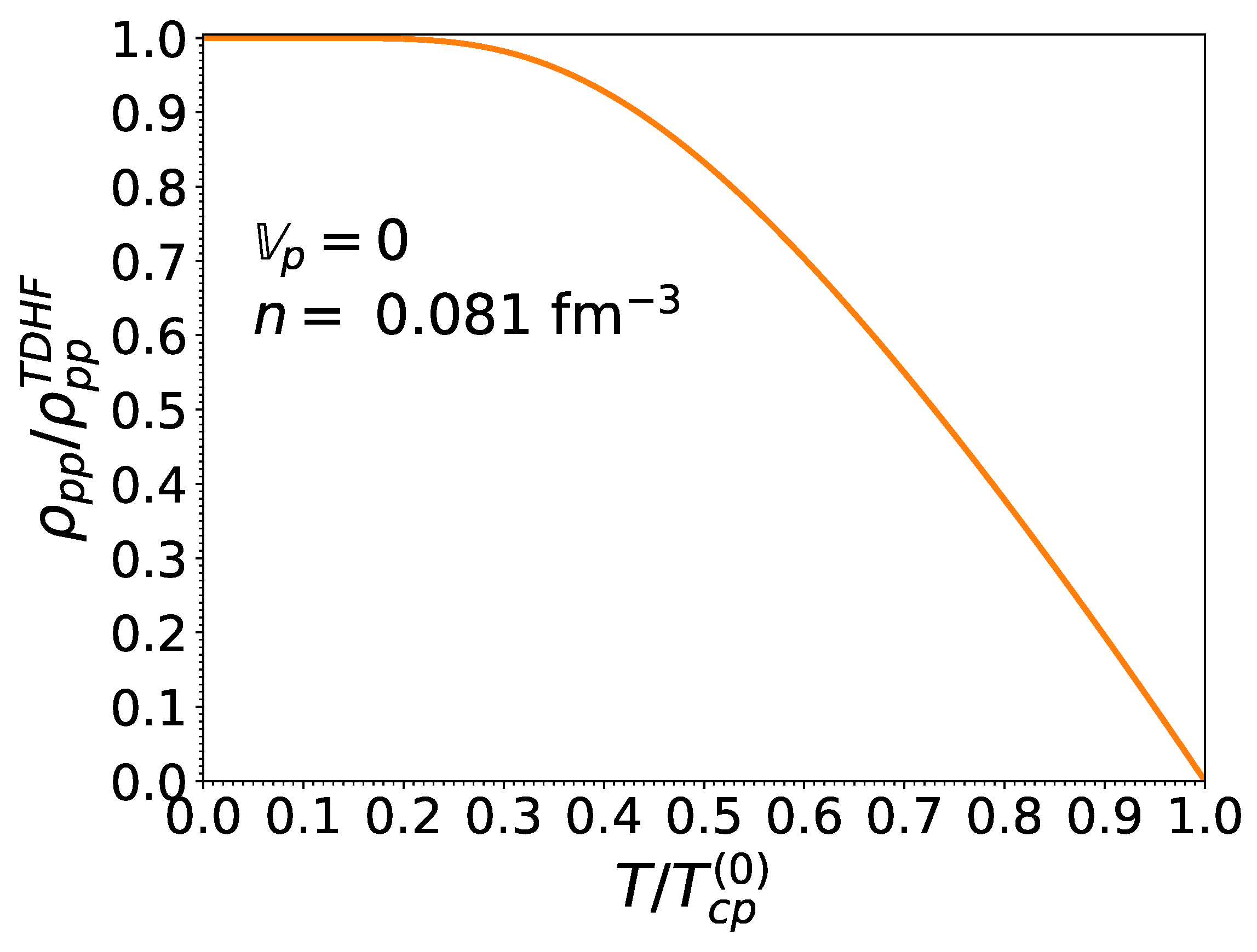
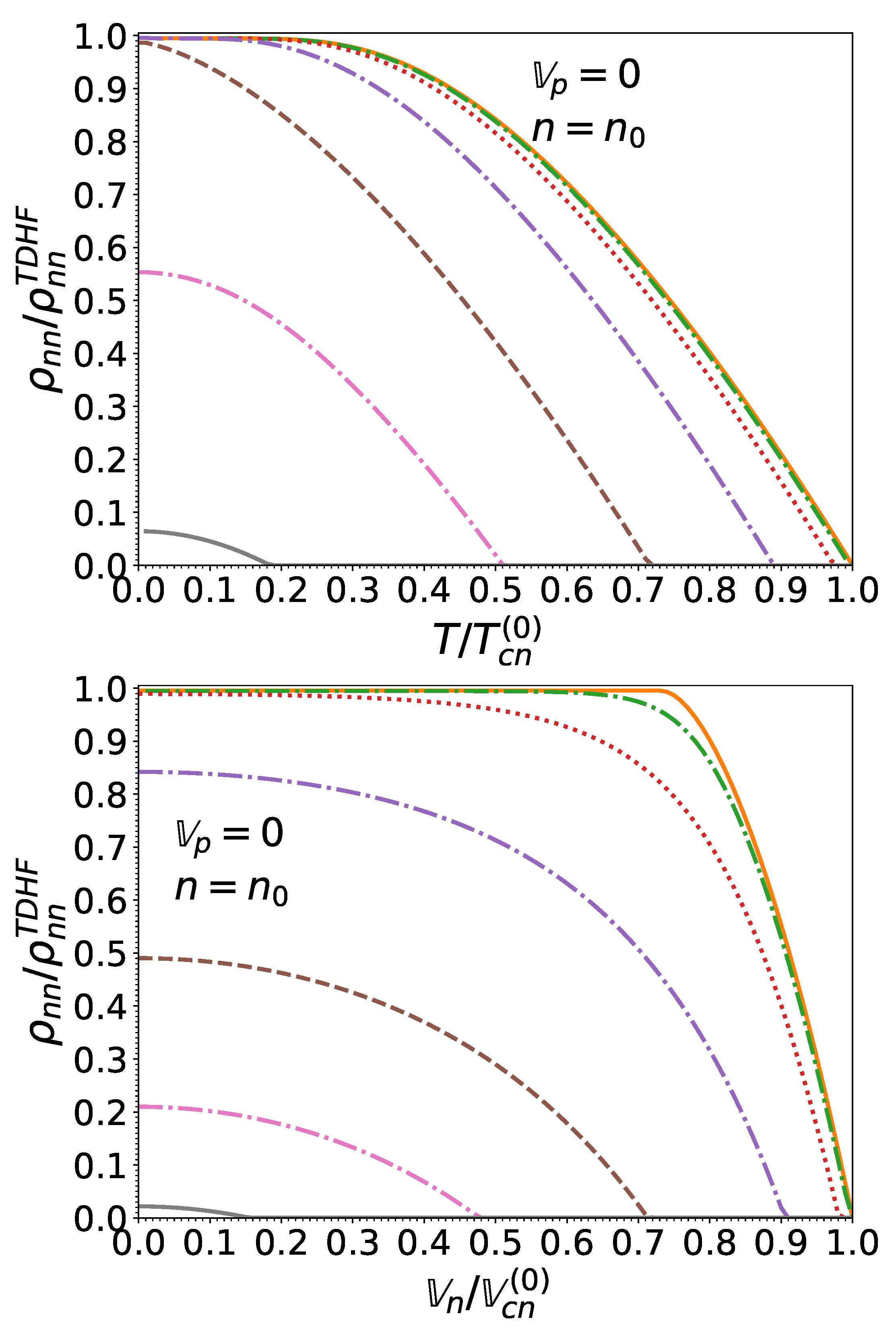
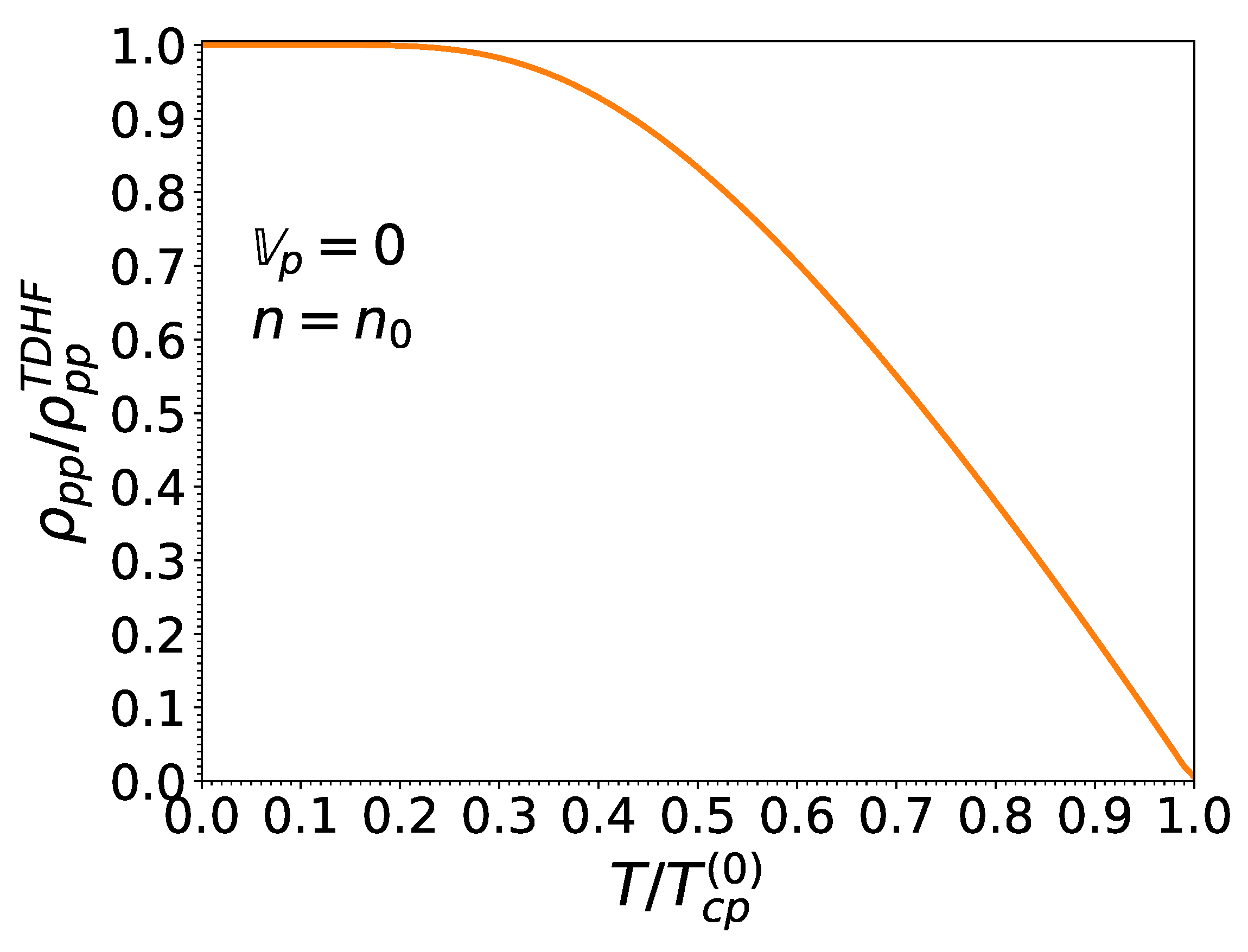
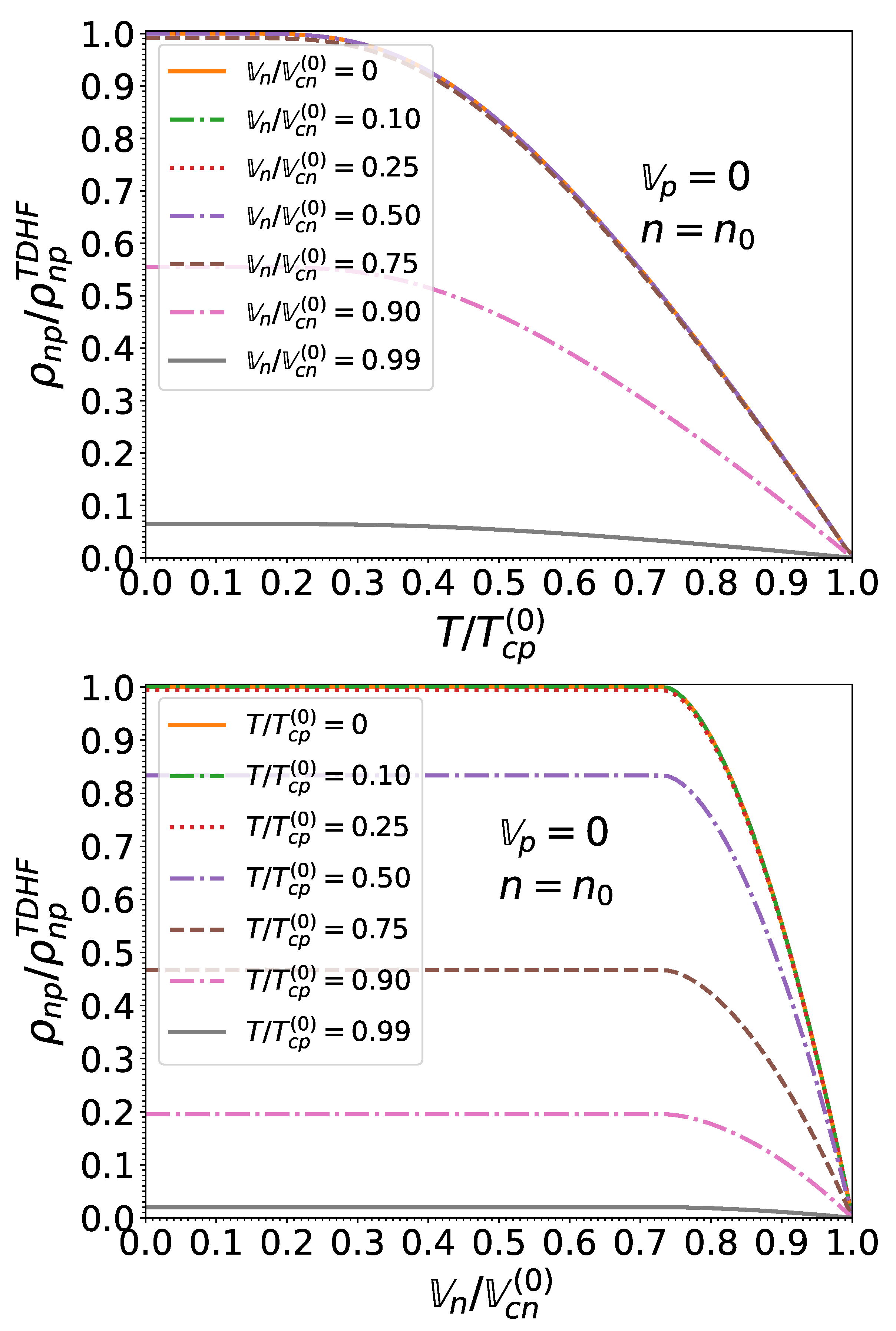
As shown in Figure 3 and Figure 4, the gaps for both neutrons and protons decrease monotonically with increasing temperature and effective superfluid velocity due to the excitation of quasiparticles. For vanishing effective superfluid velocities (i.e., in the absence of mass flow ), the temperature dependence of the pairing gaps is well fitted by the following expression [55]:
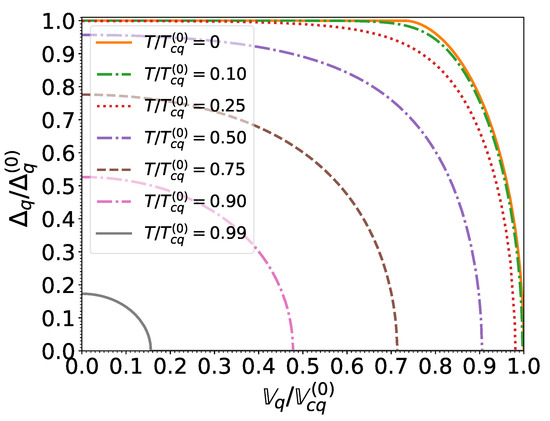
Figure 3.
S nucleon pairing gap relative to that at zero temperature and in the absence of superflow, as a function of the normalized effective superfluid velocity for different normalized temperatures .
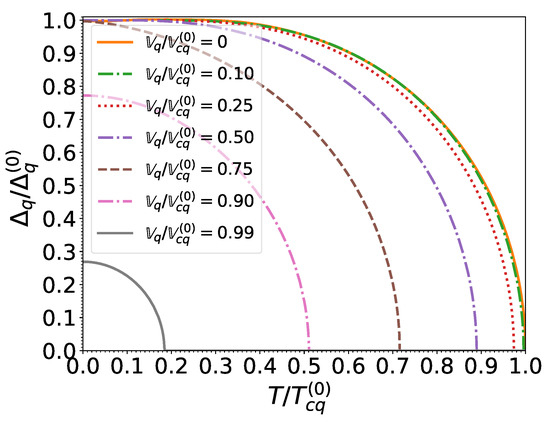
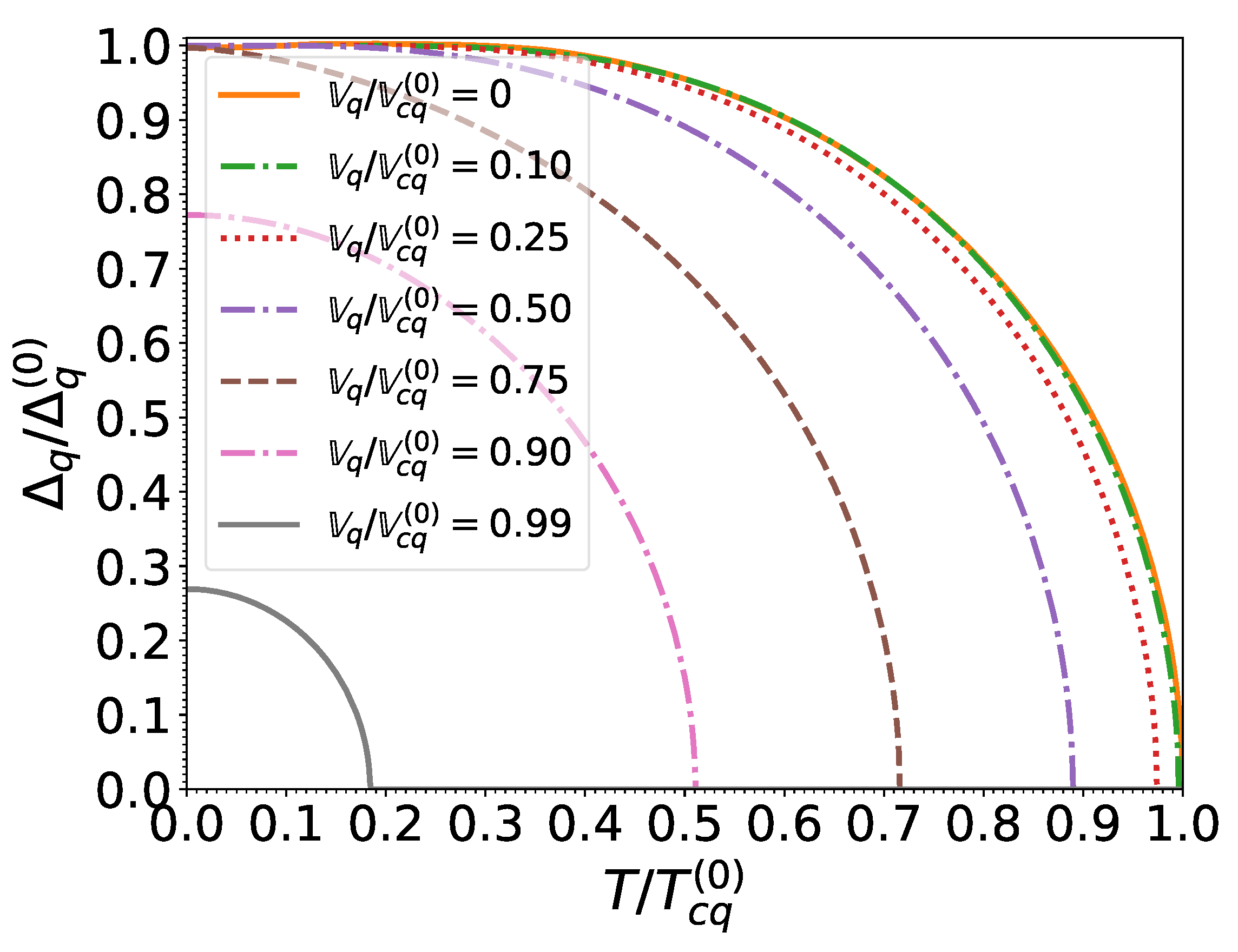
Figure 4.
S nucleon pairing gap relative to that at zero temperature and in the absence of superflow, as a function of the normalized temperature for different normalized effective superfluid velocities .
This same formula was applied in [13] to evaluate the entrainment matrix. At zero temperature, the pairing gap remains equal to until the effective superfluid velocity reaches Landau’s critical velocity , which for BCS condensates is given by [56]
Beyond this point, the pairing gap decreases with increasing effective superfluid velocity and vanishes for . We find that this behavior is well reproduced by the following interpolating formula:
The maximum relative error does not exceed 0.13%.
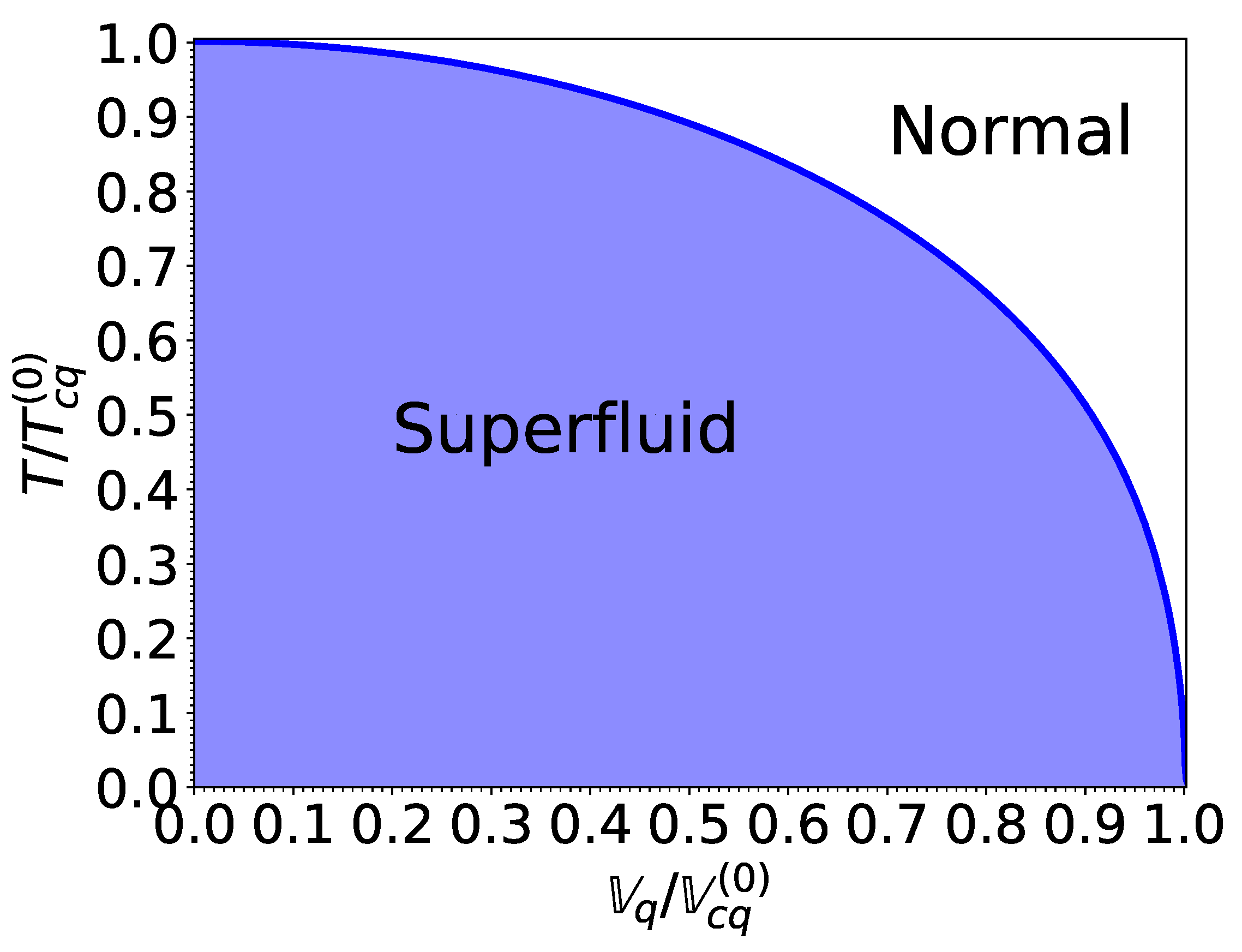
The critical temperature and critical effective superfluid velocity delimiting the superfluid and normal phases, plotted in Figure 5 is well fitted by the following expression:
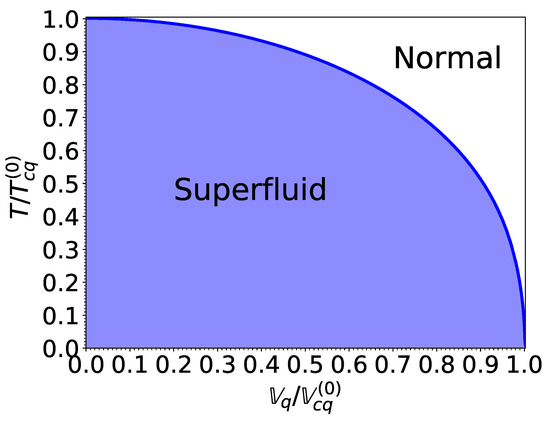
Figure 5.
Phase diagram for the nucleon species q in terms of the normalized temperature and the normalized effective superfluid velocity .
This interpolation is valid for both neutrons and protons. The errors are contained within the thickness of the lines in Figure 5.
The universality observed in the superfluid properties of both neutrons and protons (after a suitable choice of normalizations) is the consequence of the weak-coupling regime, as discussed in Section 2.5. Indeed, as shown in Equation (65), the normalized pairing gaps are independent of the pairing strength (hence also of the associated pairing cutoff ) and depend only on the rescaled temperature and effective superfluid velocity . Estimating the exact pairing gaps from Equation (77) and substituting in Equation (65) lead to a very good approximation for the exact pairing gaps at finite temperatures and arbitrary effective superfluid velocities. The largest absolute deviations are found at the crust-core interface: they are of order of for neutrons and lie within the numerical errors for protons.
3.4. Reduced Chemical Potentials
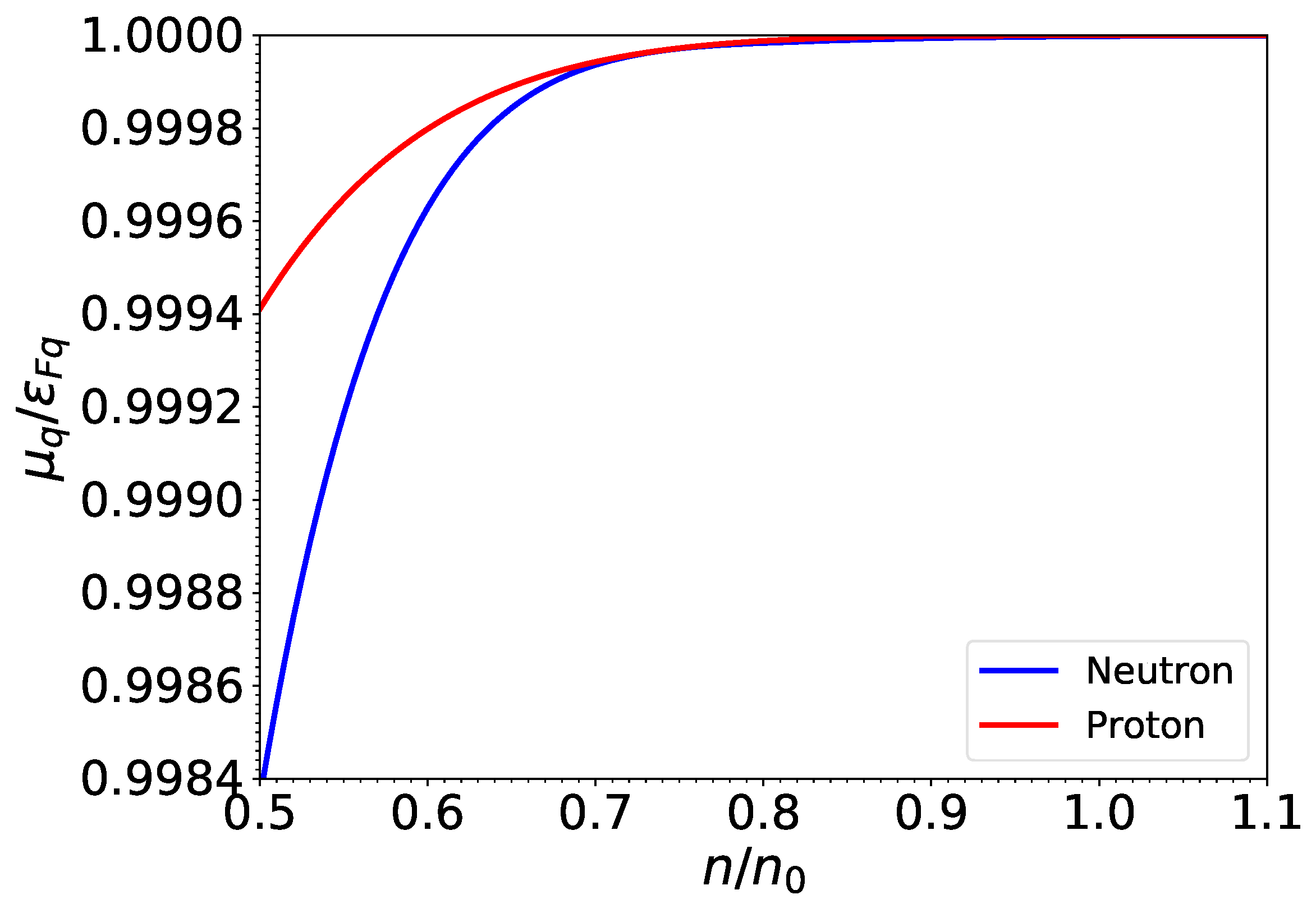
The TDHFB theory allows the determination of the chemical potentials consistently with the pairing gaps. Let us recall that in Landau’s theory adopted in previous studies [13,14,15], the reduced chemical potential was approximated by the corresponding Fermi energy ; effects induced by pairing, temperature, and currents were therefore ignored. To assess the precision of this approximation, we have computed numerically by solving simultaneously Equations (43) and (44) varying the temperature and the neutron effective superfluid velocity. The largest relative errors between and the Fermi energy we have found (at the crust-core interface) are 0.14% for neutrons and 0.052% for protons. Such errors have been obtained for low temperatures and small effective superfluid velocities for which pairing effects are the most important. Focusing on these conditions, we have plotted in Figure 6 the ratio as a function of density. As expected, the higher the density, the more precise are Landau’s approximations. To a large extent, the small deviations between and stem from the rather small pairing gaps predicted by the functional BSk24. Larger deviations cannot be excluded if another functional is adopted. In any case, let us recall that both Equations (43) and (44) should be solved simultaneously to obtain fully consistent pairing gaps and chemical potentials.
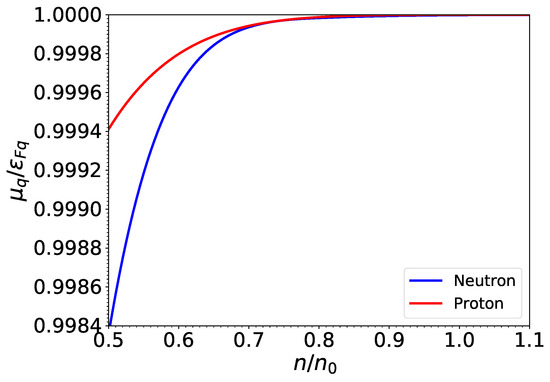
Figure 6.
Reduced chemical potentials relative to the corresponding Fermi energy for matter in beta-equilibrium at baryon densities prevailing in neutron-star cores in units of the saturation density . Results obtained at and for .
3.5. Functions
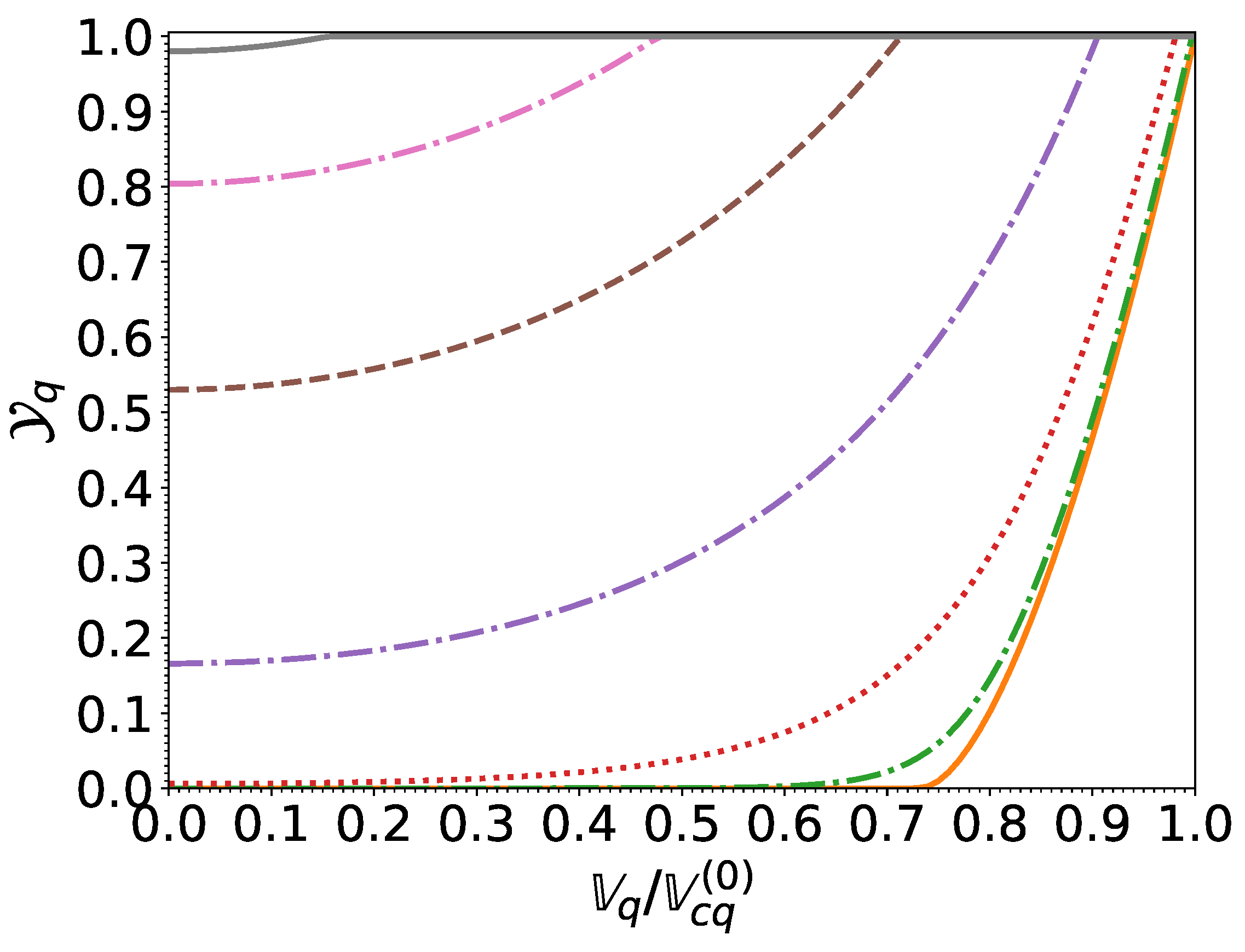
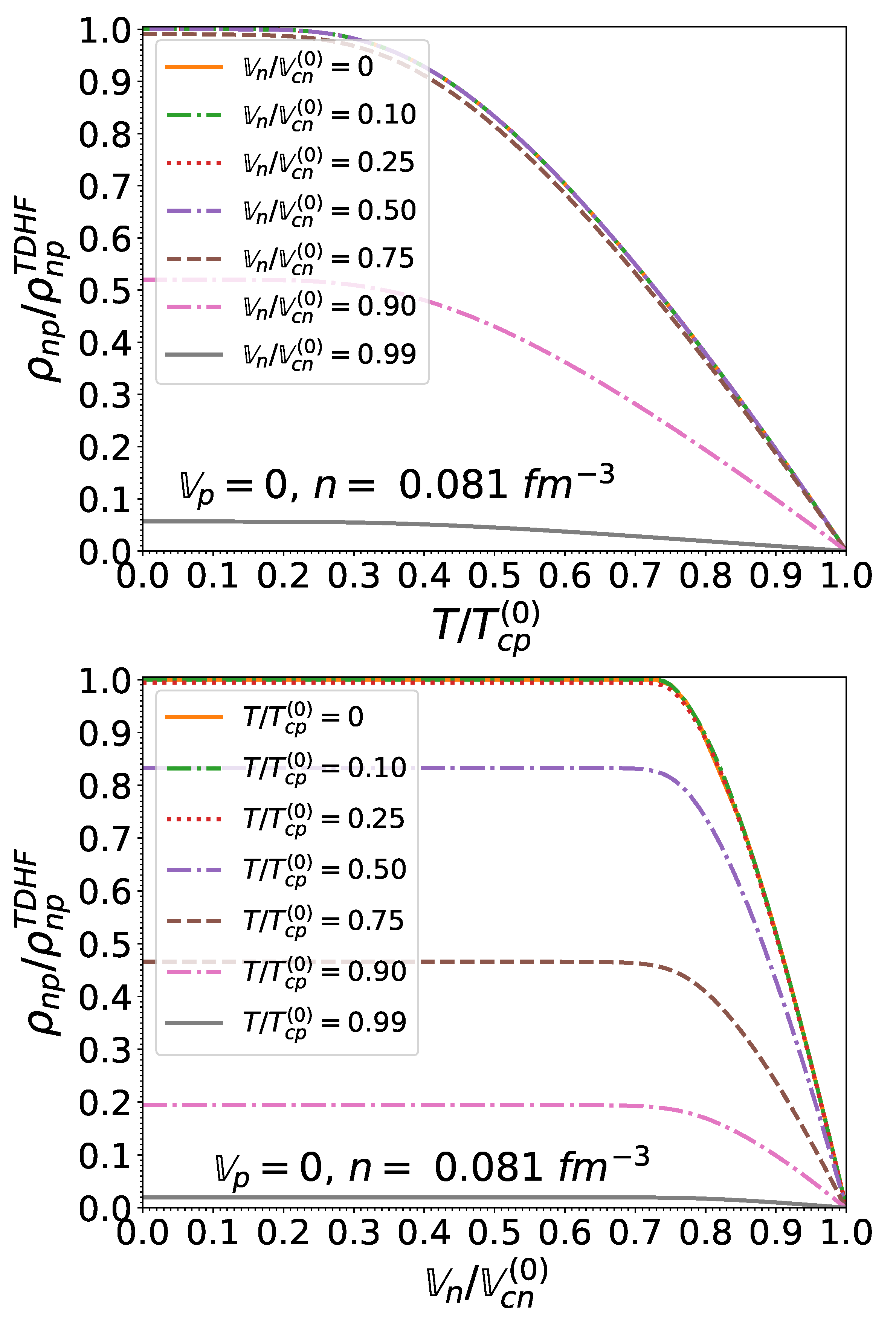
Having computed the pairing gaps as well as the reduced chemical potentials at finite temperatures and for arbitrary effective superfluid velocities by solving Equations (43) and (44), we can now evaluate the functions from Equation (38). When expressed in terms of the dimensionless ratios and , results are found to be essentially independent of density and are summarized in Figure 7 and Figure 8.
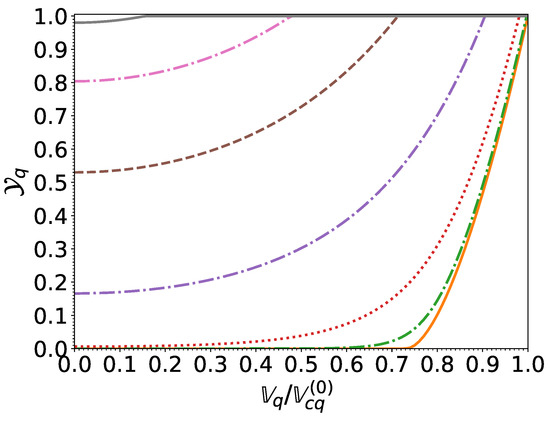
Figure 7.
as a function of the normalized effective superfluid velocity for different normalized temperatures . The legend of the curves is the same as in Figure 3.
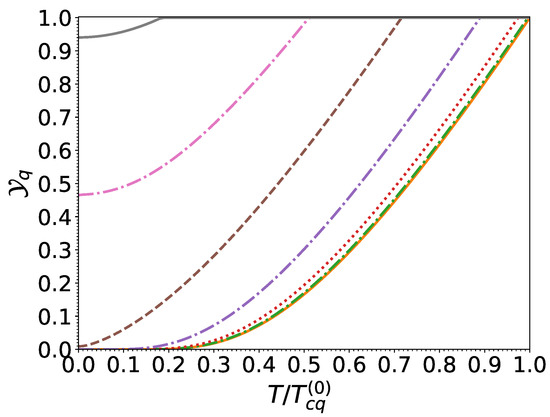
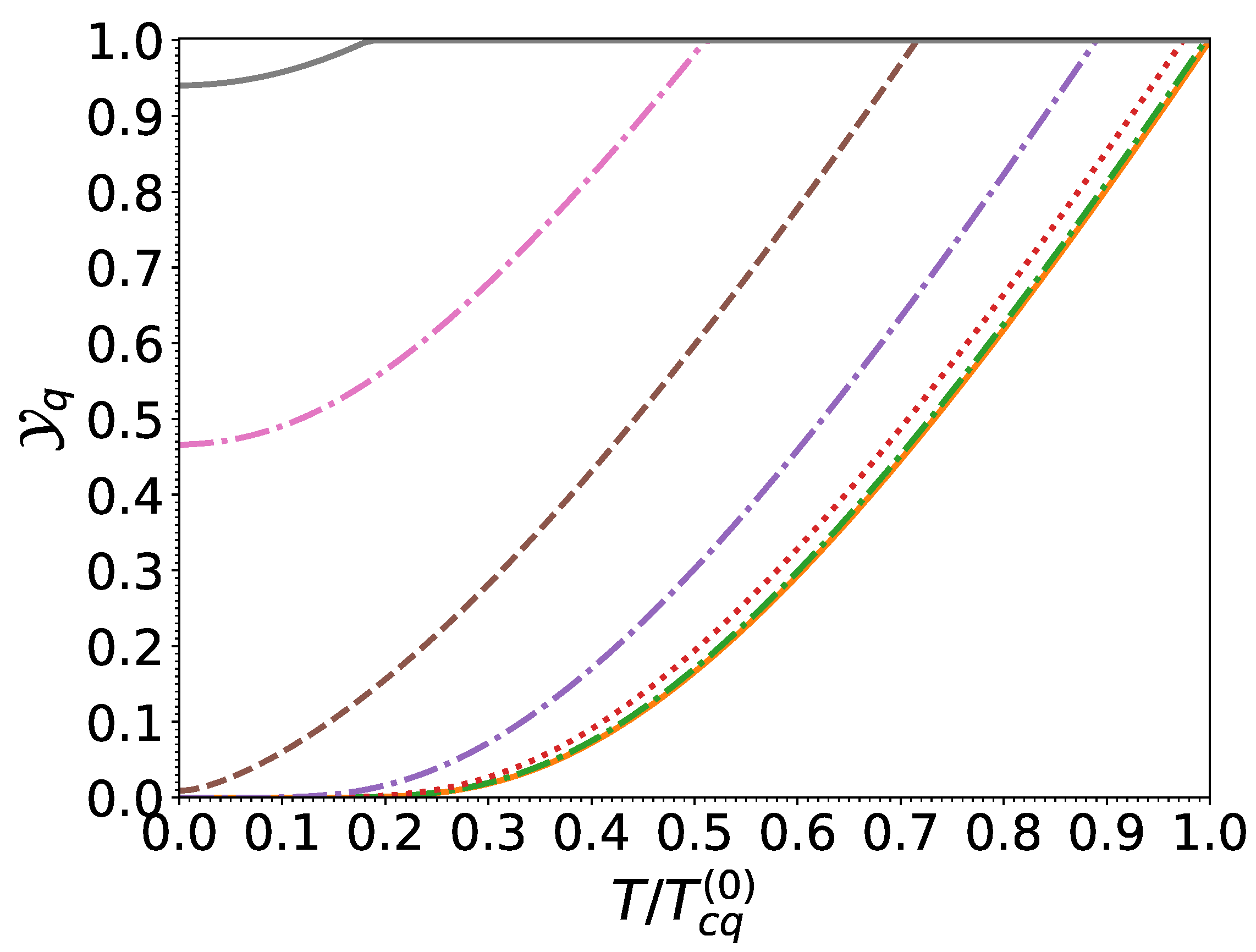
Figure 8.
as a function of the normalized temperature for different normalized effective superfluid velocities . The legend of the curves is the same as in Figure 4.
The functions are well approximated by the functions defined by Equation (62) where the pairing gaps are computed from Equation (59) and provided are evaluated from Equation (77). Since the deviations decrease with increasing density, we have focused on the crust-core interface. The absolute errors are found to be at most of order for and for . It follows from Equation (67) that the function is universal. In the absence of superflow , the temperature dependence of the functions can be well fitted by the following expression [57] (errors not exceeding 2.6%):
with computed using the interpolation (80).
3.6. Effective versus True Superfluid Velocities
The results we have presented so far have been conveniently expressed in terms of the effective superfluid velocities , which are related to the original superfluid velocities by Equations (29) and (32). These relations are highly nontrivial, recalling that the coefficients , defined by (21)–(25), depend on through the functions .
So far, we have treated the effective superfluid velocities as free parameters. In reality however, and are determined by the dynamics of the star, as pointed out in the previous analysis of entrainment effects in [15]. In particular, in the study of low-frequency oscillations, it is a very good approximation to assume that the electric current in the normal frame vanishes, as shown in the classical work of [58]. Considering that leptons are co-moving with quasiparticle excitations, the previous condition reads (in the normal frame). It immediately follows from Equation (53) that . In the following, we will restrict to this case as in [15] since it is of most physical interest. Under such condition, the vectors and are aligned, and are given by
These superfluid velocities depend on the baryon density n, the temperature T and the neutron effective superfluid velocity . Please note that under Landau’s approximations, the norm of (85) reduces to Equation (79) of [15] (these authors adopted the notation for , for the neutron effective mass , for the neutron effective superfluid velocity and for the neutron true superfluid velocity ; the Landau parameters are given by Equation (100) of [17]).
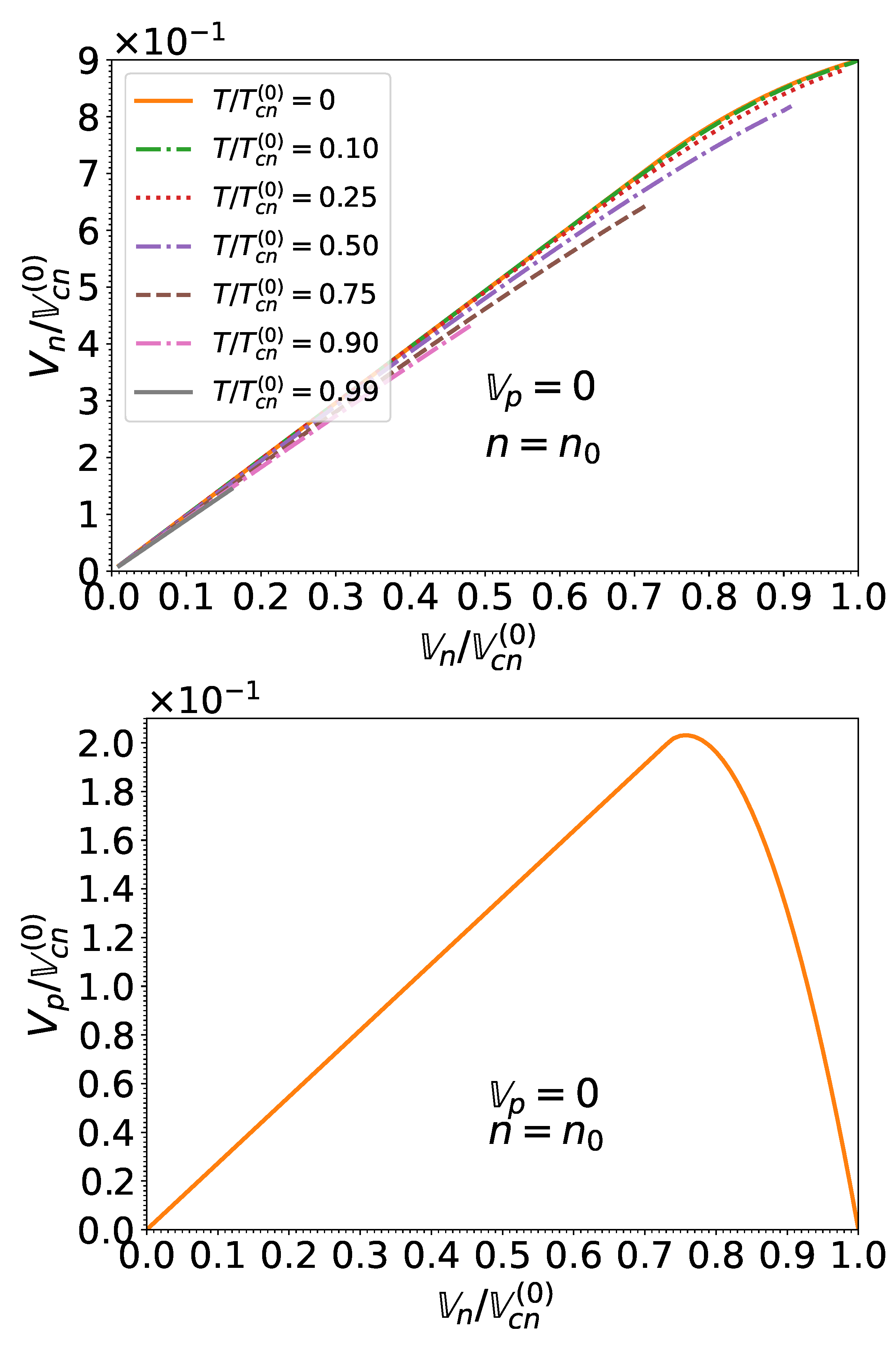
Results for the norms, considering matter in beta-equilibrium, are displayed in Figure 9 and Figure 10 for two different densities. These superfluid velocities are only defined in the superfluid phase, for effective superfluid velocities and temperatures lower than their associated critical values given by (83). Indeed, in the normal phase, the abnormal densities vanish identically and the associated superfluid velocities are therefore ill defined. However, this has no physical implications since the superfluid velocities are irrelevant in this case.
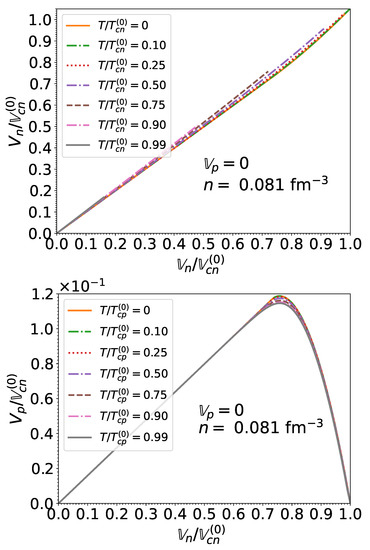
Figure 9.
Upper panel: neutron superfluid velocity relative to the corresponding critical velocity as a function of the normalized effective neutron superfluid velocity in matter in beta-equilibrium at the crust-core interface for different temperatures. Results were obtained for . Lower panel: same for the proton superfluid velocity .
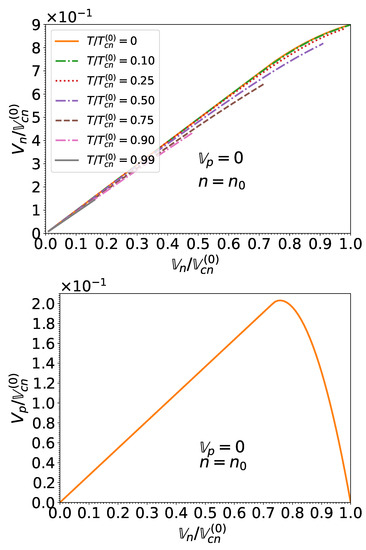
Figure 10.
Same as Figure 9 at saturation density . Please note that for the proton superfluid velocity , results for temperatures are all contained within the thickness of the solid line.
Although the neutron superfluid velocity is roughly equal to the effective superfluid velocity, , the proton superfluid velocity exhibits a more complicated behavior as a function of . From Equation (86), we have . For sufficiently low neutron effective superfluid velocities, therefore increases linearly with . However, increases with leading to a decrease of (for ), which vanishes when corresponding to .
3.7. Entrainment Matrix
Having computed the pairing gaps, chemical potentials, and functions we can now determine the entrainment matrix from Equation (19). To better see the influence of temperature and superflows, results will be compared to those obtained at zero temperature and in the limit of small currents (conditions for which pairing can be ignored) using the following expression that we have previously calculated within the time-dependent Hartree–Fock (TDHF) theory [16]:
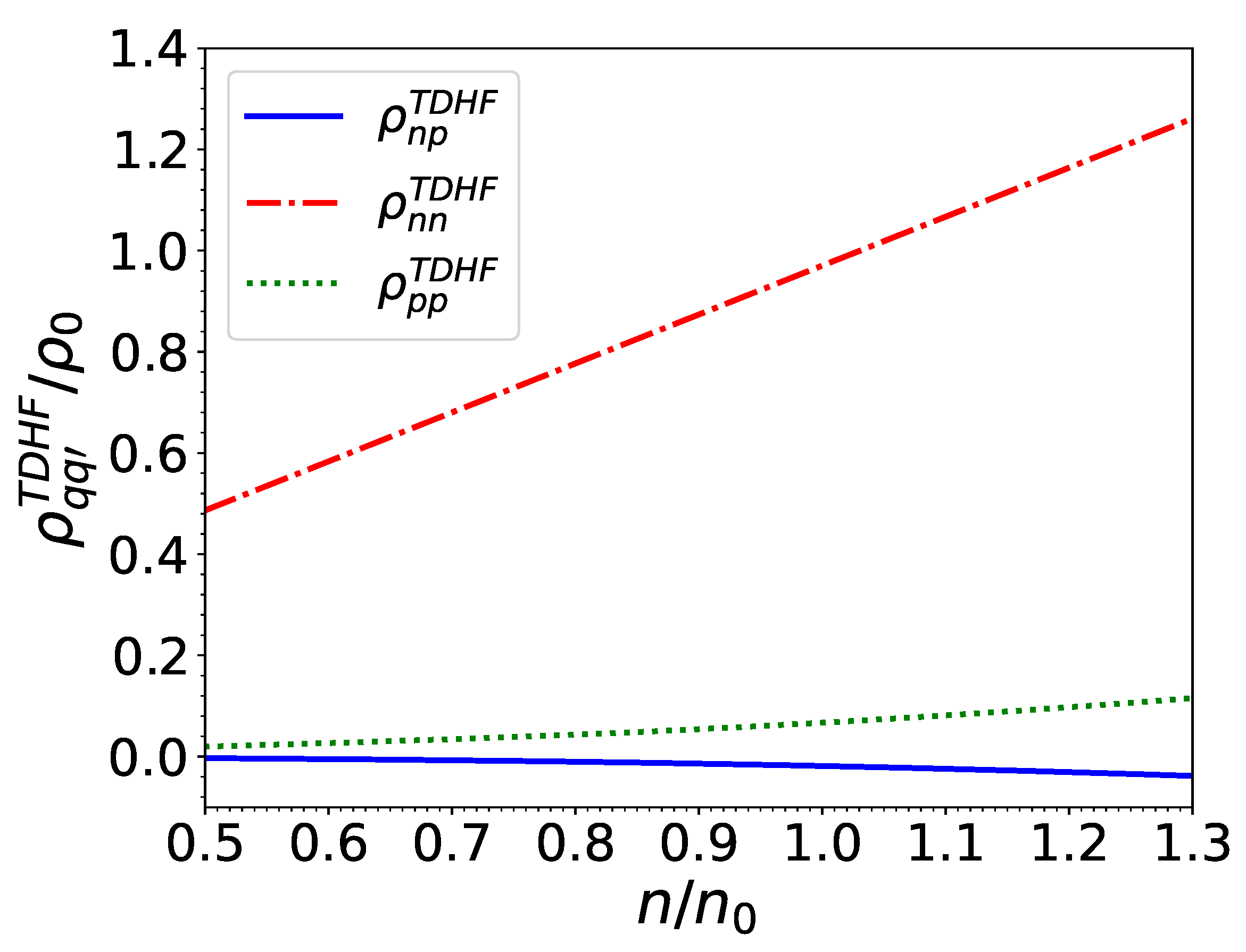
These matrix elements are shown in Figure 11 for matter in beta-equilibrium at densities relevant for the outer core of neutron stars. Results within the TDHFB theory for finite temperatures and different neutron effective superfluid velocities (recalling that we set as discussed in Section 3.6) are plotted in Figure 12, Figure 13 and Figure 14 at the crust-core interface, and in Figure 15, Figure 16 and Figure 17 at the saturation density.
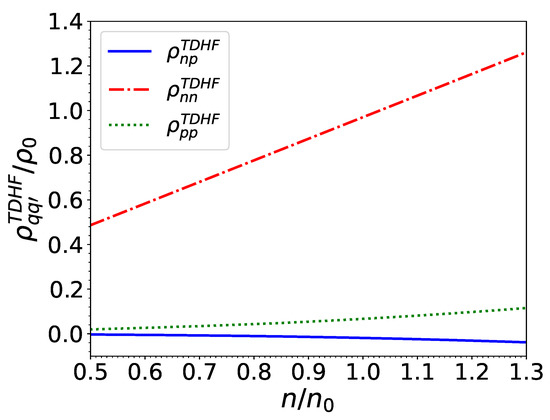
Figure 11.
Entrainment matrix elements (normalized by the saturation density ) for matter in beta-equilibrium at zero temperature and in the limit of small currents at baryon densities prevailing in neutron-star cores in units of the saturation density .
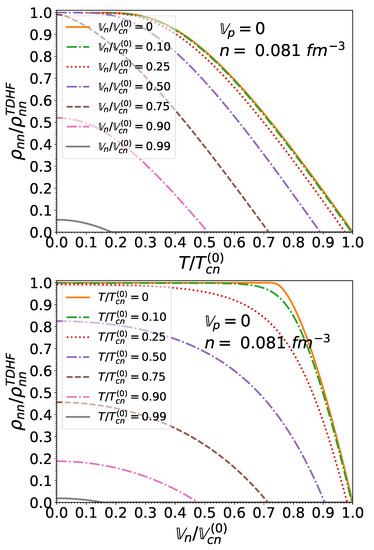
Figure 12.
Dimensionless entrainment matrix element as a function of the normalized effective superfluid velocity and the normalized temperature for matter in beta-equilibrium at the crust-core interface and for .
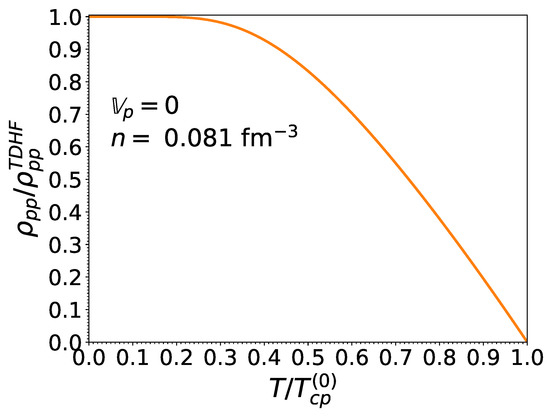
Figure 13.
Dimensionless entrainment matrix element as a function of the normalized temperature , for matter in beta-equilibrium at the crust-core interface and for . Results obtained for different neutron effective superfluid velocities are indistinguishable.
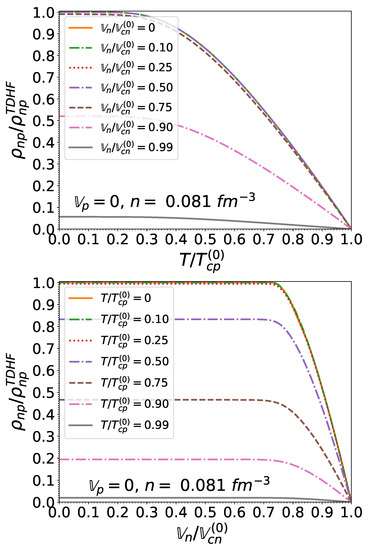
Figure 14.
Dimensionless entrainment matrix element as a function of the normalized effective superfluid velocity and the normalized temperature , for matter in beta-equilibrium at the crust-core interface and for .
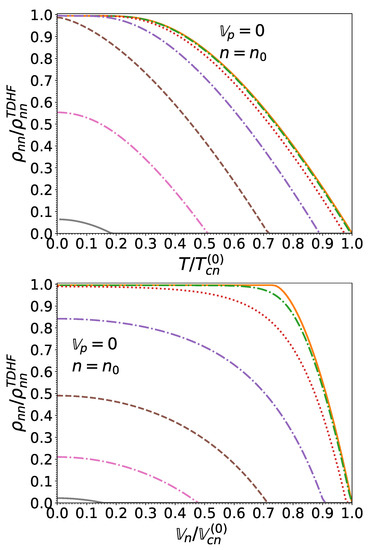
Figure 15.
Same as Figure 12 at the saturation density using the same notation for the meaning of the different curves.
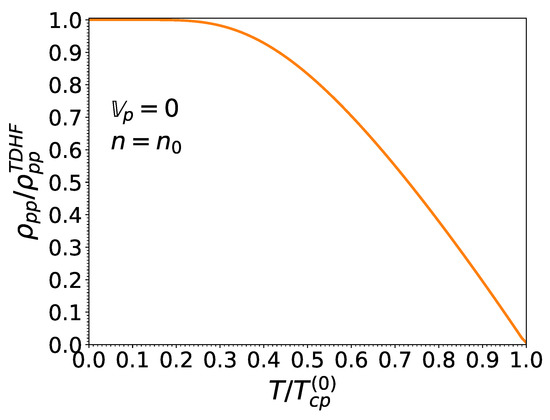
Figure 16.
Same as Figure 13 at the saturation density .
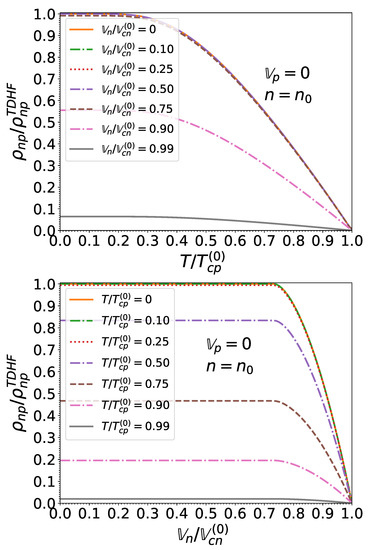
Figure 17.
Same as Figure 14 at the saturation density .
Quite remarkably, the entrainment matrix at remains independent of the neutron effective superfluid velocity provided the latter does not exceed Landau’s critical velocity. In other words, the expressions obtained in [16] in the limit of vanishing small effective superfluid velocities are actually exact for any effective superfluid velocity lying below Landau’s critical value. This can be traced back to the vanishing of the function for , as can be seen in Figure 7. This also entails that the entrainment matrix does not depend on the pairing gaps in this regime, thus justifying a posteriori our application of the TDHF theory [16] instead of TDHFB [17] since the gaps can thus artificially be set to zero. However, the TDHFB theory is still required for the determination of the actual value for .
At finite but sufficiently low temperatures, the entrainment matrix remains weakly dependent on the neutron effective superfluid velocity provided . For higher neutron effective superfluid velocities, the entrainment matrix elements and are reduced, even at . The element is essentially independent of . The influence of T and becomes increasingly important as these parameters approach their critical value. In particular, and both vanish when : neutron superfluidity is destroyed and the neutron mass is thus entirely transported by the normal fluid, as can be seen from Equation (1). On the other hand, protons remain superconducting but are no longer entrained by neutrons: the two species are dynamically uncoupled. The proton mass current (2) thus reduces to the familiar expression for a single superfluid.
3.8. Chemical Potentials
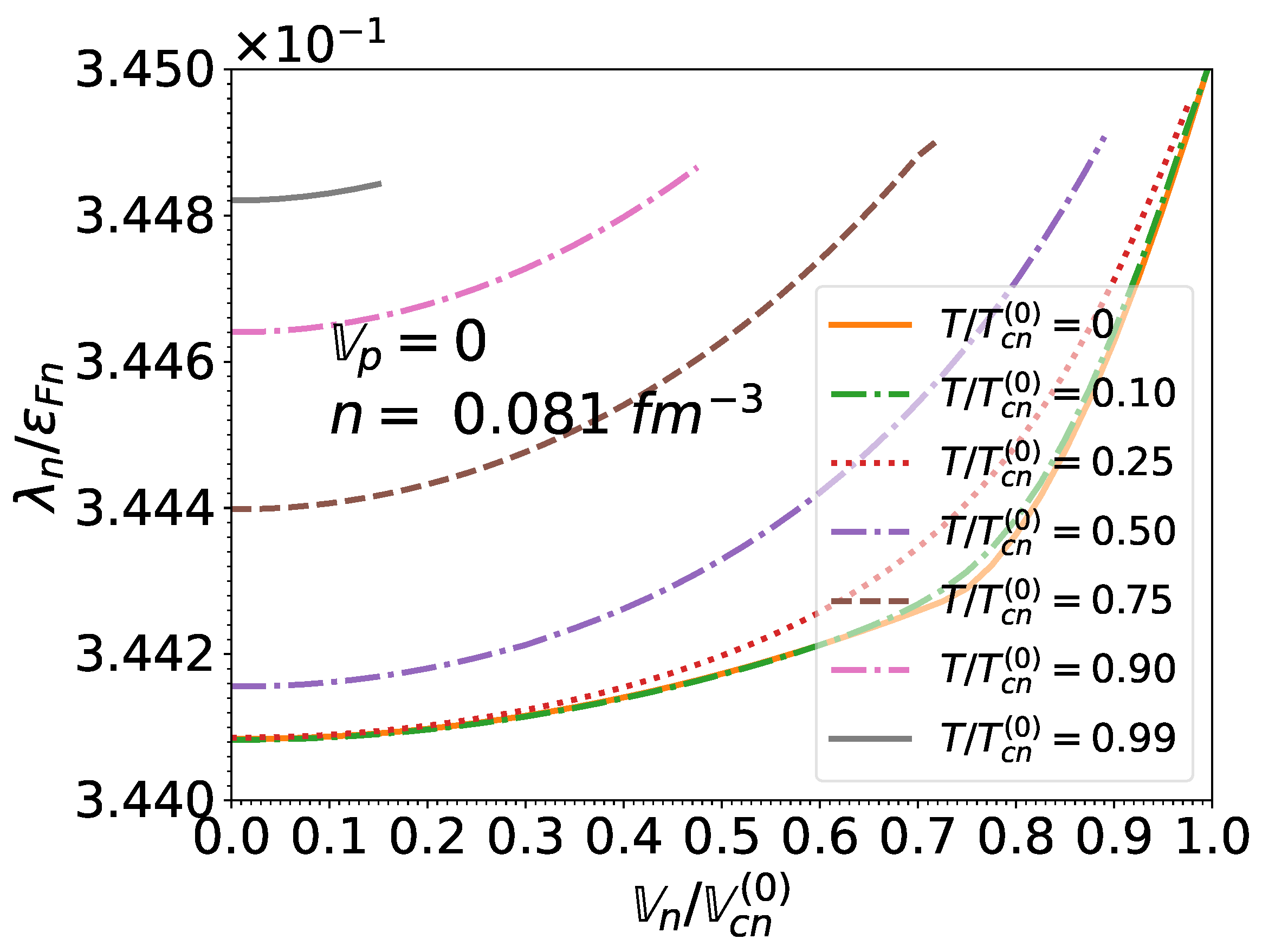
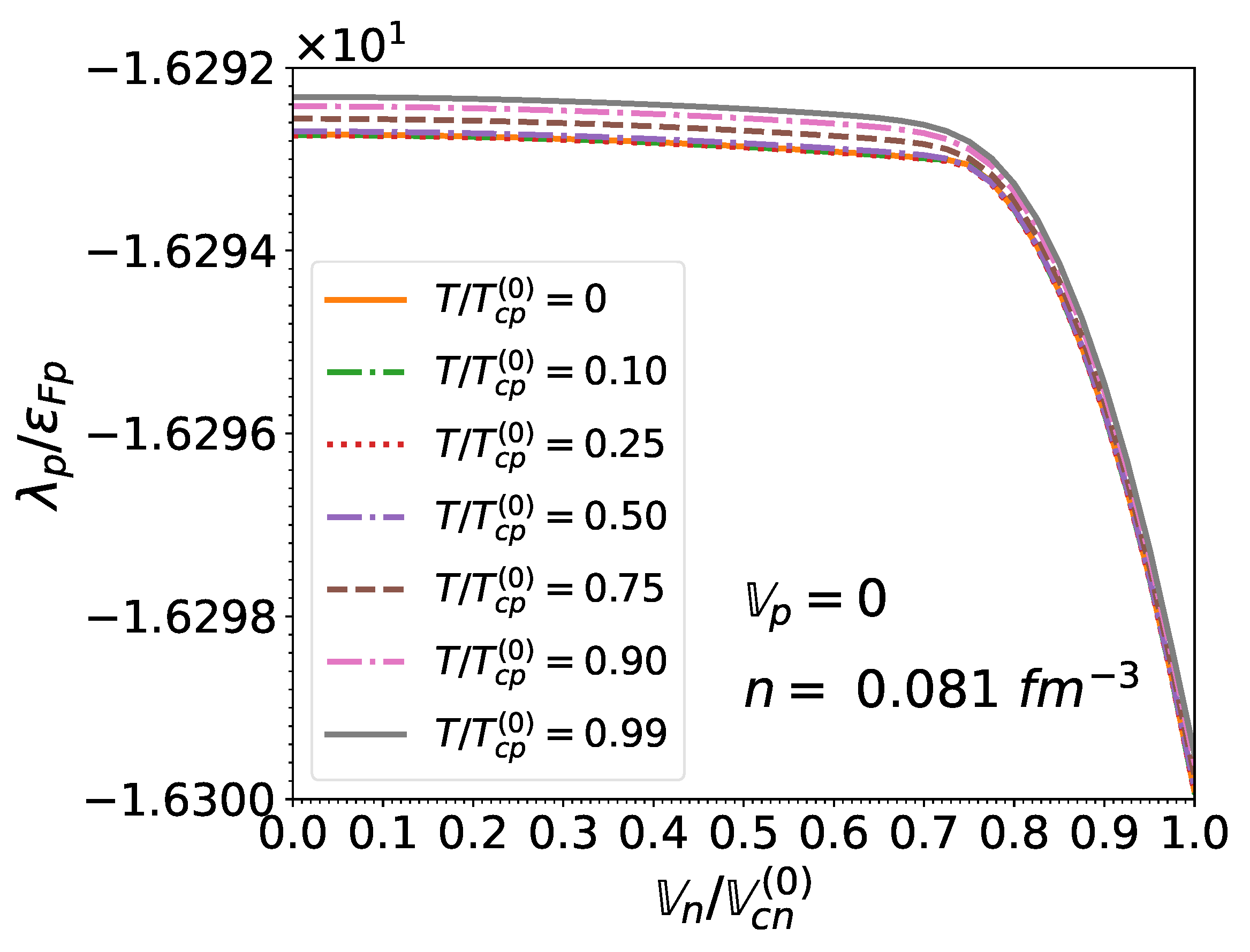
Knowing the relation between the effective superfluid velocities and the superfluid velocities , given by Equations (85) and (86) respectively, and using Equation (71) for the potentials together with Equation (50) for the momentum densities and Equation (51) for the kinetic-energy densities , we can compute the true chemical potentials from Equations (48) and (49). Results for (as discussed in Section 3.6) are plotted in Figure 18 for and in Figure 19 for respectively. Although the chemical potentials are found to be very weakly dependent on the temperature and on the neutron effective superfluid velocity (in the regime for which superfluidity exists), they deviate substantially from their corresponding Fermi energies due to the contribution from the potential .
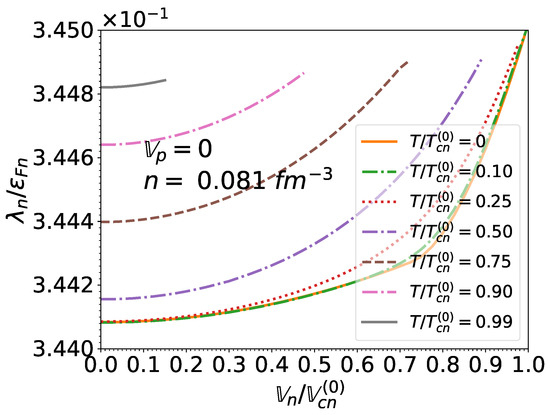
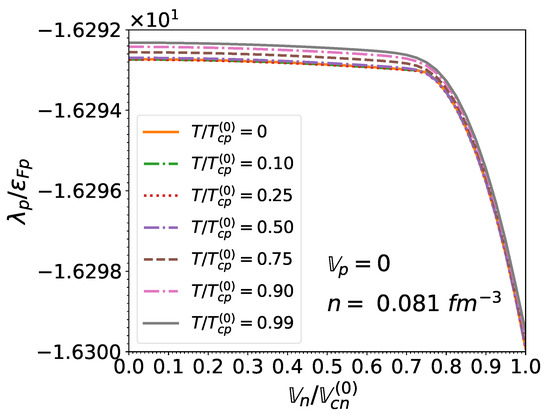
Figure 18.
Upper panel: neutron chemical potential normalized to the associated Fermi energy as a function of the normalized neutron effective superfluid velocity and of the normalized temperature for matter in beta-equilibrium at the crust-core interface and for . Lower panel: same for the proton chemical potential .
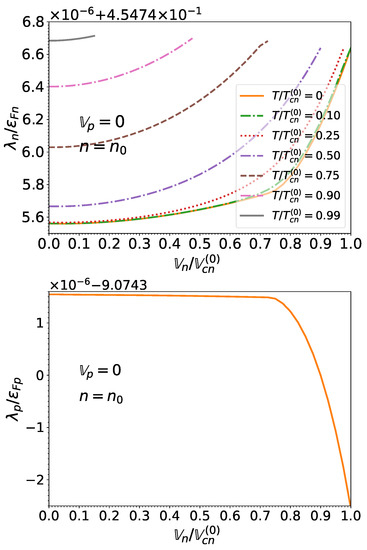
Figure 19.
Same as Figure 18 at the saturation density . Please note that for the proton chemical potential , results for temperatures (ranging from 0 to ) are all contained within the thickness of the solid line.
4. Conclusions
We have studied the neutron–proton superfluid mixture present in the outer core of a neutron star in the framework of the nuclear-energy-density functional theory. In particular, we have calculated consistently the S pairing gaps of each nucleon species q, their chemical potentials , and the entrainment matrix elements relating the mass currents to the so-called superfluid “velocities” (actually representing superfluid momenta per unit mass) in the normal-fluid rest frame.
To this end, we have solved numerically the self-consistent TDHFB equations with the Brussels–Montreal functional BSk24 [18] for matter in beta-equilibrium over the whole range of temperatures and velocities for which nuclear superfluidity can exist using the composition published in [19]. We have considered the full TDHFB equations without any approximation. In particular, the vector potentials and the contributions from the momentum densities to the potentials and to the kinetic densities have been fully taken into account. We have shown that represents the total momentum density of a given nucleon species q, accounting not only for the superfluid momentum density but also for the momentum density carried by the quasiparticles, as shown in Equation (54). Because the true velocity of the nucleon species q in the normal frame is related to the effective superfluid velocity introduced in Equation (29) through Equation (53), appears as the natural variable to characterize the superflow of the nucleon species q.
The S proton pairing gaps at zero temperature and in the absence of flows are found to be significantly smaller than the neutron gaps , unlike those generally considered in neutron-star simulations. Although proton gaps are mainly determined by the empirical interpolation (74) between the reference gaps in symmetric nuclear matter and pure neutron matter, they turn out to be consistent with recent diagrammatic calculations taking into account medium-polarization effects and considering both two- and three-body interactions [52]. We have shown that the gaps are accurately reproduced by the approximate formula (77).
The normalized S pairing gaps and the fraction of quasiparticles are found to be universal functions of and , with the critical temperature and critical velocity given by Equations (78) and (79) respectively, in the sense that they depend neither on the composition nor on the density, and are the same for both neutrons and protons. This result can be understood from the fact that S nucleon superfluidity in the core of neutron stars is in the (weak-coupling) BCS regime. We have found that the temperature dependence of the normalized pairing gaps in the absence of flows is well fitted by Equation (80) proposed in [55]. We have obtained new accurate interpolating formulas for describing the velocity-dependence of the normalized pairing gaps at zero temperature (82), as well as for the critical temperatures (83). For arbitrary temperatures and velocities, the pairing gaps can be determined with a very good accuracy by solving numerically Equation (59) instead of the full TDHFB equations.
We have found that the approximations reducing the TDHFB equations to Landau’s theory provide accurate results for the entrainment matrix provided the critical temperatures in the absence of superflow are given. Moreover, the reduced chemical potentials defined by Equation (35) are well approximated by the corresponding Fermi energies given by Equation (41). However, this conclusion may change depending on the functional, especially if the adopted one predicts stronger pairing. Moreover, numerical solutions of the full TDHFB equations are still required for calculating the chemical potentials .
Together with the results published in [19,20,21,22] for the composition and the equation of state, our calculations provide consistent microscopic inputs for modeling the global structure and dynamics of superfluid neutron stars. Although we have considered the specific functional BSk24 because it has been shown to be in excellent agreement with existing nuclear data and astrophysical observations [23,44], we have also derived all the necessary equations to evaluate superfluid properties for any other functional of the Brussels–Montreal type (this includes all the functionals based on standard Skyrme effective nucleon-nucleon interactions). Extension of the TDHFB theory to account for PF neutron superfluidity in the inner core of massive neutron stars is left for future studies.
Author Contributions
Conceptualization, N.C. and V.A.; methodology, V.A. and N.C.; software, V.A.; validation, V.A. and N.C.; formal analysis, V.A.; investigation, V.A.; resources, N.C.; data curation, V.A.; writing—original draft preparation, V.A. and N.C.; writing—review and editing, N.C. and V.A.; visualization, V.A.; supervision, N.C.; project administration, N.C.; funding acquisition, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Fonds de la Recherche Scientifique (Belgium) under Grant No. PDR T.004320. This work was also partially supported by the European Cooperation in Science and Technology action (EU) CA16214.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| TDHFB | time-dependent Hartree–Fock–Bogoliubov |
| TDHF | time-dependent Hartree–Fock |
| NM | (Pure) Neutron matter |
| SM | Symmetric matter |
Appendix A. Weak-Coupling Approximation
Adopting Landau’s approximations discussed in Section 2.5, the gap equation reads
where the pairing strength is given by Equation (73), the density of single-particle states by Equation (58) and Landau’s quasiparticle energy by Equation (63). The lower bound of the integral consistent with the approximate single-particle energies (56) is .
Focusing on the superfluid phase () such that , dividing Equation (A1) by yields
Let us remark that in the limit , and is equal to 1 when evaluated at since . Taking the limit of Equation (A1) in the absence of currents and evaluating it at zero temperature, we thus obtain the approximate gap equation for
We can divide both sides of Equation (A3) by . Therefore, the left-hand side of Equation (A2) can be expressed as
Following [15], the weak-coupling approximation allows us to replace the inverse hyperbolic sine function by its asymptotic form . Taking the limit and and eliminating leads to Equation (59). Please note that unlike the original gap Equation (A1), the limit can be taken here since the integral does not exhibit any divergence.
References
- Chamel, N. Superfluidity and Superconductivity in Neutron Stars. J. Astrophys. Astron. 2017, 38, 43. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Andersson, N. Rotational evolution of young pulsars due to superfluid decoupling. Nat. Phys. 2012, 8, 787–789. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Chugunov, A.I.; Kantor, E.M. Instability Windows and Evolution of Rapidly Rotating Neutron Stars. Phys. Rev. Lett. 2014, 112, 151101. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 015806. [Google Scholar] [CrossRef]
- Andersson, N. A Superfluid Perspective on Neutron Star Dynamics. Universe 2021, 7, 17. [Google Scholar] [CrossRef]
- Andreev, A.F.; Bashkin, E.P. Three-velocity hdrodynamics of superfluid solutions. Sov. Phys. JETP 1975, 42, 164–167. [Google Scholar]
- Carter, B.; Khalatnikov, I.M. Canonically Covariant Formulation of Landau’s Newtonian Superfluid Dynamics. Rev. Math. Phys. 1994, 6, 277–304. [Google Scholar] [CrossRef]
- Prix, R. Variational description of multifluid hydrodynamics: Uncharged fluids. Phys. Rev. D 2004, 69, 043001. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Kantor, E.M. Velocity-dependent energy gaps and dynamics of superfluid neutron stars. Mon. Not. R. Astron. Soc. 2013, 428, L26–L30. [Google Scholar] [CrossRef]
- Dommes, V.A.; Kantor, E.M.; Gusakov, M.E. Temperature-dependent oscillation modes in rotating superfluid neutron stars. Mon. Not. R. Astron. Soc. 2019, 482, 2573–2587. [Google Scholar] [CrossRef]
- Kantor, E.M.; Gusakov, M.E. Entrainment matrix for BSk energy-density functionals. J. Phys. Conf. Ser. 2020, 1697, 012005. [Google Scholar] [CrossRef]
- Kantor, E.M.; Gusakov, M.E.; Dommes, V.A. Resonance suppression of the r -mode instability in superfluid neutron stars: Accounting for muons and entrainment. Phys. Rev. D 2021, 103, 023013. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Haensel, P. The entrainment matrix of a superfluid neutron-proton mixture at a finite temperature. Nucl. Phys. A 2005, 761, 333–348. [Google Scholar] [CrossRef]
- Leinson, L.B. Non-linear approach to the entrainment matrix of superfluid nucleon mixture at zero temperature. Mon. Not. R. Astron. Soc. 2017, 470, 3374–3387. [Google Scholar] [CrossRef]
- Leinson, L.B. The entrainment matrix of a superfluid nucleon mixture at finite temperatures. Mon. Not. R. Astron. Soc. 2018, 479, 3778–3790. [Google Scholar] [CrossRef]
- Chamel, N.; Allard, V. Entrainment effects in neutron-proton mixtures within the nuclear energy-density functional theory: Low-temperature limit. Phys. Rev. C 2019, 100, 065801. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Entrainment effects in neutron-proton mixtures within the nuclear energy-density functional theory. II. Finite temperatures and arbitrary currents. Phys. Rev. C 2021, 103, 025804. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals-I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Comparison between the Thomas-Fermi and Hartree-Fock-Bogoliubov Methods in the Inner Crust of a Neutron Star: The Role of Pairing Correlations. Universe 2020, 6, 206. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Mutafchieva, Y.D.; Chamel, N.; Stoyanov, Z.K.; Pearson, J.M.; Mihailov, L.M. Role of Landau-Rabi quantization of electron motion on the crust of magnetars within the nuclear energy density functional theory. Phys. Rev. C 2019, 99, 055805. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N.; Sourie, A. Role of the symmetry energy and the neutron-matter stiffness on the tidal deformability of a neutron star with unified equations of state. Phys. Rev. C 2019, 100, 035801. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N. Role of dense matter in tidal deformations of inspiralling neutron stars and in gravitational waveforms with unified equations of state. Phys. Rev. C 2021, 103, 025801. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Yasui, S.; Inotani, D.; Nitta, M. Coexistence phase of 1S0 and 3P2 superfluids in neutron stars. Phys. Rev. C 2020, 101, 055806. [Google Scholar] [CrossRef]
- Blaizot, J.; Ribka, G. Quantum Theory of Finite Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Dobaczewski, J.; Flocard, H.; Treiner, J. Hartree-Fock-Bogolyubov description of nuclei near the neutron-drip line. Nucl. Phys. A 1984, 422, 103–139. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Theory of Superconductivity: From Weak to Strong Coupling; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Chamel, N.; Pearson, J.M.; Fantina, A.F.; Ducoin, C.; Goriely, S.; Pastore, A. Brussels–Montreal Nuclear Energy Density Functionals, from Atomic Masses to Neutron Stars. Acta Phys. Pol. B 2015, 46, 349. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XVI. Inclusion of self-energy effects in pairing. Phys. Rev. C 2016, 93, 034337. [Google Scholar] [CrossRef]
- Bertsch, G.F.; Esbensen, H. Pair correlations near the neutron drip line. Ann. Phys. 1991, 209, 327–363. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Nazarewicz, A.A.; Werner, A.A. Closed shells at drip-line nuclei. Phys. Scr. Vol. 1995, 56, 15–22. [Google Scholar] [CrossRef]
- Chamel, N.; Goriely, S.; Pearson, J. Further explorations of Skyrme–Hartree–Fock–Bogoliubov mass formulas. IX: Constraint of pairing force to 1S0 neutron-matter gap. Nucl. Phys. A 2008, 812, 72–98. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Recent breakthroughs in Skyrme-Hartree-Fock-Bogoliubov mass formulas. Eur. Phys. J. A 2009, 42, 547–552. [Google Scholar] [CrossRef]
- Chamel, N. Effective contact pairing forces from realistic calculations in infinite homogeneous nuclear matter. Phys. Rev. C 2010, 82, 014313. [Google Scholar] [CrossRef]
- Chamel, N.; Goriely, S.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XI. Stabilizing neutron stars against a ferromagnetic collapse. Phys. Rev. C 2009, 80, 065804. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XII. Stiffness and stability of neutron-star matter. Phys. Rev. C 2010, 82, 035804. [Google Scholar] [CrossRef]
- Goriely, S. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XV: The spin-orbit coupling. Nucl. Phys. A 2015, 933, 68–81. [Google Scholar] [CrossRef]
- Cao, L.G.; Lombardo, U.; Shen, C.W.; Giai, N.V. From Brueckner approach to Skyrme-type energy density functional. Phys. Rev. C 2006, 73, 014313. [Google Scholar] [CrossRef]
- Gulminelli, F.; Fantina, A.F. The Equation of State of Neutron Stars and the Role of Nuclear Experiments. Nucl. Phys. News 2021, 31, 9–13. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Carreau, T.; Fantina, A.F.; Gulminelli, F. Uncertainties in the pasta-phase properties of catalysed neutron stars. Astron. Astrophys. 2021, 654, A114. [Google Scholar] [CrossRef]
- Abbott, B.P.; LIGO Scientific Collaboration; Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F. Properties of the nuclear medium. Rep. Prog. Phys. 2012, 75, 026301. [Google Scholar] [CrossRef]
- Lombardo, U.; Schulze, H.J.; Zuo, W. Induced Pairing Interaction in Neutron Star Matter. In Fifty Years of Nuclear BCS: Pairing in Finite Systems; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2013; pp. 338–347. [Google Scholar] [CrossRef]
- Guo, W.; Dong, J.M.; Shang, X.; Zhang, H.F.; Zuo, W.; Colonna, M.; Lombardo, U. Proton-proton 1S0 pairing in neutron stars. Nucl. Phys. A 2019, 986, 18–25. [Google Scholar] [CrossRef]
- Zuo, W.; Li, Z.; Lu, G.; Li, J.; Scheid, W.; Lombardo, U.; Schulze, H.J.; Shen, C. 1S0 proton and neutron superfluidity in beta-stable neutron star matter. Phys. Lett. B 2004, 595, 44–49. [Google Scholar] [CrossRef]
- Zhou, X.R.; Schulze, H.J.; Zhao, E.G.; Pan, F.; Draayer, J.P. Pairing gaps in neutron stars. Phys. Rev. C 2004, 70, 048802. [Google Scholar] [CrossRef]
- Levenfish, K.P.; Yakovlev, D.G. Specific heat of neutron star cores with superfluid nucleons. Astron. Rep. 1994, 38, 247–251. [Google Scholar]
- Bardeen, J. Critical Fields and Currents in Superconductors. Rev. Mod. Phys. 1962, 34, 667–681. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Yakovlev, D.G. Thermal conductivity of electrons and muons in neutron star cores. Nucl. Phys. A 1995, 582, 697–716. [Google Scholar] [CrossRef]
- Mendell, G. Superfluid Hydrodynamics in Rotating Neutron Stars. I. Nondissipative Equations. Astrophys. J. 1991, 380, 515. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).