A First-Quantized Model for Unparticles and Gauge Theories around Conformal Window

Abstract

We first quantize an action proposed by Casalbuoni and Gomis in 2014 that describes two massless relativistic scalar particles interacting via a conformally invariant potential. The spectrum is a continuum of massive states that may be interpreted as unparticles. We then obtain in a similar way the mass operator for a deformed action in which two terms are introduced that break the conformal symmetry: a mass term and an extra position-dependent coupling constant. A simple Ansatz for the latter leads to a mass operator with linear confinement in terms of an effective string tension $\sigma$. The quantized model is confining when $\sigma \ne 0$ and its mass spectrum shows Regge trajectories. We propose a tensionless limit in which highly excited confined states reduce to (gapped) unparticles. Moreover, the low-lying confined bound states become massless in the latter limit as a sign of conformal symmetry restoration and the ratio between their masses and $\sqrt{\sigma }$ stays constant. The originality of our approach is that it applies to both confining and conformal phases via an effective interacting model.

1. Introduction

It is known that some asymptotically free gauge theories with $N_f$ light fermion flavours and $SU\left(N\right)$ gauge group have a conformal window, i.e., there exists an energy range in which the beta function vanishes. This conformal window occurs at various values of $N_f$ and $N$, depending on the fermion representation, see [1] for an extensive list of examples obtained by inspection of the two-loop beta function. For example, $SU\left(3\right)$ gauge theory with 12 light quarks flavours in the fundamental representation is conformal, as confirmed by five-loop and nonperturbative calculations [2,3]. $SU\left(2\right)$ gauge theory with 2 quark flavours in the adjoint representation can also be mentioned [4,5], or 2 quark flavours in the two-index symmetric representation [6]. Note that conformal windows are expected to be present for other gauge groups than $SU\left(N\right)$, like $Sp\left(2N\right)$ and $SO\left(N\right)$ [7]. Many evidences showing the existence of a conformal window for specific gauge theories have been found by resorting to lattice QCD methods, see e.g., the reviews [8,9,10,11,12]. General algorithms actually exist for $SU\left(N\right)$ theories with quarks in arbitrary representations [13].

To our knowledge, no effective model—we mean a simple enough action so as to allow for analytical calculations—has been proposed to mimic confining gauge theories when they approach the conformal window starting from a confining phase. Our starting point has been proposed in Ref. [14], where an action describing two scalar relativistic particles with conformal invariant interaction has been presented. The latter action reads

$$S_C=\alpha \int d\tau {\left(\frac{{\dot{x}}_1^2{\dot{x}}_2^2}{r^4}\right)}^{1/4},$$

(1)

with $\alpha$ a dimensionless parameter, $x_i^{\mu }=x_i^{\mu }\left(\tau \right)$ the parametric equations for the two particles in the $(D+1)$—dimensional Minkowski spacetime with metric $\eta =$ diag$(-+\cdots +)$ in inertial coordinates, $\tau$ an evolution parameter and $r^{\mu }:=x_2^{\mu }-x_1^{\mu }$. For any vector with components $v^{\mu }$, $v^2:={\eta }_{\mu \nu }{v}^{\mu }{v}^{\nu }=:v·v$ is the squared norm in the Lorentzian sense. In Section 2 we first review and quantize the action $S_C$. In particular, while reproducing some steps of the canonical analysis of [14], we also detail some issues that were not presented therein for the sake of conciseness but that we need for the quantization of the model. We link the spectrum obtained after quantization to unparticles, originally introduced as a nontrivial scale-invariant sector in low-energy effective field theories [15], see also [16,17].

The model is generalized in two ways that break conformal invariance. In Section 3 we introduce a mass term for the interacting particles. The quantization leads to unparticle spectrum with a mass gap. Then a confining interaction is introduced in Section 4 via a change of the form ${\alpha }^2\to {\alpha }^2{U}^2\left(r^2\right)$. The quantization of our model is then performed and the spectrum is analytically computed. The transition from the confining phase to the conformal phase is finally studied and unparticles are shown to emerge from the confined spectrum. The idea that unparticles may be “hidden” in a gauge theory’s conformal window has been developed in [18]. We finally argue that the present model provides a toy model to illustrate the latter proposal.

2. Conformal Phase

2.1. Classical Analysis

Let us review the conformally-invariant action presented by Casalbuoni and Gomis in Refs. [14,19]. The aim of their presentation was to show the existence of higher-spin-type conserved currents in their model while ours is rather to prepare the ground for the quantization of our model.

In the case of two massless particles, the authors of [14] start from the action

$$S_0[x_1^{\mu },e_1,x_2^{\mu },e_2]=\int d\tau \left(\frac{{\dot{x}}_1^2}{2e_1}+\frac{{\dot{x}}_2^2}{2e_2}\right),$$

(2)

with $e_i$$(i=1,2)$ the einbeins, and add an interaction term that couples the two massless particles in a conformally-invariant way:

$$S[x_1^{\mu },e_1,x_2^{\mu },e_2]=\int d\tau \left(\frac{{\dot{x}}_1^2}{2e_1}+\frac{{\dot{x}}_2^2}{2e_2}-\frac{{\alpha }^2}{4}\frac{\sqrt{e_1{e}_2}}{r^2}\right),$$

(3)

where we recall that $r^2:=r^{\mu }{r}^{\nu }{\eta }_{\mu \nu }=:r·r$ and where we have chosen the potential to be repulsive. In the above action, the coupling constant $\alpha$ is dimensionless. Since the action is manifestly Poincaré invariant it suffices to prove that it is invariant under dilations and special conformal transformations. As for the dilations, it is easy to see that the transformations $x_i^{\mu }\mapsto \lambda x_i^{\mu }$, $e_i\mapsto {\lambda }^2{e}_i$ preserve the action. The invariance under special conformal transformations is established by defining them as a succession of a Poincaré translation followed by an inversion and another Poincaré translation, where the inversion is the transformation

$$x_i^{\mu }\mapsto \frac{x_i^{\mu }}{x_i^2},e_i\mapsto \frac{e_i}{x_i^4},r^2\mapsto \frac{r^2}{x_1^2{x}_2^2}.$$

(4)

The interested reader may find additional information in the following lecture notes. The conformal invariance of the action is then readily checked.

Note that one can eliminate the two auxiliary variables $e_1\left(\tau \right)$ and $e_2\left(\tau \right)$ by virtue of their own field equations, which results [14] in the incarnation (1) of the action. We mention for completeness Ref. [20] in which it is shown that action (3) may be modified in a simple way so that it models two particles interacting conformally in Snyder space.

The action (3) does not depend on the derivatives ${\dot{e}}_i$, hence there are two primary constraints:

$${\pi }_1\approx 0,{\pi }_2\approx 0,$$

(5)

where ${\pi }_i$ is the conjugate variable to $e_i$ and where the symbol “≈” denotes a weak equality, i.e., an equality which holds on the constraint surface. One then derives the canonical Hamiltonian associated with the Lagrangian action (3):

$$\begin{array}{cc}\hfill H_c& =\frac{e_1{p}_1^2}{2}+\frac{e_2{p}_2^2}{2}+\frac{{\alpha }^2}{4}\frac{\sqrt{e_1{e}_2}}{r^2}+{\dot{e}}_1{\pi }_1+{\dot{e}}_2{\pi }_2\approx \frac{e_1{p}_1^2}{2}+\frac{e_2{p}_2^2}{2}+\frac{{\alpha }^2}{4}\frac{\sqrt{e_1{e}_2}}{r^2}\hfill \end{array}$$

(6)

as well as the total Hamiltonian

$$\begin{array}{cc}\hfill H_T(p_i,x_i,e_i,{\pi }_i,{\lambda }_1,{\lambda }_2)& =\frac{e_1{p}_1^2}{2}+\frac{e_2{p}_2^2}{2}+\frac{{\alpha }^2}{4}\frac{\sqrt{e_1{e}_2}}{r^2}+{\lambda }^1{\pi }_1+{\lambda }^2{\pi }_2.\hfill \end{array}$$

(7)

The invariance of the primary constraint under the dynamical evolution leads to two secondary constraints:

$$\begin{array}{cc}\hfill \{{\pi }_1,H_T\}=\frac{1}{2}\left(- p_1^2-\frac{{\alpha }^2}{4r^2}\sqrt{\frac{e_2}{e_1}}\right) =:{\varphi }_1\approx 0,& \{{\pi }_2,H_T\}=\frac{1}{2}\left(- p_2^2-\frac{{\alpha }^2}{4r^2}\sqrt{\frac{e_1}{e_2}}\right) =:{\varphi }_2\approx 0.\hfill \end{array}$$

(8)

Pursuing the consistency algorithm with these two constraints gives

$$\begin{array}{cc}\hfill \{{\varphi }_1,H_T\}& =- \frac{{\alpha }^2}{16r^2}\left(- {\lambda }_1\sqrt{\frac{e_2}{e_1^3}}+\frac{{\lambda }_2}{\sqrt{e_1{e}_2}}\right) + \frac{{\alpha }^2}{4r^4}\left(\sqrt{e_1{e}_2}{p}_1·r+\sqrt{\frac{e_2^3}{e_1}}{p}_2·r\right) =:{\varphi }_3\hfill \end{array}$$

(9)

and $\{{\varphi }_2,H_T\}=-\frac{e_1}{e_2}{\varphi }_3$. One can identically solve ${\varphi }_3=0$ by fixing one of the Lagrange multipliers, say ${\lambda }_1\left(\tau \right)$:

$${\lambda }_1={\tilde{\lambda }}_2{e}_1+C,{\tilde{\lambda }}_2:=\frac{{\lambda }_2}{e_2},C:=-\frac{4e_1}{r^2}(e_1{p}_1·r+e_2{p}_2·r),$$

(10)

which gives rise to the following expression for the total Hamiltonian:

$$\begin{array}{cc}\hfill & H_T=H_c+{\lambda }_2\frac{e_1}{e_2}{\pi }_1-\frac{4e_1}{r^2}\left[e_1{p}_1.r+e_2{p}_2.r\right]{\pi }_1+{\lambda }_2{\pi }_2=H_c+{\tilde{\lambda }}_2(e_1{\pi }_1+e_2{\pi }_2)+C{\pi }_1.\hfill \end{array}$$

(11)

At this stage it is worth saying that the same analysis can be performed even if $\alpha$ is a function $\alpha \left(r\right)$: Although breaking conformal symmetry, this case is important for our purpose and will be discussed in Section 4.

Coming back to the Hamiltonian (11), since ${\tilde{\lambda }}_2$ is an arbitrary function, one may take $e_1{\pi }_1+e_2{\pi }_2$ as our new primary first-class constraint. Its Poisson brackets with ${\pi }_1$ and ${\pi }_2$ is weakly zero while it is strongly zero with ${\varphi }_1$ and ${\varphi }_2$. Furthermore, $H_T$ is first-class since it does not explicitly depend on time. From the fact that the bracket of two first-class functions is first-class and the computation

$$\{e_1{\pi }_1+e_2{\pi }_2,H_T\}=e_1{\varphi }_1+e_2{\varphi }_2-C{\pi }_1=:{\gamma }_2,$$

(12)

one derives that ${\gamma }_2$ is another first-class constraint. To summarise, there are two first-class (FC) constraints (one is primary and the other is secondary) and two second-class (SC) constraints (one is primary and the other is secondary):

$$\begin{array}{ccc}\hfill \mathrm{FC}& :{\gamma }_1:=e_1{\pi }_1+e_2{\pi }_2\left(\mathrm{primary}\right),\hfill & \hfill {\gamma }_2:=e_1{\varphi }_1+e_2{\varphi }_2-C{\pi }_1\left(\mathrm{secondary}\right),\end{array}$$

(13)

$$\begin{array}{ccc}\hfill \mathrm{SC}& :{\chi }_1:={\pi }_1\left(\mathrm{primary}\right),\hfill & \hfill {\chi }_2:={\varphi }_1\left(\mathrm{secondary}\right).\end{array}$$

(14)

One has

$$\{{\gamma }_1,{\gamma }_2\}=-{\gamma }_2,\{{\gamma }_2,H_T\}={\tilde{\lambda }}_2{\gamma }_2,\{{\gamma }_1,H_T\}={\gamma }_2.$$

(15)

The number f of degrees of freedom is given by the number of phase-space variables minus twice the number of first-class constraints minus the number of second-class constraints. The number of degrees of freedom for the conformally-invariant interacting system (3) is therefore given by $f=4(D+1)+4-4-2=4D+2$, which differs from the counting obtained for the non-interacting system that produces $f=4D$. If one considers the free limit $\alpha \to 0$, the limiting value should therefore not be considered. This is also clear from the form (1) of the action. In fact, one can show that the Dirac conjecture is not satisfied by the constrained system at hand. It turns out that first-class constraints are all gauge symmetry generators if four conditions established in Chapter 3 of [21] are respected. One of these conditions is that the secondary second-class constraints should not appear in the Poisson bracket of the first-class constraints with the primary second-class constraint. With ${\gamma }_a$ the first-class constraints and ${\chi }_{\alpha }$ the second-class constraints, in general one has that

$$\{{\gamma }_a,{\chi }_{\alpha }\}=C_{a\alpha }^b{\gamma }_b+C_{a\alpha }^{\beta }{\chi }_{\beta },$$

(16)

and the condition mentioned above is that the matrix elements $C_{a{\alpha }_1}^{\beta \ne {\beta }_1}$ must be equal to zero, where ${\alpha }_1$ and ${\beta }_1$ refer to the primary constraints. In our case, this condition means that the quantities $C_{{\sigma }_i{\pi }_1}^{{\varphi }_1}$ should be null quantities. However,

$$\{{\sigma }_2,{\pi }_1\}={\pi }_1\frac{4}{r^2}(2e_1{p}_1.r+e_2{p}_2.r)+{\varphi }_1,$$

(17)

showing that $C_{{\sigma }_2{\pi }_1}^{{\varphi }_1}\ne 0$. Therefore, at least one condition imposed in [21] is not satisfied, which implies that the Dirac conjecture is not true in our case. The first-class constraints are not necessarily all generators of gauge transformations and one must use the chain algorithm of [22] to determine these generators; see e.g., Appendix A for some details about it.

The field equations are obtained by taking the Poisson bracket of the dynamical variables with the total Hamiltonian (11). They explicitly read

$$\begin{array}{cc}\hfill {\dot{x}}_1^{\mu }& =e_1{p}_1^{\mu }+\frac{4{\pi }_1}{r^2}{e}_1^2{r}^{\mu }\approx e_1{p}_1^{\mu },{\dot{x}}_2^{\mu }=e_2{p}_2^{\mu }+\frac{4{\pi }_1}{r^2}{e}_1{e}_2{r}^{\mu }\approx e_2{p}_2^{\mu },\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\dot{p}}_1^{\mu }& =-{\alpha }^2\frac{\sqrt{e_1{e}_2}}{2r^4}{r}^{\mu }+{\pi }_1\frac{8e_1}{r^4}{r}^{\mu }(e_1{p}_1.r+e_2{p}_2.r)-{\pi }_1\frac{4e_1}{r^2}(e_1{p}_1^{\mu }+e_2{p}_2^{\mu })\approx -{\alpha }^2\frac{\sqrt{e_1{e}_2}}{2r^4}{r}^{\mu },\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\dot{p}}_2^{\mu }& =+{\alpha }^2\frac{\sqrt{e_1{e}_2}}{2r^4}{r}^{\mu }-{\pi }_1\frac{8e_1}{r^4}{r}^{\mu }(e_1{p}_1.r+e_2{p}_2.r)+{\pi }_1\frac{4e_1}{r^2}(e_1{p}_1^{\mu }+e_2{p}_2^{\mu })\approx +{\alpha }^2\frac{\sqrt{e_1{e}_2}}{2r^4}{r}^{\mu },\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\dot{e}}_1& ={\tilde{\lambda }}_2{e}_1-\frac{4e_1}{r^2}(e_1{p}_1·r+e_2{p}_2·r)\equiv {\tilde{\lambda }}_2{e}_1+C,{\dot{e}}_2={\tilde{\lambda }}_2{e}_2,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\dot{\pi }}_1& ={\varphi }_1-{\tilde{\lambda }}_2{\pi }_1+{\pi }_1(\frac{8e_1}{r^2}{p}_1.r+\frac{4}{r^2}{e}_2{p}_2.r)\approx 0,{\dot{\pi }}_2={\varphi }_2-{\tilde{\lambda }}_2{\pi }_2+{\pi }_1\frac{4}{r^2}{e}_1{p}_2.r\approx 0.\hfill \end{array}$$

(22)

The second class constraints can be dropped by adopting the Dirac bracket defined in terms of the inverse of the matrix

$${\mathsf{\Omega }}_{\alpha \beta }:=\{{\chi }_{\alpha },{\chi }_{\beta }\}= \left(\begin{array}{cc}0& \mathcal{D}\\ -\mathcal{D}& 0\end{array}\right),$$

(23)

where ${\left({\chi }_{\alpha }\right)}_{\alpha =1,2}=({\pi }_1,{\varphi }_1)$ denotes the two second class constraints and $\mathcal{D}:=\{{\pi }_1,{\varphi }_1\}=-\frac{{\alpha }^2}{16r^2}\sqrt{\frac{e_2}{e_1^3}}$. One can then consider the reduced phase space where one strongly sets ${\pi }_1$ and ${\varphi }_1$ to zero. The first-class constraint ${\gamma }_2\approx 0$ therefore leads to the constraint ${\varphi }_2\approx 0$, since the einbein $e_2$ is required to be non vanishing. By using that ${\varphi }_1$ is strongly set to zero, the equation ${\varphi }_2\approx 0$ yields a constraint where the einbeins $e_1$ and $e_2$ have been eliminated [14]:

$$p_1^2{p}_2^2\approx \frac{{\alpha }^4}{16r^4}.$$

(24)

This equation is one of the main results of [14], that terminates their canonical analysis. We pursue their analysis in order to derive a more tractable constraint in view of the quantization. We express (24) in the relative (−) and centre-of-mass (+) variables

$$p_{\pm }^{\mu }:=p_1^{\mu }\pm p_2^{\mu },q_{\pm }^{\mu }:=\frac{1}{2}(x_1^{\mu }\pm x_2^{\mu })$$

(25)

that satisfy the canonical Poisson bracket relations

$$\{q_{+}^{\mu },q_{-}^{\nu }\}=0,\{p_{+}^{\mu },p_{-}^{\nu }\}=0,\{q_{\pm }^{\mu },p_{\pm }^{\nu }\}={\eta }^{\mu \nu }.$$

(26)

In the new coordinate system and once the second class constraints ${\left({\chi }_{\alpha }\right)}_{\alpha =1,2}=({\pi }_1,{\varphi }_1)$ have been strongly set to zero, the resulting first-class constraint (24) reads

$$\begin{array}{c}\hfill (p_{+}^2+p_{-}^2-2p_{+}.p_{-})(p_{+}^2+p_{-}^2+2p_{+}.p_{-})-\frac{{\alpha }^4}{16q_{-}^4}\approx 0.\end{array}$$

(27)

In these coordinates, the canonical equations of motion (18)–(22) read:

$$\begin{array}{cc}\hfill {\dot{q}}_{+}^{\mu }& =\frac{1}{4}(p_{+}^{\mu }(e_1+e_2)+p_{-}^{\mu }(e_1-e_2)),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\dot{q}}_{-}^{\mu }& =\frac{1}{4}(p_{+}^{\mu }(e_1-e_2)+p_{-}^{\mu }(e_1+e_2)),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\dot{p}}_{+\mu }& =0,{\dot{p}}_{-}^{\mu }=+\frac{{\alpha }^2}{8q_{-}^4}\sqrt{e_1{e}_2}{q}_{-}^{\mu },\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\dot{e}}_1& ={\tilde{\lambda }}_2{e}_1+C,{\dot{e}}_2={\tilde{\lambda }}_2{e}_2,{\dot{\pi }}_1=0,{\dot{\pi }}_2=0.\hfill \end{array}$$

(31)

Obviously, the total momentum $p_{+}^{\mu }$ is preserved by the dynamics, which simply reflects the invariance of the system under constant spacetime translations. Since Equation (27) is not totally tractable yet, we will completely fix the gauge by finding two gauge-fixing conditions $C_a=0$ such that the bracket matrix with entries $M_{ab}:=\{C_a,{\gamma }_b\}$ is non-degenerate, effectively resulting in a second-class system. We propose the following gauge-fixing conditions

$$\begin{array}{c}\hfill C_1:=p_{+}·p_{-}=0,C_2:=e_1{e}_2-1=0,\end{array}$$

(32)

and readily check that the bracket matrix

$$M= \left(\begin{array}{cc}\{C_1,{\gamma }_1\}& \{C_2,{\gamma }_1\}\\ \{C_1,{\gamma }_2\}& \{C_2,{\gamma }_2\}\end{array}\right) \approx \left(\begin{array}{cc}0& 2e_1{e}_2\\ -{\alpha }^2\frac{\sqrt{e_1{e}_2}}{8q_{-}^4}{p}_{+}.p_{-}& -\frac{e_1{e}_2}{q_{-}^2}{q}_{-}.(p_{+}(e_1+e_2)+p_{-}(e_1-e_2))\end{array}\right)$$

(33)

is invertible, as we wished. In the gauge $C_1=0$ and in the Lorentz frame where the (preserved) total momentum is $p_{+}^{\mu }=(M,0,0,0)$, we have $p_{-}^{\mu }=(0,{\overrightarrow{p}}_{-})$ and $p_1^2=p_2^2$: there is a balanced energy distribution among the two particles. Although this case will not be investigated here, it has been shown in [23] that massless bound states can also be considered by using similar methods.

The first two field equations of (31) indicate that one can further impose the condition

$$e_1-e_2=0,$$

(34)

which leads to ${\dot{q}}_{+}^i=0$ and ${\dot{q}}_{-}^0=0$. Indeed, let us assume $e_1=e_2$ and therefore $e_1=1=e_2$ on account of $C_2=0$. The two conditions $e_1=1=e_2$ can obviously be reached by virtue of the primary constraints (5). We call this gauge the unit einbein gauge. Equation (29) shows that $q_{-}.p_{+}$ is a constant that one considers to be zero in order to have $q_{-}^0=0$ in the Lorentz frame adopted. From the first two equations of (31), the constraint $e_1=e_2$ is consistent provided $C=\frac{e_1}{q_{-}^2}{q}_{-}.[p_{+}(e_1+e_2)+p_{-}(e_1-e_2)]$ is zero when $e_1-e_2=0$. It is straightforward to check that it is indeed the case from the fact that $q_{-}.p_{+}$ is zero, as we have just shown. We therefore set $q_{-}=(0,{\overrightarrow{q}}_{-})$. The three-vector ${\overrightarrow{q}}_{+}$ is set to zero, in accordance with translation invariance of the system. From the equations of motion and in the gauge chosen, it is clear that the only dynamical variables are ${\overrightarrow{q}}_{-}$ and ${\overrightarrow{p}}_{-}$.

In the gauges and Lorentz frame we have chosen, Equation (27) becomes

$$\begin{array}{c}\hfill {(p_{+}^2+p_{-}^2)}^2\approx \frac{{\alpha }^4}{16q_{-}^4}.\end{array}$$

(35)

Instead of extracting the square root of the above equation, with the ambiguity in which branch to pick, we recall that the remaining first-class constraint ${\gamma }_2\approx 0$ now reads ${\varphi }_2\approx 0$ that leads, in the gauges we have chosen:

$$p_{+}^2+p_{-}^2=-\frac{{\alpha }^2}{4q_{-}^2}.$$

(36)

Finally one is led to the following dispersion relation

$$M^2={\overrightarrow{p}}_{-}^2+\frac{{\alpha }^2}{4{\overrightarrow{q}}_{-}^2}.$$

(37)

2.2. Quantization

In a Schrödinger quantization scheme, Equation (37) defines the eigenequation

$$\left(-{▵}_{-}+ \frac{{\alpha }^2}{4{\overrightarrow{q}}_{-}^2}\right)\mathsf{\Psi }\left({\overrightarrow{q}}_{-}\right)=M^2\mathsf{\Psi }\left({\overrightarrow{q}}_{-}\right).$$

(38)

The spherical symmetry of this operator allows to work with hyperspherical coordinates ${\overrightarrow{q}}_{-}=(q_{-},{\widehat{\mathsf{\Omega }}}_D)$ and to set

$$\mathsf{\Psi }\left({\overrightarrow{q}}_{-}\right)=R\left(q_{-}\right)Y_{\ell ,m_a}\left({\widehat{\mathsf{\Omega }}}_D\right),$$

(39)

with $Y_{\ell ,m_a}\left({\widehat{\mathsf{\Omega }}}_D\right)$ the spherical harmonics in D dimensions, $\ell \in \mathbb{N}$, $m_a\in \mathbb{Z}$ and $a=1,\dots ,(D-1)$. Explicit forms can be found for example in [24]. More precisely, the squared mass operator is a Schrödinger Hamiltonian with repulsive inverse-squared potential:

$$- R^{″}\left(q_{-}\right)-\frac{D-1}{q_{-}}{R}^{\prime }\left(q_{-}\right)+\frac{\ell (\ell +D-2)}{q_{-}^2}R\left(q_{-}\right)+\frac{{\alpha }^2}{4q_{-}^2}R\left(q_{-}\right)=M^{2}R\left(q_{-}\right).$$

(40)

Hence the mass spectrum is continuous and the eigenstates are scattering states:

$$\begin{array}{ccc}\hfill M^2& =& {\mu }^2,\hfill \\ \hfill R\left(q_{-}\right)& \sim & \left(q_{-}\right){}^{1-\frac{D}{2}}{J}_{\lambda +\frac{D}{2}-1}\left(\mu q_{-}\right),\hfill \end{array}$$

(41)

where $\mu \in {\mathbb{R}}^{+}$ and where $J_{\lambda +\frac{D}{2}}$ is a Bessel function of the first kind. The generalized angular-momentum index $\lambda$ is defined by

$$\lambda (\lambda +D-2)=\ell (\ell +D-2)+\frac{{\alpha }^2}{4}$$

(42)

where $\lambda >0$ guarantees a solution that is regular at the origin. Because ${\alpha }^2>0$, the radial function actually never vanishes at the origin. The interested reader may find in [25] a detailed discussion of the inverse-squared potential in quantum mechanics.

Our model in the conformal phase contains a continuum of bosonic states with arbitrary mass $M\ge 0$. We identify this continuous spectrum with unparticles, originally introduced as a nontrivial scale-invariant sector in low-energy effective field theories [16]. As discussed in [26,27,28,29], such an unparticle sector arises from a continuum of scalar fields with arbitrary mass; an effective Lagrangian of the form $L\sim {\partial }_{\mu }\varphi {\square }^{-\delta }{\partial }^{\mu }\varphi$ with $\delta >0$ is then found for a scalar unparticle [26,27]. An originality of the present work is to provide a realization of unparticles as binary states of two interacting massless particles through action (3).

3. Massive Particles and Gapped Unparticles

We first recall the action for a massive relativistic particle in Minkowski spacetime:

$$S^{\left(m\right)}[x^{\mu },e]=\int d\tau \left(\frac{{\dot{x}}^2}{2e}-\frac{e}{2}{m}^2\right),$$

(43)

where the variable e is required to be nonvanishing. The above action has a smooth massless limit $m\to 0$.

The whole constraint analysis that we have reviewed from [14] and presented above can be repeated in the case one adds a mass term to the original action. By considering the action

$$S_0^{\left(m\right)}[x_1^{\mu },e_1,x_2^{\mu },e_2]=\int d\tau \left(\frac{{\dot{x}}_1^2}{2e_1}+\frac{{\dot{x}}_2^2}{2e_2}-m^2(\frac{e_1}{2}+\frac{e_2}{2})-\frac{{\alpha }^2}{4}\frac{\sqrt{e_1{e}_2}}{r^2}\right)$$

(44)

that clearly breaks conformal invariance through the presence of the mass terms, it is straightforward to see that both the number and nature of the constraints remain unchanged compared to the massless case reviewed in great details above. There remains two first-class constaints $\left\{{\gamma }_a^{\left(m\right)}\right\}$, $a=1,2$ (one primary and one secondary) and two second-class constraints $\left\{{\chi }_{\alpha }^{\left(m\right)}\right\}$, $\alpha =1,2$ (one primary and one secondary). We adopt the same gauge-fixing conditions as in the massless case. The set of conditions $\{C_1=0,C_2=0,{\gamma }_1^{\left(m\right)}\approx 0,{\gamma }_2^{\left(m\right)}\approx 0\}$ defines a set of second-class constraints so that the corresponding operators each become the zero operator upon quantization.

In the massless case one had the constraint (35). In presence of the mass terms in (44), following the same procedure, one is led to the dispersion relation

$$M^2={\overrightarrow{p}}_{-}^2+\frac{{\alpha }^2}{4{\overrightarrow{q}}_{-}^2}+4m^2,$$

(45)

and, after quantization, to the spectrum (41) with $M^2={\mu }^2+4m^2$. The continuous spectrum is bounded from below by $M=2m$.

It has previously been noticed that coupling an unparticle to an electroweak sector leads to an unparticle spectrum with mass gap via a kind of Brout-Englert-Higgs mechanism [30]. Note also that unparticle models with a mass gap are nothing but hidden-valley models [31]. We can finally mention Ref. [32], in which gapped unparticles emerge as continuous Kaluza-Klein modes of a five-dimensional model with a brane. The action (44) may be seen as a first proposal to generate gapped unparticles from two massive interacting particles. It is worth mentioning that such an action might be used in the modelling of near-threshold neutral charm meson molecules, since it has been argued in [33] that such states (like the X(3872) which is very close to the $D_0^{\ast }{\overline{D}}^0$ threshold) may be seen as unparticles.

4. From the Confining to the Conformal Phase

As starting point we propose the action

$$S=\int d\tau \left[\frac{{\dot{x_1}}^2}{2e_1}+\frac{{\dot{x_2}}^2}{2e_2}-m^2\left(\frac{e_1}{2}+\frac{e_2}{2}\right) - \frac{{\alpha }^2{U}^2\left(r^2\right)}{4}\frac{\sqrt{e_1{e}_2}}{r^2}\right].$$

(46)

Both the mass term and the extra interaction term with the function $U\left(r^2\right)$ break conformal invariance. One obviously recovers action (3) in the limit $m\to 0$ and by setting $U=1$.

The replacement of ${\alpha }^2$ by the position dependent coupling ${\alpha }^2{U}^2\left(r^2\right)$ breaks conformal invariance but do not lead to drastic changes in the canonical constraint analysis. Although there appear terms proportional to $U^{\prime }\left(r^2\right)$ from the Poisson bracket of the total Hamiltonian with the secondary constraints, one is still able to ensure that the latter constraints are preserved during dynamical evolution by identically solving the equation ${\varphi }_3=0$ for the function ${\lambda }_1$. The latter function takes a more complicated form than the one given in the massless case reviewed in Section 2. Here we obtain

$${\lambda }_1=\frac{e_1}{e_2}{\lambda }_2+C+8e_1{ln}^{\prime }U\left(r^2\right)r·(p_2{e}_2+p_1{e}_1),$$

(47)

where the function C is given in (10). The additional terms proportional to the derivative of the function $U\left(r^2\right)$ make no difference for the rest of the canonical analysis. Proceeding as in the previous sections, it is straightforward to find the following dispersion relation:

$$M^2={\overrightarrow{p}}_{-}^2+\frac{{\alpha }^2{U}^2\left(q_{-}^2\right)}{4{\mathrm{q}}_{-}^2}+4m^2.$$

(48)

We now use the Ansatz

$$U^2\left(q_{-}^2\right)=1+\frac{4}{{\alpha }^2}{\sigma }^2{q}_{-}^4,$$

(49)

where the term in $q_{-}^4$ can be seen as the first nontrivial term in the power expansion of any function $U^2\left(q_{-}^2\right)$: a term in $q_{-}^2$ would only redefine m. As we will show in the following, Equation (49) mimics a linear confinement, typical of $(3+1)—$dimensional Yang-Mills theories in their confining phase. We therefore assume that the action (46) with potential (49) is a relevant effective model to describe binary states in gauge theories around their conformal window, just as a Nambu-Goto Lagrangian is a relevant effective model for light mesons ($\rho$, $f_0$, …) in the confined phase, see e.g., [34,35].

As in Section 2, we may set $q_{-}^0=0$, so that $q_{-}^2={\mathrm{q}}_{-}^2$. With the Ansatz (49), the mass operator (48) is now a $D—$dimensional harmonic oscillator with arbitrary angular momentum: $M^2={\overrightarrow{p}}_{-}^2+\frac{{\alpha }^2}{4q_{-}^2}+{\sigma }^2{q}_{-}^2+4m^2$. Its spectrum reads [24]

$$\begin{array}{ccc}\hfill M^2& =& 2\sigma \left(2n+\lambda +\frac{D}{2}\right) + 4m^2,\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill R\left(q_{-}\right)& =& {\left[\frac{2\mathsf{\Gamma }(n+1){\sigma }^{\lambda +\frac{D}{2}}}{\mathsf{\Gamma }(n+\lambda +\frac{D}{2})}\right]}^{\frac{1}{2}}{q}_{-}^{\lambda }{\mathrm{e}}^{-\frac{\sigma q_{-}^2}{2}}{L}_n^{\lambda +\frac{D}{2}-1}\left(\sigma q_{-}^2\right),\hfill \end{array}$$

(51)

with $L_n^{\alpha }$ the generalized Laguerre polynomials and $\lambda$ given by Equation (42). The spectrum contains massive states showing Regge trajectories, i.e., $M^2\sim \ell$ or n at large ℓ or n. Such a behaviour is observed experimentally in light meson spectroscopy, see e.g., Ref. [36] and references therein. For this reason the massive states we observe in the confined phase will be referred to as “mesons”.

An more general ansatz of the form $U^2\left(q_{-}^2\right)=1-\frac{4}{{\alpha }^2}{\delta }^2{q}_{-}^2+\frac{4}{{\alpha }^2}{\sigma }^2{q}_{-}^4$ leads to the mass spectrum

$$\begin{array}{c}\hfill M^2=2\sigma \left(2n+\lambda +\frac{D}{2}\right) + 4m^2-{\delta }^2.\end{array}$$

(52)

The mass scale $\delta$ could be used to fine-tune the ground-state mass ($n=\ell =0)$. For example, the value ${\delta }^2=2\sigma (1+\sqrt{{(D-2)}^2+{\alpha }^2})+4m^2$ leads to a massless ground state. However, such a value causes $U^2\left(q_{-}^2\right)$ to be negative for some values of $q_{-}^2$ since ${\delta }^2>\alpha \sigma$. In our model, the existence of a massless ground state demands to drop the positivity of the potential.

Let us now focus on the low-lying confined spectrum (n and ℓ finite) when approaching the conformal window, that is in the limit $\sigma \to 0$ and $m\to 0$. According to (50), the mass of low-lying states will go to zero as already suggested in [37,38,39]: Light mesons are expected to become massless as a signal of conformal symmetry restoration. Their masses scale as $\sqrt{\sigma }$, which is a behaviour observed in lattice QCD in the case of $SU\left(2\right)$ QCD with one adjoint Dirac quark flavour: The ratios $M/\sqrt{\sigma }$ are found to be constant for the lightest (pseudo)scalar states (mesons and glueball) as the fermion mass goes to zero in order to restore conformal invariance [40]. Moreover, it is observed that the mass ratios of two meson masses are constant near the conformal window as suggested by Equation (50). This feature has been observed in $SU\left(2\right)$ gauge theory with two adjoint quarks [41].

It has to be noticed that the methodoloy used in most of the lattice QCD studies of theories with conformal window is to choose $N$, $N_f$ and the quark representation such that the conformal window is a priori reached. The quark mass m starts from a nonzero value and the conformal window is reached by taking the limit $m\to 0$; the masses of bound states scale as $m^{\frac{1}{1+\gamma }}$ with $\gamma$ the anomalous mass dimension. That parameter is then fitted on the lattice data to characterise the theory under study. The interested reader may find a review of computed values of $\gamma$ in Ref. [38]. This parameter can hardly be guessed from our effective approach: The behaviours of $\sigma \left(m\right)$ and $\alpha \left(m\right)$ are not constrained by our model.

Other states of the spectrum are worth of interest: radially excited states such that

$$n\to \infty \mathrm{as}\sigma \to 0\mathrm{with}\sigma n=\frac{{\mu }^2}{4}\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d},$$

(53)

$\mu$ being an arbitrary (but finite) energy scale parameter. In this tensionless limit, the mass (50) remains finite. At large n one can use a Mehler-Heine-type formula for Laguerre polynomials, see Theorem 4.1 of [42]

$$L_n^{\lambda +\frac{D}{2}-1}\left(\frac{{\left(\mu q_{-}\right)}^2}{4n}\right) \sim n^{\lambda +\frac{D}{2}-1}{q}_{-}^{-\lambda -\frac{D}{2}+1}{\mathrm{e}}^{\frac{{\left(\mu q_{-}\right)}^2}{8n}}{J}_{\lambda +\frac{D}{2}-1}\left(\mu q_{-}\right),$$

(54)

and [43]

$$\frac{\mathsf{\Gamma }(n+1)}{\mathsf{\Gamma }(n+\lambda +\frac{D}{2})}\sim n^{1-\lambda -\frac{D}{2}}.$$

(55)

The spectrum (50) approaches to our unparticle sector (41) as $n\to +\infty$ up to the rescaling $R\to \sqrt{n}R$. The harmonic oscillator functions are indeed normalized to unity, which leads to the vanishing of R as $\sigma \to 0$ since scattering states can only be normalized to $\delta (\mu -{\mu }^{\prime })$ in principle.

Our limit (53) is actually consistent with the results of [44] showing that, in field theory, an unparticle sector can be generated by a tower of massive states with mass $M_n^2=\mathsf{\Delta }n$ when the mass spacing parameter $\mathsf{\Delta }$ goes to zero.

5. Concluding Comments

The action (46) appears to be an interesting toy model to describe the transition from confining to conformal phases of a Banks-Zaks-type gauge theory [15] in terms of binary states. It predicts that the low-lying bound states in the confining phase become massless when approaching the conformal window with a universal behaviour, the ratios of masses and $\sqrt{\sigma }$ being a constant. Highly excited radial states give rise to a unparticle sector in the conformal phase. The unparticle spectrum has a mass gap or not depending on whether the conformal symmetry is broken or not by a mass term. A schematic drawing of this picture is given is Figure 1.

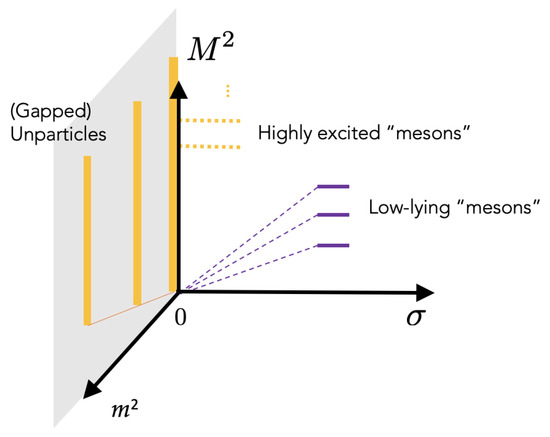
Figure 1. Schematic representation of the mass spectrum generated by the model defined by Equations (46) and (49). The behaviours of states with fixed n (purple lines) and with fixed $\sigma n$ (dotted orange lines) are represented in the $m=0$ plane. The spectrum of gapped unparticles is represented in the $\sigma =0$ plane (solid orange lines).

Notice that the radial wave equation we derived in the present paper also appears from a bottom-up AdS/CFT perspective, see e.g., [45]. Interestingly, in the paper [46] where they consider a $U\left(1\right)$-invariant gauge theory in AdS${}_4$ propagating a vector field and a complex scalar field, a nontrivial profile for the scalar field near the conformal infinity of AdS${}_4$ introduces two dimensionful constants m and v that break conformal symmetry of the dual theory. Various limits where $m\to 0$ and $v\to 0$ relate a discrete spectrum with a massless Goldstone boson to a continuous Banks-Zaks-type spectrum for the scalar conformal operator in the dual CFT${}_3$. The approach of [46] enables a simultaneous discussion of spontaneous and dynamical symmetry breaking in a CFT at strong coupling. Some bridges may presumably be drawn between our model and the AdS/QCD framework, although it is out of the scope of the present paper. The interested reader may find a detailed discussions of mesons in AdS/QCD in the review [47].

One may finally wonder to what kind of gauge theory our toy model best applies. Similarities with $SU\left(2\right)$ QCD with one adjoint quark [40] have been commented in the text. However, our model is a priori better suited to model gauge theories with scalar matter than with fermionic matter, the variables $x_i\left(\tau \right)$ being then identified with two “particles” of scalar matter. The existence of a conformal window is not limited to gauge theories with fermionic matter, as discussed in Appendix B. For example, a lattice study of $N_f=5$ scalar SU(2) Yang-Mills theory is affordable with current computers and could be performed to check the present model. We hope that such results will become available in the future.

Although we did not explicitly mention it, the present work and quoted references focus on zero-temperature gauge theories. The interplay between conformal window crossing and confinement/deconfinement transition may lead to new interesting phenomena, as discussed in [48]. For example, a correspondence has been found between conformal QCD with $N_f=7$ and QCD with $N_f=2$ at $T\approx 2T_c$ ($T_c$ is the deconfinement temperature). To what extent the action (46) can be generalized at finite-temperature and bring relevant information is a problem that we leave for future works.