Superconducting Phases in Neutron Star Cores
Abstract
:1. Introduction
2. The Ginzburg–Landau Formalism
2.1. Entrainment and Local Phase Invariance
2.2. Connection with Previous Work
3. Superconducting Ground States
3.1. The Free Energy Density
3.2. The Helmholtz and Gibbs Free Energies
3.3. The Numerical Model
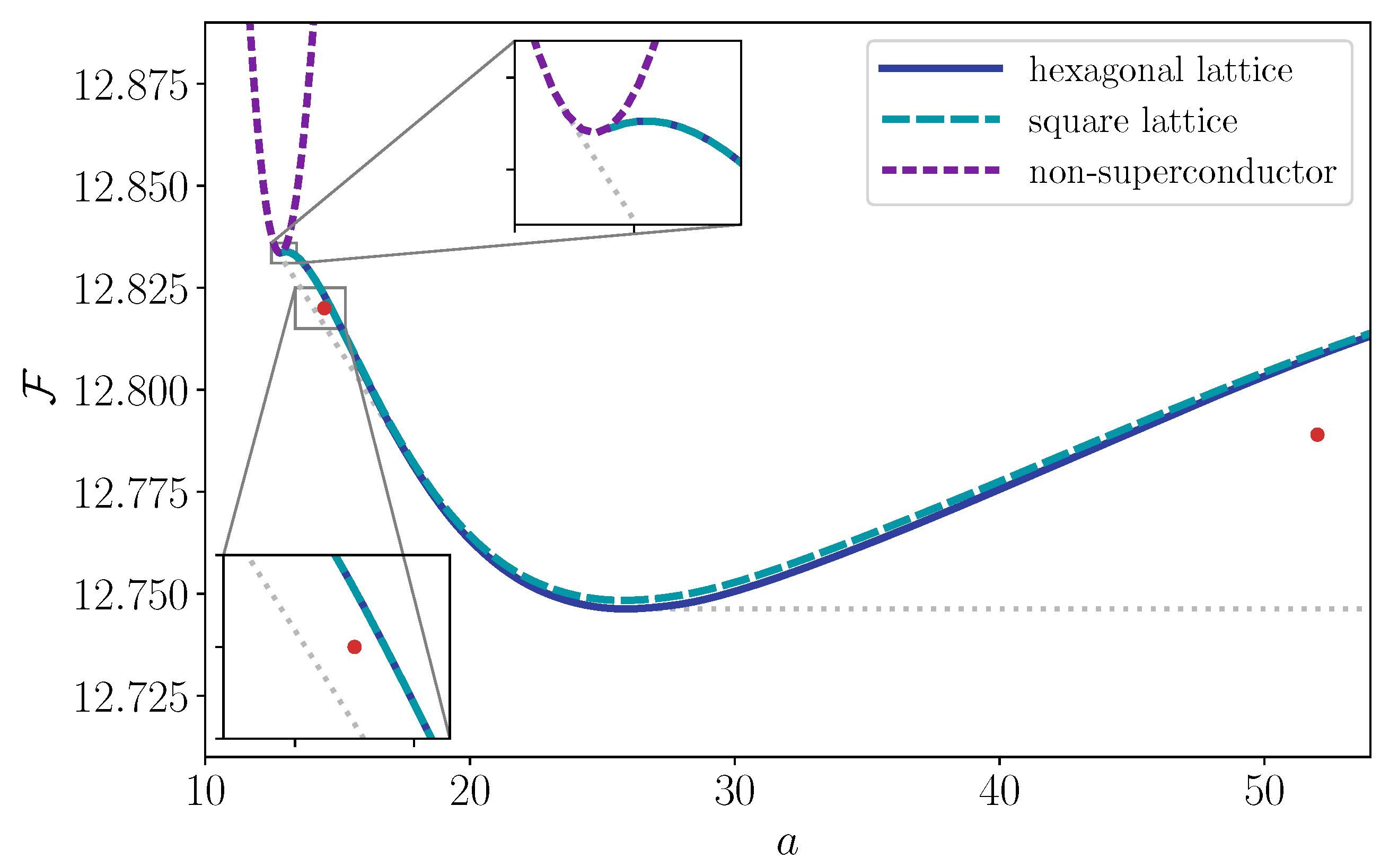
- for a square lattice, we take and ;
- for a hexagonal lattice, we take and .
- for the ground state is non-superconducting;
- for the ground state is a mixture of non-superconductor and a hexagonal fluxtube lattice;
- for the ground state is a hexagonal fluxtube lattice;
- for the ground state is a mixture of a hexagonal fluxtube lattice and the Meissner state.
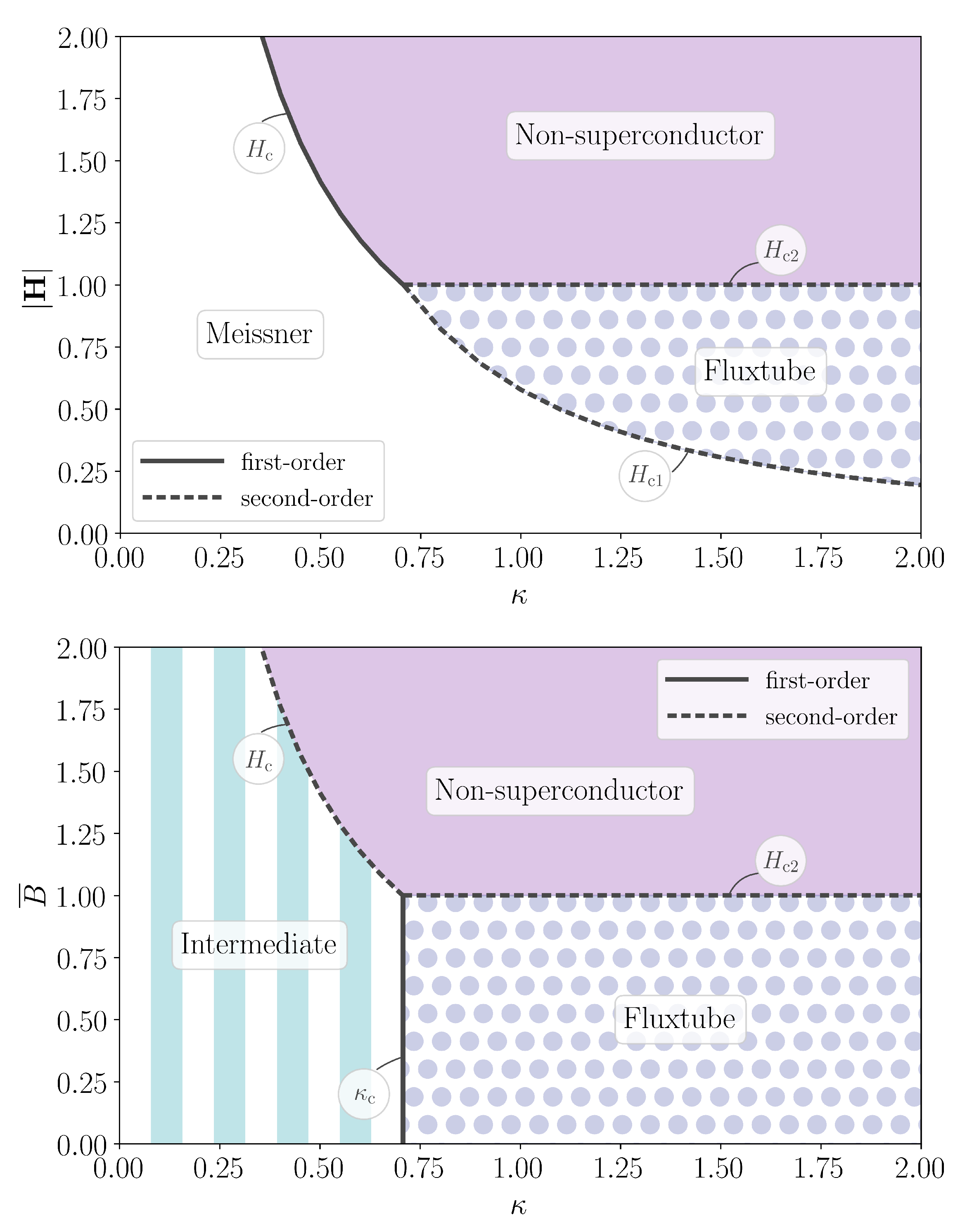
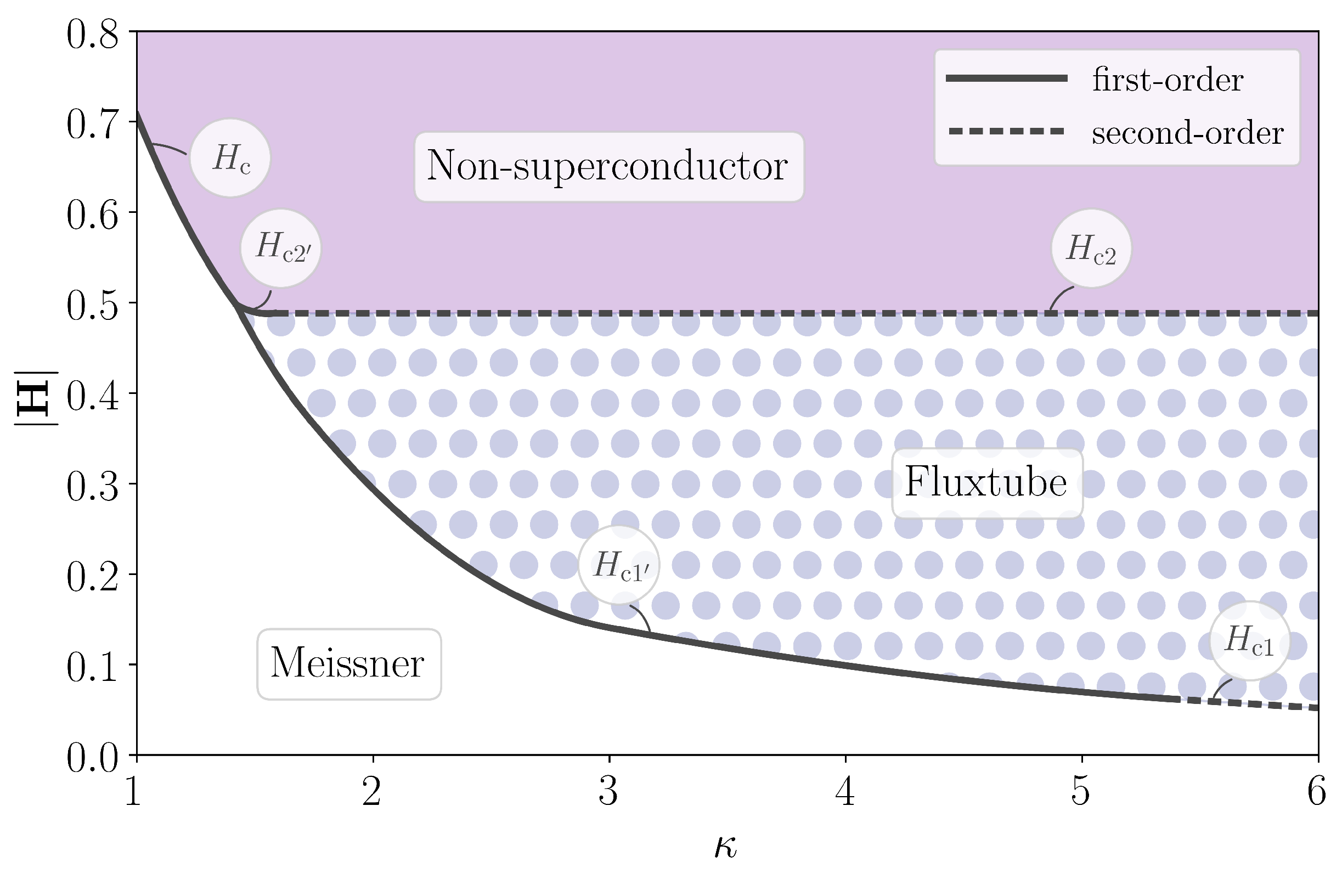
3.4. Phase Diagrams
4. Phase Transitions with
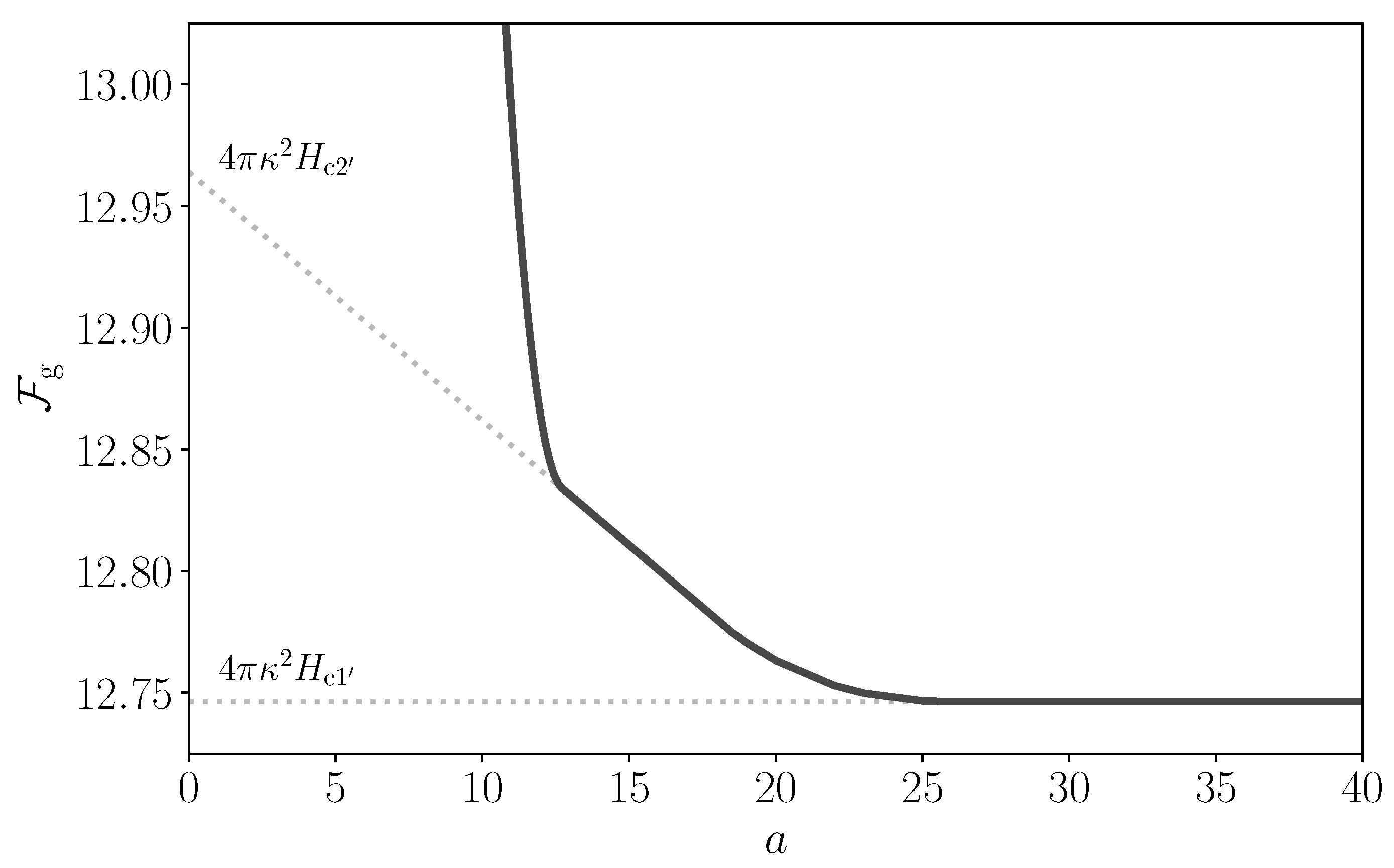
4.1. The Critical Field,
4.2. The Lower Critical Field, vs.
4.3. The Upper Critical Field, vs.
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Minimization of the Free Energy
Appendix B. Long-Range Interaction between Fluxtubes
- Within each cell, the solution can be approximated as a linear perturbation to the single fluxtube solution;
- On the boundary of the cell, the solution can be approximated as the Meissner solution plus a superposition of linear, independent perturbations produced by the fluxtubes.
- Rather than computing the interaction energy for a lattice, they considered a pair of fluxtubes. However, this is generally not a steady state, i.e., it is not a solution of the Euler–Lagrange Equations (A7). This violates a basic assumption underlying the derivation.
- They chose to include some, but not all, of the higher-order terms in their calculation, leading to a result that lacks certain symmetries expected on physical grounds. By contrast, in deriving Equation (A14), we have consistently neglected all terms of higher order than , and the result is antisymmetric between and .
- Their formula (C8) for the interaction energy depends on the location of the Wigner–Seitz cell boundary, relative to the fluxtube lattice. As we emphasized above, the location of the fluxtube within its cell is immaterial, and therefore should not change the result.
Appendix C. Weakly Nonlinear Lattice Solution

References
- Baym, G.; Pethick, C.; Pines, D. Superfluidity in Neutron Stars. Nature 1969, 224, 673–674. [Google Scholar] [CrossRef]
- Mendell, G. Superfluid Hydrodynamics in Rotating Neutron Stars. I. Nondissipative Equations. Astrophys. J. 1991, 380, 515. [Google Scholar] [CrossRef]
- Sedrakian, D.M.; Sedrakian, A.D.; Zharkov, G.F. Type I superconductivity of protons in neutron stars. Mon. Not. R. Astron. Soc. 1997, 290, 203–207. [Google Scholar] [CrossRef] [Green Version]
- Buckley, K.B.; Metlitski, M.A.; Zhitnitsky, A.R. Vortices and type-I superconductivity in neutron stars. Phys. Rev. C 2004, 69, 055803. [Google Scholar] [CrossRef] [Green Version]
- Buckley, K.B.; Metlitski, M.A.; Zhitnitsky, A.R. Neutron stars as type-I superconductors. Phys. Rev. Lett. 2004, 92, 151102. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.; Good, G.; Reddy, S. Isospin asymmetry and type-I superconductivity in neutron star matter. Phys. Rev. C 2005, 72, 055801. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Good, G. Flux tubes and the type-I/type-II transition in a superconductor coupled to a superfluid. Phys. Rev. B 2008, 78, 024510. [Google Scholar] [CrossRef] [Green Version]
- Haber, A.; Schmitt, A. Critical magnetic fields in a superconductor coupled to a superfluid. Phys. Rev. D 2017, 95, 116016. [Google Scholar] [CrossRef] [Green Version]
- Babaev, E.; Speight, M. Semi-Meissner state and neither type-I nor type-II superconductivity in multicomponent superconductors. Phys. Rev. B 2005, 72, 180502. [Google Scholar] [CrossRef] [Green Version]
- Moshchalkov, V.; Menghini, M.; Nishio, T.; Chen, Q.H.; Silhanek, A.V.; Dao, V.H.; Chibotaru, L.F.; Zhigadlo, N.D.; Karpinski, J. Type-1.5 Superconductivity. Phys. Rev. Lett. 2009, 102, 117001. [Google Scholar] [CrossRef] [Green Version]
- Babaev, E.; Carlström, J.; Speight, M. Type-1.5 superconducting state from an intrinsic proximity effect in two-band superconductors. Phys. Rev. Lett. 2010, 105, 067003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gutierrez, J.; Raes, B.; Silhanek, A.V.; Li, L.J.; Zhigadlo, N.D.; Karpinski, J.; Tempere, J.; Moshchalkov, V.V. Scanning Hall probe microscopy of unconventional vortex patterns in the two-gap MgB2 superconductor. Phys. Rev. B 2012, 85, 094511. [Google Scholar] [CrossRef] [Green Version]
- Babaev, E.; Carlström, J.; Silaev, M.; Speight, J.M. Type-1.5 superconductivity in multicomponent systems. Physica C 2017, 533, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Muzikar, P.; Pethick, C.J. Flux bunching in type-II superconductors. Phys. Rev. B 1981, 24, 2533–2539. [Google Scholar] [CrossRef]
- Sedrakian, A.D.; Sedrakian, D.M. Superfluid core rotation in pulsars. I. Vortex cluster dynamics. Astrophys. J. 1995, 447, 305. [Google Scholar] [CrossRef]
- Stairs, I.H.; Lyne, A.G.; Shemar, S.L. Evidence for free precession in a pulsar. Nature 2000, 406, 484–486. [Google Scholar] [CrossRef]
- Shabanova, T.V.; Lyne, A.G.; Urama, J.O. Evidence for free precession in the pulsar B1642-03. Astrophys. J. 2001, 552, 321–325. [Google Scholar] [CrossRef] [Green Version]
- Haberl, F.; Turolla, R.; de Vries, C.P.; Zane, S.; Vink, J.; Méndez, M.; Verbunt, F. Evidence for precession of the isolated neutron star RX J0720.4-3125. Astron. Astrophys. 2006, 451, L17–L21. [Google Scholar] [CrossRef]
- Ashton, G.; Jones, D.I.; Prix, R. Comparing models of the periodic variations in spin-down and beamwidth for PSR B1828-11. Mon. Not. R. Astron. Soc. 2016, 458, 881–899. [Google Scholar] [CrossRef]
- Sedrakian, A.; Wasserman, I.; Cordes, J.M. Precession of isolated neutron stars. I. Effects of imperfect pinning. Astrophys. J. 1999, 524, 341–360. [Google Scholar] [CrossRef] [Green Version]
- Link, B. Constraining hadronic superfluidity with neutron star precession. Phys. Rev. Lett. 2003, 91, 101101. [Google Scholar] [CrossRef] [Green Version]
- Sedrakian, A. Type-I superconductivity and neutron star precession. Phys. Rev. D 2005, 71, 083003. [Google Scholar] [CrossRef]
- Charbonneau, J.; Zhitnitsky, A. Novel mechanism for type I superconductivity in neutron stars. Phys. Rev. C 2007, 76, 015801. [Google Scholar] [CrossRef] [Green Version]
- Glampedakis, K.; Andersson, N.; Jones, D.I. Stability of precessing superfluid neutron stars. Phys. Rev. Lett. 2008, 100, 081101. [Google Scholar] [CrossRef] [Green Version]
- Gügercinoğlu, E.; Alpar, M.A. Vortex creep against toroidal flux lines, crustal entrainment, and pulsar glitches. Astrophys. J. Lett. 2014, 788, L11. [Google Scholar] [CrossRef] [Green Version]
- Graber, V.; Cumming, A.; Andersson, N. Glitch rises as a test for rapid superfluid coupling in neutron stars. Astrophys. J. 2018, 865, 23. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N. Vortex pinning in the superfluid core of neutron stars and the rise of pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 493, L98–L102. [Google Scholar] [CrossRef]
- Alpar, M.A. Flux-vortex pinning and neutron star evolution. J. Astrophys. Astron. 2017, 38, 44. [Google Scholar] [CrossRef] [Green Version]
- Drummond, L.V.; Melatos, A. Stability of interlinked neutron vortex and proton flux-tube arrays in a neutron star—II. Far-from-equilibrium dynamics. Mon. Not. R. Astron. Soc. 2018, 475, 910–920. [Google Scholar] [CrossRef] [Green Version]
- Dobaczewski, J.; Dudek, J. Time-odd components in the mean field of rotating superdeformed nuclei. Phys. Rev. C 1995, 52, 1827–1839. [Google Scholar] [CrossRef] [Green Version]
- Chamel, N.; Haensel, P. Entrainment parameters in a cold superfluid neutron star core. Phys. Rev. C 2006, 73, 045802. [Google Scholar] [CrossRef] [Green Version]
- Yakovlev, D.G.; Kaminker, A.D.; Gnedin, O.Y.; Haensel, P. Neutrino emission from neutron stars. Phys. Rep. 2001, 354, 1–155. [Google Scholar] [CrossRef] [Green Version]
- Yakovlev, D.G.; Pethick, C.J. Neutron star cooling. Annu. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Levenfish, K.P.; Shibanov, Y.A. Cooling of neutron stars and superfluidity in their cores. Phys. Uspekhi 1999, 42, 737–778. [Google Scholar] [CrossRef] [Green Version]
- Kaminker, A.D.; Haensel, P.; Yakovlev, D.G. Nucleon superfluidity vs. observations of cooling neutron stars. Astron. Astrophys. 2001, 373, L17–L20. [Google Scholar] [CrossRef] [Green Version]
- Kaminker, A.D.; Yakovlev, D.G.; Gnedin, O.Y. Three types of cooling superfluid neutron stars: Theory and observations. Astron. Astrophys. 2002, 383, 1076–1087. [Google Scholar] [CrossRef] [Green Version]
- Kobyakov, D.N. Surface energy of magnetized superconducting matter in neutron star cores. Phys. Rev. C 2020, 102, 045803. [Google Scholar] [CrossRef]
- Bedaque, P.F.; Rupak, G.; Savage, M.J. Goldstone bosons in the 3P2 superfluid phase of neutron matter and neutrino emission. Phys. Rev. C 2003, 68, 065802. [Google Scholar] [CrossRef] [Green Version]
- Alpar, M.A.; Langer, S.A.; Sauls, J.A. Rapid postglitch spin-up of the superfluid core in pulsars. Astrophys. J. 1984, 282, 533–541. [Google Scholar] [CrossRef]
- Babaev, E. Unconventional rotational responses of hadronic superfluids in a neutron star caused by strong entrainment and a Σ− hyperon gap. Phys. Rev. Lett. 2009, 103, 231101. [Google Scholar] [CrossRef] [Green Version]
- Sinha, M.; Sedrakian, A. Magnetar superconductivity versus magnetism: Neutrino cooling processes. Phys. Rev. C 2015, 91, 035805. [Google Scholar] [CrossRef]
- Kobyakov, D.N.; Pethick, C.J. Two-component superfluid hydrodynamics of neutron star cores. Astrophys. J. 2017, 836, 203. [Google Scholar] [CrossRef] [Green Version]
- Drummond, L.V.; Melatos, A. Stability of interlinked neutron vortex and proton flux tube arrays in a neutron star: Equilibrium configurations. Mon. Not. R. Astron. Soc. 2017, 472, 4851–4869. [Google Scholar] [CrossRef]
- Silaev, M.; Babaev, E. Microscopic derivation of two-component Ginzburg–Landau model and conditions of its applicability in two-band systems. Phys. Rev. B 2012, 85, 134514. [Google Scholar] [CrossRef] [Green Version]
- Andreev, A.F.; Bashkin, E.P. Three-velocity hydrodynamics of superfluid solutions. J. Exp. Theor. Phys. 1976, 42, 164–167. [Google Scholar]
- Allard, V.; Chamel, N. 1S0 pairing gaps, chemical potentials and entrainment matrix in superfluid neutron-star cores for the Brussels–Montreal functionals. Universe 2021, 7, 470. [Google Scholar] [CrossRef]
- Graber, V.; Andersson, N.; Hogg, M. Neutron stars in the laboratory. Int. J. Mod. Phys. D 2017, 26, 1730015. [Google Scholar] [CrossRef]
- Esry, B.D.; Greene, C.H.; Burke, J.P., Jr.; Bohn, J.L. Hartree–Fock theory for double condensates. Phys. Rev. Lett. 1997, 78, 3594–3597. [Google Scholar] [CrossRef]
- Law, C.K.; Pu, H.; Bigelow, N.P.; Eberly, J.H. “Stability Signature” in two-species dilute Bose–Einstein condensates. Phys. Rev. Lett. 1997, 79, 3105–3108. [Google Scholar] [CrossRef]
- Bashkin, E.P.; Vagov, A.V. Instability and stratification of a two-component Bose–Einstein condensate in a trapped ultracold gas. Phys. Rev. B 1997, 56, 6207–6212. [Google Scholar] [CrossRef]
- Riboli, F.; Modugno, M. Topology of the ground state of two interacting Bose–Einstein condensates. Phys. Rev. A 2002, 65, 063614. [Google Scholar] [CrossRef] [Green Version]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Press: New York, NY, USA, 2004. [Google Scholar]
- Wood, T.S.; Mesgarnezhad, M.; Stagg, G.W.; Barenghi, C.F. Quasiperiodic boundary conditions for three-dimensional superfluids. Phys. Rev. B 2019, 100, 024505. [Google Scholar] [CrossRef] [Green Version]
- Kramer, L. Thermodynamic behavior of type-II superconductors with small κ near the lower critical field. Phys. Rev. B 1971, 3, 3821–3825. [Google Scholar] [CrossRef]
- Svistunov, B.V.; Babaev, E.S.; Prokof’ev, N.V. Superfluid States of Matter; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Abrikosov, A.A. On the magnetic properties of superconductors of the second group. J. Exp. Theor. Phys. 1957, 5, 1174–1182. [Google Scholar]
- Kleiner, W.H.; Roth, L.M.; Autler, S.H. Bulk solution of Ginzburg-Landau equations for type II superconductors: Upper critical field region. Phys. Rev. 1964, 133, 1226–1227. [Google Scholar] [CrossRef]
- Chamel, N. Two-fluid models of superfluid neutron star cores. Mon. Not. R. Astron. Soc. 2008, 388, 737–752. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 015806. [Google Scholar] [CrossRef]
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars [review article]. Phys. Rep. 2005, 411, 325–375. [Google Scholar] [CrossRef] [Green Version]
- Glampedakis, K.; Andersson, N.; Samuelsson, L. Magnetohydrodynamics of superfluid and superconducting neutron star cores. Mon. Not. R. Astron. Soc. 2011, 410, 805–829. [Google Scholar] [CrossRef] [Green Version]
- Pippard, A.B. The surface energies of superconductors. Proc. Camb. Phil. Soc. 1951, 47, 617. [Google Scholar] [CrossRef]
- Lewis, H.W. Surface Energies in Superconductors. Phys. Rev. 1956, 104, 942–947. [Google Scholar] [CrossRef]
- Jones, P.B. Neutron superfluid spin-down and magnetic field decay in pulsars. Mon. Not. R. Astron. Soc. 1991, 253, 279. [Google Scholar] [CrossRef]
- Gusakov, M.E. Force on proton vortices in superfluid neutron stars. Mon. Not. R. Astron. Soc. 2019, 485, 4936–4950. [Google Scholar] [CrossRef] [Green Version]
- Perez, F.; Granger, B.E. IPython: A system for interactive scientific computing. Comput. Sci. Eng. 2007, 9, 21–29. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006. [Google Scholar]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Harris, C.R.; Jarrod Millman, K.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; pp. 56–61. [Google Scholar]
- Jones, E.; Oliphant, T.E.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.scipy.org/ (accessed on 16 March 2020).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Taub, A.H. Stability of general relativistic gaseous masses and variational principles. Commun. Math. Phys. 1969, 15, 235–254. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wood, T.S.; Graber, V. Superconducting Phases in Neutron Star Cores. Universe 2022, 8, 228. https://doi.org/10.3390/universe8040228
Wood TS, Graber V. Superconducting Phases in Neutron Star Cores. Universe. 2022; 8(4):228. https://doi.org/10.3390/universe8040228
Chicago/Turabian StyleWood, Toby S., and Vanessa Graber. 2022. "Superconducting Phases in Neutron Star Cores" Universe 8, no. 4: 228. https://doi.org/10.3390/universe8040228
APA StyleWood, T. S., & Graber, V. (2022). Superconducting Phases in Neutron Star Cores. Universe, 8(4), 228. https://doi.org/10.3390/universe8040228






