The I-Love-Q Relations for Superfluid Neutron Stars
Abstract
1. Introduction
2. General Relativistic Two-Fluid Formalism
2.1. Nonrotating Stars
2.2. Slowly Rotating Stars
2.3. Tidally Deformed Nonrotating Stars
3. Equations of State
3.1. Two-Fluid Polytropic Model
3.2. Relativistic Mean Field Model
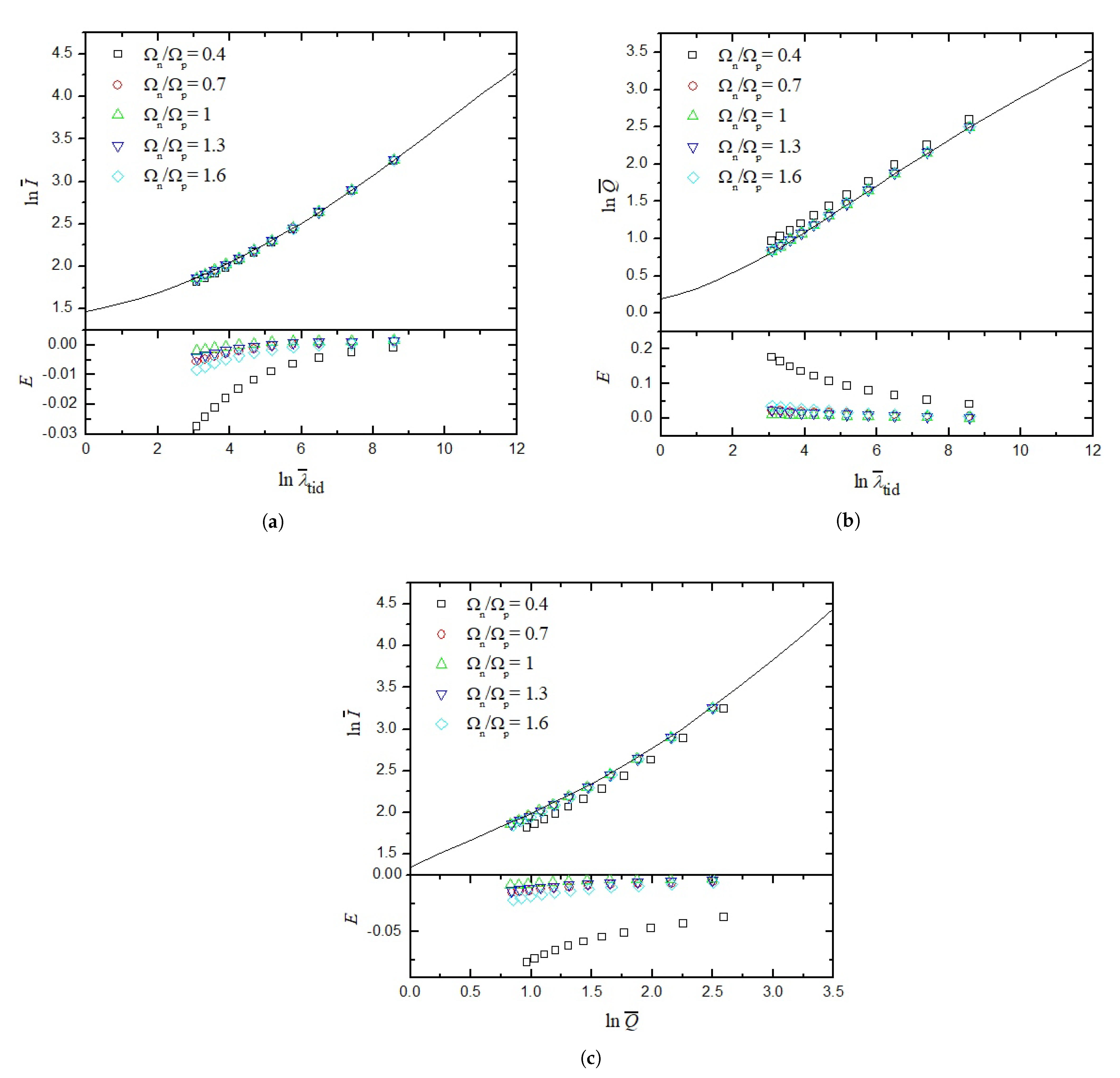
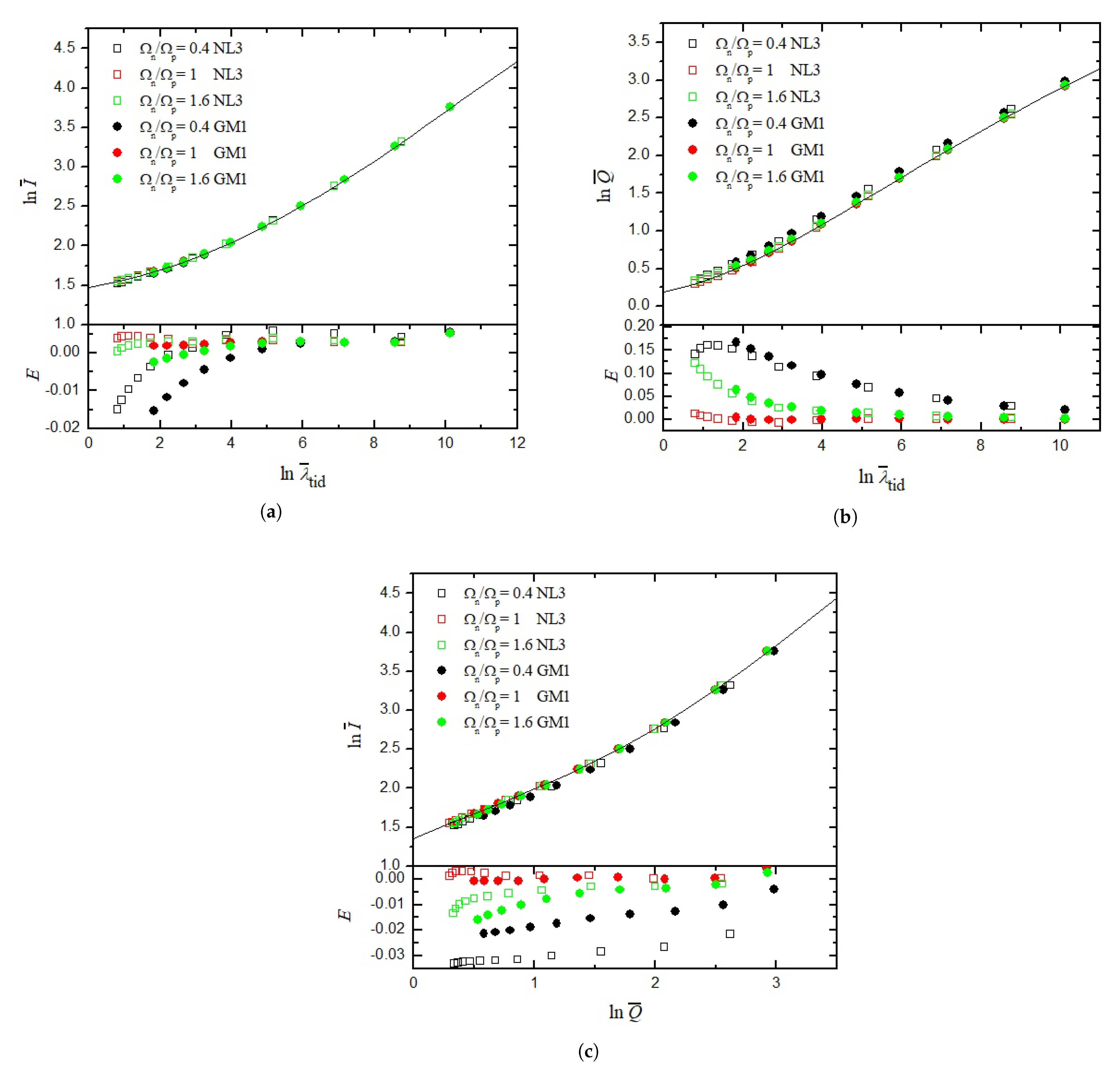
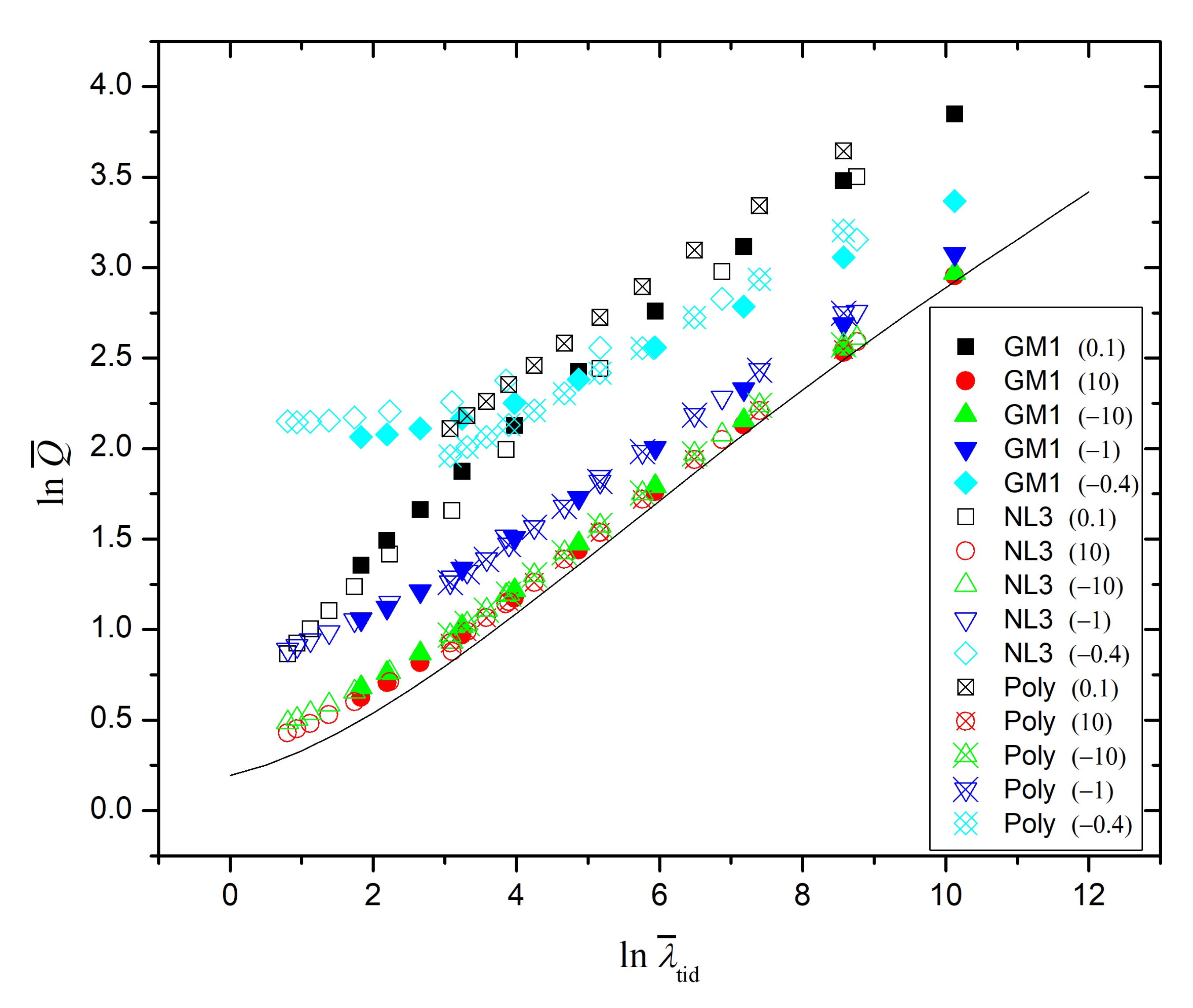
4. Numerical Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef] [PubMed]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J.W. Neutron Star Tidal Deformabilities Constrained by Nuclear Theory and Experiment. Phys. Rev. Lett. 2018, 121, 062701. [Google Scholar] [CrossRef] [PubMed]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Li, B.A.; Krastev, P.G.; Wen, D.H.; Zhang, N.B. Towards understanding astrophysical effects of nuclear symmetry energy. Eur. Phys. J. A 2019, 55, 117. [Google Scholar] [CrossRef]
- Carson, Z.; Steiner, A.W.; Yagi, K. Constraining nuclear matter parameters with GW170817. Phys. Rev. D 2019, 99, 043010. [Google Scholar] [CrossRef]
- Tsui, L.K.; Leung, P.T. Probing the Interior of Neutron Stars with Gravitational Waves. Phys. Rev. Lett. 2005, 95, 151101. [Google Scholar] [CrossRef]
- Lau, H.K.; Leung, P.T.; Lin, L.M. Inferring physical parameters of compact stars from their f-mode gravitational wave signals. Astrophys. J. 2010, 714, 1234. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q: Unexpected Universal Relations for Neutron Stars and Quark Stars. Science 2013, 341, 365–368. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q relations in neutron stars and their applications to astrophysics, gravitational waves, and fundamental physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Yagi, K. Multipole Love relations. Phys. Rev. D 2014, 89, 043011. [Google Scholar] [CrossRef]
- Chan, T.K.; Sham, Y.H.; Leung, P.T.; Lin, L.M. Multipolar universal relations between f-mode frequency and tidal deformability of compact stars. Phys. Rev. D 2014, 90, 124023. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Delsate, T.; Gürlebeck, N.; Steinhoff, J. I-Q Relation for Rapidly Rotating Neutron Stars. Phys. Rev. Lett. 2014, 112, 201102. [Google Scholar] [CrossRef]
- Pappas, G.; Apostolatos, T.A. Effectively Universal Behavior of Rotating Neutron Stars in General Relativity Makes Them Even Simpler than Their Newtonian Counterparts. Phys. Rev. Lett. 2014, 112, 121101. [Google Scholar] [CrossRef]
- Pappas, G. Unified description of astrophysical properties of neutron stars independent of the equation of state. Mon. Not. R. Astron. Soc. 2015, 454, 4066–4084. [Google Scholar] [CrossRef][Green Version]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. R. Astron. Soc. 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Bozzola, G.; Stergioulas, N.; Bauswein, A. Universal relations for differentially rotating relativistic stars at the threshold to collapse. Mon. Not. R. Astron. Soc. 2017, 474, 3557–3564. [Google Scholar] [CrossRef]
- Luk, S.S.; Lin, L.M. Universal Relations for Innermost Stable Circular Orbits around Rapidly Rotating Neutron Stars. Astrophys. J. 2018, 861, 141. [Google Scholar] [CrossRef]
- Riahi, R.; Kalantari, S.Z.; Rueda, J.A. Universal relations for the Keplerian sequence of rotating neutron stars. Phys. Rev. D 2019, 99, 043004. [Google Scholar] [CrossRef]
- Sun, W.; Wen, D.; Wang, J. New quasiuniversal relations for static and rapid rotating neutron stars. Phys. Rev. D 2020, 102, 023039. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate universal relations for neutron stars and quark stars. Phys. Rep. 2017, 681, 1. [Google Scholar] [CrossRef]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 737–806. [Google Scholar] [CrossRef]
- Lackey, B.D.; Pürrer, M.; Taracchini, A.; Marsat, S. Surrogate model for an aligned-spin effective-one-body waveform model of binary neutron star inspirals using Gaussian process regression. Phys. Rev. D 2019, 100, 024002. [Google Scholar] [CrossRef]
- Schmidt, P.; Hinderer, T. Frequency domain model of f-mode dynamic tides in gravitational waveforms from compact binary inspirals. Phys. Rev. D 2019, 100, 021501. [Google Scholar] [CrossRef]
- Andersson, N.; Pnigouras, P. The seismology of Love: An effective model for the neutron star tidal deformability. arXiv 2019, arXiv:1905.00012. [Google Scholar]
- Barkett, K.; Chen, Y.; Scheel, M.A.; Varma, V. Gravitational waveforms of binary neutron star inspirals using post-Newtonian tidal splicing. Phys. Rev. D 2020, 102, 024031. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Stergioulas, N.; Kokkotas, K.D. Breakdown of I-Love-Q Universality in Rapidly Rotating Relativistic Stars. Astrophys. J. 2013, 781, L6. [Google Scholar] [CrossRef]
- Haskell, B.; Ciolfi, R.; Pannarale, F.; Rezzolla, L. On the universality of I-Love-Q relations in magnetized neutron stars. Mon. Not. R. Astron. Soc. 2013, 438, L71–L75. [Google Scholar] [CrossRef]
- Martinon, G.; Maselli, A.; Gualtieri, L.; Ferrari, V. Rotating protoneutron stars: Spin evolution, maximum mass, and I-Love-Q relations. Phys. Rev. D 2014, 90, 064026. [Google Scholar] [CrossRef]
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I-Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Lau, S.Y.; Leung, P.T.; Lin, L.M. Tidal deformations of compact stars with crystalline quark matter. Phys. Rev. D 2017, 95, 101302. [Google Scholar] [CrossRef]
- Lau, S.Y.; Leung, P.T.; Lin, L.M. Two-layer compact stars with crystalline quark matter: Screening effect on the tidal deformability. Phys. Rev. D 2019, 99, 023018. [Google Scholar] [CrossRef]
- Lombardo, U.; Schulze, H.J. Superfluidity in Neutron Star Matter. In Physics of Neutron Star Interiors; Blaschke, D., Glendenning, N., Sedrakian, A., Eds.; Springer: Berlin, Germany, 2001; pp. 30–53. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 401–454. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 1–56. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Pines, D. Superfluidity in Neutron Stars. Nature 1969, 224, 673–674. [Google Scholar] [CrossRef]
- Yu, H.; Weinberg, N.N. Resonant tidal excitation of superfluid neutron stars in coalescing binaries. Mon. Not. R. Astron. Soc. 2016, 464, 2622–2637. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Effects of Hyperons in Binary Neutron Star Mergers. Phys. Rev. Lett. 2011, 107, 211101. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Radice, D.; Ott, C.D.; Roberts, L.F.; Mösta, P.; Galeazzi, F. How loud are neutron star mergers? Phys. Rev. D 2016, 94, 024023. [Google Scholar] [CrossRef]
- Perego, A.; Bernuzzi, S.; Radice, D. Thermodynamics conditions of matter in neutron star mergers. Eur. Phys. J. A 2019, 55. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Relativistic fluid dynamics: Physics for many different scales. arXiv 2020, arXiv:gr-qc/2008.12069. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N.; Pereira, J.P. Tidal deformations of neutron stars with elastic crusts. Phys. Rev. D 2020, 101, 103025. [Google Scholar] [CrossRef]
- Carter, B. Covariant theory of conductivity in ideal fluid or solid media. In Relativistic Fluid Dynamics; Anile, A.M., Choquet-Bruhat, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–64. [Google Scholar] [CrossRef]
- Comer, G.L.; Langlois, D. Hamiltonian formulation for multi-constituent relativistic perfect fluids. Class. Quantum Gravity 1993, 10, 2317–2327. [Google Scholar] [CrossRef]
- Comer, G.L.; Langlois, D. Hamiltonian formulation for relativistic superfluids. Class. Quantum Gravity 1994, 11, 709–721. [Google Scholar] [CrossRef]
- Carter, B.; Langlois, D. Relativistic models for superconducting-superfluid mixtures. Nucl. Phys. B 1998, 531, 478–504. [Google Scholar] [CrossRef]
- Langlois, D.; Sedrakian, D.M.; Carter, B. Differential rotation of relativistic superfluid in neutron stars. Mon. Not. R. Astron. Soc. 1998, 297, 1189–1201. [Google Scholar] [CrossRef]
- Andersson, N. A Superfluid Perspective on Neutron Star Dynamics. Universe 2021, 7, 17. [Google Scholar] [CrossRef]
- Comer, G.L.; Langlois, D.; Lin, L.M. Quasinormal modes of general relativistic superfluid neutron stars. Phys. Rev. D 1999, 60, 104025. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Slowly rotating general relativistic superfluid neutron stars. Class. Quantum Gravity 2001, 18, 969–1002. [Google Scholar] [CrossRef]
- Char, P.; Datta, S. Relativistic tidal properties of superfluid neutron stars. Phys. Rev. D 2018, 98, 084010. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L.; Langlois, D. Oscillations of general relativistic superfluid neutron stars. Phys. Rev. D 2002, 66, 104002. [Google Scholar] [CrossRef]
- Lin, L.M.; Andersson, N.; Comer, G.L. Oscillations of general relativistic multifluid/multilayer compact stars. Phys. Rev. D 2008, 78, 083008. [Google Scholar] [CrossRef]
- Prix, R.; Novak, J.; Comer, G.L. Relativistic numerical models for stationary superfluid neutron stars. Phys. Rev. D 2005, 71, 043005. [Google Scholar] [CrossRef]
- Sourie, A.; Oertel, M.; Novak, J. Numerical models for stationary superfluid neutron stars in general relativity with realistic equations of state. Phys. Rev. D 2016, 93, 083004. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Pani, P.; Gualtieri, L.; Ferrari, V. Tidal Love numbers of a slowly spinning neutron star. Phys. Rev. D 2015, 92, 124003. [Google Scholar] [CrossRef]
- Landry, P. Tidal deformation of a slowly rotating material body: Interior metric and Love numbers. Phys. Rev. D 2017, 95, 124058. [Google Scholar] [CrossRef]
- Datta, S.; Char, P. Effect of superfluid matter of a neutron star on the tidal deformability. Phys. Rev. D 2020, 101, 064016. [Google Scholar] [CrossRef]
- Comer, G.L.; Joynt, R. Relativistic mean field model for entrainment in general relativistic superfluid neutron stars. Phys. Rev. D 2003, 68, 023002. [Google Scholar] [CrossRef]
- Comer, G.L. Slowly rotating general relativistic superfluid neutron stars with relativistic entrainment. Phys. Rev. D 2004, 69, 123009. [Google Scholar] [CrossRef]
- Kheto, A.; Bandyopadhyay, D. Isospin dependence of entrainment in superfluid neutron stars in a relativistic model. Phys. Rev. D 2014, 89, 023007. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Shen, G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C 2010, 82, 055803. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the Λ in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414–2417. [Google Scholar] [CrossRef]
- Yagi, K.; Stein, L.C.; Pappas, G.; Yunes, N.; Apostolatos, T.A. Why I-Love-Q: Explaining why universality emerges in compact objects. Phys. Rev. D 2014, 90, 063010. [Google Scholar] [CrossRef]
- Sham, Y.H.; Chan, T.K.; Lin, L.M.; Leung, P.T. Unveiling the university of I-Love-Q relations. Astrophys. J. 2015, 798, 121. [Google Scholar] [CrossRef]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807. [Google Scholar] [CrossRef]
- Ray, P.S.; Guillot, S.; Ho, W.C.G.; Kerr, M.; Enoto, T.; Gendreau, K.C.; Arzoumanian, Z.; Altamirano, D.; Bogdanov, S.; Campion, R.; et al. Anti-glitches in the Ultraluminous Accreting Pulsar NGC 300 ULX-1 Observed with NICER. Astrophys. J. 2019, 879, 130. [Google Scholar] [CrossRef]
- Serim, M.M.; Şahiner, Ş.; Çerri-Serim, D.; İnam, S.Ç.; Baykal, A.L. Discovery of a glitch in the accretion-powered pulsar SXP 1062. Mon. Not. R. Astron. Soc. 2017, 471, 4982–4989. [Google Scholar] [CrossRef]


| Model | b | c | |||
|---|---|---|---|---|---|
| NL3 | 15.739 | 10.530 | 5.324 | 0.002055 | |
| GM1 | 11.785 | 7.148 | 4.410 | 0.002948 |
| Poly_2 | Poly_4 | Poly_8 | |
|---|---|---|---|
| 0.1 | 2.22 (59%) | 2.46 (76%) | 2.66 (91%) |
| 0.2 | 1.66 (18%) | 1.79 (28%) | 1.96 (40%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeung, C.-H.; Lin, L.-M.; Andersson, N.; Comer, G. The I-Love-Q Relations for Superfluid Neutron Stars. Universe 2021, 7, 111. https://doi.org/10.3390/universe7040111
Yeung C-H, Lin L-M, Andersson N, Comer G. The I-Love-Q Relations for Superfluid Neutron Stars. Universe. 2021; 7(4):111. https://doi.org/10.3390/universe7040111
Chicago/Turabian StyleYeung, Cheung-Hei, Lap-Ming Lin, Nils Andersson, and Greg Comer. 2021. "The I-Love-Q Relations for Superfluid Neutron Stars" Universe 7, no. 4: 111. https://doi.org/10.3390/universe7040111
APA StyleYeung, C.-H., Lin, L.-M., Andersson, N., & Comer, G. (2021). The I-Love-Q Relations for Superfluid Neutron Stars. Universe, 7(4), 111. https://doi.org/10.3390/universe7040111






