Equation of State and Composition of Proto-Neutron Stars and Merger Remnants with Hyperons
Abstract
:1. Introduction
2. Relativistic Density Functional with Density-Dependent Couplings
2.1. Equation of State
2.2. Choice of Coupling Constants
2.3. Thermodynamic Conditions in Supernovas and Merger Remnants
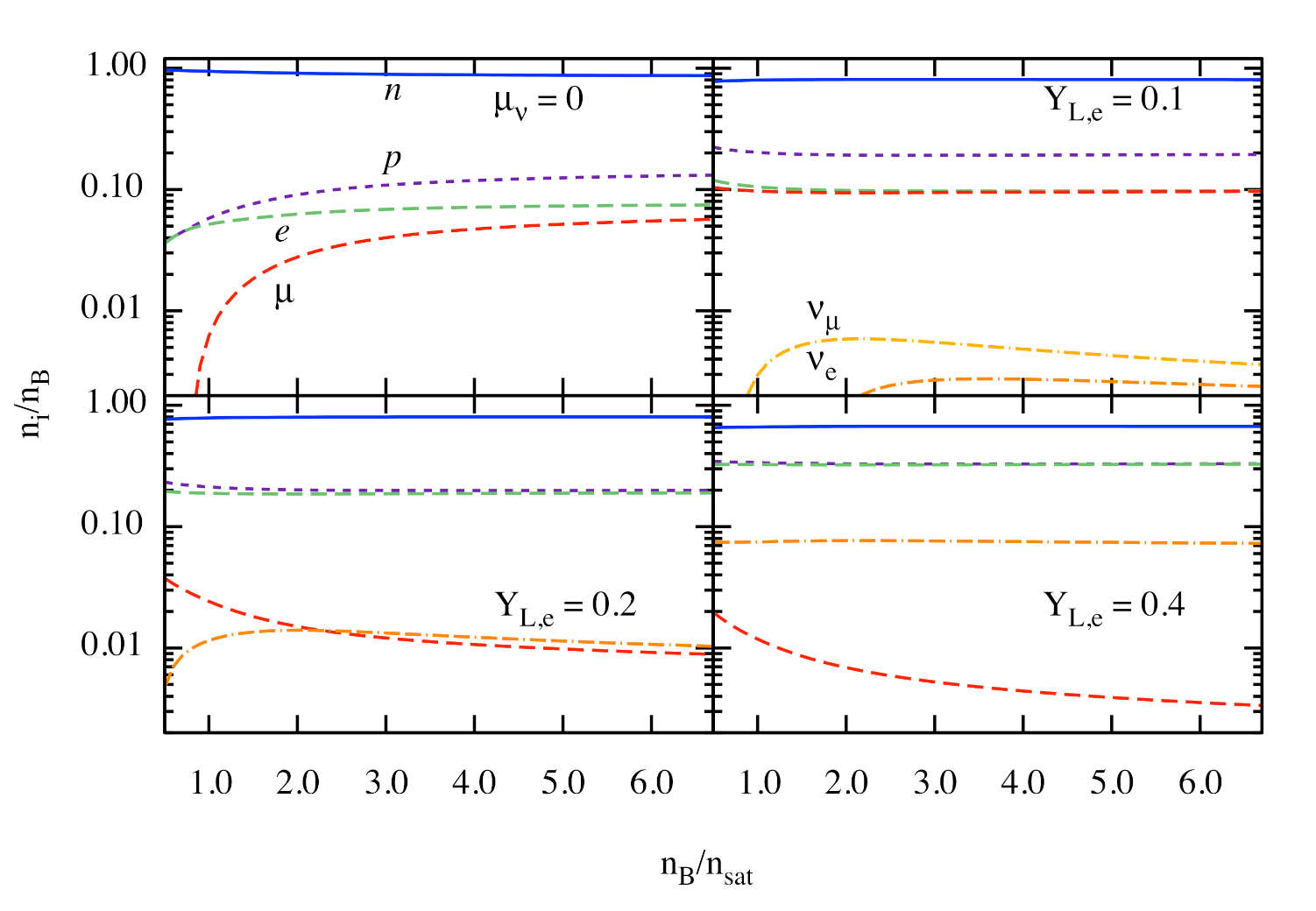
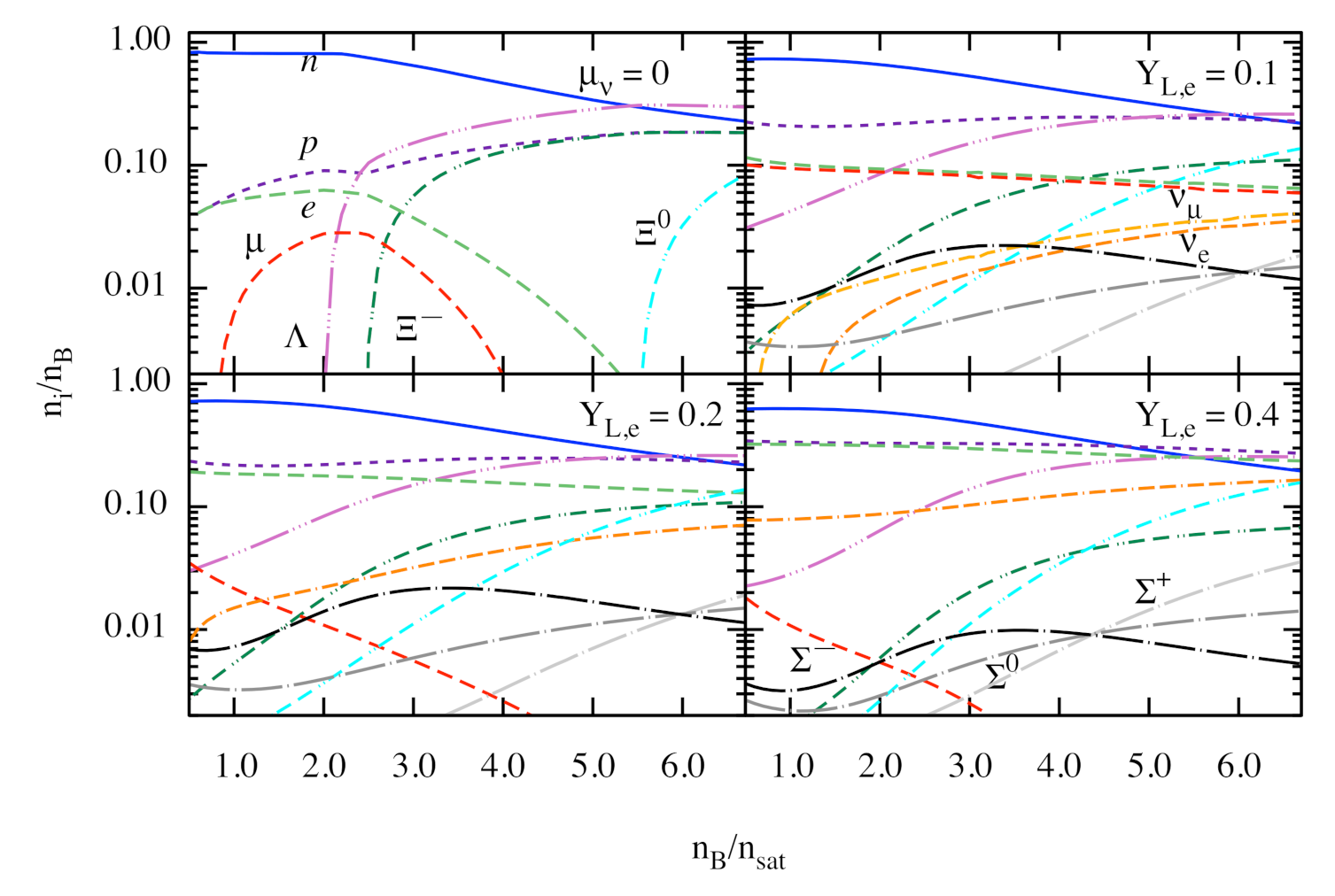
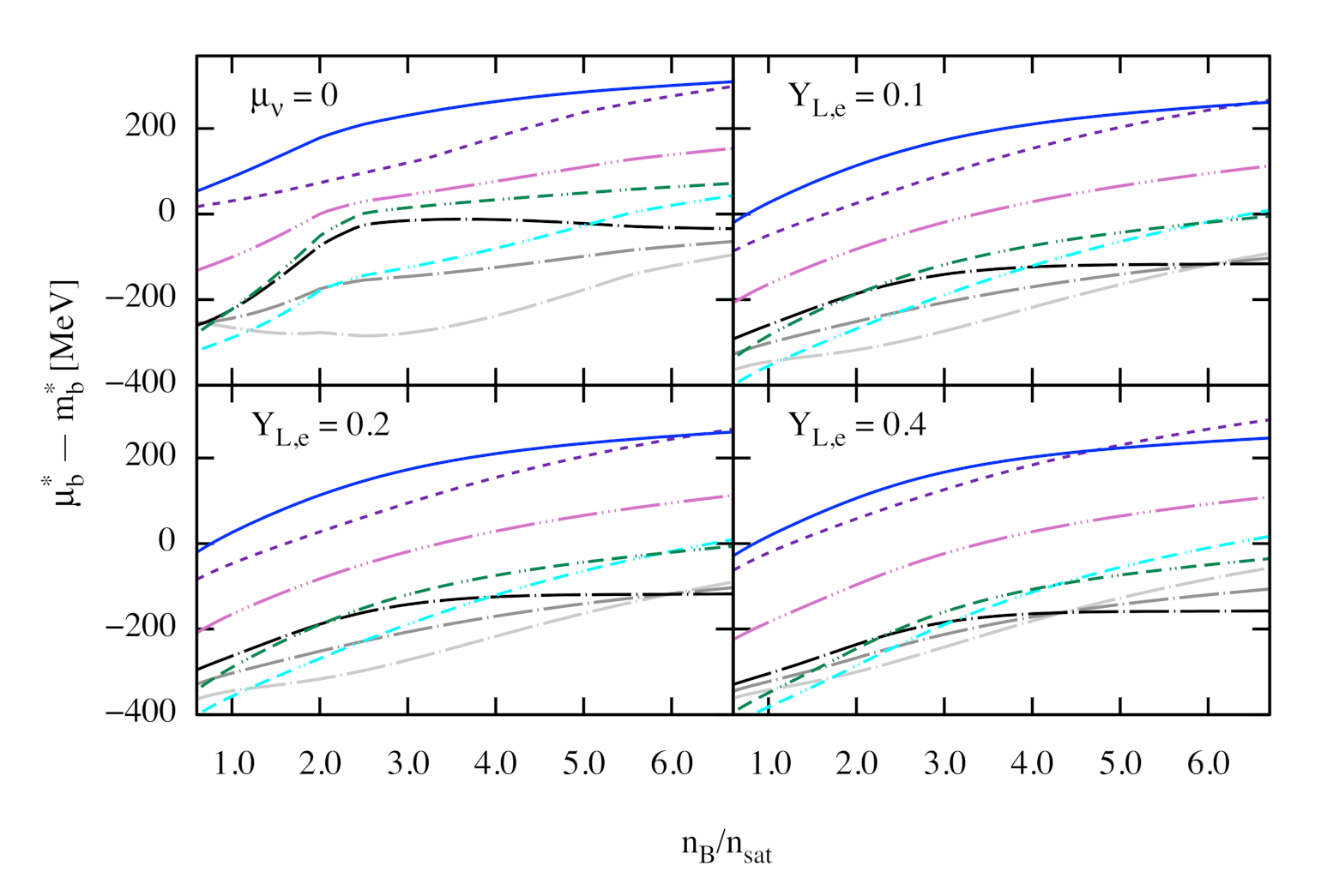
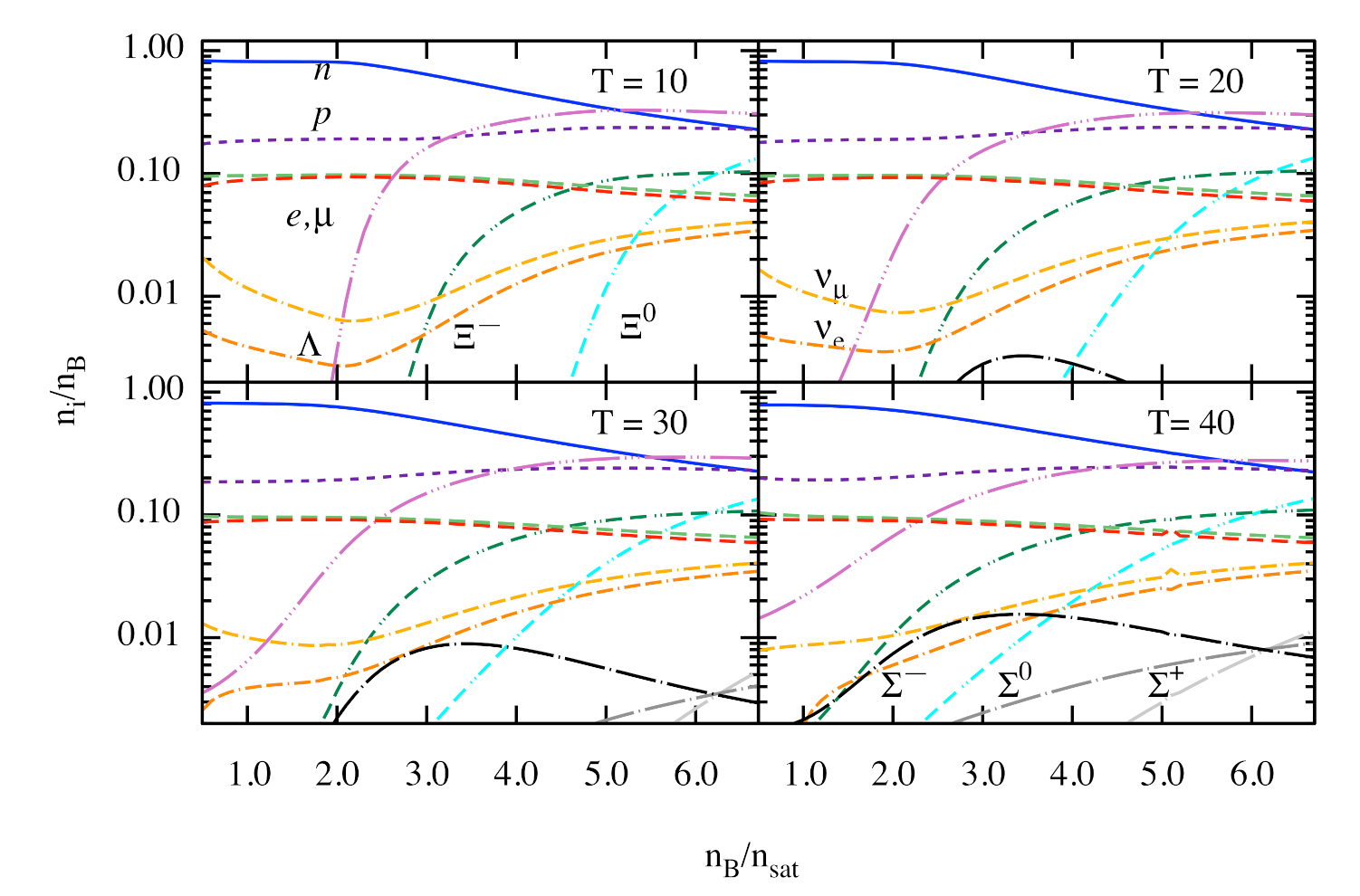
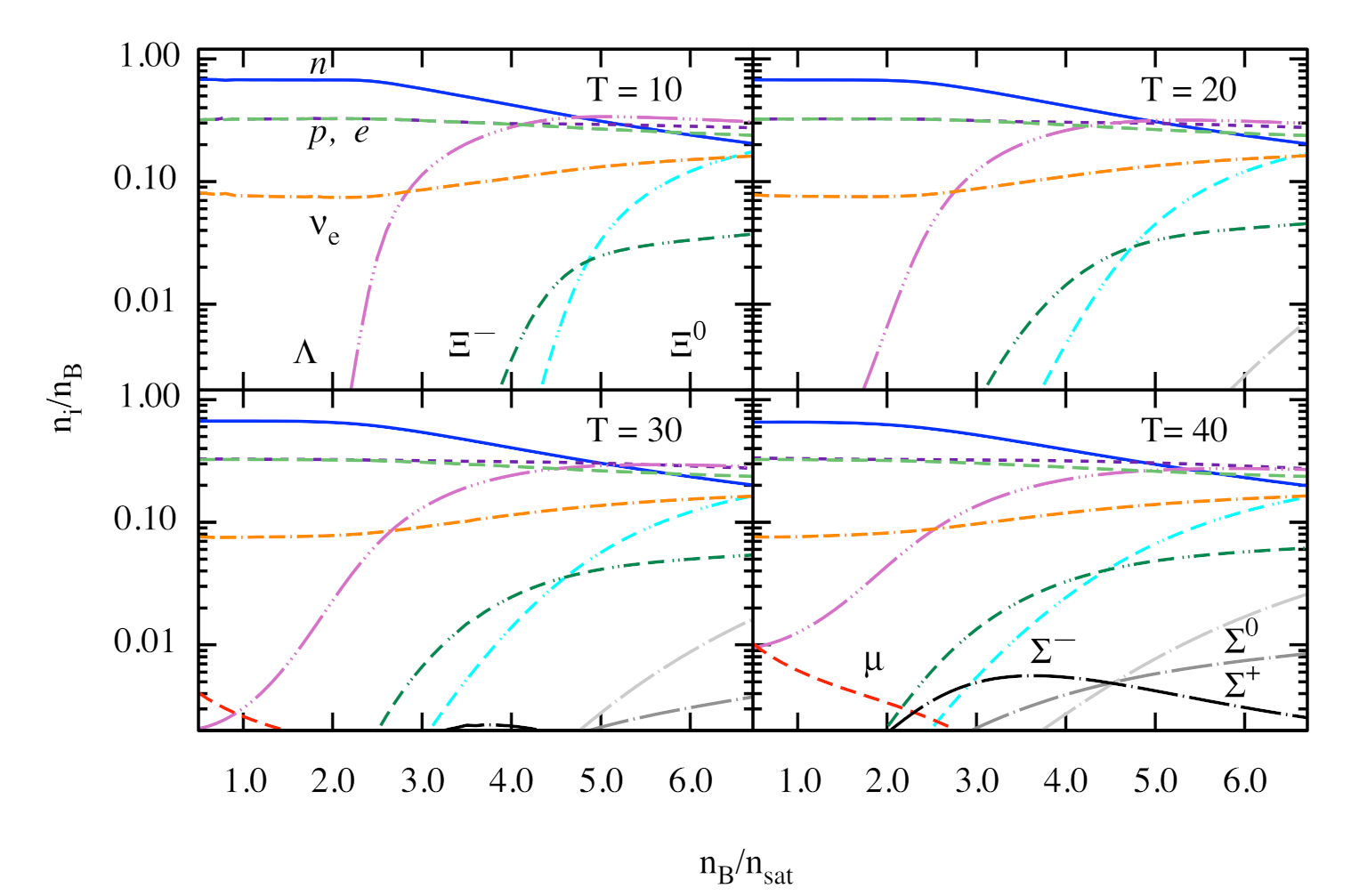
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef] [Green Version]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of Proto–Neutron Stars. Astrophys. J. 1999, 513, 780–804. [Google Scholar] [CrossRef] [Green Version]
- Janka, H.T.; Langanke, K.; Marek, A.; Martinez-Pinedo, G.; Mueller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef] [Green Version]
- Mezzacappa, A.; Lentz, E.J.; Bruenn, S.W.; Hix, W.R.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N.; et al. A Neutrino-Driven Core Collapse Supernova Explosion of a 15 M Star. arXiv 2015, arXiv:1507.05680. [Google Scholar]
- O’Connor, E.P.; Couch, S.M. Exploring Fundamentally Three-dimensional Phenomena in High-fidelity Simulations of Core-collapse Supernovae. Astrophys. J. 2018, 865, 81. [Google Scholar] [CrossRef]
- Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Ranea-Sandoval, I.F. Hot quark matter and (proto-) neutron stars. Phys. Rev. C 2019, 100, 015803. [Google Scholar] [CrossRef] [Green Version]
- Burrows, A.; Radice, D.; Vartanyan, D.; Nagakura, H.; Skinner, M.A.; Dolence, J.C. The overarching framework of core-collapse supernova explosions as revealed by 3D FORNAX simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2715–2735. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Yamada, S.; Suzuki, H. Dynamics and Neutrino Signal of Black Hole Formation in Nonrotating Failed Supernovae. I. Equation of State Dependence. Astrophys. J. 2007, 667, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Fischer, T.; Whitehouse, S.C.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. The neutrino signal from protoneutron star accretion and black hole formation. Astron. Astrophys. 2009, 499, 1–15. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. Black Hole Formation in Failing Core-Collapse Supernovae. Astrophys. J. 2011, 730, 70. [Google Scholar] [CrossRef] [Green Version]
- da Silva Schneider, A.; O’Connor, E.; Granqvist, E.; Betranhandy, A.; Couch, S.M. Equation of State and Progenitor Dependence of Stellar-mass Black Hole Formation. Astrophys. J. 2020, 894, 4. [Google Scholar] [CrossRef]
- Shibata, M.; Taniguchi, K. Coalescence of Black Hole-Neutron Star Binaries. Living Rev. Relativ. 2011, 14, 6. [Google Scholar] [CrossRef] [Green Version]
- Faber, J.A.; Rasio, F.A. Binary Neutron Star Mergers. Living Rev. Relativ. 2012, 15. [Google Scholar] [CrossRef] [Green Version]
- Rosswog, S. The multi-messenger picture of compact binary mergers. Int. J. Mod. Phys. D 2015, 24, 1530012–1530052. [Google Scholar] [CrossRef] [Green Version]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Harris, S.P. β equilibrium in neutron-star mergers. Phys. Rev. C 2018, 98, 065806. [Google Scholar] [CrossRef] [Green Version]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Sedrakian, A.; Li, J.J.; Weber, F. Hyperonization in Compact Stars. arXiv 2021, arXiv:2105.14050. [Google Scholar]
- Burgio, G.F.; Schulze, H.J.; Vidaña, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Oertel, M.; Fantina, A.F.; Novak, J. Extended equation of state for core-collapse simulations. Phys. Rev. C 2012, 85, 055806. [Google Scholar] [CrossRef] [Green Version]
- Colucci, G.; Sedrakian, A. Equation of state of hypernuclear matter: Impact of hyperon-scalar-meson couplings. Phys. Rev. C 2013, 87, 055806. [Google Scholar] [CrossRef]
- Oertel, M.; Gulminelli, F.; Providência, C.; Raduta, A.R. Hyperons in neutron stars and supernova cores. Eur. Phys. J. 2016, A52, 50. [Google Scholar] [CrossRef] [Green Version]
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I-Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef] [Green Version]
- Dexheimer, V.; de Oliveira Gomes, R.; Schramm, S.; Pais, H. What do we learn about vector interactions from GW170817? J. Phys. G 2019, 46, 034002. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Oertel, M.; Providencia, C. Hyperons in hot dense matter: What do the constraints tell us for equation of state? Publ. Astron. Soc. Aust. 2018, 35, 44. [Google Scholar] [CrossRef] [Green Version]
- Weber, F.; Farrell, D.; Spinella, W.M.; Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Maloney, I. Phases of Hadron-Quark Matter in (Proto) Neutron Stars. Universe 2019, 5, 169. [Google Scholar] [CrossRef] [Green Version]
- Stone, J.R.; Dexheimer, V.; Guichon, P.A.M.; Thomas, A.W. Hot Dense Matter in The Quark-Meson-Coupling Model (QMC): Equation of State and Composition of Proto-Neutron Stars. arXiv 2019, arXiv:1906.11100. [Google Scholar]
- Roark, J.; Du, X.; Constantinou, C.; Dexheimer, V.; Steiner, A.W.; Stone, J.R. Hyperons and quarks in proto-neutron stars. Mon. Not. R. Astron. Soc. 2019, 486, 5441–5447. [Google Scholar] [CrossRef]
- Raduta, A.R.; Oertel, M.; Sedrakian, A. Proto-neutron stars with heavy baryons and universal relations. Mon. Not. R. Astron. Soc. 2020, 499, 914–931. [Google Scholar] [CrossRef]
- Stone, J.R.; Dexheimer, V.; Guichon, P.A.M.; Thomas, A.W.; Typel, S. Equation of state of hot dense hyperonic matter in the Quark-Meson-Coupling (QMC-A) model. Mon. Not. R. Astron. Soc. 2021, 502, 3476–3490. [Google Scholar] [CrossRef]
- Alford, M.G.; Haber, A. Strangeness-changing rates and hyperonic bulk viscosity in neutron star mergers. Phys. Rev. C 2021, 103, 045810. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Implications from GW170817 for Δ-isobar Admixed Hypernuclear Compact Stars. Astrophys. J. Lett. 2019, 874, L22. [Google Scholar] [CrossRef] [Green Version]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars with sequential first-order phase transitions and heavy-baryon envelopes. Phys. Rev. D 2020, 101, 063022. [Google Scholar] [CrossRef] [Green Version]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D. Ring, New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Providência, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef] [Green Version]
- Sedrakian, A. The physics of dense hadronic matter and compact stars. Prog. Part. Nucl.Phys. 2007, 58, 168–246. [Google Scholar] [CrossRef] [Green Version]
- Typel, S. Relativistic Mean-Field Models with Different Parametrizations of Density Dependent Couplings. Particles 2018, 1, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Sinha, M.; Mukhopadhyay, B.; Sedrakian, A. Hypernuclear matter in strong magnetic field. Nucl. Phys. A 2013, 898, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Thapa, V.B.; Sinha, M.; Li, J.J.; Sedrakian, A. Equation of State of Strongly Magnetized Matter with Hyperons and Δ-Resonances. Particles 2020, 3, 660–675. [Google Scholar] [CrossRef]
- Dexheimer, V.; Marquez, K.D.; Menezes, D.P. Delta Baryons in Neutron-Star Matter under Strong Magnetic Fields. arXiv 2021, arXiv:2103.09855. [Google Scholar]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Δ isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]
- Cai, B.J.; Fattoyev, F.J.; Li, B.A.; Newton, W.G. Critical density and impact of Δ(1232) resonance formation in neutron stars. Phys. Rev. C 2015, 92, 015802. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Y.; Li, A.; Hu, J.N.; Sagawa, H. Δ(1232) effects in density-dependent relativistic Hartree-Fock theory and neutron stars. Phys. Rev. C 2016, 94, 045803. [Google Scholar] [CrossRef] [Green Version]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Delta isobars in relativistic mean-field models with σ-scaled hadron masses and couplings. Nucl. Phys. A 2017, 961, 106–141. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, H.S.; Mitra, G.; Mishra, R.; Panda, P.K.; Li, B.A. Neutron star matter with Δ isobars in a relativistic quark model. Phys. Rev. C 2018, 98, 045801. [Google Scholar] [CrossRef] [Green Version]
- Ribes, P.; Ramos, A.; Tolos, L.; Gonzalez-Boquera, C.; Centelles, M. Interplay between Δ Particles and Hyperons in Neutron Stars. Astrophys. J. 2019, 883, 168. [Google Scholar] [CrossRef]
- de Swart, J.J. The Octet Model and its Clebsch-Gordan Coefficients. Rev. Mod. Phys. 1963, 35, 916–939. [Google Scholar] [CrossRef] [Green Version]
- van Dalen, E.N.E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with Λ-hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef] [Green Version]
- Friedman, E.; Gal, A. Constraints on Ξ-nuclear interactions from capture events in emulsion. arXiv 2021, arXiv:2104.00421. [Google Scholar]
- Inoue, T.; HAL QCD Collaboration. Strange nuclear physics from QCD on lattice. In Proceedings of the 13th International Conference on HyperNuclear and Strange Particle Physics: HYP2018, Portsmouth, VR, USA, 24–29 June 2018; American Institute of Physics Conference Series. 2019; Volume 2130, p. 020002. [Google Scholar]
- Sasaki, K. ΛΛ and NΞ interactions from Lattice QCD near the physical point. Nucl. Phys. A 2020, 998, 121737. [Google Scholar]
- Bollig, R.; Janka, H.T.; Lohs, A.; Martinez-Pinedo, G.; Horowitz, C.; Melson, T. Muon Creation in Supernova Matter Facilitates Neutrino-driven Explosions. Phys. Rev. Lett. 2017, 119, 242702. [Google Scholar] [CrossRef] [Green Version]
- Guo, G.; Martínez-Pinedo, G.; Lohs, A.; Fischer, T. Charged-Current Muonic Reactions in Core-Collapse Supernovae. Phys. Rev. D 2020, 102, 023037. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. Damping of density oscillations in neutrino-transparent nuclear matter. Phys. Rev. C 2019, 100, 035803. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Haber, A.; Harris, S.P.; Zhang, Z. Beta equilibrium under neutron star merger conditions. arXiv 2021, arXiv:2108.03324. [Google Scholar]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity of baryonic matter with trapped neutrinos. Phys. Rev. D 2019, 100, 103021. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk Viscous Damping of Density Oscillations in Neutron Star Mergers. arXiv 2020, arXiv:2006.07975. [Google Scholar] [CrossRef]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity from Urca processes: npeμ-neutrino-trapped matter. arXiv 2021, arXiv:2108.07523. [Google Scholar]
- Bart, S.; Chrien, R.E.; Franklin, W.A.; Fukuda, T.; Hayano, R.S.; Hicks, K.; Hungerford, E.V.; Michael, R.; Miyachi, T.; Nagae, T.; et al. Σ Hyperons in the Nucleus. Phys. Rev. Lett. 1999, 83, 5238–5241. [Google Scholar] [CrossRef]
- Dover, C.; Gal, A. Hyperon-nucleus potentials. Prog. Part. Nucl. Phys. 1984, 12, 171–239. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic Mean-Field Models with Scaled Hadron Masses and Couplings: Hyperons and Maximum Neutron Star Mass. Nucl. Phys. A 2016, 950, 64–109. [Google Scholar] [CrossRef] [Green Version]
- Lopes, L.L.; Menezes, D.P. Hypernuclear matter in a complete SU(3) symmetry group. Phys. Rev. C 2014, 89, 025805. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.O.; Dexheimer, V.; Schramm, S.; Vasconcellos, C.A.Z. Many-body forces in the equation of state of hyperonic matter. Astrophys. J. 2015, 808, 8. [Google Scholar] [CrossRef] [Green Version]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Equation of State for Neutron Stars With Hyperons and Quarks in the Relativistic Hartree-Fock Approximation. Astrophys. J. 2015, 813, 135. [Google Scholar] [CrossRef] [Green Version]
- Ambartsumyan, V.A.; Saakyan, G.S. The Degenerate Superdense Gas of Elementary Particles. Sov. Astron. 1960, 4, 187. [Google Scholar]
- Sedrakian, A. Light clusters in dilute heavy-baryon admixed nuclear matter. Eur. Phys. J. A 2020, 56, 258. [Google Scholar] [CrossRef]
- Khadkikar, S.; Raduta, A.R.; Oertel, M.; Sedrakian, A. Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state. Phys. Rev. C 2021, 103, 055–811. [Google Scholar] [CrossRef]


| Meson (i) | (MeV) | |||||
| 550.1238 | 1.3881 | 1.0943 | 1.7057 | 0.4421 | 10.5396 | |
| 783 | 1.3892 | 0.9240 | 1.4620 | 0.4775 | 13.0189 | |
| 763 | 0.5647 | — | — | — | 7.3672 |
| 2/3 | 0 | 0.6106 | 0.4777 | ||
| 2/3 | 2 | 0.4426 | 0.4777 | ||
| 1/3 | 1 | 0.3024 | 0.9554 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sedrakian, A.; Harutyunyan, A. Equation of State and Composition of Proto-Neutron Stars and Merger Remnants with Hyperons. Universe 2021, 7, 382. https://doi.org/10.3390/universe7100382
Sedrakian A, Harutyunyan A. Equation of State and Composition of Proto-Neutron Stars and Merger Remnants with Hyperons. Universe. 2021; 7(10):382. https://doi.org/10.3390/universe7100382
Chicago/Turabian StyleSedrakian, Armen, and Arus Harutyunyan. 2021. "Equation of State and Composition of Proto-Neutron Stars and Merger Remnants with Hyperons" Universe 7, no. 10: 382. https://doi.org/10.3390/universe7100382
APA StyleSedrakian, A., & Harutyunyan, A. (2021). Equation of State and Composition of Proto-Neutron Stars and Merger Remnants with Hyperons. Universe, 7(10), 382. https://doi.org/10.3390/universe7100382







