Abstract
Finite-temperature equation of state (EoS) and the composition of dense nuclear and hypernuclear matter under conditions characteristic of neutron star binary merger remnants and supernovas are discussed. We consider both neutrino free-streaming and trapped regimes which are separated by a temperature of a few MeV. The formalism is based on covariant density functional (CDF) theory for the full baryon octet with density-dependent couplings, suitably adjusted in the hypernuclear sector. The softening of the EoS with the introduction of the hyperons is quantified under various conditions of lepton fractions and temperatures. We find that , , and hyperons appear in the given order with a sharp density increase at zero temperature at the threshold being replaced by an extended increment over a wide density range at high temperatures. The hyperon survives in the deep subnuclear regime. The triplet of s is suppressed in cold hypernuclear matter up to around seven times the nuclear saturation density, but appears in significant fractions at higher temperatures, MeV, in both supernova and merger remnant matter. We point out that a special isospin degeneracy point exists where the baryon abundances within each of the three isospin multiplets are equal to each other as a result of (approximate) isospin symmetry. At that point, the charge chemical potential of the system vanishes. We find that under the merger remnant conditions, the fractions of electron and -on neutrinos are close and are about 1%, whereas in the supernova case, we only find a significant fraction (∼10%) of electron neutrinos, given that in this case, the -on lepton number is zero.
1. Introduction
Several astrophysical scenarios lead to the formation of hot, neutrino-rich compact objects which contain nuclear and hypernuclear matter at finite temperature. One such scenario arises in the core-collapse supernova and proto-neutron star context, where a hot proto-neutron star is formed during the contraction of the supernova progenitor and subsequent gravitational detachment of the remnant from the expanding ejecta [1,2,3,4,5,6,7]. A related scenario arises in the case of stellar black-hole formation when the progenitor mass is so large (typically tens of solar masses) that the formation of a stable compact object is not possible and a black hole is inevitably formed [8,9,10,11]. Finally, the binary neutron star mergers offer yet another scenario where finite temperature nuclear and hypernuclear matter play an important role [12,13,14,15]. In the “hot” stage of evolution of these objects the thermodynamics of the matter is characterized by several parameters, for example, density, temperature and lepton fraction. This is in contrast to the case of cold (essentially zero-temperature) compact stars whose thermodynamics is fully determined by a one-parameter EoS relating pressure to energy density under approximate -equilibrium. An important feature of the hot stages of evolution of compact stars is the trapped neutrino component above the trapping temperature MeV—a regime where the neutrino mean-free-path is shorter than the size of the star [16]. As is well known, neutrinos affect significantly the composition of matter and are important for the energy transport and dynamics of supernova and binary neutron star mergers.
After the first observation of a massive compact star in 2010 [17] which was followed by further observations of such objects [18,19] the interest in the covariant density functional (CDF) theories of superdense matter resurged because its parameters became subject to astrophysical constraints in addition to the (low-density) constraints coming from laboratory nuclear physics (for reviews see [20,21,22]). CDF based models tuned to the astrophysical constraints that account for the finite temperature, neutrino component, and strangeness in the form of hyperons appeared in recent years [23,24,25,26,27,28,29,30,31,32,33,34].
In this work, we study the EoS and composition of nuclear and hypernuclear matter both in the neutrino free and neutrino-trapped regimes within the CDF formalism. Our numerical implementation is based on that of Ref. [24] but also includes the hidden strangeness and mesons which account for the interactions amongst hyperons. In addition, instead of using SU(3) symmetry arguments of Ref. [24] in the scalar sector, we adjust the parameters to the depths of hyperon potentials, as already done in Refs. [35,36,37] in the case of zero-temperature EoS. In this work, we use, for the sake of conciseness, a single nucleonic CDF with parameters chosen according DDME2 parameterization [38]. A similar nucleonic DDME2-model-based finite temperature EoS has been presented in Ref. [32], where the couplings in the hyperonic sector were taken from Ref. [39] which differ from the ones adopted here. In this work, we do not address microscopic models of hypernuclear matter which predict too low masses associated for hyperonic stars, see Refs. [22,40] for reviews.
This work is organized as follows. Section 2 is devoted to the formal aspects of EoS and the composition of matter at finite temperatures. The CDF formalism is discussed in Section 2.1 and the choice of the baryon–meson coupling constants is addressed in Section 2.2. The thermodynamic conditions of baryonic matter relevant to neutron star mergers and supernovas are discussed in Section 2.3. Our numerical results are given in Section 3. Section 4 provides a short summary. We use the natural (Gaussian) units with , and the metric signature .
2. Relativistic Density Functional with Density-Dependent Couplings
2.1. Equation of State
We start with a description of the formalism of CDF as applied to hyperonic matter. In this work, we adopt the DDME2 parameterization [38] which is based on the version of the theory that uses density-dependent coupling constants for the meson-baryon interactions [41].
The Lagrangian of the stellar matter is given by
where the baryon Lagrangian is given by
where the b-sum is over the baryon octet; are the Dirac fields of baryons with masses ; , and are the mesonic fields and are the coupling constants that are density-dependent. The - and -meson fields only couple to hyperons. The mesonic part of the Lagrangian is given by
where , , , and are the meson masses and , and stand for the field-strength tensors of vector mesons
The leptonic Lagrangian is given by
where are leptonic fields and are their masses. The lepton index includes electrons and -ons. In hot stellar matter, one needs to include also the three flavors of neutrinos whenever they are trapped. An approximate estimate of the temperature above which neutrinos are trapped is MeV. We will neglect henceforth the strong magnetic fields present in certain classes of compact stars and drop the gauge part of the Lagrangian. For the inclusion of these effects see Refs. [42,43,44]. We do not consider in this work the non-strange members of the baryons decuplet—the -resonances [35,45,46,47,48,49,50]; for a review, see [21].
The partition function of the matter can be evaluated in the mean-field and infinite system approximations from which one finds the pressure and energy density
with the contributions due to mesons and baryons given by
where is the spin degeneracy factor of the baryon octet. The lepton contribution is given by
where for electrons and -ons and 1 for neutrinos of all flavors. The single particle energies of baryons and leptons are given by and , respectively, where the effective (Dirac) baryon masses in the mean-field approximation are given by
Next, is the Fermi distribution function at temperature T. The effective baryon chemical potentials are given by
where is the chemical potential, is the third component of baryon isospin and the rearrangement self-energy , which arises from density-dependence of the coupling constants, is given by
In the mean-field approximation the meson expectation values are given by
where the meson fields now stand for their mean-field values; the scalar number density is given by , whereas the baryon number density is given by . Explicitly, they are given by
2.2. Choice of Coupling Constants
The coupling constants are functions of baryon density, . This accounts for modifications of interactions by the medium at zero temperature; the extrapolation to finite temperature neglects the influence of temperature on the self-energies of baryons at beyond-mean-field level. The nucleon–meson couplings are given by
where is the saturation density, and
For completeness, we list the values of parameters in Table 1.

Table 1.
The values of parameters of the DDME2 CDF.
The density-dependent functions are subject to constraints , and .
Fixing the hyperonic coupling constants involves two sources of information: (a) the couplings of hyperons to the vector mesons are chosen according to the SU(6) spin-flavor symmetric model [51]; (b) their couplings to the scalar mesons are chosen such as to reproduce their phenomenological potential depths at the saturation density, which are determined from experiments.
We express the hyperonic couplings in terms of their ratios to the corresponding couplings of nucleons: for and , . For -hyperons, we adopt [35], which is close to the value determined in Ref. [52] through fits to the -hypernuclei. The likely range of the potentials for and hyperons are
where the value MeV has been given in [53] and is much deeper than the one expected from Lattice 2019 results [54,55]. The adopted values of the coupling constants are taken from Ref. [35] and are listed in Table 2. Note that it is implicitly assumed that the couplings of mesons to hyperons have the same density dependence as for nucleons. The hidden strangeness mesons have masses and MeV, with the density dependence of their couplings coinciding with those of the couplings of the - and -mesons, respectively.

Table 2.
The ratios of the couplings of hyperons to mesons. See text for explanations.
2.3. Thermodynamic Conditions in Supernovas and Merger Remnants
Next, we adopt our hypernuclear CDF to the stellar conditions, specifically to the cases of supernovas and binary neutron star mergers. As already mentioned, two regimes arise depending on the ratio of the neutrino mean-free-path to the size of the system: the neutrino free regime in the case of this ratio being much larger than unity, and the trapped neutrino regime in the opposite case. Trapped neutrinos are in thermal equilibrium and are characterized by appropriate Fermi distribution functions at the matter temperature. Numerical simulations provide the lepton fractions that we adopt in our static (time-independent) description. We assume that the lepton number is conserved in each family, which implies that the neutrino oscillations are neglected. The -leptons are neglected because of their large mass. For supernova matter, the predicted electron and muon lepton numbers are typically and [1,6,29], where we introduced partial lepton densities normalized by the baryon density , where refers to the positron and —to the anti-muon. Note, however, that may vary significantly along with a supernova profile in a time-dependent manner. Furthermore, muonization in the matter can lead to a small (of the order ) fraction of -ons [56,57] which we neglect here. In the case of neutron star mergers, the hot remnant emerges from the material of initial cold neutron stars, and the lepton fractions are assumed for the remnant of a merger. The adopted values reflect (approximately) those of the pre-merger cold neutron stars.
The stellar matter is in weak equilibrium and is charge neutral. The equilibrium with respect to the weak processes requires
where and are the baryon and charge chemical potentials, with are the thermodynamic chemical potentials of the baryons. The charge neutrality condition is given in terms of the partial densities of charged baryons as
Introducing the partial charge density normalized by the baryonic density , the charge neutrality condition can be written
The free streaming and trapped neutrino regimes are characterized by
where are the lepton chemical potentials which are associated with the lepton number and , which are conserved separately. Combining the weak-equilibrium and charge neutrality conditions we are now in a position to compute the EoS of stellar matter both in the trapped and free streaming neutrino regimes. Note that it is implicitly assumed that the matter is under detailed balance with respect to Urca processes; if this condition is violated, then an additional “isospin chemical potential” arises [58,59]. Additionally, note that we do not constrain particles to their Fermi surfaces and any corrections associated with the finite temperature features of the Fermi distribution function are included in our -equilibratium condition.
3. Numerical Results
Our numerical procedure involves a solution of self-consistent equations for the meson fields and the scalar and baryon densities for fixed values of temperature, density, and lepton numbers and , which are chosen according to the physical conditions characteristic for supernovas and merger remnants, as specified in Section 2.3. In this work, we concentrate on the features of EoS and particle fractions (or abundances) in the matter under various thermodynamic conditions.
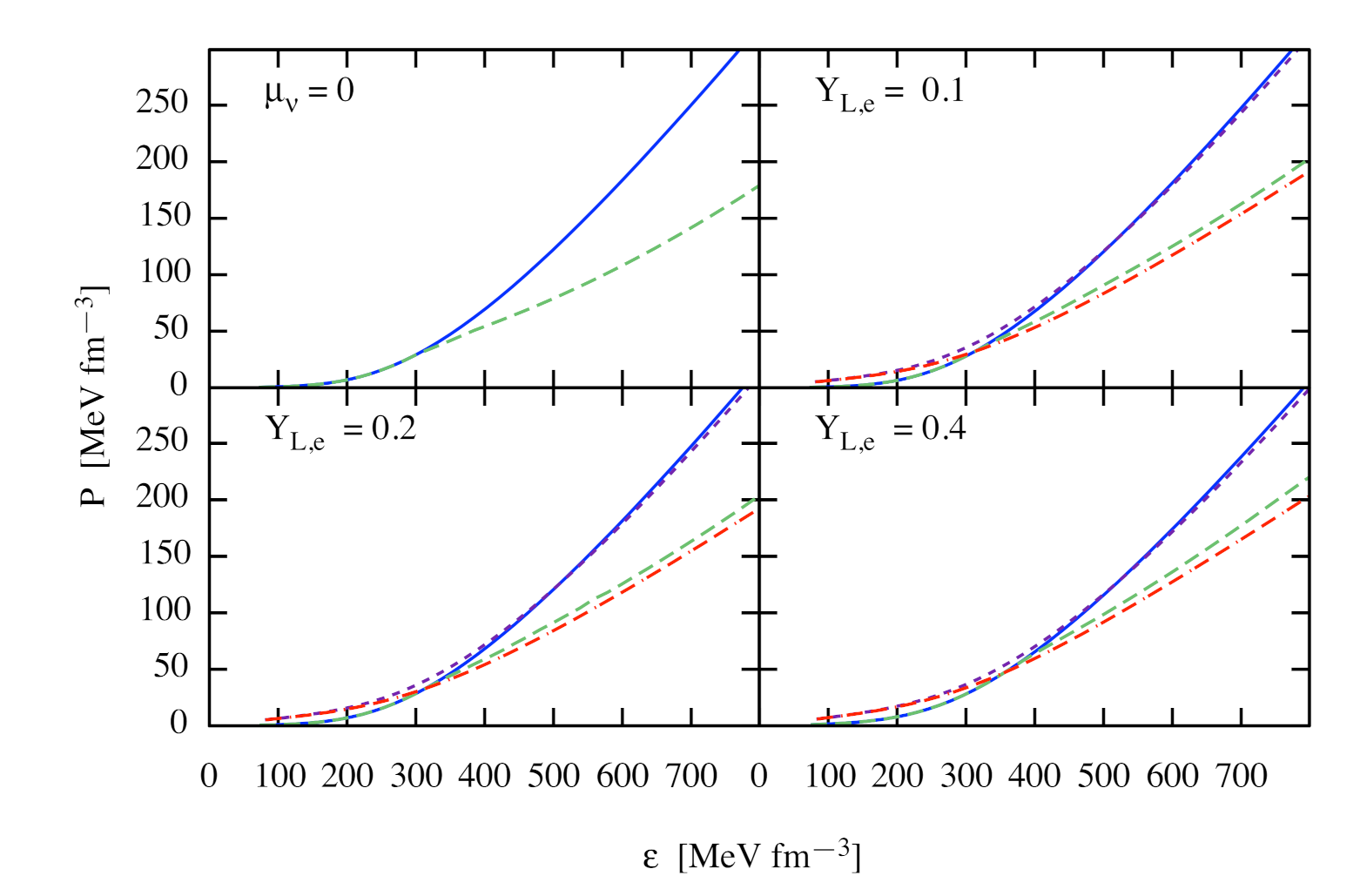
Figure 1 shows the EoS for nucleonic and hyperonic matter at temperature MeV in the -equilibrium and neutrino-free case, as well as at and 50 MeV with trapped neutrinos and several values of . The -on fractions are chosen as for and . The non-zero is characteristic of merger remnants whereas zero is characteristic for supernovas. The key well-known feature of the onset of hyperons seen in Figure 1 is the softening of the EoS, i.e., the shift of pressure to lower values above the energy-density for the onset of hyperons. It is further seen that for a higher temperature, the pressure is larger at low densities and is lower at high densities independent of the presence of hyperons.
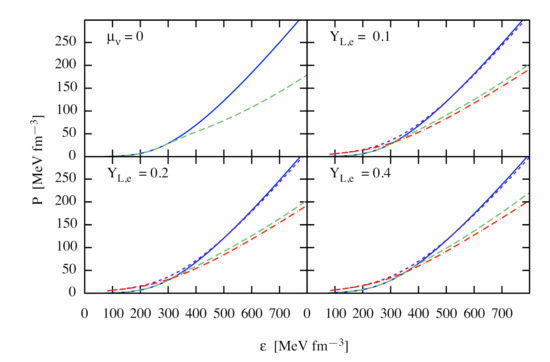
Figure 1.
Dependence of the pressure on the energy density. The panel labeled corresponds to neutrino-free -equilibrium case without (solid) and with (dashed) hyperons at MeV. (Varying the temperature up to does not produce visible changes.) The remaning panels show results for the neutrino trapped matter at MeV (solid—without hyperons and long-dashed—with hyperons) and 50 MeV (short-dashed—without hyperons and double-dash-dotted—with hyperons) for . The -on fractions are (upper right panel) and for and 0.4 (lower row). The case is characteristic of a merger remnant, whereas —to supernova.
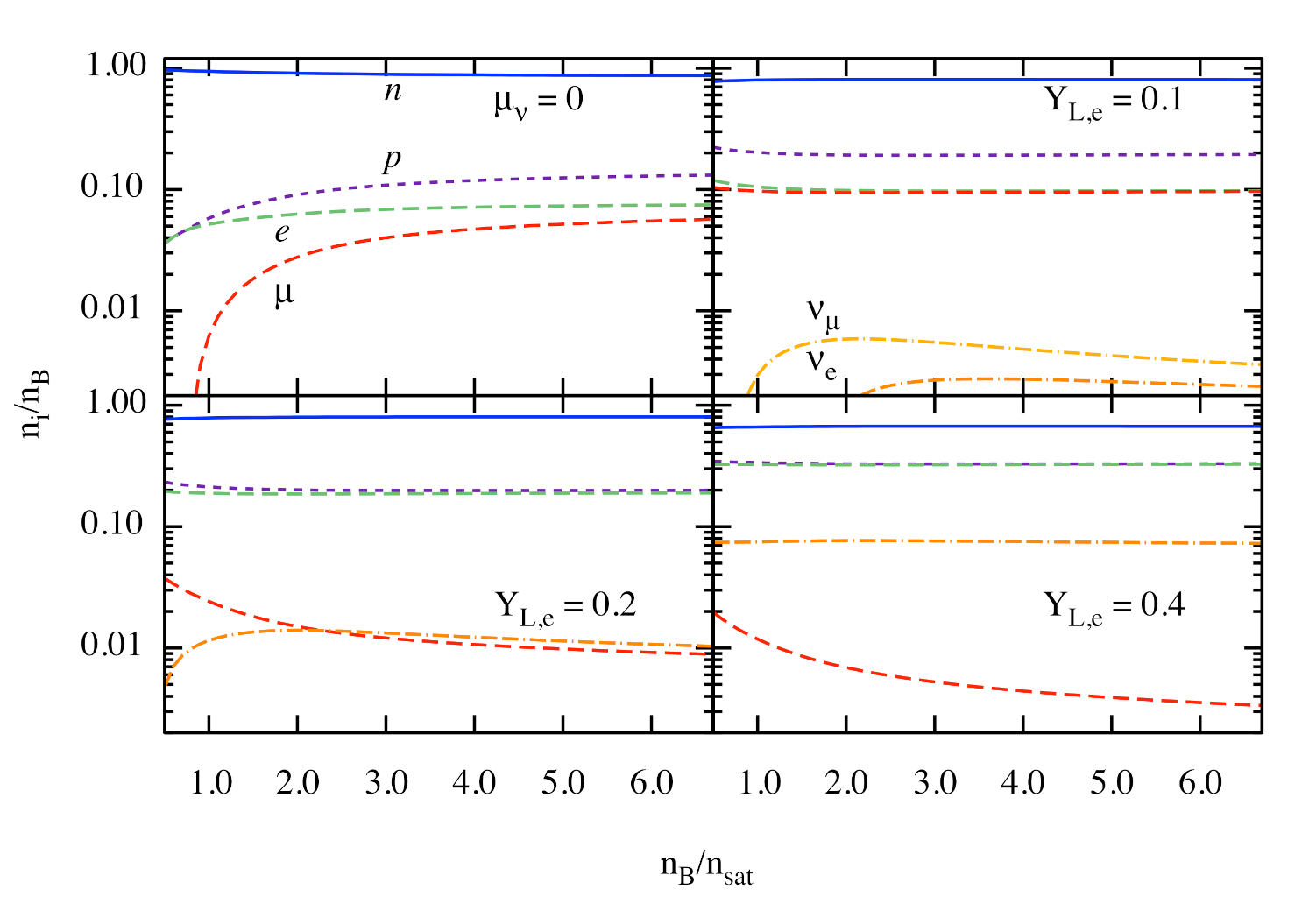
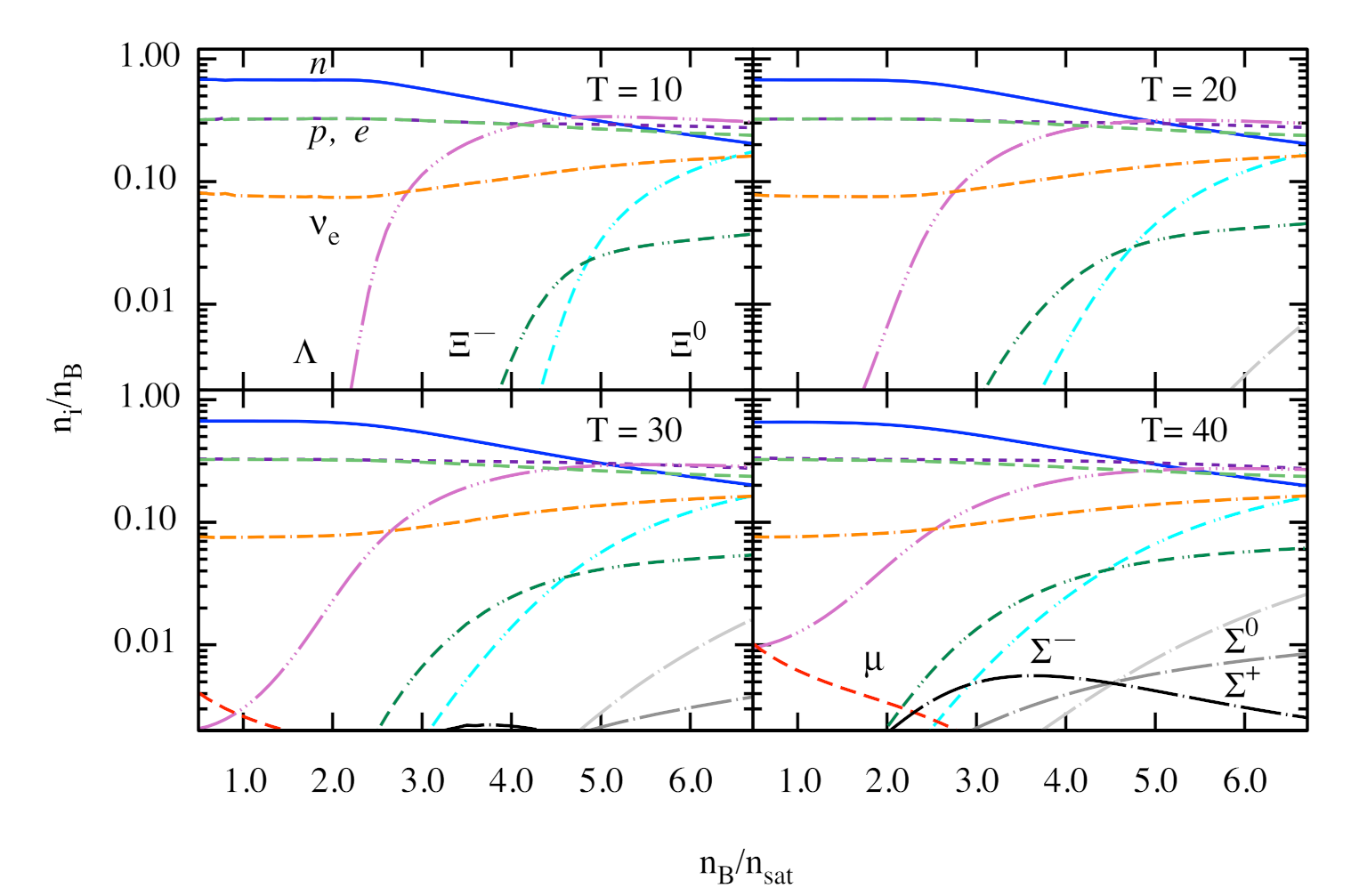
Figure 2 shows the particle number densities in -matter normalized by baryon density as a function of baryon density normalized by fm . The case corresponds to the -equilibrium neutrino-free case at MeV, whereas the cases correspond to the trapped neutrino regime at MeV. The choices of match those of Figure 1. In contrast to the neutrino-transparent case, where the muons appear above a threshold density around where , in the neutrino-trapped regime, the electron and muon contributions are almost equal under merger conditions (), and there is a visible fraction of -on neutrinos. Thus, the charge neutrality is maintained through the balance of negative charges of both types of leptons with protons. From the upper right panel of Figure 2, we see that the net neutrino numbers become negative at low densities for both lepton families, indicating that there are more antineutrinos than neutrinos in the low-density and high-temperature regime of neutron star merger matter.
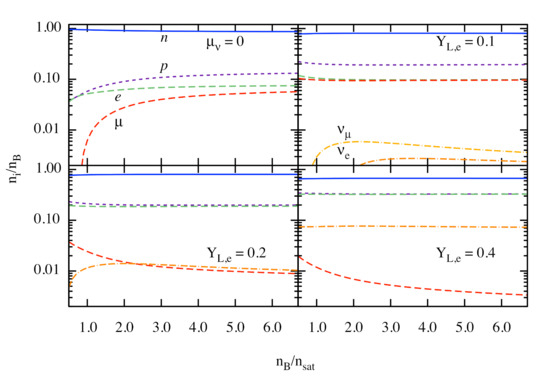
Figure 2.
Dependence of the particle fractions on the baryon density normalized by the saturation density. The panels show the composition of matter in -equilibrium at MeV in the neutrino-free case () and for neutrino-trapped matter at MeV for several values of the electron lepton faction , with the -on component satisfying and for , where is the -on lepton fraction.
Note that the proton fraction remains below the threshold for the Urca processes to operate in the low-temperature neutrino-free regime. In the high-temperature regime, the phase-space for Urca processes opens due to the thermal smearing of Fermi surfaces of baryons. This has important ramifications on the oscillations of post-merger remnants through the damping effect of the bulk viscosity driven by Urca processes [34,58,60,61,62].
Under the supernova conditions, -ons are greatly suppressed and the corresponding neutrinos are extinct. Then, the near equality of proton and electron abundances is required by charge neutrality. Note that the -on abundances need not vanish, as also includes the contributions from muonic neutrinos and antineutrinos. The small -on fraction seen in the lower panels of Figure 2 is compensated by an equal fraction of muonic antineutrinos required by the condition . The isospin asymmetry in supernova matter is reduced with increasing and, consequently, the difference between the neutron and proton abundances gradually vanishes. The electron-neutrino population increases as well. In the cases , the -on neutrino fraction is comparable to that of electron-neutrinos, as their lepton numbers are set equal. In the lower panels of Figure 2, they are absent because we enforced the condition .
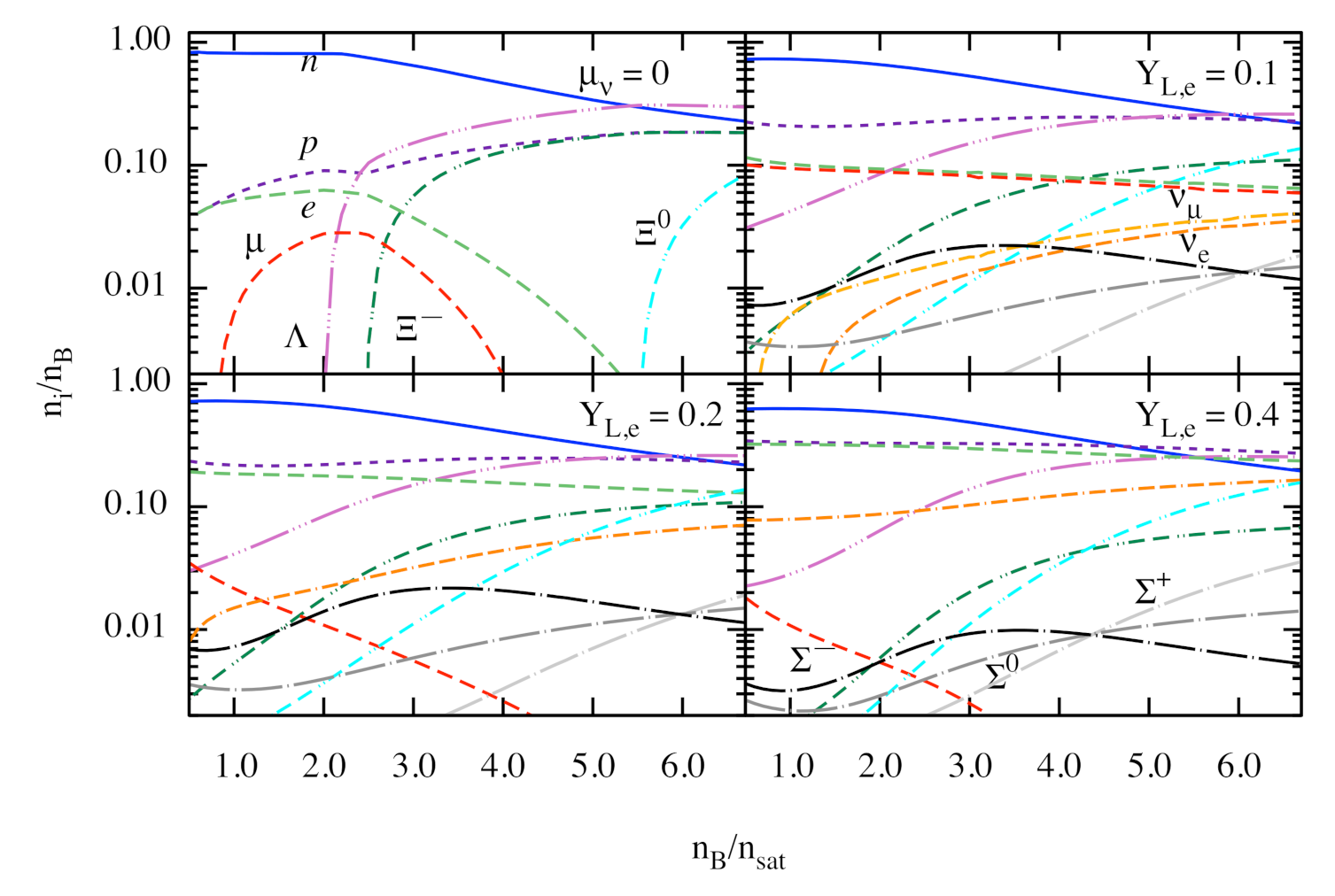
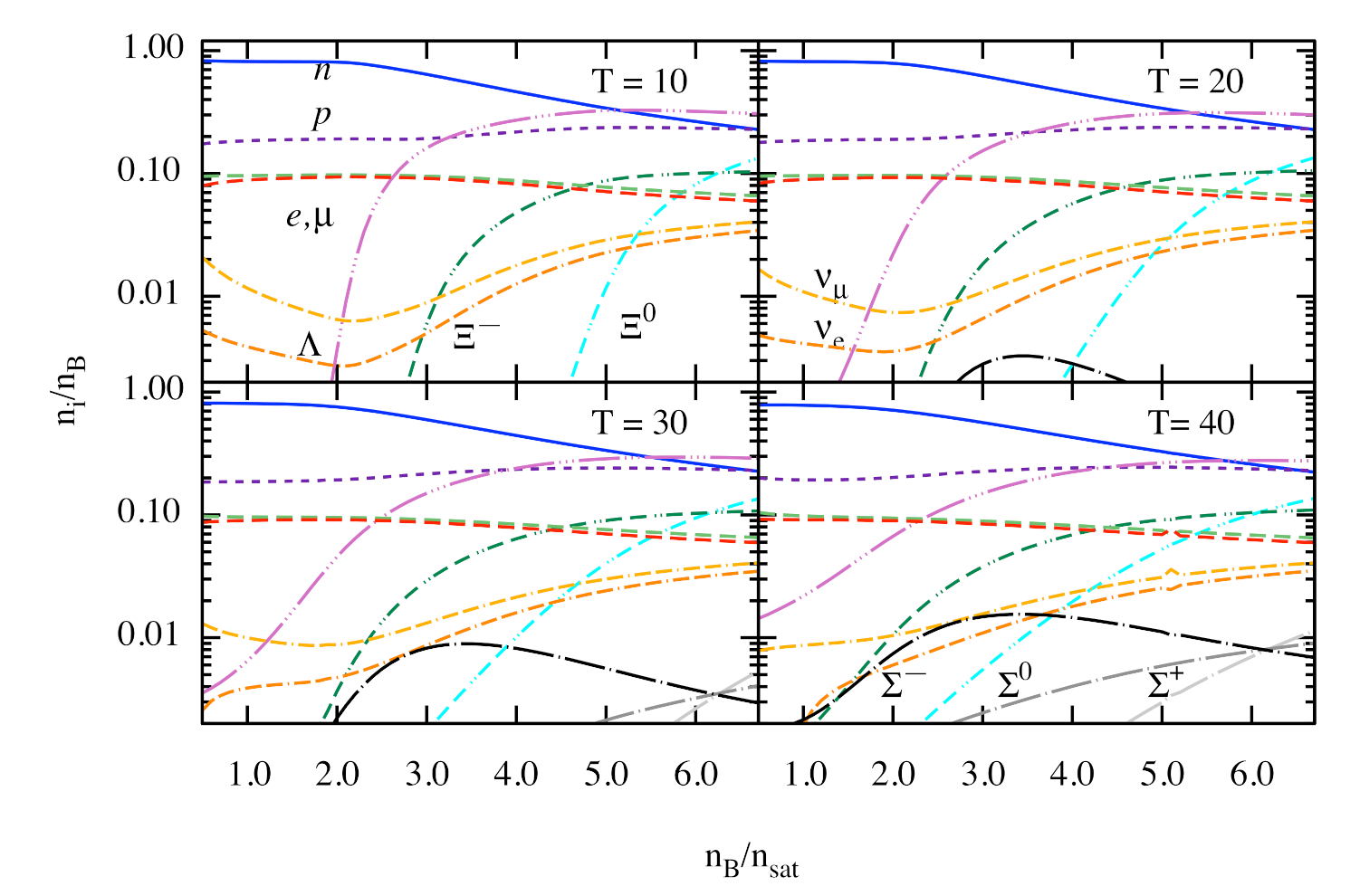
Figure 3 shows the same as Figure 2, but it includes the full baryon octet. Hyperons appear at densities above the saturation, in the following sequence: , and . The onset of hyperon in the low-temperature matter occurs at densities outside the range shown. The reason for the shift of hyperons to high densities is the adopted highly repulsive potential value in nuclear matter [63,64,65,66,67,68]. This ordering is at variance to the case of free hyperonic gas, where was predicted to be the first hyperon to nucleate [69], and more elaborate models which assign weakly repulsive potential, see, e.g., [24]. However, the triplet of is present for MeV independent of the values of lepton numbers. It is interesting that and fractions interchange their roles from being most abundant to least abundant -hyperon with increasing density at a special intersection point where the abundances of all the s coincide. Note that the location of this special point depends on the choice of . Furthermore, it is seen that the intersection point of n and p fractions, as well as that of and fractions, are located close to the intersection point of s.
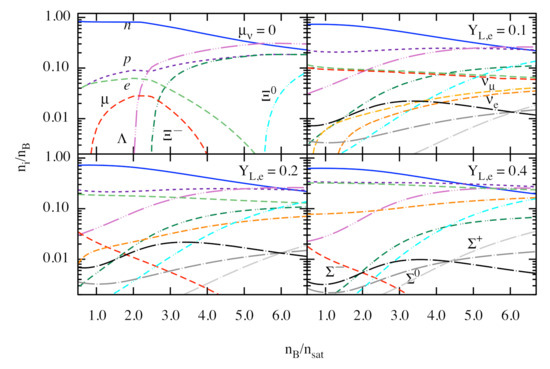
Figure 3.
Same as in Figure 2, but for the full baryon octet with the -on component satisfying the conditions (upper right) and for (lower row). In the low-temperature, -equilibrium case, the , and appear in the given order with a sharp increase in their fractions at the corresponding density thresholds. At high temperature MeV the density thresholds are located at lower densities (some are outside figure’s scale) and the triplet appears. The fractions of hyperons are shown by dash-triple-dot lines, that of by double-dash-double-dot lines and that of by dash-single-dot lines. The electron and -ons neutrinos are shown by double-dash-dot lines; the electrons and -ons by long-dashed lines, protons by short-dashed lines and, finally, neutrons by solid lines.
This feature can be understood by examining the -equilibrium conditions (25)–(27). If there is a point within the density range considered where the proton fraction reaches the neutron fraction (which means due to Equation (19)), then the charge chemical potential vanishes at that point (due to the density scaling (22), the contribution of the -meson mean-field to the effective baryon chemical potentials (14) is negligible at high densities, resulting in ). This results in a single chemical potential for the full baryon octet at that special isospin degeneracy point. This implies, in turn, almost equal values of effective chemical potentials and, therefore, equal baryon fractions within a given isospin-multiplet.
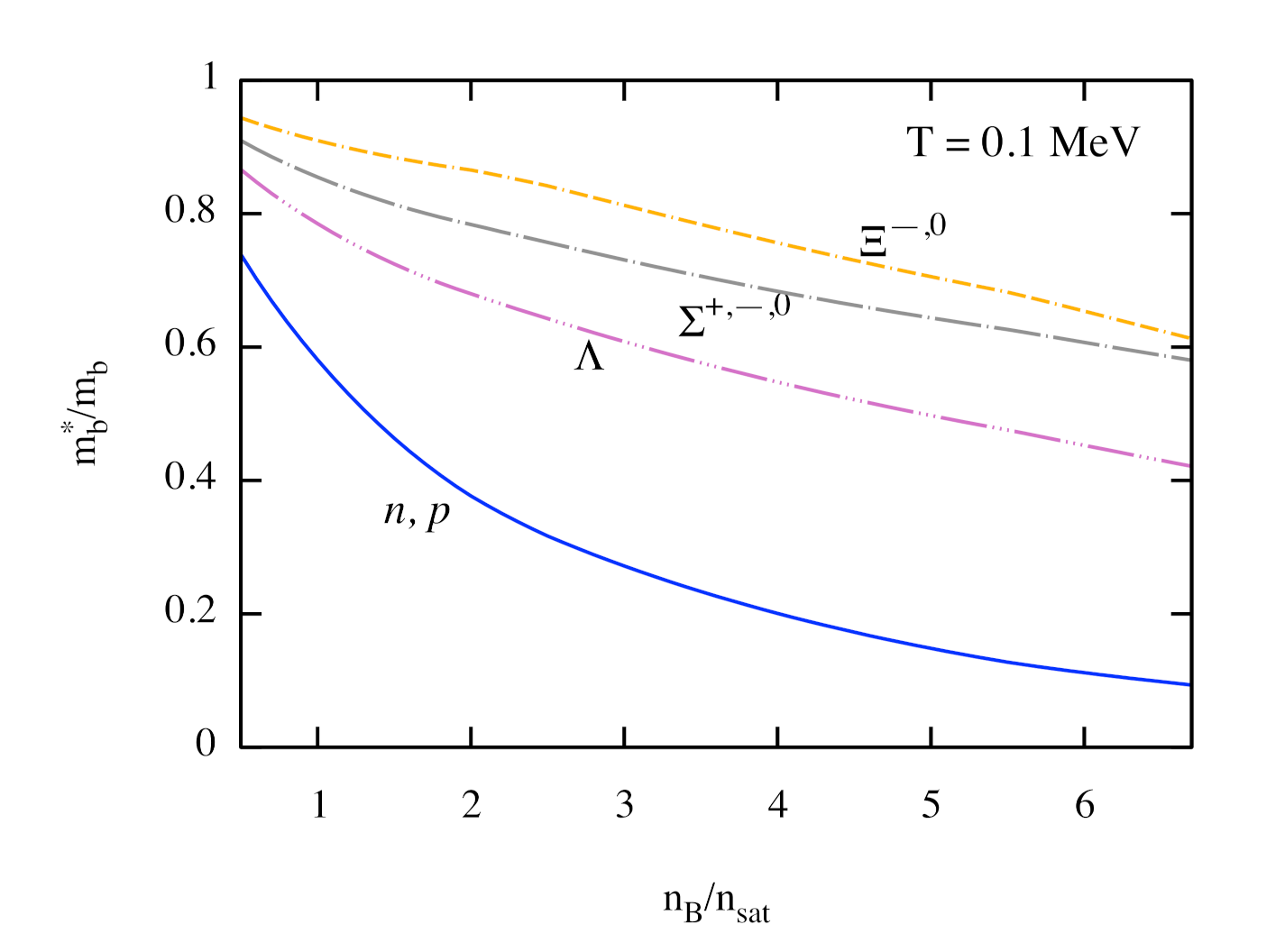
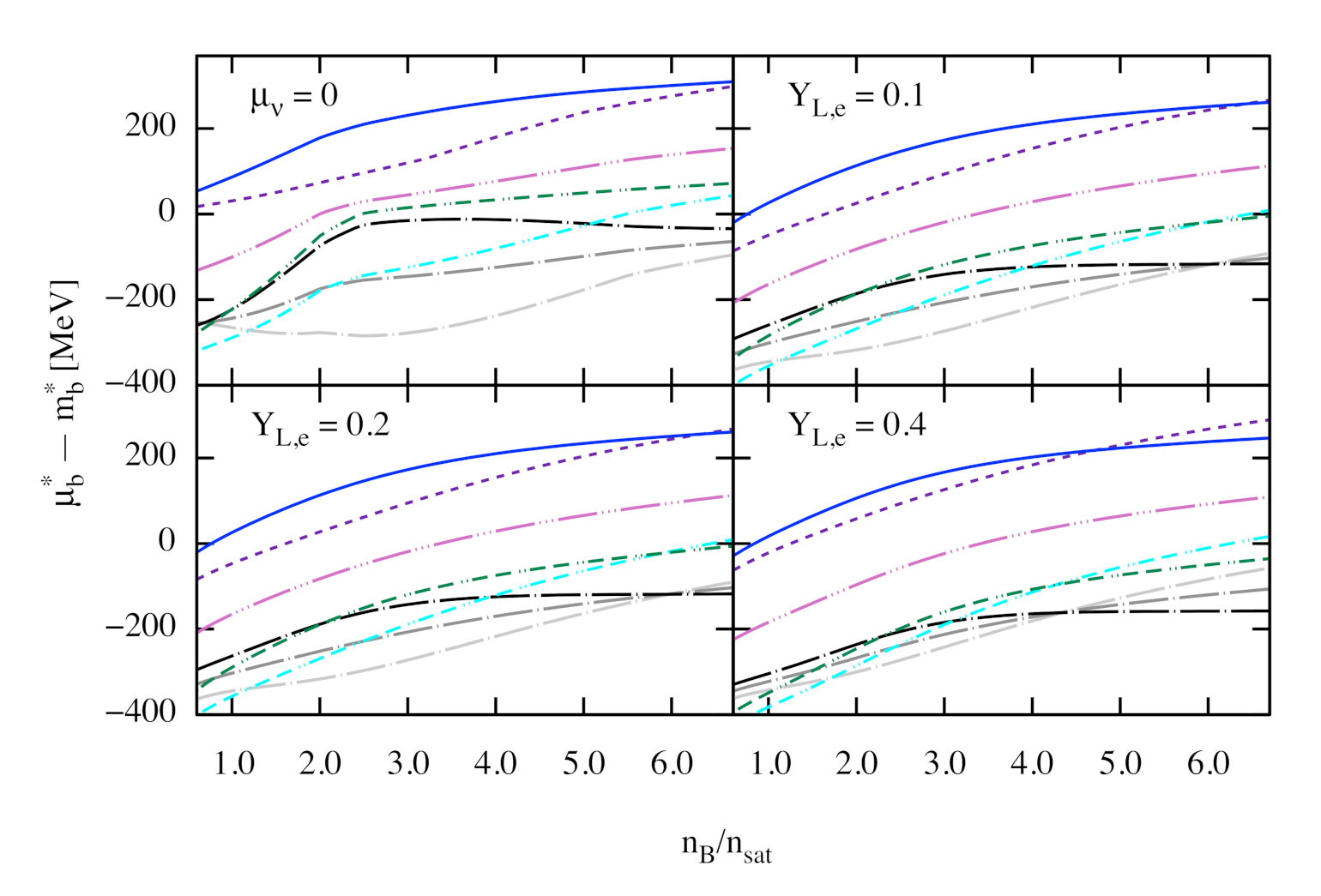
Figure 4 shows the effective masses of baryons as a function of density at MeV and in -equilibrium. The effective masses of isospin multiplets (), and are degenerate. The temperature dependence of the effective masses of baryons is very weak and, for the sake of clarity, is not shown.
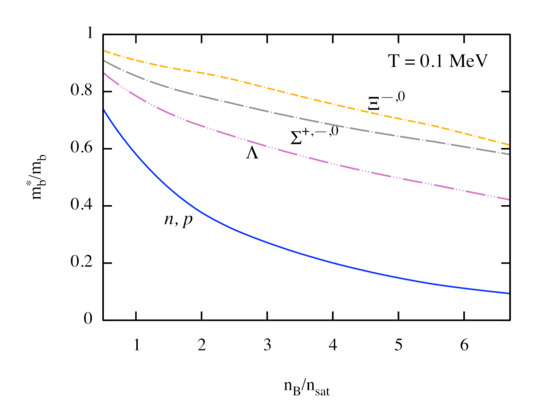
Figure 4.
Dependence of effective masses of baryons on the density at MeV and in -equilibrium. Each isospin multiplet is shown by a single line due to the degeneracy in their masses.
Figure 5 shows the effective baryon chemical potentials minus their effective masses, which clearly show the special intersection points within each multiplet at all values of the lepton fractions in the neutrino-trapped matter. Note that the effective masses within each multiplet are equal in our model, see Figure 4 above. On the left side of the intersection point we have , which according to the conditions (25)–(27) puts the baryon abundances within each multiplet in the charge-decreasing order (i.e., baryons with smaller charges are more abundant). Above the intersection point , the ordering of baryon fractions within each multiplet is reversed. Similar behaviour of baryon abundances was found also in Refs. [6,32], where the composition of hot stellar matter was shown at constant entropy-per-baryon and the composition of matter also included the quartet of -resonances. Note that in the ideal case of exact isospin symmetry, the intersection points of the three isospin-multiplets , and would be located exactly at the same density. The small deviations of these three points from each other (which increase gradually with increasing ) reflect the fact that the isospin symmetry is approximate.
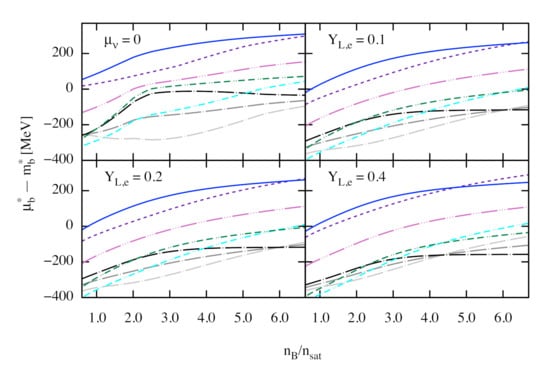
Figure 5.
Dependence of baryon effective chemical potentials (computed from their effective masses) on the normalized baryon density . The line styles for each baryon and the values of the temperature and lepton fractions for each panel match those in Figure 3. The intersection (isospin degeneracy) points of chemical potentials of the same isospin-multiples is clearly visible at all values of lepton fractions in the neutrino-trapped matter.
The difference between almost equal abundances of leptons for and the remaining cases is related to our choice of to reflect merger remnant conditions (first case) and supernova conditions (second case). This difference also propagates to the abundances of electron and -on neutrinos, which are present in almost equal quantities in the first case, whereas in the second case, the -on neutrinos are replaced by a much smaller amount of -on antineutrinos. Hyperons affect the way the charge neutrality is maintained at high density. In low-temperature and -equilibrated matter it is enforced by equal abundances of protons and hyperons with electrons and -ons being extinct at high densities. At finite temperature, the electrons are abundant and the presence of hyperon only induces some splitting between the electron and proton fractions, which becomes less pronounced with increasing . The fractions of -ons and their neutrinos in the merger remnant case () are as significant as those of electrons and electron-neutrinos, respectively, but they do not play any significant role in the supernova case where . In contrast to the pure nucleonic matter where the neutrino abundances remain constant or decrease slowly with baryon density, the hypernuclear matter features increasing neutrino abundances with density because of decreasing lepton fractions at fixed and .
It is further seen that finite temperatures induce a significant shift of the hyperon thresholds to lower densities (which lie outside of the density range considered). This is in accordance with the recent observation that low-density hot nuclear matter may feature a significant fraction of strangeness (-particles) as well as -resonances in addition to light clusters and free nucleons [70]. Note also that the -hyperon abundances become larger than those of neutrons at high density, i.e., these species are the dominant baryonic component in the matter for . This results mainly from the weaker repulsive coupling of s to -meson which enhances their abundances compared to neutrons. The weaker renormalization of ’s mass due to coupling to and mesons than that of neutron is less important.
Figure 6 shows the particle fractions in the hypernuclear matter in the temperature range MeV and electron and -on fraction fixed by the condition characteristic of neutron star binary mergers. It is seen that the abundances of neutrons, protons, electrons and -ons are weakly dependent on the temperature. Due to equal lepton numbers, the electron and -on abundances are close to each other with the small electron excess reflected in the dominance of -on neutrinos over the electron-neutrinos. At high densities, the neutrino abundances are almost independent of the temperature as well, but they decrease with increasing temperature and, eventually, become negative at temperatures between 40 and 50 MeV in the low-density domain (see also the upper right panel of Figure 3).
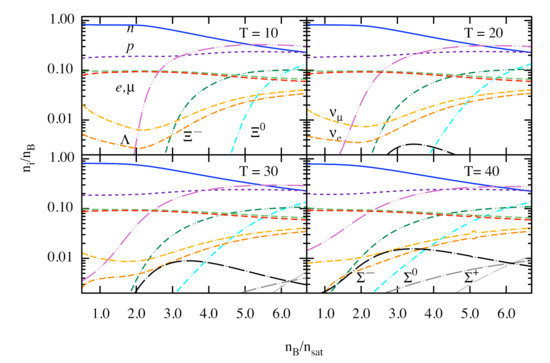
Figure 6.
Same as in Figure 3, but for the fixed electron and -on lepton fractions and temperatures , 20, 30 and 40 MeV. The lepton number fractions are characteristic for binary neutron star mergers.
Hyperons have sharply increasing fractions at the thresholds at MeV, which replicates those at low temperatures and in neutrino-free regimes. With increasing temperature, the thresholds of the appearance of the hyperons move to the lower densities, with the threshold moving to a density below . The high-density limit shows the following new features: (a) the becomes the most abundant baryon by exceeding the neutron fraction; the hyperon overtakes and becomes the second-most abundant hyperon. Note that the upper right panel of Figure 3 differs from the panels shown here only by the temperature ( MeV); therefore, our comments here parallel the statements made earlier in the context of Figure 3. Turning to the s, we note that their abundances are noticeable for MeV and the occurrence of the special interchange point of isospin degeneracy is seen again for MeV and MeV.
In Figure 7, we show the same as in Figure 6 but for and , which physically corresponds to the case of supernova matter. Many general trends seen for baryon abundances remain the same under these new conditions. An interesting new feature is the near equipartition between neutrons, , and protons at high density , with fraction approaching this group above . As for leptons, the main effect arises from the drop of -on fraction to below 1% and less for MeV. For , this number climbs to a few percent (see Figure 3, lower panels). Because of this, the charge neutrality is mainly maintained by the equality of the abundances of protons and electrons, with slight disparity introduced by at high density. The most striking difference is the strong enhancement of electron-neutrino abundances for all temperatures, with a very weak dependence on the temperature of the environment.
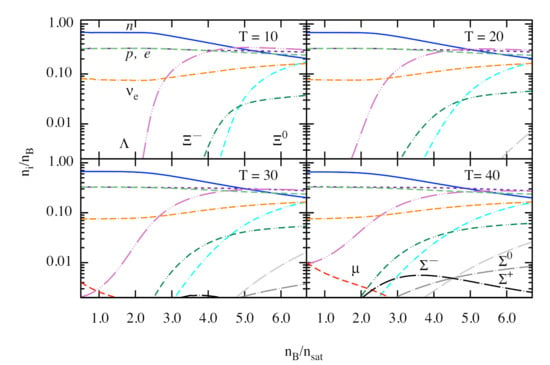
Figure 7.
Same as in Figure 6, but for the fixed and , i.e., the lepton number fractions are characteristic for supernova.
4. Conclusions
In this work, we explored the finite-temperature EoS of nuclear and hypernuclear matter within the CDF formalism. Formally, our study uses essentially the same approach as that of Ref. [24], but it includes additional hidden-strangeness mesons and employs a different strategy to fix the hyperonic couplings in the scalar sector by adjusting these to the depths of hyperon potential in nuclear matter. We performed parameter studies varying the temperature, density and lepton fraction within two scenarios: the binary merger remnant scenario with equal numbers of electron and -on lepton numbers and the supernova scenario with non-zero electron and zero -on lepton numbers. In all cases, the well-known feature of softening of the EoS with the inclusion of hyperons is reproduced. Even though the temperature dependence of the EoS is not strong (see Figure 1), it has significant impact on the radii and masses of compact stars (see for example, refs. [32,71]). The abundances of particles in a baryon–lepton mixture in a merger remnant and a supernova were explored within the CDF formalism. The main features are: (a) at finite temperatures, the sharp increase in hyperon fractions at the thresholds is replaced by a gradual increase over a density range allowing for a significant fraction of hyperons, especially s, at sub-saturation densities, as shown in Figure 3, Figure 6, and Figure 7. (b) At large densities , the most abundant baryon is , as in the strongly relativistic regime, the difference between the (bare) masses of the neutron and is not important. The weaker coupling of meson to than to nucleon results in a a weaker renormalization of mass (see Figure 4) which disfavors hyperons. However, the weaker repulsive coupling of s to -meson promotes their abundances compared to neutrons, which eventually leads to their dominance at high densities. Note that the -meson coupling is exponentially suppressed at high densities and it does not play any considerable role. Note also that the roles played by - and -mesons are similar to that of - and -mesons, but are quantitatively less important. (c) The triplet of hyperons, which is completely suppressed in the cold regime of hypernuclear matter, emerges at temperatures above 20 MeV, with significant fractions of compatible to that of at low densities and high temperatures MeV. (d) In the neutrino-trapped regime, there is always a special isospin degeneracy point where the charge chemical potential of the system vanishes. At that point, the baryon abundances within each of the three isospin-multiplets are equal to each other as a result of (approximate) isospin symmetry. (e) We find a significant difference between the neutrino abundances in the merger remnant and supernova cases. In the first case, there are comparable numbers of electron and -on neutrinos (the electron and -on lepton numbers being equal). In the second case, electron neutrino abundance is much larger and -on neutrinos are absent (there is only a small fraction of -on anti-neutrinos in this case, typically less than a percent). This, of course, reflects the choices of and for these cases, but the abundances are not trivially related to lepton numbers.
Author Contributions
A.S. and A.H. equally contributed to all stages of this project. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Volkswagen Foundation (Hannover, Germany) grant No. 96 839. A. S. was funded by Deutsche Forschungsgemeinschaft (DFG) Grant No. SE1836/5-1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying this article will be shared on reasonable request to the corresponding author.
Acknowledgments
The author acknowledge the networking opportunities offered by the European COST Action “PHAROS” (CA16214).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef] [Green Version]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of Proto–Neutron Stars. Astrophys. J. 1999, 513, 780–804. [Google Scholar] [CrossRef] [Green Version]
- Janka, H.T.; Langanke, K.; Marek, A.; Martinez-Pinedo, G.; Mueller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef] [Green Version]
- Mezzacappa, A.; Lentz, E.J.; Bruenn, S.W.; Hix, W.R.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N.; et al. A Neutrino-Driven Core Collapse Supernova Explosion of a 15 M Star. arXiv 2015, arXiv:1507.05680. [Google Scholar]
- O’Connor, E.P.; Couch, S.M. Exploring Fundamentally Three-dimensional Phenomena in High-fidelity Simulations of Core-collapse Supernovae. Astrophys. J. 2018, 865, 81. [Google Scholar] [CrossRef]
- Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Ranea-Sandoval, I.F. Hot quark matter and (proto-) neutron stars. Phys. Rev. C 2019, 100, 015803. [Google Scholar] [CrossRef] [Green Version]
- Burrows, A.; Radice, D.; Vartanyan, D.; Nagakura, H.; Skinner, M.A.; Dolence, J.C. The overarching framework of core-collapse supernova explosions as revealed by 3D FORNAX simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2715–2735. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Yamada, S.; Suzuki, H. Dynamics and Neutrino Signal of Black Hole Formation in Nonrotating Failed Supernovae. I. Equation of State Dependence. Astrophys. J. 2007, 667, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Fischer, T.; Whitehouse, S.C.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. The neutrino signal from protoneutron star accretion and black hole formation. Astron. Astrophys. 2009, 499, 1–15. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. Black Hole Formation in Failing Core-Collapse Supernovae. Astrophys. J. 2011, 730, 70. [Google Scholar] [CrossRef] [Green Version]
- da Silva Schneider, A.; O’Connor, E.; Granqvist, E.; Betranhandy, A.; Couch, S.M. Equation of State and Progenitor Dependence of Stellar-mass Black Hole Formation. Astrophys. J. 2020, 894, 4. [Google Scholar] [CrossRef]
- Shibata, M.; Taniguchi, K. Coalescence of Black Hole-Neutron Star Binaries. Living Rev. Relativ. 2011, 14, 6. [Google Scholar] [CrossRef] [Green Version]
- Faber, J.A.; Rasio, F.A. Binary Neutron Star Mergers. Living Rev. Relativ. 2012, 15. [Google Scholar] [CrossRef] [Green Version]
- Rosswog, S. The multi-messenger picture of compact binary mergers. Int. J. Mod. Phys. D 2015, 24, 1530012–1530052. [Google Scholar] [CrossRef] [Green Version]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Harris, S.P. β equilibrium in neutron-star mergers. Phys. Rev. C 2018, 98, 065806. [Google Scholar] [CrossRef] [Green Version]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Sedrakian, A.; Li, J.J.; Weber, F. Hyperonization in Compact Stars. arXiv 2021, arXiv:2105.14050. [Google Scholar]
- Burgio, G.F.; Schulze, H.J.; Vidaña, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Oertel, M.; Fantina, A.F.; Novak, J. Extended equation of state for core-collapse simulations. Phys. Rev. C 2012, 85, 055806. [Google Scholar] [CrossRef] [Green Version]
- Colucci, G.; Sedrakian, A. Equation of state of hypernuclear matter: Impact of hyperon-scalar-meson couplings. Phys. Rev. C 2013, 87, 055806. [Google Scholar] [CrossRef]
- Oertel, M.; Gulminelli, F.; Providência, C.; Raduta, A.R. Hyperons in neutron stars and supernova cores. Eur. Phys. J. 2016, A52, 50. [Google Scholar] [CrossRef] [Green Version]
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I-Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef] [Green Version]
- Dexheimer, V.; de Oliveira Gomes, R.; Schramm, S.; Pais, H. What do we learn about vector interactions from GW170817? J. Phys. G 2019, 46, 034002. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Oertel, M.; Providencia, C. Hyperons in hot dense matter: What do the constraints tell us for equation of state? Publ. Astron. Soc. Aust. 2018, 35, 44. [Google Scholar] [CrossRef] [Green Version]
- Weber, F.; Farrell, D.; Spinella, W.M.; Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Maloney, I. Phases of Hadron-Quark Matter in (Proto) Neutron Stars. Universe 2019, 5, 169. [Google Scholar] [CrossRef] [Green Version]
- Stone, J.R.; Dexheimer, V.; Guichon, P.A.M.; Thomas, A.W. Hot Dense Matter in The Quark-Meson-Coupling Model (QMC): Equation of State and Composition of Proto-Neutron Stars. arXiv 2019, arXiv:1906.11100. [Google Scholar]
- Roark, J.; Du, X.; Constantinou, C.; Dexheimer, V.; Steiner, A.W.; Stone, J.R. Hyperons and quarks in proto-neutron stars. Mon. Not. R. Astron. Soc. 2019, 486, 5441–5447. [Google Scholar] [CrossRef]
- Raduta, A.R.; Oertel, M.; Sedrakian, A. Proto-neutron stars with heavy baryons and universal relations. Mon. Not. R. Astron. Soc. 2020, 499, 914–931. [Google Scholar] [CrossRef]
- Stone, J.R.; Dexheimer, V.; Guichon, P.A.M.; Thomas, A.W.; Typel, S. Equation of state of hot dense hyperonic matter in the Quark-Meson-Coupling (QMC-A) model. Mon. Not. R. Astron. Soc. 2021, 502, 3476–3490. [Google Scholar] [CrossRef]
- Alford, M.G.; Haber, A. Strangeness-changing rates and hyperonic bulk viscosity in neutron star mergers. Phys. Rev. C 2021, 103, 045810. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Implications from GW170817 for Δ-isobar Admixed Hypernuclear Compact Stars. Astrophys. J. Lett. 2019, 874, L22. [Google Scholar] [CrossRef] [Green Version]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars with sequential first-order phase transitions and heavy-baryon envelopes. Phys. Rev. D 2020, 101, 063022. [Google Scholar] [CrossRef] [Green Version]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D. Ring, New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Providência, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef] [Green Version]
- Sedrakian, A. The physics of dense hadronic matter and compact stars. Prog. Part. Nucl.Phys. 2007, 58, 168–246. [Google Scholar] [CrossRef] [Green Version]
- Typel, S. Relativistic Mean-Field Models with Different Parametrizations of Density Dependent Couplings. Particles 2018, 1, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Sinha, M.; Mukhopadhyay, B.; Sedrakian, A. Hypernuclear matter in strong magnetic field. Nucl. Phys. A 2013, 898, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Thapa, V.B.; Sinha, M.; Li, J.J.; Sedrakian, A. Equation of State of Strongly Magnetized Matter with Hyperons and Δ-Resonances. Particles 2020, 3, 660–675. [Google Scholar] [CrossRef]
- Dexheimer, V.; Marquez, K.D.; Menezes, D.P. Delta Baryons in Neutron-Star Matter under Strong Magnetic Fields. arXiv 2021, arXiv:2103.09855. [Google Scholar]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Δ isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]
- Cai, B.J.; Fattoyev, F.J.; Li, B.A.; Newton, W.G. Critical density and impact of Δ(1232) resonance formation in neutron stars. Phys. Rev. C 2015, 92, 015802. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Y.; Li, A.; Hu, J.N.; Sagawa, H. Δ(1232) effects in density-dependent relativistic Hartree-Fock theory and neutron stars. Phys. Rev. C 2016, 94, 045803. [Google Scholar] [CrossRef] [Green Version]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Delta isobars in relativistic mean-field models with σ-scaled hadron masses and couplings. Nucl. Phys. A 2017, 961, 106–141. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, H.S.; Mitra, G.; Mishra, R.; Panda, P.K.; Li, B.A. Neutron star matter with Δ isobars in a relativistic quark model. Phys. Rev. C 2018, 98, 045801. [Google Scholar] [CrossRef] [Green Version]
- Ribes, P.; Ramos, A.; Tolos, L.; Gonzalez-Boquera, C.; Centelles, M. Interplay between Δ Particles and Hyperons in Neutron Stars. Astrophys. J. 2019, 883, 168. [Google Scholar] [CrossRef]
- de Swart, J.J. The Octet Model and its Clebsch-Gordan Coefficients. Rev. Mod. Phys. 1963, 35, 916–939. [Google Scholar] [CrossRef] [Green Version]
- van Dalen, E.N.E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with Λ-hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef] [Green Version]
- Friedman, E.; Gal, A. Constraints on Ξ-nuclear interactions from capture events in emulsion. arXiv 2021, arXiv:2104.00421. [Google Scholar]
- Inoue, T.; HAL QCD Collaboration. Strange nuclear physics from QCD on lattice. In Proceedings of the 13th International Conference on HyperNuclear and Strange Particle Physics: HYP2018, Portsmouth, VR, USA, 24–29 June 2018; American Institute of Physics Conference Series. 2019; Volume 2130, p. 020002. [Google Scholar]
- Sasaki, K. ΛΛ and NΞ interactions from Lattice QCD near the physical point. Nucl. Phys. A 2020, 998, 121737. [Google Scholar]
- Bollig, R.; Janka, H.T.; Lohs, A.; Martinez-Pinedo, G.; Horowitz, C.; Melson, T. Muon Creation in Supernova Matter Facilitates Neutrino-driven Explosions. Phys. Rev. Lett. 2017, 119, 242702. [Google Scholar] [CrossRef] [Green Version]
- Guo, G.; Martínez-Pinedo, G.; Lohs, A.; Fischer, T. Charged-Current Muonic Reactions in Core-Collapse Supernovae. Phys. Rev. D 2020, 102, 023037. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. Damping of density oscillations in neutrino-transparent nuclear matter. Phys. Rev. C 2019, 100, 035803. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.G.; Haber, A.; Harris, S.P.; Zhang, Z. Beta equilibrium under neutron star merger conditions. arXiv 2021, arXiv:2108.03324. [Google Scholar]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity of baryonic matter with trapped neutrinos. Phys. Rev. D 2019, 100, 103021. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk Viscous Damping of Density Oscillations in Neutron Star Mergers. arXiv 2020, arXiv:2006.07975. [Google Scholar] [CrossRef]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity from Urca processes: npeμ-neutrino-trapped matter. arXiv 2021, arXiv:2108.07523. [Google Scholar]
- Bart, S.; Chrien, R.E.; Franklin, W.A.; Fukuda, T.; Hayano, R.S.; Hicks, K.; Hungerford, E.V.; Michael, R.; Miyachi, T.; Nagae, T.; et al. Σ Hyperons in the Nucleus. Phys. Rev. Lett. 1999, 83, 5238–5241. [Google Scholar] [CrossRef]
- Dover, C.; Gal, A. Hyperon-nucleus potentials. Prog. Part. Nucl. Phys. 1984, 12, 171–239. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic Mean-Field Models with Scaled Hadron Masses and Couplings: Hyperons and Maximum Neutron Star Mass. Nucl. Phys. A 2016, 950, 64–109. [Google Scholar] [CrossRef] [Green Version]
- Lopes, L.L.; Menezes, D.P. Hypernuclear matter in a complete SU(3) symmetry group. Phys. Rev. C 2014, 89, 025805. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.O.; Dexheimer, V.; Schramm, S.; Vasconcellos, C.A.Z. Many-body forces in the equation of state of hyperonic matter. Astrophys. J. 2015, 808, 8. [Google Scholar] [CrossRef] [Green Version]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Equation of State for Neutron Stars With Hyperons and Quarks in the Relativistic Hartree-Fock Approximation. Astrophys. J. 2015, 813, 135. [Google Scholar] [CrossRef] [Green Version]
- Ambartsumyan, V.A.; Saakyan, G.S. The Degenerate Superdense Gas of Elementary Particles. Sov. Astron. 1960, 4, 187. [Google Scholar]
- Sedrakian, A. Light clusters in dilute heavy-baryon admixed nuclear matter. Eur. Phys. J. A 2020, 56, 258. [Google Scholar] [CrossRef]
- Khadkikar, S.; Raduta, A.R.; Oertel, M.; Sedrakian, A. Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state. Phys. Rev. C 2021, 103, 055–811. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).