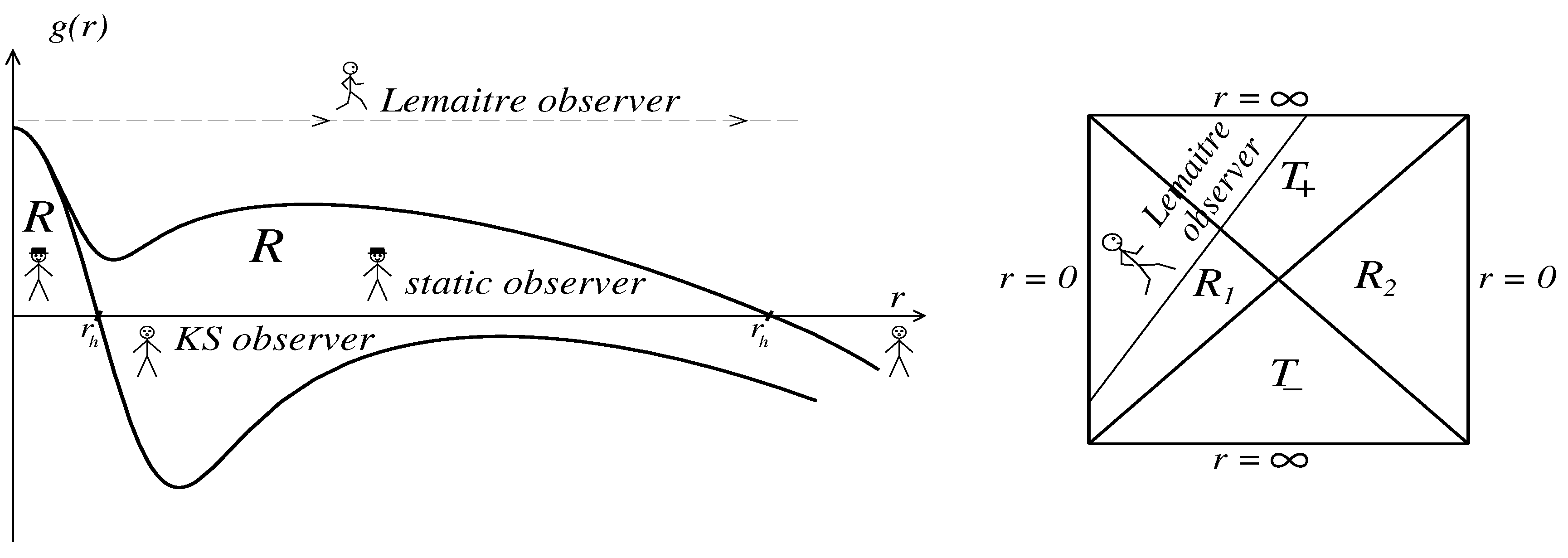1. Introduction
| Which arrow does fly forever? |
| An arrow which hits the goal. |
| Vladimir Nabokov |
Einstein introduced a cosmological term
into his equations describing Gravity as a Geometry represented by the geometric tensor
and generated by the distribution of energy-matter represented by its stress-energy tensor
to achieve the concordance with the Mach principle, which was one of his primary motivations [
1,
2]. Mach’s principle stated that some matter has the property of inertia due to the presence of some other matter in the universe [
3]. It is expected that the field equations (
1) would have reasonable solutions only in the presence of a matter. However, Einstein found the regular solution to the equations
, the Minkowski geometry, which perfectly describes inertial motion in the absence of matter. The primary task of
was thus to eliminate reasonable solutions in the case when
, following the logic dictated by Mach’s principle [
4].
Soon after, de Sitter found a reasonable solution with
and without
[
5]. In the same year, 1917, Einstein used the basic property of
as the universal repulsion to construct the static universe model with a uniformly distributed matter and non-zero
[
6]. However, when in 1929 Hubble finally confirmed the linear relations discovered by him between redshifts and distances for galaxies, which testified that the universe is undoubtedly expanding [
7], Einstein decided to exclude
from his equations as “the biggest fault” in his career [
8].
Many years later,
was rehabilitated and invoked to provide the reason for the initial universe expansion and powering it due to generic repulsive character of the de Sitter geometry independent on a particular model underlying the de Sitter vacuum [
9,
10] (for a review [
11]). The Einstein cosmological term
is associated with the maximally symmetric de Sitter vacuum,
, (
) with
by virtue of the contracted Bianchi identities resulting in
. It is specified by the equation of state
which implies generically negative pressure. In accordance with the standard definition of a pressure as related to a force preventing contraction, the negative pressure acts in the opposite direction and may lead to an unlimited contraction. In the de Sitter geometry, the intrinsic contraction of the negative pressure is transformed into the intrinsic gravitational repulsion,
. This is what provides a mechanism able (i) to drive accelerated expansion in the universe and (ii) to avoid singularities replacing them with the de Sitter vacuum.
De Sitter vacuum is identified as the best candidate for a dark energy (DE), which fills our universe in about 75% of its density (for a review [
12,
13]). Sometimes one can read in the literature that the nature of a dark energy is unknown. This is rather not true. The truth is that the de Sitter vacuum as a highly symmetric continuous medium dominates in our universe as its basic ingredient, which powers its accelerated expansion. There exist infinitely many distributions of matter that behave like a cosmological term in the Einstein equations,
([
14] and references therein), but ultimately it is the repulsive gravity of the de Sitter vacuum that explains the results of astronomical observations. The numerous examples are presented by various DE models, which involve
or mimic its behavior ([
15,
16,
17] and references therein). The intensively explored problem is what kind of a particular matter associated with the de Sitter vacuum fits better in the physical context of our universe state and evolution in confrontation with observations (for a review [
18,
19]).
The requirement
excludes a self-consistent description of its whole evolution from the large initial value to the small today value by the Einstein cosmological term
. The possibility to describe evolution between an initial and final de Sitter vacua in the frame of one theoretical scheme is provided by the algebraic classification of stress-energy tensors, which includes stress-energy tensors with the algebraic structure such that
[
20,
21] and the vacuum equation of state holds only in one or two space dimensions (
). They correspond to a variable cosmological term [
21] and describe essentially anisotropic vacuum dark fluid [
22], which can be evolving and clustering dependently on the choice of a coordinate mapping. It can be identified as an anisotropic kind of quintessence, which was originally introduced in general treatment by the equation of state
with
[
23] (for a recent review [
24]). In the anisotropic case, its definition extends to
and
,
, where
and, in the general case, is coordinate-dependent. It represents a time-evolving and spatially inhomogeneous dark energy which can evolve between initial, final and intermediate (if necessary) de Sitter vacua ([
25] and references therein). By the Einstein equations, they generate spacetimes whose the basic features are determined by geometry independently on underlying particular models for
(for a review [
26]).
The Einstein equations admit the class of regular solutions with the source terms specified by
[
20] and satisfying the Weak Energy Condition (WEC), which implies the non-negative energy density as measured by any local observer on a time-like curve. In cosmology they describe relaxing cosmological constant ([
27] and references therein). Its evolution between different values is provided by the intrinsic anisotropy of
, therefore it cannot be described by the isotropic FLRW cosmological models and requires applying the cosmological models of the Lemaître class for anisotropic and inhomogeneous perfect fluid (for a review [
28]). Solutions of this class also represent compact objects with the de Sitter vacuum interiors: regular black holes and self-gravitating solitons replacing naked singularities: G-lumps, described by the Einstein equations [
29,
30], and electromagnetic solitons, described by the nonlinear electrodynamics minimally coupled to gravity [
31]. Their masses are generically related to the interior de Sitter vacuum and spacetime symmetry breaking from the de Sitter group [
30].
The majority of regular black holes presented in the literature belongs to this class. Information on their interiors can be in principle extracted from observations of black holes shadows ([
32] and references therein). Gravitational solitons G-lumps replacing naked singularities are defined in the spirit of the Coleman lumps as non-singular, non-dissipative, self-gravitating, compact objects related by their own self-interaction [
33]. Regular primordial black holes with the de Sitter interiors, their remnants and gravitational solitons G-lumps can be considered as dark matter (DM) candidates with the DE interiors. The de Sitter vacuum interiors determine their observational signatures and provide their observational identification (for a review [
34]).
The story of the abandonment of
by Einstein and its spectacular revitalization in cosmology, overshadowed his primary idea to introduce
as a quantity significantly related to inertia. The question of how to connect them goes back to another of Einstein’s profound proposals to describe an elementary particle by a regular solution of nonlinear field equations as a “bunched field” located in the confined region with the maximal field tension and energy [
35].
In the contemporary view, massive particles acquire masses by the Higgs mechanism involving the de Sitter vacuum as its fundamental ingredient (a false vacuum). Incorporating the de Sitter vacuum, the Higgs mechanism implicitly incorporates the intrinsic relation between mass, gravity and spacetime symmetry breaking revealed in the frame of General Relativity for all objects with the de Sitter vacuum interiors [
36]. In all cases when a particle acquires its mass by the Higgs mechanism, its mass is generically related to gravity and spacetime symmetry, since the de Sitter vacuum generates the de Sitter geometry in the region of its involvement and leads to dynamical participation of gravity in the region of interaction. For example, despite that gravity is frequently assumed to be too weak to be essential on the electroweak scale, gravity of the intrinsically involved de Sitter vacuum leads to the bi-maximal neutrino mixing in the interaction vertex, which allows to explain the observed mass square differences for neutrino and to evaluate the gravito-electroweak scale in accordance with the existing theories of the gravito-electroweak unification ([
37,
38,
39] and references therein). Another example concerns the appearance of the minimal length scale in the annihilation reaction
[
40,
41]. Experimental data reveal with a 5
significance the existence of a characteristic minimal length
cm at the scale
TeV. The calculations of the differential cross-section QED-
including radiative effects up to
predict an increase in the total cross-section. Contrary to these predictions, the
fit displays the minimum with the negative fit parameter. This result can be understood by applying an extended electron model suggested by nonlinear electrodynamics coupled to gravity (NED-GR) and satisfying WEC, which predicts, for an arbitrary gauge invariant Lagrangian, the existence of a spinning electrically charged electromagnetic soliton, asymptotically Kerr–Newman for a distant observer with the gyromagnetic ratio
, the same as for the Dirac electron [
31]. Generic features of the electromagnetic soliton allow to interpret the minimal length in the annihilation reaction
as the distance of the closest approach of the annihilating particles at which their electromagnetic attraction is balanced by the gravitational repulsion of the de Sitter vacuum.
In
Section 2, we present the basic features of regular spacetimes in which the central de Sitter vacuum
evolves to the de Sitter vacuum
with
.
Section 3 outlines the Lemaître cosmological models with special attention to the model singled out by the Holographic Principle. In
Section 4, we present the dynamical features and observational signatures of regular black holes and solitons with the de Sitter vacuum interiors. In
Section 5, we overview the role of the de Sitter vacuum as providing the intrinsic relation of mass generation by the Higgs mechanism with gravity and spacetime symmetry breaking.
Section 6 contains conclusions.
2. Spacetimes with Two de Sitter Vacua
In this section we overview the general basic features of spherically symmetric spacetimes with two de Sitter vacua, in the center and at infinity, including the course of quantum evaporation of the horizons towards the stable final products with the de Sitter vacuum.
The Einstein equations contain the class of regular spherical solutions with the de Sitter center generated by source terms
able to relate the central de Sitter vacuum with other de Sitter vacua if needed and specified by [
20,
21]
A medium specified by
satisfies the
dependent equation of state [
20]
and can be identified as an anisotropic quintessence defined by two EOS parameters,
and
related to principal pressures
;
[
25] due to the symmetry of stress-energy tensors
.
If
satisfies WEC, it requires
which leads to
, the density monotonically increases towards the center where the stress-energy tensor takes the de Sitter value
,
and the spacetime symmetry restores to the de Sitter group [
30,
42] (see also [
26] and references therein).
A central singularity at appears in the Schwarzschild solution to the Einstein equations obtained for the empty space, (no matter). In a singularity, all curvature invariants diverge to infinity and all geodesics terminate. Luckily, it is confined by the event horizon, which allows for application of the Schwarzschild solution in astrophysics as describing external fields of massive spherical objects including black holes.
The early proposals on replacing a Schwarzschild singularity with the de Sitter vacuum were based on hypotheses of self-regulation of geometry by vacuum polarization effects [
43], of the existence of the limiting curvature of the Planck scale,
[
44], and of symmetry restoration to the de Sitter group at the GUT scale [
20,
45]. The key point is that in the course of a gravitational collapse, all fields evidently contribute to vacuum polarization, and hence the resulting vacuum expectation value of the stress-energy tensor transforms in gravity via the Einstein equation resulting in a vacuum polarization by the gravitational field [
20,
30]. In the case of the symmetry restoration to the de Sitter group at the GUT scale, the de Sitter vacuum appears with the density
, and the problem can be treated semi-classically. The above hypotheses on the de Sitter vacuum instead of a singularity were confirmed in the frame of the quadratic gravity [
46], “renormalization group improving” [
47], non-commutative geometry approach [
48], and an ultraviolet quantum gravity [
49,
50].
In the case of two vacuum scales, at the origin and at infinity, a stress-energy tensor evolves between two de Sitter vacua, and spacetime has not more than three horizons [
25,
51].
In the Schwarzschild coordinates, the metrics are described by [
52]
The stress-energy tensors responsible for these metrics evolve between the de Sitter vacuum with
as
and the de Sitter vacuum with
as
. The metrics (
4) tend for
to the de Sitter metric with
and for
to the Schwarzschild–de Sitter metric with
where
is the total mass, and ultimately tend to the de Sitter metric with
.
Geometry is characterized by three basic length scales
and by the parameter
q relating de Sitter vacuum scales
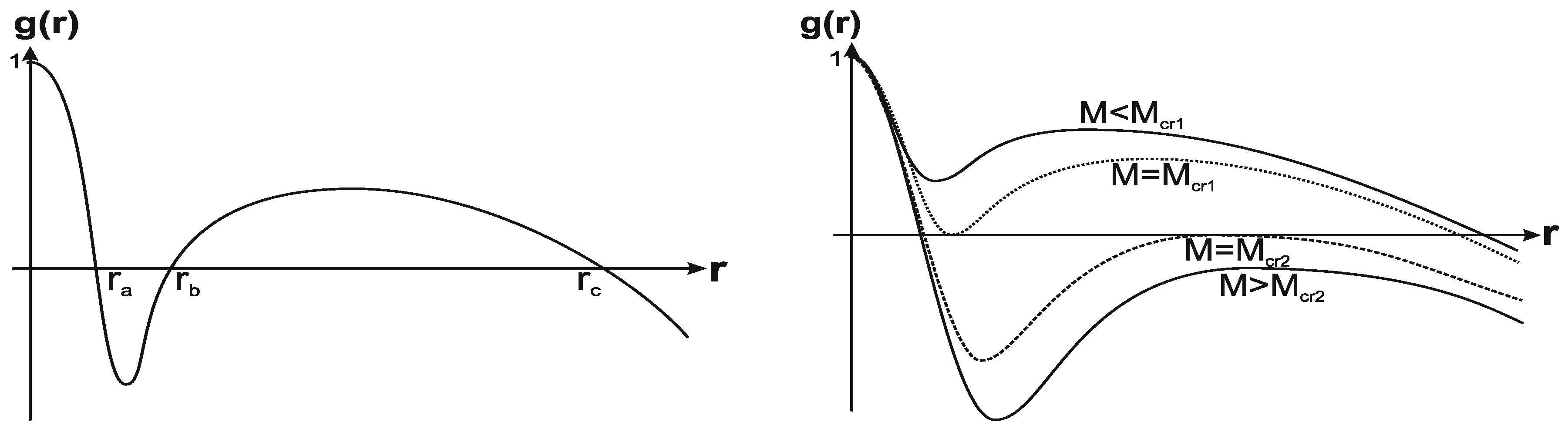
Spacetime with two vacuum scales represents the following possible configurations: a regular cosmological black hole with the mass constrained within
, confined by the event horizon
and the internal horizon
in the universe with the cosmological horizon
(
Figure 1 Left); two double-horizon states,
and
, two one-horizon states (
Figure 1 Right), two one-horizon states with the inflection point instead of the minimum (
Figure 2 Left, curves
and
), and the triple horizon state (the curve
in
Figure 2 Left) in which
. The critical masses
converge at a certain value
to
(
Figure 2 Right) [
53].
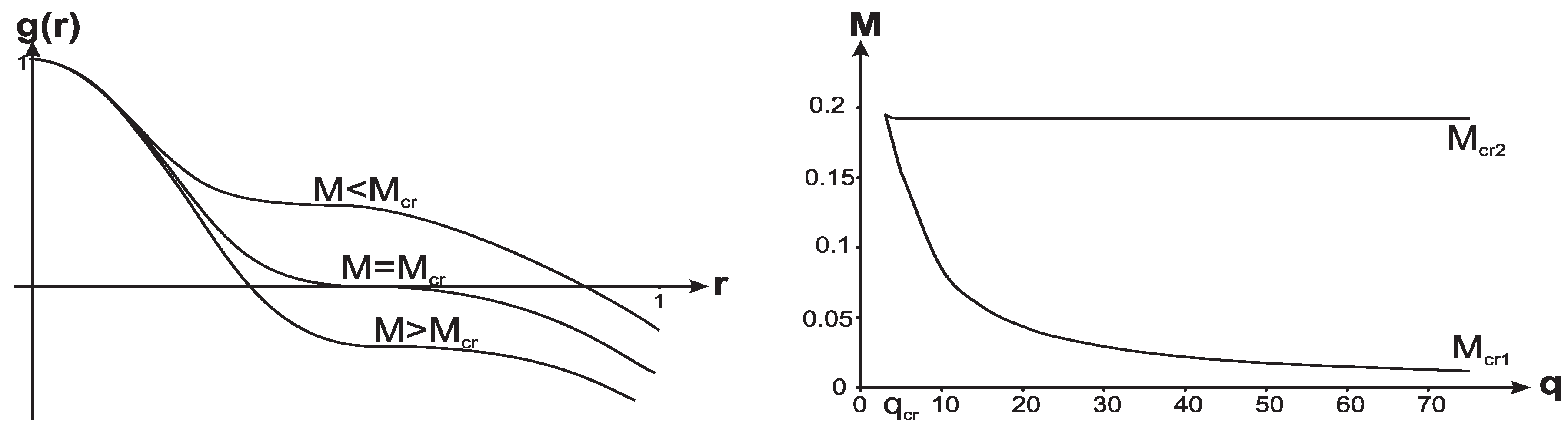
In spacetimes with the de Sitter interior there exists an additional characteristic length scale
. In thermodynamics of the horizons it appears as the scaling scale in the constraint on the form of a density profile by the course of evolution of the total mass
M dictated by the horizons evaporation [
54].
The quantum temperature and the entropy of a horizon [
55], and its specific heat [
54] are given by:
and directly relate the character and stability of a product of evaporation to the extrema of its metric function
. During quantum evaporation, the internal horizon (which is the cosmological horizon for the region
) and the cosmological horizon
move outwards by virtue of the second law of thermodynamics. Behavior of
on each of the horizons determines behavior of the mass
M and leads to its decreasing in the course of evaporation. As a result, the black hole horizon moves inwards. This imposes the constraint on the
r-dependence of the density profile which should involve the scaling
[
54] (for more details [
53]; for a review [
56,
57]). The process of the black hole evaporation is directed towards the double-horizon state,
(the curve
in
Figure 1 Right), where the temperature vanishes and specific heat is positive by virtue of (
6), hence the end-product of evaporation is the thermodynamically stable remnant generically related to vacuum dark energy via its interior de Sitter vacuum. Its mass is determined as
[
29,
54] where the coefficient
depends on the form of the density profile.
The case of
(
Figure 1 Right) presents gravitational solitons G-lumps replacing naked singularities and defined in the spirit of the Coleman lumps as non-singular non-dissipative compact objects related by their own self-interaction [
33]. Basic properties of regular black holes, their remnants and G-lumps are overviewed in
Section 4.
The spacetime with
evolves towards the double horizon state
with zero temperature and negative specific heat by virtue of (
6), which represents the thermodynamically unstable regularized version of the Nariai spacetime [
53].
The configuration with
evolves towards the triple-horizon spacetime with
(shown in
Figure 2 Left), which is absolutely thermodynamically stable due to its infinite positive specific heat according to (
6). Equations
determine uniquely
and hence
for a given value of
[
54]. This case is outlined in the next section.
Spacetime has two characteristic surfaces, the zero gravity surface
at which the strong energy condition,
is violated and the gravitational acceleration changes its sign replacing the gravitational attraction by the gravitational repulsion, and the zero curvature surface
at which the scalar curvature
R changes the sign [
29,
53]. Since both of them are ultimately defined through the density and its derivative,
and
, their explicit definitions involve scaling
.
The characteristic scale
appears explicitly in the simple semiclassical model of the vacuum polarization in the spherical gravitational field [
20]
based on the hypothesis of symmetry restoration in the course of a gravitational collapse since all fields evidently contribute to vacuum polarization, and hence to a stress-energy tensor and to gravity [
20,
29,
30]. This density profile has been applied for producing the pictures illustrating the generic dynamical behavior. In this geometry, the scale
directly defines the zero gravity surface by
and the zero curvature surface by
[
20,
29].
In the regular spherically symmetric spacetime with the de Sitter center at the background de Sitter vacuum quantum evaporation of the horizons results in two stable end-products: regular double-horizon black hole remnant with the interior de Sitter vacuum and absolutely stable triple-horizon spacetime with determined by dynamics of the horizon evaporation.
3. Cosmologies with the Relaxing Cosmological Constant
In this section, we overview the basic properties of the Lemaître cosmological models that describe evolution between an initial and final de Sitter vacuum, and distinguish the special class of models singled our by the Holographic Principle, in which quantum evaporation of the cosmological horizon determines the density of the final de Sitter vacuum.
The Lemaître class cosmological models with the different principal pressures describe in general a spatially inhomogeneous and anisotropic universe and contain the FRLW isotropic and homogeneous models as the particular cases with the equal principal pressures.
The spherically symmetric Lemaître cosmological models are described by the line element
Cosmological coordinates
are the Lagrange (comoving) coordinates. The Einstein equations in the comoving reference frame have the form [
58]
Equation (
12) yields [
58]
where
is an integration function. Putting (
13) into (
9) gives the equation of motion
For the vacuum dark energy with
, the first integration in (
14) gives
For regular cosmological models
as
and
as
. An arbitrary integration function
should be put zero. The second integration in (
14) yields
The third arbitrary integration function
is called the bang-time function [
59].
The transformation of the Schwarzschild coordinates to the cosmological coordinates
, where the Lemaître coordinate
R is introduced as the congruence parameter of the family of the radial geodesics and
is the proper time along a geodesic, is given by [
51]
where
is the integral of motion along a geodesic. The metric takes the form [
25,
51]
which shows that behavior of the Lemaître cosmological models is conditioned by the behavior of the metric function
in (
4). Comparing the metric (
18) with the metric (
8) taking into account (
13), we find
and
[
51].
For expanding models, in accordance with (
17),
, and
r is a function of
, so we can choose
[
51]. For
, the equation (
16) reduces to
For the choice
preferred by the observational data for our Universe (
), we have
, and evolution starts from the time-like regular surface
and the metric (
8) takes the FLRW form with the de Sitter scale factor
where
and
.
For the open models (, ) the evolution starts from the surface with the de Sitter initial state . For the closed models (, ), the evolution starts from the time-like surface defined by and presented by the de Sitter initial state .
For all Lemaître class models the non-singular non-simultaneous de Sitter bang is followed by the anisotropic stage with the expansion in the transversal direction,
, and shrinking in the radial direction,
until
. At this stage of highly anisotropic behavior
-decay supports a subsequent energy transfer to radiation typical for inflationary scenarios with reheating after inflation [
27,
51,
60,
61] (for a review on
decay [
28,
62]).
In the limit
, the metric (
8) reduces to the de Sitter form. For
it reads
For the density profile (
7) this occurs around
years when
starts to dominate according to the observational data [
27].
Global structure of spacetime is presented by the Penrose–Carter conformal diagrams, which represent the maximal analytic extension for solutions of Equation (
4). Diagrams are plotted in coordinates related to radial photons, which follow the null geodesics
, the light cones are oriented under the angle
. The
and
regions are defined by the sign of the gradient
,
, the sign “+” for the
regions (one-way traffic regions, light cones directed inwards for
regions and outwards for
regions), and the sign “−” for
regions (static, two-way traffic regions, each light cone directed both inwards and outwards). The sign here depends on the sign of the metric function
, since
. The global structure of the one-horizon spacetime is the same as the global structure for the de Sitter spacetime (
Figure 3 right).
Lemaître observers have to their disposal the whole manifold from the initial de Sitter bang surface to infinity.
The global structure of the double-horizon spacetimes (curves
and
in
Figure 1 Right) and possibilities for Lemaître observers are shown in
Figure 4 where the internal horizons are denoted as
, the black hole horizons as
and the cosmological horizons as
. KS observers shown in
Figure 3 Left and in
Figure 4, populate
regions of the spacetime manifold, described by the regular cosmological models of the Kantowski–Sachs type
. These are homogeneous anisotropic T-models in which evolution starts with a null bang from the Killing horizon (
in
Figure 3,
and
in
Figure 4), and pre-bang information from their past beyond the horizons is available for KS observers [
51,
63].
For spacetime with the global structure contains the infinite sequence, extended in the time direction, of two subsequent regions separated by the double horizons , and regions between the horizons and infinities.
The global structure for the case contains the infinite sequence, extended in the spacelike direction, of regions beyond the horizons , and two subsequent regions, between the horizons and the double horizons , and between and infinity.
As well as in one-horizon cases, cosmological evolution starts with the nonsingular non-simultaneous de Sitter bang from the time-like surface for (), and from the time-like surface where for ().
In both cases Lemaître observers have at their disposal the whole manifold from the past infinity of the region
to the future infinity in the region
. In the case shown in
Figure 4 Left, they can start from
in the
region, pass two
regions, arrive at the surface
, then pass two
regions and arrive at
in the region
. In the case in
Figure 4 Right, they can start from
in the region
, pass through the
region, arrive at
in the
region, then pass through the
region, and arrive at
in the region
.
The Lemaître observers have essentially more possibilities in the spacetimes with three horizons, which are presented in the next section as causally related to regular black holes [
52,
60,
64].
The triple-horizon spacetime (the curve
in
Figure 2 Left) represents the most promising class of cosmological models. According to (
6), it has the finite entropy, zero temperature and infinite positive specific heat, which makes it absolutely thermodynamically stable [
27,
65].
The triple-horizon spacetime is singled out by the Holographic Principle formulated as the requirement that the number of quantum degrees of freedom contained in a certain spatial volume is bounded from above by the surface area of this region [
66], and leading to the conjecture that a physical system can be entirely specified by the data stored on its boundary [
67]. Evaporation to the triple-horizon state is guided by the quantum dynamics of the horizon evaporation, and the basic parameters characterizing the final state are completely determined by the data stored at its boundary (the triple horizon), defined by three algebraic equations:
which determine uniquely the horizon radius
, the mass
and the parameter
which allows to determine
by choosing the density profile and the vacuum scale for
. For the
scale
GeV, and the density profile (
7) we find the value of
within the range
, which contains the observational value
[
68]. Moreover, these data are stored at the triple-horizon boundary of the universe actually forever due to its infinite scrambling time [
65], defined for a quantum system as the time needed to thermalize information [
69]. A universal bound on a scrambling time
is estimated as [
70]
where
A is a certain constant. Quantum evaporation towards the triple-horizon state
stops at
, so that the triple-horizon boundary has the infinite scrambling time and reliably stores the value of the density
for the final de Sitter vacuum [
27,
65].
The Lemaître class cosmological models with dark energy specified by describe the cosmological evolution between the initial and final de Sitter vacuum. The initial de Sitter vacuum powers the first inflation and supports the subsequent energy transfer to radiation in agreement with the standard inflationary scenarios. For the special class of the Lemaître cosmological models, the density of the final de Sitter vacuum is determined by the quantum evaporation of the cosmological horizon. For the particular model with the initial de Sitter vacuum of the GUT scale due to symmetry restoration by the gravitational vacuum polarization, the final de Sitter vacuum state is achieved around years when starts to dominate according to observations, and its value appears in agreement with the observational data.
4. Regular Black Holes and Gravitational Solitons G-Lumps with the de Sitter Vacuum Interiors
In this section we overview the basic generic properties and observational signatures of spherically and axially symmetric compact objects with the de Sitter interiors: regular black holes and gravitational solitons G-lumps, which are non-singular non-dissipative self-gravitating particle-like structures without horizons replacing naked singularities.
The global structure of spacetime with three horizons, which represent the maximal analytic extension for solutions of Equation (
4) with the metric function
shown in
Figure 1 Left, is presented by the Penrose–Carter conformal diagram displayed in
Figure 5.
Global structure contains an infinite sequence of the regular black and white holes,
and
, the regular asymptotically de Sitter regions
at
and
at
, the parallel (causally disconnected) universes
,
, and the horizons
,
,
. The surfaces
and
are the null surfaces (
) ([
51] and references therein). The sequence of these structures is extended in both time (upwards in the diagram) and space directions. Any observer on a time-like curve (including Lemaître observers of the previous section) can start in some universes
and travel towards the future regions of the manifold presented by this Penrose–Carter diagram ([
34] and references therein).
Existence of the de Sitter vacuum in the interior regions of regular black holes provides an opportunity of appearance of baby universes inside a black hole. The question of arising a new universe inside a black hole was considered in 1989 in [
71] on the basis of the hypothesis on the existence of the limiting curvature at the Planck scale with adopting the equation of state for the de Sitter vacuum,
. Analysis of a smooth de Sitter–Schwarzschild transition with arising of a closed world in the future of the original universe has been presented in [
44].
The model for arising a baby universe inside a black hole was proposed in 1990 starting from a little false vacuum bubble in the Minkowski space evolving, via quantum tunneling, into the larger bubble with formation of a black hole and further classical evolution of the vacuum bubble to a new universe beyond the black hole horizon [
72].
The question of a quantum birth of new universes inside a regular black hole with the de Sitter interior due to quantum instabilities of the de Sitter vacuum has been considered in [
60] for the closed, open and flat universes. The case of arising of a closed universe is shown in
Figure 6 Left [
60], and for open universes in
Figure 6 Right [
60,
73]. The picture in
Figure 6 Left is plotted for the asymptotically flat spacetime (
), but the situation with arising closed baby universes is similar for the spacetime with two vacuum scales and three horizons shown in
Figure 5.
In
Figure 6 Right, the region
corresponds to the region
in
Figure 5 and the region
corresponds to a part of the region
. The events
E and
in
Figure 6 Right are creations of the causally disconnected universes. The curved lines are the world lines of co-moving observers. At the spacelike surface
, the phase transition occurs from the inflationary to the radiation dominated stage [
73]. Multiple births of universes from the initial de Sitter vacuum have been noted still in 1975 in [
9]. In the spacetime with the global structure
Figure 5, the birth of open and flat baby universes can occur in any of an infinite numbers of the
regions inside a black hole, and looks like what is shown in
Figure 6 Right. In [
64] we presented a review of the literature on baby universes, and estimations of the probability of baby universes arising in the future of a regular black hole with the de Sitter vacuum interior in some of its
regions.
Information about the interior de Sitter vacuum in a regular black hole can be extracted from the rotating black hole shadows due to the asymmetry of a shadow dependent on the black hole angular momentum. The shadow of a black hole presents its direct image over an image of a bright distance source of radiation. The shadow is formed by the photon gravitational capture cross-section confined by the innermost unstable photon orbits ([
74,
75] and references therein). Current observational possibilities are provided by the Event Horizon Telescope Collaboration [
76] verified by the first observation of the black hole shadow in M 87 [
77].
Regular rotating black holes with the de Sitter vacuum interiors are described by the de Sitter–Kerr geometries [
78] with the metrics of the Kerr–Schild class [
79] obtained from the spherical metrics (
4) by the general Gürses-Gürsey formalism [
80], which includes the Newman–Janis complex translation [
81] typically applied for construction of particular solutions. In the Boyer–Lindquist coordinates, the Gürses-Gürsey metric reads (in the units
) [
80]
where
a is the angular momentum, the Lorentz signature is [- + + +],
,
, and
. The surfaces of constant
r are the oblate confocal ellipsoids
, which degenerate, for
, to the equatorial disk
bounded by the ring
[
74]. The disk (
25) is filled with the rotating de Sitter vacuum, which is the basic generic feature of all regular rotating objects specified by (
2) and described by the metrics (
24) (for a review [
82]).
The shape of the shadow of a regular rotating black hole depends on the interior density: the gravitational capture cross section is less than that for the Kerr black hole, and the difference depends essentially on the form of the density profile [
32]. Comparison of a regular black hole shadow with the observed shadow and with the shadow of the Kerr black hole of the same mass can provide information about the interior content of a regular black hole (for a detailed analysis and a review [
32]).
The comparative analysis for two particular regular black holes, with the density profile (
7) and with the phenomenologically regularized Newtonian profile [
83] reveals also the essential dependence of their shadows on the pace of density decreasing [
32].
The regularized Newtonian profile is given by [
83]
where
is the density of the de Sitter vacuum on the disk
and
.
The cutoff length scale
in Equation (
26) is proportional to the de Sitter radius
. The parameter
B is directly related to
:
, where
is the density at
, which represents the energy density of self-interaction [
78,
83], in accordance with the Zel’dovich idea [
84] to associate the cosmological constant with self-interaction energy.
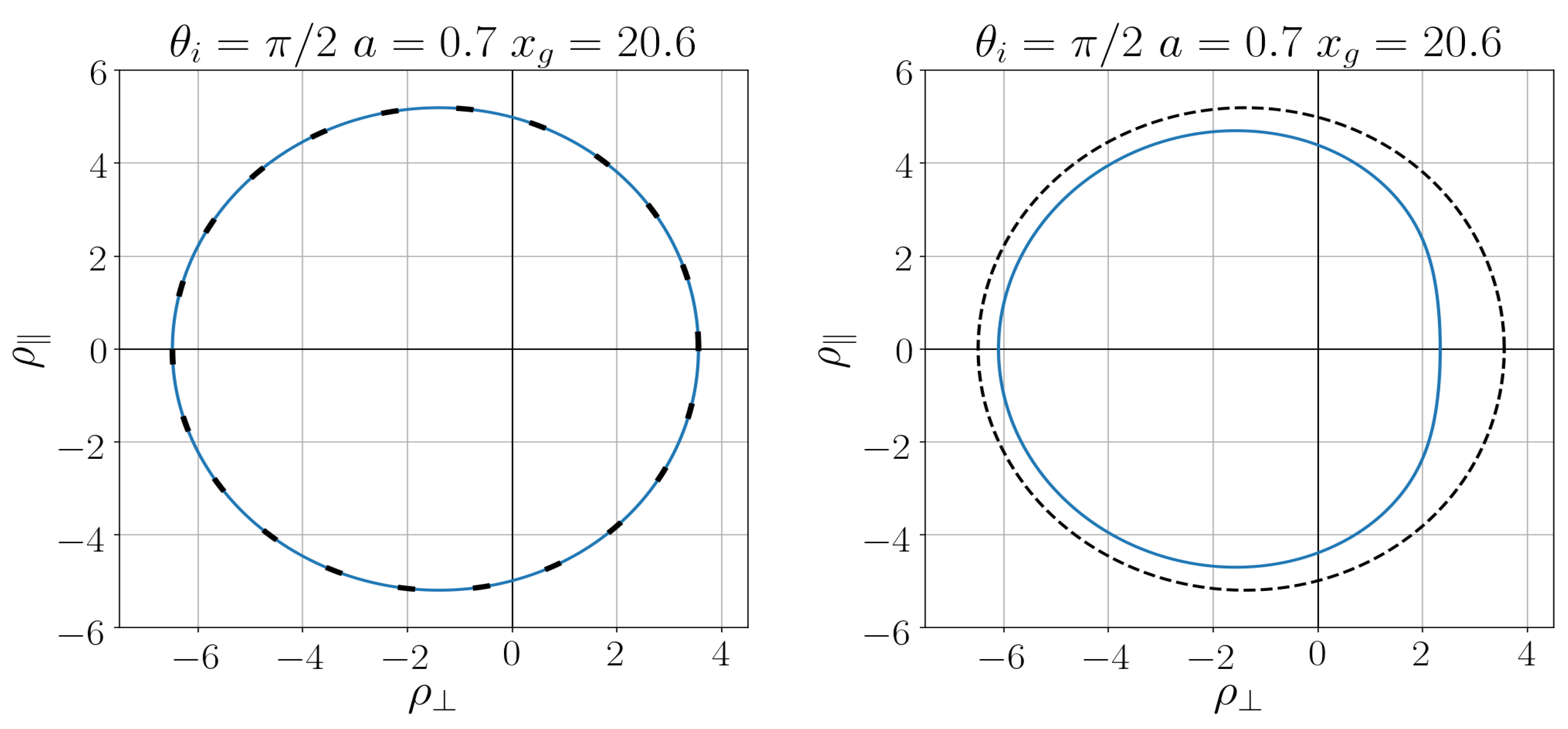
In
Figure 7 [
32] we show the comparison of the regular black shadow with that for the Kerr black hole for both density profiles (
7) and (
26).
For a black hole with slowly decreasing density (
26), the difference of its shadow from the Kerr shadow is much more substantial than for a quickly decreasing density (
7), which testifies for the essential dependence of shadows on the pace of the density decreasing [
32].
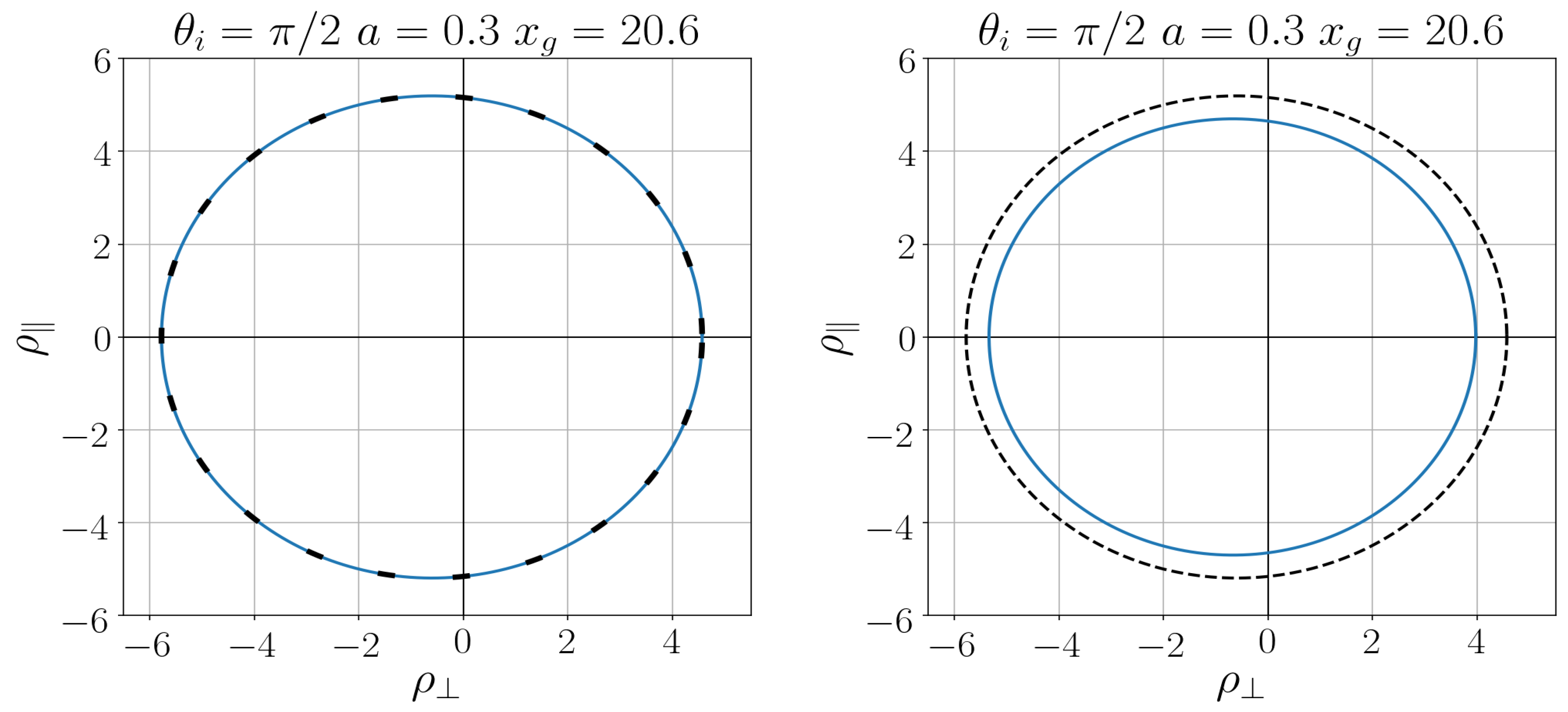
As follows from detailed numerical analysis, differences related to spin parameter
a are less essential than those related to the pace of the density decreasing, as we can see in
Figure 8 [
32].
Restoring the density profile of a black hole from its observed shadow can give information about the character of its interior.
Another way to reveal an interior de Sitter vacuum is provided by specific observational signatures of regular black hole (RBH) remnants and gravitational solitons G-lumps in their contribution to heavy dark matter candidates [
22,
85,
86] (for a review [
34]).
The general criteria for RBHs stability to external perturbations (valid for a wide class of the density profiles) have been presented for regular black holes in [
87] and for G-lumps in [
22].
The question of primordial black holes and their remnants as heavy DM candidates has been discussed in the literature for more than thirty five years [
88,
89,
90]. In the case of regular compact objects this list should be completed by G-lumps replacing naked singularities.
Regular primordial black holes and G-lumps with the de Sitter vacuum interiors are formed at the early inflationary stage(s) by the quantum collapse of density fluctuations related to primordial inhomogeneities [
91]. Their observational signatures as heavy DM candidates can therefore serve as the signatures for inhomogeneity of the early universe [
86]. Primordial RBH remnants and G-lumps can form graviatoms-gravitationally bound (
) quantum systems, by capturing available charged particles ([
34,
91] and references therein).
Observational signatures of RBH remnants, G-lumps and graviatoms provide information about the scale of the interior de Sitter vacuum. Regular objects with the GUT scale interiors [
20,
45], where baryon and lepton numbers are not conserved, may induce a proton decay in the matter of an underground detector. The rough estimate of the cross-section by the geometrical size of a nucleon would lead to one event per
years in one ton of a detector matter. In the 1 km
detector, like IceCUBE, there could be expected up to 300 events per year [
86], which can be an observational signature in heavy DM searches in the IceCUBE experiment [
86].
An additional observational signature for graviatoms is provided by their electromagnetic radiation with the characteristic frequency essentially depending on the scale of the interior de Sitter vacuum. Most promising is the oscillatory radiation [
91]. For the density profile (
7) the energy
appears within the range of observational possibilities (for cosmic photons up to
GeV [
92]).
Global structure of spacetime of a regular black hole contains an infinite sequence of universes, white and black holes and the interior regions of the de Sitter vacuum which provide a possibility for the birth of baby universes in the future of black holes. A regular rotating black hole can be identified by comparison of its shadow with the observed black hole shadow, which yields information about its interior content and allows one to decide whether it contains a singularity or the de Sitter vacuum. Interior de Sitter vacuum of RBH remnants and G-lumps can be identified by their observational signatures as heavy DM candidates.
5. De Sitter Vacuum in Particle Physics
In this section, we overview the intrinsic relation of the Higgs mechanism with gravity and spacetime symmetry ensured by the de Sitter vacuum incorporated in the Higgs mechanism as its basic ingredient (a false vacuum with ).
In the Higgs mechanism, particles acquire masses via spontaneous symmetry breaking of scalar field(s) from a symmetric false vacuum state (
) [
93,
94,
95]. The de Sitter vacuum involved in this process generates in the region of interaction the de Sitter geometry, so that gravity and hence spacetime are undoubtedly intrinsically involved in the mass generation (for a recent review including the existing in the literature proposals concerning the relation of mass with gravity and with spacetime symmetry [
36]).
A particle equipped with mass propagates further in an observer space with the Minkowski geometry, hence also breaking of spacetime symmetry from the de Sitter group to the Poincaré group is intrinsically incorporated in the mass generation by the Higgs mechanism [
36].
Below we outline the observational case that displays and verifies this fact. It is referred to as “the negative mass square problem” for neutrino. The value given by the Particle Data Group in 1994 [
96]
was later confirmed by observations at the level around
[
97] (for a review [
36]).
In particle physics theory there is no exact gauge symmetry to protect the lepton number, so it is expected to be violated and neutrinos to acquire masses, eventually due to mixing the non-degenerate mass eigenstates at the gravito-electroweak scale
GeV [
98,
99].
The de Sitter symmetry group induced by the Higgs mechanism in the gravito-electroweak vertex requires the description of a particle state in the vertex by the eigenstates of the Casimir invariant
of the Casimir operator
in the de Sitter spacetime. To study the behavior of mass in transition from the de Sitter group in the interaction vertex to the Poincaré group in the observer region, we concentrate on the behavior of
, which is defined as [
100]
where
and
;
take the values
. In the interaction region
([
37], justification below), and the operator
is approximated by
The generators of rotations
and generators of the Lorentz boosts
are given by [
101]
for the right-handed and left-handed fields, respectively;
denotes the Pauli matrices.
This gives for the Casimir operator
and its eigenvalues
[
38]
The additional term related to the eigenvalues of the product of the Pauli matrices (which is the unit matrix) appears due to the change in the spacetime symmetry.
The state
appears as a linear superposition of two different mass eigenstates
with equal weights. The de Sitter symmetry in the gravito-electroweak vertex produces an exact bi-maximal mixing for neutrinos. For
,
becomes negative, which testifies that arising of “negative mass square” follows directly from the essential involvement of the de Sitter vacuum in the gravito-electroweak vertex [
37,
38].
The de Sitter radius
is related to the density of the de Sitter vacuum
as
, and the mass-squared difference is given by [
38]
Relating
to the gravito-electroweak scale
, we get the relation between the mass square difference and the unification scale [
37]
This allows to read off the gravito-electroweak scale from the known observational data on mass square differences for the atmospheric and solar neutrino obtained in the two-flavor mixing approximation
[
99], which gives ([
37] and references therein)
The mass square differences for neutrinos provided by the de Sitter mixing, Equation (
31), give for these observational data the value for
at the same scale as predicted by theories of gravito-electroweak unification ([
36] and references therein).
Our aim in [
37,
38] was to find the reason for the appearance of the negative mass squares for neutrino and then to apply the results for evaluation of the gravito-electroweak scale from the observational data. The reason was found without any assumptions or approximations as provided by the intrinsic involvement of the de Sitter symmetry in the interaction vertex.
The evaluation of the gravito-electroweak scale was given with the approximation Equation (
28). Now let us estimate the accuracy of this approximation. The de Sitter spacetime is characterized by the constant non-zero curvature, while the Minkowski geometry is the case of zero curvature, which corresponds to
. The transition from the de Sitter symmetry in the interaction vertex to the Minkowski symmetry in the observer region in general occurs continuously. The characteristic length scale for the de Sitter geometry is
related to the de Sitter vacuum density as
. The density
is related to the gravito-electroweak unification scale as
, where the scale
is directly related to the observational data by Equation (
33). The data on the atmospheric and solar neutrino give the scales (
34) for
which ultimately give
cm, and
cm. For neutrino with the mass
eV, its Compton wavelength is
cm. The relation
estimates the accuracy of approximation
in Equation (
28) as
for
obtained with the data on the atmospheric neutrino, and
for
obtained with the data on the solar neutrino. With this accuracy, the scales (
34) appear in agreement with the scales predicted by theories of gravito-electroweak unification.
Another observational case directly related to participation of the de Sitter vacuum in mass generation, is the appearance of a minimal length scale
= 1.57
cm in the annihilation reaction
at the energy E = 1.253 TeV with the
significance [
41]. Experiments have been carried out from 1989 to 2003 with the data from VENUS, TOPAZ, ALEPH, DELPHI, L3 and OPAL at the center-of-mass energies from
= 55 GeV to 207 GeV. Working out the data in the QED-
with a scattering center as a point and the radiative corrections up to
predicted an increase in the total cross-section, but the
fit, shown in
Figure 9, displayed the minimum with the negative fit parameter
, where
here is the QED cutoff parameter ([
41] and references therein).
Contradiction of the results of experiments with the QED predictions displays a non-point-like behavior of particles and suggests an extended particle approach in a situation when its characteristic size exceeds the test distances. In the case of the electron, both its classical radius cm and the Compton size cm are much larger than the characteristic length .
In the models of the extended electron, constructed for more than a hundred years since its discovery by Sir Joseph John Thomson in 1897, just these two sizes have been typically imposed. The early models concentrated on the problem of preventing an electron from flying apart by the Coulomb repulsion, which resulted in understanding the necessity to introduce
cohesive forces of non-electromagnetic origin (the Poincaré stress) [
102] (for a review [
41]).
In the Einstein–Maxwell equations with the linear electrodynamics, electrically charged spinning objects are described by the Kerr–Newman solution presented in 1965 and corresponding to
in (
24), with the associated electromagnetic potential
[
103]. As was discovered by Carter in 1968 [
104], the angular momentum
, and an asymptotic magnetic momentum
yield the same gyromagnetic ratio
as predicted by the Dirac equation for a spinning particle, however the Kerr–Newman solution cannot describe an electron due to the global causality violation involving the region of a distant observer in the relevant case of the absence of the event horizon [
104].
Since then, construction of the extended electron models was carried out by matching the Kerr–Newman metric outside with some model of an interior source inside. Contemporary comprehensive models comprise a lepton Bag model in which the external Kerr–Newman solution is matched to the free of gravity (flat) superconducting interior by the domain wall boundary interpolating between them ([
105,
106] and references therein), and the models focused on the significant role of the electron spin [
107,
108] (for a recent review [
36]).
The annihilation reaction
is the purely electromagnetic reaction, proceeding with the exchange of a virtual electron in the
t and
u channels and forbidden
s channel. It can be, in principle, approached by applying as a model an electromagnetic spinning soliton related by electromagnetic and gravitational interactions and described by nonlinear electrodynamics coupled to gravity (NED-GR). The more that introducing nonlinear electrodynamics by Born and Infeld was originally motivated by the aim to describe the electron and electromagnetic field in the frame of one physical entity (electromagnetic field) and to avoid divergences of physical quantities [
109]. This was performed by imposing an upper cutoff on the electric field related to the electron radius, nevertheless the geometry remained singular [
109].
In NED-GR, this aim can be achieved in full and in a self-consistent way. The regular objects are described by source-free dynamical equations for electromagnetic fields, while the gravitational field is determined from the Einstein equations with stress-energy tensors for their own electromagnetic fields, which belong to the class .
Their inherent part is the interior de Sitter vacuum, able to prevent a formation of singularities (and thus to avoid divergences) by its intrinsic negative pressure [
31]. The de Sitter vacuum fills an equatorial disk (
25) [
31,
110] (for a review [
82,
111]). The metric (
24) on the disk is intrinsically flat but the density achieves the maximum presented by the de Sitter vacuum, so that gravity is not only essential but its intensity is maximal [
31]. For
the metric (
24) approaches the Kerr–Newman asymptotic form with the gyromagnetic relation
appropriate for a spinning particle.
The interior equatorial disk (
25) of the de Sitter vacuum has properties of a perfect conductor and ideal diamagnetic [
31] and is confined by the superconducting ring current, which serves as a non-dissipative source of the electromagnetic fields of an NED-GR spinning object responsible for its unlimited life time [
112], and as the source of its intrinsic magnetic momentum [
113]. For the electron modeled by the electromagnetic soliton its known magnetic momentum gives the value of its superconducting ring current
[
113].
Masses of NED-GR objects are generically related to the interior de Sitter vacuum, and breaking of spacetime symmetry from the de Sitter group in the origin to the Poincaré group at infinity in the asymptotically flat spacetime (
24) (for more information a review [
26]).
Basic model-independent features of an electromagnetic soliton visualizing the electron as an extended particle, can shed some light on the physical mechanism responsible for a minimal length scale in the annihilation reaction
[
41]. A characteristic de Sitter cutoff
on electromagnetic self-energy can be roughly estimated by
[
83]. Adopting for the interior de Sitter vacuum the electroweak scale
GeV related to the electron mass, we obtain the de Sitter radius
cm. It gives for the characteristic length scale at which electromagnetic attraction is balanced by de Sitter gravitational repulsion,
cm, close enough to the minimal length scale
.
More detailed analysis [
41] gives additional information about the origin of the minimal length scale
. At a certain stage of the annihilation process, the interaction region is obviously neutral and spinless, and can be modeled by a spherical lump with the de Sitter vacuum interior, asymptotically Schwarzschild as
. For all such structures there exists the characteristic zero gravity surface
, at which the strong energy condition (
) is violated and beyond which the gravitational acceleration becomes repulsive [
21,
29]. For a lump with the energy
TeV, the radius of zero gravity surface is
cm, and the scale
cm appears inside a region of the repulsive gravity. The minimal length
can be interpreted as a distance of the closest approach of annihilating particles at which the effect of gravitational repulsion of the interior de Sitter vacuum becomes crucial.
This observational case promotes the extended massive particle approach, essential at the distances smaller then a particle size, while for the distances substantially exceeding its size, the point-like idealization evidently works.
The de Sitter vacuum is incorporated in the Higgs mechanism as its false vacuum state, which leads to incorporation of gravity and breaking of spacetime symmetry in mass generation. Applying the Casimir operators in the de Sitter space for description of particle states in the interaction vertex allows to explain the negative mass square problem for neutrino and to evaluate the gravito-electroweak scale from the atmospheric and solar neutrino data in agreement with the predictions of gravito-electroweak theories. The NED-GR equations predict, for an arbitrary gauge invariant lagrangian without additional requirements except WEC, the existence of electrically charged spinning solitons, with the gyromagnetic ratio for a distant observer. Their inherent part is the interior de Sitter vacuum, which allows to explain the appearance of the minimal length scale in the annihilation reaction .
6. Conclusions
Repulsive gravity of the de Sitter vacuum () provides the reason for the universe expansion, powers the first inflationary stage and supports the present accelerated expansion of our universe due to the basic properties of the de Sitter geometry independent on the choice of an underlying particular model for . The de Sitter vacuum keeps the position of the best candidate for a dark energy since 1995, the various models of a dark energy specified by with , give in confrontation with observations of the value . The contribution of the de Sitter vacuum to the universe density approaches 75%, which allows to consider it as its basic ingredient.
The Einstein equations admit the class of spherically symmetric and axially symmetric regular solutions with the source terms specified by () which describe, dependently on the choice of a coordinate mapping, cosmological evolution between an initial and final de Sitter vacua and regular compact objects with the de Sitter vacuum interiors: the regular black holes and gravitational solitons G-lumps replacing naked singularities.
Cosmological evolution between two de Sitter vacua, initial and present, is described in the frame of one theoretical scheme by the Lemaître class regular cosmological models. For the special class of the Lemaître models, absolutely thermodynamically stable and distinguished by the Holographic Principle, spacetime symmetry provides a mechanism for relaxing a cosmological constant to a tightly fixed non-zero value for the density of the final de Sitter vacuum.
The observational signatures of regular black holes (presented by shadows of rotating black holes), as well as of their remnants and G-lumps as heavy dark matter coordinates, can in principle give information about the scale of their interior de Sitter vacuum.
For all these objects mass is generically related to the interior de Sitter vacuum and breaking of spacetime symmetry from the de Sitter group in the origin.
De Sitter vacuum as the basic ingredient of the Higgs mechanism (the false vacuum with ), provides the intrinsic relation of the mass generation with gravity and spacetime symmetry breaking. It generates the de Sitter geometry in the region of its involvement and leads to dynamical participation of gravity in the region of interaction. Gravity of the de Sitter vacuum leads to the bi-maximal neutrino mixing in the interaction vertex, which explains the data on the mass square differences for neutrino and allows to evaluate from these data the gravito-electroweak scale in agreement with the theories of the gravito-electroweak unification.
Nonlinear electrodynamics coupled to gravity stress-energy tensors of electromagnetic fields have the algebraic structure such that . As a result, all regular electrically charged spinning objects with positive density have an interior de Sitter vacuum and mass related to gravity and spacetime symmetry breaking. This is displayed in the appearance of the minimal length scale in the annihilation reaction . The QED predictions with the radiative corrections up to contradict the results of experiments, which suggest an extended particle approach in a situation when its characteristic size exceeds the test distances. Application of the electromagnetic spinning solitons allows to interpret the minimal length as the distance of the closest approach of annihilating particles at which their electromagnetic attraction is effectively balanced by the gravitational repulsion of their interior de Sitter vacuum.