Excess of Soft Dielectrons and Photons

Abstract

Spectra of unbound electron–positron pairs (dielectrons, in brief) and photons from decays of parapositronia produced in ultraperipheral collisions of electrically charged objects are calculated. Their shapes at energies of the NICA collider are demonstrated. Soft dielectrons and photons are abundantly produced. The relevance of these processes to the astrophysical problem of cooling electron–positron pairs and the intense emission of 511 keV photons from the Galactic center is discussed.

Excess of soft dileptons and photons over their supply from all well established sources is a widely known fact in particle physics and in astrophysics. It is reasonable to assume that electromagnetic fields are responsible for this effect. The outcome of a collision of two charged objects is especially soft if they do not come too close to one another but pass at large distances (impact parameters) and only their electromagnetic fields interact. These processes were named ultraperipheral because of the large spatial extension of electromagnetic forces. It is shown here that very soft dielectrons and photons are produced in these grazing collisions.

Electromagnetic interactions of rapidly moving charged objects were first considered by Fermi [1,2] in 1924. He derived the formula for the intensity of the electromagnetic field created in such processes. This field can be treated in terms of equivalent photons as was done by Weizsäcker [3] and Williams [4] in 1934. The same year, Landau and Lifshitz [5] published their result on the energy dependence of the cross section of dielectrons production in high energy cosmic rays ions collisions. This is still the most rapidly increasing (with energy increase) cross section known in particle physics. Asymptotically, it is proportional to ${ln}^3\gamma$, where $\gamma =E_c/M_c$ is the Lorentz-factor, $E_c$ and $M_c$ are the energy and the mass of a colliding particle. The two-photon collisions in electromagnetic fields create soft dileptons and $CP$-even resonances (see, e.g., [6,7,8,9,10,11,12,13,14,15,16,17,18]). These processes have been recorded in collider experiments. Further progress in measurements of ever softer products is required. The ultraperipheral processes can be responsible for the recorded excess of soft dileptons in accelerator experiments as well as for the rapid cooling of the electron–positron clouds in the Universe and for the famous excess of 511 keV photons emitted from the Galactic center.

The spectra of dielectrons and photons created in ultraperipheral collisions can be obtained from the general expression for the total cross section

$${\sigma }_{up}\left(X\right)=\int d{x}_{1}d{x}_2\frac{dn}{d{x}_1}\frac{dn}{d{x}_2}{\sigma }_{\gamma \gamma }\left(X\right),$$

(1)

derived in the equivalent photon approximation. Feynman diagrams of ultraperipheral processes contain the subgraphs of two-photon interactions leading to production of some final states X (e.g., $e^{+}{e}^{-}$ pairs). These blobs can be represented by the cross sections of these processes. Therefore, ${\sigma }_{\gamma \gamma }\left(X\right)$ in (1) denotes the total cross section of interaction of two photons from the electromagnetic clouds surrounding colliding objects and $dn/d{x}_i$ describe the density of photons carrying the share $x_i$ of the energy of the objects.

In what follows, we examine the collisions of heavy Au ${}^{79+}$-ions at the NICA collider. The photon fluxes $dn/d{x}_i$ are calculated from the flux of electromagnetic fields surrounding the colliding ions. They are shown in many textbooks on quantum electrodynamics. The distribution of equivalent photons generated by a moving nucleus with the charge $Ze$ and carrying a fraction of the nucleon energy x integrated over the transverse momentum up to some value (see, e.g., [19]) can be denoted as

$$\frac{dn}{dx}=\frac{2Z^2\alpha }{\pi x}ln\frac{u\left(Z\right)}{x}.$$

(2)

Soft photons carrying small fractions x of the nucleon energy dominate in these fluxes. The physical meaning of the ultraperipherality parameter $u\left(Z\right)$ is the ratio of the maximum adoptable transverse momentum to the nucleon mass as the only massless parameter of the problem. It differs numerically in various approaches [6,7,8,9,10,11,12,13,14,15,16,17,18]. It depends on charges $Z_{i}e$, sizes and impact parameters of colliding objects (form factors and absorptive factors) as well as, in principle, on the considered processes.

The cross section ${\sigma }_{\gamma \gamma }\left(X\right)$ to be inserted in (1) in case of creation of the unbound dielectrons X looks [19,20] as

$${\sigma }_{\gamma \gamma }\left(X\right)=\frac{2\pi {\alpha }^2}{M^2}[(3-z^4)ln\frac{1+z}{1-z}-2z(2-z^2)],$$

(3)

where $z=\sqrt{1-\frac{4m^2}{M^2}}$, m is the electron mass and M is the dielectron mass. This cross section tends to 0 at the threshold $M=2m$ and decreases as $\frac{1}{M^2}lnM$ at very large M.

The distribution of masses M of dielectrons is obtained after inserting Equations (2) and (3) into Equation (1) and leaving free one integration there. One gets

$$\frac{d\sigma }{dM}=\frac{128{(Z\alpha )}^4}{3\pi M^3}[(1+\frac{4m^2}{M^2}-\frac{8m^4}{M^4})ln\frac{1+\sqrt{1-\frac{4m^2}{M^2}}}{1-\sqrt{1-\frac{4m^2}{M^2}}}-(1+\frac{4m^2}{M^2})\sqrt{1-\frac{4m^2}{M^2}}]{ln}^3\frac{u\sqrt{s_{nn}}}{M},$$

(4)

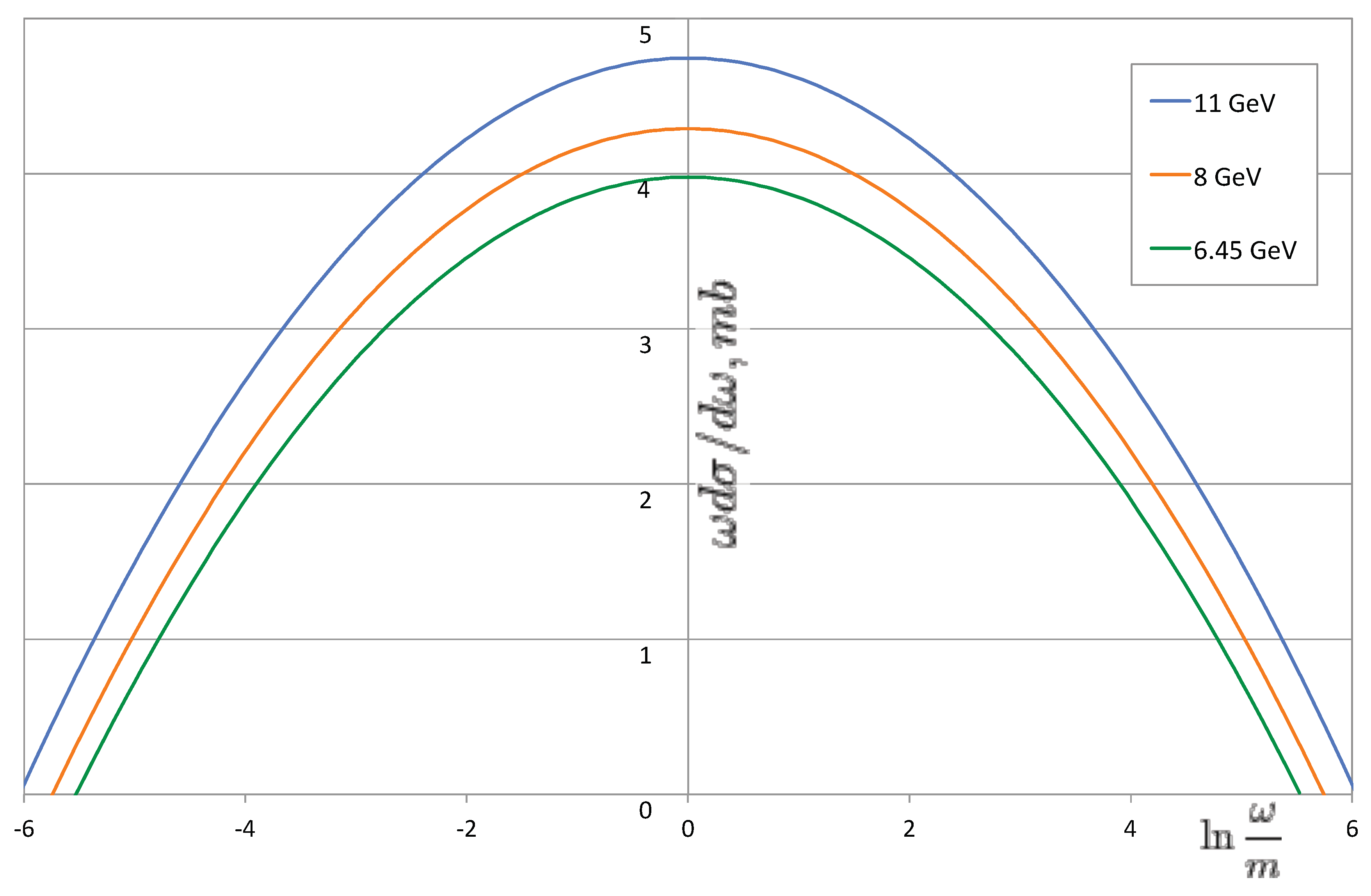
where $\sqrt{s_{nn}}$ is the c.m.s. energy per a nucleon pair. The dielectron distribution (4) is shown in Figure 1 for three NICA energies ranging from 11 to 8 GeV and 6.45 GeV per nucleon. The parameter u = 0.02 has been chosen in accordance with its value obtained in [8], where careful treatment of nuclei form factors is done. The total cross section of ultraperipheral production of unbound pairs is

$$\sigma (ZZ(\gamma \gamma )\to ZZ{e}^{+}{e}^{-})=\frac{28}{27}\frac{Z^4{\alpha }^4}{\pi m^2}{ln}^3\frac{u^2{s}_{nn}}{4m^2}.$$

(5)

The sharp peak at very low masses M in Figure 1 demonstrates the most important feature of ultraperipheral processes—the abundant production of soft dielectrons with masses of the order of several electron masses $m=0.511$ MeV (effectively, less than 50 MeV). Their direct registration is a major problem in accelerator experiments as shown in a recent paper of ALICE Collaboration at LHC on observed soft-dielectron excess in proton-proton collisions at $\sqrt{s}$ = 13 TeV [21]. Unfortunately, the dielectrons with masses less than 150 MeV were inaccessible there for recording. However, recording dielectrons with masses down to this limit marks substantial progress relative to the previosly achieved lower limit, which was several times higher. Special adjustment of the magnetic fields at LHC was required to get this value. As can be seen in Figure 1, the limit of 150 MeV is still well above the masses in the area of abundant ultraperipheral production of dielectrons.

Surely, the excess of dielectrons might be recorded at NICA energies, but some special experimental technique is needed. The spectrum of dielectrons created per 1 GeV interval shown in Figure 1 is extremely soft. The experimental challenge of dielectron measurements is the high combinatorial background, as well. The background from all other nuclear sources including thermal radiation and freeze-out cocktail is negligibly small compared to the contribution of ultraperipheral processes at low masses shown in Figure 1. That is easily seen if Figure 1 is matched with the left panel in Figure 17 of [22], which depicts a dielectron invariant mass spectrum $dN/dM$ simulated for central Au + Au collisions at $\sqrt{s_{nn}}$ = 6.45 GeV [23]. For comparison of the ordinates, the values of $d\sigma /dM$ in Figure 1 must be normalized to the total cross section about 5 kb at 6.45 GeV. The extremely strong excess of dielectrons with masses below 10 MeV is predicted.

Some slight excess of positrons can appear in the observed state of dileptons due to the so-called bound-free process when the created electron is captured by one of the colliding nuclei. This effect can limit the luminosity and lead to some damage of the collider. Its cross section was recently estimated at NICA energies in [24]. It is much smaller than that for unbound pairs. Therefore, this effect does not change our conclusions.

The NICA energy interval also permits the ultraperipheral production of positronia and ${\pi }^0$-mesons. Creation of parapositronia is especially interesting because their decay products at rest are two gamma-quanta with energies about 511 keV. For ${\pi }^0$’s, this energy is 67.5 MeV. Their recording requires a different technique and looks somewhat simpler than in the case of dielectrons. The origin of the strong line at 511 keV emitted from the Galactic center has not been explained yet [25]. Studies at NICA collider can help in resolving this puzzle.

The total cross section of the direct production of parapositronia in two-photon interactions (6) is much lower than the cross section for creation of unbound pairs (5):

$${\sigma }_{Ps}=\frac{16Z^4{\alpha }^2\Gamma }{3m^3}{ln}^3\frac{u\sqrt{s_{nn}}}{m}.$$

(6)

However, the final products differ. One must record the gamma-quanta instead of electrons. Their energy distribution is obtained from Equation (1) by omitting one of the integrations there and inserting the resonance cross section for ${\sigma }_{\gamma \gamma }(X)$ (see, e.g., [6]). For Au–Au collisions at NICA one gets

$$\omega \frac{d\sigma }{d\omega }=\frac{4Z^4{\alpha }^2\Gamma }{m^3}({ln}^2\frac{u\sqrt{s_{nn}}}{m}-{ln}^2\frac{\omega }{m}),$$

(7)

where $\Gamma \approx 5.2·{10}^{-15}$ GeV is the decay width of the parapositronium.

This distribution (7) is shown in Figure 2 as $\omega d\sigma /d\omega$ for three energies of NICA ranging from 11 to 8 GeV and 6.45 GeV per nucleon. Again, the parameter u = 0.02 is chosen in accordance with its value obtained in [8].

As expected, the photon spectra are concentrated near the electron mass 511 keV and they are rather wide. The motion of parapositronia produced in ultraperipheral collisions at high enough energies of NICA is responsible for the broadened spectra in Figure 2. In general, the direct ultraperipheral production of parapositronia is about a million times less effective than the creation of dielectrons as estimated from Equations (5) and (6).

The estimates done above in the equivalent photon approximation are, strictly speaking, valid at very high energies. The preasymptotical corrections can become important at NICA energies (see, e.g., [6,24]) and ask for different values of the ultraperipherality parameter u. On the other hand, its application at low lepton masses (electrons!) is also questionable. Nevertheless, the qualitative feature of soft outcome in these processes is well established.

Coming now to geophysics, it is worthwhile to remark that the 511 keV photons from the parapositronia clouds have been recorded [26] during the thunderstorms in the Earth atmosphere. Strong electromagnetic fields there favor somehow the creation of parapositronia at rest. Regarding the astrophysical observation of a narrow line at 511 ± 2.2 keV stemming from the Galactic center, it would be reasonable to assume that this line originates from decays of very slow parapositronia. Huge clouds of them formed during "the Galactic thunderstorms" must exist in the Galactic center to emit this strong and narrow line. The initially created soft dielectrons can be in charge of their formation. Different astrophysical objects are claimed to produce the dense clouds of the electron-positron plasma. Besides, some microscopic mechanism of soft dielectron production active inside the objects must be at the origin of these parapositronia in the Universe.

The process of ultraperipheral production of dielectrons by the electromagnetic fields of moving charged particles is a good candidate for providing extremely soft dielectrons as shown above. It is especially intense in collisions of the relativistic heavy ions. Here, the cross sections are proportional to the factor $Z^4{\alpha }^4$ (i.e., enlarged by $Z^4$ compared to the singly charged particles) and strongly increase with increasing energy as ${ln}^3\gamma$. However, their values are still large enough even for protons with lower energies because of the smaller ultraperipherality parameter. As shown in Figure 1, the masses of produced dielectrons are very small. It means that the relative velocities of electrons and positrons are not high. Dielectrons, produced initially by this process, would further cool down, e.g., by bremsstrahlung or again due to mutual ultraperipheral collisions of (already soft!) electrons and/or positrons with creation of additional dielectrons in the reaction $e^{\pm }{e}^{\pm }\to e^{\pm }{e}^{\pm }{e}^{+}{e}^{-}$. Thus, the density of the electron–positron plasma increases while the energies of electron–positron pairs diminish so that they come almost to rest and are able to form extremely slow moving parapositronia. The cross section of this process at small dielectron masses is quite large $\sigma \propto \pi r_0^2\approx 250$ mb, where $r_0\approx 2.8\times {10}^{-15}$ m is the classical electron radius. The width of the photon spectrum would become much narrower than demonstrated in Figure 2, which was computed for direct ultraperipheral production of parapositronia at rather high energies of colliding nuclei. The competition between the increasing density of the electron–positron plasma and the decreasing cross section of ultraperipheral processes near the threshold must be studied. This new hypothesis needs further foundations and theoretical efforts to become acceptable.