Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction
Abstract
1. Introduction
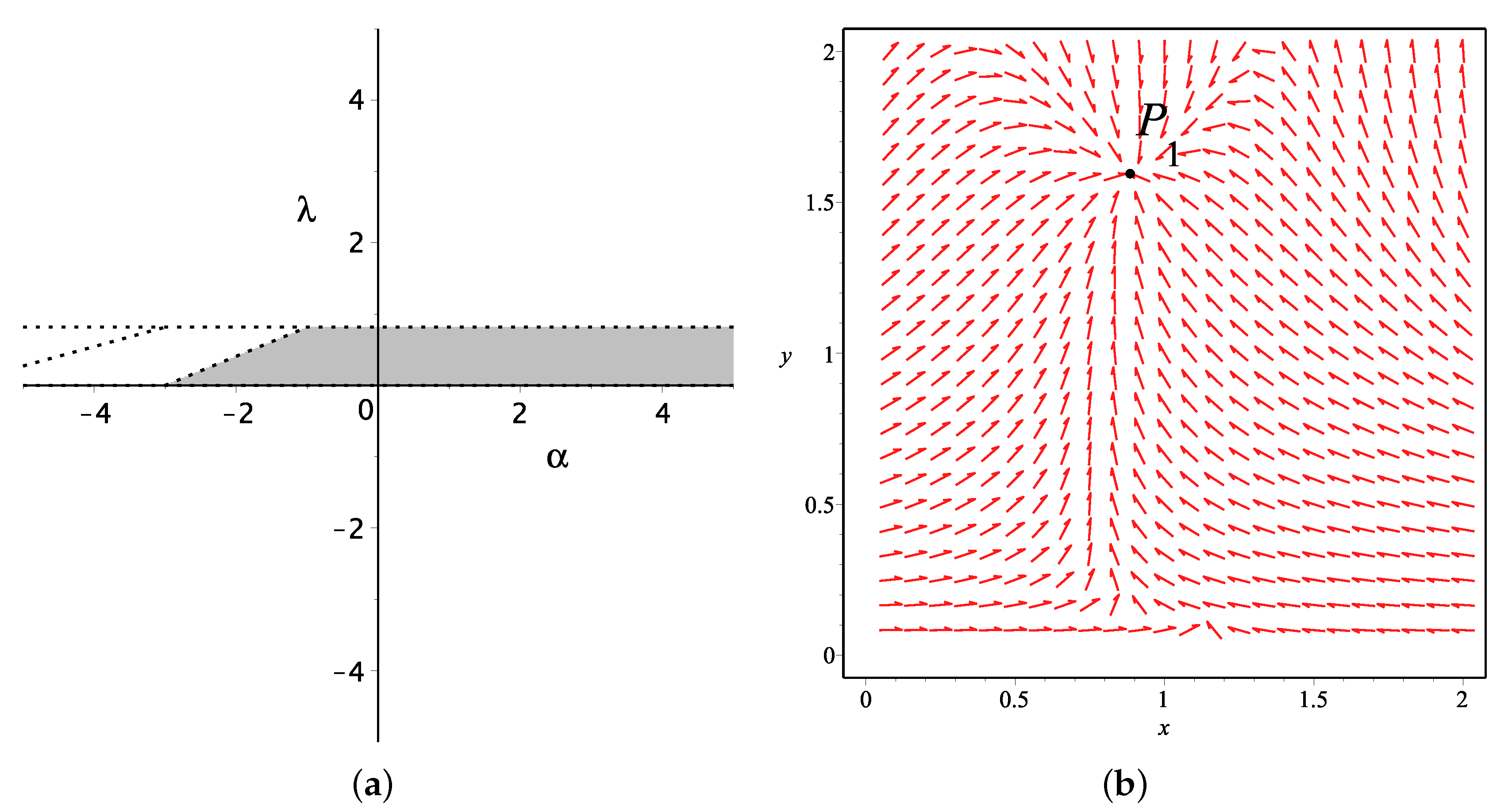
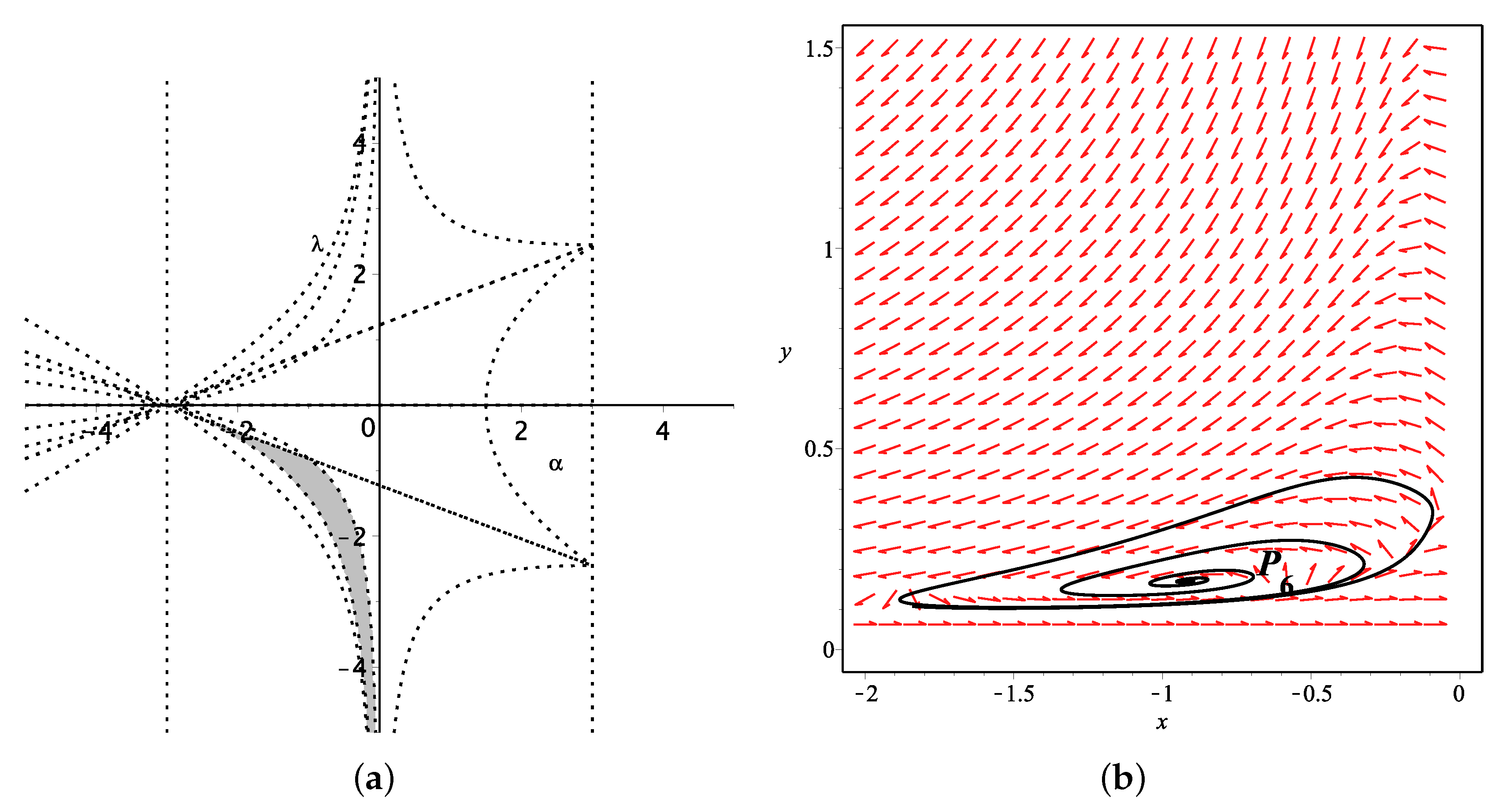
2. The Power Law K-Essence Dark Energy Model and Its Stability Analysis
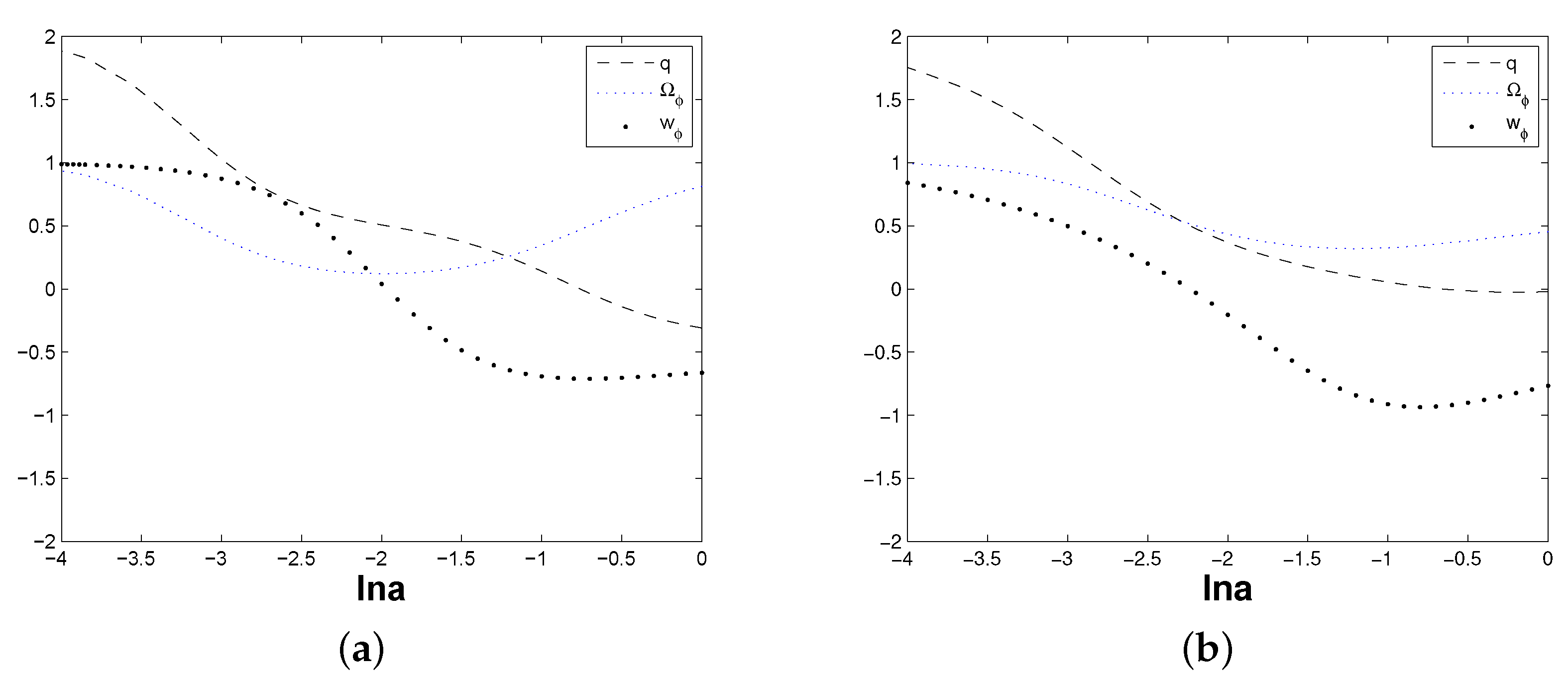
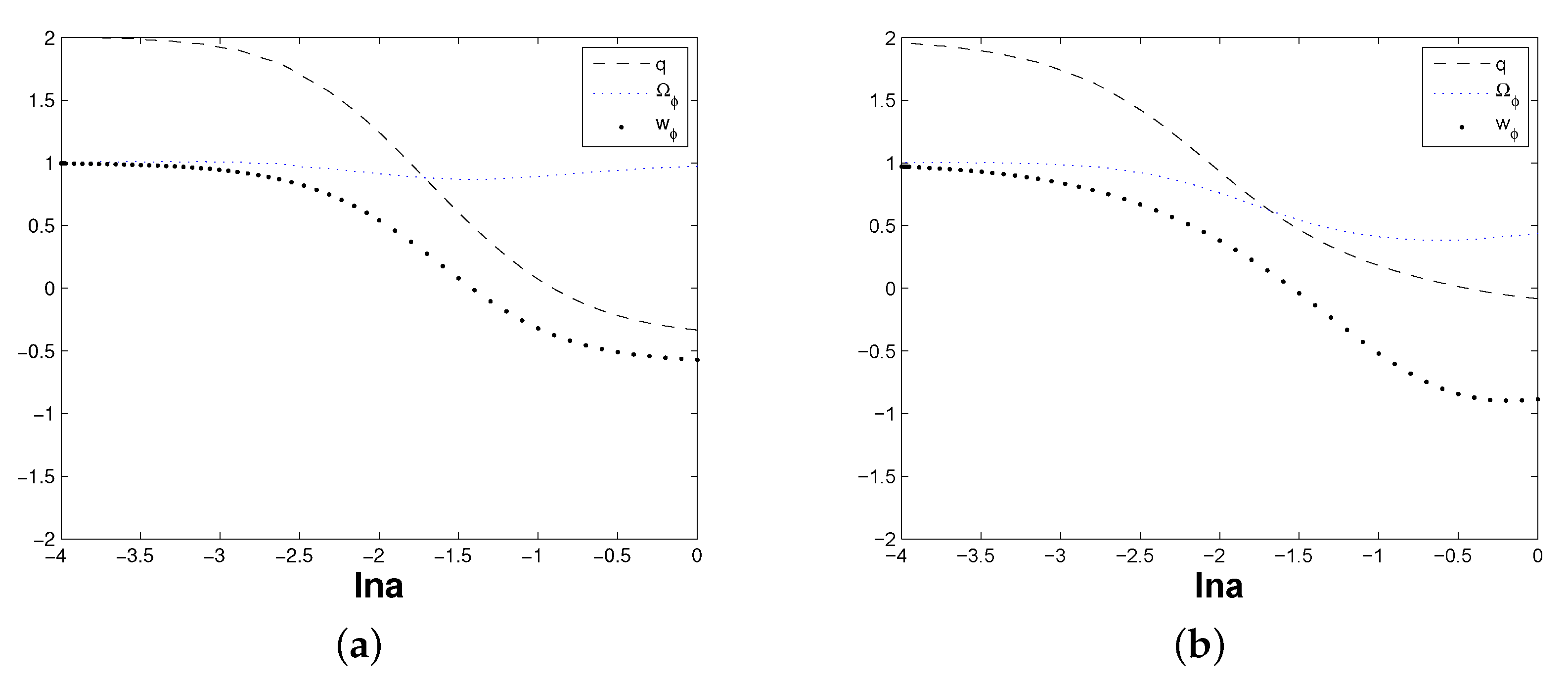
3. The Analysis of Stability for This Dark Energy Model with Interaction
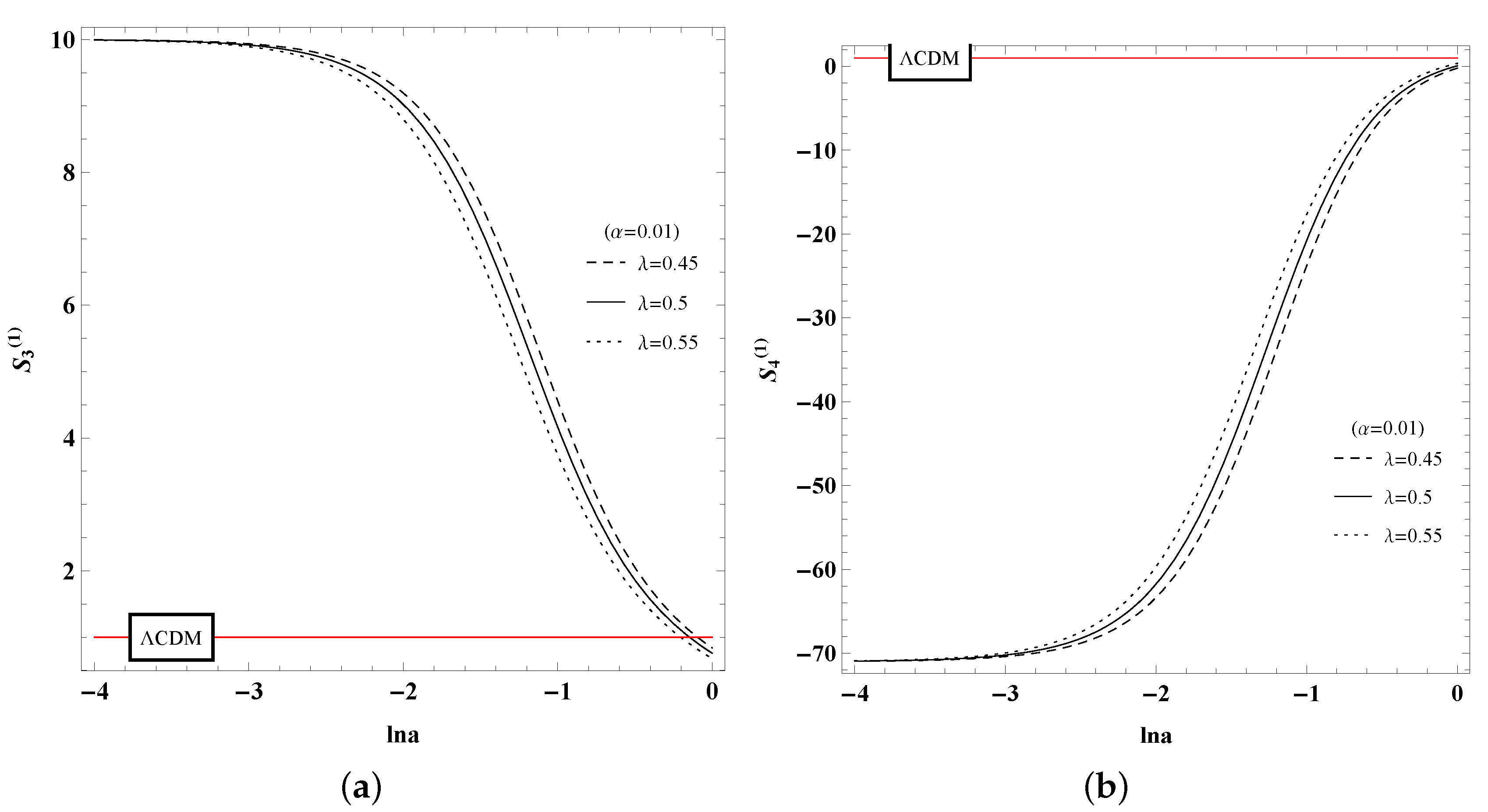
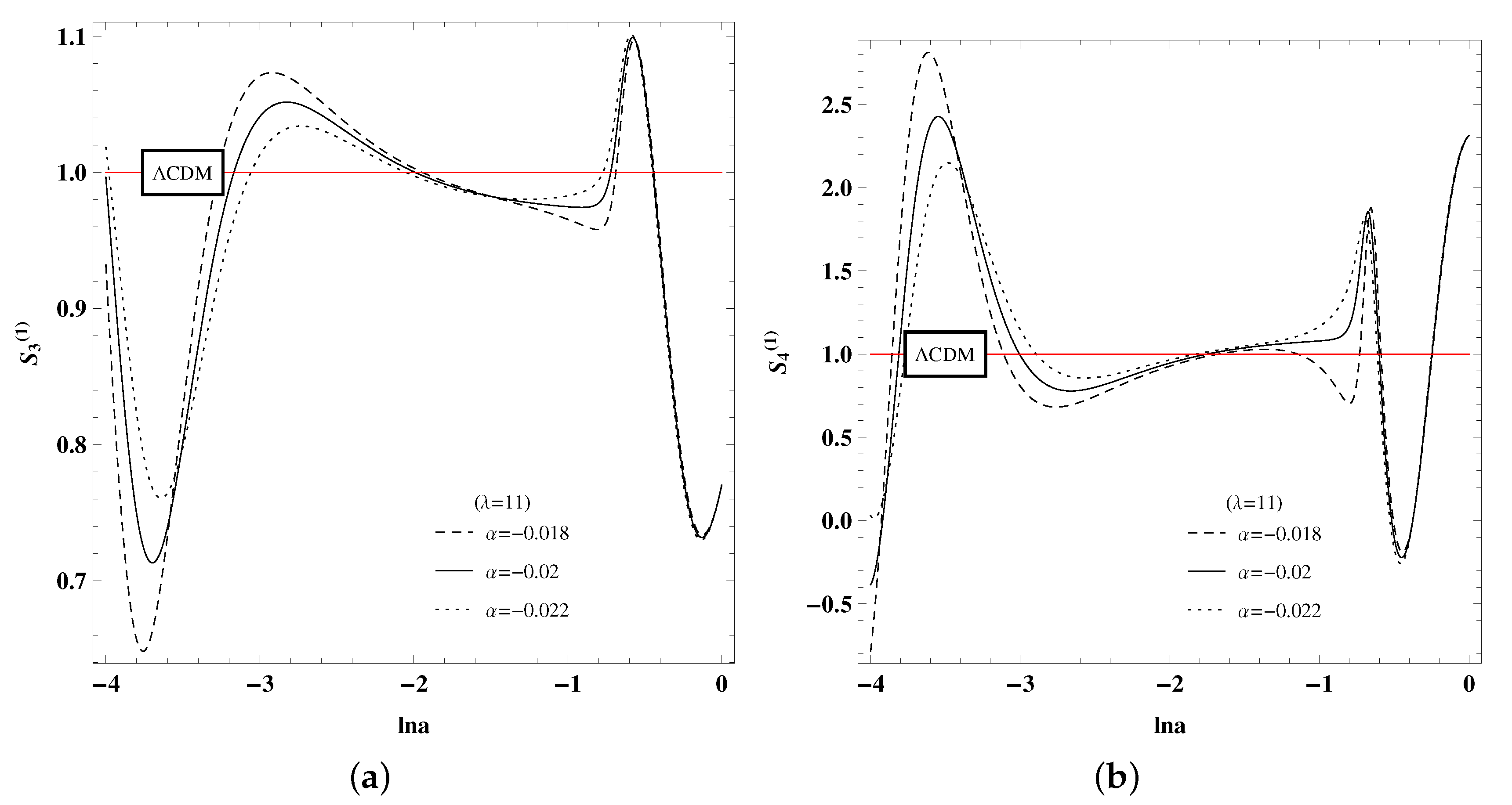
4. The Geometric Diagnostic of Statefinder Hierarchy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. [The Supernova Cosmology Project] Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP)* observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. J. 2020, 641, 1–67. [Google Scholar]
- Xu, L.X.; Lu, J.B.; Wang, Y.T. Revisiting generalized Chaplygin gas as a unified dark matter and dark energy model. Eur. Phys. J. C 2012, 72, 1883. [Google Scholar] [CrossRef]
- Xu, L.X.; Wang, Y.T.; Noh, H. Modified Chaplygin gas as a unified dark matter and dark energy model and cosmic constraints. Eur. Phys. J. C 2012, 72, 1931. [Google Scholar] [CrossRef]
- Yang, W.Q.; Li, H.; Wu, Y.B.; Lu, J.B. Cosmological implications of the dark matter equation of state. Int. J. Mod. Phys. D 2017, 26, 1750013. [Google Scholar] [CrossRef]
- Du, M.H.; Yang, W.Q.; Xu, L.X.; Pan, S.; Mota, D.F. Future constraints on dynamical dark-energy using gravitational-wave standard sirens. Phys. Rev. D 2019, 100, 043535. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than −1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Commun. Dark Energy. Theor. Phys. 2011, 56, 525–604. [Google Scholar]
- Yang, R.J.; Zhang, S.N. The age problem in the ΛCDM model. Mon. Not. R. Astron. Soc. 2010, 407, 1835–1841. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242. [Google Scholar] [CrossRef]
- Huang, Q.G.; Wang, K. How the dark energy can reconcile Planck with local determination of the Hubble constant. Eur. Phys. J. C 2016, 76, 506. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.Q.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 083539. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.Q.; Valentino, E.D.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Grav. 2013, 30, 214003. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.L.; Zhang, X.M. Dark Energy Constraints from the Cosmic Age and Supernova. Phys. Lett. B 2005, 607, 35–41. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. K-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. A Dynamical Solution to the Problem of a Small Cosmological Constant and Late-time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef]
- Rendall, A.D. Dynamics of k-essence. Class. Quant. Grav. 2006, 23, 1557–1570. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely kinetic k-essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. A k-essence Model of Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. Unified Model of k-Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 80, 103508. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically Driven Quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Chimento, L.P.; Feinstein, A. Power-law expansion in k-essence cosmology. Mod. Phys. Lett. A 2004, 19, 761–768. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Battye, R.A.; Pace, F. Approximation of the potential in scalar field dark energy models. Phys. Rev. D 2016, 94, 063513. [Google Scholar] [CrossRef]
- Wang, B. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Chimento, L.P. Linear and nonlinear interactions in the dark sector. Phys. Rev. D. 2010, 81, 043525. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Pan, S.; Yang, W.Q. Dynamics of nonlinear interacting dark energy models. Int. J. Mod. Phys. D 2019, 28, 1950161. [Google Scholar] [CrossRef]
- Yang, W.Q.; Pan, S.; Barrow, J.D. Large-scale stability and astronomical constraints for coupled dark-energy models. Phys. Rev. D. 2018, 97, 043529. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, Y.B.; Chi, J.N.; Yu, Z.; Xu, D.F. Diagnosing Tsallis holographic dark energy models with interactions. Mod. Phys. Lett. A 2020, 33, 2050044. [Google Scholar] [CrossRef]
- Yang, R.J.; Chen, B.H.; Li, J.; Qi, J.Z. The evolution of the power law k-essence cosmology. Astrophys. Space Sci. 2015, 356, 399–405. [Google Scholar] [CrossRef][Green Version]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D. 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Bahamonde, S.; Boehmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rep. 2018, 775, 1–122. [Google Scholar] [CrossRef]
- Leon, G.; Saridakis, E.N. Phase-space analysis of Horava-Lifshitz cosmology. J. Cosmol. Astropart. Phys. 2009, 2009, 006. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef]
- Wu, Y.B.; Zhang, C.Y.; Lu, J.B.; Lu, J.W.; Zhang, X.; Qi, Q.M.; Fan, B. Analysis on modified Chaplygin gas as dark energy model. Mod. Phys. Lett. A 2015, 30, 1550005. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the Expanding Universe and Dark Energy using the Statefinder Diagnostic. Mon. Not. R. Asron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Arabsalmani, M.; Sahni, V. The Statefinder hierarchy: An extended null diagnostic for concordance cosmology. Phy. Rev. D. 2011, 83, 043501. [Google Scholar] [CrossRef]
- Li, J.; Yang, R.J.; Chen, B.H. Discriminating dark energy models by using the statefinder hierarchy and the growth rate of matter perturbations. J. Cosmol. Astropart. Phys. 2014, 2014, 043. [Google Scholar] [CrossRef]
- Cui, J.L.; Yin, L.; Wang, L.F.; Li, Y.H.; Zhang, X. A closer look at interacting dark energy with statefinder hierarchy and growth rate of structure. J. Cosmol. Astropart. Phys. 2014, 2014, 024. [Google Scholar] [CrossRef]
- Liu, W.Z.; Liu, D.J. Statefinder Diagnostic for Quintessence with or without Thermal Interaction. Int. J. Mod. Phys. D 2009, 18, 43–52. [Google Scholar] [CrossRef]
- De-Santiago, J.; Cervantes-Cota, J.L. Generalizing a Unified Model of Dark Matter, Dark Energy, and Inflation with Non Canonical Kinetic Term. Phys. Rev. D 2011, 83, 063502. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Unnikrishnan, S.; Sriramkumar, L. A note on perfect scalar fields. Phys. Rev. D 2010, 81, 103511. [Google Scholar] [CrossRef]
- Christopherson, A.J.; Malik, K.A. The non-adiabatic pressure in general scalar field system. Phys. Lett. B 2009, 675, 159–163. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686–4690. [Google Scholar] [CrossRef]
- Yang, R.J.; Gao, X.T. Phase-space analysis of a class of k-essence cosmology. Class. Quantum Gravity 2011, 28, 065012. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Unified phantom cosmology: Inflation, dark energy and dark matter under the same standard. Phys. Lett. B 2006, 632, 597–604. [Google Scholar] [CrossRef]
- Carloni, S.; Elizalde, E.; Silva, P.J. An analysis of the phase space of Horava-Lifshitz cosmologies. Class. Quant. Grav. 2010, 27, 045004. [Google Scholar] [CrossRef]
- He, J.; Wu, Y.B.; Fu, M.H. Dynamical Attractor of Modified Chaplygin Gas. Chin. Phys. Lett. 2008, 25, 347. [Google Scholar]




| Name | Existence | Stability | q | |||
|---|---|---|---|---|---|---|
| 1 | ||||||
| none | 1 | |||||
| 1 | ||||||
| none | 1 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.-H.; Wu, Y.-B.; Xu, D.-F.; Dong, W.; Zhang, N. Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction. Universe 2020, 6, 244. https://doi.org/10.3390/universe6120244
Chen B-H, Wu Y-B, Xu D-F, Dong W, Zhang N. Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction. Universe. 2020; 6(12):244. https://doi.org/10.3390/universe6120244
Chicago/Turabian StyleChen, Bo-Hai, Ya-Bo Wu, Dong-Fang Xu, Wei Dong, and Nan Zhang. 2020. "Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction" Universe 6, no. 12: 244. https://doi.org/10.3390/universe6120244
APA StyleChen, B.-H., Wu, Y.-B., Xu, D.-F., Dong, W., & Zhang, N. (2020). Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction. Universe, 6(12), 244. https://doi.org/10.3390/universe6120244








