Quantum Mixmaster as a Model of the Primordial Universe
Abstract
1. Introduction
1.1. Motivation
1.2. Our Approach
1.3. Former Results on Mixmaster
1.4. Outline of the Article
2. The Classical Model
2.1. General Features of the Mixmaster Model
2.2. Approaches to the Anisotropy Potential
2.2.1. Well-Known Approximations
2.2.2. Perturbed Toda System
3. Quantization and Semi-Classical Formula: General Features
3.1. What is Quantization?
3.2. Integral Quantization
- (i)
- To there corresponds , where is the identity in ,
- (ii)
- To a real function there corresponds a(n) (essentially) self-adjoint operator in .
3.3. Integral Quantization and Semi-Classical Formula: Phase-Space Portraits
3.4. Affine Covariant Integral Quantization
3.4.1. General Settings
3.4.2. Properties of Acs Quantization
3.4.3. Affine Semi-Classical Portrait
3.5. Weyl–Heisenberg Integral Quantization
3.5.1. General Settings
3.5.2. Properties of the Weyl–Heisenberg Integral Quantization
3.5.3. Weyl–Heisenberg Semi-Classical Portrait
4. Quantization of the Mixmaster Hamiltonian
4.1. General Settings
4.2. Acs ⊕ Canonical Quantization
The Quantum Framework
4.3. Acs ⊕ Covariant Weyl–Heisenberg Integral Quantization
4.3.1. The Framework
4.3.2. Underlying Toda System
5. Quantum Dynamical Studies
5.1. Semi-Classical Lagrangian and Dynamical Equations
- (a)
- is a -time-dependent ACS, the fiducial vector being constrained by as in the Section 3.4.3,
- (b)
- is the unitary operator resulting from the substitution in the operator defined in Equation (64),
- (c)
- is an arbitrary fixed value of q.
5.2. Adiabatic and Nonadiabatic Approximations
5.2.1. Adiabatic (Born–Oppenheimer) Approximation
5.2.2. Nonadiabatic (Vibronic) Approximation
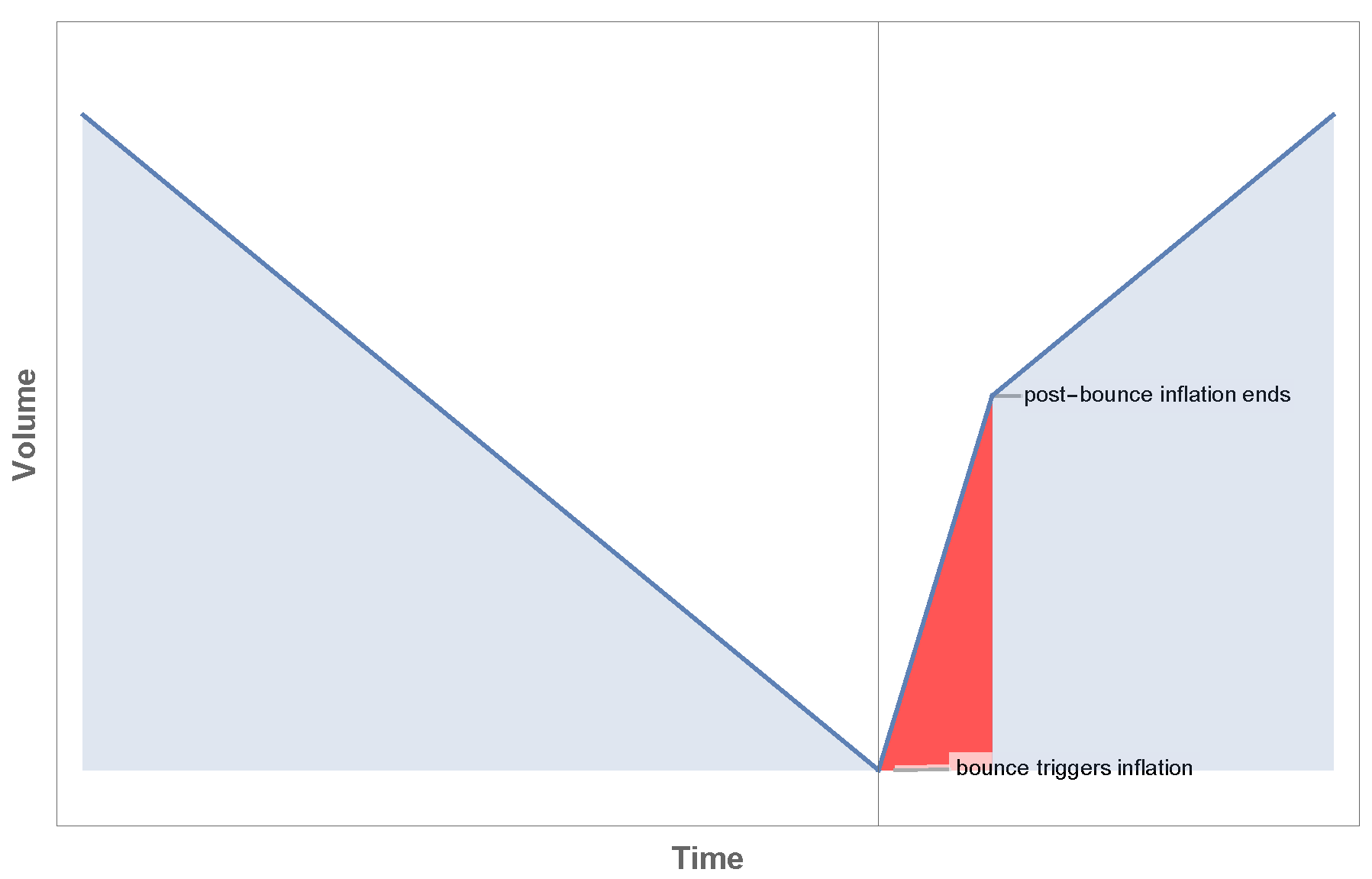
5.3. Nonadiabatic Bounce and Inflationary Phase
- (i)
- What is the regime of validity of the adiabatic approximation?
- (ii)
- What are the precise factors on which the excitation (or decay) of anisotropy depends?
- (iii)
- What is the amount of anisotropic energy that can be produced in a violent bouncing cosmological scenario?
- (a)
- to describe properly the quantum entanglement of degrees of freedom (operator in Equation (75)) before building the semi-classical Hamiltonian;
- (b)
- to avoid the harmonic approximation of the Bianchi IX potential, which is broken for high excitations close to the bounce.
A First Attempt to Obtain a Complete Semi-Classical Framework
6. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PGWs | Primordial gravitational waves |
| CMB | Cosmic microwave background |
| FRW | Friedman-Robertson–Walker |
| BKL | Belinskii, Khalatnikov and Lifshitz |
| CS | Coherent states |
| ACS | Affine coherent states |
| WH | Weyl–Heisenberg |
| UIR | Unitary Irreducible representation |
| IR/UV | Infra-red/Ultra-violet |
Appendix A. Toda Approximation
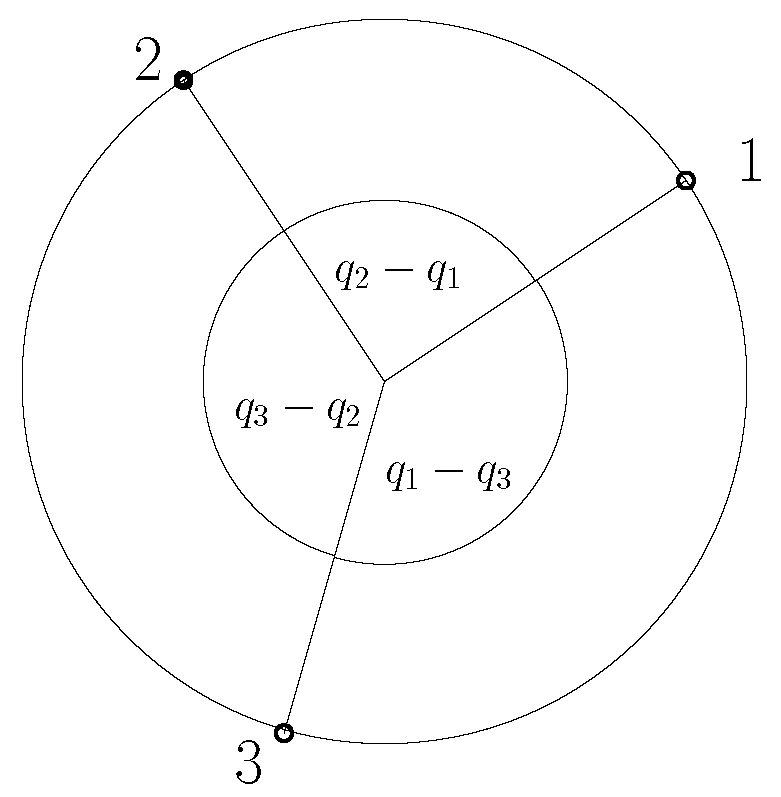
Appendix B. Coefficients Due to the Fiducial Vector of the ACS
References
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Planck Collaboration; et al. Planck 2015 results-XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Boyle, L.A. Gravitational Waves and the Early Universe. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2006. [Google Scholar]
- DECi-Hertz Interferometer Gravitational Wave Observatory. Available online: http://tamago.mtk.nao.ac.jp/decigo/index_E.html (accessed on 29 December 2019).
- Lite (Light) Satellite for the Studies of B-Mode Polarization and Inflation from Cosmic Background Radiation Detection. Available online: http://litebird.jp/eng/ (accessed on 29 December 2019).
- Cosmic Origins Explorer. Available online: http://www.core-mission.org (accessed on 29 December 2019).
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary paradigm in trouble after Planck2013. Phys. Lett. B 2013, 723, 261. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The Ekpyrotic Universe: Colliding Branes and the Origin of the Hot Big Bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N. Cosmology without inflation. Phys. Rev. D 2008, 78, 063506. [Google Scholar] [CrossRef]
- Misner, C.W. Mixmaster Universe. Phys. Rev. Lett. 1969, 22, 1071. [Google Scholar] [CrossRef]
- Bogoyavlensky, O.I. Methods in the Qualitative Theory of Dynamical Systems in Astrophysics and Gas Dynamics; Springer: Berlin, Germany, 1985. [Google Scholar]
- Belinskii, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. A general solution of the Einstein equations with a time singularity. Adv. Phys. 1982, 31, 639. [Google Scholar] [CrossRef]
- Belinskii, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 1970, 19, 525. [Google Scholar] [CrossRef]
- Bergeron, H.; Czuchry, E.; Gazeau, J.-P.; Małkiewicz, P.; Piechocki, W. Singularity avoidance in a quantum model of the Mixmaster universe. Phys. Rev. D 2015, 92, 124018. [Google Scholar] [CrossRef]
- Bergeron, H.; Czuchry, E.; Gazeau, J.-P.; Małkiewicz, P.; Piechocki, W. Smooth Quantum Dynamics of Mixmaster Universe. Phys. Rev. D 2015, 92, 061302(R). [Google Scholar] [CrossRef]
- Bergeron, H.; Czuchry, E.; Gazeau, J.-P.; Małkiewicz, P. Vibronic framework for quantum mixmaster universe. Phys. Rev. D 2016, 93, 064080. [Google Scholar] [CrossRef]
- Bergeron, H.; Czuchry, E.; Gazeau, J.-P.; Małkiewicz, P. Nonadiabatic bounce and an inflationary phase in the quantum mixmaster universe. Phys. Rev. D 2016, 93, 124053. [Google Scholar] [CrossRef]
- Hu, B.L.; Regge, T. Perturbations on the Mixmaster Universe. Phys. Rev. Lett. 1972, 29, 1616. [Google Scholar] [CrossRef]
- Hu, B.L. Scalar Waves in the Mixmaster Universe. I. The Helmholtz Equation in a Fixed Background. Phys. Rev. D 1973, 8, 1048. [Google Scholar] [CrossRef]
- Hu, B.L. Scalar waves in the mixmaster universe. II. Particle creation. Phys. Rev. D 1974, 9, 3263. [Google Scholar] [CrossRef]
- Hu, B.L. Separation of tensor equations in a homogeneous space by group theoretical methods. J. Math. Phys. 1974, 15, 1748. [Google Scholar] [CrossRef]
- Hu, B.L.; Fulling, S.A.; Parker, L. Quantized Scalar Fields in a Closed Anisotropic Universe. Phys. Rev. D 1973, 8, 2377. [Google Scholar] [CrossRef]
- Slagter, R.J. Numerical solutions of high-frequency perturbations in Bianchi type IX models. Astroph. J. 1983, 268, 513. [Google Scholar] [CrossRef]
- Slagter, R.J. Behavior of higher modes of gravitational waves and gauge-invariant density perturbations in Bianchi IX cosmological models. Astroph. J. 1984, 286, 379. [Google Scholar] [CrossRef]
- Klauder, J.R. Enhanced quantization: A primer. J. Phys. A 2012, 45, 285304. [Google Scholar] [CrossRef]
- Klauder, J.R. Completing canonical quantization, and its role in nontrivial scalar field quantization. arXiv 2013, arXiv:1308.4658. [Google Scholar]
- Klauder, J.R. Enhanced Quantization, Particles, Fields & Gravity; World Scientific: Singapore, 2015. [Google Scholar]
- Uggla, C. Hamiltonian Cosmology. In Dynamical Systems in Cosmology; Wainwright, J., Ellis, G.F.R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bergeron, H.; Czuchry, E.; Gazeau, J.-P.; Malkiewicz, P. Integrable Toda system as a quantum approximation to the anisotropy of the mixmaster universe. Phys. Rev. D 2018, 98, 083512. [Google Scholar] [CrossRef]
- Berry, M. Regular and irregular motion. In Topics in Nonlinear Mechanics; Jorna, S., Ed.; American Institute of Physics Conference Proceedings No. 46; American Institute of Physics: College Park, MD, USA, 1978; p. 16. [Google Scholar]
- Hénon, M. Integrals of the Toda lattice. Phys. Rev. B 1974, 9, 1926. [Google Scholar] [CrossRef]
- Flaschka, M. The Toda lattice. II. Existence of integrals. Phys. Rev. B 1974, 9, 1924. [Google Scholar] [CrossRef]
- Ford, J.; Stoddard, S.D.; Turner, J.S. On the Integrability of the Toda Lattice. Prog. Theor. Phys. 1973, 50, 1547. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.-P. Integral quantizations with two basic examples. Ann. Phys. 2014, 344, 43. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.-P. Coherent States, Wavelets and their Generalizations. In Theoretical and Mathematical Physics, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Gazeau, J.-P.; Murenzi, R. Covariant affine integral quantization(s). J. Math. Phys. 2016, 57, 052102. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Heller, B. POVM Quantization. Axioms. 2015, 4, 1. [Google Scholar] [CrossRef]
- Bergeron, H.; Curado, E.M.F.; Gazeau, J.-P.; Rodrigues, L.M.C.S. Weyl–Heisenberg integral quantization(s): A compendium. arXiv 2017, arXiv:1703.08443. [Google Scholar]
- Gazeau, J.-P. From Classical to Quantum Models: The Regularising Rôle of Integrals, Symmetry and Probabilities. Found. Phys. 2018, 48, 1648. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.-P. Variations à la Fourier-Weyl-Wigner on Quantizations of the plane and the Half-Plane. Entropy 2018, 20, 787. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Koide, T.; Noguera, D. Quantum Smooth Boundary Forces from Constrained Geometries. J. Phys. A Math. Theor. 2019, 52, 445203. [Google Scholar] [CrossRef]
- Perelomov, A.M. Generalized Coherent States and their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Weyl, H. Gruppentheorie und Quantenmechanik; Hirzel: Leipzig, Germany, 1928. [Google Scholar]
- Weyl, H. The Theory of Groups and Quantum Mechanics; Dover: New York, NY, USA, 1931. [Google Scholar]
- Grossmann, A. Parity operator and quantization of δ functions. Commun. Math. Phys. 1976, 48, 191. [Google Scholar] [CrossRef]
- Daubechies, I. On the distributions corresponding to bounded operators in the Weyl quantization. Commun. Math. Phys. 1980, 75, 229. [Google Scholar] [CrossRef]
- Daubechies, I.; Grossmann, A. An integral transform related to quantization. I. J. Math. Phys. 1980, 21, 2080. [Google Scholar] [CrossRef]
- Daubechies, I.; Grossmann, A.; Reignier, J. An integral transform related to quantization. II. J. Math. Phys. 1983, 24, 239. [Google Scholar] [CrossRef]
- Bergeron, H.; Dapor, A.; Gazeau, J.-P.; Małkiewicz, P. Smooth big bounce from affine quantization. Phys. Rev. D 2014, 89, 083522. [Google Scholar] [CrossRef]
- Bergeron, H.; Dapor, A.; Gazeau, J.-P.; Małkiewicz, P. Smooth Bounce in Affine Quantization of Bianchi I. Phys. Rev. D 2015, 91, 124002. [Google Scholar] [CrossRef]
- Almeida, C.R.; Bergeron, H.; Gazeau, J.-P.; Scardua, A.C. Three examples of quantum dynamics on the half-line with smooth bouncing. Ann. Phys 2018, 392, 206–228. [Google Scholar] [CrossRef]
- Frion, E.; Almeida, C.R. Affine quantization of the Brans-Dicke theory: Smooth bouncing and the equivalence between the Einstein and Jordan frames. Phys. Rev. D 2019, 99, 023524. [Google Scholar] [CrossRef]
- Klauder, J.R.; Aslaksen, E.W. Elementary Model for Quantum Gravity. Phys. Rev. D 1970, 2, 272. [Google Scholar] [CrossRef]
- Klauder, J.R. An affinity for affine quantum gravity. Proc. Steklov Inst. Math. 2011, 272, 169. [Google Scholar] [CrossRef]
- Fanuel, M.; Zonetti, S. Affine quantization and the initial cosmological singularity. Europhys. Lett. 2013, 101, 10001. [Google Scholar] [CrossRef][Green Version]
- Stenzel, M.B. Holomorphic Sobolev spaces and the generalized Segal-Bargmann transform. J. Funct. Anal. 1994, 165, 44. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics, II. Fourier Analysis, Self-Adjointness; Academic Press: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Gesztesy, F.; Kirsch, W.; Reine, J. Schrödinger Operators in L2() with Pointwise Localized Potential. Angew. Math. 1985, 362, 28. [Google Scholar]
- Bergeron, H.; Czuchry, E.; Gazeau, J.; Małkiewicz, P. Spectral properties of the quantum Mixmaster universe. Phys. Rev. D 2017, 96, 043521. [Google Scholar] [CrossRef]
- Kac, M.; van Moerbeke, P. On some periodic Toda lattices. Proc. Natl. Acad. Sci. USA 1975, 72, 1627–1629. [Google Scholar] [CrossRef]
- van Moerbeke, P. The spectrum of Jacobi matrices. Invent. Math. 1976, 37, 45. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. The Quantum mechanical Toda lattice. Ann. Phys. 1980, 124, 347. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. The Quantum mechanical Toda lattice II. Ann. Phys. 1981, 133, 304. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.-P.; Małkiewicz, P. Primordial gravitational waves in a quantum model of big bounce. J. Cosmol. Astropart. Phys. 2018, 2018, 057. [Google Scholar] [CrossRef]
- Hazra, D.K. A Shafieloo and T Souradeep, Primordial power spectrum from Planck. J. Cosmol. Astropart. Phys. 2014, 2014, 011. [Google Scholar] [CrossRef]
- Durakovic, A.; Hunt, P.; Mukherjee, S.; Sarkar, S.; Souradeep, T. Reconstruction of a direction-dependent primordial power spectrum from Planck CMB data. J. Cosmol. Astropart. Phys. 2018, 2018, 012. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergeron, H.; Czuchry, E.; Gazeau, J.P.; Małkiewicz, P. Quantum Mixmaster as a Model of the Primordial Universe. Universe 2020, 6, 7. https://doi.org/10.3390/universe6010007
Bergeron H, Czuchry E, Gazeau JP, Małkiewicz P. Quantum Mixmaster as a Model of the Primordial Universe. Universe. 2020; 6(1):7. https://doi.org/10.3390/universe6010007
Chicago/Turabian StyleBergeron, Hervé, Ewa Czuchry, Jean Pierre Gazeau, and Przemysław Małkiewicz. 2020. "Quantum Mixmaster as a Model of the Primordial Universe" Universe 6, no. 1: 7. https://doi.org/10.3390/universe6010007
APA StyleBergeron, H., Czuchry, E., Gazeau, J. P., & Małkiewicz, P. (2020). Quantum Mixmaster as a Model of the Primordial Universe. Universe, 6(1), 7. https://doi.org/10.3390/universe6010007







