Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres
Abstract
1. Introduction
2. Rotating vs. Inertial Frame
2.1. Metric
2.2. Electrodynamics
2.3. Doppler Effect
2.4. Maxwell Equations in a Rotating Coordinate System
3. Electromagnetic Field Inside and Outside the Star
4. Particle Motion in the Magnetosphere
- following magnetic field lines in the corotating frame.
- following magnetic field lines in the inertial frame in addition to a corotation imposed by the stellar rotation.
- following the ultra-relativistic radiation reaction limit leading to the so-called Aristotelian dynamics. Actually, this limit can be explained by Newtonian dynamics in a stationary regime balancing electric acceleration and radiation friction.
4.1. Corotating Frame
4.2. Corotating Velocity
4.3. Aristotelian Dynamics
5. Numerical Simulation of Rotating Magnetospheres
5.1. Numerical Schemes
5.2. Force-Free Magnetospheres
5.3. Radiative Magnetospheres
6. Differentially Rotating Magnetospheres
7. Radiation from the Magnetosphere
8. Discussion
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Chandrasekhar, S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of Stars. Phys. Z. Der Sowjetunion 1932, 1, 285–288. [Google Scholar]
- Woltjer, L. X-Rays and Type I Supernova Remnants. Astrophys. J. 1964, 140, 1309–1313. [Google Scholar] [CrossRef]
- Spruit, H.C. Origin of neutron star magnetic fields. AIP Conf. Proc. 2008, 983, 391–398. [Google Scholar]
- Manchester, R.N.; Taylor, J.H. Observed and derived parameters for 330 pulsars. Astron. J. 1981, 86, 1953–1973. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Belfiore, A.; Bellazzini, R.; et al. The Second Fermi Large Area Telescope Catalog of Gamma-Ray Pulsars. Astrophys. J. Suppl. Ser. 2013, 208, 17. [Google Scholar] [CrossRef]
- Guillot, S.; Kerr, M.; Ray, P.S.; Bogdanov, S.; Ransom, S.; Deneva, J.S.; Arzoumanian, Z.; Bult, P.; Chakrabarty, D.; Gendreau, K.C.; et al. NICER X-ray Observations of Seven Nearby Rotation-Powered Millisecond Pulsars. arXiv 2019, arXiv:1912.05708. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869–880. [Google Scholar] [CrossRef]
- Rizzi, G.; Ruggiero, M. Relativity in Rotating Frames: Relativistic Physics in Rotating Reference Frames; Fundamental Theories of Physics; Springer Science+Business Media: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Jackson, J.D. Electrodynamique Classique: Cours et Exercices D’electromagnétisme; Dunod: Paris, Franch, 2001. [Google Scholar]
- Gourgoulhon, E. Relativité Restreinte: Des Particules à L’astrophysique; EDP Sciences: Les Ulis, France, 2010. [Google Scholar]
- Beskin, V.S. MHD Flows in Compact Astrophysical Objects: Accretion, Winds and Jets, 2010 Edition ed; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Deutsch, A.J. The electromagnetic field of an idealized star in rigid rotation in vacuo. Ann. D’Astrophys. 1955, 18, 1–10. [Google Scholar]
- Belinsky, V.; de Paolis, F.; Lee, H.W.; Ruffini, R. Radiation from a relativistic rotating magnetic dipole: Magnetic synchrotron effect. Astron. Astrophys. 1994, 283, 1018–1024. [Google Scholar]
- Roberts, W.J. Electromagnetic multipole fields of neutron stars. Astrophys. J. Suppl. Ser. 1979, 41, 75–86. [Google Scholar] [CrossRef]
- Bai, X.N.; Spitkovsky, A. Uncertainties of Modeling Gamma-ray Pulsar Light Curves Using Vacuum Dipole Magnetic Field. Astrophys. J. 2010, 715, 1270–1281. [Google Scholar] [CrossRef]
- Bai, X.N.; Spitkovsky, A. Modeling of Gamma-ray Pulsar Light Curves Using the Force-free Magnetic Field. Astrophys. J. 2010, 715, 1282. [Google Scholar] [CrossRef]
- Romani, R.W.; Yadigaroglu, I.A. Gamma-ray pulsars: Emission zones and viewing geometries. Astrophys. J. 1995, 438, 314–321. [Google Scholar] [CrossRef]
- Dyks, J.; Rudak, B. Two-Pole Caustic Model for High-Energy Light Curves of Pulsars. Astrophys. J. 2003, 598, 1201–1206. [Google Scholar] [CrossRef]
- Dyks, J.; Harding, A.K.; Rudak, B. Relativistic Effects and Polarization in Three High-Energy Pulsar Models. Astrophys. J. 2004, 606, 1125–11421. [Google Scholar] [CrossRef]
- Cheng, K.S.; Ruderman, M.; Zhang, L. A Three-dimensional Outer Magnetospheric Gap Model for Gamma-Ray Pulsars: Geometry, Pair Production, Emission Morphologies, and Phase-resolved Spectra. Astrophys. J. 2000, 537, 964–976. [Google Scholar] [CrossRef]
- Herold, H.; Ertl, T.; Ruder, H. Generation of relativistic particles in pulsar magnetospheres. Mitteilungen Der Astron. Ges. Hambg. 1985, 63, 174. [Google Scholar]
- Mestel, L. Stellar Magnetism; International Series of Monographs on Physics 99; Clarendon: Oxford, UK, 1999. [Google Scholar]
- Pétri, J. General-relativistic pulsar magnetospheric emission. Mon. Not. R. Astron. Soc. 2018, 477, 1035–1064. [Google Scholar] [CrossRef]
- Pétri, J. Pulsar gamma-ray emission in the radiation reaction regime. Mon. Not. R. Astron. Soc. 2019, 484, 5669–5691. [Google Scholar] [CrossRef]
- Jackson, E.A. A new pulsar atmospheric model. I - Aligned magnetic and rotational axes. Astrophys. J. 1976, 206, 831–841. [Google Scholar] [CrossRef]
- Finkbeiner, B.; Herold, H.; Ertl, T.; Ruder, H. Effects of radiation damping on particle motion in pulsar vacuum fields. Astron. Astrophys. 1989, 225, 479–487. [Google Scholar]
- Michel, F.; Li, H. Electrodynamics of neutron stars. Phys. Rep. 1999, 318, 227–297. [Google Scholar] [CrossRef]
- Landau, L.; Lifchitz, E. Physique Théorique: Tome 2, Théorie des Champs; Mir: Moscou, Russie, 1989. [Google Scholar]
- Gruzinov, A. Aristotelian Electrodynamics solves the Pulsar: Lower Efficiency of Strong Pulsars. arXiv 2013, arXiv:1303.4094. [Google Scholar]
- Moffett, D.A.; Hankins, T.H. Multifrequency Radio Observations of the Crab Pulsar. Astrophys. J. 1996, 468, 779–783. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kazanas, D.; Fendt, C. The axisymmetric pulsar magnetosphere. Astrophys. J. 1999, 511, 351. [Google Scholar] [CrossRef]
- Spitkovsky, A. Time-dependent Force-free Pulsar Magnetospheres: Axisymmetric and Oblique Rotators. Astrophys. J. 2006, 648, L51–L54. [Google Scholar] [CrossRef]
- Komissarov, S.S. Simulations of the axisymmetric magnetospheres of neutron stars. Mon. Not. R. Astron. Soc. 2006, 367, 19–31. [Google Scholar] [CrossRef]
- Timokhin, A.N. On the force-free magnetosphere of an aligned rotator. Mon. Not. R. Astron. Soc. 2006, 368, 1055–1072. [Google Scholar] [CrossRef]
- Kalapotharakos, C.; Contopoulos, I.; Kazanas, D. The extended pulsar magnetosphere. Mon. Not. R. Astron. Soc. 2012, 420, 2793–2798. [Google Scholar] [CrossRef]
- Pétri, J. The pulsar force-free magnetosphere linked to its striped wind: time-dependent pseudo-spectral simulations. Mon. Not. R. Astron. Soc. 2012, 424, 605–619. [Google Scholar] [CrossRef]
- Cao, G.; Zhang, L.; Sun, S. Spectral simulations of an axisymmetric force-free pulsar magnetosphere. Mon. Not. R. Astron. Soc. 2016, 455, 4267–4273. [Google Scholar] [CrossRef][Green Version]
- Cao, G.; Zhang, L.; Sun, S. An oblique pulsar magnetosphere with a plasma conductivity. Mon. Not. R. Astron. Soc. 2016, 461, 1068–1075. [Google Scholar] [CrossRef][Green Version]
- Pétri, J. General relativistic monopole magnetosphere of neutron stars: A pseudo-spectral discontinuous Galerkin approach. Mon. Not. R. Astron. Soc. 2015, 447, 3170–3188. [Google Scholar] [CrossRef]
- Pétri, J. General-relativistic force-free pulsar magnetospheres. Mon. Not. R. Astron. Soc. 2016, 455, 3779–3805. [Google Scholar] [CrossRef]
- Li, J.; Spitkovsky, A.; Tchekhovskoy, A. Resistive Solutions for Pulsar Magnetospheres. Astrophys. J. 2012, 746, 60. [Google Scholar] [CrossRef]
- Kalapotharakos, C.; Kazanas, D.; Harding, A.; Contopoulos, I. Toward a Realistic Pulsar Magnetosphere. Astrophys. J. 2012, 749, 2. [Google Scholar] [CrossRef]
- Canuto, C. (Ed.) Spectral Methods: Fundamentals in Single Domains; Scientific Computation; Springer: Berlin, Germany; New York, NY, USA, 2006. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier: Boston, UK, 2005. [Google Scholar]
- Kosloff, D.; Tal-Ezer, H. A Modified Chebyshev Pseudospectral Method with an O(N-1$) Time Step Restriction. J. Comput. Phys. 1993, 104, 457–469. [Google Scholar] [CrossRef]
- Parfrey, K.; Beloborodov, A.M.; Hui, L. Introducing PHAEDRA: A new spectral code for simulations of relativistic magnetospheres. Mon. Not. R. Astron. Soc. 2012, 423, 1416–1436. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Dover: Minella, NY, USA, 2001. [Google Scholar]
- Gruzinov, A. Stability in Force-Free Electrodynamics. arXiv 1999, arXiv:Astro-ph/9902288. [Google Scholar]
- Lyubarskii, Y.E. A model for the energetic emission from pulsars. Astron. Astrophys. 1996, 311, 172–178. [Google Scholar] [CrossRef]
- Kirk, J.G.; Skjæraasen, O.; Gallant, Y.A. Pulsed radiation from neutron star winds. Astron. Astrophys. 2002, 388, L29–L32. [Google Scholar] [CrossRef]
- Michel, F.C. Magnetic structure of pulsar winds. Astrophys. J. 1994, 431, 397–401. [Google Scholar] [CrossRef]
- Coroniti, F.V. Magnetically striped relativistic magnetohydrodynamic winds—The Crab Nebula revisited. Astrophys. J. 1990, 349, 538–545. [Google Scholar] [CrossRef]
- Pétri, J.; Kirk, J.G. The Polarization of High-Energy Pulsar Radiation in the Striped Wind Model. Astrophys. J. 2005, 627, L37–L40. [Google Scholar] [CrossRef]
- Pétri, J. A unified polar cap/striped wind model for pulsed radio and gamma-ray emission in pulsars. Mon. Not. R. Astron. Soc. 2011, 412, 1870–1880. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kalapotharakos, C.; Kazanas, D. A New Standard Pulsar Magnetosphere. Astrophys. J. 2014, 781, 46. [Google Scholar] [CrossRef][Green Version]
- Philippov, A.A.; Spitkovsky, A. Ab Initio pulsar magnetosphere: Three-dimensional particle-in-cell simulations of axisymmetric pulsars. Astrophys. J. Lett. 2014, 785, L33. [Google Scholar] [CrossRef]
- Cerutti, B.; Philippov, A.; Parfrey, K.; Spitkovsky, A. Particle acceleration in axisymmetric pulsar current sheets. Mon. Not. R. Astron. Soc. 2015, 448, 606–619. [Google Scholar] [CrossRef]
- Ferraro, V.C.A. The Non-uniform Rotation of the Sun and its Magnetic Field. Mon. Not. R. Astron. Soc. 1937, 97, 458–472. [Google Scholar] [CrossRef]
- Davidson, R.C. An Introduction to the Physics of Nonneutral Plasmas; Addison-Wesley: Redwood, CA, USA, 1990. [Google Scholar]
- Dubin, D.H.E. Collisional transport in non-neutral plasmas. Phys. Plasmas 1998, 5, 1688–1694. [Google Scholar] [CrossRef]
- Dubin, D.H.E.; O’Neil, T.M. Trapped nonneutral plasmas, liquids, and crystals (the thermal equilibrium states). Rev. Mod. Phys. 1999, 71, 87–172. [Google Scholar] [CrossRef]
- Krause-Polstorff, J.; Michel, F.C. Electrosphere of an aligned magnetized neutron star. Mon. Not. R. Astron. Soc. 1985, 213, 43P–49P. [Google Scholar] [CrossRef]
- Pétri, J.; Heyvaerts, J.; Bonazzola, S. Global static electrospheres of charged pulsars. Astron. Astrophys. 2002, 384, 414–432. [Google Scholar] [CrossRef]
- Hones, E.W.; Bergeson, J.E. Electric field generated by a rotating magnetized sphere. J. Geophys. Res. 1965, 70, 4951–4958. [Google Scholar] [CrossRef]
- Pétri, J.; Heyvaerts, J.; Bonazzola, S. Diocotron instability in pulsar electrospheres. I. Linear analysis. Astron. Astrophys. 2002, 387, 520–530. [Google Scholar] [CrossRef][Green Version]
- Pétri, J.; Heyvaerts, J.; Bonazzola, S. Cross-field charge transport by the diocotron instability in pulsar magnetospheres with gaps. Astron. Astrophys. 2003, 411, 203–213. [Google Scholar] [CrossRef]
- Pétri, J. Non-linear evolution of the diocotron instability in a pulsar electrosphere: Two-dimensional particle-in-cell simulations. Astron. Astrophys. 2009, 503, 1–12. [Google Scholar] [CrossRef]
- Pétri, J. Relativistic stabilisation of the diocotron instability in a pulsar “cylindrical” electrosphere. Astron. Astrophys. 2007, 469, 843–855. [Google Scholar] [CrossRef][Green Version]
- Pétri, J. The magnetron instability in a pulsar’s cylindrical electrosphere. Astron. Astrophys. 2008, 478, 31–41. [Google Scholar] [CrossRef]
- Manchester, R.N. Radio Emission Properties of Pulsars. In Neutron Stars and Pulsars; Becker, W., Ed.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2009; pp. 19–39. [Google Scholar]
- Mitra, D. Nature of Coherent Radio Emission from Pulsars. J. Astrophys. Astron. 2017, 38, 52. [Google Scholar] [CrossRef]
- Blaskiewicz, M.; Cordes, J.M.; Wasserman, I. A relativistic model of pulsar polarization. Astrophys. J. 1991, 370, 643–669. [Google Scholar] [CrossRef]
- Pétri, J.; Mitra, D. Joint radio and X-ray modelling of PSR J1136+1551. Mon. Not. R. Astron. Soc. 2020, 491, 80–91. [Google Scholar] [CrossRef]
- Bilous, A.V.; Watts, A.L.; Harding, A.K.; Riley, T.E.; Arzoumanian, Z.; Bogdanov, S.; Gendreau, K.C.; Ray, P.S.; Guillot, S.; Ho, W.C.G.; et al. A NICER view of PSR J0030+0451: Evidence for a global-scale multipolar magnetic field. arXiv 2019, arXiv:1912.05704. [Google Scholar] [CrossRef]
- Pétri, J. The illusion of neutron star magnetic field estimates. Mon. Not. R. Astron. Soc. 2019, 485, 4573–4587. [Google Scholar] [CrossRef]
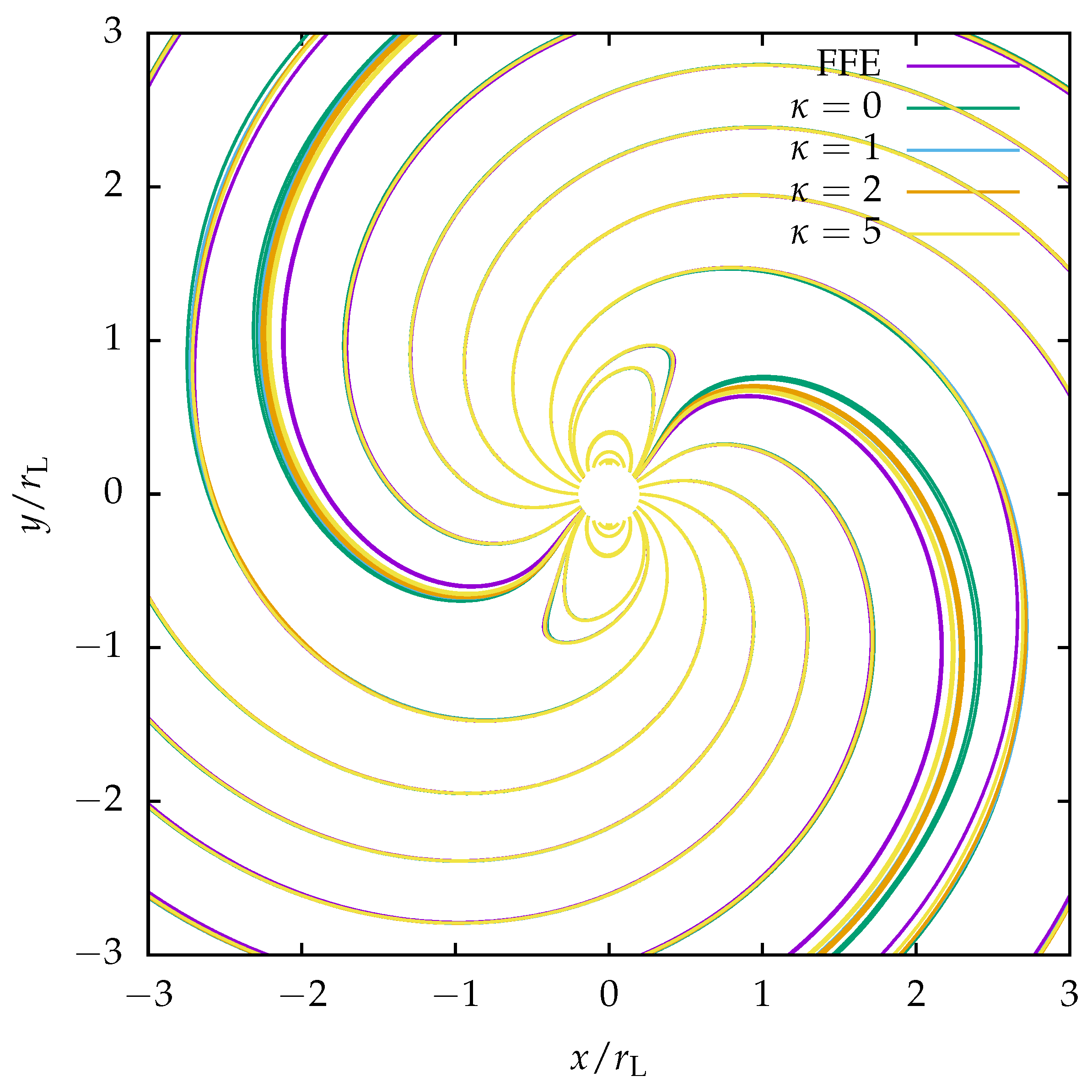
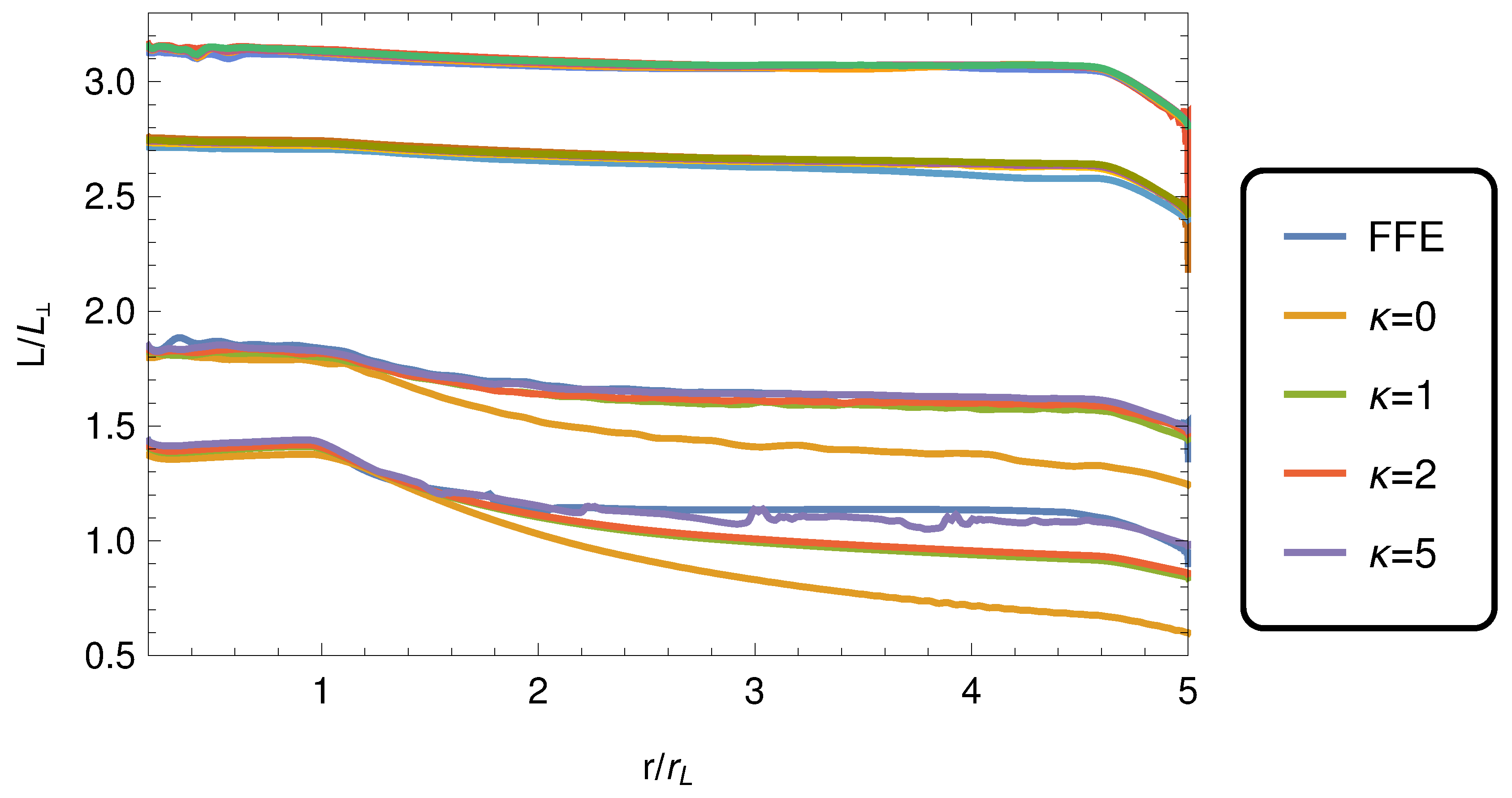
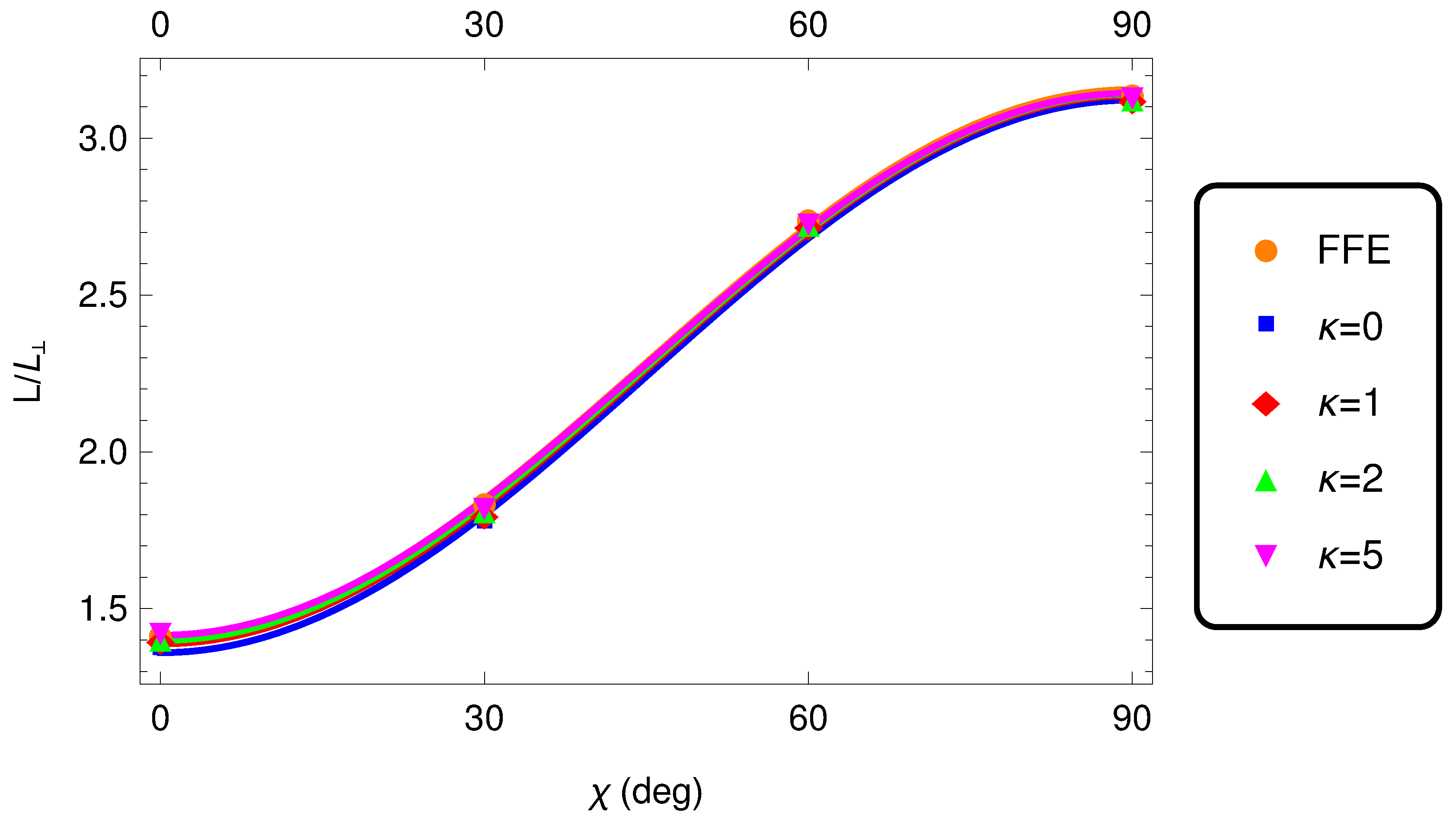

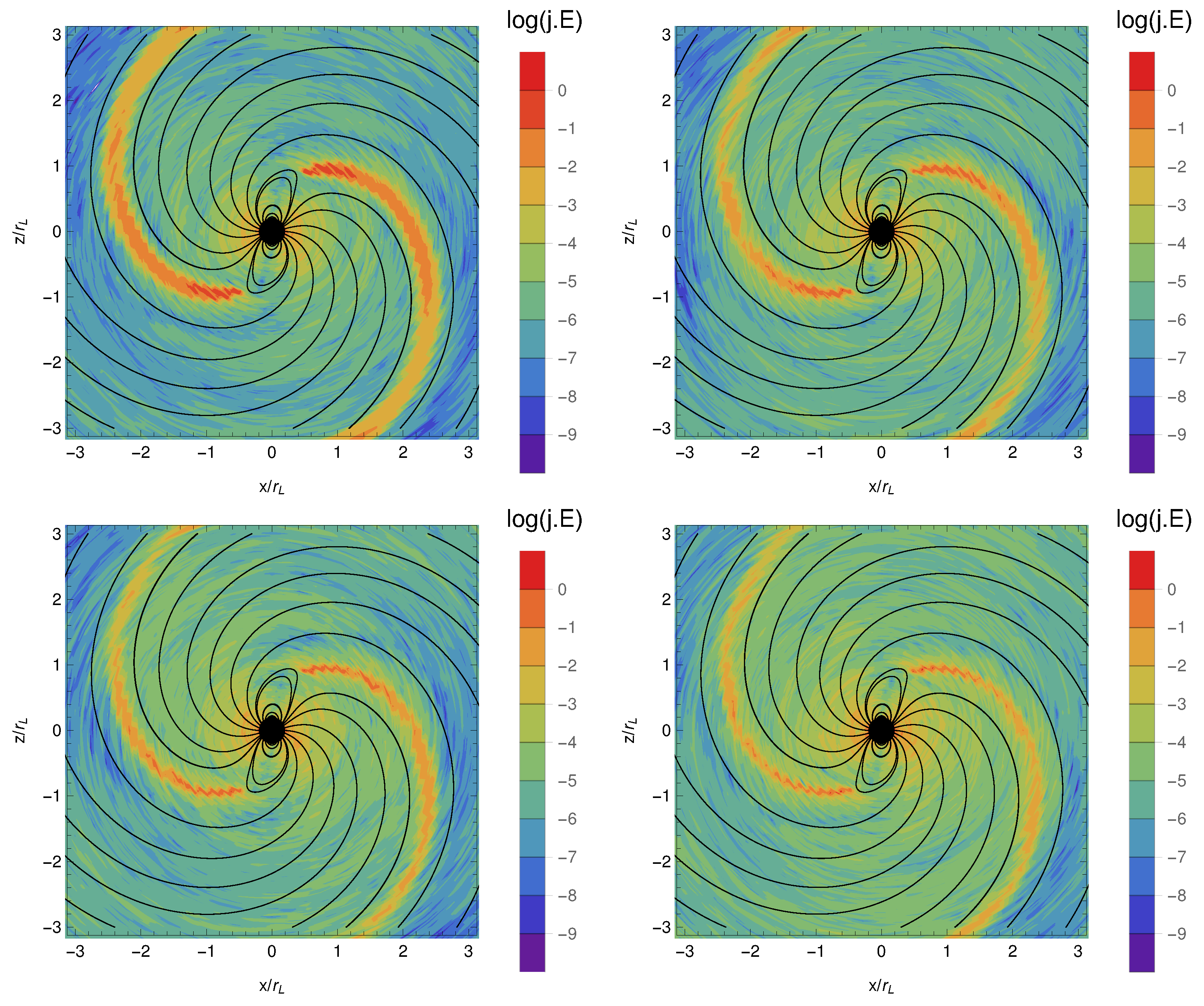
| Regime | a | b |
|---|---|---|
| FFE | 1.42 | 1.73 |
| 1.36 | 1.75 | |
| 1.39 | 1.76 | |
| 1.40 | 1.74 | |
| 1.42 | 1.73 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pétri, J. Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres. Universe 2020, 6, 15. https://doi.org/10.3390/universe6010015
Pétri J. Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres. Universe. 2020; 6(1):15. https://doi.org/10.3390/universe6010015
Chicago/Turabian StylePétri, Jérôme. 2020. "Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres" Universe 6, no. 1: 15. https://doi.org/10.3390/universe6010015
APA StylePétri, J. (2020). Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres. Universe, 6(1), 15. https://doi.org/10.3390/universe6010015




