Possible Origins and Properties of an Expanding, Dark Energy Providing Dark Multiverse
Abstract
1. Introduction
2. Summary of Previous Work on the DM-Concept
3. Two Scenarios for the Origin of the Dark Multiverse
3.1. Quasiclassical Approximation of the Quantum Regime
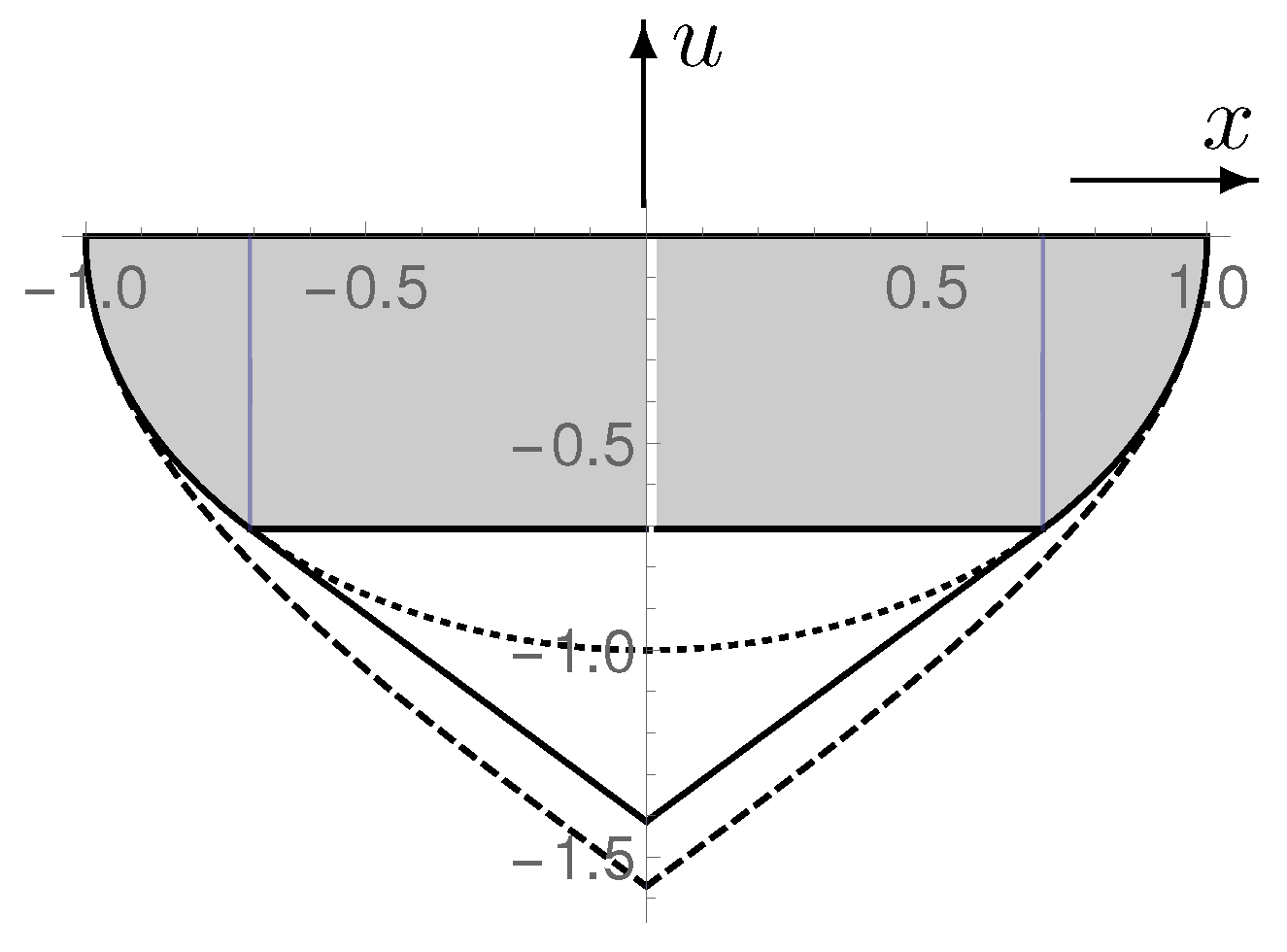
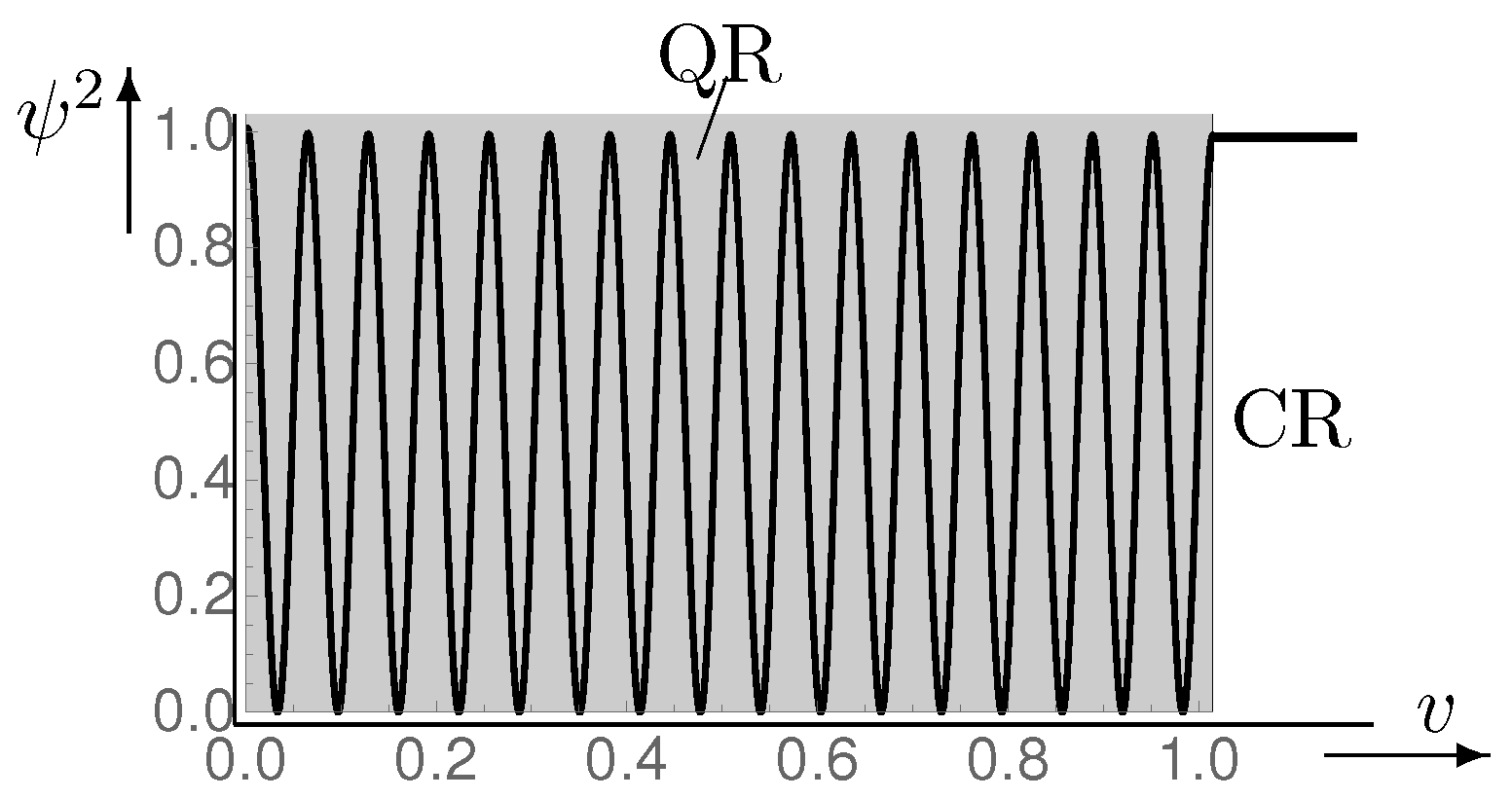
- Creation from nothing through tunneling. It is interesting to look into the question of whether a tunneling solution of Equation (8) is also possible when , as in the HH-approach, forms a semicircle (page 86 of Ref. [7]) so that no point is distinguished. Accordingly, we demand the validity of the equationand determine from Equation (8) in such a way that Equation (12) is satisfied. From the latter follows . Inserting this in Equation (8), eliminating u by use of Equation (12), and resolving with respect to yieldsThis treatment of the QR is an approximation which is getting worse the deeper one gets into it. In that sense, the negative values of the density may perhaps not be taken seriously. However, for , a singularity appears that is just what should be avoided in a quantum treatment.There are two ways to get out of this situation with a viable solution.1. the solution (13), yielding in the range , is continued into the range by a straight line with the slope following from Equation (8) for .2. The solution (13) is cut off at .Both possibilities are shown in Figure 1. The truncated HH-like solution, supplemented by two straight lines, has a peak which constitutes a distinguished point and must therefore be regarded as a tunneling solution of the VL-type. It represents an alternative to the solution (45) of Ref. [2], or , but does not comply with the HH-concept.
- HH-like primordial state. In the case of the solution cut off at with , the situation changes. If the two end points are connected by a horizontal straight line and the resulting corners rounded, one arrives at a solution, whose boundary, although not having a constant curvature, does not contain any point which could be interpreted as a temporal beginning. Although this solution results from the effort to construct a VL-like tunneling solution, it makes sense to accept it as a solution compatible with the HH-intention, so that the fourth spatial coordinate (which resulted from time by a Wick Rotation) is on equal footing to the others. It is obvious that the treatment of this model with the WdW-equation in the context of QG is much more appropriate because of its time independence.
3.2. Employing Quantum Gravity with Use of a Wheeler-De Witt Equation
3.2.1. Creation from Nothing
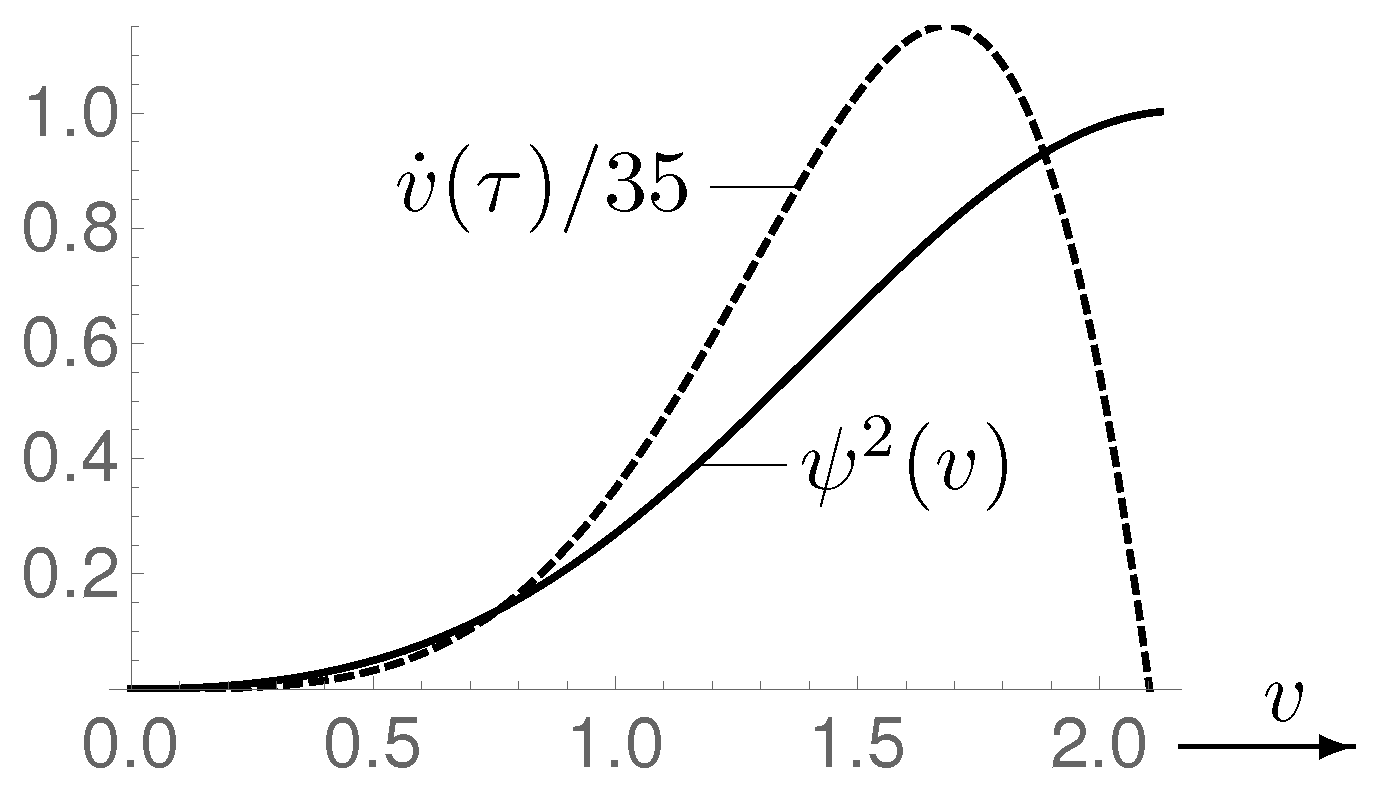
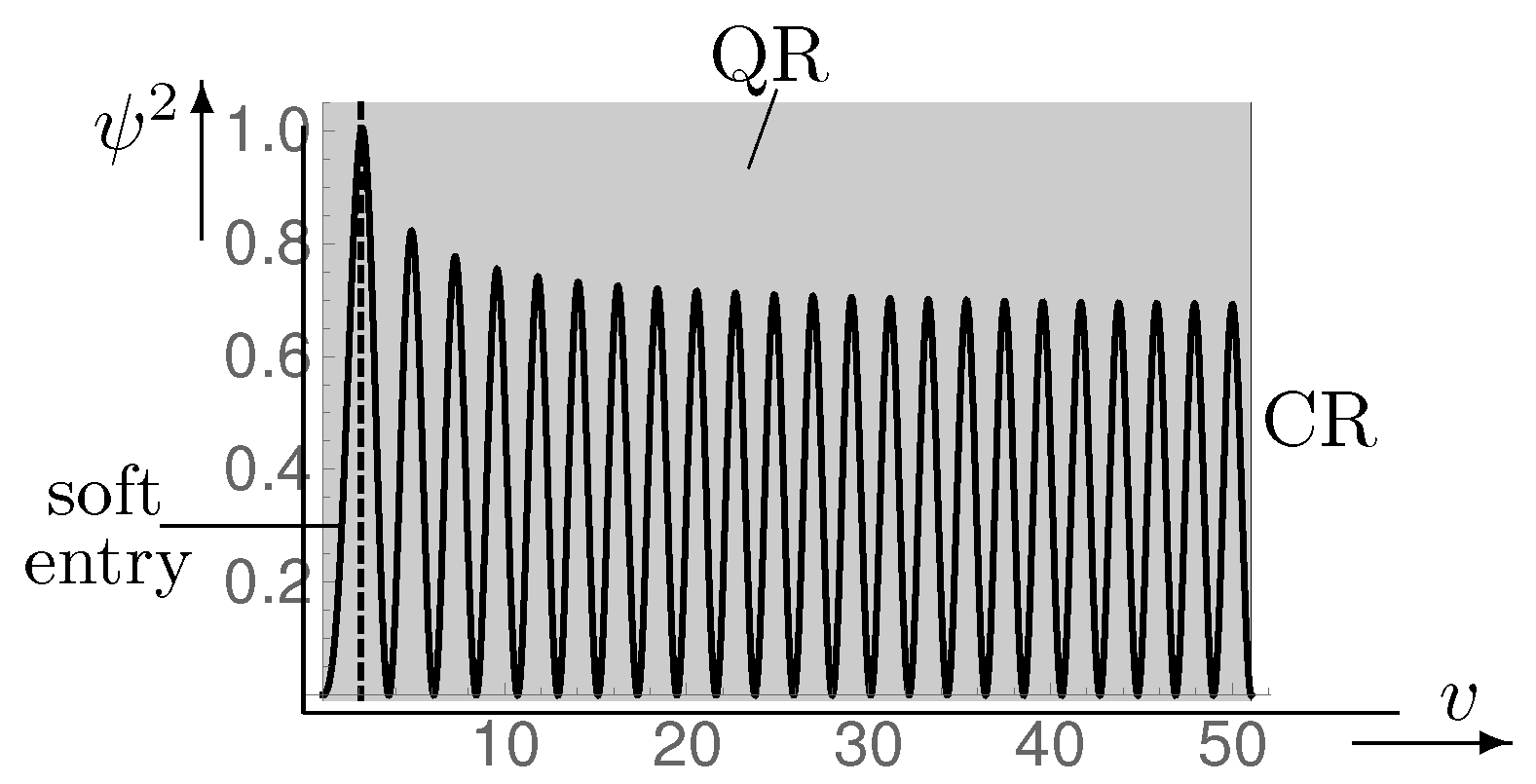
- Solution in the QR. In finding the right solution for a creation from nothing, we restrict ourselves to the option 2, for which we must solve Equation (A9) (with ),According to pages 203–206 of Ref. [11], a solution is considered the best, for which is largest at and decreases fast with increasing x because it roughly corresponds to the tunneling through the potential barrier given by the factor ∼ near in Equation (A8). We take the position that probability statements make sense only within an already existing multiverse, while conclusions based on such statements about the start of the tunneling are external, that is, they come from nowhere and must be regarded as meaningless. In the selection of a solution for an equivalent process, being suggested as a viable alternative on page 204 of Ref. [11] with reference to Ref. [10], we rely entirely on the probability interpretation of and choose so that with increasing v its square permanently increases. The solution shown in Figure 2 has this property; in the place where it is linked with the wave function for the CR, it satisfies the further constraint , which is explained further down. In the next paragraph, another argument is developed which supports our selection. Although derived with the goal of a tunneling process, this solution has nothing in common with the latter and therefore should be named differently, e.g., “soft entry”. Equation (14) has, of course, also a genuine tunneling solution, which can be treated in exactly the same way as our “soft entry” solution.
- Interpretation. Contributions to the literature on QG such as [14,15,16] give the impression that too little information is available for the assignment and interpretation of the WdW-equation. In Ref. [16], the interesting suggestion is made to use the de Broglie–Bohm interpretation for this purpose. According to this, from the representation of the wave function, particle trajectories satisfying are derived. Unfortunately, this is not possible in our case because the solutions of Equation (14) are real whence . Therefore, we develop an alternative, which, like the de Broglie–Bohm approach, leaves quantum mechanics completely unchanged and concerns only its interpretation. Under application to the solutions of Equation (14), it consists essentially in reversing the step that leads from the classical to the quantum-mechanical description. Specifically, for the spatial density of the quantum mechanical momentum, we make the ansatz( is obtained from Equations (A2)–(A4)) by which it is identified with the classical momentum. The multiplication of the left side by i constitutes the return to classical values and can be interpreted as reverse Wick rotation. With Equations (4), , , and going over to dimensionless quantities, and resolving with respect to , the last equation becomesThis means that the DM moves to larger values of until it terminates the entry process, if everywhere . The velocity and , up to a normalization factor the probability density of our “soft entry” solution, are depicted in Figure 2. From that, it becomes particularly clear that our solution is suitable for describing a creation from nothing. Regarding the dynamics, one could even say, at least for this solution that in the QR the role of time is taken over by the probability density .
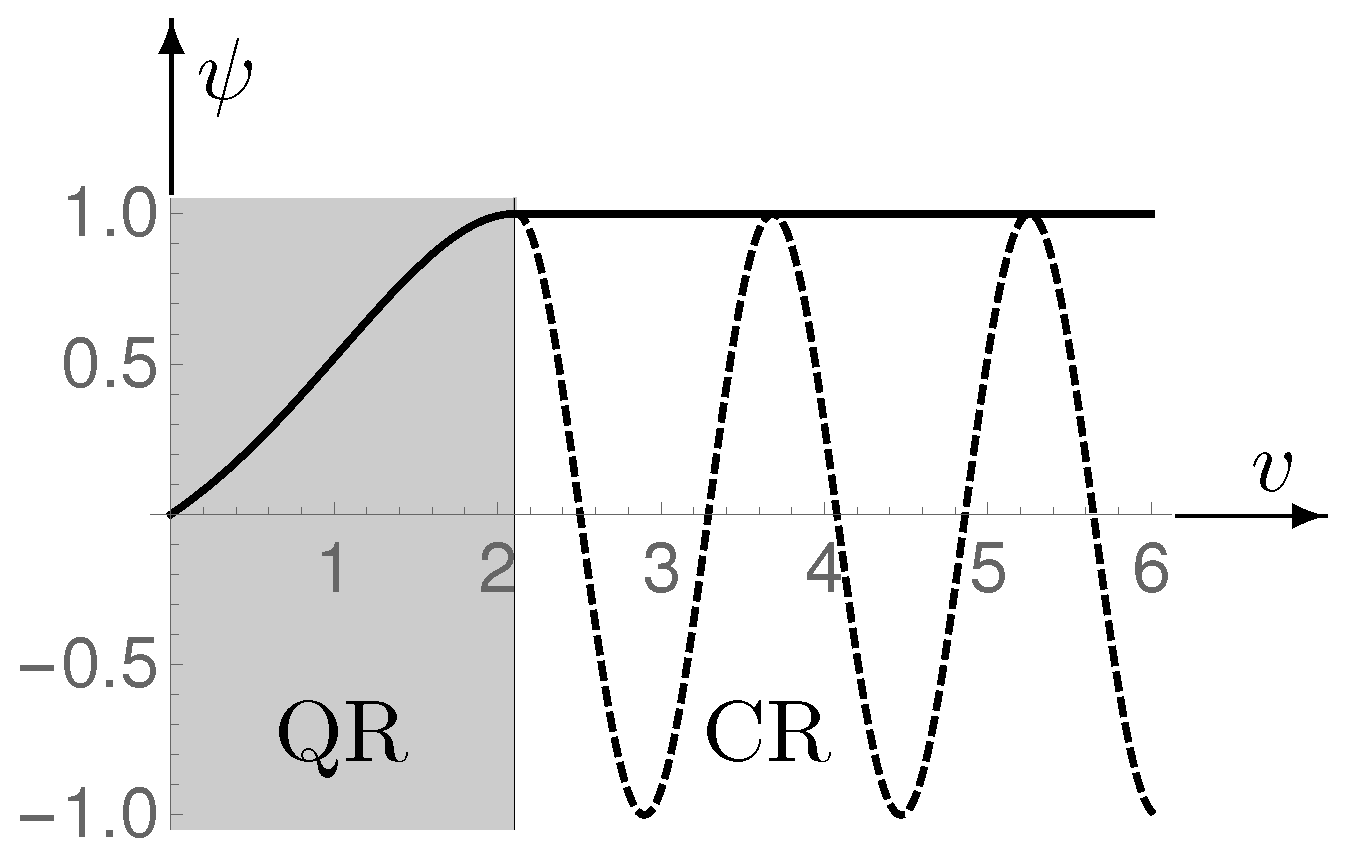
- Wave function of the the CR. We want to connect the wave function of the QR with that of the CR and have to determine the latter. For this, it is advantageous to use the interpretation of the classical solution based on Equations (5) and (6) with a friction term because then the minisuperspace contains only the one variable v. Furthermore, we can use the fact that we already know the classical solution (9), which satisfies the equationWe first consider the quantisation of the latter in the minisuperspace spanned by a or x resp. This can be done in the same way as in the derivation of Equation (A7). With , Equation (17) becomes . The equation corresponding to Equation (A2) is obtained by setting , and . With this, one can go directly to Equation (A6) and from there to dimensionless quantities, ending up at the WdW-equationIts general solution iswhere are Bessel functions, and a and b are integration constants. As mentioned in the introduction to Section 3.2, the solution depends on the volume . Furthermore, for , the envelope of the Bessel functions is whence, due to the factor in front of , the envelope of decays with u as . This solution would actually lead the DM-expansion to ever smaller probabilities, so absolutely not what one would reasonably expect.The situation turns for the better, if we employ the minisuperspace spanned by v. The corresponding WdW-equation can be easily deduced from Equation (18) by replacing in it by according to Equation (A10). The resulting equation isand has the solutionwhere is an integration constant. This solution must be continuously and with continuous derivative be connected to the solution for the QR, that of Equation (14). For the latter as well as for Equation (20), it holds that together with also is a solution, where C is a freely selectable constant. This allows us to freely set the value of one of the two solutions at the junction and to continuously join the other. Due to the extremely small value of , the derivative of the solution (21) for the CR is essentially equal to zero for all v. It follows that the derivative of the solution for the QR must be virtually zero at the junction. For the sake of simplicity, we therefore demand that the derivative of both solutions is exactly zero at the junction. With the boundary condition for the QR-solution at the border to the CR, it follows from Equation (16) that there also and thus must apply. Thus, QG requires the same boundary condition as the quasi-classical approximation.Figure 3 shows the solutions thus obtained. The joining point is or and not as in Section 3.1. This is due to the requirement and the fact that Equation (14) does not allow a solution with and . The classical solution (21) is entered twice in the figure, once over (horizontal straight line), and once over (dashed curve).
- Normalization of and corresponding probabilities. The freely selectable factor C in the solutions of Equations (14) and (20) allows a particularly simple fulfillment of the normalization condition (A11), for which onlymust be chosen. The normalized solution is then . This does not only apply to the solution for the QR, but also to combined solutions for the QR and the CR. For comparing states that have been traversed up to a certain time (corresponding volume ), it appears reasonable to extend the normalization range from up to . Over time, the upper boundary becomes larger and larger, with the result that the probability density of fixed and duly normalized intermediate states becomes ever smaller. Therefore, it is obviously useless to compare intermediate states of different normalization. In other words, it only makes sense to compare states with the same normalization, which amounts to determining the ratio of their probabilities. However, this is just as well obtained from a wave function without normalization, which is valid for the entire range. (This is the reason why our figures are not based on normalized wave functions.)For interpreting the dynamics of the system described by the wave function (21), the probability density can not be used as in the case of the “soft entry” solution. The reason is that it has many local maxima, and the system would remain with one of them, once it has reached it. This problem can be solved by considering the set of values between two successive zeros as a single quantum state of the classical system. This range has the size following from or and corresponds to the x-range orwhere Bohr radius. Regarding the dynamics, we assume that the system jumps from one state to the next in leaps of the length . In this interpretation, up to an uninteresting factor, the probability density of the various system states is given by the average of the local density over a half period, that is, byWith our solution, the probability of the different states does not decrease as with the solution (19) based on the usual minisuperspace. However, it does not increase as desired either. This can, however, be improved by taking advantage of the fact that the classical dynamic is an evolution in time, and by relating the probability density not to volume but to time (using instead of ). Settingfor we employ the classical solution: from and use of Equation (9), we get and finallywhere v does the jumps of height described above. Plotted above v, thus follows a staircase-like curve of the slope . Once again, the incremental probability of the individual quantum states can be considered as a substitute for time.
3.2.2. Modified HH-Approach
- Depictive model. In this section, we investigate an alternative to the HH-approach which differs comparatively more from the latter than the approach in Section 3.1. We now assume that the timeless primordial state is a 4D-sphere of radius in a 4D-space (coordinates ) of constant positive curvature, uniformly filled with DE of the 3D-density . It can be represented by the surfaceof a 5D-sphere in a Euclidean 5D-space. Assuming that the 3D-subspace spanned by is homogeneous and isotropic, its metric belongs to the class of metrics with line elementwhere and . For both and , a 3D-space of the same metric is transversed, so one can say that, for given a, two identical homogeneous, isotropic and closed 3D-spaces of Volume exist. Due to the factor , not present in the representation (24) of the surface of the initial 5D-sphere, the metric of its homogeneous and isotropic 3D-sub-spaces is a subclass of the metrics of Equation (24). We must therefore find out which restrictions result for the expansion parameter a. According to Equation (24), for , from which it follows that and . A maximum value of a follows from the fact that the total volume of 3D-sub-spaces, belonging to the range of permissible a values, may not be larger than the surface of the initially given sphere in the Euclidean 5D-space, and is given byThe surface of the Euclidean 5D-sphere is invariant under rotations , each of which leads to another set of homogeneous and isotropic 3D-sub-spaces, which for given all have the same metric and shape. All in all, we get a number3 of similar 3D-sub-spaces, which, based on their abundance, are equally probable. We assume that each of them can serve as a timeless primordial state of the DM. (An important difference to the HH-model is that the latter has only one coordinate which can turn from space-like to time-like; furthermore, the initial state is represented only by the lower part of the 4D-sphere, while the upper part is reserved for the evolution in time, see pages 80–83 of Ref. [7].)
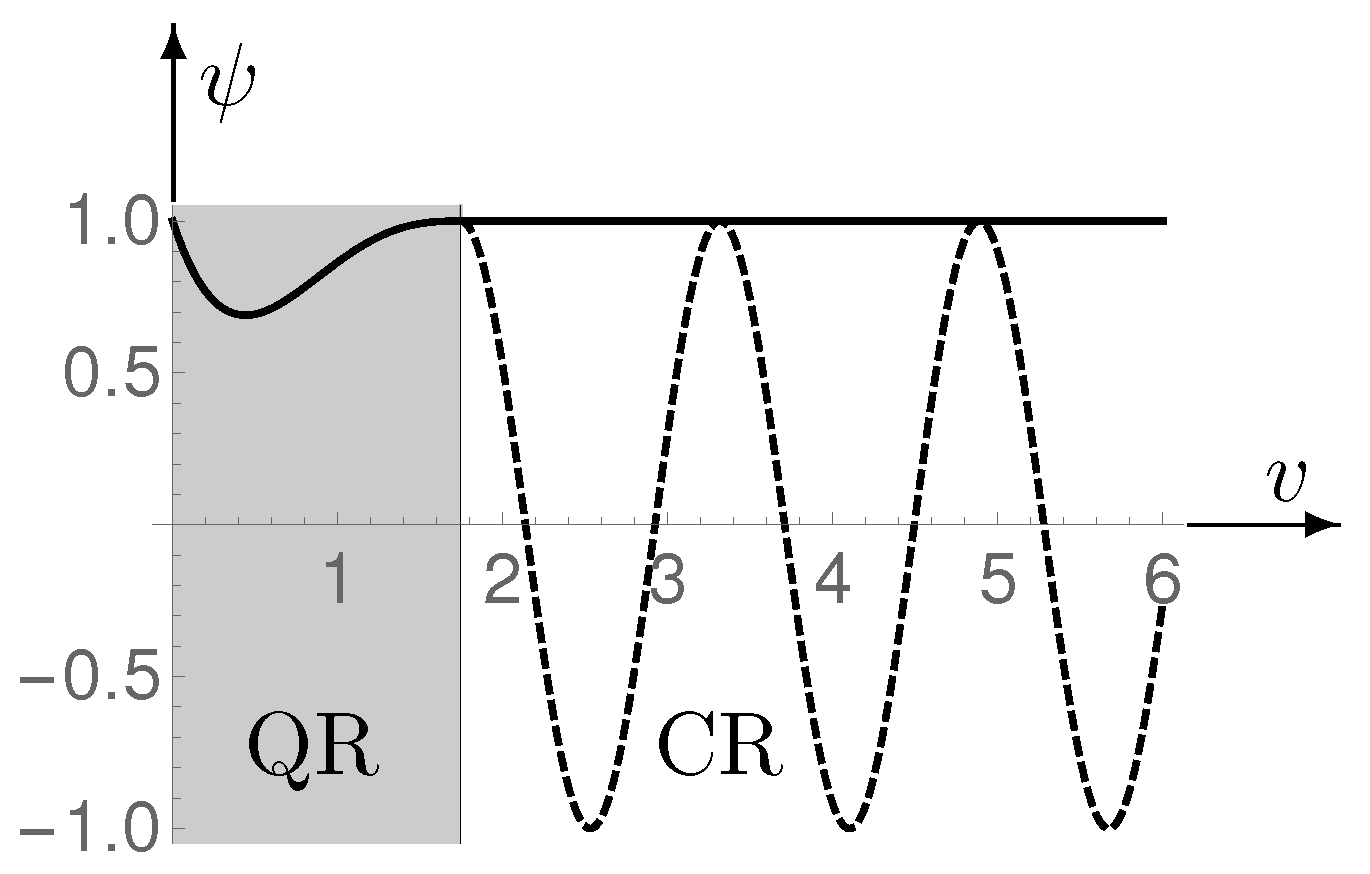
- Treatment in the framework of quantum gravity. For the above model, which is partly based on classical ideas, a suitable solution of the WdW-equation for the QR is to be found. Because we again want to have a continuous connection between the solutions for the QR and the CR, once again we impose the boundary conditions and . In order to implement our concept from above as accurately as possible, we look for a solution in the QR whose probability density is as constant as possible. This condition can only roughly be satisfied (see Figure 4). Furthermore, it appears reasonable to require for this timeless state that its total momentum disappears, i.e.,Therefore, must apply what can be easily satisfied. (Note that zero is the only value for which the total momentum is not imaginary.) In Figure 4, a solution satisfying the above requirements is entered together with the properly adapted classical solution , Equation (21).Both in the HH-concept, used as a model, and in the present concept, the transition from the time-independent primordial state in four spatial dimensions to a time-dependent evolution in three spatial dimensions represents a critical point. (In the original version of the HH-concept [6], it appears somewhat non-transparent [17] by being accomplished via transition probabilities. In a later contribution—see pages 85–86 of Ref. [7]—the transition is explicitly performed by linking the purely spatial solution for the QR with the time-dependent solution for the CR, the same as done by us in this and in Section 3.2.1.)A look at the averaged probability density in the CR does not reveal why the DM should make this transition. In our case, it could slightly be favored by the fact that each of the four spatial coordinates and, in addition, coordinates resulting from them by a rotation (if allowed by LQG) are eligible for the transition to a time coordinate. However, another means can help: because a transition from space to time is concerned, it offers itself to relate the probability density in the CR to the time interval as in Section 3.2.1. According to Equation (23), due to the prefactor , starts with an extremely small value which is smaller than by many orders of magnitude. However, since it is a probability assessment of the same state, it must be considered as equivalent. In this way, the transition from space to time is associated with a corresponding change in relating the probability densities. Thus, the transition from purely spatial to time-dependent states finally leads to an evolution with increasing probabilities.
4. Critical Comments on the Quantum Results
4.1. Notes on the Storage and Transmission of Information
4.2. Notes on the Primordial States
4.3. Primordial State with Large Volume
5. Properties of the CR-Solution
5.1. Initial Equilibrium between DE and Matter
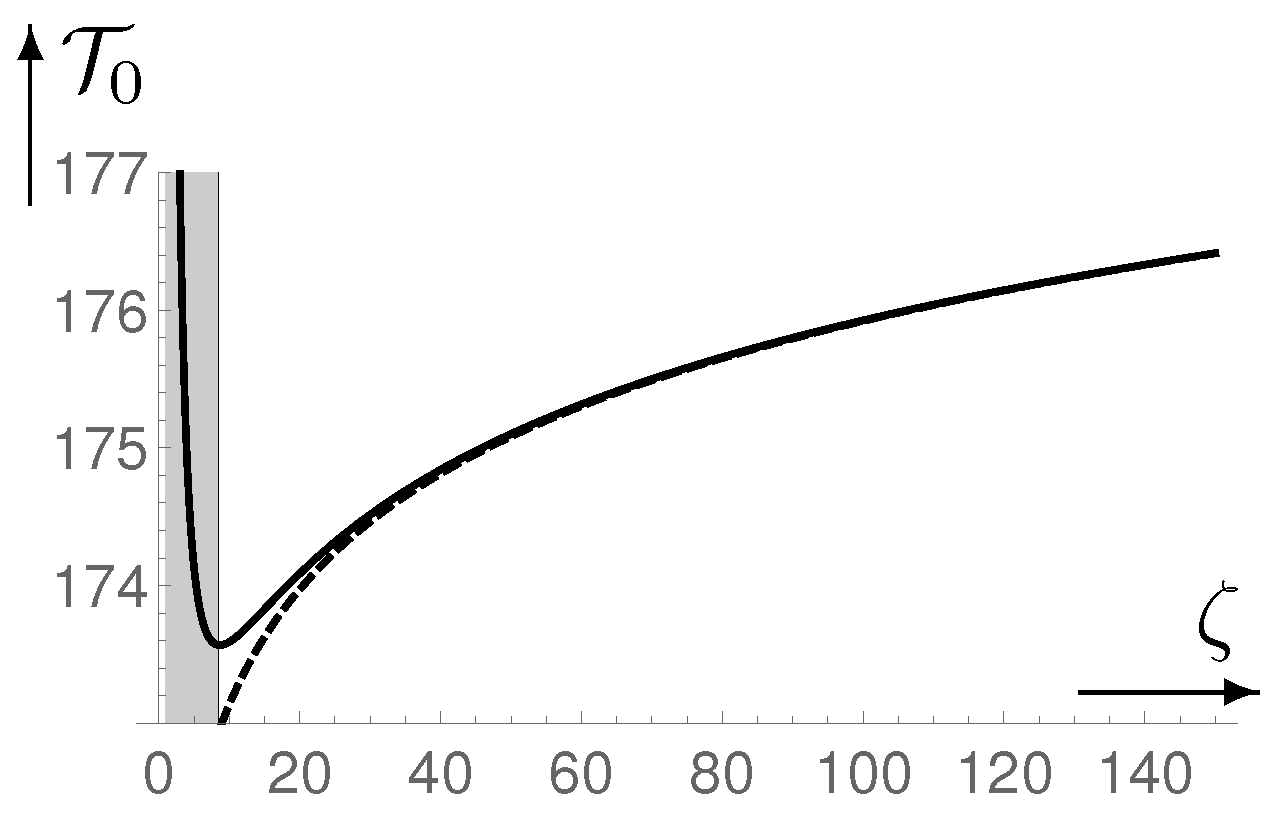
5.2. Minimum Age of the Dark Multiverse
5.3. Irreversibility of the Friction-Involving Interpretation
5.4. Behavior of the DE in Our Universe
6. Discussion
Funding
Conflicts of Interest
Abbreviations
| M | multiverse |
| U | our universe |
| DE | dark energy |
| DM | dark multiverse |
| QR | quantum regime |
| CR | classical regime |
| VL | Vilenkin–Linde |
| HH | Hartle–Hawking |
| QG | quantum gravity |
| LQG | loop quantum gravity |
| WdW | Wheeler–de Witt |
| FL | Friedmann–Lemaître |
Appendix A
References
- Rebhan, E. Model of a multiverse providing the dark energy of our universe. Int. J. Mod. Phys. A 2017, 32, 1750149. [Google Scholar] [CrossRef]
- Rebhan, E. Acceleration of cosmic expansion through huge cosmological constant progressively reduced by submicroscopic information transfer. Int. J. Mod. Phys. A 2018, 33, 1850137. [Google Scholar] [CrossRef]
- Vilenkin, A. Creation of universes from nothing. Phys. Lett. B 1982, 117, 25–28. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum origin of the universe. Nucl. Phys. B 1985, 252, 141–152. [Google Scholar] [CrossRef]
- Linde, A.D. Quantum creation of the inflationary universe. Lett. Nuovo Cim. 1984, 39, 401–405. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave function of the universe. Phys. Rev. B 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Hawking, S.; Penrose, R. The Nature of Space and Time; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- DeWitt, C.M.; Wheeler, J.A. (Eds.) Lectures in Mathematics and Physics. In Batelle Rencontres; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Coleman, S. Why there is nothing rather than something: A theory of the cosmological constant. Nucl. Phys. B 1988, 310, 643–668. [Google Scholar] [CrossRef]
- Linde, A. Particle Physics and Inflationary Cosmology; Contemporary Concepts Physics 5; Harwood Academic Publishers: Reading, UK, 1990; pp. 1–362. [Google Scholar]
- Rovelli, C. Reality Is Not What It Seems: The Journey to Quantum Gravity; Penguin Publishing Group: London, UK, 2017. [Google Scholar]
- Vilenkin, A.; Yamada, M. Tunneling wave function of the universe. arXiv 2018, arXiv:1808.02032v2. [Google Scholar] [CrossRef]
- Peres, A. Critique of the Wheeler-DeWitt Equation. In On Einstein’s Path. Essays in Honor of Engelbert Schucking; Harvey, A., Ed.; Springer: New York, NY, USA, 1999; pp. 367–379. [Google Scholar]
- Patrick, P. Using Trajectories in Quantum Cosmology. arXiv 2018, arXiv:1902.00796v1. [Google Scholar]
- Pinto-Neto, N.; Fabris, J.C. Quantum cosmology from the de Broglie–Bohm perspective. Class. Quantum Gravity 2013, 30, 143001. [Google Scholar] [CrossRef]
- Vilenkin, A. Many Worlds in One; Hill and Wang: New York, NY, USA, 2006; pp. 190–191. [Google Scholar]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory; Cambridge University Press: Camebridge, UK, 2014; Available online: http://www.cpt.univ-mrs.fr/~rovelli/IntroductionLQG.pdf (accessed on 27 May 2019).
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 23, 287. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Energy cost of information transfer. Phys. Rev. Lett. 1981, 46, 623–626. [Google Scholar] [CrossRef]
- Bremermann, H.J. Optimization through evolution and recombination. In Self-Organizing Systems 1962; Yovits, M.C., Jacobi, G.T., Goldstein, G.D., Eds.; Spartan Books: Washington, DC, USA, 1962; pp. 93–106. [Google Scholar]
| 1 | For later purposes (Section 4.1), we consider here a slightly more general case. Unfortunately, when Ref. [2] was written down for printing, in the derivation of Equation (26) there (Equation (7) here), two different types of calculation were mixed up, which resulted in two sign errors. For correction, the following substitutions must be made there: in Equation (22), and in the unnumbered equation immediately thereafter. The resulting Equation (26) is, however, correct. |
| 2 | Note that by this assumption or resp. the term in Equation (2) drops out, i.e., the friction term plays a role only in the CR. |
| 3 | Due to space-related quantum effects, this number could be quite small. |
| Generally | n = 3 | n = 4 | |
|---|---|---|---|
| 2/n | 2/3 | 1/2 | |
| (n−2)/n | 1/3 | 1/2 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rebhan, E. Possible Origins and Properties of an Expanding, Dark Energy Providing Dark Multiverse. Universe 2019, 5, 178. https://doi.org/10.3390/universe5080178
Rebhan E. Possible Origins and Properties of an Expanding, Dark Energy Providing Dark Multiverse. Universe. 2019; 5(8):178. https://doi.org/10.3390/universe5080178
Chicago/Turabian StyleRebhan, Eckhard. 2019. "Possible Origins and Properties of an Expanding, Dark Energy Providing Dark Multiverse" Universe 5, no. 8: 178. https://doi.org/10.3390/universe5080178
APA StyleRebhan, E. (2019). Possible Origins and Properties of an Expanding, Dark Energy Providing Dark Multiverse. Universe, 5(8), 178. https://doi.org/10.3390/universe5080178




