Phases of Hadron-Quark Matter in (Proto) Neutron Stars

Abstract

In the first part of this paper, we investigate the possible existence of a structured hadron-quark mixed phase in the cores of neutron stars. This phase, referred to as the hadron-quark pasta phase, consists of spherical blob, rod, and slab rare phase geometries. Particular emphasis is given to modeling the size of this phase in rotating neutron stars. We use the relativistic mean-field theory to model hadronic matter and the non-local three-flavor Nambu–Jona-Lasinio model to describe quark matter. Based on these models, the hadron-quark pasta phase exists only in very massive neutron stars, whose rotational frequencies are less than around 300 Hz. All other stars are not dense enough to trigger quark deconfinement in their cores. Part two of the paper deals with the quark-hadron composition of hot (proto) neutron star matter. To this end we use a local three-flavor Polyakov–Nambu–Jona-Lasinio model which includes the ’t Hooft (quark flavor mixing) term. It is found that this term leads to non-negligible changes in the particle composition of (proto) neutron stars made of hadron-quark matter.

1. Introduction

Neutron stars are extremely compact objects. They are typically about 20 to 30 km across and spin rapidly, often making many hundreds of rotations per second (pulsar PSR J1748-2446ad is the fastest spinning neutron star known to date, rotating at 716 Hz.) Depending on mass and rotational frequency, gravity compresses the matter in the core regions of neutron stars to densities that are several times higher than the density of atomic nuclei. At such enormous densities, atomic nuclei are squeezed so tightly together that new types of particles and novel states of matter may be created. These include the creation of hyperons and delta isobars and the formation of a mixed phase of hadrons and quarks deep in the central regions of neutron stars. As shown by Glendenning [1,2], the quark-hadro mixed phase region could segregate phases by net charge to minimize the total energy of the system, leading to the formation of a hadron-quark Coulomb lattice. Since this lattice is qualitatively similar to the hypothesized “nuclear pasta” structures in the crustal regions of neutron stars [1,2,3,4,5], it is referred to as hadron-quark pasta phase.1 All these possibilities make neutron stars and the events creating them (e.g., GW 170817) superb astrophysical laboratories for a wide range of physical studies. With observational data accumulating rapidly from both orbiting (HST, ATHENA, NICER) and ground based (skA, FAST, LIGO, VIRGO) observatories there has never been a more exciting time than today to study neutron stars.

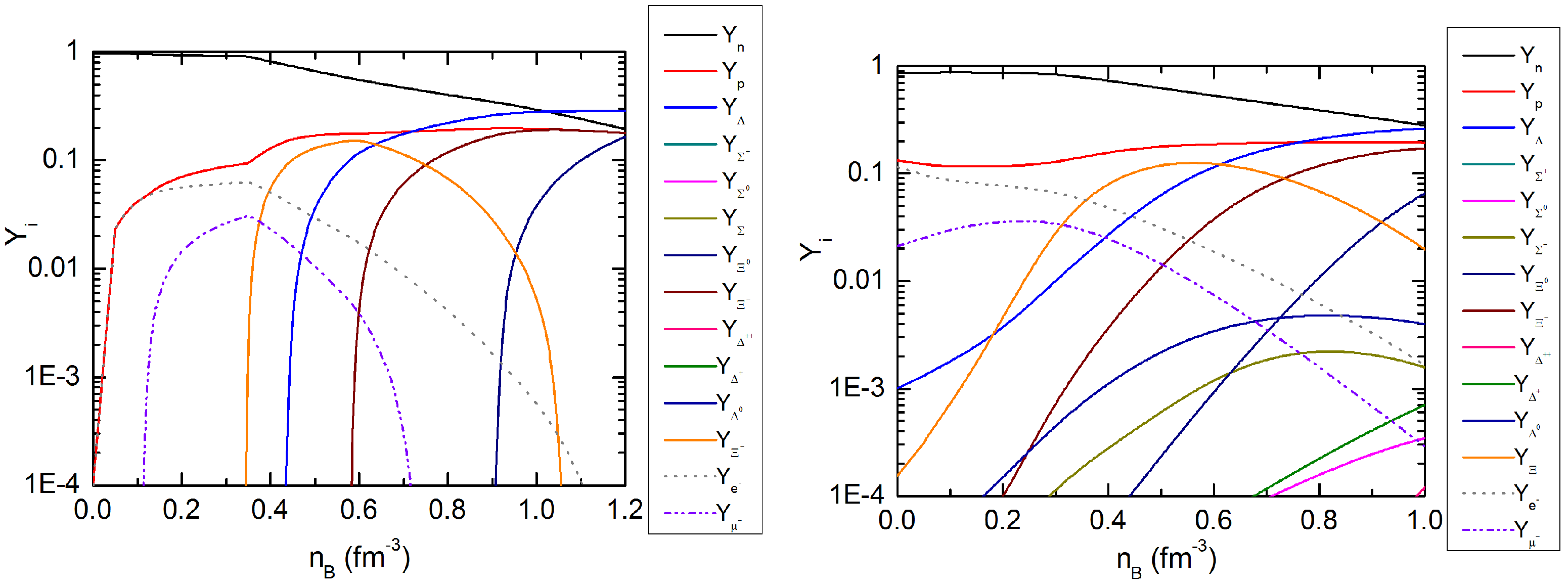
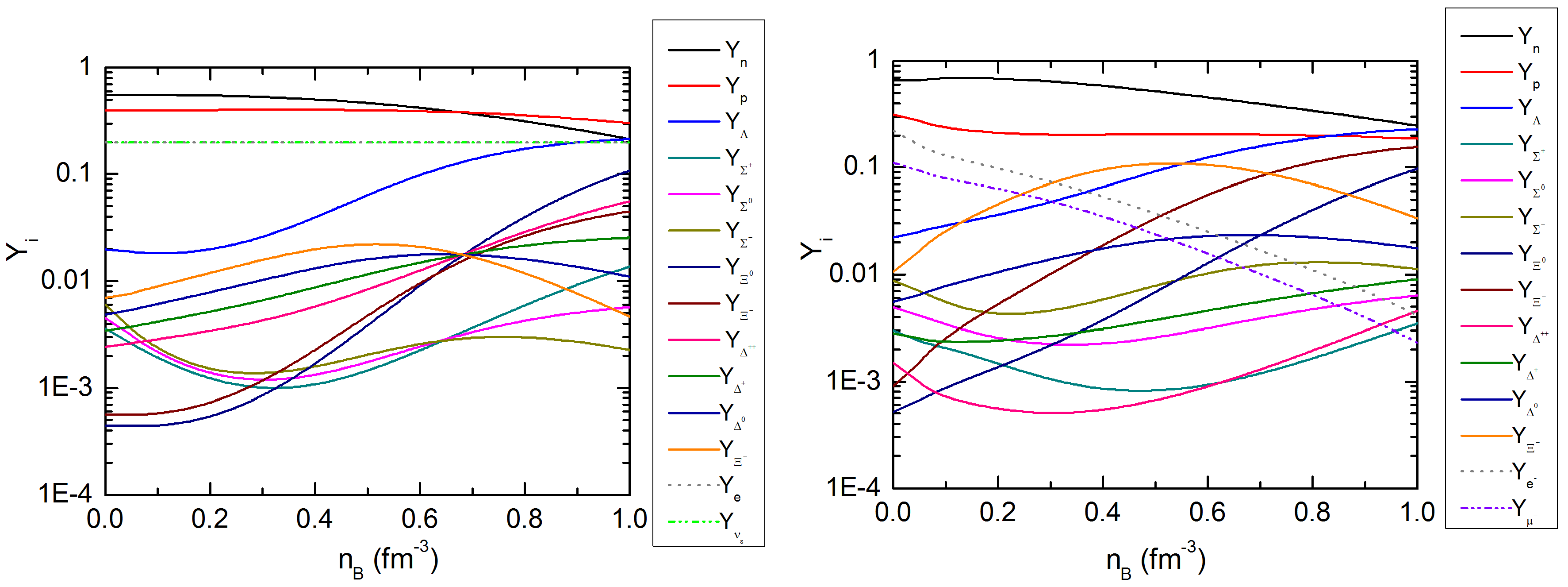
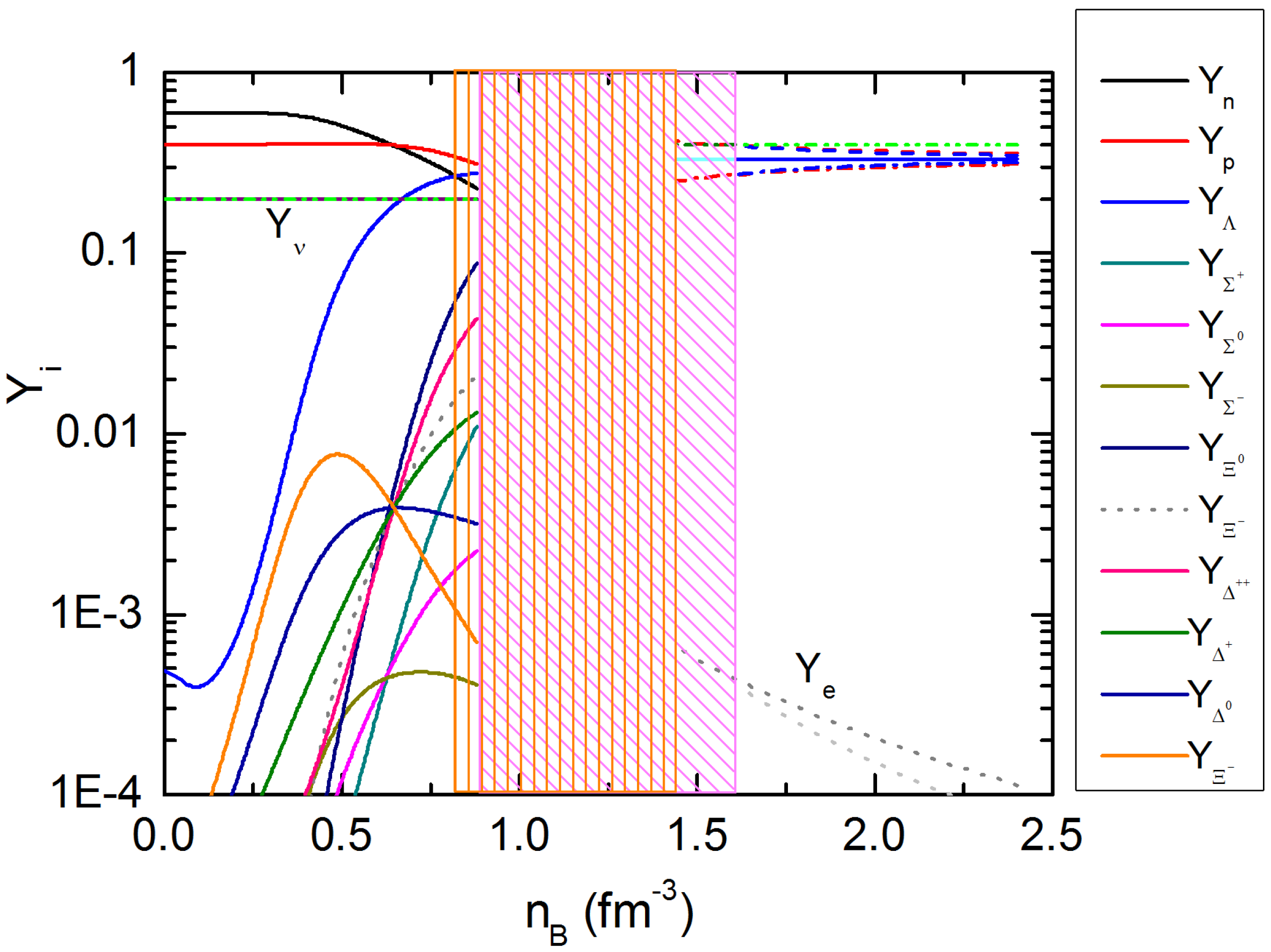
2. Hadronic Composition of Neutron Star Matter at Finite Temperature

A neutron star is born as a result of the gravitational collapse of the iron core of a massive evolved progenitor star (M∼8–$25M_{\odot }$) in a type-II supernova explosion. The iron core of such a star collapses when its mass reaches the Chandrasekhar limit, which depends on the mass of the progenitor star. Due to the Fermi pressure of the nucleons, the collapse stops when nuclear matter density is reached and the core bounces back. Shortly after core bounce (some 10 ms) a hot, lepton rich neutron star, called a proto-neutron star, is formed [8,9,10,11,12,13]. This star consists of a shocked envelope with an entropy per baryon of s∼4–10 (in units of the Boltzmann constant) and an unshocked core with s∼1. The envelope and the core contain nearly the same mass of about 0.6–0.8 $M_{\odot }$. During the so-called Kelvin-Helmholtz cooling phase the lepton number decreases in the proton-neutron star due to the loss of neutrinos and the proto-neutron star evolves in about 10 to 30 s to a hot, lepton poor neutron star with an entropy per baryon of s∼1–2. After several minutes, this hot neutron star cools to a cold neutron star with temperatures $T<1$ MeV, which then continues to slowly cool via neutrino and photon emission until its thermal radiation becomes too weak to be detectable with X-ray telescopes, after about ${10}^7$ years.

To study hot hadronic matter at conditions that exist in the cores of (proto) neutron stars, we use the relativistic nuclear mean-field (RMF) approximation and choose the GM1L, HV, and DD2 nuclear parametrizations listed in

Table 1. Properties of symmetric nuclear matter at saturation density for the hadronic parametrizations GM1L, DD2, and HV considered in this work.

Saturation Property	GM1L [1,14]	DD2 [21]	HV [22]
$n_0$ (fm${}^{-3}$)	0.153	0.149	0.145
$E_0$ (MeV)	−16.30	−16.02	−15.98
$K_0$ (MeV)	300.0	242.7	285
$m^{*}$/$m_N$	0.70	0.56	0.77
J (MeV)	32.5	32.8	36.8
$L_0$ (MeV)	55.0	55.3	–

that satisfy current constraints from studies of symmetric nuclear matter and from observations of neutron stars. The GM1L parametrization is based on the standard RMF model and was proposed in Refs. [1,14] but has been constructed to satisfy recent constraints from symmetric nuclear matter at saturation density while simultaneously being able to satisfy the $2.01M_{\odot }$ mass constraint set by PSR J0348+0432 with the inclusion of hyperons in SU(3) flavor symmetry. The DD2 parametrization is also based on the standard RMF approach but utilizes a density dependent meson-baryon coupling scheme, with the parameters of the density dependence set such that the model reproduces the properties of finite nuclei [15,16,17,18]. The lagrangian of the density-dependent relativistic mean-field model is given by [17,18,19,20]

$$\begin{array}{ccc}\mathcal{L}& =& {\sum }_B{\overline{\psi }}_B\left[{\gamma }_{\mu }[i{\partial }^{\mu }-g_{\omega B}\left(n\right){\omega }^{\mu }-g_{\rho B}\left(n\right)\mathit{\tau }·{\mathit{\rho }}^{\mu }]-[m_B-g_{\sigma B}\left(n\right)\sigma ]\right]{\psi }_B+\frac{1}{2}({\partial }_{\mu }\sigma {\partial }^{\mu }\sigma -m_{\sigma }^2{\sigma }^2)\hfill \\ & -& \frac{1}{3}{\tilde{b}}_{\sigma }{m}_N{\left[g_{\sigma N}\left(n\right)\sigma \right]}^3-\frac{1}{4}{\tilde{c}}_{\sigma }{\left[g_{\sigma N}\left(n\right)\sigma \right]}^4-\frac{1}{4}{\omega }_{\mu \nu }{\omega }^{\mu \nu }+\frac{1}{2}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }+\frac{1}{2}{m}_{\rho }^2{\mathit{\rho }}_{\mu }·{\mathit{\rho }}^{\mu }-\frac{1}{4}{\mathit{\rho }}_{\mu \nu }·{\mathit{\rho }}^{\mu \nu },\hfill \end{array}$$

(1)

where $g_{\sigma B}\left(n\right)$, $g_{\omega B}\left(n\right)$ and $g_{\rho B}\left(n\right)$ are density dependent meson-baryon coupling constants and $n={\sum }_{B=N,Y,\Delta }{n}_B$ is the total baryon number density. In this work we consider all members of the spin-$1/2$ baryon octet, which include nucleons $N=(n,p)$ and hyperons $Y=(\Lambda ,{\Sigma }^{-},{\Sigma }^0,{\Sigma }^{+},{\Xi }^{-},{\Xi }^0)$, as well as the spin $3/2$ delta isobar quartet $({\Delta }^{-},{\Delta }^0,{\Delta }^{+}$, ${\Delta }^{++})$. The density dependent coupling constants are given by [19]

$$g_{iB}\left(n\right)=g_{iB}\left(n_0\right)a_i\frac{1+b_i{(\frac{n}{n_0}+d_i)}^2}{1+c_i{(\frac{n}{n_0}+d_i)}^2},$$

(2)

for $i=\sigma ,\omega$, and

$$g_{\rho B}\left(n\right)=g_{\rho B}\left(n_0\right)\exp \left[-a_{\rho }\left(\frac{n}{n_0}-1\right)\right]$$

(3)

for the $\rho$ meson. This approach is parametrized to reproduce the properties of symmetric nuclear matter at saturation density $n_0$. The parametrizations used in this work (GM1L, HV, and DD2) are shown in Table 1. The properties listed in this table are the energy per nucleon ($E_0$), nuclear incompressibility ($K_0$), isospin asymmetry energy (J), and effective nucleon mass ($m^{*}/m_N$). The isovector meson-baryon coupling constant is treated density-dependent. Its numerical value has been fit to the slope of the asymmetry energy ($L_0$) at $n_0$.

The parameters $a_i$, $b_i$, $c_i$, $d_i$, and $a_{\rho }$ in Equations (2) and (3) are fixed by the binding energies, charge and diffraction radii, spin-orbit splittings, and the neutron skin thickness of finite nuclei. The density dependence of the meson-baryon couplings of the DD2 parametrization eliminates the need for non-linear self-interactions of the $\sigma$-meson field. The non-linear terms [23,24] of the $\sigma$-meson field in Equation (1) therefore only contribute to the GM1L and HV models. The meson–hyperon coupling constants have been determined following the Nijmegen extended soft core (ESC08) model [25]. The relative isovector meson-hyperon coupling constants were scaled with the hyperon isospin. For the $\Delta$-isobar we used $x_{\sigma \Delta }=x_{\omega \Delta }=1.1$ and $x_{\rho \Delta }=1.0$, where $x_{i\Delta }=g_{i\Delta }/g_{iN}$ (for details, see Ref. [14]).

The meson mean-field equations following from Equation (1) are given by

$$\begin{array}{ccc}\hfill m_{\sigma }^2\overline{\sigma }& =& \sum _B{g}_{\sigma B}\left(n\right)n_B^s-{\tilde{b}}_{\sigma }{m}_N{g}_{\sigma N}\left(n\right){\left(g_{\sigma N}\left(n\right)\overline{\sigma }\right)}^2-{\tilde{c}}_{\sigma }{g}_{\sigma N}\left(n\right){\left(g_{\sigma N}\left(n\right)\overline{\sigma }\right)}^3,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill m_{\omega }^2\overline{\omega }& =& \sum _B{g}_{\omega B}\left(n\right)n_B,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill m_{\rho }^2\overline{\rho }& =& \sum _B{g}_{\rho B}\left(n\right)I_{3B}{n}_B,\hfill \end{array}$$

(6)

where $I_{3B}$ is the 3-component of isospin and $n_B^s$ and $n_B$ are the scalar and particle number densities of each baryon B, given by

$$\begin{array}{ccc}\hfill n_B^s& =& {\gamma }_B\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\left[f_{B-}\left(p\right)-f_{B+}\left(p\right)\right]\frac{m_B^{*}}{E_B^{*}},\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill n_B& =& {\gamma }_B\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\left[f_{B-}\left(p\right)-f_{B+}\left(p\right)\right].\hfill \end{array}$$

(8)

The quantity $f_{B\mp }$ denotes the Fermi-Dirac distribution function, and $E_B^{*}$ stands for the effective single-baryon energy,

$$f_{B\mp }\left(p\right)=\frac{1}{exp\left[\frac{E_B^{*}\left(p\right)\mp {\mu }_B^{*}}{T}\right]+1},E_B^{*}\left(p\right)=\sqrt{p^2+m_B^{*2}}.$$

(9)

The quantity ${\gamma }_B=2J_B+1$ accounts for the spin degeneracy, and $m_B^{*}=m_B-g_{\sigma B}\left(n\right)\overline{\sigma }$ denotes the effective baryon mass. The effective baryon chemical potential, ${\mu }_B^{*}$, is defined as

$${\mu }_B^{*}={\mu }_B-g_{\omega B}\left(n\right)\overline{\omega }-g_{\rho B}\left(n\right)\overline{\rho }{I}_{3B}-\tilde{R},$$

(10)

where $\tilde{R}$ is the so-called rearrangement term given by

$$\begin{array}{c}\hfill \tilde{R}=\sum _B\left(\frac{\partial g_{\omega B}\left(n\right)}{\partial n}{n}_B\overline{\omega }+\frac{\partial g_{\rho B}\left(n\right)}{\partial n}{I}_{3B}{n}_B\overline{\rho }-\frac{\partial g_{\sigma B}\left(n\right)}{\partial n}{n}_B^s\overline{\sigma }\right),\end{array}$$

(11)

which is important for achieving thermodynamic consistency. The total baryonic pressure of the matter follows from

$$\begin{array}{ccc}\hfill P& =& \sum _B\frac{{\gamma }_B}{3}\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\frac{p^2}{E_B^{*}}[f_{B-}\left(p\right)+f_{B+}\left(p\right)]-\frac{1}{2}{m}_{\sigma }^2{\overline{\sigma }}^2+\frac{1}{2}{m}_{\omega }^2{\overline{\omega }}^2+\frac{1}{2}{m}_{\rho }^2{\overline{\rho }}^2\hfill \\ & -& \frac{1}{3}{\tilde{b}}_{\sigma }{m}_N{\left(g_{\sigma N}\left(n\right)\overline{\sigma }\right)}^3-\frac{1}{4}{\tilde{c}}_{\sigma }{\left(g_{\sigma N}\left(n\right)\overline{\sigma }\right)}^4+n\tilde{R},\hfill \end{array}$$

(12)

while the energy density of the system follows from the standard Gibbs relation $ϵ(P,T,n)=-P+TS+{\sum }_B{\mu }_B{n}_B$.

To complete the description of the matter in the cores of (proto) neutron stars, leptons (L) need to be included in the treatment. Leptons can be treated as free, relativistic Fermions whose total thermodynamic potential is given by (${\gamma }_L=2$)

$${\Omega }_{\mathrm{L}}=-\sum _L\frac{{\gamma }_L}{3}\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\frac{p^2}{E_L}[f_{L-}\left(p\right)+f_{L+}\left(p\right)],$$

(13)

with

$$\begin{array}{ccc}\hfill f_{L\mp }\left(p\right)& =& \frac{1}{exp\left[\frac{E_L\left(p\right)\mp {\mu }_L}{T}\right]+1},E_L\left(p\right)=\sqrt{p^2+m_L^2}.\hfill \end{array}$$

(14)

The sum in Equation (13) is over electrons and muons (with masses $m_L$) as well as over massless neutrinos, ${\nu }_e$. Neutrinos do not contribute to cold neutron stars matter, but are present in the cores of newly formed proto-neutron stars.

3. Electric Charge Neutrality, Chemical Equilibrium and Conserved Charges

The composition of the matter in (proto-) neutron stars is constrained by the conditions of electric charge neutrality, chemical equilibrium, and baryon number conservation. Electric charge neutrality and baryon number conservation leads to

$$\sum _B{q}_B{n}_B+\sum _L{q}_L{n}_L=0\mathrm{and}\sum _B{n}_B-n=0,$$

(15)

where $q_B$ and $q_L$ denote the electric charges of baryons and leptons, respectively, and $n_B$ and $n_L$ are the respective number densities of these particles. The condition of chemical equilibrium among the different particle species present at a given density reads

$${\mu }_B={\mu }_n+q_B({\mu }_e-{\mu }_{{\nu }_e}),$$

(16)

where ${\mu }_n$, ${\mu }_e$, and ${\mu }_{{\nu }_e}$ are the chemical potentials of neutrons, electrons, and neutrinos, respectively. The lepton chemical potentials obey

$${\mu }_e={\mu }_{\mu }+{\mu }_{{\nu }_e}+{\mu }_{{\overline{\nu }}_{\mu }}.$$

(17)

Neutrinos are trapped in the core during the very early stages in the life of a neutron star. Accepted lepton fractions at that stage of stellar evolution are [8]

$$\begin{array}{ccc}\hfill Y_{Le}& =& \frac{n_e+n_{{\nu }_e}}{n}=\xi \simeq 0.4,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill Y_{L\mu }& =& \frac{n_{\mu }+n_{{\nu }_{\mu }}}{n}=0.\hfill \end{array}$$

(19)

During this stage the system is characterized by three independent chemical potentials, ${\mu }_n$, ${\mu }_e$, and ${\mu }_{{\nu }_e}$, which, together with the hadronic field equations and the conditions of electric charge neutrality and baryon number conservation, determine the composition of hot (proto-) neutron star matter. The condition $Y_{L\mu }=0$ has to be imposed in addition since no muons are present when neutrinos are trapped. When a proto-neutron star cools down, the matter in the core becomes transparent to neutrinos quickly, leading to ${\mu }_{{\nu }_e}={\mu }_{{\overline{\nu }}_{\mu }}=0$ for cold neutron stars. In this case, the number of independent chemical potentials reduces from three to two (${\mu }_n$ and ${\mu }_e$). Figure 1 shows the equation of state (EoS) of neutron star matter at three different temperatures. The matter is composed of neutrons, protons, hyperons, delta isobars, and leptons in chemical equilibrium with each other. Since the number of hyperons and delta isobars in the matter increases drastically with temperature, the pressure at a given density drops for increasing temperatures.

In Figure 2 and Figure 3 we show the particle compositions of neutron stars at zero as well as finite temperature. As can be seen, the complexity of the compositions intensifies quickly with increasing temperature, lepton content, and assumptions about the neutrino population.

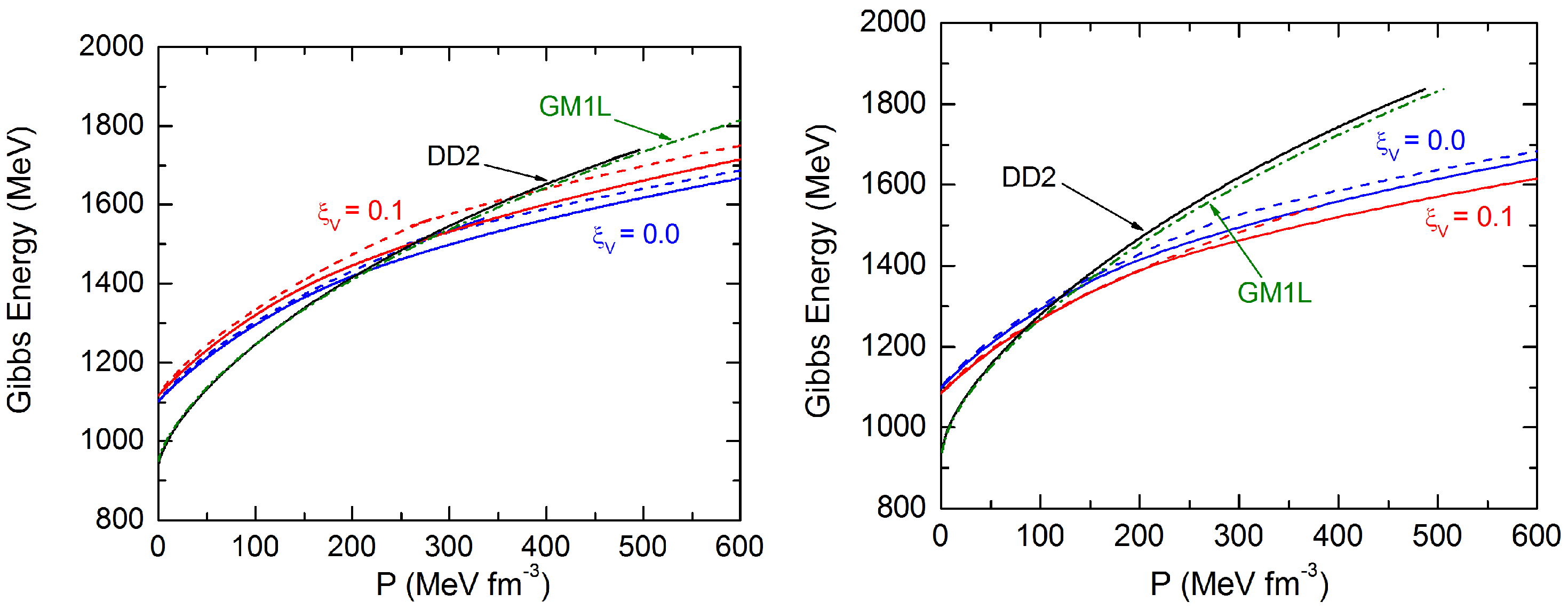
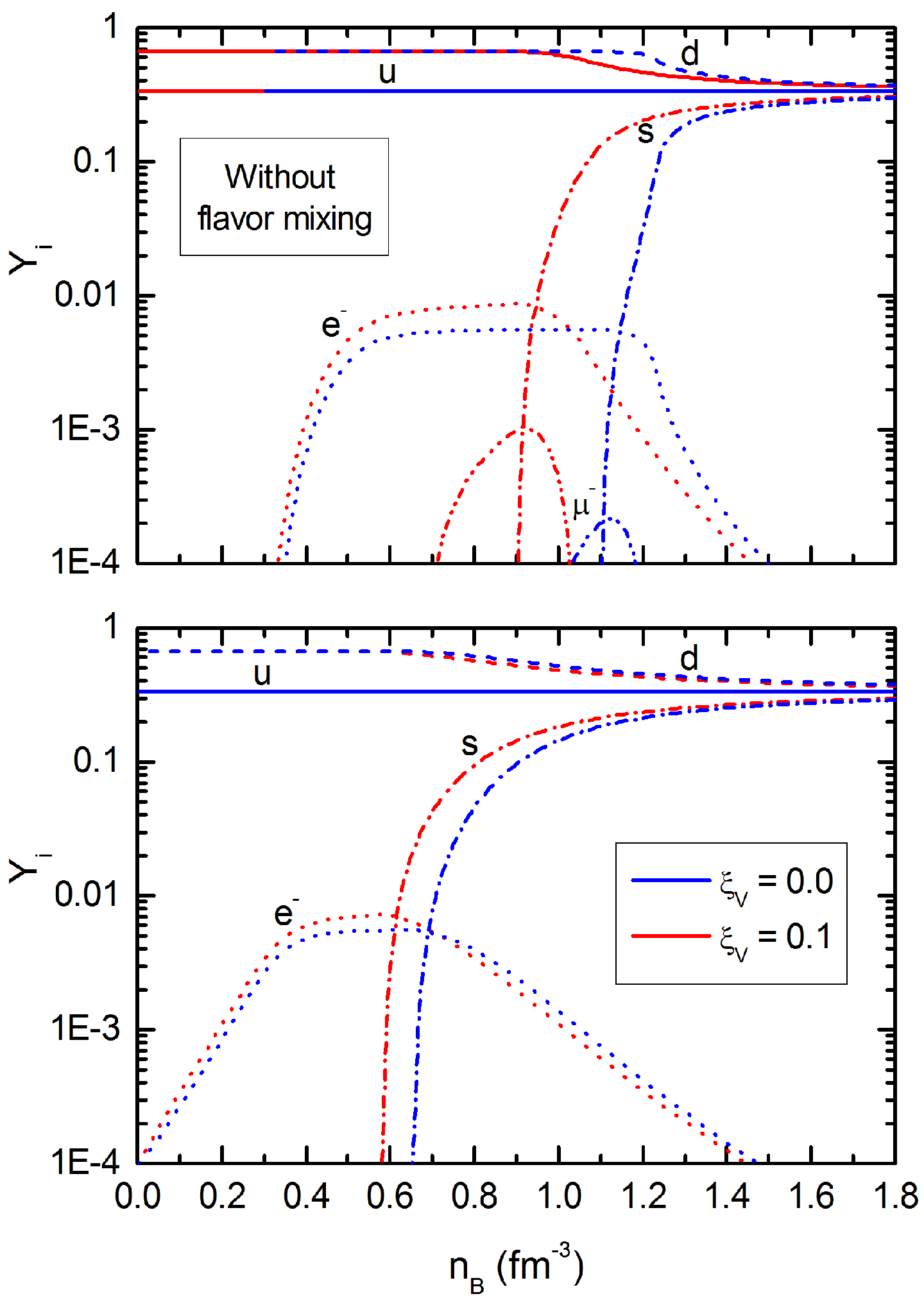
4. Quark Matter Modeled with the Non-Local NJL Model

A model widely used to describe the properties of deconfined 3-flavor quark matter is the Nambu–Jona-Lasinio model [26]. In the following, we present a non-local extension of this model (denoted n3NJL). The effective action of this model reads (for details, see Refs. [27,28])

$$\begin{array}{ccc}{S}_E& =& \int d^{4}x\left\{\overline{\psi }\left(x\right)\left[-i\cancel{\partial }/+\widehat{m}\right]\psi \left(x\right)-\frac{G_S}{2}\left[j_a^S\left(x\right)j_a^S\left(x\right)+j_a^P\left(x\right)j_a^P\left(x\right)\right]\right.\hfill \\ & & -\frac{H}{4}{T}_{abc}\left[j_a^S\left(x\right)j_b^S\left(x\right)j_c^S\left(x\right)-3j_a^S\left(x\right)j_b^P\left(x\right)j_c^P\left(x\right)\right]\left.-\frac{G_V}{2}\left[j_V^{\mu }\left(x\right)j_{V,\mu }\left(x\right)\right]\right\},\hfill \end{array}$$

(20)

where $\psi \equiv {(u,d,s)}^T$ and $\widehat{m}$ denotes the current quark mass matrix give by $\widehat{m}=\mathrm{diag}(m_u,m_d,m_s)$. The currents $j_a^{S,P}\left(x\right)$ and $j_V^{\mu }\left(x\right)$ depend on form factors which describe non-local interactions among the quarks. The quantity $T_{abc}$ in the ’t Hooft term accounts for quark-flavor mixing. The current quark mass $\overline{m}$ of up and down quarks and the coupling constants $G_S$ and H in Equation (20) are fitted to the pion decay constant, $f_{\pi }$, and meson masses $m_{\pi }$, $m_K$, $m_{{\eta }^{\prime }}$ [29,30]. This leads to $\overline{m}=6.2$ MeV, $\Lambda =706.0$ MeV, $G_S{\Lambda }^2=15.04$, and $H{\Lambda }^5=-337.71$. The current mass of the strange quark is treated as a free parameter. Its value is set to $m_s=140.7$ MeV. It is customary to express the vector interaction, $G_V$, in terms of the strong coupling constant, $G_S$, according to ${\xi }_V\equiv G_V/G_S$. The value of ${\xi }_V$ is then typically varied from 0 to around $0.09$.

The expression of the thermodynamic potential that follows from $S_E$ of Equation (20) is given, for the mean-field approximation, by

$$\begin{array}{c}\Omega =-\frac{3}{{\pi }^3}{\sum }_{f=u,d,s}{\int }_0^{\infty }d{p}_0{\int }_0^{\infty }dp\ln \left\{\left[{\widehat{\omega }}_f^2+M_f^2\left({\omega }_f^2\right)\right]\frac{1}{{\omega }_f^2+m_f^2}\right\}-\frac{3}{{\pi }^2}{\sum }_{f=u,d,s}{\int }_0^{\sqrt{{\mu }_f^2-m_f^2}}dp{p}^2\times \hfill \\ \left[\left({\mu }_f-E_f\right)\theta \left({\mu }_f-m_f\right)\right]-\frac{1}{2}\left[{\sum }_{f=u,d,s}\left({\overline{\sigma }}_f{\overline{S}}_f+\frac{G_S}{2}{\overline{S}}_f^2\right)+\frac{H}{2}{\overline{S}}_u{\overline{S}}_d{\overline{S}}_s\right]-{\sum }_{f=u,d,s}\frac{{\overline{\omega }}_f^2}{4G_V}.\hfill \end{array}$$

(21)

The quantities ${\overline{\sigma }}_f$, ${\overline{\omega }}_f$, and ${\overline{S}}_f$ denote the scalar, vector, and auxiliary mean-fields of quarks, respectively. The quantity $E_f$ denotes the energy-momentum relation of free quarks given by $E_f=\sqrt{{\mathit{p}}^2+m_f^2}$. The symbol ${\omega }_f^2$ stands for ${\omega }_f^2={(p_0+i{\mu }_f)}^2+{\mathit{p}}^2$. The relation of the momentum-dependent quark masses reads $M_f({\omega }_f^2)=m_f+{\overline{\sigma }}_{f}g({\omega }_f^2)$. The quantities $g({\omega }_f^2)=\exp (-{\omega }_f^2/{\Lambda }^2)$ are Gaussian form factors, which describe the nonlocal nature of the interactions among quarks [28]. The quantities ${\overline{S}}_f$ denote auxiliary mean fields [31]. The scalar and vector quark mean-fields are obtained by minimizing the thermodynamic potential, $\partial \Omega /\partial {\overline{\sigma }}_f=0$ and $\partial \Omega /\partial {\overline{\omega }}_f=0$. The number densities of quarks are obtained from the thermodynamic potential as $n_f=\partial \Omega /\partial {\mu }_f$.

To determine the equation of state of the system is given in terms of the quark mean-fields ${\overline{\sigma }}_f$, ${\overline{\omega }}_f$ and the neutron and electron chemical potentials ${\mu }_n$ and ${\mu }_e$. The pressure $p_Q$ and the energy density ${ϵ}_Q$ of the system at zero temperature are given by

$$P_Q={\Omega }_0-\Omega ,$$

(22)

and

$${ϵ}_Q=-P_Q+\sum _{f=u,d,s}{n}_f{\mu }_f+\sum _{\lambda =e^{-},{\mu }^{-}}{n}_{\lambda }{\mu }_{\lambda },$$

(23)

where ${\Omega }_0$ is chosen such that $P_Q$ vanishes at $T=\mu =0$ [27,28].

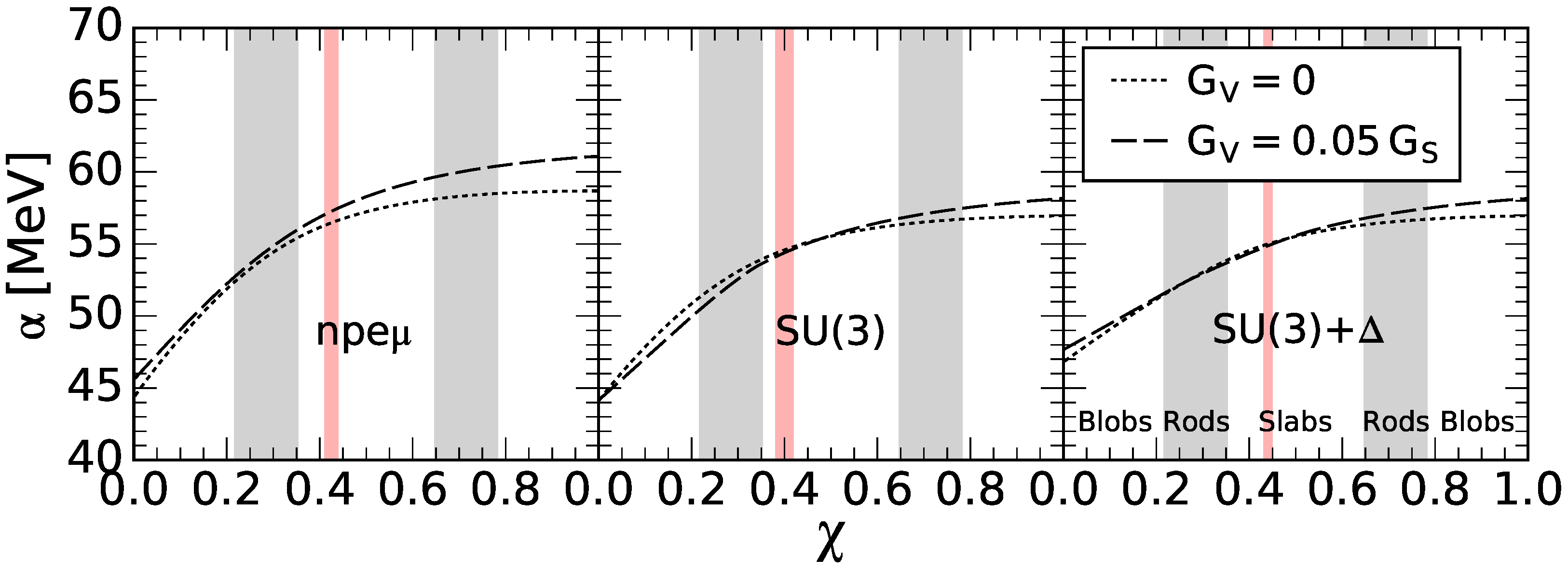
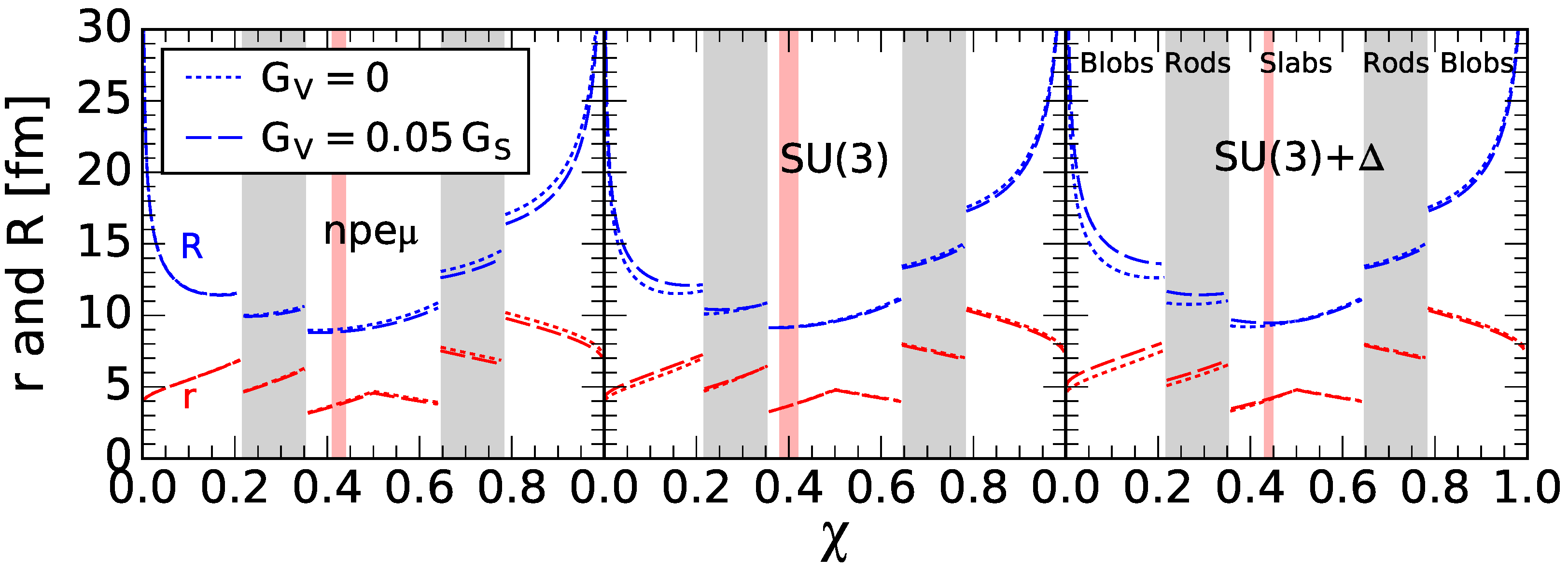
5. Pasta Structure of the Hadron-Quark Phase

In this section, we provide a brief discussion of the mathematical treatment of the mixed phase region of hadrons and quarks in neutron stars. The starting point is the Gibbs condition for phase equilibrium between hadronic (H) matter and quark (Q) matter [1,2],

$$\begin{array}{c}\hfill P_H({\mu }_n,{\mu }_e,\left\{{\varphi }_H\right\})=P_Q({\mu }_n,{\mu }_e,\left\{{\varphi }_Q\right\}),\end{array}$$

(24)

where $P_H$ and $P_Q$ denote the pressures of hadronic matter and quark matter, respectively [1,2]. The quantities $\left\{{\varphi }_H\right\}$ and $\left\{{\varphi }_Q\right\}$ in Equation (24) collectively denote the field variables of hadronic ($\overline{\sigma }$, $\overline{\omega }$, $\overline{\rho }$) and quark (${\overline{\sigma }}_f$, ${\overline{\omega }}_f$, ${\overline{S}}_f$) matter as well as the Fermi momenta ($k_B$, $k_{\lambda }$) that characterize a solution of the equations of hadronic matter described in Section 2. The quantity $\chi \equiv V_Q/V$ describes the volume proportion of quark matter, $V_Q$, in the unknown volume V. $\chi$, therefore, varies between 0 and 1, where 0 means that 0% quark matter is present and 1 means that the matter consist of 100% quark matter. Equation (24) is solved subject to the conditions of global baryon number conservation and global electric charge conservation. The global conservation of baryon charge is expressed as [1,2]

$$\begin{array}{c}\hfill n_b=\chi n_Q({\mu }_n,{\mu }_e,\left\{{\varphi }_Q\right\})+(1-\chi )n_H({\mu }_n,{\mu }_e,\left\{\varphi \right\}),\end{array}$$

(25)

where $n_Q$ and $n_H$ are the baryon number densities of the quark and hadronic phases, respectively. Global electric charge neutrality is given by [1,2]

$$\begin{array}{c}\hfill 0=\chi n_Q({\mu }_n,{\mu }_e,\left\{{\varphi }_Q\right\})+(1-\chi )n_H({\mu }_n,{\mu }_e,\left\{\varphi \right\}),\end{array}$$

(26)

where $q_Q$ and $q_H$ denoting the electric charge densities of the quark phase and hadronic phase, respectively.

As demonstrated by Glendenning [1,2], a mixed phase of hadron-quark matter may arrange itself in such a way that the total energy of the system is minimized. For matter described by global electric charge neutrality, this is the same as minimizing the contributions to the total energy due to phase segregation, which includes the surface and Coulomb energy contributions. Mathematically, the relations for the Coulomb (${ϵ}_C$) and the surface (${ϵ}_S$) energy densities are given by [1,2,32]

$$\begin{array}{ccc}\hfill {\mathcal{E}}_C& =& 2\pi e^2{\left[q_H\left(\chi \right)-q_Q\left(\chi \right)\right]}^2{r}^{2}x{f}_D\left(x\right),\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\mathcal{E}}_S& =& Dx\alpha \left(\chi \right)/r,\hfill \end{array}$$

(28)

where $q_H$ denotes the charge density of the hadronic phase and $q_Q$ stands for the charge density of the quark phase. The symbol r is the radius of the rare phase structures (i.e., quark blobs embedded in hadronic matter at the onset of phase equilibrium). The surface tension between hadronic matter and quark matter is denoted by $\alpha \left(\chi \right)$ where $0\le \chi \le 1$. The quantity $f_D\left(x\right)$ in Equation (27) is defined as

$$f_D\left(x\right)=\frac{1}{D+2}\left[\frac{1}{D-2}(2-D{x}^{1-2/D})+x\right],$$

(29)

where D is the dimensionality of the lattice and $x\equiv \min (\chi ,1-\chi )$. The phase rearrangements will result in the formation of geometrical structures of the rare phase distributed in a lattice that is immersed in the dominant phase. For the sake of simplicity, the rare phase structures are approximated by spherical blobs, rods, and slabs. The spherical blobs populate sites in a three dimensional ($D=3$) body centered cubic (BCC) lattice, the rods in a two dimensional ($D=2$) triangular lattice, and the slabs in a simple one dimensional ($D=1$) lattice. At a volume ratio of $\chi =0.5$ both hadronic and quark matter exist as slabs in the same proportion, and at $\chi >0.5$ the hadronic phase becomes the rare phase with its geometry evolving in reverse order (from slabs to rods to blobs) with increasing density [1,2,32].

The determination of the surface tension, $\alpha$, of the quark-hadro interface is hampered by the fact that a single theory that can accurately describe both hadronic matter and quark matter does not exist. We therefore make use of an approximation proposed by Gibbs where the surface tension is taken to be proportional to the difference in the energy densities of the interacting phases,

$$\alpha \left(\chi \right)=\eta L\left[{\mathcal{E}}_Q\left(\chi \right)-{\mathcal{E}}_H\left(\chi \right)\right].$$

(30)

The quantity L is proportional to the surface thickness which should be on the order of the range of the strong interaction (1 fm). The quantity $\eta$ denotes a proportionality constant. For the results shown in this work we maintained the energy density proportionality but set the parameter $\eta =0.08$ so that the surface tension falls below 70 MeV fm${}^{-2}$, which is a reasonable upper limit for the existence of a hadron-quark mixed phase [33]. The surface tension as a function of $\chi$ is given in Figure 4 for the nuclear GM1L parametrization introduced in Section 2.

The size of the rare phase structures is given by the radius (r) and is determined by minimizing the sum of the Coulomb and surface energies, $\partial ({\mathcal{E}}_C+{\mathcal{E}}_S)/\partial r$, and solving for r

$$r\left(\chi \right)={\left(\frac{D\alpha \left(\chi \right)}{4\pi e^2{f}_D\left(\chi \right){\left[q_H\left(\chi \right)-q_Q\left(\chi \right)\right]}^2}\right)}^{\frac{1}{3}}.$$

(31)

Rare phase structures are centered in the primitive cell of the lattice, taken to be a Wigner-Seitz cell of the same geometry as the rare phase structure. The Wigner–Seitz cell radius R is set so that the primitive cell is charge neutral, i.e., $R\left(\chi \right)=r{x}^{-1/D}$.

In Figure 5 we show r and R as a function of the quark fraction in the mixed phase. Both r and R increase with an increase in the baryonic degrees of freedom, particularly when $\chi \lesssim 0.5$ and the vector interaction is included.

The transport properties of a hypothetical quark-hadro Coulomb lattice in the core of a neutron star and the neutrino emissivity in this phase have been investigated in Refs. [32,34,35,36].

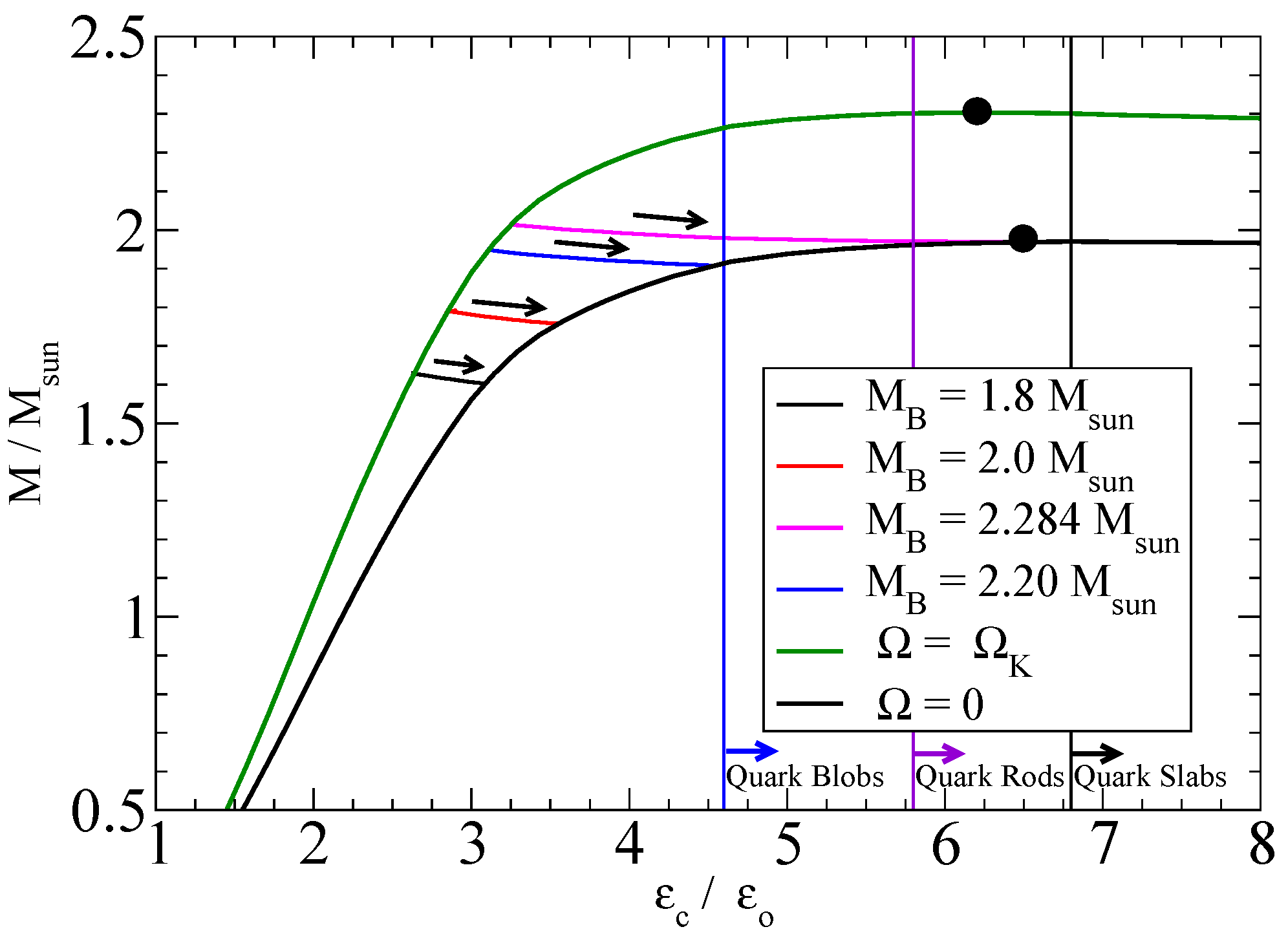
6. Hadron-Quark Lattices in the Cores of Rotating Neutron Stars

In this section we use the equations of state discussed in Section 2 and Section 4 to explore the possible existence of hadron-quark lattices in the cores of (cold) rotating neutron stars. Depending on rotational frequency, such stars are highly deformed and experience significant density changes (up to 50%) in their cores which drastically alters their core compositions. The line element that is used to model rotating neutron stars has the form [37]

$$\begin{array}{c}\hfill d{s}^2=-e^{2\nu }d{t}^2+e^{2\psi }{(d\varphi -\omega dt)}^2+e^{2\mu }d{\theta }^2+e^{2\lambda }d{r}^2,\end{array}$$

(32)

where $\nu$, $\psi$, $\mu$ and $\lambda$ denote metric functions and $\omega$ stand for the angular velocity of the local inertial frames. Each quantity depends on the radial coordinate r, the polar angle $\theta$, and on the rotating star’s angular velocity $\Omega$. The metric functions and the frame dragging frequency are to be computed from Einstein’s field equation,

$$R^{\kappa \sigma }-\frac{1}{2}R{g}^{\kappa \sigma }=8\pi T^{\kappa \sigma },$$

(33)

where $T^{\kappa \sigma }=T^{\kappa \sigma }(ϵ,P\left(ϵ\right))$ denotes the energy momentum tensor of the stellar matter, whose equation of state is given by $P\left(ϵ\right)$. The other quantities in Equation (33) are the Ricci tensor $R^{\kappa \sigma }$, the curvature scalar R, and the metric tensor, $g^{\kappa \sigma }$. A strict limit on rapid rotation is given by the Kepler frequency, ${\Omega }_{\mathrm{K}}$, at which mass shedding from the equator terminates stable rotation. This frequency is of great theoretical value because it sets an absolute limit on rapid rotation, but it may not be accessible to neutron stars as other instabilities set tighter constraints on stable rotation [38,39]. As a case in point, even the most rapidly spinning neutron star observed to date, PSR J1748-244ad, spinning at 716 Hz (i.e., 1.4 milliseconds) [40], rotates only at a fraction of the Kepler frequency.

The general relativistic expression for the Kepler frequency is obtained by evaluating $\delta \int d{s}^2=0$ in the star’s equatorial plane, which leads to [37,38]

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{K}}=\omega +\frac{{\omega }_{,r}}{2{\psi }_{,r}}+e^{\nu -\psi }\sqrt{\frac{{\nu }_{,r}}{{\psi }_{,r}}+{\left(\frac{{\omega }_{,r}}{2{\psi }_{,r}}{e}^{\psi -\nu }\right)}^2},\end{array}$$

(34)

where ${}_r\equiv \partial /\partial r$. This equation is to be computed self-consistently in combination with Einstein’s field equation at the equator of a rotating neutron star.

In Figure 6 we show the gravitational mass versus central energy density relationships for both neutron stars spinning at their Kepler frequencies, as well as non-rotating neutron stars. As one moves along either of these two lines, the baryon mass $M_B$ of the stars changes, increasing with larger central density. Isolated neutron stars spinning down due to the loss of energy would follow a path of constant baryon mass, from the Kepler frequency curve down to the non-rotating one. Four such evolutionary paths (marked with arrows) are depicted in Figure 6.

One sees that neutron stars with baryon masses less than $2.20M_{\odot }$ do not become dense enough during spin down to produce hadron-quark phases in their cores. This is only possible for the most massive neutron stars of our study, which contains a Coulomb lattice made of quark blobs and quark rods if the star’s rotational frequency has dropped to 300 Hz (25% of ${\Omega }_{\mathrm{K}}$). Other quark phases (e.g., quark slabs) would not be present in stable neutron stars.

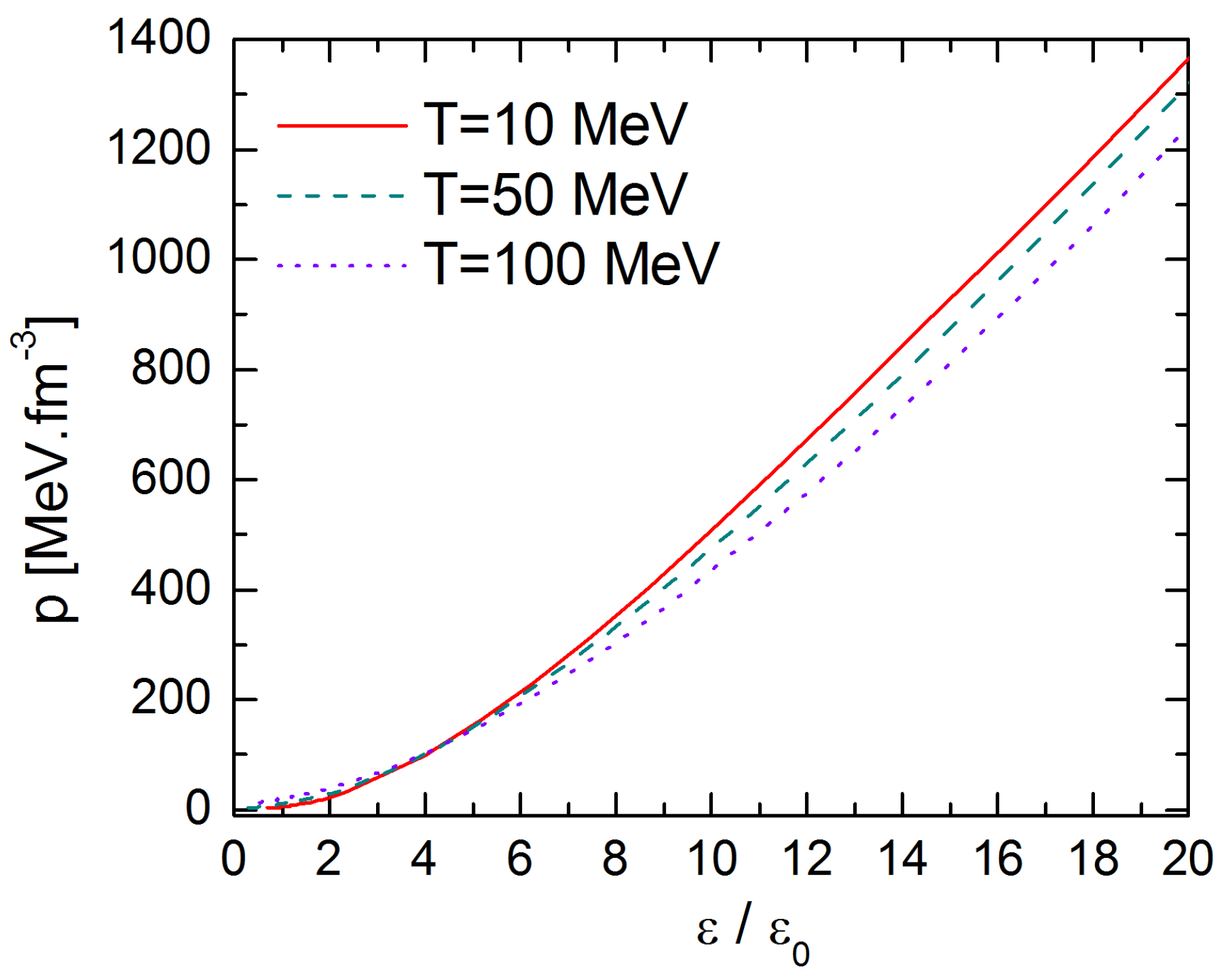
7. Quark Matter at Finite Temperature Modeled with the Local PNJL Model

The non-local 3-flavor NJL model has been introduced in Section 4. This model has then be used, together with the model for hadronic matter introduced in Section 2, to determine the possible possible pasta structure of hadrons and quarks in the hadron-quark mixed phase of neutron star matter. In this section, we introduce a local version of the Polyakov–Nambu–Jona-Lasinio (PNJL) model which will be used to study quark matter at zero as well as at finite temperatures [13,41,42,43]. The Polyakov loop effective potential, which relates quark confinement to color confinement, is included, so that from here on we refer to this model as PNJL. The general expression for the mean-field thermodynamic potential of the model can be written as

$$\Omega ={\Omega }_{\mathrm{reg}}+{\Omega }_{\mathrm{free}}+{\Omega }_0+{\Omega }_v+\mathcal{U}(\Phi ,T),$$

(35)

where ${\Omega }_0$ is defined by the condition that $\Omega$ vanishes at zero temperature and chemical potential, $T=\mu =0$. Allowing for three independent chemical potentials ${\mu }_f$ for the three quark flavors $f=(u,d,s)$, the SU(3) regularized thermodynamic potential in the presence of the quark condensates ${\sigma }_f=〈\overline{f}f〉$ reads

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{reg}}=-2N_c\sum _f{\int }_0^{\Lambda }\frac{{\mathrm{d}}^{3}p}{{\left(2\pi \right)}^3}{E}_f+G_s({\sigma }_u^2+{\sigma }_d^2+{\sigma }_s^2)+4H{\sigma }_u{\sigma }_d{\sigma }_s,\end{array}$$

(36)

and the corresponding free term is given by

$$\begin{array}{c}\hfill {\Omega }_{\mathrm{free}}=-2T\sum _{f,c}{\int }_0^{\infty }\frac{{\mathrm{d}}^{3}p}{{\left(2\pi \right)}^3}\{\ln \left(1+e^{-\frac{E_f-{\mu }_f+ic{\varphi }_3}{T}}\right)+\ln \left(1+e^{-\frac{E_f+{\mu }_f-ic{\varphi }_3}{T}}\right)\},\end{array}$$

(37)

where $N_c=3$ is the number of quark colors and $E_f=\sqrt{p^2+M_f^2}$ is the energy of a quark of flavor f. The color background fields due the coupling to the Polyakov loop are ${\varphi }_c=c{\varphi }_3$, i.e., ${\varphi }_r=-{\varphi }_g={\varphi }_3$ and ${\varphi }_b=0$. The sums over the flavor and color indices are over $f=(u,d,s)$ and $c=(r,g,b)$, respectively. The constituent quark masses $M_f$ are given by

$$M_f=m_f-2G_s{\sigma }_f-2H{\sigma }_j{\sigma }_k,$$

(38)

with $f,j,k=u,d,s$ indicating cyclic permutations of the quark flavors. For our calculations we have used the Polyakov loop effective potential as given in Ref. [44],

$$\begin{array}{ccc}\hfill \mathcal{U}(\Phi ,T)& =& \left[-\frac{1}{2}{a}_1(T,T_0){\Phi }^2+a_2(T,T_0)ln(1-6{\Phi }^2+8{\Phi }^3-3{\Phi }^4)\right]T^4,\hfill \end{array}$$

(39)

where the coefficients $a_1(T,T_0)$ and $a_2(T,T_0)$ are fixed by Lattice QCD simulations of gluon dynamics and the traced Polyakov loop $\Phi =[2cos({\varphi }_3/T)+1]/3$ [30,45]. The parameter $T_0$ denotes the critical temperature of the deconfinement phase transition. The effective potential is key to describe the phase transition from the color confined state ($T<T_0$, with the minimum of the effective potential at $\Phi =1$) to the color deconfined state ($T>T_0$, with the minima of the effective potential at $\Phi =0$). $T_0$ is the only free parameter of the Polyakov loop once the effective potential has been chosen. In this work we will set $T_0=195.0$ MeV [46]. The scalar coupling constant, $G_s$, the ’t Hooft coupling constant, H, the quark masses, and the three-momentum ultraviolet cutoff, $\Lambda$, are model parameters. The respective values of these quantities are $m_u=m_d=5.5$ MeV, $m_s=140.7$ MeV, $\Lambda =602.3$ MeV, $G_s{\Lambda }^2=3.67$ and $H{\Lambda }^5=-12.36$ [47]. The grand canonical thermodynamic potential ${\Omega }_{\mathrm{v}}$ due to vector interactions among quarks is given by

$${\Omega }_{\mathrm{v}}=-G_{\mathrm{v}}\sum _f{n}_f^2,$$

(40)

where the number density of a quark of flavor f in the mean field approximation is given by

$$n_f=\frac{N_c}{3{\pi }^2}{[{({\mu }_f-2G_{\mathrm{v}}{n}_f)}^2-M_f^2]}^{3/2}.$$

(41)

As already mentioned in Section 4, the vector coupling constant $G_{\mathrm{v}}$ is treated as a free parameter and is generally expressed in terms of the strong coupling constant $G_s$, that is, ${\xi }_{\mathrm{v}}\equiv G_v/G_s$.

The minimization of the thermodynamic potential with respect to the quark condensates and the Polyakov-loop color field ${\varphi }_3$ leads to a system of coupled, non-linear equations that are to be solved numerically together with the conditions of electric charge neutrality, baryon number conservation, and chemical equilibrium, similar to the ones discussed in Section 3 for hadronic matter. Once the thermodynamic potential has been computed, the system’s pressure, $P=-\Omega$, and the quark number density, $n_q={\sum }_f{n}_f$, can readily be determined. The EoS of quark matter then follows as $ϵ(P,T,n_f)=-P+TS+{\sum }_f{\mu }_f{n}_f$, where $S=\frac{\partial P}{\partial T}$ and $n_f=\frac{\partial P}{\partial {\mu }_f}$.

To construct the hadron-quark phase transition we, as described in Section 5, the Gibbs condition $G_H(P,T,\left\{{\varphi }_H\right\})=G_Q(P,T,\left\{{\varphi }_Q\right\})$, where $G_H$ respectively $G_Q$ denote the Gibbs free energy per baryon of the hadronic (H) and the quark (Q) phase at a given pressure and transition temperature. The Gibbs energy of each phase ($i=H,Q$) is given by

$$\begin{array}{c}\hfill G_i(P,T)=\sum _j\frac{n_j}{n}{\mu }_j,\end{array}$$

(42)

where the sum over j is over all the particles present in each phase. Figure 7 shows the Gibbs energy of hadronic matter and quark matter as a function of pressure. A sharp (Maxwell-like) first-order phase transition is assumed. Values of ${\xi }_{\mathrm{v}}=0$ and $0.1$ have been chosen for the ratio of the vector-to-scalar quark coupling constant to demonstrate the dependence of the Gibbs energy on the repulsion among quarks. The points where the curves cross each other mark the location of phase equilibrium between hadronic and quark matter.

Figure 8 shows the composition of cold quark matter in chemical equilibrium computed for ${\xi }_{\mathrm{v}}=0$ and $0.1$.

It turns out that the ’t Hooft term responsible for quark flavor mixing alters the quark population significantly, which, in turn, severely changes the populations of leptons and muons.

In Figure 9, we show the hadron quark composition of hot neutron star matter. Neutrinos are included. This composition, therefore, corresponds to matter that may exist in the cores of proto-neutron stars. The shaded areas indicate a sharp (Maxwell) hadron-quark phase transition, computed for the DD2 nuclear parametrization. Three-flavor quark matter is described by the local PNJL model described above.

As can be seen, quark flavor mixing shifts the hadron-quark phase transition toward a smaller baron number density. This trend is to be expected from the results for the particle densities shown in Figure 8, which shows that flavor mixing shifts the presence of quarks to lower densities.

8. Summary and Future Prospects

The purpose of this paper is to provide a short overview of the role of quark matter for neutron star matter at different temperatures. As shown, the hadron-quark composition of such matter depends critically on temperature. For proto-neutron star matter neutrinos are to be included in the treatment too, which also impacts the various particle fractions present at a given temperature and density. If hadron-quark matter exists in cold neutron star, it may form a Coulomb lattice. As demonstrated here (for a non-local version of the NJL model), this lattice would be made almost entirely of spherical quark blobs. The size of the lattice depends on the central density of a neutron star, which, most interestingly, links the size of the lattice to the spin-frequency of a neutron star. We find that the lattice could be produced during spin-down of massive pulsars, once their spin frequency has dropped below around 300 Hz (∼25% of the Kepler frequency). The study of quark matter with a local PNJL shows that the ’t Hooft quark flavor mixing term leads to non-negligible changes in the particle composition of (proto-) neutron stars made of hadron-quark matter.

We have analyzed the role of the ’t Hooft mixing term, associated with the axial U(1) symmetry anomaly of QCD, for quark matter that is locally electrically charge neutral, color neutral, and in chemical equilibrium (i.e., matter under neutron star matter conditions). This symmetry is expected to be restored (not necessarily together with chiral symmetry) at high temperature, which implies that the mixing coupling constant $H\to 0$. For high-density matter as existing in the cores of neutron stars, the mixing (six-point interaction) term is less relevant than the four-point scalar and vector interaction terms (see Equations (20) and (21)). At the mean-field level, the axial U(1) symmetry anomaly of QCD does not change the thermodynamics of the quarks [48].

Our results show that the inclusion of the mixing term lowers the pressure at which the quark-hadro phase transition occurs. It will be interesting to explore how the mixing term modifies the possible formation of a pasta phase in the hadron-quark mixed phase if color super-conductivity is taken into account, since the mixing term can destabilize a color superconductor by preventing the formation of diquark condensates [49].

The existence of a solid hadron-quark pasta phase in the core of a neutron star may be linked to sudden pulsar spin-ups (glitches) and the subsequent healing of the pulsar period. A very prominent example of a pulsar that displays regular glitch activity is PSR J0537–6910. The glitch rate of this pulsar is 3.2 yr${}^{-1}$ [50]. A link between pulsar glitches and solid neutron-matter cores inside of neutron stars has been pointed out may years ago already [51,52,53]. This suggests that one should investigate the connection between a solid hadron-quark pasta phase and the pulsar glitch phenomenon. In particular, it needs to be studied whether or not the sudden release of elastic energy stored in a solid hadron-quark pasta phase could explain macro-glitches (which are related to sudden changes in the rotational frequency of a pulsar on the order of $\Delta \Omega /\Omega$∼${10}^{-6}$) at the rate (months to years) at which pulsar glitches are typically observed. Another issue that needs to be investigated concerns the role of neutron superfluidity. Since neutron stars with and without hadron-quark matter cores contain nuclear crusts with identical compositions (but varying thickness), both types of stars possess nuclear crusts containing ${}^1{\mathrm{S}}_0$ neutron superfluids. The situation is less clear for the neutrons in the cores of both types of stars. It needs to be studied if both types of stars may possess ${}^3{\mathrm{S}}_1$ neutrons superfluids in their cores, or whether this phase is restricted to neutron stars without quark matter cores.

Gravitational-wave detectors such as LIGO and VIRGO have opened up a new observational window on the inner workings of neutron stars. This is particularly the case for the neutron stars in the elliptic galaxy NGC 4993 that produced the gravitational-wave event GW170817 observed with LIGO and VIRGO in 2017. The detection of the gravitational and electromagnetic waves produced by the coalescence of these neutron stars has offered an unprecedented opportunity for imposing constraints on the quark-hadro composition of neutron stars and the equation of state associated with such objects (see Refs. [54,55,56], and references therein).