1. Introduction
The theory behind particle physics, called for historic reasons the standard model (SM), is based on local gauge symmetries In certain cases, broken symmetries were introduced in order to explain the fundamental experimental observations, the most important ones being parity violation and the Brout–Englert–Higgs (BEH) mechanism of spontaneous symmetry breaking. Left-handed currents could take care of parity violation observed in weak interactions, and using the BEH mechanism, the standard model could account for the masses of the elementary fermions and bosons. In spite of the excellent agreement between the experimental data and the predictions and fitting of the standard model, several mysteries stayed unsolved in particle physics. Numerous extensions for the standard model were proposed to solve those, the most popular one being supersymmetry, a broken fermion-boson symmetry. It helps to interpret the dark matter of cosmology within particle physics and also to solve the hierarchy problem, the quadratic divergence of the calculated mass of the Higgs boson in the standard model. Other problems unsolved in the framework of the standard model are the lack of antimatter in the Universe and baryogenesis, as well as neutrino oscillations. In this review, we shall try to summarize these concepts and the corresponding experimental evidence in high-energy physics.
2. Fundamental Particles in the Standard Model
According to the standard model, the world consists of two kinds of particles, fermions and bosons, different by their spins, intrinsic angular momenta, measured in units of
ℏ, the reduced Planck constant. The fermions in general have half-integer spins:
, whereas the spins of the bosons are integer:
The elementary (fundamental) fermions of the standard model are the leptons and the quarks of three families (see
Table 1) with
; those are also called matter particles, as our matter consists of the fermions of the first family. The elementary bosons have integer spins; those mediating the three interactions, the photon, the eight gluons, and the three weak bosons have
, whereas the Higgs boson is a scalar particle with zero spin. The LEP experiments have shown by measuring the decay width of the Z boson that only those three families exist with light enough neutrinos to allow for the Z →
decay process.
The term elementary means that those particles are point-like and structureless, with no excited state. The fundamental fermions have three families, consisting of a pair of quarks and a pair of leptons each. All fermions have antiparticles of opposite charges, but similar other properties. The leptons can propagate freely, but the quarks are confined in composite particles, the hadrons. They are either composite fermions, bound states of three quarks, the baryons (like the proton and neutron), and three antiquarks, antibaryons (like the antiproton), or bosons composed of a quark and an antiquark, the mesons (like the pion). The quarks in the hadrons are bound together by the strong interaction, and because of the two possible compositions, its three-state source is called color charge; in analogy with human sight, they are called the colorless states.
3. Interactions in the Standard Model
The standard model includes three basic interactions derived from local gauge invariances. A fully invariant color-SU(3) accounts for the strong interaction from local SU(3), but the other two are united in a local U(1)⊗SU(2) gauge invariance as an electroweak interaction partially broken by the spontaneous symmetry breaking BEH mechanism. The strong interaction originates from the color charge of the quarks with its three colors, and it is mediated by eight massless gluons carrying both color and anti-color. The weak interaction has three heavy weak bosons as mediators, W and Z, whereas that of of the electromagnetism is the massless and neutral photon. Due to Heisenberg’s uncertainty principle, these bosons are virtual when they mediate the interactions. A virtual photon as mediator has a finite mass when transferring energy and momentum between two charged particles, and the heavy W boson is many orders of magnitude lighter when mediating the nuclear beta decay. However, they are real particles; they can be also emitted and observed experimentally: everybody can see the visible photons, and even the weak bosons and the gluons can be observed and studied when emitted in high-energy collisions and decay to leptons or hadron showers, jets.
A fermion enters into an interaction if it possesses the corresponding charge. The weak interaction operates on all basic fermions as all of them carry the weak isospin, the electromagnetic one on those having electric charges or magnetic moments, and the strong interaction on the colored fermions, i.e., on the quarks. The photon does not carry charges, but the W boson is electrically charged. The gluons carry the color charge, and so, they have self-interaction as well. In order to ensure a better agreement between theory and experiment, one also needs the existence of a scalar boson, a particle with its charges and spin zero. In the standard model, that scalar particle is the Higgs boson.
The standard model was very thoroughly tested in high-energy experiments, mostly at LEP, the Large Electron-Positron collider of CERN (see
Figure 1). All elementary particles of the model were identified and studied experimentally, and much experimental evidence was collected for the three-state color and fractional electric charges of the quarks, as well as for the properties of the gluons and of the heavy weak bosons. Lately, the high-energy experiments concentrated on searching for the only missing particle, the Higgs boson, acquiring more and more precise new data. The latter was achieved mainly at the electron-positron colliders and all results are in reasonable agreement with the predictions of the standard model.
4. Testing the Standard Model
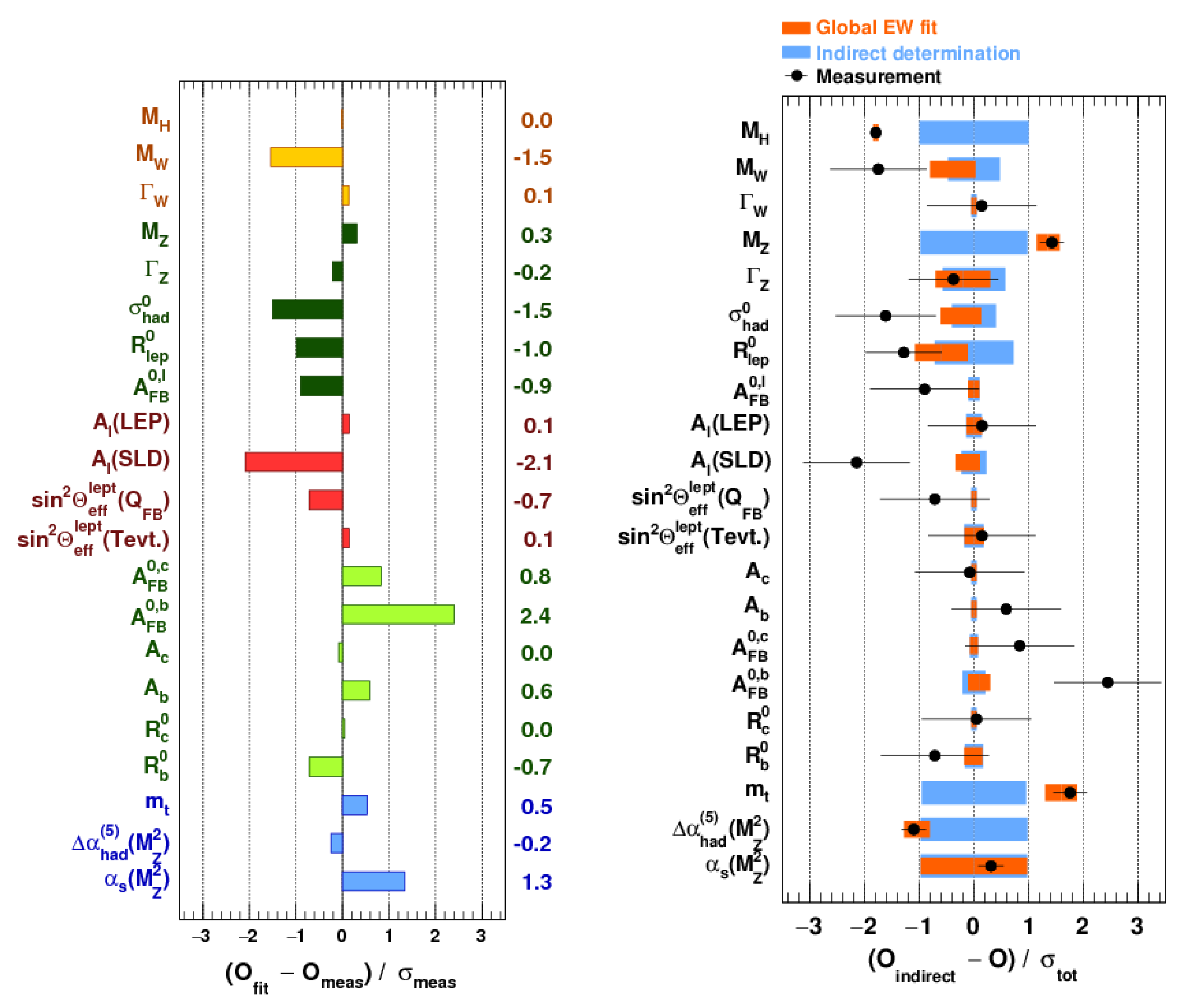
Figure 1 summarizes the present situation of testing the standard model by comparing measured and calculated values for key parameters [
1] using the collected experimental information. On the left plot, relative deviations are shown between the fitted and measured parameter values: that is, a global electroweak fit. On the right side, besides the global fit (in red), another fit is plotted (in blue) with the measured value of the given parameter not included in the fit; that shows the degree of determination of the given parameter by the rest of the measurements, i.e., the sensitivity of the model to the values of the parameters. We can conclude that all parameters agree within their experimental uncertainties with the theoretical predictions. This picture became complete with the measurement of the Higgs boson mass at 125 GeV/
. It is interesting that the standard model calculations are not too sensitive to its mass value, the fit without including the Higgs measurement would predict a somewhat lighter Higgs boson (
Figure 1, right) with a quite large uncertainty.
Spontaneous Symmetry Breaking
One can derive the three basic interactions from local gauge symmetries, but they cannot produce masses for the elementary fermions and the weak bosons (the photon and the gluons are massless). The model must violate some of those symmetries in order to create masses. Symmetry violation plays a key role in the standard model. Several theoreticians published
spontaneous symmetry breaking in 1964 independently [
2,
3,
4,
5], and it is now called the
BEH mechanism after
R. Brout, F. Englert, and P.W. Higgs, although for a long time, it was quoted as the
Higgs mechanism.
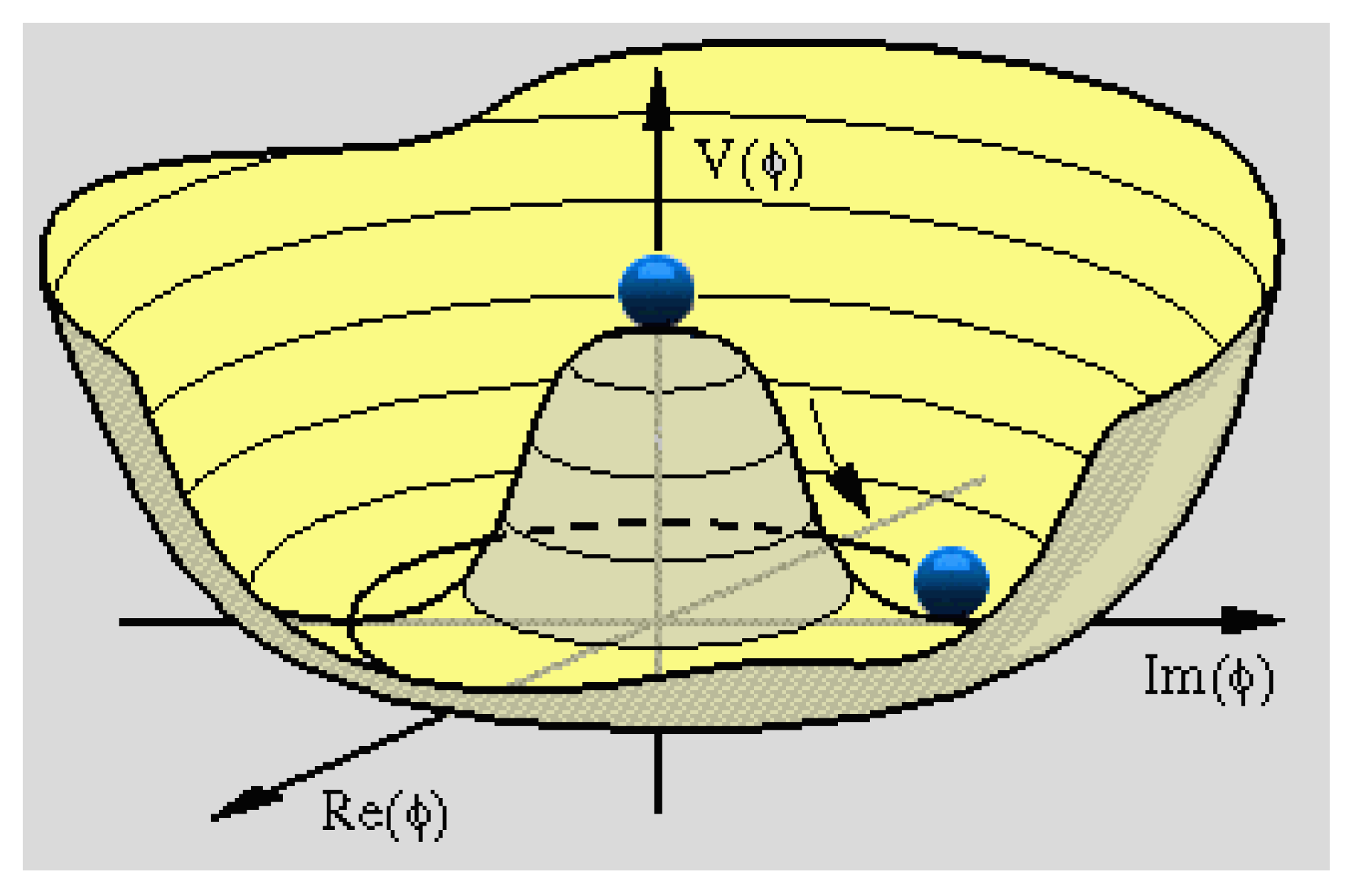
The BEH mechanism assumes that the electroweak vacuum is filled by a potential that spontaneously breaks its perfect symmetry. This can be illustrated by a Mexican hat (
Figure 2): its axial symmetry is not violated by a ball on its top, but the ball should roll down, thereby spontaneously breaking the symmetry. The axial symmetry of the potential allows us the choose such a coordinate system where the position of the minimum is determined by one real parameter only (this corresponds to the ball laying on the imaginary axis in
Figure 2), that is the vacuum expectation value of the BEH field, determined by the Fermi constant to be
GeV.
The BEH potential has a complex doublet field, adding four degrees of freedom to those of the standard model: three of them are used to produce the masses for the weak bosons, and the fourth one makes a scalar particle, the Higgs boson, which is needed by the theory. Thus, the scalar boson appears as a by-product of the mass-creation mechanism. The masses of the weak bosons can actually be calculated by the standard model using the value of the weak coupling (called Fermi constant at low energies) deduced from the beta-decay measurements. Moreover, the BEH mechanism allows us to add fermion mass terms to the electroweak Lagrangian with the fermion masses as free parameters.
We have to emphasize that the masses of the macroscopic objects in our world are predominantly due to the energy content of the proton and the neutron; the quark and electron masses from the BEH mechanism add only a few percent to them.
5. Search for the Higgs Boson
All of the fundamental particles of the standard model, the fermions of
Table 1, and the bosons mediating the interactions were observed and studied by the high-energy experiments well before the launch of the LHC, but the Higgs boson was not yet. Before the observation of the Higgs boson, the BEH mechanism had no direct experimental proof, and several alternative theories existed (although they had to create a scalar particle, usually as a
bound state). Fitting the standard model has limited, but did not determine the mass of the Higgs boson. This is well demonstrated by the right plot of
Figure 1: the Higgs boson mass is not that tightly determined by the rest of the standard model measurements. Thus, the particle physics community invested an incredible amount of effort in searching for the Higgs boson.
5.1. Hunting for the Higgs Boson
In the accelerator experiments, the Higgs boson was searched for at ever-increasing energies by ever-increasing collaborations, usually in the following steps:
Compose a complete SM background using Monte Carlo simulation including all types of possible events normalized to their cross sections.
Simulate Higgs-boson signals of all possible production and decay processes with all possible Higgs-boson masses.
Put all these through your own detector simulation to get events analogous to the measured ones.
Calculate the number of events expected for signal and background at various conditions at the actually collected experimental luminosity.
Check whether the expected background predicted by the standard model (SM) agrees with the experimental data yield.
Optimize the event selection using the simulated events: reduce the
B background, and enhance the
S signal via maximizing a function of merit, e.g.,
or
, or using the approximate formula of Cowan et al. [
6].
Once we are happy with the simulations and the event selection, we must choose a test statistic. That could be any kind of probability variable characteristic of the given phenomenon: probabilities for having background only, signal, or combinations. A popular one is the Q likelihood ratio of signal + background over background: . Other frequently used ones are the probabilities of not having the expected signal above the expected background and the collected data, like:
, the signal confidence level assuming background only, i.e., the complete absence of the signal, or
the so-called p-value: the probability that a random fluctuation of the measured background could give the observed excess.
5.2. Exclusion at LEP
The Higgs boson of the standard model is a scalar particle: most of its quantum numbers are zero, although the BEH field is a weak isospin doublet. The main measurable property of the Higgs boson is mass, and all production and decay cross sections depend on its mass. Analyzing all the experimental data before 2012 pointed towards a Higgs-boson mass GeV/ ( GeV/ with a 95% confidence level).
In accelerator experiments, a new theoretical hypothesis is considered to be excluded if its signal does not appear at a ≥95% confidence level and observed if its appearance exceeds five uncertainties, i.e., its signal
over the background, where
is the total experimental uncertainty according to the best honest guess of the experimentalist including both statistics and the possible systematic deviations. Some of the statistical methods used in the search and discovery of the Higgs boson have been reviewed by the author in [
7].
CERN used the last two years of the Large Electron-Positron collider (LEP) to search for the Higgs boson and collected more data (luminosity) at energies above the Z boson mass than in the previous decade altogether.
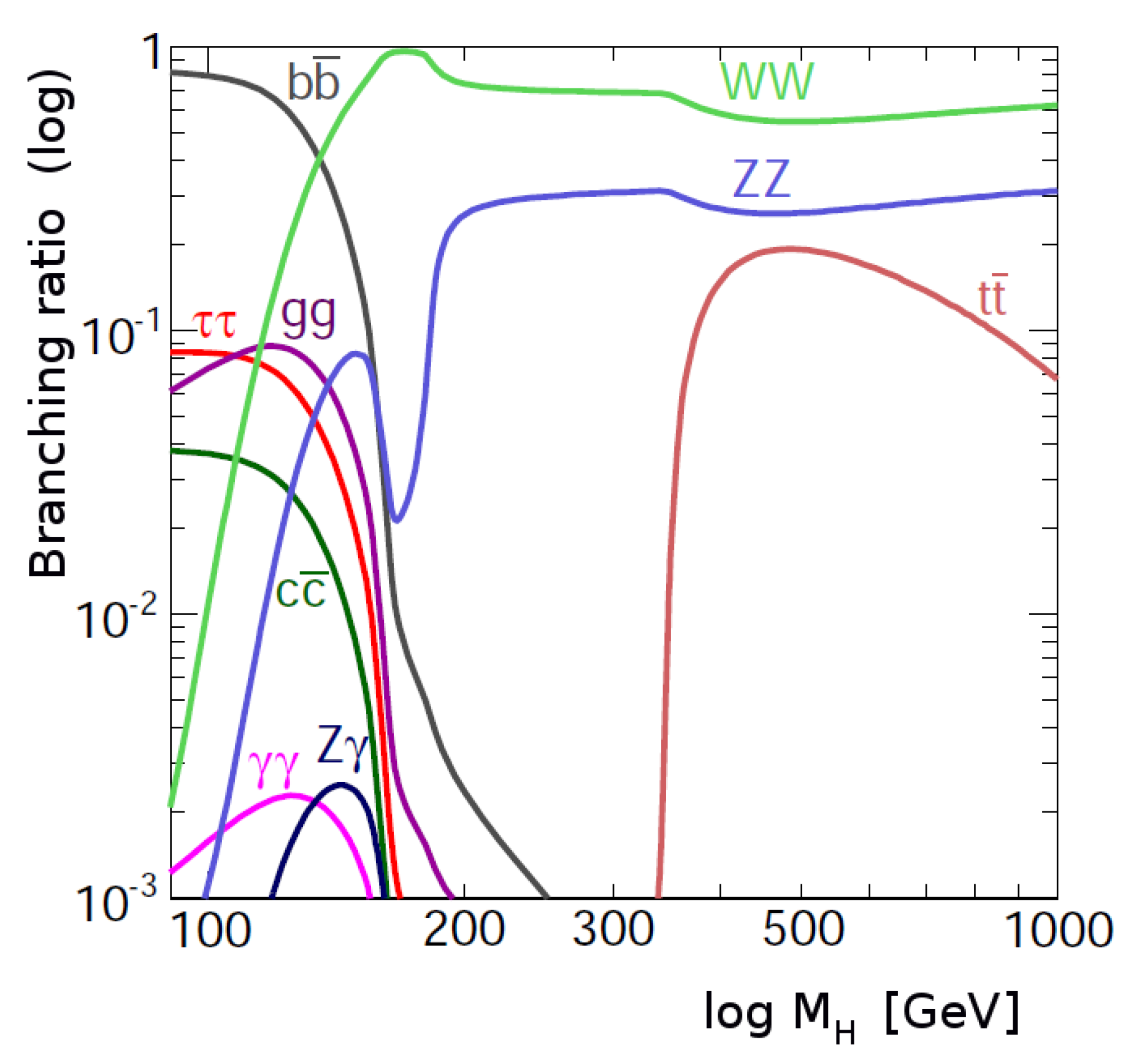
According to the standard model at LEP energies, the dominant production process is
, and the dominant Higgs boson decay is to the heaviest available fermions, a pair of b quarks [
8] (
Figure 3). At LEP, the only difference among the various search channels was the different decay process of the accompanying Z boson.
The detectors of high-energy experiments are built of cylindrical layers encircled by huge magnets including as much as possible the detector parts. This structure includes a vertex detector right around the interaction point, a tracking system of multiwire chambers or semiconductor detectors of light material for measuring the tracks of the charged particles curved in the magnetic field. The next stage is the electromagnetic calorimeter, something heavy absorbing all electrons and photons, encircled by an even heavier hadron calorimeter, absorbing the pions, protons, neutrons, etc., and outside of an all muon system, following and measuring the high-energy muons leaving the detector. The neutrinos, produced by weak interaction, escape the whole system with no interaction, and they are identified by a momentum imbalance (called missing momentum). LEP had four such large experiments located in the four collision points of the collider ring: ALEPH, DELPHI, L3, and OPAL (the present author was in OPAL).
Statistics made a bad joke at LEP: the ALEPH experiment saw a quite significant signal of a Higgs-like boson of a mass of 115 GeV/
, whereas the other LEP experiments did not observe any such signal. Finally, a common limit was determined, 114.4 GeV/
, below which the Higgs boson was excluded [
9] by a 95% confidence level. Many physicists wanted CERN to let LEP work for another year, but the simulations were not very promising for the discovery of a 115 GeV/
Higgs boson, and LEP had to be dismounted and removed from its tunnel to make space for the LHC.
5.3. Search for the Higgs Boson at the LHC
Designing the LHC and its experiments started very early, even before the start of LEP; thus, the construction of its detectors took two decades of hard work by thousands of physicists and engineers before the LHC was launched in 2009. Moreover, during its first two years, the LHC was mostly under development; the actual intensive data taking started in 2011 only.
Similarly to the former LEP ring, the Large Hadron Collider has four beam-beam interaction points with a major experiment (and in some cases, smaller ones associated with them) in each one. The two largest LHC experiments, ATLAS and CMS, have been designed with the main goal of finding the Higgs boson. These collaborations are really large. According to the official statistics, in 2016, CMS had 5250 participants (including 1916 students and 1274 engineers and technicians) from 198 institutions of 45 countries. The largest participant country was the USA, then Italy, Germany, and Russia. ATLAS has even a somewhat larger size than CMS both in the volume of the detector and in the number of participants.
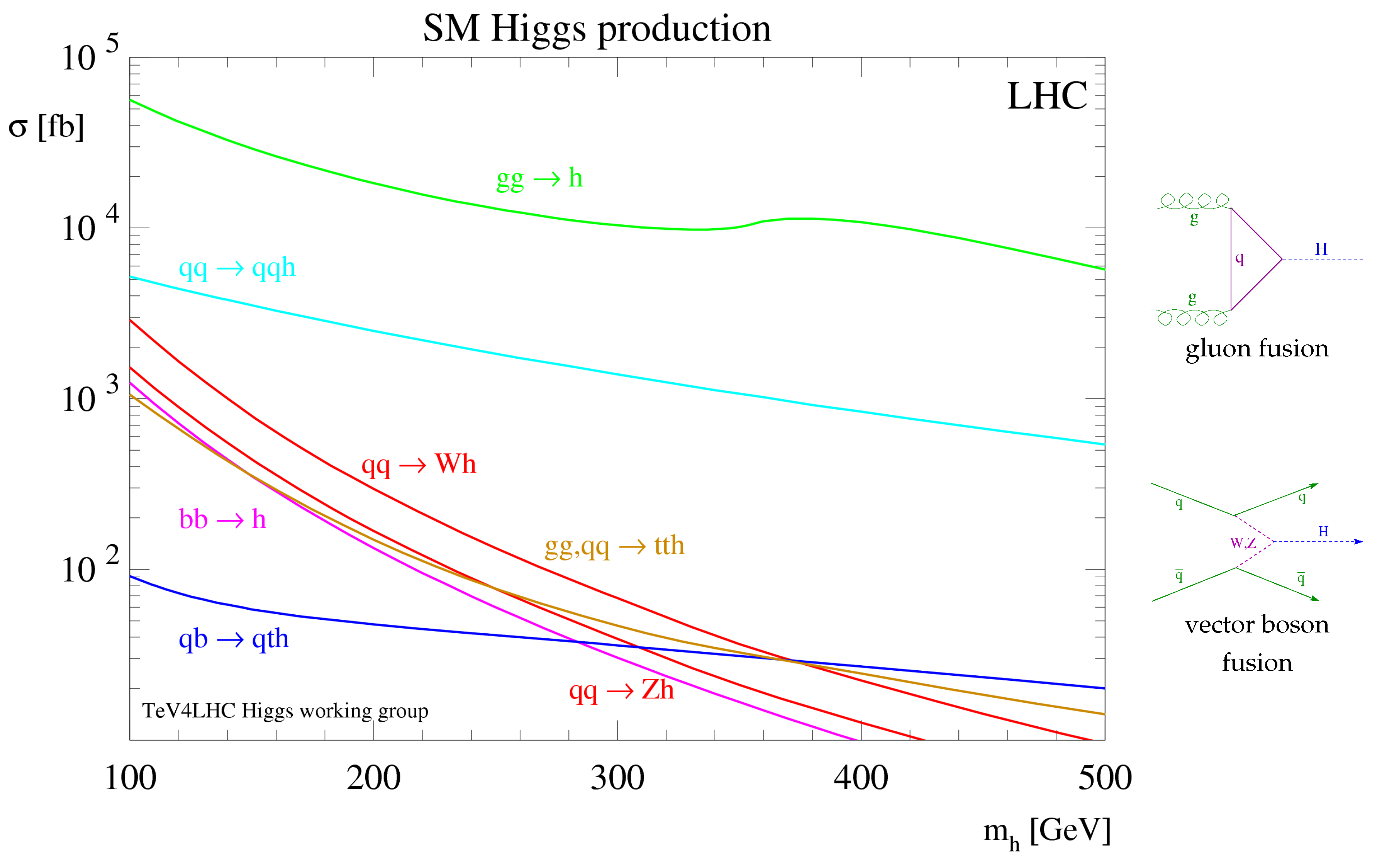
The various formation processes of the SM Higgs boson in p-p collisions at the LHC are shown in
Figure 4. Gluon fusion is by far the dominant reaction, but vector boson fusion is also quite important [
8]. From previous experimental data, the general fitting of the standard model predicted a light Higgs boson, with a mass slightly below 100 GeV/
. As LEP excluded the Higgs boson below 114 GeV/
, ATLAS and CMS had to be prepared for detecting the Higgs boson in the most difficult region,
GeV/
, with several competing decay channels (
Figure 3). Of course, if the Higgs boson were much lighter or heavier, it would have been observed earlier at LEP or at the Tevatron.
5.4. Observation at the LHC
The most promising reactions to observe a light SM Higgs boson at the LHC was theoretically predicted to be its decay either to two hard photons or decay to two Z bosons (one of them virtual, of course, as there would not be enough energy to make two 91 GeV/
bosons) and each Z decaying further to a pair of charged leptons: these two reactions could be visible above the high hadron background (see, e.g.,
Figure 5). In spite of the very low decay branching fractions (BF), these channels promised the best signal/background (S/B) ratios: for H → ZZ
→
(
), the BF is low,
, but the S/B ratio > 1, whereas for H →
, the BR is much higher,
, although S/B
. Both large LHC experiments, CMS and ATLAS designed their electromagnetic calorimeters with this in mind. The CMS one consists of 75,848 PbWO
single crystal scintillators, whereas the electromagnetic calorimeter ATLAS is a sampling one based on liquid argon shower detectors (see
Table 2).
In 2012, ATLAS and CMS announced [
10,
11] that at the LHC, at the collision energies of 7 and 8 TeV, in the two decay channels H →
and H → ZZ →
, a new boson was observed with a mass of
GeV/
by both experiments at a statistical significance of
each (i.e., that much higher than the total
uncertainties of the measurements). The properties of the observed new particle corresponded to those of the Higgs boson as predicted by the standard model.
5.5. The Two Large Experiments
A combination of ATLAS and CMS data based on 7 and 8 TeV collisions gave the mass estimation:
GeV, including both statistical and systematic uncertainties [
12]. This result was made even more convincing by the fact that the construction of ATLAS and CMS was very different. Some of these features are overviewed in
Table 2; note, e.g., that CMS has about one tenth of the volume and twice the weight of ATLAS.
5.6. Mass Measurements
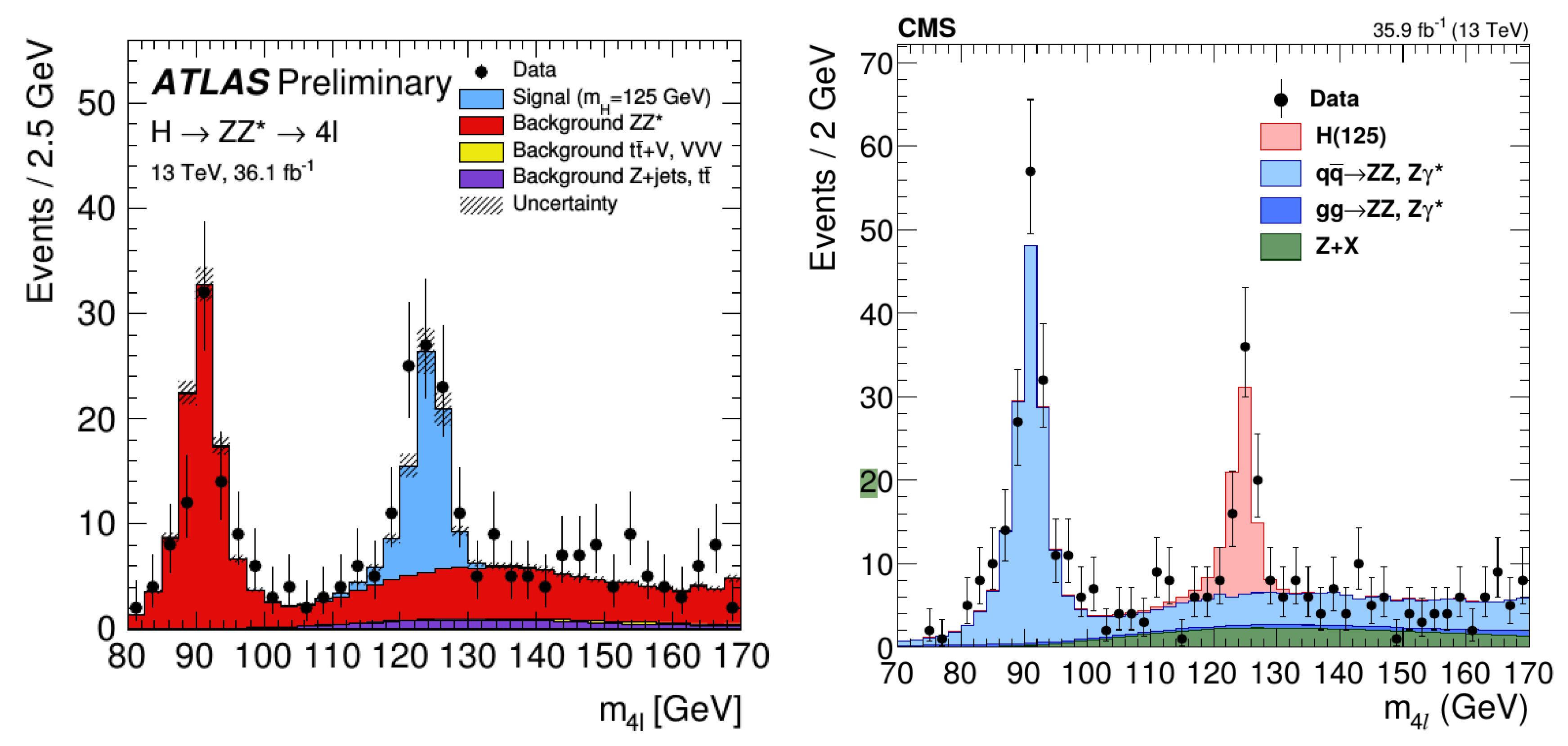
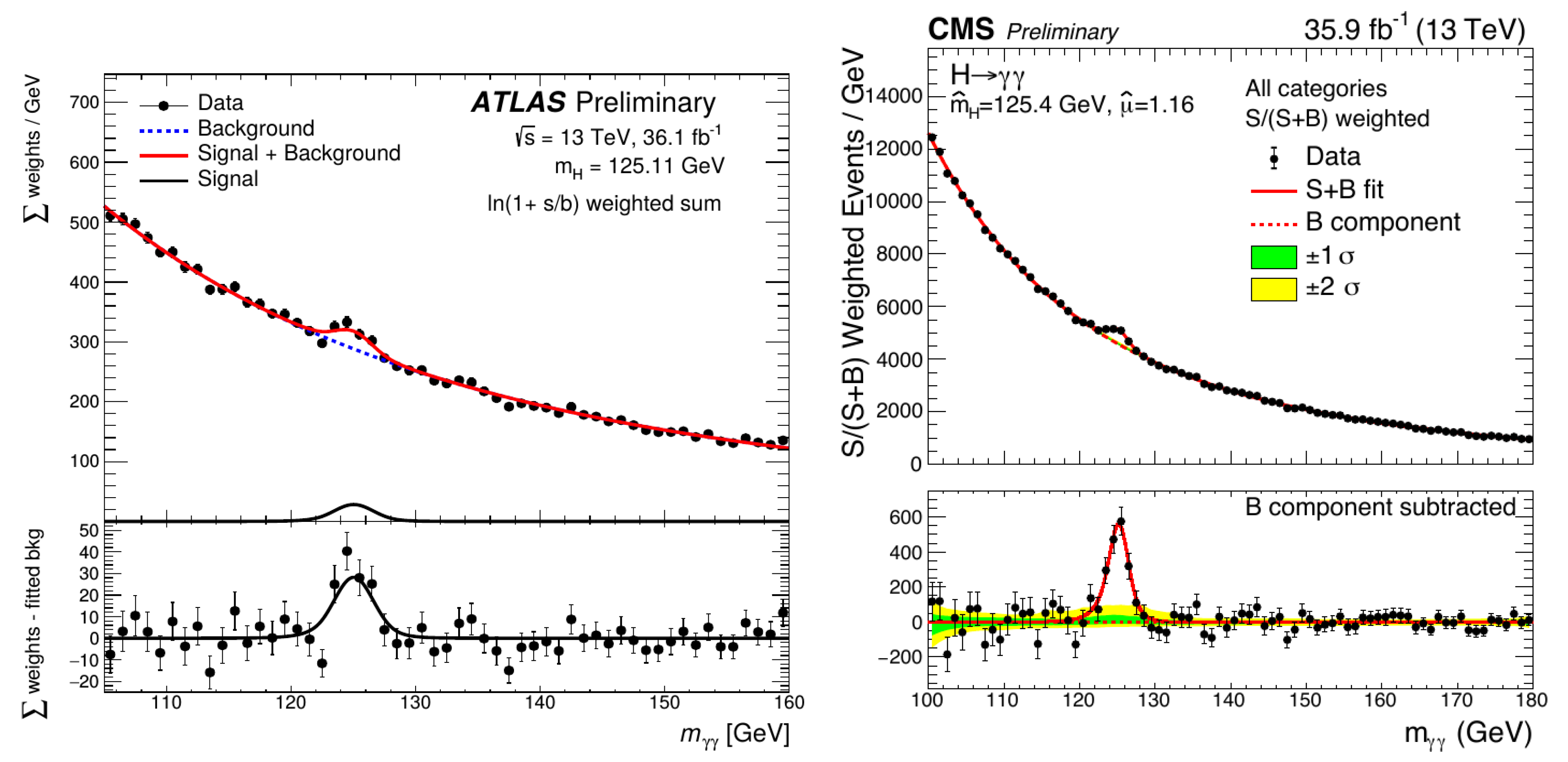
Since the original discovery, an order of magnitude more information was collected in the last three years at a higher collision energy, 13 TeV. As examples of the new measurements, let us show mass spectra measured by ATLAS and CMS at 13 TeV for H →
(
Figure 6) and for H →
(
Figure 7). The corresponding mass values for the Higgs boson are listed in
Table 3, where the first uncertainties are statistical and the second ones are systematic. Note the remarkable agreement between channels and experiments. As all results were statistically limited and only the 2016 data were used, significant improvement is expected when all 13 TeV data collected in 2016–2018 will be analyzed. One can see in
Figure 1 that these values also agree with the standard model calculations very well.
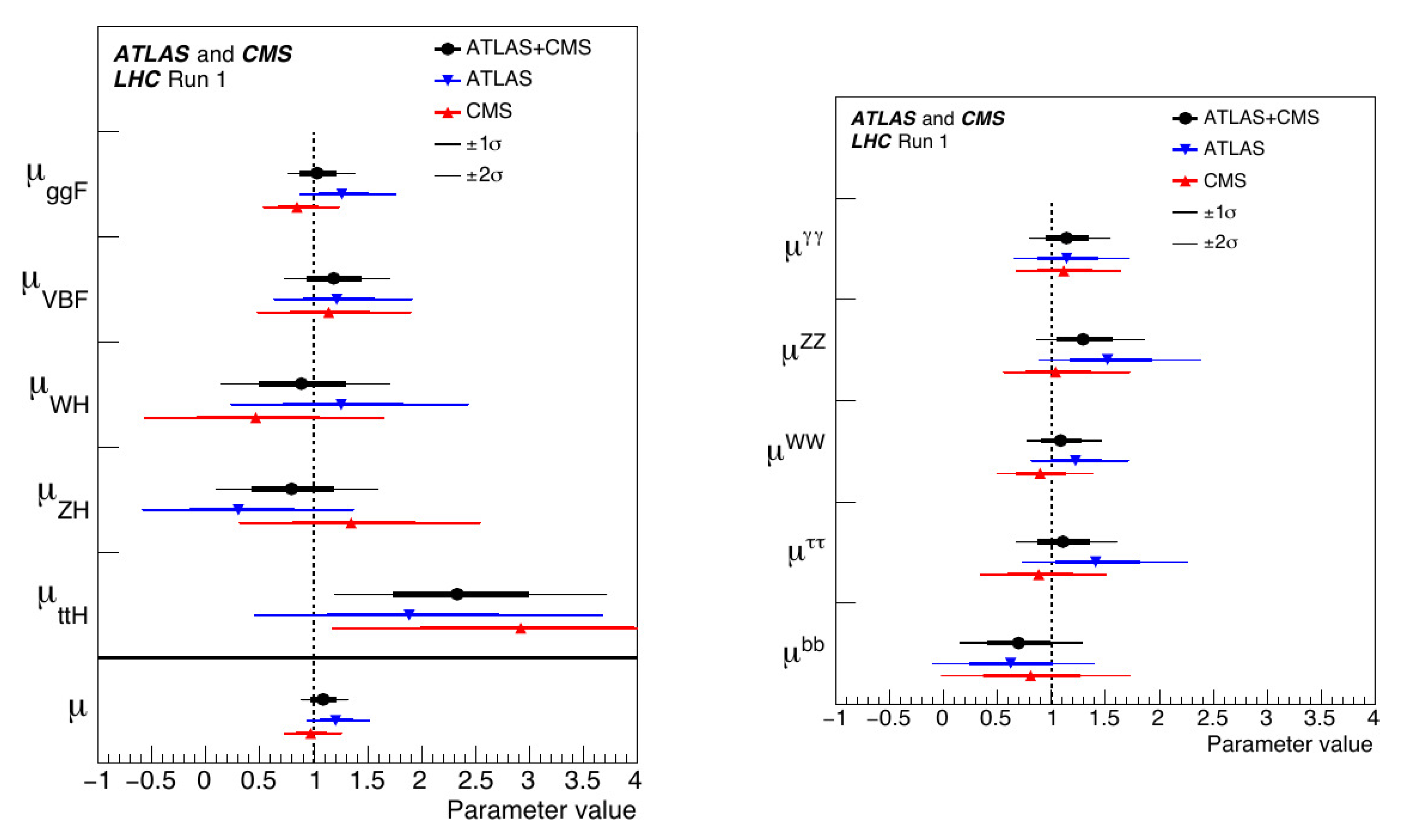
5.7. Higgs Couplings
Although much of the new data are still in analysis, all significant production and decay channels of the Higgs boson were identified and studied. The results (
Figure 8) show good agreement between the two experiments and also with the predictions for a single Higgs boson with a mass of 125 GeV/
. The decay widths were measured for all production and decay channels, and they agreed with those predicted by the standard model.
5.8. Other Decay Channels
Using the 13 TeV data enabled ATLAS and CMS to observe and study the Higgs boson using decay channels other than the most favored four-lepton and
ones. The third most significant channel is
. When in 2012, its contribution at 7 and 8 TeV (Run 1) was added to the four-lepton and
measurements, it changed the
observational significance for both experiments, increasing it for ATLAS to
and decreasing it for CMS to
. The analysis of all Run 1 data gave relative signal strengths
for ATLAS and
for CMS, but the average agreed [
16] with the standard model:
.
Another important channel is H →
. In Run 1, ATLAS and CMS together managed to observe it with a
significance [
16]. In Run 2, by a simultaneous analysis of all data obtained at 7, 8, and 13 TeV, CMS reached a
significance [
17].
In principle, the decay to a pair of b quarks has the highest cross section among the decay channels of the Higgs boson, but it is very difficult to distinguish among all the hadronic activity in the detectors. CMS has managed to observe its signal with a significance of
via using all production channels: associated with a vector boson (VH), gluon fusion (gg), vector boson fusion (VBF), and associated with a top pair (ttH); and data collected at 7, 8, and 13 TeV collision energies. The measured signal strength,
, again agreed with the SM prediction [
18].
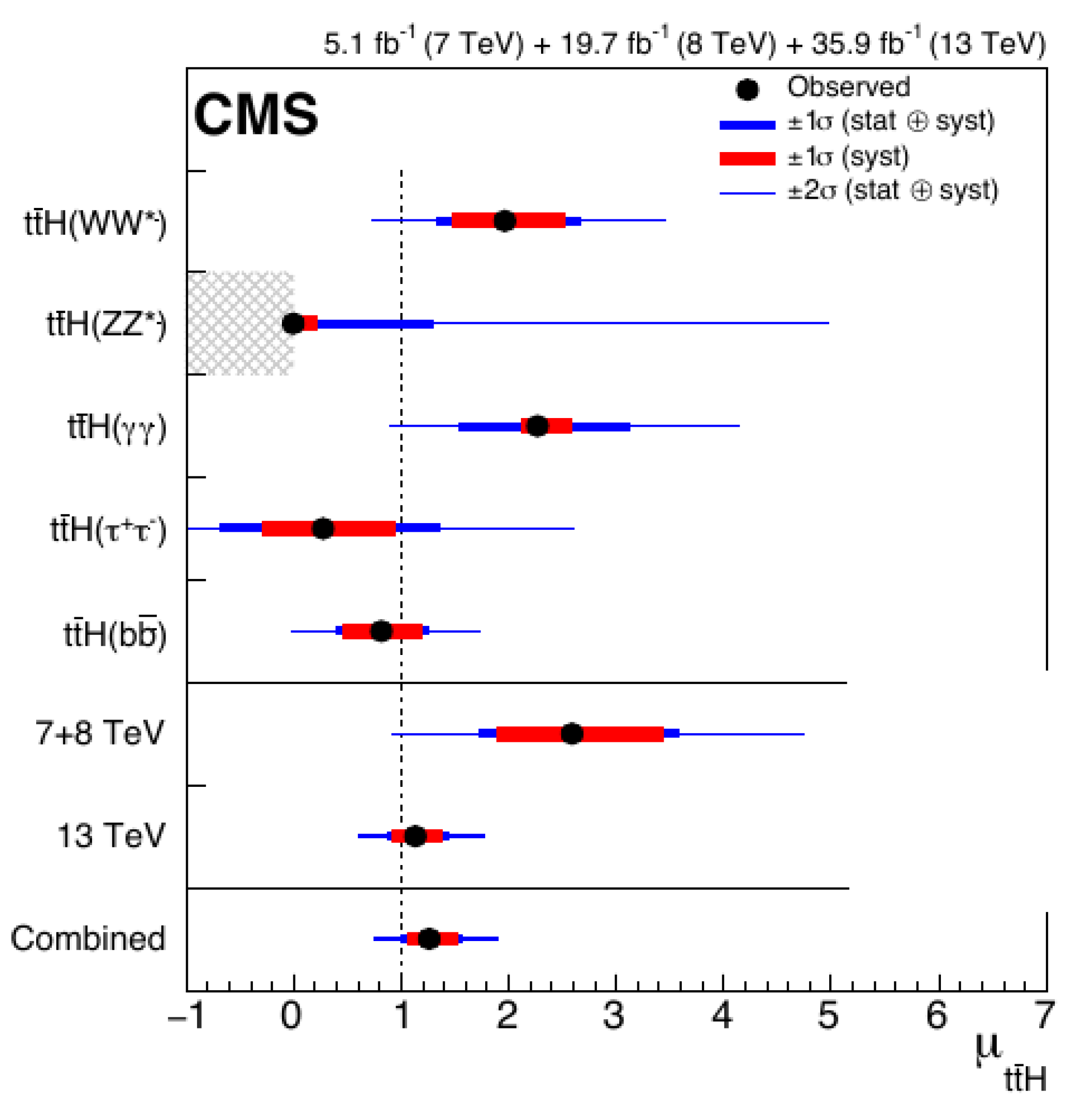
According to the standard model, the Higgs boson couples to other particles via their masses. An important test is to check its coupling to the top quark, the heaviest fermion. An analysis of all decay channels at the three LHC energies including the 2016 data gave CMS an observation (
Figure 9) of the
associated production at a
significance [
19].
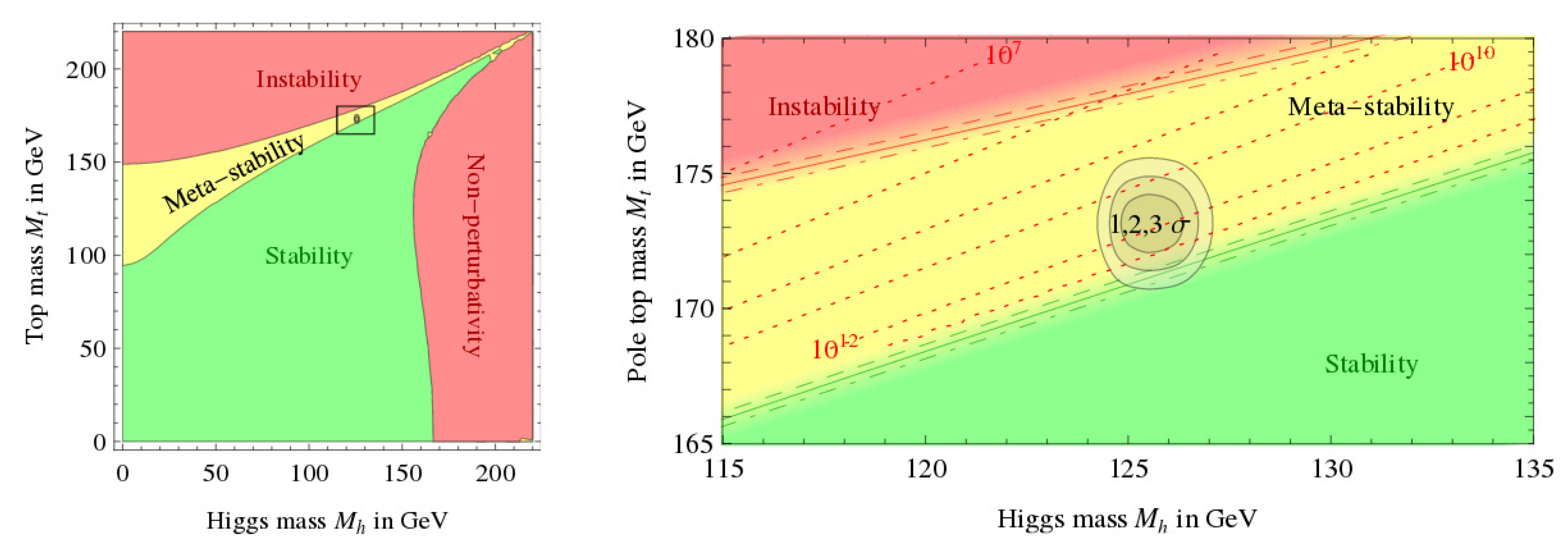
6. Vacuum Stability
The observed light mass of the Higgs boson seems to be very exciting for theoreticians, and there was even a special workshop [
20] devoted to discuss this mass value in 2013. The reason is that
GeV is at the borderline of the stability of the electroweak vacuum on the plane of top mass against Higgs mass as another fine-tuning aspect of the standard model (
Figure 10). The vacuum is considered to be stable if it has a single minimum, but it could also be metastable with more than one minima [
21].
If our vacuum is metastable and we are not in the deepest minimum, then the universe exists in a
false vacuum, and the world can shift into the deeper one by a quantum mechanical tunneling effect. In some sense, it could be the end of our world as we know it, as in the new BEH minimum, all the particles would have different masses, and also the strength of the weak interaction would change. Of course, this assumes that the standard model is valid up to extreme high energies. However, Turner and Wilczek stated in 1982 [
22] that even if our vacuum is metastable, its expected lifetime could be much longer than the age of the Universe, hence it should appear stable to us.
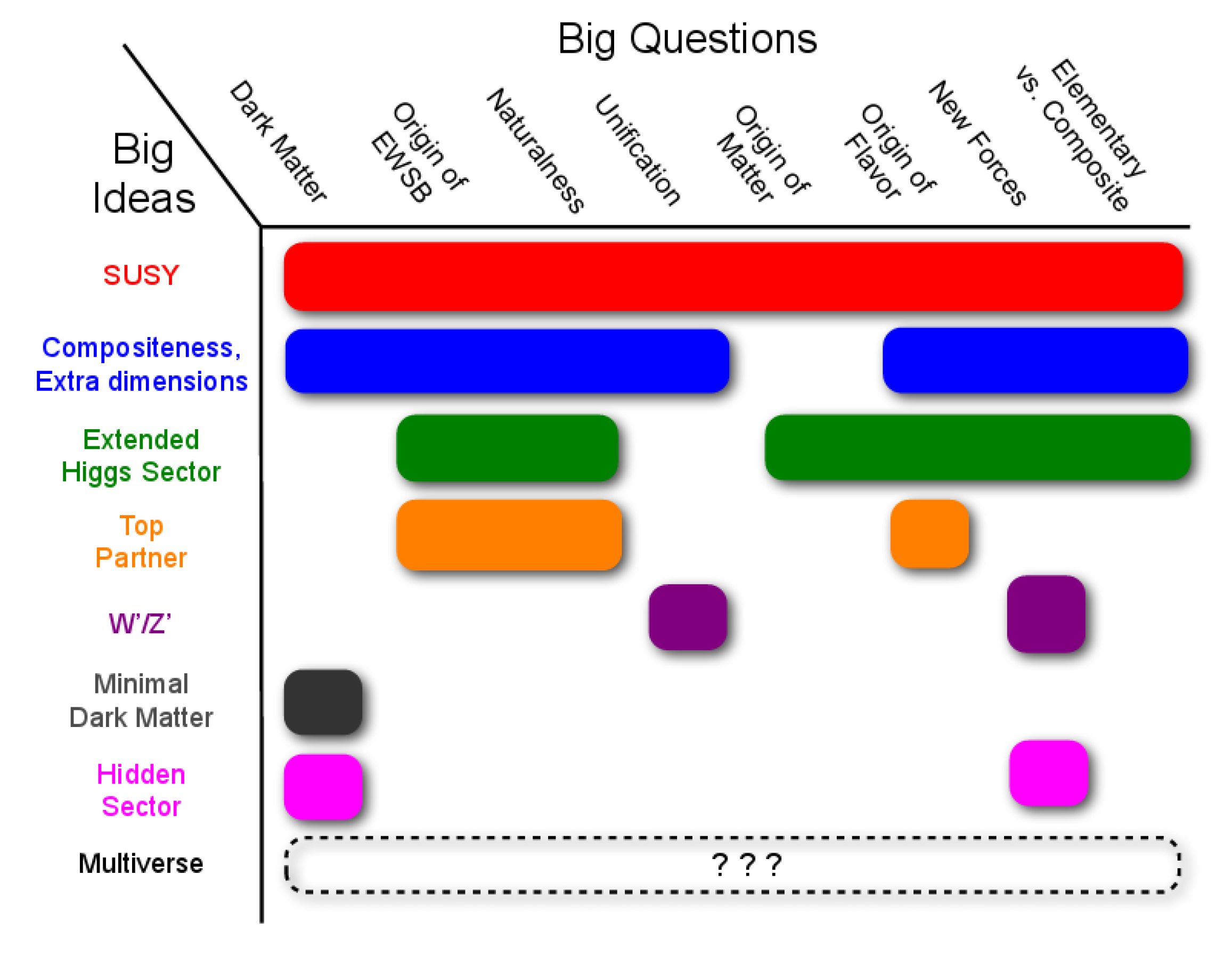
7. Problems of the Standard Model
Thus, we most likely observed the standard model Higgs boson at the LHC. This is, of course, a great success of particle physics as it has proven the BEH mechanism of mass production. However, the fact that the SM seems to describe all high-energy experimental data perfectly is in some sense a problem: it has theoretical difficulties that need new physics to resolve (
Figure 11).
The standard model cannot interpret gravity as a gauge interaction similar to the other three interactions.
It cannot account for the dark matter as a particle and cannot explain dark energy or the lack of antimatter in the Universe.
It has an ad hoc symmetry-breaking mechanism to produce masses for the elementary fermions, but cannot explain the nonzero masses of the neutrinos and their oscillation.
The fractional quantum numbers of the quarks contradict the quantization of the electric charge.
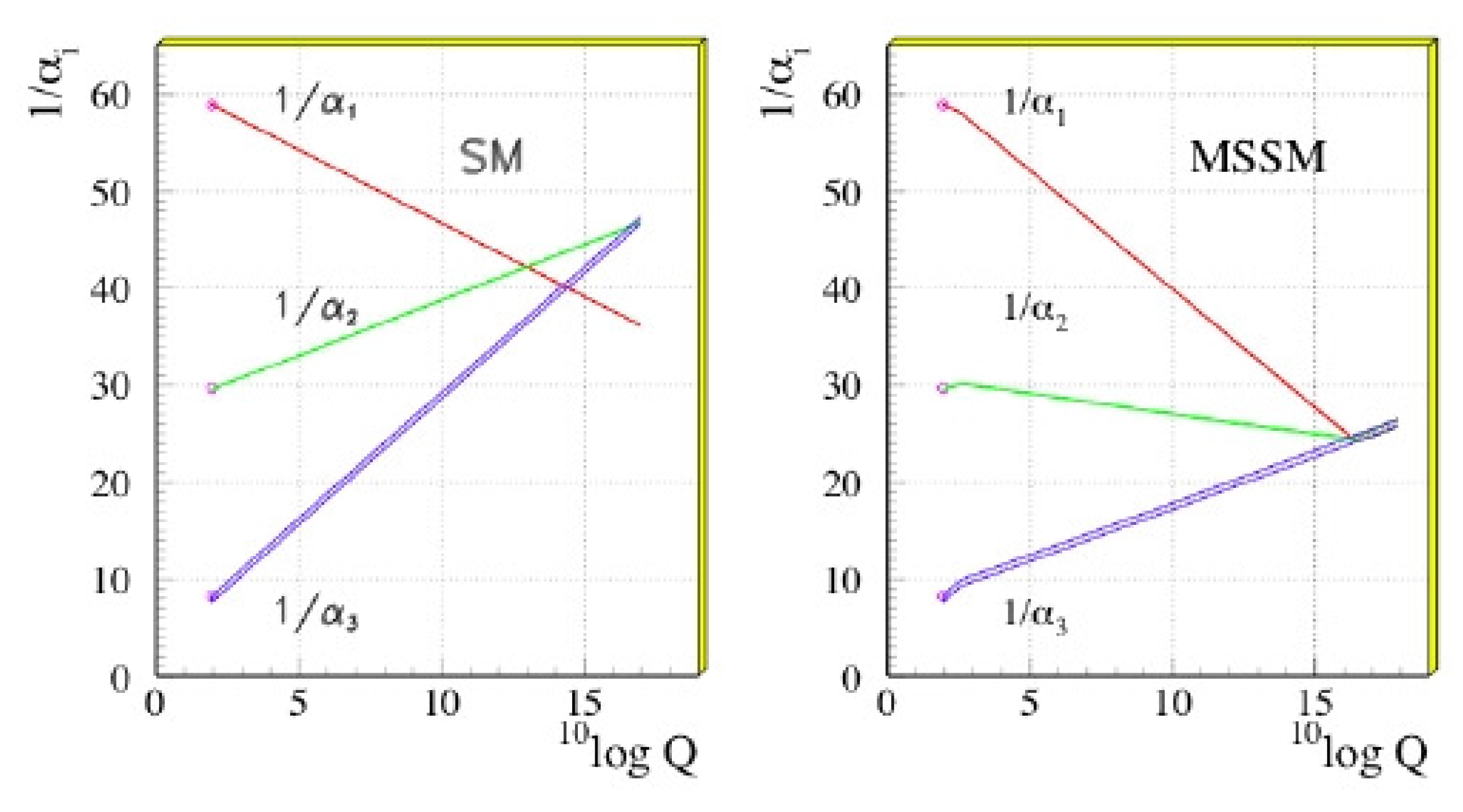
The coupling constants of the three gauge interactions converge at high energies, but do not meet (
Figure 12).
There is a magic number three for colors, charges, and fermion families with no relation to each other.
Naturalness (hierarchy) problem: The mass of the Higgs boson quadratically diverges due to radiative corrections.
The hierarchy problem would be solved if the fundamental fermions and bosons existed in pairs with the same properties, just different (one half less) spins, because the largest terms of the corrections (mainly that due to the top quark) could cancel each other.
8. Supersymmetry
Many extensions have been proposed for the standard model, solving some of the problems above [
23]. However, only one of them seems to be able to handle most of those (see
Figure 11),
supersymmetry with the short name
SUSY. SUSY is originally proposed to solve the hierarchy problem, so it assumes that fermions and bosons exist in identical pairs, with just their spins different by
. Thus the gauge bosons of the SM should have spin-half fermions and the SM fermions scalar bosons as partners. If this picture has any reality, SUSY is obviously broken at low energy, as we do not observe those partner particles: if they exist at all they must be much heavier. There are also many-many alternative extensions of the standard model proposed to solve these problems and for checking them the experiments search for deviations from SM predictions.
8.1. R Parity and LSP
SUSY’s quantum number is called
R parity,
, where
B is the baryon charge,
L is the lepton charge, and
S is the spin of the particle. It is easy to check that
for all SM particles and
for the SUSY partners. Supersymmetry can unify at high energy the gauge coupling constants (
Figure 12). Moreover, it allows including gravity and offers a good candidate for dark matter as the lightest neutral supersymmetric particle (LSP). In the case if SUSY is valid,
R parity should be conserved, as we do not see such exotic decays, possibly attributed to supersymmetry. Conservation of the
R parity would prevent the LSP from decaying. After the Big Bang, SUSY particles could also be produced in particle-antiparticle pairs, and at the end of the decay cascade, the LSP could just stay on and constitute the dark matter of the universe.
LSP production should make it possible to observe SUSY reactions: supersymmetric particles could be produced in pairs in high-energy collisions and decay via emitting ordinary and SUSY particles. At the end of the decay chain, the lightest one should escape detection, leaving behind a great portion of undetected momentum missing energy producing energetically unbalanced events. Unfortunately, leptonic weak decays produce neutrinos, resulting in similar events with missing energy, making a considerable SM background in the search for SUSY phenomena.
In order to eliminate the hierarchy problem, the numbers of ordinary and supersymmetric particle kinds should be equal, thus the left- and right-polarized fermions of the SM should have different SUSY partner bosons, with different masses. Supersymmetry in its minimal form needs two doublet BEH fields, i.e., eight symmetry-breaking fields, and after creating the three weak boson masses, five Higgs bosons will be left, three neutral and two charged ones. As we see already a 125 GeV Higgs boson, we must assume that one of the neutral minimal supersymmetric standard model (MSSM) Higgs bosons (probably the lighter one) corresponds to that one. The other neutral ones could be very heavy, but there must be two charged ones, as well. This clearly shows the importance of the Higgs sector in testing the validity of SUSY.
Due to the rather complicated nature of the proposed SUSY-breaking mechanisms, the MSSM adds 105 new particle masses and coupling constants to the original 19 parameters of the standard model. Thus, SUSY has much too many variables, impossible to test directly. There were several extremely simplified versions of the MSSM (with four or five free parameters), but those were refuted by the earliest runs of the LHC.
8.2. Search for SUSY Phenomena
Recently, the experiments gave up testing definite SUSY models with fixed parameters and rather tried to find deviations from the predictions of the standard model by analyzing events of simple topologies. For that, great amounts of very precise data are needed. Many such topologies are considered by the LHC experiments, but so far, none uncovered any difference from the SM predictions. Nonetheless, these studies are quite useful for the theoreticians, as they help to restrict the parameter space available for the various versions of MSSM. In most of the cases, the available experimental information provides mass limits for SUSY particles in various possible model scenarios from a few hundred GeV up to several TeV’s.
Thus, the LHC experiments devote much effort to find or exclude SUSY signatures. ATLAS and CMS studied hundreds of possible supersymmetric scenarios and excluded most of the hypothetical SUSY partner particles with masses below 1 TeV. For solving the hierarchy problem, one needs lighter SUSY particles: even in the case of broken supersymmetry, the mass of the partner of the top quark (the scalar top) cannot be orders of magnitude heavier than the t quark itself, as that would break the elimination of the huge corrections to the mass of the Higgs boson. Generally, the scalar t quark is assumed to be the lightest scalar quark, and the SUSY partner of the tau lepton is assumed to be the lightest among the scalar leptons (reversed particle hierarchy).
9. Unsolved Problems
As shown in
Figure 11, in addition to supersymmetry, many different theoretical extensions have been proposed in order to solve the problems of the standard model. All high-energy experiments try to search for such signatures, but so far, no convincing positive result was obtained. Of all extensions, only those models can be tested, of course, that make measurable predictions. All of the hypothetical new particles that were searched for experimentally were excluded at the masses that could be generated at the energies available at the accelerators, and thus, they have lower limits set on their masses, usually above 1 TeV.
9.1. Neutrino Oscillation
Particle oscillation appears when two interactions have different eigenstates in relation to a particle and those eigenstates have a very small mass difference (like in the case of the neutral kaons). Neutrino oscillations, the conversion of one neutrino flavor into another one, were experimentally observed among all three neutrinos and therefore established that neutrinos do have masses. These masses are extremely small, that is why they contribute very little to the measurable quantities in high-energy physics. Nevertheless, neutrino oscillation contradicts the standard model as that assumes massless neutrinos. One cannot add neutrino mass terms to the interaction Lagrangian similarly to those of the quarks and charged leptons. Massive neutrinos should have right-polarized particles and left-polarized antiparticles, which then cannot partake in the SU(2) (charged current) interaction, the only interaction available for neutrinos according to the standard model. Furthermore, for describing the neutrino oscillation, the neutrinos must have two interactions with different eigenstates, but for them, no other interaction is known. Thus, we have another symmetry breaking of unknown origin leading out of the SM world.
9.2. Antimatter
Another big mystery is the apparent lack of antimatter in our universe. According to the theory of the Big Bang, in the beginning, all energy in the Universe had to be in form of radiation, which upon expansion and cooling formed particle–antiparticle pairs, and we do not know where the antimatter went. Explanations were offered based on inflation, the fast expansion of the Universe in the very short first moments of its existence. Nevertheless, there are considerable efforts to check whether or not particle and antiparticle have really identical properties apart from the signs of their charges. At the Antiproton Decelerator of CERN, many such experiments study this question by measuring the charge, mass, and magnetic moment of the antiproton and also the spectral and gravitational properties of the antihydrogen atom, the atomic bound state of an antiproton and a positron. Thus far, none of the measurements uncovered any difference between proton and antiproton within the relative precision of .
10. Conclusions
The standard model is based on gauge symmetries, but several of them are broken. The P spatial mirror symmetry, i.e., parity conservation, is maximally violated, and the (charge + parity reflection) and T (time reversal) symmetries are also slightly broken. Nevertheless, invariance and its consequence, the matter-antimatter symmetry, seems to be fully valid. The BEH mechanism of spontaneous symmetry breaking to produce masses for the elementary particles is well established, as the Higgs boson was observed and its properties agreed very well with the predictions of the standard model. Thus, the standard model seems to be both theoretically and experimentally very well confirmed.
However, in spite of its tremendous success in reproducing experimental data, the standard model has several shortcomings, mostly theoretical problems: divergent Higgs boson mass, unknown dark matter, neutrino mass and oscillations, etc. Various extensions of the standard model were proposed to solve them, all based on breaking some (hypothetical) symmetry, but (1) none of them solves all the problems, although supersymmetry seems to take care of many of them, while (2) their predicted new particles and phenomena have not been observed yet. All particle physics experiments at present working at low and high energies are making tremendous efforts for clarifying these questions, but first of all uncover possible deviations in measurable data from the standard model.