Abstract
This contribution is an appetizer to the relatively young and fast-evolving approach to quantum cosmology based on group field theory condensate states. We summarize the main assumptions and pillars of this approach which has revealed new perspectives on the long-standing question of how to recover the continuum from discrete geometric building blocks. Among others, we give a snapshot of recent work on isotropic cosmological solutions exhibiting an accelerated expansion, a bounce where anisotropies are shown to be under control, and inhomogeneities with an approximately scale-invariant power spectrum. Finally, we point to open issues in the condensate cosmology approach.
Most important part of doing physics is theknowledge of approximation.Lev Davidovich Landau
1. Introduction
Current observational evidence strongly suggests that our universe is accurately described by the standard model of cosmology [1]. This model relies on Einstein’s theory of general relativity (GR) and assumes its validity on all scales. However, this picture proves fully inadequate to describe the earliest stages of our universe, as our concepts of spacetime and its geometry as given by GR are then expected to break down due to the extreme physical conditions encountered in the vicinity of and shortly after the Big Bang. More explicitly, it appears that our universe emerged from a singularity, as implied by the famous theorems of Penrose and Hawking [2]. From a fundamental point of view, such a singularity is unphysical, and it is expected that quantum effects lead to its resolution [3]. This motivates the development of a quantum theory of gravity in which the quintessential features of GR and quantum field theory (QFT) are consistently unified. Such a theory will revolutionize our understanding of spacetime and gravity at a microscopic level and should be able to give a complete and consistent picture of cosmic evolution.
The difficulty in making progress in this field is ultimately rooted in the lack of experiments which have access to the physics at the smallest length scales and highest energies and so would provide a clear empirical guideline for the construction of such a theory. In turn, this severe underdetermination of theory by experiment is a reason for the current presence of a plethora of contesting approaches to quantum gravity [4]. Against this backdrop, the cosmology of the very early universe represents a unique window of opportunity out of this impasse [5]. For instance, it is naturally expected that traces of quantum gravity have left a fingerprint on the spectrum of the cosmic microwave background radiation, see e.g., Refs. [6,7,8,9,10,11]. Hence, cosmology provides an ideal testbed where the predictions of such competing theories can be compared and tested against forthcoming cosmological data.
A central conviction of some approaches to quantum gravity is that it should be a non-perturbative, background-independent, and diffeomorphism-invariant theory of quantum geometry. In this sense, the spacetime continuum is renunciated and is instead replaced by degrees of freedom of a discrete and combinatorial nature.1 Particular representatives of this class of theories are the closely related canonical and covariant loop quantum gravity (LQG) [20,21,22,23], group field theory (GFT) [24,25], tensor models (TM) [26,27,28,29,30,31,32], and simplicial quantum gravity approaches such as quantum Regge calculus (QRC) [33] and Euclidean and causal dynamical triangulations (EDT, CDT) [34,35,36]. The perturbative expansion of their path integrals each yields a sum over discrete geometries and the most difficult problem for all of them then lies in the recovery of continuous spacetime geometry and GR describing its dynamics in an appropriate limit. This is challenging because it ideally requires formulating statements about the continuum by only calling upon notions rooted in the discontinuum. Taking the continuum limit in these approaches crucially depends on whether the discreteness of geometry is considered physical or unphysical therein, the proper weighting of configurations in the partition function, and the precise specification of the continuum limit itself. Consequently, strategies to reach this goal differ among them strongly, see e.g., Ref. [37] for an overview.
In the light of the above, it is vitally important to consider these approaches in a cosmological context, which has been accomplished to a varying degree of success by them. In this contribution, we give a brief and rather non-technical panorama of the GFT condensate cosmology program [38,39] which has been developed over the last few years and has so far borne promising fruits.2 This program is motivated by the idea that the mechanism for regaining a continuum geometry from a physically discrete quantum gravity substratum in GFT is provided by a phase transition to a condensate phase [40,42]. Research on the phase structure of different GFT models in terms of functional renormalization group analyses finds support for such a conjecture in terms of IR fixed points [43,44,45,46,47,48,49,50]. Further backing is provided by saddle point studies [51] and Landau–Ginzburg mean field analyses [52] which probe non-perturbative aspects of GFT models, see also Ref. [37]. In this picture, a condensate would correspond to a non-perturbative vacuum which comprises of many bosonic GFT quanta and in the context of GFT models of four-dimensional quantum gravity is tentatively interpreted as a continuum geometry. Given this basic premise, the most striking successes and milestone results of the condensate cosmology approach are the recovery of Friedmann-like dynamics of an emergent homogeneous and isotropic geometry [53], an extended accelerated phase of expansion [54,55] right after a cosmological bounce [56], a simple yet effective mechanism for dynamical isotropization of microscopic anisotropies [57,58] and the finding of an approximately scale-invariant and small-amplitude power spectrum of quantum fluctuations of the local volume over a homogeneous background geometry perturbed by small inhomogeneities [59]. In the following, we will quickly review the GFT formalism, give the basic structures behind its condensate cosmology spin-off, highlight the main results, and give an outlook for future challenges of this program.3
2. Group Field Theory
GFTs are quantum field theories which live on group configuration spaces, possess a gauge symmetry and are in particular characterized by combinatorially non-local interactions [24,25]. More precisely, the real- or complex-valued scalar field lives on d copies of a Lie group G. In models for quantum gravity, G corresponds to the local gauge group of GR and the gauge symmetry leads to an invariance of the GFT action under the (right) diagonal action of G which acts on the fields as
For quantum gravity models G is typically (or ) in the Lorentzian case, (or ) in the Riemannian case or their rotation subgroup which is the gauge group of Ashtekar–Barbero gravity. The group elements with are parallel transports which are associated with d links and A denotes a gravitational connection 1-form. The gauge symmetry guarantees the closure of the faces dual to the links to form a -simplex. For the most discussed case where , one obtains tetrahedra in this way. The metric information encoded in the fields can be retrieved via a non-commutative Fourier transform [38,39,41,57,61,62,63].
For a complex-valued field the action has the structure
where we used the shorthand notation . Since further details about the action are specified below, here the following suffices to say. The local kinetic term typically incorporates a Laplacian and a “mass term” contribution. The former is motivated by renormalization studies on GFT [64] while the latter can be related to spin foam edge weights via the GFT/spin foam correspondence [65] (see below) and hence should not be confused with a physical mass. The so-called simplicial interaction term consists of products of fields paired via convolution according to a combinatorial non-local pattern which for encodes the combinatorics of a 4-simplex. The precise details of the kinetic and interaction term are supposed to encode the Euclidean or Lorentzian embeddings of the theory [53,58,66].
With this, the perturbative expansion of the partition function
is indexed by Feynman diagrams which are dual to gluings of d-simplices.4 In this way, it provides a generating function for the covariant quantization of LQG in terms of spin foam models [22,23]. In LQG, boundary spin network states of a spin foam correspond to 3-dimensional discrete quantum geometries while the spin foam transition amplitudes interpolate in between two such boundary configurations. There, a proper imposition of the so-called simplicity constraints guarantees that - or -data in the bulk is reduced to -valued data on the boundary [70,71,72,73,74,75,76,77,78,79,80,81,82,83]. The main aspects of the GFT formulation of the currently most studied spin foam model for Lorentzian 4d quantum gravity, the so-called EPRL model [22,23], are specified by the aforementioned simplicial interaction term, that the GFT fields are defined over (thus encoding the boundary geometry) and finally the proper embedding of these data into which is realized by the dynamics and thus is encoded by the details of the kinetic and interaction term in the action. We further specify this action in Section 3.2 and Section 4.1 but note here that all the details of the interaction term have so far not been put down in terms of its boundary data [58] which, for what matters in this review, does not pose a limitation.
In the second-quantized formulation of GFT, introduced in Ref. [84], motivated by the origins of GFT in LQG, spin network boundary states are viewed as elements of the GFT Fock space wherein spin network vertices, i.e., atoms of space, correspond to fundamental quanta which are created or annihilated by the field operators of GFT.5 The GFT Fock space
is built by means of the fundamental Hilbert space of a GFT quantum which is assumed to obey bosonic statistics.6 Clearly, for and imposing gauge invariance as in Equation (1), a state in represents an open LQG spin network vertex or its dual quantum polyhedron. In particular, for a GFT quantum corresponds to a quantum tetrahedron which also is the most studied case within the condensate cosmology program [38,39,41]. In the remainder, we stick to this choice for G and d.
In this picture, many particle GFT states can be excited over the Fock vacuum which is the state devoid of any topological and quantum geometric information. Standardly, it is defined via the action of an annihilation field operator, namely
where the vacuum is normalized to 1. Given their bosonic statistics, the GFT field operators obey the canonical commutation relations
where the form of the delta distribution accounts for the imposition of gauge invariance, Equation (1).
In this framework, quantum geometric observable data can be retrieved from such states via second-quantized Hermitian operators [87], e.g., the number operator is given by
while more general one-body operators read as
wherein denote the matrix elements of a corresponding first-quantized operator. In this way, the area and volume operator of LQG can be imported into the GFT context, which is typically done by working in the spin representation introduced below.7 Hence, in GFT the discreteness of geometry is considered to be being real, rooted in its strong connections to LQG where the spectra of geometric operators are discrete (as shown to hold at the kinematical level) [88,89,90,91].
3. Group Field Theory Condensate Cosmology
The general aim of the GFT condensate cosmology program is to describe cosmologically relevant geometries by means of the formalism given above. Concretely, the goal is to approximate 3-dimensional homogeneous and extended geometries as well as their cosmological evolution in terms of GFT condensate states and their effective dynamics.
3.1. Motivation for Condensate States
As initially stated in the introduction, indications for the formation of a condensate phase have been found through the analyses of non-perturbative aspects of GFT models. In particular, functional renormalization group analyses of so-called tensorial GFTs [43,44,45,46,47,48,49] indicate a phase transition separating a symmetric from a broken/condensate phase as the “mass parameter” tends to negative values in the IR limit which is analogous to a Wilson-Fisher fixed point in the corresponding local QFT. This is illustrated in terms of the phase diagrams in Figure 1. Building on these, more work must be devoted to studying the phase structure of a (potentially colored) GFT model enriched with additional geometric data and an available simplicial quantum gravity interpretation. The hope would be that in the phase diagram of such a theory at least one phase can be found which can be interpreted as a physical continuum geometry of relevance to cosmology.8
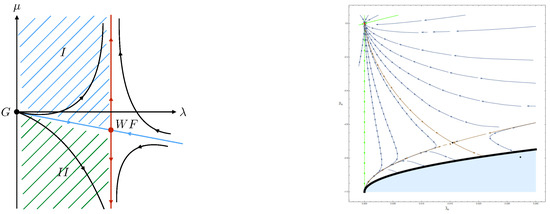
Figure 1.
Left: Phase diagram of a local scalar field theory with quartic interaction on . The “mass parameter” is denoted by while the interaction couples with . G denotes the Gaussian fixed point and the Wilson-Fisher fixed point. In the region hatched in green holds. Right: Exemplary phase diagram of a quartic tensorial GFT on (cf. Refs. [48,49]). In the analogue of region on the left-hand side, a non-vanishing expectation value of the field operator is expected to be found.
Given this central hypothesis of the GFT condensate cosmology program, the goal is to directly derive the effective dynamics for GFT condensate states from the microscopic quantum dynamics using mean field techniques inspired by the theory on Bose-Einstein condensates [96,97,98] and to extract a cosmological interpretation thereafter. Generally, a condensate phase corresponds to a non-perturbative vacuum of a theory where the expectation value of the field operator is non-vanishing, i.e., . Since such a vacuum is described by a large number N of quanta, in the GFT context this would make it suitable to model extended geometries. In addition, these quanta are occupying the same quantum geometric configuration which is desirable if a homogeneous background geometry is to emerge from the condensate. Simple trial states which capture these features are field coherent states of the form
corresponding to an infinite superposition of states which for describe disconnected quantum tetrahedra labeled by the same discrete geometric data. The latter is encoded by a single collective function, the condensate wave function . These states are field coherent since they are eigenstates of the field operator,
for which holds. Finally, in addition to the right invariance as in Equation (1), we require the invariance under the left diagonal action of G, i.e., for all to guarantee that the domain of the condensate wave function is isomorphic to the minisuperspace of homogeneous geometries [63].9,10
3.2. Effective Condensate Dynamics
The effective dynamics of such states can be obtained by taking alternative but equivalent roads. One can either study the GFT path integral in saddle point approximation or use the lowest-order truncation of the Schwinger-Dyson equations of the GFT model under consideration [38,39,41,51,52,102]. These equations can be derived when using
where is a functional of the fields. An expression encoding the effective dynamics is then extracted by setting to the identity, giving
If we evaluate the expectation value with respect to the condensate state, one yields
which is the classical equation of motion for the condensate wave function. Its solution would amount to solving the theory at tree-level. In general, this is a non-linear and non-local equation for the dynamics of the mean field and is given the interpretation of a quantum cosmology equation despite the fact that it has no direct probabilistic interpretation as compared to the equations of motion of Wheeler–DeWitt (WdW) quantum cosmology [103] and loop quantum cosmology (LQC) [104,105]. However, this does not pose a problem to extract cosmological predictions from the full theory, as we will review below.
In a next step, to extract information regarding the dynamics of such condensate systems, we extend the set of degrees of freedom of the formalism and couple a free, massless, minimally coupled real-valued scalar field to the GFT field,
This scalar field serves as a relational clock, i.e., an internal time variable, with respect to which the latter evolves. Such a procedure is common practice in classical and quantum gravity [104,105,106,107,108,109]. Notice that the expectation values of the above-introduced observables will then obviously depend on the relational clock . The precise introduction of this degree of freedom is based on the expression of the Feynman amplitudes of a given simplicial GFT model which take the form of simplicial gravity path integrals for gravity when coupled to such a scalar field, as explained in detail in Refs. [53,110]. In this discretized setting, the matter field sits on the vertices which are dual to the 4-simplices of the simplicial complex.
In this way, the action takes the general form
where is local in and and the interaction term is given by
where each corresponds to four group elements. The object is a function of all group elements, encoding the combinatorics of a 4-simplex, which when appropriately specified together with are supposed to yield the GFT formulation of the EPRL spin foam model for Lorentzian quantum gravity in [53,58,80,81].
For the remainder of this review it is important to introduce the spin representation of GFT fields. For left- and right-invariant configurations as considered in the context of the condensate program, we may give the Peter-Weyl decomposition of the condensate field as
where are the Wigner matrices and is the dimension of the corresponding irreducible representation. The representation label j is an element of the set while the indices assume the values . The objects are called intertwiners and are elements of the Hilbert space of states of a single tetrahedron, i.e.,
where corresponds to the Hilbert space of an irreducible unitary representation of . The index labels elements in a basis in . In this way, it is clear that the presence of the intertwiners with label is due to the imposition of the right invariance onto the field, while the left-invariance leads to the label , respectively. Hence, the quantum geometric content of the field is stored in the scalar functions in the spin representation
When Equation (17) is injected into the action (15), one obtains an equation of motion for the condensate field which is a non-linear tensor equation and as such is notoriously difficult to solve, see Refs. [51,85,86,111,112]. We refrain from explicating the full details of this equation in the general case here and direct the reader to the original literature where these are given in depth [53,58]. Instead, we will focus on giving some details of a specific scenario relevant to cosmology the elaboration of which has led to most of the results of the condensate program.
4. Overview of Important Results
4.1. Recovery of Friedmann-Like Dynamics and Bouncing Solutions
What allows to make progress is the focusing on the case where the condensate wave function only depends on a single-spin variable, as discussed in the following. In fact, this corresponds to an isotropic restriction which leads to a highly symmetric configuration: In this way the condensate is made of equilateral tetrahedra which are the most “isotropic” configurations in a simplicial context. In effect, the domain of the left- and right-invariant field is reduced to a 1-dimensional manifold which is parametrized by a single variable, interpreted as the volume and the configuration space is that of a homogeneous and isotropic universe [53,58].11 One thus requires the mean field to be of the form
where the identification of intertwiner labels is due to the requirement that the volume be maximized in equilateral tetrahedra [53,58]. For such field configurations the action (15) (when dropping all repeated intertwiner labels for convenience) reads as
with
and
The latter product of intertwiners can be cast into the form of a -symbol. The details of these calculations can be found in Ref. [53] and in greater detail in Ref. [58]. Again, the specific aspects of the EPRL GFT model would be encoded in the details of the objects and (and thus ). The interaction kernel is supposed to encode the Lorentzian embedding of the theory and thus what is known as the spin foam vertex amplitude with boundary -states. Though its details are yet to be put down in the GFT context, its explicit form is not relevant to the results presented below.
With the above, one obtains the equation of motion of the condensate field, i.e.,
Most generally, the contribution of the kinetic term takes the form , where and parametrize ambiguities in the EPRL GFT model [53,58] and the partial derivatives with respect to the relational clock follow from a derivative expansion with respect to the same variable [53,110]. In what follows, we will see that the requirement that the Friedmann equations be recovered allows constraining of the form of and .
To this aim, we follow Refs. [53,56] and consider the regime of the dynamics where the interaction term is sufficiently small as compared to the kinetic term. Since higher powers of the condensate field are directly proportional to the number of condensate constituents, we may refer to a regime where the interaction term is sub-dominant as being mesoscopic.12 This is a crucial approximation to recover the Friedmann equations below. Then, the equation of motion reduces to
and when using the polar decomposition of the field as , yields
together with the conserved quantities
Notice that the central term in Equation (25) diverges towards to the effect that the system exhibits a quantum bounce (elaborated further below), as long as at least one is non-vanishing, see Figure 2.
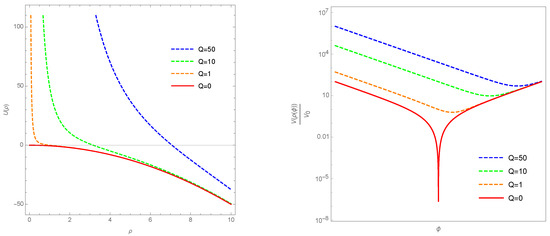
Figure 2.
Equation (25) has the form of the equation of motion of a classical point particle with potential . The potential is plotted for different values for Q while m and is kept fixed (left). Solutions to Equation (25) (initial conditions are arbitrarily chosen) lead to a plot for the volume (right). The point in relational time where the minimum of solutions is reached corresponds to the bounce. The solution for does not exhibit a bounce since the volume vanishes when turns to zero. In the plots and in this caption the label j is suppressed.
This is the case when requiring the energy density of the clock field to be non-zero. This energy density is given in terms of its conserved momentum by
where V denotes the expectation value of the volume operator. (Please note that is not to be confused with or ascribed to the mean field.) It is explicitly given by
We are now ready to give the dynamics of the volume of the emergent space, namely
as obtained in Ref. [53] and call these the generalized Friedmann equations.
The classical limit of these equations is obtained when considering sufficiently large volumes for which the terms with and in Equations (29) are suppressed. If one identifies then also (where denotes Newton’s constant), one recovers the classical Friedmann equations of GR for a flat universe in terms of the relational clock 13,
Notice that the definition of is understood as a definition in terms of the microscopic parameters (or and ) and not as an interpretation of the latter.
Another relevant situation where the dynamics of the volume can be solved exactly, is when the condensate is dominated by a single spin .14 In this case, the Equations (29) yield
where is a critical density [56]. The terms involving and correspond to quantum corrections where the one involving is responsible for the quantum bounce. To the past of this event, the emergent space contracts while it expands to the future. It should be remarked that up to the terms depending on these equations are exactly the modified Friedmann equations derived in LQC.15,16 For the bounce takes place at an energy density larger than , while for the bounce is realized for an energy density smaller than . Independently of the exact value of , a bounce will occur. It should nevertheless be clear that the physical meaning of the conserved quantity , from a fundamental point of view, is yet to be clarified. In future research it would also be important to consider the impact of different j-modes onto the dynamics. This is in principle straightforward but would then require solving Equations (29) numerically.
Finally, to contextualize, notice that a quantum gravity induced bounce falls into the more general class of bouncing cosmologies which present tentative alternatives to the standard inflationary scenario to resolve the problems of the standard model of cosmology, see Ref. [117] for an overview.17
We may list important side-results which support the findings presented above:
- In Ref. [121], it is shown that for growing relational time, the condensate dynamically settles into a low-spin configuration, i.e., it will be dominated by the lowest non-trivial representations labeled by j. This goes in hand with a classicalization of the emergent geometry [57]. Following Ref. [121], this can be seen from the general solutions to Equation (24), i.e.,which either lead to exponentially expanding and contracting or oscillating solutions depending on the sign of the argument of the root function. All models for which has a positive maximum for some (as long as is excluded18) lead toA low-spin configuration is dynamically reached if the maximum of occurs at a low . This was demonstrated for reasonable choices of and in Refs. [121] and [57] to lead to . One may then argue that the type of configuration which is usually assumed in the LQC literature can be derived from the quantum dynamics of GFT.
- A careful analysis shows that the identification only holds asymptotically for large , rendering a state-dependent function [54]. This is illustrated in Figure 3.
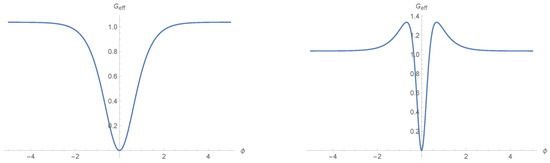 Figure 3. The effective gravitational constant as a function of relational time for to the left and to the right given in arbitrary units, taken from Ref. [54]. A bounce occurs towards situated at the origin of both plots. For large Newton’s constant is asymptotically attained. In the plots and in this caption the label j is suppressed.
Figure 3. The effective gravitational constant as a function of relational time for to the left and to the right given in arbitrary units, taken from Ref. [54]. A bounce occurs towards situated at the origin of both plots. For large Newton’s constant is asymptotically attained. In the plots and in this caption the label j is suppressed. - Another related notion of isotropic restriction has been studied in the literature so far where the condensate is built from tri-rectangular tetrahedra [57]. This produces physically equivalent results in terms of the dynamics of the volume, as one would expect when invoking naive universality arguments. Notice that both isotropic restrictions correspond to symmetry reductions applied to the quantum state and thus should by no means be equated with those performed in WdW quantum cosmology or LQC. In the latter cases, symmetry reductions are imposed before quantization and this procedure is expected to violate the uncertainty principle [103].19 In light of the above, it would be important to give a precise notion of isotropy in terms of a properly defined GFT curvature operator.
- In a related model which does not make use of the relational clock, the field content has been explicitly studied for free and effectively interacting scenarios [92]. For such static configurations one finds that the condensate consists of many GFT quanta residing in the lowest spin configurations. This is indicated by the analysis of the discrete spectra of the geometric operators, as illustrated by Figure 4. This also supports the idea that under the given isotropic restrictions, such GFT condensate states are suitable candidates to describe effectively continuous homogeneous and isotropic 3-spaces built from many smallest building blocks of the quantum geometry.
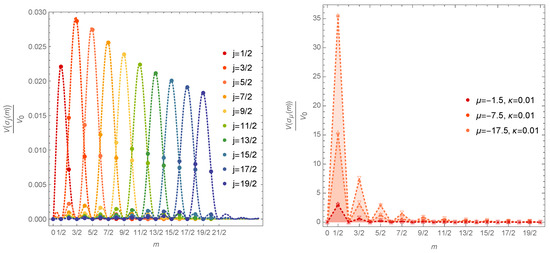 Figure 4. The spectrum to the volume operator in the free case to the left and effectively interacting case to the right. These illustrate that the geometric operators are dominated by the lowest non-trivial modes characterizing the condensate field. These plots were taken from Ref. [92] where a detailed discussion of their underlying computations can be found.
Figure 4. The spectrum to the volume operator in the free case to the left and effectively interacting case to the right. These illustrate that the geometric operators are dominated by the lowest non-trivial modes characterizing the condensate field. These plots were taken from Ref. [92] where a detailed discussion of their underlying computations can be found.
4.2. Cyclic Cosmologies and Accelerated Expansion
In a series of works the effect of simplified GFT interactions onto the cosmological dynamics has been investigated under the assumption that the spin representation j is fixed [55,57] (which may be motivated by the above-described process of reaching a low-spin configuration). Given these phenomenologically motivated interactions, the equations of motion take a simple non-linear form. Despite the fact that from a GFT point of view such interactions seem to be somewhat artificial due to their lack of a discrete geometric interpretation, they bring us nearer to the physics which we want to probe as they capture the basic non-linearity of the original GFT interactions. The form of the effective potential is given by
and we require so that the potential is bounded from below. Using the polar form of the field, we obtain the equation of motion
where we have set
To guarantee that this equation does not lead to an open cosmology expanding at a faster than exponential rate, we have . In consistency with the free case discussed above, while the sign of can be left unconstrained. A first observation from this equation of motion is its resemblance with that of a classical point particle in the potential
so that with the given signs and the bouncing contribution of strength the solutions to Equation (36) yield cyclic motions. Via Equation (28) these correspond to cyclic solutions for the dynamics of the emergent universe. Hence, we observe that bounded interactions induce a recollapse. Given that in the classical theory a recollapsing solution follows from a closed topology of 3-space, this might give an indication of how to obtain such topologies from these simple GFT condensates.
Regarding the expansion behavior of the emergent geometry, using the above-given interactions it is possible to obtain a long-lasting accelerated phase after the bounce. In fact, the free parameters may be fine-tuned to achieve any desirable value of e-folds so that this behavior can be understood as an inflationary expansion of quantum geometric origin. This becomes transparent when writing for the number of e-folds
and incorporating it in an expression for the acceleration. Since there is no notion of proper time in GFT, a sensible definition of acceleration can only be given in relational terms. In particular, we seek a definition that agrees with the standard one given in ordinary cosmology via the Raychaudhuri equation which allows us to define the acceleration as
the derivation of which is discussed in detail in Refs. [54,55]. Using this, one finds that the free case does not lead to a value of N large enough to supplant the standard inflationary mechanism in cosmology. However, the careful analysis of Ref. [55] demonstrates that with a hierarchy together with leads to which allows room for an era of accelerated expansion analogous to that of models of inflationary cosmology. If phantom energy is ruled out, only and are admissible selecting an interaction term which is in principle compatible with simplicial interactions, introduced above. These results are illustrated in Figure 5. Notice that these works emphasize the role that phenomenology can take for model building in quantum gravity.
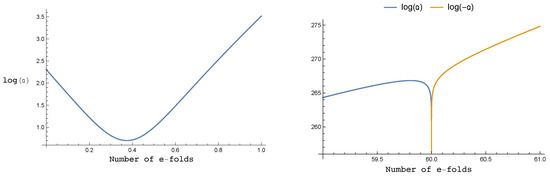
Figure 5.
The plot to the left shows the behavior of the acceleration close to the bounce while the one to the right illustrates it towards the end of inflation. These plots were taken from Ref. [55] to which we direct for details.
It should be emphasized that these findings have a purely quantum geometric origin and in particular are not based in any way on the assumption of a specific potential for the minimally coupled massless scalar field , the relational clock. This is in stark contrast to inflation which depends on the choice of potential and initial conditions of the inflaton field to yield the desired expansion behavior [124,125,126,127].
4.3. Anisotropies and Inhomogeneities
If quantum gravity is to offer the picture of the earliest moments of our universe, it must include an approximately homogeneous and isotropic background with superimposed perturbations. Given the above results an important step for the condensate cosmology program is to go beyond the considered isotropic restriction and homogeneous configurations and to study more general configurations and their dynamics. In the following, we want to briefly discuss recent advances in which the exploration of anisotropies [57,58] and inhomogeneities [59] has been commenced.
The study of anisotropic GFT configurations and their dynamics is of general importance since it would be desirable to see if at least a subset of these can agree with the observed isotropy of our universe at late times. For these one must show that anisotropies do not grow in the expanding phase. Apart from that, it is well known that bouncing cosmologies are haunted by the notorious problem of uncontrolled growth of anisotropies when the universe contracts [117]. This is the problem of the Belinsky–Khalatnikov–Lifshitz instability [128,129]. In light of this, it is interesting to understand the fate of anisotropies when approaching the quantum bounce as predicted by GFT.
Leaving the technical details aside, in Ref. [57] it has indeed been shown for rather general configurations that they dynamically isotropize in relational time by means of a simple mechanism (which is akin to the one responsible for settling the system into a low-spin configuration, as described in Section 4.1). Conversely, it is demonstrated that anisotropic contributions to the condensate become increasingly pronounced towards small volumes. This paved the way to a systematic investigation of anisotropic perturbations over an isotropic background in the vicinity of the bounce in Ref. [58]. In particular, a region in the parameter space is identified such that these anisotropies can be large at the bounce but are fully under control. From this it also follows that towards the bounce the quantum geometry of the emergent universe is rather degenerate. Furthermore, this analysis shows that the anisotropic perturbations become negligible the further away the system is from the bouncing phase and can be completely irrelevant to the dynamics before interactions kick in. Hence, after the bounce a cosmological background emerges the dynamics of which can again be cast into the form of the above-given effective Friedmann equations, thus corroborating the results of Refs. [53,56,57]. These results are illustrated in Figure 6. On more general grounds, these studies form a crucial starting point towards identifying anisotropic cosmologies, i.e., Bianchi models, within this approach and allow establishment of contact with corresponding studies in WdW [103], spin foam [130,131,132,133,134,135,136,137,138,139,140,141,142] and loop quantum cosmology [104,105].
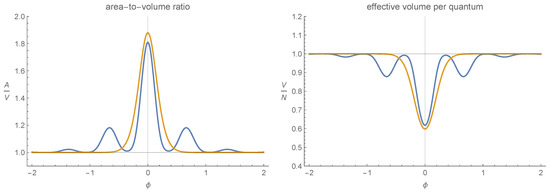
Figure 6.
The surface-area-to-volume ratio (left) and the effective volume per quantum (right) as a function of relational time. These figures demonstrate the degenerate character of the quantum geometry towards the bounce and the damping of the anisotropies in the outgoing phase. The plots were taken from Ref. [58] where detailed explanations are given.
Modern Cosmology teaches us that the seeds for structure formation are represented by inhomogeneities in the very early universe [143]. Hence, the identification and study of cosmological inhomogeneities in the condensate approach is mandatory to promote it to a realistic contestant theory of quantum cosmology. In particular, the goal would be to find a mechanism rooted in quantum geometry which explains the origins of inhomogeneities without referring to the inflationary paradigm where the inhomogeneities correspond to quantum fluctuations of the inflaton field [124].
Recent progress building on Refs. [144,145], allows extension of the formalism beyond homogeneity. In Refs. [59,146] the formalism of including a free massless scalar field [53,110] is extended to incorporate four reference scalar fields which are used as relational clocks and rods, i.e., as a physical coordinate system. Again, this procedure is common in classical and quantum gravity approaches [108,109]. In this setting quantum fluctuations (i.e., small inhomogeneities) of the local 3-volume around a nearly homogeneous background geometry are studied. Their power spectrum can be calculated, and this is shown to be approximately scale-invariant (where the scale is defined by the reference matter), the amplitude is small, and decreases as the emergent universe expands. However, it was also demonstrated that analogous statements do not hold for perturbations in the total density of the scalar fields when the gradient energy is non-negligible. Notice that the details of these arguments relied on the specific choice of condensate state which solves the condensate dynamics and thus depends on the approximation scheme summarized in Section 3.1 and Section 3.2. More recent work [147] has shown how the transition from the initial quantum fluctuations present in the deep quantum gravity regime to classical observable inhomogeneities can be accomplished. By and large, it is striking that features of the spectrum of cosmologically relevant observables can be recognized using the condensate formalism. Future research has to bridge the gap between observations of the early universe and the condensate formalism and the hope is that the incorporation of more complicated matter dynamics can reproduce observationally viable results.20
5. Discussion and Outlook
In this brief review we wanted to draw attention to key results of the GFT condensate cosmology program which illustrate its potential to provide a quantum gravitational foundation for early universe cosmology. Finally, we would like to point to open directions (if not already stated in the main body of this appetizer) and address some relations with other non-perturbative discrete quantum gravity approaches trying to extract cosmological solutions from their path integral formulations.
Beyond its application to cosmology showing a rich phenomenology, this program has revealed an interesting and powerful perspective on the extraction of continuum information from a discrete geometric setting: The field theoretic setting of GFT and specifically the use of field coherent states prove extremely useful and elegant to this aim.
To contextualize this, we may compare with the other non-perturbative and discrete path integral approaches to quantum gravity. In EDT, CDT, tensor models, the discreteness of geometry is regarded as a mathematical tool allowing us to rewrite the continuum path integral in a discrete form. The philosophy behind taking the continuum limit is rather similar among them and the goal is to study the phase structure of the respective theories via analyticity properties of the partition function. The CDT approach has been able to produce physically relevant, i.e., extended macroscopic geometries which obey effective minisuperspace dynamics [34,35,36]. This potentially highlights the role of causality in facilitating the escape from the sector of unphysical continuum geometries EDT [34,35,36] and TMs [26,27,28,29,30,31,32] are so far stuck with.
A point of criticism often invoked regarding these approaches, concerns the lack of a clear interpretation of expectation values of observables rigorously defined on a physical Hilbert space, which is in principle available in covariant LQG and GFT. Given this, GFT condensate cosmology is not the only approach which tries to extract the cosmological sector of LQG from a covariant formulation of its dynamics. In the spin foam cosmology approach, one uses the spin foam expansion which is an expansion in terms of the number of degrees of freedom [130,131,132,133,134,135,136,137]. It has mostly been studied for so-called dipole graphs (corresponding to the simplest cellular decomposition of the 3-sphere) [138,139,140] and can be extended to more general regular graphs [141,142]. A central assumption of this approach is that a fixed number of quanta of geometry captures all relevant physics. In contrast, in the condensate program one looks for continuum physics away from the Fock vacuum and does not restrict the number of quanta which can be rather large and dynamical.
Although GFT allows studying of an infinite class of simplicial complexes by construction, it provides the field theoretic approximation tools to study the physics of many LQG degrees of freedom while bypassing the treatment of highly complicated spin networks. In addition, in the spin foam context one typically studies the semi-classical limit by requiring the configurations to peak on some triangulated classical geometry [20,21,22,23].21 This point of view is also not assumed in GFT condensate cosmology, motivated by the condensate hypothesis which fixes the states to be described by the simple condensate wave function.
Being aware that the choice of simple trial states and the disregard of proper simplicial interactions so far neglects all the connectivity information of those spin networks that would be considered important for a realistic definition of a non-perturbative continuum vacuum state, it is pressing to go beyond the given simplifications. The exploration of the phenomenologically motivated interactions presented here as well as the study of dipole condensates [38,39] goes into this direction. Notice that recent work [51] in the context of the dynamical Boulatov model which is a model for Euclidean quantum gravity in has shown that non-trivial condensate solutions can be produced where simplicial interactions are fully considered. The background quantum geometries one yields in this way must be better understood but this procedure could in principle be carried over to the case in . Also, it is clear from this example that the choice of simple states does not pose a major problem since more complicated ones associated with connected graphs are then easily generated by the simplicial interaction term. In light of this, it would be important to study the relational evolution of such properly interacting condensates to see if the intriguing results regarding the accelerated expansion of the emergent geometry found via exploring the simplified interactions can be reproduced. Furthermore, studying the effect of the simplicial interaction of the Lorentzian EPRL GFT model (or any related model) onto the condensate will require putting it explicitly down in terms of its boundary data [58]. It could also be interesting to consider a colored version of such a model, given the insight that in perturbative expansion of the partition function the color degree of freedom guarantees that all terms are free of topological pathologies [67,68,69].
Apart from their impact on the dynamics, a better understanding of interactions will also allow construction of more sophisticated observables capturing curvature and cosmological anisotropies which in turn will prove indispensable to classify different emergent geometries from one another. It is nevertheless remarkable that in the regime where interactions are sub-dominant and which has been explored most so far, rich Friedmann-like dynamics can be obtained.
A related point to be focused on, touches on higher order corrections to the so-far considered condensate equation of motion and to understand if they can be neglected or if they would have a drastic impact on the cosmological interpretation of this approach. Understanding the full quantum dynamics will then shed light onto the phase structure of interesting GFT models of quantum gravity. In other words, it must be checked by means of non-perturbative techniques if a simplicial GFT model for quantum gravity can truly exhibit a phase or phases which are related to -dimensional Lorentzian continuum geometries. In the context of exploring the notion of phases in GFT, it would also be important to understand the relation in between a potential phase transition into a geometric phase for which the order parameter should vanish and the occurrence of a bounce which (by definition) forbids a zero-volume state.
At the very end, this approach will be judged by the ability to extract phenomenological signatures to see if it can be a realistic contestant theory of quantum cosmology. The development of a scenario to explain the origin of cosmological perturbations neither by the mechanism provided by inflation nor as in ordinary bounce models but rather via the quantum fluctuations of the geometry itself as given by GFT condensates is an important step into this direction.
Author Contributions
All authors contributed equally to all aspects of this manuscript.
Funding
M. S. is supported in part by the Science and Technology Facility Council (STFC), United Kingdom, under the research grant ST/P000258/1.
Acknowledgments
The authors thank the referees for their remarks which led to an improvement of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. arXiv 2018, arXiv:1807.06205. [Google Scholar]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge Monographs on Mathematical Physics; CUP: Cambridge, UK, 2011. [Google Scholar]
- De Witt, B.S. Quantum theory of gravity. i. the canonical theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Oriti, D. (Ed.) Approaches to Quantum Gravity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sakellariadou, M. Quantum Gravity and Cosmology: An intimate interplay. IOP Conf. Ser. J. Phys. Conf. Ser. 2017, 880, 012003. [Google Scholar] [CrossRef]
- Kiefer, C.; Krämer, M. Quantum Gravitational Contributions to the CMB Anisotropy Spectrum. Phys. Rev. Lett. 2012, 108, 021301. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, C.; Krämer, M. Can effects of quantum gravity be observed inthe cosmic microwave background? Int. J. Mod. Phys. 2012, D21, 1241001. [Google Scholar] [CrossRef]
- Kiefer, C.; Krämer, M. On the Observability of Quantum-Gravitational effects in the Cosmic Microwave Background. Springer Proc. Phys. 2014, 157, 531–538. [Google Scholar]
- Agullo, I.; Ashtekar, A.; Nelson, W. A Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 2012, 109, 251301. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. Extension of the quantum theory of cosmological perturbations to the Planck era. Phys. Rev. D 2013, 87, 043507. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. The pre-inflationary dynamics of loop quantum cosmology: Confronting quantum gravity with observations. Class. Quantum Gravity 2013, 30, 085014. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Field Theory, Past and Future. arXiv 2009, arXiv:0908.1964. [Google Scholar]
- Eichhorn, A. Status of the asymptotic safety paradigm for quantum gravity and matter. Found. Phys. 2018, 48, 1407–1429. [Google Scholar] [CrossRef]
- Percacci, R. Introduction to Covariant Quantum Gravity And Asymptotic Safety; World Scientific: Singapore, 2017. [Google Scholar]
- Reuter, M.; Saueressig, F. Quantum Gravity and the Functional Renormalization Group; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Blumenhagen, R.; Lüst, D.; Theisen, S. Basic Concepts of String Theory; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Connes, A. Noncommutative Geometry; Academic Press: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Chamseddine, A.H.; Fröhlich, J.; Grandjean, O. The Gravitational Sector in the Connes-Lott Formulation of the Standard Model. J. Math. Phys. 1995, 36, 6255–6275. [Google Scholar] [CrossRef][Green Version]
- Chamseddine, A.H.; Connes, A. The Spectral Action Principle. Commun. Math. Phys. 1997, 186, 731. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Background Independent Quantum Gravity: A Status Report. Class. Quantum Gravity 2004, 21, R53. [Google Scholar] [CrossRef]
- Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rovelli, C. Zakopane lectures on loop gravity. arXiv 2011, arXiv:1102.3660. [Google Scholar]
- Perez, A. The Spin Foam Approach to Quantum Gravity. Living Rev. Relativ. 2013, 16, 3. [Google Scholar] [CrossRef]
- Freidel, L. Group field theory: An Overview. Int. J. Theor. Phys. 2005, 44, 1769–1783. [Google Scholar] [CrossRef]
- Oriti, D. (Ed.) The Group field theory approach to quantum gravity. In Approaches to Quantum Gravity; Cambridge University Press: Cambridge, UK, 2009; pp. 310–331. [Google Scholar]
- Ambjørn, J.; Durhuus, B.; Jonsson, T. Three-dimensional simplicial quantum gravity and generalized matrix models. Mod. Phys. Lett. 1991, A6, 1133–1146. [Google Scholar] [CrossRef]
- Gross, M. Tensor models and simplicial quantum gravity in > 2-D. Nucl. Phys. Proc. Suppl. 1992, 25A, 144–149. [Google Scholar] [CrossRef]
- Gurau, R. Invitation to Random Tensors. SIGMA 2016, 12, 094. [Google Scholar] [CrossRef]
- Gurau, R. Random Tensors; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Rivasseau, V. The Tensor Track, IV. arXiv 2016, arXiv:1604.07860. [Google Scholar]
- Rivasseau, V. Random Tensors and Quantum Gravity. SIGMA 2016, 12, 069. [Google Scholar] [CrossRef]
- Delporte, N.; Rivasseau, V. The Tensor Track V: Holographic Tensors. arXiv 2018, arXiv:1804.11101. [Google Scholar]
- Williams, R.M. Quantum Regge Calculus. In Approaches to Quantum Gravity; Oriti, D., Ed.; Cambridge University Press: Cambridge, UK, 2009; pp. 360–377. [Google Scholar]
- Loll, R. Discrete approaches to quantum gravity in four dimensions. Living Rev. Relativ. 1998, 1, 13. [Google Scholar] [CrossRef] [PubMed]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127–210. [Google Scholar] [CrossRef]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Quantum gravity via causal dynamical triangulations. In Springer Handbook of Spacetime; Springer: Berlin, Germany, 2014; pp. 723–741. [Google Scholar]
- Pithis, A.G.A. Aspects of Quantum Gravity. Ph.D. Thesis, University of London, King’s College. Available online: https://kclpure.kcl.ac.uk/portal/en/theses/aspects-of-quantum-gravity(904af0f7-5dcc-4387-b905-32b5869db8c9).html (accessed on 31 March 2019).
- Gielen, S.; Oriti, D.; Sindoni, L. Cosmology from Group Field Theory Formalism for Quantum Gravity. Phys. Rev. Lett. 2013, 111, 031301. [Google Scholar] [CrossRef] [PubMed]
- Gielen, S.; Oriti, D.; Sindoni, L. Homogeneous cosmologies as group field theory condensates. J. High Energy Phys. 2014, 1406, 013. [Google Scholar] [CrossRef]
- Oriti, D. The Universe as a Quantum Gravity Condensate. In “Testing Quantum Gravity with Cosmology” of Comptes Rendus Physique; Barrau, A., Ed.; Académie des Sciences: Paris, France, 2017. [Google Scholar]
- Gielen, S.; Sindoni, L. Quantum Cosmology from Group Field Theory Condensates: A Review. SIGMA 2016, 12, 082. [Google Scholar] [CrossRef]
- Oriti, D. Disappearance and emergence of space and time in quantum gravity. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2014, 46, 186–199. [Google Scholar] [CrossRef]
- Benedetti, D.; Geloun, J.B.; Oriti, D. Functional Renormalisation Group Approach for Tensorial Group Field Theory: A Rank-3 Model. J. High Energy Phys. 2015, 3, 084. [Google Scholar] [CrossRef]
- Benedetti, D.; Lahoche, V. Functional Renormalization Group Approach for Tensorial Group Field Theory: A Rank-6 Model with Closure Constraint. Class. Quantum Gravity 2016, 33, 095003. [Google Scholar] [CrossRef]
- Geloun, J.B.; Koslowski, T.A. Nontrivial UV behavior of rank-4 tensor field models for quantum gravity. arXiv 2016, arXiv:1606.04044. [Google Scholar]
- Carrozza, S.; Lahoche, V. Asymptotic safety in three-dimensional SU(2)-Group Field Theory: Evidence in the local potential approximation. Class. Quantum Gravity 2017, 34, 115004. [Google Scholar] [CrossRef]
- Geloun, J.B.; Koslowski, T.A.; Oriti, D.; Pereira, A.D. Functional Renormalization Group analysis of rank 3 tensorial group field theory: The full quartic invariant truncation. Phys. Rev. D 2018, 97, 126018. [Google Scholar] [CrossRef]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalisation Group analysis of a Tensorial Group Field Theory on R3. EPL (Europhys. Lett.) 2015, 112, 31001. [Google Scholar] [CrossRef]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalisation Group analysis of Tensorial Group Field Theories on Rd. Phys. Rev. D 2016, 94, 024017. [Google Scholar] [CrossRef]
- Carrozza, S. Flowing in Group Field Theory Space: A Review. SIGMA 2016, 12, 070. [Google Scholar] [CrossRef]
- Geloun, J.B.; Kegeles, A.; Pithis, A.G.A. Minimizers of the equilateral dynamical Boulatov model. Eur. Phys. J. C 2018, 78, 996. [Google Scholar] [CrossRef]
- Pithis, A.G.A.; Thürigen, J. Phase transitions in group field theory: The Landau perspective. Phys. Rev. D 2018, 98, 126006. [Google Scholar] [CrossRef]
- Oriti, D.; Sindoni, L.; Wilson-Ewing, E. Emergent Friedmann dynamics with a quantum bounce from quantum gravity condensates. Class. Quantum Gravity 2016, 33, 224001. [Google Scholar] [CrossRef]
- de Cesare, M.; Sakellariadou, M. Accelerated expansion of the Universe without an inflaton and resolution of the initial singularity from Group Field Theory condensates. Phys. Lett. B 2017, 764, 49–53. [Google Scholar] [CrossRef]
- de Cesare, M.; Pithis, A.G.A.; Sakellariadou, M. Cosmological implications of interacting Group Field Theory models: Cyclic Universe and accelerated expansion. Phys. Rev. D 2016, 94, 064051. [Google Scholar] [CrossRef]
- Oriti, D.; Sindoni, L.; Wilson-Ewing, E. Bouncing cosmologies from quantum gravity condensates. Class. Quantum Gravity 2017, 34, 04LT01. [Google Scholar] [CrossRef]
- Pithis, A.G.A.; Sakellariadou, M. Relational evolution of effectively interacting GFT quantum gravity condensates. Phys. Rev. D 2017, 95, 064004. [Google Scholar] [CrossRef]
- de Cesare, M.; Sakellariadou, M.; Pithis, A.G.A.; Oriti, D. Dynamics of anisotropies close to a cosmological bounce in quantum gravity. Class. Quantum Gravity 2018, 35, 015014. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D. Cosmological perturbations from full quantum gravity. Phys. Rev. D 2018, 98, 106019. [Google Scholar] [CrossRef]
- Calcagni, G.; Gielen, S.; Oriti, D. Group field cosmology: A cosmological field theory of quantum geometry. Class. Quantum Gravity 2012, 29, 105005. [Google Scholar] [CrossRef]
- Freidel, L.; Livine, E.R. 3d Quantum Gravity and Effective Non-Commutative Quantum Field Theory. Phys. Rev. Lett. 2006, 96, 221301. [Google Scholar] [CrossRef]
- Baratin, A.; Dittrich, B.; Oriti, D.; Tambornino, J. Non-commutative flux representation for loop quantum gravity. Class. Quantum Gravity 2011, 28, 175011. [Google Scholar] [CrossRef]
- Gielen, S. Quantum cosmology of (loop) quantum gravity condensates: An example. Class. Quantum Gravity 2014, 31, 155009. [Google Scholar] [CrossRef]
- Ben Geloun, J. On the finite amplitudes for open graphs in Abelian dynamical colored Boulatov-Ooguri models. J. Phys. A 2013, 46, 402002. [Google Scholar] [CrossRef][Green Version]
- Reisenberger, M.P.; Rovelli, C. Spacetime as a Feynman diagram: The connection formulation. Class. Quantum Gravity 2001, 18, 121. [Google Scholar] [CrossRef]
- Oriti, D.; Rosati, G. Non-commutative Fourier transform for the Lorentz group via the Duflo map. Phys. Rev. D 2019, 99, 106005. [Google Scholar] [CrossRef]
- Gurau, R. Colored Group Field Theory. Commun. Math. Phys. 2011, 304, 69–93. [Google Scholar] [CrossRef]
- Bonzom, V.; Gurau, R.; Rivasseau, V. Random tensor models in the large N limit: Uncoloring the colored tensor models. Phys. Rev. D 2012, 85, 084037. [Google Scholar] [CrossRef]
- Gurau, R. Lost in translation: Topological singularities in group field theory. Class. Quantum Gravity 2010, 27, 235023. [Google Scholar] [CrossRef]
- De Pietri, R.; Freidel, L. so(4) Plebanski Action and Relativistic Spin Foam Model. Class. Quantum Gravity 1999, 16, 2187–2196. [Google Scholar] [CrossRef]
- Barrett, J.W.; Crane, L. A Lorentzian Signature Model for Quantum General Relativity. Class. Quantum Gravity 2000, 17, 3101–3118. [Google Scholar] [CrossRef]
- Perez, A.; Rovelli, C. Spin foam model for Lorentzian General Relativity. Phys. Rev. D 2001, 63, 041501. [Google Scholar] [CrossRef]
- Freidel, L.; Krasnov, K. A New Spin Foam Model for 4d Gravity. Class. Quantum Gravity 2008, 25, 125018. [Google Scholar] [CrossRef]
- Engle, J.; Livine, E.; Pereira, R.; Rovelli, C. LQG vertex with finite Immirzi parameter. Nucl. Phys. 2008, B799, 136. [Google Scholar] [CrossRef]
- Dupuis, M.; Livine, E.R. Lifting SU(2) Spin Networks to Projected Spin Networks. Phys. Rev. D 2010, 82, 064044. [Google Scholar] [CrossRef]
- Ding, Y.; Rovelli, C. Physical boundary Hilbert space and volume operator in the Lorentzian new spin-foam theory. Class. Quantum Gravity 2010, 27, 205003. [Google Scholar] [CrossRef]
- Freidel, L.; Speziale, S. On the Relations between Gravity and BF Theories. SIGMA 2012, 8, 032. [Google Scholar] [CrossRef]
- Kaminksi, W.; Kisielowski, M.; Lewandowski, J. Spin-Foams for All Loop Quantum Gravity. Class. Quantum Gravity 2010, 27, 095006, Erratum in 2012, 29, 049502. [Google Scholar]
- Speziale, S.; Wieland, W.M. The twistorial structure of loop-gravity transition amplitudes. Phys. Rev. D 2012, 86, 124023. [Google Scholar] [CrossRef]
- Geloun, J.B.; Gurau, R.; Rivasseau, V. EPRL/FK Group Field Theory. Europhys. Lett. 2010, 92, 60008. [Google Scholar] [CrossRef][Green Version]
- Baratin, A.; Oriti, D. Quantum simplicial geometry in the group field theory formalism: Reconsidering the Barrett-Crane model. New J. Phys. 2011, 13, 125011. [Google Scholar] [CrossRef]
- Han, M.; Zhang, M. Asymptotics of Spinfoam Amplitude on Simplicial Manifold: Euclidean Theory. Class. Quantum Gravity 2012, 29, 165004. [Google Scholar] [CrossRef]
- Baratin, A.; Oriti, D. Group field theory with non-commutative metric variables. Phys. Rev. Lett. 2010, 105, 221302. [Google Scholar] [CrossRef]
- Oriti, D. Group field theory as the 2nd quantization of Loop Quantum Gravity. Class. Quantum Gravity 2016, 33, 085005. [Google Scholar] [CrossRef]
- Girelli, F.; Livine, E.R.; Oriti, D. 4d Deformed Special Relativity from Group Field Theories. Phys. Rev. D 2010, 81, 024015. [Google Scholar] [CrossRef]
- Girelli, F.; Livine, E.R. A Deformed Poincare Invariance for Group Field Theories. Class. Quantum Gravity 2010, 27, 245018. [Google Scholar] [CrossRef]
- Oriti, D.; Pranzetti, D.; Ryan, J.P.; Sindoni, L. Generalized quantum gravity condensates for homogeneous geometries and cosmology. Class. Quantum Gravity 2015, 32, 235016. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Knot Theory and Quantum Gravity. Phys. Rev. Lett. 1988, 61, 1155. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Smolin, L. Loop space representation of quantum general relativity. Nucl. Phys. B 1990, 331, 80152. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–622, Erratum in 1995, 456, 753. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Spin networks and quantum gravity. Phys. Rev. D 1995, 52, 57435759. [Google Scholar] [CrossRef]
- Pithis, A.G.A.; Sakellariadou, M.; Tomov, P. Impact of nonlinear effective interactions on GFT quantum gravity condensates. Phys. Rev. D 2016, 94, 064056. [Google Scholar] [CrossRef]
- Kegeles, A.; Oriti, D.; Tomlin, C. Inequivalent coherent state representations in group field theory. Class. Quantum Gravity 2018, 35, 125011. [Google Scholar] [CrossRef]
- Kotecha, I.; Oriti, D. Statistical Equilibrium in Quantum Gravity: Gibbs states in Group Field Theory. New J. Phys. 2018, 20, 073009. [Google Scholar] [CrossRef]
- Chirco, G.; Kotecha, I.; Oriti, D. Statistical equilibrium of tetrahedra from maximum entropy principle. Phys. Rev. D 2019, 99, 086011. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation, 1st ed.; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-Gonzalez, R. (Eds.) Emergent Nonlinear Phenomena in Bose-Einstein Condensates Theory and Experiment; Springer: Berlin, Germany, 2008. [Google Scholar]
- Yukalov, V.I. Theory of cold atmos: Bose-Einstein statistics. Laser Phys. 2016, 26, 062001. [Google Scholar] [CrossRef]
- Oriti, D.; Pranzetti, D.; Sindoni, L. Horizon entropy from quantum gravity condensates. Phys. Rev. Lett. 2016, 116, 211301. [Google Scholar] [CrossRef] [PubMed]
- Oriti, D.; Pranzetti, D.; Sindoni, L. Black Holes as Quantum Gravity Condensates. Phys. Rev. D 2018, 97, 066017. [Google Scholar] [CrossRef]
- Oriti, D. The Universe as a Quantum Gravity Condensate, Extended Version of the Invited Contribution to the Special Issue “Testing Quantum Gravity with Cosmology” of Comptes Rendus Physique; Académie des Sciences: Paris, France, 2017. [Google Scholar]
- Sindoni, L. Effective equations for GFT condensates from fidelity. arXiv 2014, arXiv:1408.3095. [Google Scholar]
- Kiefer, C. Quantum Gravity, 3rd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quantum Gravity 2011, 28, 213001. [Google Scholar] [CrossRef]
- Banerjee, K.; Calcagni, G.; Martin-Benito, M. Introduction to Loop Quantum Cosmology. SIGMA 2012, 8, 016. [Google Scholar] [CrossRef]
- Dittrich, B. Partial and complete observables for canonical General Relativity. Class. Quantum Gravity 2006, 23, 6155–6184. [Google Scholar] [CrossRef]
- Rovelli, C. Partial observables. Phys. Rev. D 2002, 65, 124013. [Google Scholar] [CrossRef]
- Brown, D.; Kuchar, K. Dust as a standard of space and time in canonical quantumgravity. Phys. Rev. D 1995, 51, 5600–5629. [Google Scholar] [CrossRef]
- Giesel, K.; Thiemann, T. Scalar material referencesystems and loop quantum gravity. Class. Quantum Gravity 2015, 32, 135015. [Google Scholar] [CrossRef]
- Li, Y.; Oriti, D.; Zhang, M. Group field theory for quantum gravity minimally coupled to a scalar field. Class. Quantum Gravity 2017, 34, 195001. [Google Scholar] [CrossRef]
- Fairbairn, W.J.; Livine, E.R. 3d spinfoam quantum gravity: Matter as a phase of the group field theory. Class. Quantum Gravity 2007, 24, 5277. [Google Scholar] [CrossRef]
- Livine, E.R.; Oriti, D.; Ryan, J.P. Effective Hamiltonian Constraint from Group Field Theory. Class. Quantum Gravity 2011, 28, 245010. [Google Scholar] [CrossRef]
- Adjei, E.; Gielen, S.; Wieland, W. Cosmological evolution as squeezing: A toy model for groupfield cosmology. Class. Quantum Gravity 2018, 35, 105016. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. A relational Hamiltonian for group field theory. Phys. Rev. D 2019, 99, 086017. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D. Quantum cosmology from quantum gravity condensates: Cosmological variables and lattice-refined dynamics. New J. Phys. 2014, 16, 123004. [Google Scholar] [CrossRef]
- Calcagni, G. Loop quantum cosmology from group field theory. Phys. Rev. D 2014, 90, 064047. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. Found. Phys. 2017, 47, 797–850. [Google Scholar] [CrossRef]
- de Cesare, M. Limiting curvature mimetic gravity for group field theory condensates. Phys. Rev. D 2019, 99, 063505. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Mimetic gravity: A review of recent developments and applications to cosmology and astrophysics. Adv. High Energy Phys. 2017, 2017, 3156915. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Mukhanov, V. Resolving Cosmological Singularities. J. Cosmol. Astropart. Phys. 2017, 1703, 009. [Google Scholar] [CrossRef]
- Gielen, S. Emergence of a low spin phase in group field theory condensates. Class. Quantum Gravity 2016, 33, 224002. [Google Scholar] [CrossRef]
- Alesci, E.; Cianfrani, F. Quantum-Reduced Loop Gravity: Cosmology. Phys. Rev. D 2013, 87, 083521. [Google Scholar] [CrossRef]
- Alesci, E.; Cianfrani, F. Quantum reduced loop gravity: Universe on a lattice. Phys. Rev. D 2015, 92, 084065. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambrige, UK, 2005. [Google Scholar]
- Linde, A. Inflationary Cosmology after Planck 2013. arXiv 2014, arXiv:1402.0526. [Google Scholar]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary paradigm in trouble after Planck 2013. Phys. Lett. B 2013, 723, 261–266. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J. Implications of Planck 2015 for inflationary, ekpyrotic and anamorphic bouncing cosmologies. Class. Quantum Gravity 2016, 33, 044001. [Google Scholar] [CrossRef]
- Belinsky, V.; Khalatnikov, I.; Lifshitz, E. Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 1970, 19, 525. [Google Scholar] [CrossRef]
- Lifshitz, E.; Khalatnikov, I. Investigations in relativistic cosmology. Ad. Phys. 1963, 12, 185. [Google Scholar] [CrossRef]
- Bianchi, E.; Rovelli, C.; Vidotto, F. Towards Spin-foam Cosmology. Phys. Rev. D 2010, 82, 084035. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. On the spinfoam expansion in cosmology. Class. Quantum Gravity 2010, 27, 145005. [Google Scholar] [CrossRef]
- Bianchi, E.; Krajewski, T.; Rovelli, C.; Vidotto, F. Cosmological constant in spinfoam cosmology. Phys. Rev. D 2011, 83, 104015. [Google Scholar] [CrossRef]
- Hellmann, F. On the Expansions in Spin Foam Cosmology. Phys. Rev. D 2011, 84, 103516. [Google Scholar] [CrossRef]
- Livine, E.R.; Martin-Benito, M. Classical Setting and Effective Dynamics for Spinfoam Cosmology. Class. Quantum Gravity 2013, 30, 035006. [Google Scholar] [CrossRef]
- Schroeren, D. Decoherent Histories of Spin Networks. Found. Phys. 2013, 43, 310–328. [Google Scholar] [CrossRef][Green Version]
- Rennert, J.; Sloan, D. A Homogeneous Model of Spinfoam Cosmology. Class. Quantum Gravity 2013, 30, 235019. [Google Scholar] [CrossRef]
- Rennert, J.; Sloan, D. Anisotropic Spinfoam Cosmology. Class. Quantum Gravity 2014, 31, 015017. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Stepping out of Homogeneity in Loop Quantum Cosmology. Class. Quantum Gravity 2008, 25, 225024. [Google Scholar] [CrossRef]
- Battisti, M.V.; Marciano, A.; Rovelli, C. Triangulated Loop Quantum Cosmology: Bianchi IX and inhomogenous perturbations. Phys. Rev. D 2010, 81, 064019. [Google Scholar] [CrossRef]
- Borja, E.F.; Diaz-Polo, J.; Garay, I.; Livine, E.R. Dynamics for a 2-vertex Quantum Gravity Model. Class. Quantum Gravity 2010, 27, 235010. [Google Scholar] [CrossRef]
- Vidotto, F. Many-nodes/many-links spinfoam: The homogeneous and isotropic case. Class. Quantum Gravity 2011, 28, 245005. [Google Scholar] [CrossRef]
- Borja, E.F.; Garay, I.; Vidotto, F. Learning about Quantum Gravity with a Couple of Nodes. SIGMA 2012, 8, 015. [Google Scholar] [CrossRef]
- Mukhanov, V.; Feldman, H.A.; Brandenberger, R. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Gielen, S. Perturbing a quantum gravity condensate. Phys. Rev. D 2015, 91, 043526. [Google Scholar] [CrossRef]
- Gielen, S. Identifying cosmological perturbations in group field theory condensates. J. High Energy Phys. 2015, 1508, 010. [Google Scholar] [CrossRef]
- Gielen, S. Group field theory and its cosmology in a matter reference frame. Universe 2018, 4, 103. [Google Scholar] [CrossRef]
- Gielen, S. Inhomogeneous universe from group field theory condensate. J. Cosmol. Astropart. Phys. 2019, 1902, 013. [Google Scholar] [CrossRef]
- Gerhardt, F.; Oriti, D.; Wilson-Ewing, E. The separate universe framework in group field theory condensate cosmology. Phys. Rev. D 2018, 98, 066011. [Google Scholar] [CrossRef]
- Dittrich, B. The continuum limit of loop quantum gravity—A framework forsolving the theory. arXiv 2014, arXiv:1409.1450. [Google Scholar]
- Dittrich, B. From the discrete to the continuous: Towards a cylindrically con-sistent dynamics. New J. Phys. 2012, 14, 123004. [Google Scholar] [CrossRef]
- Dittrich, B.; Eckert, F.C.; Martin-Benito, M. Coarse graining methods for spin net and spin foam models. New J. Phys. 2012, 14, 035008. [Google Scholar] [CrossRef]
- Dittrich, B.; Schnetter, E.; Seth, C.J.; Steinhaus, S. Coarse graining flow of spin foam intertwiners. Phys. Rev. D 2016, 94, 124050. [Google Scholar] [CrossRef]
- Bahr, B. On background-independent renormalization of spin foam models. Class. Quantum Gravity 2017, 34, 075001. [Google Scholar] [CrossRef]
- Bahr, B.; Steinhaus, S. Numerical evidence for a phase transition in 4d spin foam quantum gravity. Phys. Rev. Lett. 2016, 117, 141302. [Google Scholar] [CrossRef]
- Bahr, B.; Steinhaus, S. Hypercuboidal renormalization in spinfoam quantum gravity. Phys. Rev. D 2017, 95, 126006. [Google Scholar] [CrossRef]
- Steinhaus, S.; Thürigen, J. Emergence of Spacetime in a restricted Spin-foam model. Phys. Rev. D 2018, 98, 026013. [Google Scholar] [CrossRef]
- Bahr, B.; Rabuffo, G.; Steinhaus, S. Renormalization of symmetry restricted spin foam models with curvature in the asymptotic regime. Phys. Rev. D 2018, 98, 106026. [Google Scholar] [CrossRef]
| 1 | The introduction of discrete structures can be motivated to bypass the issue of perturbative non-renormalizability of GR within the continuum path integral formulation. Alternative points of view of dealing with this issue would be to assume the existence of a non-perturbative (i.e., interacting) fixed point for gravity in the UV as done by the asymptotic safety program [12,13,14,15] or to increase the amount of symmetries as compared to GR and QFT with the aim to regain perturbative renormalizability as proposed by string theory [16]. Yet another view, as presented by non-commutative geometry, is that above the Planck scale the concept of geometry collapses and spacetime is replaced by a non-commutative manifold [17,18,19]. |
| 2 | For previous articles giving a review account of the program, we refer to Refs. [40,41]. |
| 3 | Another way to relate GFT to cosmology was brought forward in Ref. [60]. This work is closer to canonical quantum cosmology (either Wheeler–DeWitt or loop quantum cosmology) in the sense that it is built on a minisuperspace model, i.e., symmetry reduction is applied before quantization and not afterwards as in the condensate program. |
| 4 | Notice that by attributing an additional combinatorial degree of freedom named color to the fields, one can guarantee that the terms of the perturbative expansion are free of topological pathologies [67,68,69]. |
| 5 | A detailed discussion on the subtle differences in between the Fock space of GFT and the kinematical Hilbert space of LQG, which are mostly related to the absence of the so-called cylindrical consistency and equivalence in the former, is found in Ref. [84]. |
| 6 | The assumption of bosonic statistics is crucial for the condensate cosmology program where spacetime is thought to arise from a GFT condensate. To justify this choice of statistics from a fundamental point of view is an open problem, see Ref. [84] for a discussion and Refs. [67,68,69,85,86] for explorations into other statistics. |
| 7 | We refer e.g., to Appendix C of Ref. [58] for an extensive discussion of this matter for the case of the volume operator. |
| 8 | Complementarily to the application of functional methods to study the notion of phases in this context, research on the algebraic foundations of GFT has shown the existence of representations which are unitarily inequivalent to the one of the GFT Fock space and that are potentially related to different phases of GFT models, in particular to condensate phases [92,93,94,95]. |
| 9 | In principle, more complex composite states can be constructed so as to encode connectivity information in between GFT quanta and topological information to model e.g., spherical geometries [87,99,100]. |
| 10 | One may also take the view that the existence of a condensate phase transition is of less pronounced importance for such condensate states to be suitable non-perturbative states of physical relevance. We refer to Ref. [101] for a detailed discussion. |
| 11 | We comment below on an alternative notion of isotropy which has been explored so far in the literature. However, notice that such a reduction is a common simplification also applied in the closely related contexts of tensor models for quantum gravity [26,27,28,29,30,31,32] and lattice gravity approaches [33,34,35,36]. |
| 12 | Notice that the term “mesoscopic” used here only refers to the number of quanta N so far. Detailed studies must determine the exact range of N for such a regime to hold true and relate it to a range of length scales in the future. Conversely, this would necessitate to study the regimes of very small and very large N where the simple field coherent state ansatz is expected to be inapplicable. |
| 13 | We exemplify the link to the standard Friedmann equations of GR for a flat universe in proper time t as compared to those in relational time via the first Friedmann equation, i.e.,
|
| 14 | This is akin to what is done in LQC, where one assumes that the links of the underlying spin network are all identically labeled, with being the most studied case [104,105]. We will present a possible dynamical mechanism leading to a single-spin condensate further below. |
| 15 | In fact, these background dynamics are understood to generalize the effective dynamics of LQC which can be retained as a special case. We refer to Refs. [113,114] where this point was further explored. |
| 16 | In the given picture, the cosmological dynamics expressed by the expansion of the volume is vastly driven by a growing occupation number [115,116]. It should be remarked that this is a GFT realization of the lattice refinement of LQC [104,105]. |
| 17 | In Ref. [118] the relations between the condensate program and mimetic gravity were explored. Mimetic gravity is a Weyl-symmetric extension of GR [119] proposed to mimic the effects of cold dark matter within the context of modifications of GR. In the context of limiting curvature mimetic gravity, it is possible to realize non-singular bouncing cosmologies in the sense that it is possible to reproduce their background dynamics. This has been shown for the case of LQC [120] and very recently for the case of the effective dynamics of GFT condensates [118]. |
| 18 | We refer to Refs. [84,121] for a discussion touching on the subtle differences in between the Hilbert spaces of GFT and LQG especially relevant to the point of the zero-mode . |
| 19 | For a recent attempt at imposing a quantum counterpart of the classical symmetry reduction in the LQG context, we refer to Refs. [122,123]. |
| 20 | Notice that this proposal of incorporating inhomogeneities has recently been further developed using the separate universe approach to describe long-wavelength scalar perturbations [148]. |
| 21 | A different and interesting take on regaining the continuum in spin foam models is presented by the spin foam coarse graining and renormalization program for which we refer to Refs. [149,150,151,152,153,154,155,156,157]. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).