Thermodynamic Geometry of Yang–Mills Vacua

Abstract

We study vacuum fluctuation properties of an ensemble of $SU\left(N\right)$ gauge theory configurations, in the limit of many colors, viz. $N_c\to \infty$, and explore the statistical nature of the topological susceptibility by analyzing its critical behavior at a non-zero-vacuum parameter $\theta$ and temperature T. We find that the system undergoes a vacuum phase transition at the chiral symmetry restoration temperature as well as at an absolute value of $\theta$. On the other hand, the long-range correlation length solely depends on $\theta$ for the theories with critical exponent $e=2$ or $T=T_d+1$, where $T_d$ is the decoherence temperature. Furthermore, it is worth noticing that the unit-critical exponent vacuum configuration corresponds to a non-interacting statistical basis pertaining to a constant mass of ${\eta }^{\prime }$.

1. Introduction

Quantum chromo-dynamics (QCD) as a Yang–Mills (YM) gauge theory has opened interesting avenues in understanding strong nuclear processes and decay reactions [1,2,3]. Therefore, the stability of nuclear particles, viz. the determination of the lifetime of a particle or decay rate of a given nuclear reaction is one of the most interesting research issues since the proposition of modern gauge field theory [4]. As particles are considered to be in certain excited states, we are going to examine the stability of vacuum configurations under variations of the parameters. Such an intrinsic principle has been highly successful when applied in studying both the particle properties and decay rate-based applications [2]. This analysis follows further since it is easy in its implementation and it requires a finite amount of parameter tuning. Indeed, the fluctuation geometric characterizations in question are the best alternative for offering stability properties of the QCD vacuum, as a statistical system. This follows from the fact that the intrinsic geometric consideration takes account of configuration uncertainties and generally allows for a clear-cut determination of regular and singular domains of the vacuum parameters.

Motivated from Witten’s work on CP breaking and duality principle between large N gauge theories and string theory on certain spacetimes in the realm of wrapped six-branes describing a set of adjacent vacua which are separated by domain walls [5], the above observation is further supported by the fact that a class of stringy vacua remains insensitive to temperature variations as well as certain parametric deviations; see, for instance, extremal black hole configurations in string theory [6]. Fluctuation theory [7,8,9,10,11,12,13]-based parametric modeling appears to be one of the best methods to explicate the stability of a given statistical system. This is because the intrinsic geometric approach enables us to determine both the local and global stability characteristics of a chosen configuration.

The parameters concerning the parity odd bubbles [3,14] are the vacuum angle $\theta$ and temperature T of the undermining configuration. Therefore, the phase determination of an ensemble of QCD vacua, viz. the local and global characterizations, depend on the fluctuation range of $\{\theta ,T\}$. In this line of research, [14] leads us to provide an appropriate mathematical expression and an intrinsic parameterization to the free energy of parity odd-bubble configuration. From this outset, the present paper focuses on the determination of stable embedding functions under intrinsic geometric fluctuations concerning the minimization of vacuum uncertainties. Indeed, for an arbitrary non-equilibrium gauge or field theory configuration, the above parametric geometric hypothesis can be carried forward in terms of the associated effective potential parameterized via moduli fields. Such an intrinsic stability analysis of gauge theory vacuum configurations we leave open for future research.

In light of our geometric study, important issues pertaining to the statistical stability of parity odd bubbles are determined as an undermining embedding [15] via fluctuation theory analysis [7,8] of free energy and effective potential of a given large N gauge theory configuration [3]. The parametric determination of free energy of such a configuration is based on an extension of scattering theory and anomaly cancellation [3,16]. A novel formulation is consequently made realizable in stabilizing parity odd-bubble ensembles via the present consideration. Namely, our intrinsic geometric method as outlined in the sequel is very generic in its own right and it opens various possible directions for further investigations. One of the fundamental issues on which we focus in this paper is an appropriate stability determination of an ensemble of QCD vacua. To do so, one traditionally assumes that one of the parameters of the vacuum lies in a subset of the parametric family of the physical system, i.e., the free energy [3] depends on the vacuum parameter $\theta$. For instance, see [5] concerning spontaneous breaking of CP symmetry and large N gauge theories in four-dimensional spacetimes.

Kharzeev, Pisarski and Tytgat [14] offered an extension of fundamental principles such as Witten’s scattering theory analysis [3] and Veneziano’s anomaly consideration [16] for the associated mesons concerning parity odd bubbles. From a closer perspective, such an analysis of the large N gauge theory takes account of the free energy determination. Specifically, it allows a straightforward relation of vacuum settings in terms of the associated effective field theory model parameters. Notice further that the consideration of vacuum fluctuations is insensitive to supersymmetry and gauge coupling deviations, and the output is approximately equivalent to a large N pure $SU\left(N\right)$ gauge theory ensemble. In this paper, to explore the stability of such ensembles, we focus on the design of a stable parity odd-bubble vacuum region from the perspective of intrinsic Riemannian geometry.

Based on the covariant geometric consideration, we offer stability analysis of parity odd-bubble ensembles in general. The fluctuation theory approach—based on the large N free energy evaluation [14] with an incorporation of non-zero temperature and anomalous couplings of mesons—enabling improved stability structures of bounded particles and associated decays, is presented in this paper. Graphical representations of local and global parametric fluctuations are shown for the limiting large N configuration. We anticipate that the geometric framework is particularly well suited for a variety of practical applications. It turns out that the mathematical design procedure thus illustrated can further be extended for an arbitrary vacuum ensemble. Indeed, there exists a broad class of perspective investigations as far as this representation is concerned. This is one of the real virtues of stabilization of parity odd-bubble vacuum ensembles. The present analysis of parity odd bubbles can in turn be pushed further in explicating the intrinsic nature of large hadron collider (LHC) data [17] concerning the standard model of particle physics and associated background disturbances arising from vacuum fluctuations.

A priori, we have considered the above intrinsic geometric analysis for a class of equilibrium statistical configurations involving extremal and non-extremal black holes in string theory [6,18,19,20,21,22,23,24] and M-theory [25,26,27,28], and shown that such ensembles possess rich intrinsic geometric structures; see for instance [29,30,31,32,33,34,35,36]. Concerning the physics of black holes, black strings, black rings, and black branes in general, there has been much well-focused attention on equilibrium statistical fluctuation perspective of string theory vacua [29,30,31,32,33,34,35,36], to explicate the nature of undermining parametric pair correlation functions and stability of the associated string theory solution containing a set of branes and antibranes. Indeed, there have earlier been several general notions analyzed in condensed-matter physics [7,8,9,10,37,38], as well. Based on the above motivations, we focus our attention on large N gauge theory configurations as mentioned above with given equilibrium parameters $\{\theta ,T\}$. Therefore, we examine possible parametric local pair correlations and the associated global correlation length undermining the parity odd hot QCD bubbles. In a nutshell, the present research, when analyzed in terms of system parameters, offers an intriguing dimension to fluctuating vacuum ensembles.

The questions that we attempt to answer in this paper are: (i) under what constraints a considered vacuum ensemble is (un)stable; and (ii) how its parametric vacuum correlation functions scale in terms of the chosen fluctuating parity odd-bubble parameters. With such a definite covariant geometric description of a consistent equilibrium statistical system, we can indeed determine a complete set of non-trivial local correlation relations of gauge theory vacuum configurations. It is worth mentioning further that similar considerations hold for the four-dimensional black hole solutions in general relativity [39,40,41,42], and equilibrium (un)attractor black holes [43,44,45,46,47,48], as well. Moreover, based on the Legendre-transformed finite-temperature chemical configurations [49,50], we have explored the above thermodynamic type stability analysis under parametric fluctuations of the 2- and 3-flavor hot QCD systems [51,52,53,54].

Furthermore, it follows that there exist various approaches examining properties of thermodynamic systems in terms of differential geometric concepts; see [55] towards the metric structure of thermodynamic equilibrium states, its associated Legendre invariance in the thermodynamic phase space and new Legendre invariant metrics that render important geometric properties of the Weinhold’s metric tensor. Concerning the physics of black holes, the geometrothermodynamics describes the stability structures and phase transition curves in various gravity theories in a coordinate-independent manner, [56] for an overview. The concept of Legendre invariant geometrothermodynamics is equally applied to asymptotically anti-de Sitter black holes; see [57] for the associated thermodynamic implications. In short, one finds that the scalar curvature of the thermodynamic metric of all known black holes in higher dimensions is proportional to the heat capacity.

Following the above fundamentals, the phase transition curves that geometrically correspond to curvature singularities arise as the divergencies of the concerned heat capacity. This anticipates that the thermodynamic interactions are measured by the scalar curvature of the thermodynamic metric tensor; see [58] towards a new approach regarding the geometrical concepts of black hole thermodynamics, phase transitions, and possible extensions for thermodynamic systems with finitely many extensive parameters, [59] for the case of two-dimensional charged black holes and [60] towards the geometrothermodynamics of the most general static spherically symmetric topological black holes of Horava–Lifshitz gravity and their thermodynamic geometries emerging from the fluctuations over an equilibrium manifold. Further studies exist concerning the notion of the Legendre invariance, geometrical thermodynamics, and coordinate dependence; for instance, see [56] towards the ensemble dependence in black hole geometrothermodynamics for a class of Einstein-Maxwell-Gauss-Bonnet black holes with a non-zero cosmological constant and [61] towards the associated study of 3D charged-dilaton black holes. In this concern, we have provided the concerned Legendre transforms of the free energy for the particular configurations with a given critical exponent $e\in \{1,2,3\}$ that corresponds to distinct sectors in the space of parameters. The phase transition structures are clarified through the respective parameter space scalar curvatures as in Equations (26)–(28) below. In the above outset, we herewith pronounce that the consideration of differential geometry plays a vital role in studying stability properties of both the gauge theory and field theory configurations.

As per the above introduction, the present work analyzes the properties of a $SU\left(N\right)$ gauge theory from an intrinsic geometric perspective of dynamical system in the space of its parameters. As mentioned above, the idea is largely motivated from some of our previous works and pioneering works of Weinhold, Ruppeiner, and other scholars. Following the same, the core of this work is based on the use of the free energy expression that was proposed by Kharzeev, Pisarski and Tytgat [62] as an embedding; see [15] for an introduction. Here, the energy is considered as a function of the temperature T and the vacuum parameter $\theta$. Notice that our attention lies in understanding the nature of parametric fluctuations near the confining-deconfining phase.

In this paper, we geometrically address the issue of the vacuum stability of an ensemble of gauge theory configurations. First, the analysis is carried out in the vicinity of a critical point, when the temperature approaches the deconfining one, $T\to T_d^{-}$, where $T_d^{-}$ is the limiting value of $T_d$ when it is approached from the left. Extending the analysis based on this free energy expression for other values of the temperature T in nearby regions of the transition point is carried out infinitesimally and hence diffeomorphically the embedding [15] is granted to exist. Moreover, we analyze the cases for different values of the critical exponent $\alpha$ which up to a few decimal places reads as $\alpha \sim -0.0135$, as determined by Pisarski and Wilzcec [63]. In this concern, we have not taken any specific value of $\alpha$. We have provided the above value of $\alpha$ solely for a reference purpose that corresponds to the standard Kharzeev–Pisarski–Tytgat model of the free energy.

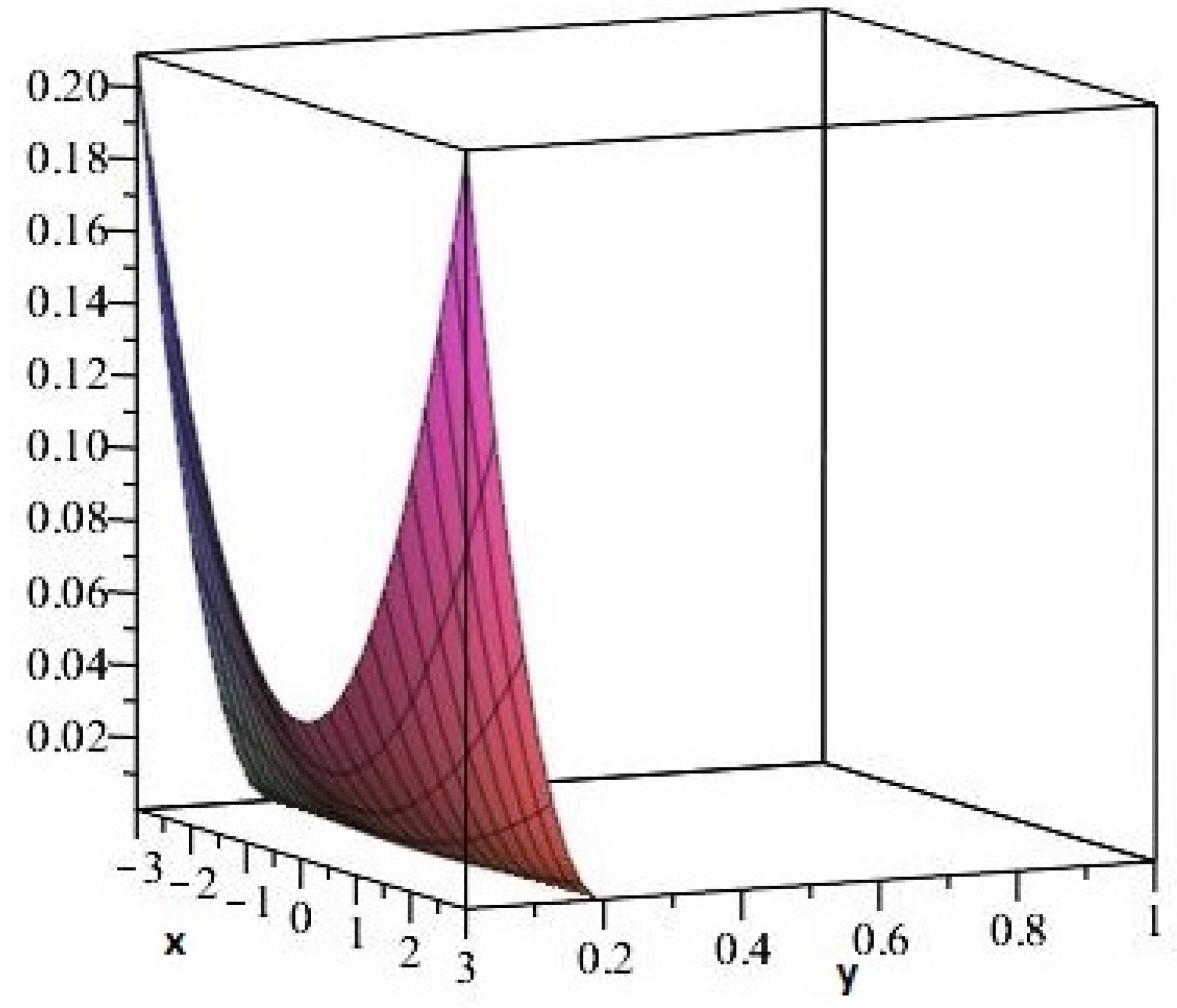
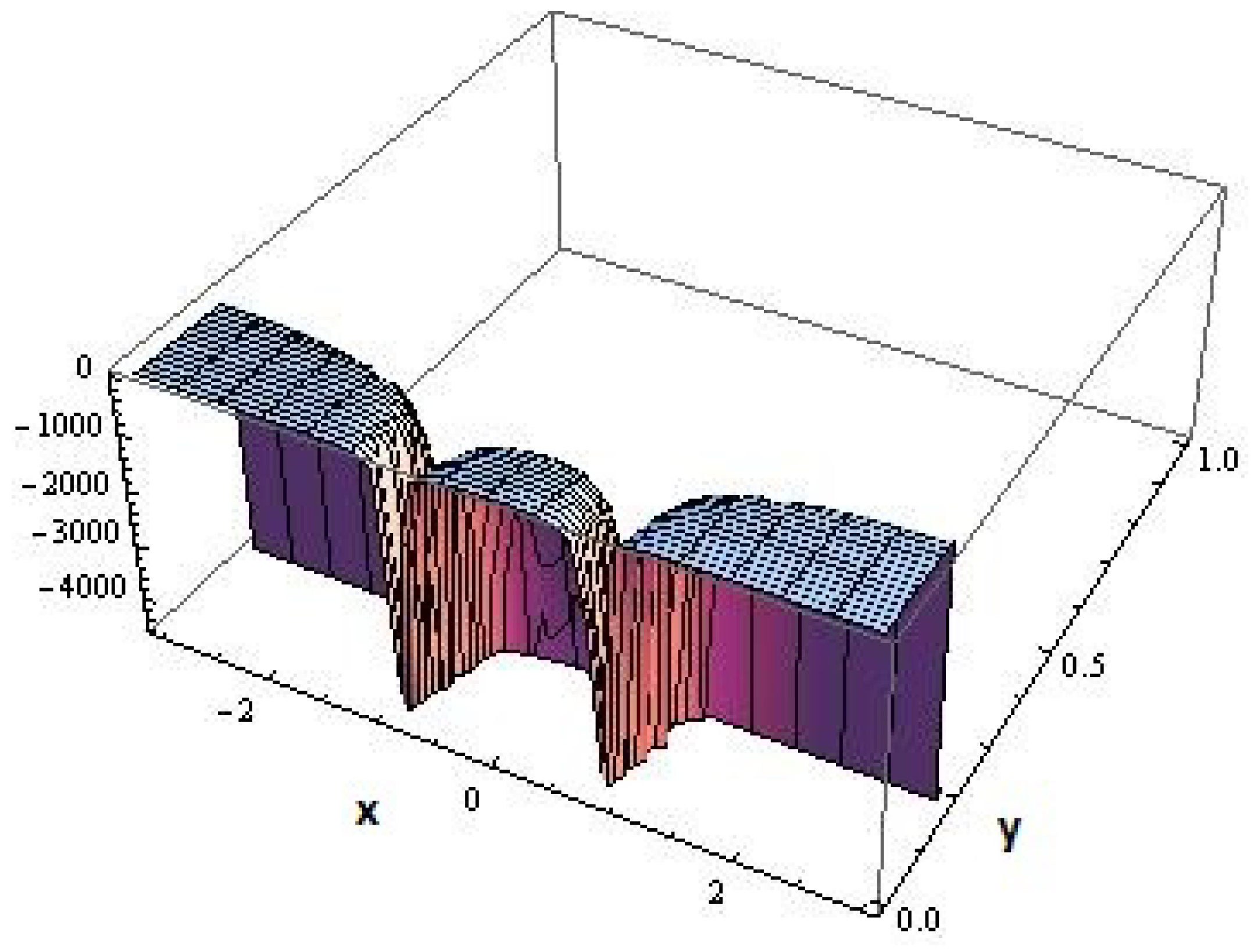
With the above motivations, we offer the local and global stability criteria of an ensemble of large N parity odd bubbles under fluctuations of the vacuum angle $\theta$ and QCD temperature T. As the function of $\{\theta ,T\}$, the free energy $F(\theta ,T)$ under consideration [14] is depicted in the Figure 1. The stability characteristics is demonstrated for a suitable set of parameters $\{\theta ,T\}$ rendering a specific parameterization as an undermining embedding [15]. Namely, as far as the parity odd bubbles are concerned, the free energy offers such an intrinsic characterization of vacuum fluctuations as the following real embedding

$$(\theta ,T)\hookrightarrow F(\theta ,T)$$

(1)

From the general $SU\left(N\right)$ gauge theory parametrization equation in the large N limit [14], the stability of component diagram is brought to attention. It is worth mentioning that this formulation is made possible for the first time towards the intrinsic geometric stability analysis of an ensemble of parity odd bubbles. The proposed methodology of intrinsic geometry is rather very generic and different Legendre-transformed versions of the present consideration are possible. We leave an intrinsic classification of such transformations open for future investigations.

In this paper, we focus on the metric geometries originating from the energy representations. By employing standard notions of the intrinsic Riemannian geometry, the rest of paper is devoted to determining local and global stability properties of an ensemble of fluctuating parity odd-bubble configurations. In Section 2, we give a review of YM theory, and the framework of the embedding geometry via the formation of an admissible energy surface. Section 3 is devoted to examining the fundamental intrinsic geometric setup in light of fluctuation theory. For an ensemble of fluctuating YM vacua, we highlight the statistical correlation outcomes as emerging via our free energy-based embedding geometry. In Section 4 we examine the stability properties arising from fluctuations of the free energy $F(\theta ,T)$ as a function of $\{\theta ,T\}$ concerning an underlying ensemble of parity odd-bubble configurations. Finally, in Section 5, we offer our fluctuation geometric conclusions and perspective directions for future research.

2. Review of the Model

Let us begin by considering an ensemble of $SU\left(N\right)$ gauge theory in the large color limit $N\to \infty$. In the following, we exploit the large N expansion [64] to investigate the stability behavior of statistical ensembles at a non-zero temperature, especially while examining local and global statistical correlation functions concerning the corresponding topological susceptibility. Namely, by invoking joint fluctuations of the vacuum parameter $\theta$ and temperature T, we wish to examine both the nature and order of confining-deconfining phase transitions. Before doing so, we offer a brief recap of the YM gauge theory [1,2,3], fluctuation theory [7,8], and an outline of fluctuating gauge theory vacuum ensembles in the realm of embedding theory.

2.1. Recaps on YM Theory

As mentioned in the introduction, recall that the deconfining temperature is defined as the temperature $T_{\chi }$ corresponding to the restoration of the chiral symmetry. Secondly, for a given YM theory [1,2,3,14], it is well known that the topological charge density can be expressed as the following total derivative

$$Q\left(x\right)=\frac{g^2}{32{\pi }^2}tr\left(G_{\alpha \beta }{\tilde{G}}^{\alpha \beta }\right)={\partial }_{\alpha }{K}^{\alpha },$$

(2)

where $K^{\alpha }$ is a gauge-dependent current.

In terms of the above charge $Q\left(x\right)$, the topological susceptibility is defined as the two-point function of Q, viz. we have

$${\lambda }_{YM}=\frac{{\partial }^{2}F(\theta ,T)}{\partial {\theta }^2}=\int d^{4}x<Q\left(x\right)|Q\left(0\right)>,$$

(3)

where $\theta$ is conjugate to the topological charge density Q and the zero-temperature free energy $F(\theta ,0)=E\left(\theta \right)$ is termed as the $\theta$-dependent vacuum energy. Since $Q\left(x\right)$ is a total space-time derivative of the gauge-dependent current $K^{\alpha }$, the topological susceptibility ${\lambda }_{YM}$ receives only instantonic contributions order by order, in the $\frac{1}{N}$-expansion [64,65]. In this case, it follows that the topological susceptibility satisfies the following leading-order behavior

$${\lambda }_{YM}\left(T\right)={\lambda }_{YM}\left(0\right)e^{-aN},$$

(4)

where $a=\frac{8{\pi }^2}{g^{2}N}$ for a single instanton contribution. Also see [66] for $C{P}^N$ modes in $(1+1)$ dimensions. At $T=0$, Witten [65] suggested that quantum fluctuations generate a non-zero value for the ${\lambda }_{YM}\left(0\right)$, over essentially vanishing semi-classical fluctuations to the deconfining phase of the topological susceptibility, viz. one has ${\lambda }_{YM}\left(0\right)\sim N^0$. Combining the above two phases with the setup of [16,65], one has the following leading-order topological susceptibility

$$\begin{array}{c}\hfill {\lambda }_{YM}\left(T\right)\sim \{\begin{array}{cc}{e}^{-aN};& T\ne 0,\\ N^0;& T=0\end{array}\end{array}$$

(5)

as a function of the temperature T. In line with Witten’s scattering theory analysis [65] and Veneziano’s anomaly cancellation [16], generalizations to a non-zero-temperature configuration [14] have further been considered with anomalous couplings of mesons in the literature; for instance see [67] for observations concerning radiative decays beyond chiral limit, topological susceptibility and associated Witten-Veneziano mass formula in the measurements of ${\eta }^{\prime }\left(\eta \right)\to \gamma \gamma$. The above setup results in the following $\theta$ dependent free energy

$$F(\theta ,T)=A(1+c{\theta }^2){(T_d-T)}^{2-\alpha },$$

(6)

where A is a known constant, c controls the strength of anomaly and $\alpha$ is critical exponent of the system. In fact, for a given deconfining phase, the transition temperature $T_d$, Ref. [14] suggests a small negative value of $\alpha$, namely, $\alpha =-0.013$. Notice that the $U_{A\left(1\right)}$ anomaly can induce chiral phase transitions in hot QCD configurations with a dense background [68]. Our analysis finds importance in the stability of QCD; see [69] for fluctuations at finite-temperature and quark chemical potential, and [70] for an associated two flavor anomalous QCD vacuum fluctuations in the context of massive baryonic models. In the above setup of $SU\left(N\right)$ YM gauge theory, we consider an ensemble of YM vacua. More precisely, we focus on the meta-stable states parametrized by finitely many (in)equilibrium statistical parameters of the chosen YM gauge theory configuration.

2.2. Admissible Energy Surfaces

In the sequel, motivated from fluctuations away from the vacuum fixed-point systems in light of scattering theory—namely, the Witten’s ${\eta }^{\prime }$ mass formula [3,5] and associated complete algebraic saturation of Ward identities in the double limit of Veneziano [16]—we wish to study statistical stability characterizations of the underlying vacuum fluctuations as a function of the system parameters $\{\theta ,T\}$. In particular, we focus our attention on fluctuations of topological susceptibility vanishing at the critical temperature line $T=T_d$, where $T_d$ is the decoherence temperature of the chosen QCD vacuum system under consideration.

To discuss the stability properties of such a statistical system, let us consider an ensemble of meta-stable states acting as regions of non-zero-vacuum angle $\theta$ at a given non-zero-temperature T. Then, the fluctuation theory setup [7] enables us to examine the statistical stability properties of an ensemble of fluctuating colored $SU\left(N\right)$ gauge theory vacuum configurations. In general, this is achieved by introducing an admissible intrinsic surface

$${\mathcal{M}}_2:=\left\{(T,\theta )\right|T<T_d,\theta \equiv \theta +2\pi \}$$

(7)

Here, we focus on the statistical ensembles with sufficiently light quark masses to statistically address the signature and production of mesons including the $\eta$ and ${\eta }^{\prime }$ mesons. This allows us to concentrate on the probabilistic admissibility of normally forbidden processes, e.g., $\eta \to {\pi }^0{\pi }^0$, concerning the $SU\left(N\right)$ gauge theory in the large N limit. Our conclusions are based on Witten’s formula pertaining to the $U\left(N\right)$ problem in light of $\frac{1}{N}$ expansion, i.e., the hadronic phase is cold, viz. the ${\eta }^{\prime }$ mass vanishes at the critical temperature line $T=T_d$.

3. Fluctuation Theory Perspective

In this subsection, we provide a fundamental intrinsic geometric setup of the fluctuation theory along with statistical outcomes concerning an ensemble of YM vacua. Our consideration is physically based on meta-stable states, which act like geometric regions of non-zero $\theta$ and T, forming a two-dimensional intrinsic surface ${\mathcal{M}}_2$, as above in Equation (7). In the sequel, we may consider ${\mathcal{M}}_2$ as an inner product space of the admissible system of parameters $\{\theta ,T\}$. Namely, it follows that the surface ${\mathcal{M}}_2$ defines the following map

$$\{\theta ,T\}{\mapsto }^{F}F(\theta ,T):{\mathcal{M}}_2\hookrightarrow \mathbb{R}.$$

(8)

The above embedding involving Riemannian geometry on a two-dimensional surface of fluctuating parameters $\{\theta ,T\}$ can be explicated as follows. Given a differentiable manifold ${\mathcal{M}}_2$ of dimension 2, a Riemannian metric g on it is defined as a family of positive definite inner products as

$$g_p:T_p{\mathcal{M}}_2\times T_p{\mathcal{M}}_2⟶\mathbb{R},$$

(9)

where $p\in {\mathcal{M}}_2$ such that the map $p\mapsto g_p(X\left(p\right),Y\left(p\right))$ gives a smooth function as the real embedding ${\mathcal{M}}_2\hookrightarrow \mathbb{R}$ for any pair of differentiable vector fields $\{X,Y\}$ on ${\mathcal{M}}_2$.

Physically, we can view the Riemannian metric g on ${\mathcal{M}}_2$ as a symmetric $(0,2)$ tensor possessing the positive definiteness property of the metric $g(X,X)>0$ for any non-zero tangent vector X. For the above real manifold ${\mathcal{M}}_2$ of dimension 2, a local coordinate system $\left\{x^i\right|i=1,2\}$ on it can be designed in terms of the fluctuation parameters $\{\theta ,T\}$. To offer an intrinsic geometric analysis, we may define the vacuum angle $x_1:=\theta$ between 0 and $2\pi$ as in Equation (7) or in a shifted interval, for example, from $-\pi$ to $+\pi$, and $x_2$ as the ratio $T/T_0$ with $T_0$ as a reference temperature that defines the unit of measurements. Furthermore, without loss of generality, we may set the prefactor $A=1$, as in Equation (6). In a system of local coordinates on the above parametric surface ${\mathcal{M}}_2$ given by doubled real valued functions $\{\theta ,T\}$ with the corresponding vector fields $\left\{\frac{\partial }{\partial \theta },\frac{\partial }{\partial T}\right\}$ on ${\mathcal{M}}_2$ forming a tangent basis of the tangent manifold $T_p{\mathcal{M}}_2$ at each point of the parametric surface ${\mathcal{M}}_2$. At each point $p\in {\mathcal{M}}_2$, it follows further that the components of the metric tensor can be expressed as the following inner product

$$g_{ij}\left(p\right):=g_p\left({\left(\frac{\partial }{\partial x^i}\right)}_p,{\left(\frac{\partial }{\partial x^j}\right)}_p\right),i,j=1,2.$$

(10)

with respect to a chosen local coordinate system $(x^1,x^2)$ on the parametric surface ${\mathcal{M}}_2$ as the vacuum parameters $\{\theta ,T\}$. Equivalently, in terms of the dual cotangent basis $\{d{x}^1,d{x}^2\}$, it follows that the metric tensor for ${\mathcal{M}}_2$ can be written as

$$g=\sum _{i,j=1,2}{g}_{ij}\mathrm{d}{x}^i\otimes \mathrm{d}{x}^j$$

(11)

Following the above inner product structure corresponding to the Riemannian metric tensor $g_{ij}$, the fluctuation manifold of the vacuum parameters $\{\theta ,T\}$ renders us a two-dimensional differentiable Riemannian surface $({\mathcal{M}}_2,g)$. For standard differential geometric notions such as flow components, correlation components such as the elements of the Hessian matrix of a defining embedding function, Christoffel connection functions, and Riemannian scalar curvature, there are numerous applications in all domains of the energy scale, from condensed-matter systems to high-energy configurations. For such an explicit evaluation of differential geometric notions in different domains of research, see [29,30,31,32,33,34,35,36] for string theory vacua of branes and antibranes, [7,8,9,10,37,38] for configurations in condensed-matter physics and [51,52,53,54] for hot QCD systems with two and three flavors.

In this paper, we first specialize in examining the vacuum temperature fluctuations whose free energy $F(\theta ,T)$ we have given in the foregoing subsection. In this setup, we consider a probabilistic interpretation of the parity odd-bubble configurations concerning the parity violation, viz. the question of whether the $\eta$ particle decays to two pions or instead to the usual three pions [14]. We also propose a global variable, namely, the intrinsic scalar curvature on the fluctuating free energy surface ${\mathcal{M}}_2$ to measure the statistical interaction properties and long-range global correlation length of an underlying ensemble of parity odd bubbles.

For a fixed number of fermion flavors as $N\to \infty$, it is worth recalling that the large N limit of $SU\left(N\right)$ gauge theory is very much gluonic in nature [14] because $N^2$ gluons totally dominate the N-quarks. At a large value of N, it is well known that the confinement of quarks occurs [71,72], thus at a low temperature, we can focus entirely on vacuum correlations of the mesons and glueballs. Therefore, by the term “confinement” we mean that all the traces of the color indices disappear, and herewith the bound states thus formed are solely characterizable via symmetries of the considered gauge theory model, e.g., spin, parity, etc.

In the sequel, we consider the setup of an arbitrary large N gauge theory in which massless quarks couple to the gluons. As far as the physics at low temperature is concerned, we further know that the chiral symmetry breaks down to a diagonal subgroup of the flavors; see for example [14,16]. Thus, we may assume in standard fashion that chiral symmetry is restored at chiral temperature $T_{\chi }$ with $T_{\chi }=T_d$, where $T_d$ is the decoherence temperature. To simplify the above consideration, we may deal with an intrinsic scale of the deconfining transition as to be the same as that of the gluball masses, which is achieved by taking the decoherence temperature limit $T_d\to 1$, as $N\to \infty$. To investigate the ensemble properties of $SU\left(N\right)$ gauge theory, we may thus focus on the large N limit of the YM gauge theory without confinement, e.g., the N-component vector model with YM coupling $g^2$ such that $g^{2}N$ remains fixed in the limit of $N\to \infty$.

Since the gluons dominate the free energy above the deconfining temperature, viz. $T\ge T_d$, it follows that the effects of quarks can be neglected in this range of temperature T. The crucial thing which we therefore obtain is the nature of deconfining phase transitions in concerning an ensemble of vacuum $SU\left(N\right)$ gauge theories. Namely, we focus on an ensemble of $SU\left(N\right)$ meta-stable states undermining parity odd-bubble vacuum phase transitions. This enables us to determine phase transition curves on an intrinsic geometric surface ${\mathcal{M}}_2$ of the vacuum fluctuation parameters $\{\theta ,T\}$ concerning the ensemble of parity odd bubbles.

As a result, we obtain statistical correlations as a function of the critical exponent under the fluctuations of $(\theta ,T)$. In fact, we find that the global statistical correlation exists, even if we switch off the vacuum parameter $\theta$ and temperature T, viz. take the limits $\theta \to 0$ and $T\to 0$. In this limit, we have a non-zero value of the correlation area $A(\theta ,T)\sim R(\theta ,T)$, where $R(\theta ,T)$ is the scalar curvature on the parametric surface ${\mathcal{M}}_2$. Namely, in Section 4 below, we have shown that our statistical analysis of the YM free energy vacuum fluctuations renders the following limiting correlation area

$$\tilde{A}=li{m}_{\theta \to 0,T\to 0}A(\theta ,T)\propto -\frac{T_d^{e-2}}{e-1},$$

(12)

Herewith, we observe that the $SU\left(N\right)$ gauge theory vacuum configuration, even in the limit of zero-temperature and zero-vacuum parameter $\theta$, corresponds to an interacting statistical ensemble. This follows in particular from a non-vanishing value of the correlation length $l=\sqrt{\tilde{A}}$. Therefore, we see that the limiting statistical configuration becomes strongly interacting about the unit-critical exponent, as $l\to \infty$ whenever $e\to 1$. Moreover, we notice that l never vanishes as long as the decoherence temperature $T_d$, corresponding to the chiral symmetry restoration temperature of meta-stable states, takes a non-zero finite value.

4. Free Energy Fluctuations

In this section, we provide fluctuation theory analysis towards the study of stability and phase structures of an ensemble of YM vacua under variations of the model parameters $(\theta ,T)$. What follows in this concern is that we specialize ourselves for physically well-suited values of the configuration parameters towards the graphical description regarding the stability of parity odd-bubble ensembles. Although our investigation of the present paper remains valid for any embedding geometric configuration, we nevertheless wish to illustrate it for a class of large N vacua, which are of an immediate interest to us in concerning the fluctuating parity odd bubbles. Here, the parameter $\theta$ is the vacuum angle arising as a translational shift to the total angle of phases. In the subsequent analysis, we invariably denote a locally deconfining QCD phase by the corresponding decoherence temperature as $T_d$ or d and the exponent as $\alpha$ or e. Moreover, we observe that the stability analysis considered in the framework of intrinsic geometry remains valid for general effective field theory configurations. Therefore, we anticipate further that such an investigation remains consistent for an arbitrary fluctuating gauge theory configuration. Subsequently, to offer a qualitative picture of our analysis, we may set the values of the model constants as $c=0.5,d=0.197$ and $e=-0.013$ corresponding to the hot QCD deconfining phase [14]. 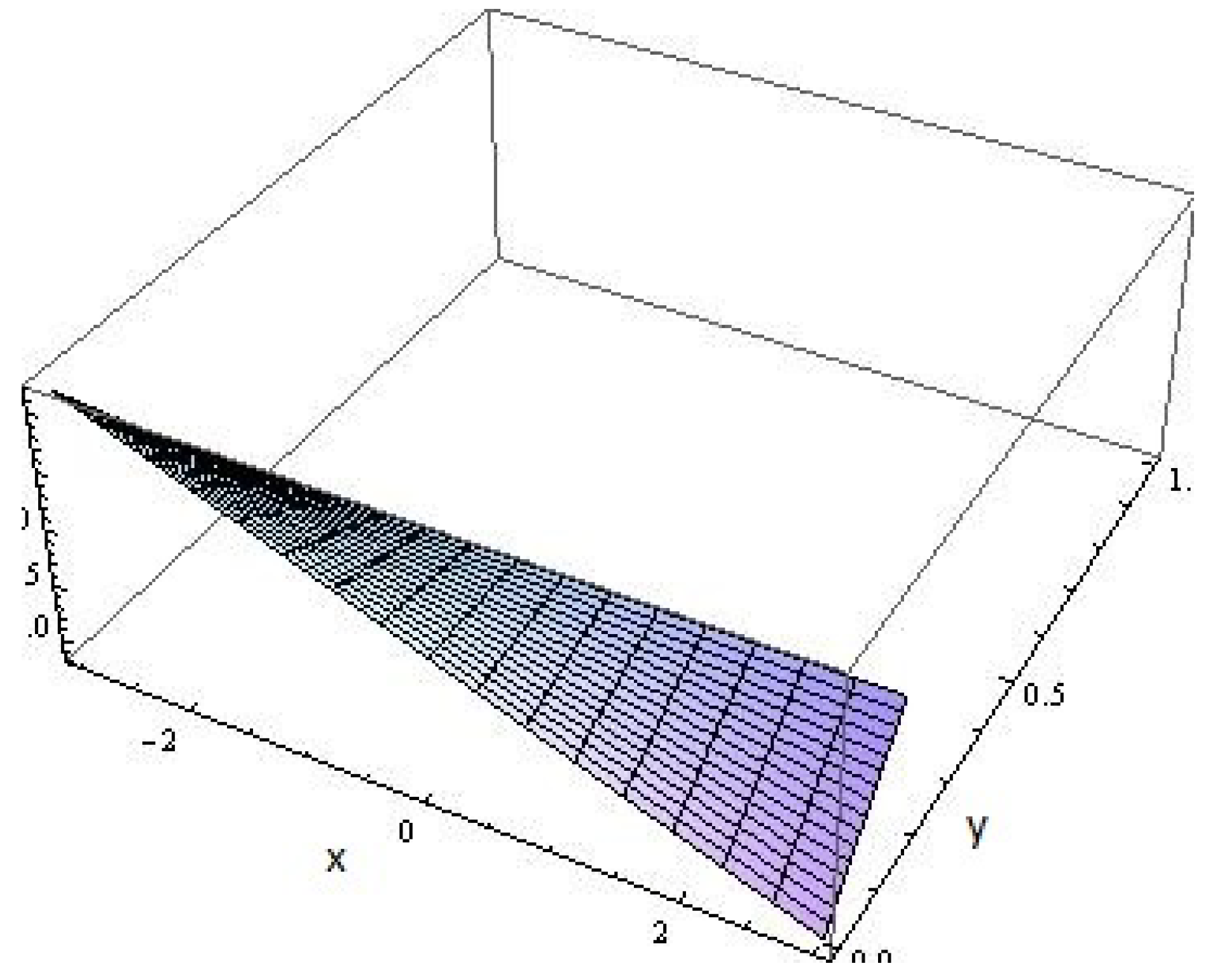Therefore, the free energy of the interest is depicted in Figure 1, showing the nature of its qualitative variations.

Given an ensemble of parity odd bubbles, we consider the intrinsic geometric analysis to determine the stability properties of an ensemble of large N vacua. The stability criteria under present consideration offers an apt method for ascertaining the required values of system parameters and therefore the underlying local and global stability properties of an ensemble of fluctuating parity odd bubbles. In the sequel, we denote the vacuum angle by x as a number between $(-\pi ,+\pi )$, temperature by y as the ratio $T/T_0$, where the temperature T and reference temperature $T_0$ are measured in K. In this setup, the decoherence temperature $T_d$ can be expressed as $T_{0}d$. Thus, without loss of generality, we may set $T_0=1$, wherefore it follows that the free energy [14] concerning the deconfining phase transition can be represented as per the following expression

$$F(x,y)=\left(1+c{x}^2\right){(d-y)}^{2-e},$$

(13)

where c is the coefficient of the anomaly and e is the critical exponent. It is worth observing that the free energy $F(x,y)$ as given in Equation (13) vanishes identically at the decoherence temperature, viz. $y=d$. Furthermore, $F(x,y)$ becomes independent of the temperature y at the value of critical exponent $e=2$ and it becomes independent of the vacuum angle x at vanishing anomaly contribution $c=0$. At the origin $x=0$ and $y=0$ of an underlying real fluctuation surface ${\mathcal{M}}_2\left(\mathbb{R}\right)$, we see that the free energy $F(x,y)$ possesses a constant value of $d^{2-e}$.

Herewith, we observe that the flow components of free energy fluctuations are

$$\begin{array}{c}{F}_x(x,y)=2cx{(d-y)}^{2-e},\hfill \\ F_y(x,y)=-(2-e)(1+c{x}^2){(d-y)}^{1-e}\hfill \end{array}$$

(14)

In this case, we hereby observe that the flow equations defined as $F_x=0=F_y$ contribute to the fact that the vacuum parameter x vanishes identically and temperature y remains fixed at its decoherence value d. However, we see that the value of the critical exponent e plays a crucial role in determining the fixed points of the free energy $F(x,y)$. Namely, the choice of $e=2$ makes the first flow equation $F_x=0$ independent of the temperature y, while the choice of $e=1$ makes the second flow equation $F_y=0$ independent of y. Furthermore, if the vacuum angle is allowed to become an imaginary number, then the value $x=\pm i/\sqrt{c}$ constitutes a complex fixed point of $F(x,y)$. Here, the flow components $F_x$ and $F_y$ arise as the dual Legendre variables corresponding to x and y respectively. In the sequel of this section, we explain the possible roles of the critical exponent e while determining the local and global statistical correlations concerning an ensemble of parity odd bubbles.

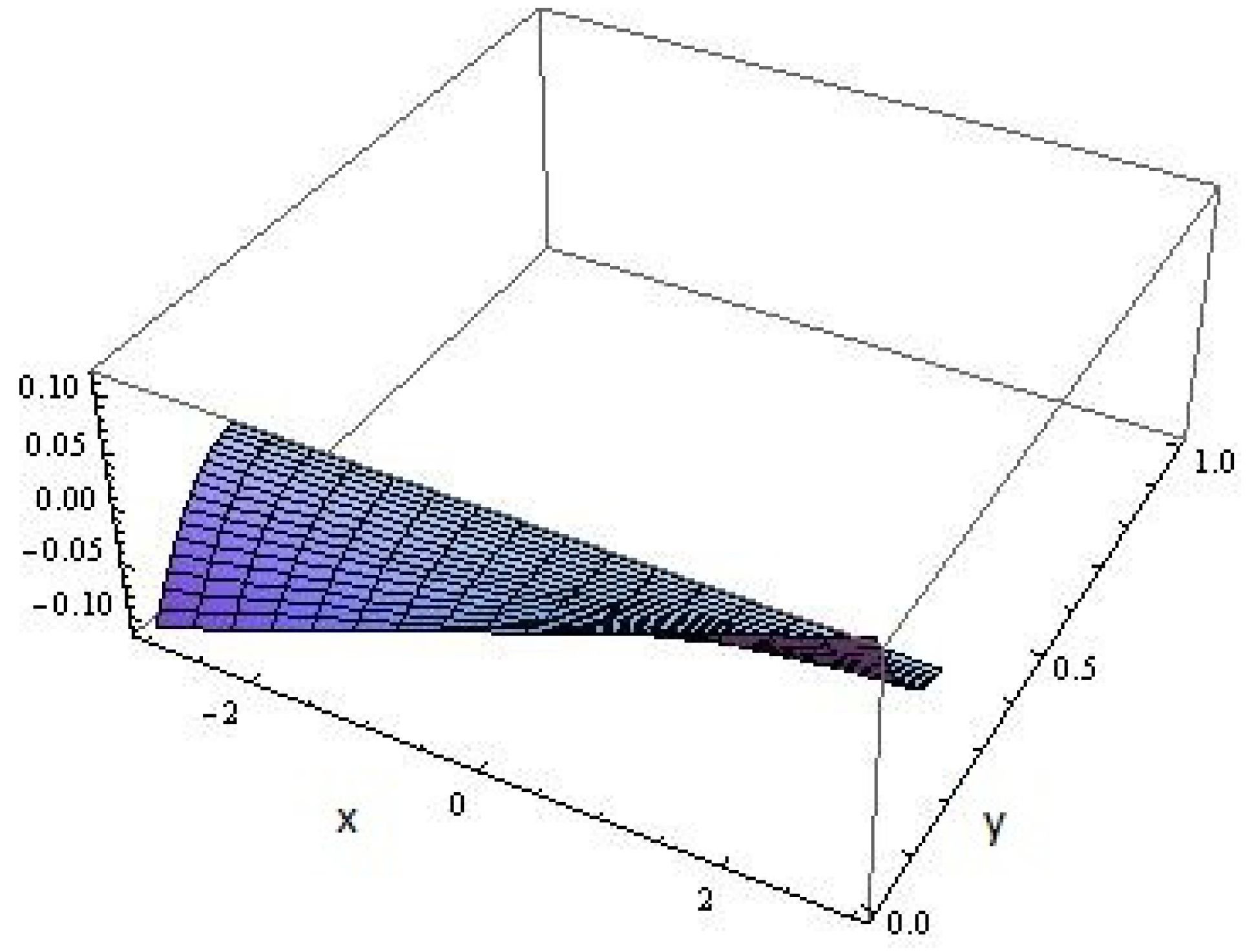
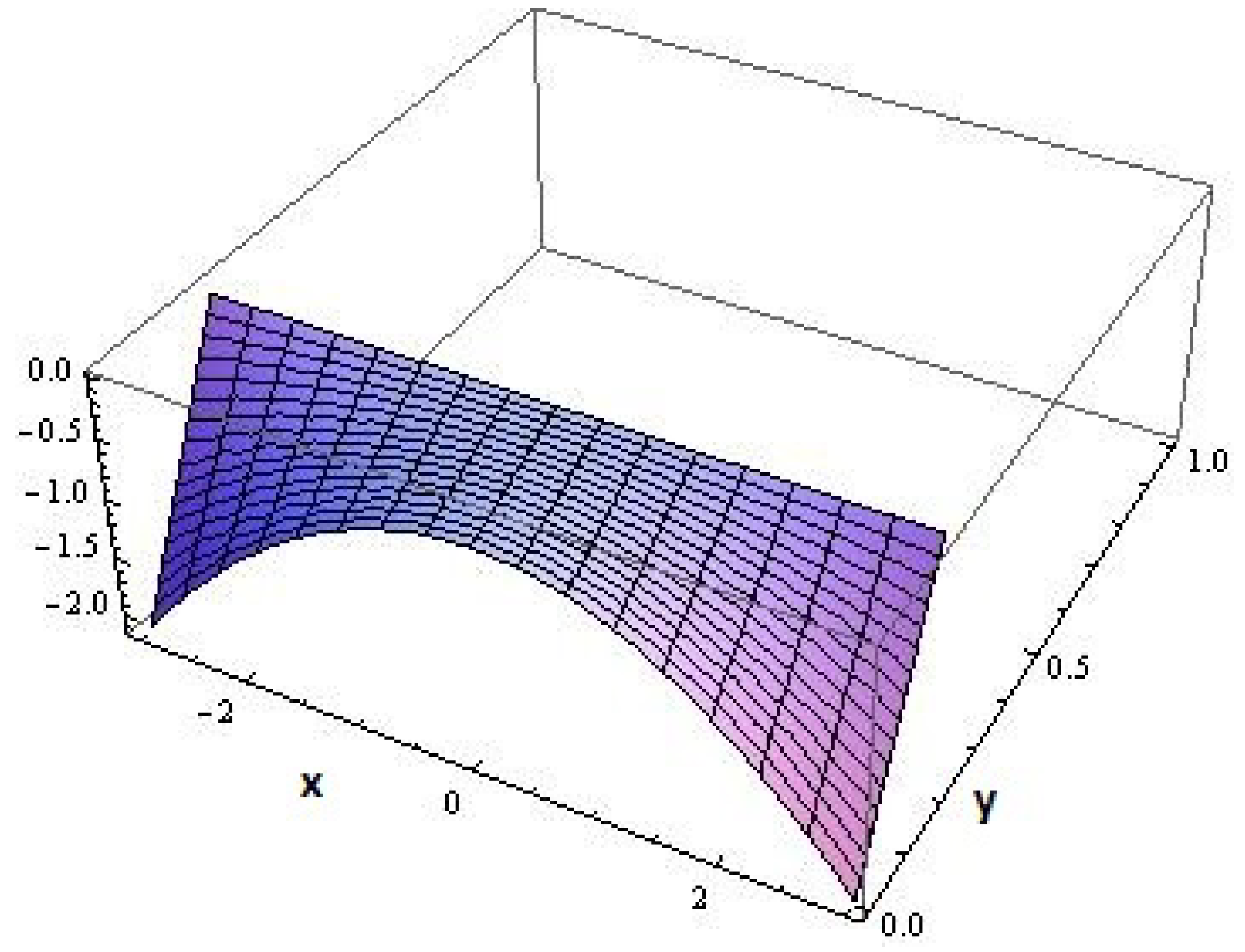
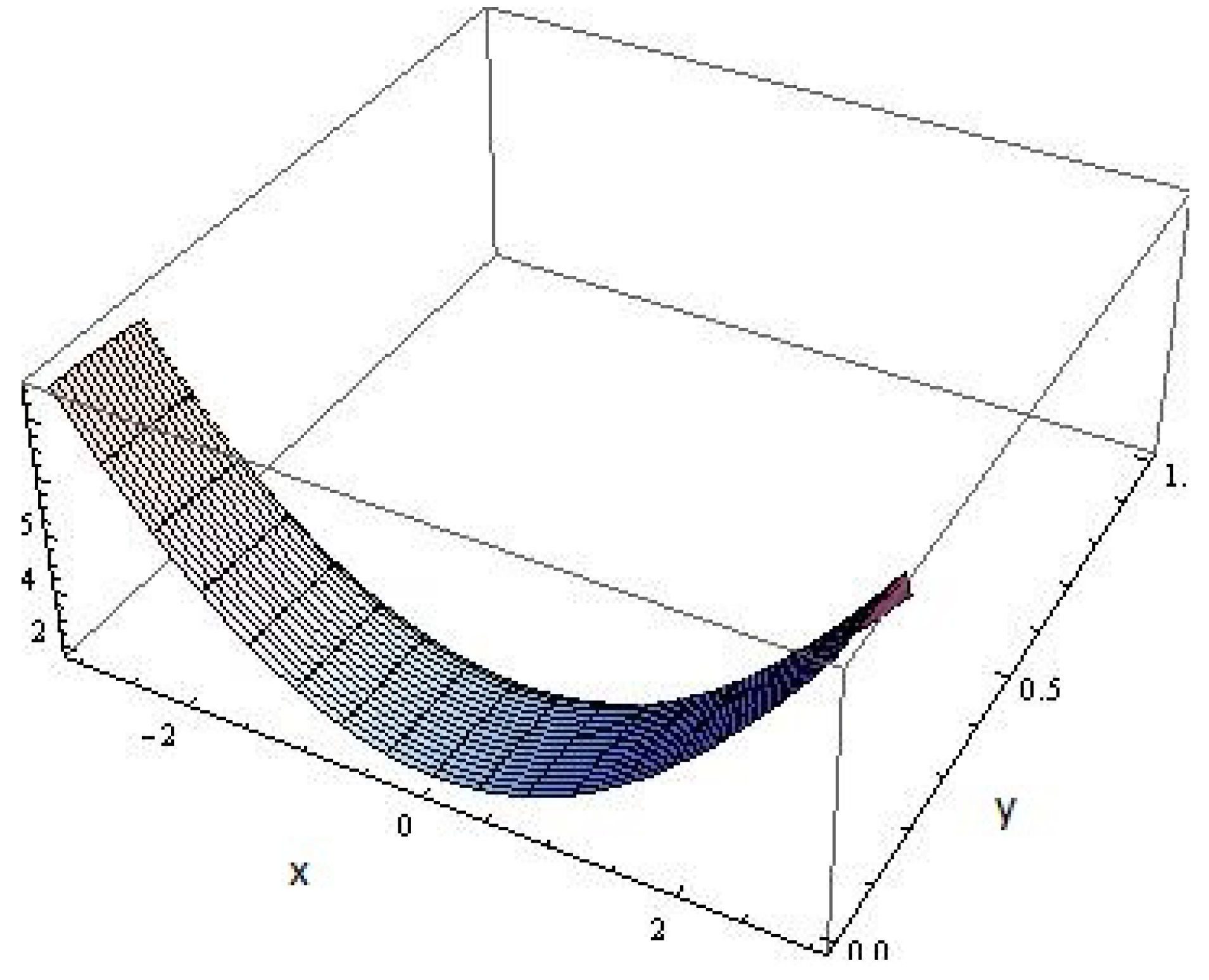
The concerned graphical representations of the flow components $\{F_{\theta },F_T\}$ are shown in the Figure 2 and Figure 3 with their respective magnitudes of variations in the range $(-0.1,+0.1)$ and $(0.0,-2.0)$.

To discuss the Legendre transformations of the free energy $F(x,y)$ as in Equation (13), let $(p,q)$ be the dual variable corresponding to $(x,y)\in {\mathcal{M}}_2$, that is, the new variables p and q are defined as the flow components $\{F_x,F_y\}$ as in Equation (14). Therefore, by inverting the flow equations $p:=F_x$ and $q:=F_y$ as the new equations $x\equiv x(p,q)$ and $y\equiv y(p,q)$, whenever it is possible, the Legendre transform of $F(x,y)$ is defined as the dual function in p and q as

$$\begin{array}{c}\hfill F^{★}(p,q)=p.x+q.y-F(x,y)\end{array}$$

(15)

Notice that the Legendre transform $F^{★}(p,q)$ exists if we can invert the flow equations as a pair of new representations $x\equiv x(p,q)$ and $y\equiv y(p,q)$. From the flow components $\{F_x,F_y\}$ as above in Equation (14), it follows that the variables $\{x,y\}$ satisfy the expressions

$$\begin{array}{c}x(p,q)-\frac{p}{2c}{(d-y)}^{e-2}=0,\\ {(d-y(p,q))}^{1-e}+\frac{p^2}{4c}{(d-y(p,q))}^{e-3}-\frac{q}{e-2}=0\end{array}$$

(16)

Therefore, we see that the Legendre transformation of the free energy $F(x,y)$ may not exist in general because of the inversion of a pair of nonlinear algebraic equations. In the sequel, we provide the concerned specific Legendre transforms of the free energy for particular values of the critical exponent $e\in \{1,2,3\}$ that corresponds to distinct sectors in the space of parameters. The concerned phase transition curves are highlighted through the thermodynamic scalar curvature as in Equations (26)–(28) below.

For the case of $e=1$, from the above Equation (16) it follows that we have

$$\begin{array}{cc}x(p,q)=\hfill & \pm i\sqrt{\frac{1+2cq}{c}},\hfill \\ y(p,q)=\hfill & d\mp i\frac{p}{2c}\sqrt{\frac{c}{1+2cq}}\hfill \end{array}$$

(17)

In this case, we see that the Legendre transform $F^{★}(p,q)$ as in Equation (15) reads as the blow complex valued function

$$F_{e=1}^{★}(p,q)=qd\pm \frac{ip}{2\sqrt{c+2q{c}^2}}(2-q+6qc)$$

(18)

For configurations with $e=2$, from Equation (16) we find that $p=2cx$ and $q=0$. Therefore, from Equation (16) it follows that the associated Legendre transform of the free energy $F(x,y)$ as in Equation (13) simplifies as

$$F_{e=2}^{★}(p,q)=\frac{p^2}{4c}-1$$

(19)

For the case of $e=3$, it follows that the old coordinates x and y reduce as

$$\begin{array}{cc}x(p,q)=\hfill & \pm \frac{p}{\sqrt{4c^{2}q-c{p}^2}},\hfill \\ y(p,q)=\hfill & d\mp \frac{2c}{\sqrt{4c^{2}q-c{p}^2}}\hfill \end{array}$$

(20)

From Equation (16), we find that the corresponding Legendre transform of the free energy $F(x,y)$ as in Equation (13) is given by

$$F_{e=3}^{★}(p,q)=qd\pm \frac{p^2-4cq}{\sqrt{4c^{2}q-c{p}^2}}$$

(21)

With the above motivations, we wish to describe the intrinsic stability of an ensemble of parity odd bubbles with fluctuating vacuum angle x and temperature y. The parametric correlations are described by the Hessian matrix of the underlying free energy $F(x,y)$, defined with a set of desired corrections over a chosen temperature y below the decoherence temperature d. Following Equation (13), we see that the components of the metric tensor g on the surface ${\mathcal{M}}_2\left(\mathbb{R}\right)$—defined via the Hessian matrix $Hess\left(F\right(x,y\left)\right)$ of $F(x,y)$—reduce as the following expressions:

$$\begin{array}{ccc}\hfill F_{xx}& =& 2c{(d-y)}^{2-e},\hfill \\ \hfill F_{xy}& =& -2cx(2-e){(d-y)}^{1-e},\hfill \\ \hfill F_{yy}& =& (1-e)(2-e)\left(1+c{x}^2\right){(d-y)}^{-e}\hfill \end{array}$$

(22)

In this framework, we notice that the intrinsic geometric nature of parametric vacuum pair correlations divulges local notions of fluctuating hot QCD bubbles. Namely, at the decoherence temperature $y=d$, we see that all the local pair correlations $\left\{F_{ij}\right|i,j=x,y\}$ vanish identically for all $x,y\in {\mathcal{M}}_2\left(\mathbb{R}\right)$. Meanwhile, for systems with critical exponent $e=2$, only the local vacuum pair correlation $F_{xx}$ survives with a constant value of $2c$, where c is the anomaly factor of the chosen vacuum ensemble. On the other hand, for the systems with unit-critical exponents $e=1$, we find that the local temperature pair correlation function $F_{yy}$ further vanishes identically, while it is interesting to notice in this case that the local vacuum pair correlation function $F_{xx}$ becomes linear in temperature y, and the local cross-correlation function $F_{xy}$ modulates linearly in the vacuum angle x.

Thus, the fluctuating bubble ensemble may intrinsically be examined in terms of the parameters of the underlying large N gauge theory configuration. Moreover, it is evident for a given vacuum bubble system that the principle components of the metric tensor $\{F_{xx},F_{yy}\}$, which signify self-pair correlations, are positive definite functions over a range of the vacuum angle and temperature. 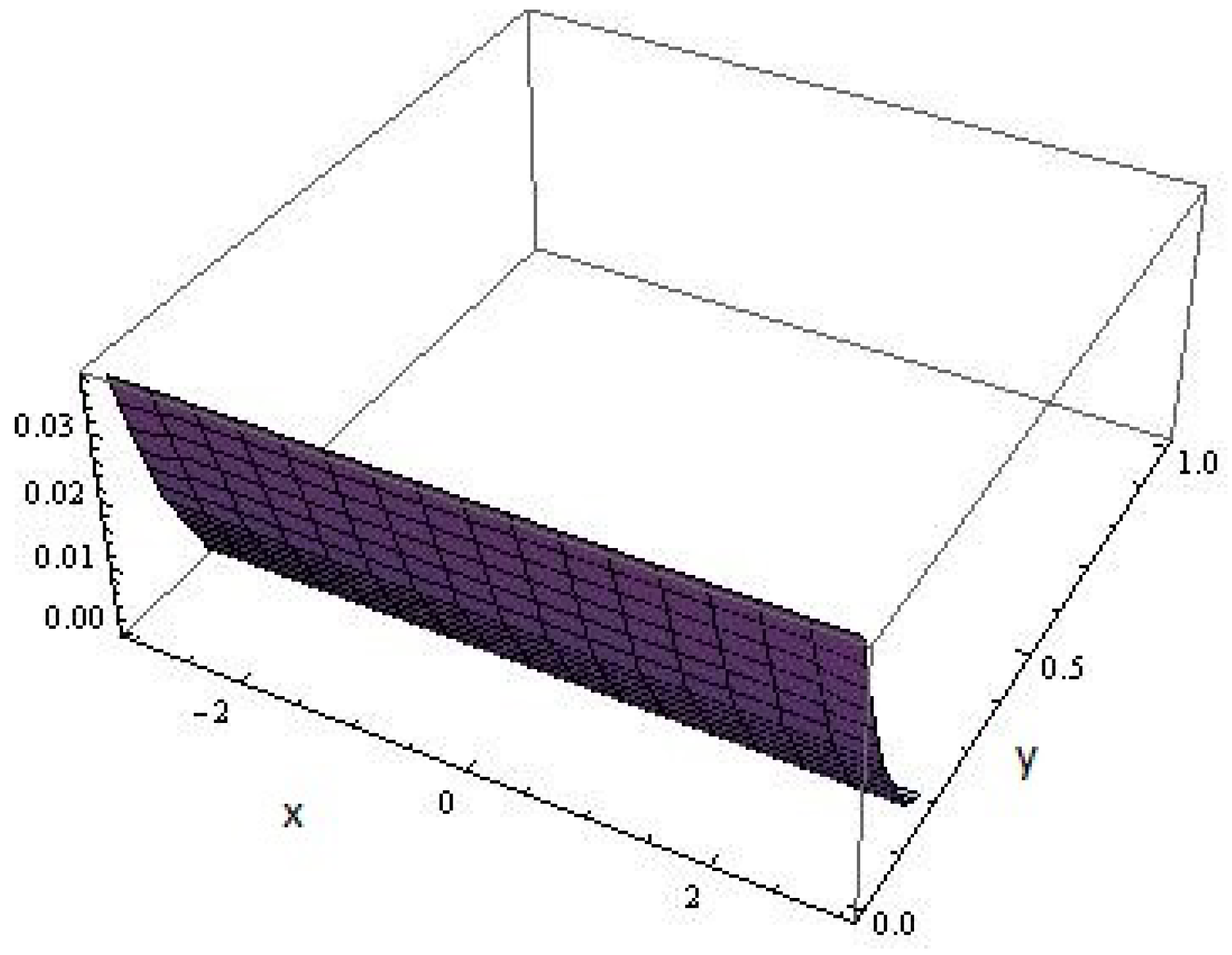Physically, this signifies a set of heat capacities against the intrinsic interactions on the configuration surface $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$ of the undermining ensemble of parity odd bubbles. The graphical representation of the metric components as the local vacuum correlation functions $\{F_{xx},F_{xy},F_{yy}\}$ as respectively depicted in the Figure 4, Figure 5 and Figure 6 show that their respective orders of magnitude are ${10}^{-2}$, ${10}^0$ and ${10}^1$.

Furthermore, it is not difficult to see that the determinant of the metric tensor reduces to the following expression

$$\begin{array}{cc}\hfill \left|\right|g\left|\right|(x,y)& =-4c^2{(2-e)}^2{x}^2{(d-y)}^{2-2e}\hfill \\ & +2c(1-e)(2-e)(1+c{x}^2){(d-y)}^{2-2e}\hfill \end{array}$$

(23)

For configurations with $e=2$, from Equation (22) we see that the parametric correlations satisfy $F_{xx}=2c$ and $F_{xy}=0=F_{yy}$, therefore they correspond to an ill-defined metric tensor g with its vanishing determinant $\left|\right|g\left|\right|=0$. This corresponds to a degenerate surface of $\{x,y\}$. In general, it is worth mentioning that the parity odd-bubble configuration corresponds to a degenerate statistical ensemble for either an absolute value of the vacuum angle x satisfying

$$\begin{array}{c}\hfill \left|x\right|=\left(\frac{e-1}{e-3}\right)c^{-1/2}\end{array}$$

(24)

or the temperature stays fixed at the decoherence temperature, viz. we have $y=d$, or the critical exponent takes a fixed constant value of $e=2$. Over the domain of the system parameters $\{x,y\}$, we notice that the Gaussian fluctuations form a stable statistical configuration, as long as the determinant of the metric tensor $\left|\right|g\left|\right|(x,y)$ remains a positive function on the parametric surface $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$ as a function of the vacuum angle x and temperature y, which is in the regions where we have $1<e<3$ with a given anomaly constant $c>0$. 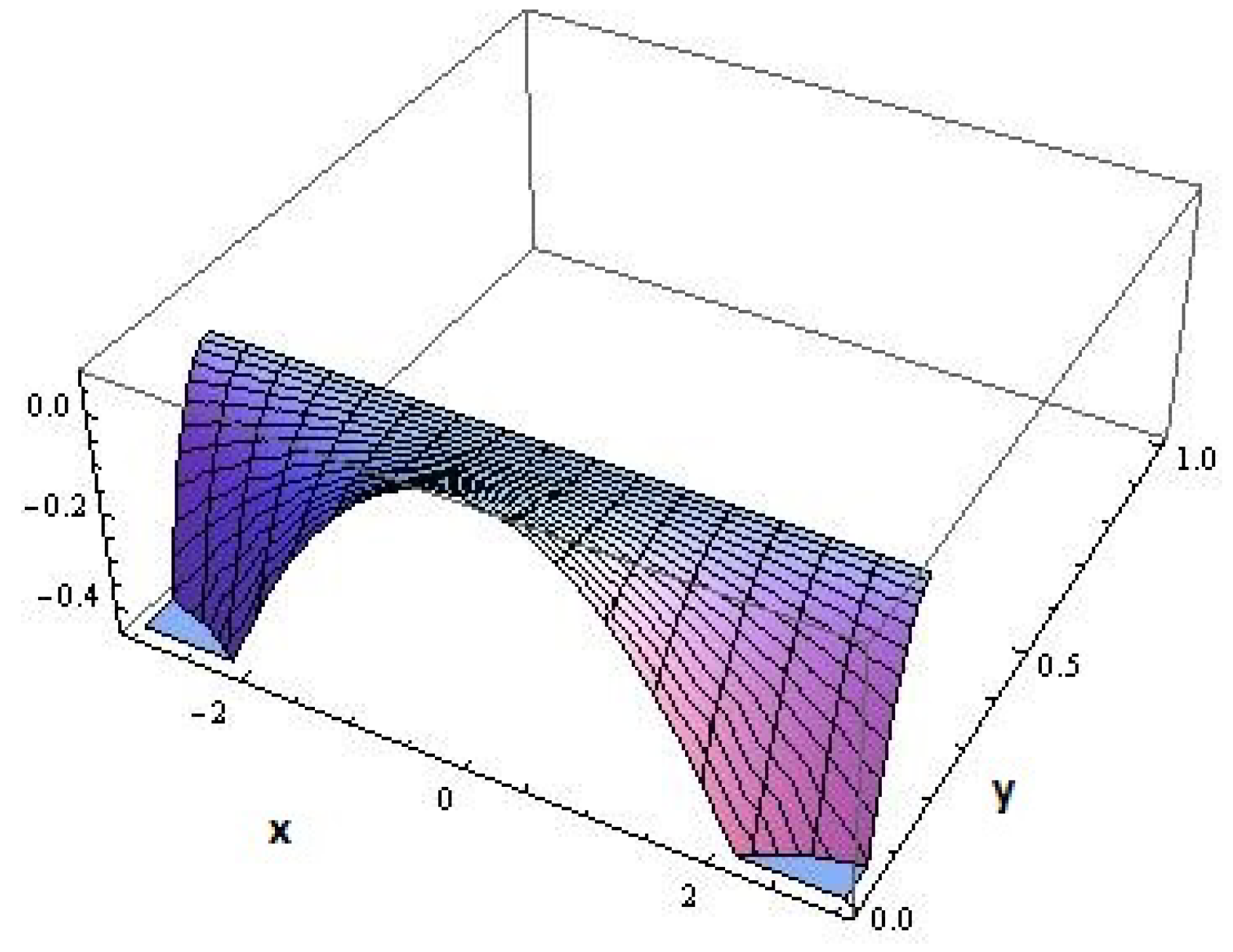The graphical representation of the determinant of the metric tensor $\left|\right|g\left|\right|$ as offered in the Figure 7 with respect to fluctuations of $\{x,y\}$ shows a negative amplitude of the order $-0.5$.

To examine the global nature of local transformations in the space of the parameters $\{x,y\}$ whose fluctuations form an intrinsic real surface $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$, we first need to determine the functional behavior of the associated Christoffel connection functions. In fact, a direct computation shows that the limiting non-trivial Christoffel connections can be expressed in terms of the third derivative of the free energy. Herewith, we see that the various distinct Christoffel components, which arise in the numerator of the intrinsic scalar curvature [7], reduce to the following expressions

$$\begin{array}{ccc}\hfill F_{111}& =& 0,\hfill \\ \hfill F_{112}& =& -2c(2-e){(d-y)}^{1-e},\hfill \\ \hfill F_{122}& =& 2c(1-e)(2-e)x{(d-y)}^{-e},\hfill \\ \hfill F_{222}& =& (1-e)(2-e)e(1+c{x}^2){(d-y)}^{-(1+e)}\hfill \end{array}$$

(25)

Therefore, we observe that the pure vacuum Christoffel component vanishes identically for all values of $x,y\in {\mathcal{M}}_2$, while the remaining components vanish as well for an ensemble with the critical exponent $e=2$. Furthermore, the pure temperature Christoffel component $F_{222}$ vanishes for the vanishing critical exponent ensembles and that of for $e=1,2$. It is clear to see that the mixed Christoffel component $F_{122}$ vanishes for both the integer values $e\in \{1,2\}$. As per this notion of thermodynamic geometry [7], the global nature of phase transition curves can thus be examined over the range of vacuum angle x and QCD temperature y describing a fluctuating ensemble of parity odd bubbles. In particular, we find that the scalar curvature reads as

$$\begin{array}{c}\hfill R(x,y)=\frac{k(e-1){(d-y)}^{e-2}}{{\left(1-e+c(e-3)x^2\right)}^2}\end{array}$$

(26)

We see that the scalar curvature vanishes for the value of the unit-critical exponent, viz. $e=1$. It follows further that the scalar curvature vanishes identically at the decoherence temperature $y=d$, unless the system possessed $e=2$. This implies that the decoherence temperature limit $y\to d$ could also be viewed as the decoupling of statistical interactions or equivalently the formation of thermodynamic equilibrium limit. 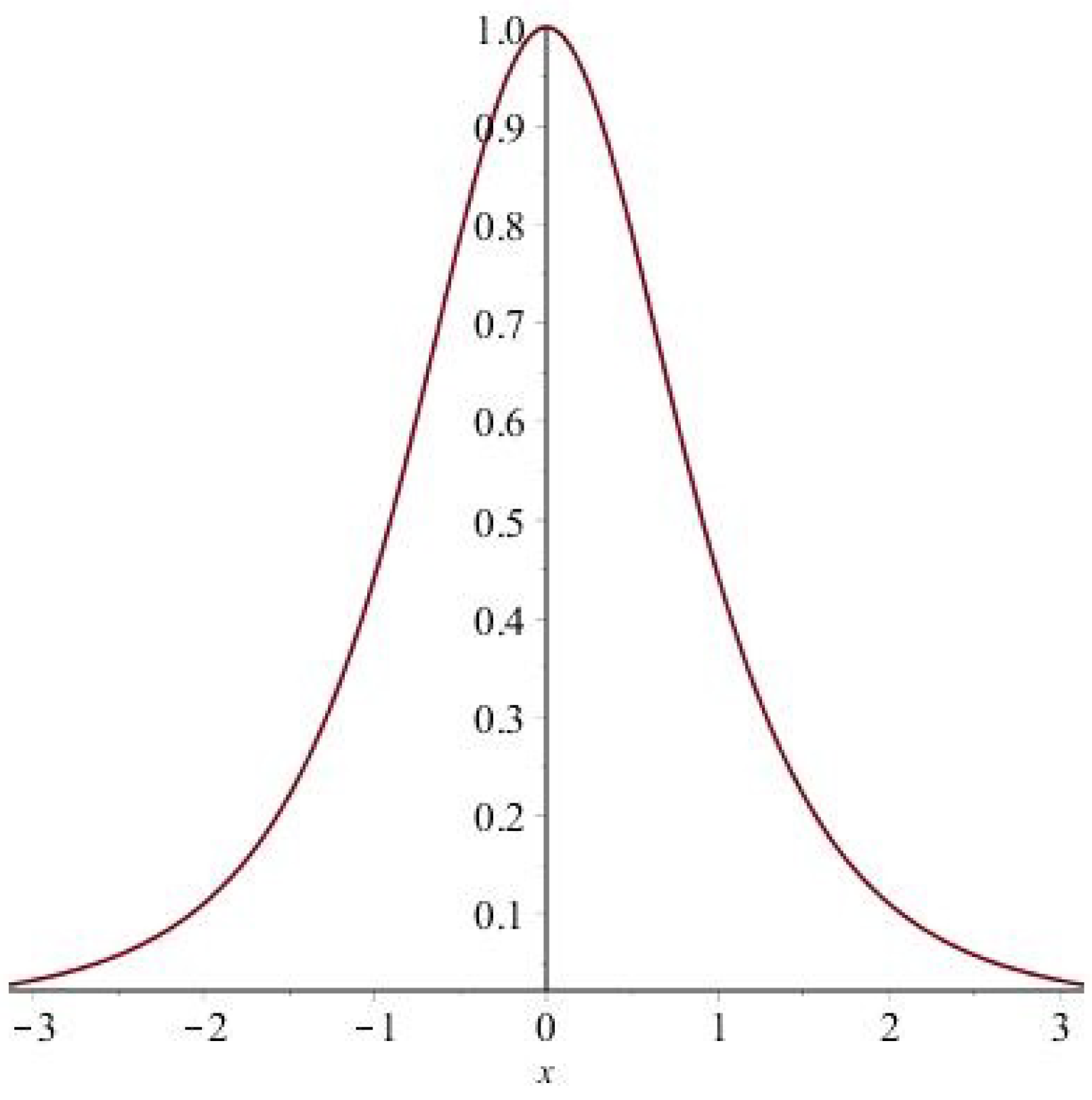For systems with critical exponent $e=2$, we however observe that the scalar curvature becomes independent of temperature y. As a function of the vacuum parameter x, we note in this case that the limiting scalar curvature reduces as the following singly peaked squared Lorentzian function

$$\begin{array}{c}\hfill R\left(x\right)=\frac{k}{{\left(1+c{x}^2\right)}^2},\end{array}$$

(27)

as a function of x. In this case, we note that the scalar curvature remains regular for all $x,y\in {\mathcal{M}}_2\left(\mathbb{R}\right)$, and hence there are no vacuum phase transitions in the limiting configuration of $e=2$. Herewith, from the above Equation (27), we see the corresponding long-range global correlation length $l(x,y)$ as the square root of the scalar curvature $R(x,y)$ becomes independent of both the temperature y and decoherence temperature d for the limiting configurations with critical exponent $e=2$. For a given value of the anomaly factor $c=0.5$, the graphical depiction of the above specific scalar curvature $R\left(x\right)$ as shown in the Figure 8 in the vacuum angle fluctuation range of $-\pi \le x\le \pi$ demonstrates a Lorentzian type peak of the unit order of magnitude.

Similarly, for an arbitrary ensemble with critical exponent $e=3$, we find that the scalar curvature $R(x,y)$ becomes independent of the vacuum angle x. As a function of the system temperature y, we observe that it satisfies an equation of a straight line of slope $-k/2$ and intercept $kd/2$, viz. we have the following limiting scalar curvature

$$\begin{array}{c}\hfill R\left(y\right)=-\frac{k}{2}y+\frac{kd}{2},\end{array}$$

(28)

where k is the standard Boltzmann constant. It is worth mentioning further that the slope of the above straight line remains independent of the chosen statistical ensemble, while the intercept depends solely on the decoherence temperature d of the underlying vacuum system. Importantly, we see that the scalar curvature remains regular for all $x,y\in {\mathcal{M}}_2\left(\mathbb{R}\right)$, and hence there are no vacuum phase transitions in this limiting case of $e=3$, as well.

On the other hand, we find that the intrinsic scalar curvature as given in Equation (26) doubly diverges for the following absolute value of the vacuum angle

$$\left|x\right|=\pm \sqrt{\frac{1}{c}\left(\frac{e-1}{e-3}\right)},$$

(29)

whenever the system possesses a critical exponent $e\notin \{1,2,3\}$ and $y\ne d$, as the phenomenon of decoupling happens at the decoherence temperature. Therefore, under Gaussian fluctuations, the present examination shows that a typical parity odd-bubble hot QCD configuration is globally regular over all possible domains of the parameters $\{x,y\}$ except for the two values of the vacuum angle x as given in the Equation (29). Furthermore, the graphical depiction of the scalar curvature as represented in Figure 9 shows that there exists a band of structures with a relatively large negative peak of an order of the magnitude $-5\times {10}^3$.

As a matter of the fact, the correlation length of the underlying nearly equilibrium vacuum system is globally characterized by the square root of the scalar curvature $R(x,y)$ of the surface $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$. This follows directly from the fact that the scalar curvature $R(x,y)$, arising from the Gaussian fluctuations of the free energy $F(x,y)$ as a function of the vacuum angle and hot QCD temperature $\{x,y\}$, vanishes identically at the decoherence temperature $y=d$ and diverges for the above-mentioned double absolute values of x; see in particular the Equation (29).

Notice furthermore that at the deconfining phase, the transition point corresponding to the critical exponent $e=-0.013$, the underlying Weinhold geometry of the parity odd-bubble vacuum ensemble corresponds to a well-defined statistical basis and is a negatively curved manifold as long as we have $e<1$, and the system remains in the deconfining phase, viz. we have the temperature range $y<d$, except for the configurations with $e=2$. In this case, we observe further that the underlying fluctuation manifold ${\mathcal{M}}_2$ becomes Ricci flat for the initial value of the critical exponent, viz. $e=1$, therefore the corresponding vacuum configuration corresponds to a non-interacting statistical system. Moreover, this system generically never diverges, namely undergoes a phase transition for a class of well-defined values of system parameters $\{x,y\}\equiv \{\theta ,T\}$, except for those x satisfying Equation (29) concerning the denominator of the scalar curvature $R(x,y)$, whose roots determine the underlying global pathologies and statistical singularities, if any.

In particular, the vacuum configurations with unit-critical exponents lead to a non-interacting statistical basis. This is because the aforementioned scalar curvature as in Equation (26) vanishes identically at the unit value of the critical exponent. In other words, for $e=1$, it follows from Equation (26) that we have $R(x,y)=0$ for all $(x,y)\in {\mathcal{M}}_2$. Therefore, the configurations with $e=1$ correspond to a non-interacting statistical system. Physically, this corresponds to a constant mass of the ${\eta }^{\prime }$ that arises as a trivial consequence of the vanishing of the thermodynamic scalar curvature. Namely, for the configurations with $e=1$, we see that the free energy concerning the confining-deconfining phase transitions varies as the difference of the temperature from it’s decoherence value that may be treated as the origin of the fluctuation manifold for a variable vacuum angle.

This illustrates the statistical structures of an ensemble of parity odd bubbles originating via the free energy fluctuations with an incorporation of anomalous couplings to the associated mesons. We may further see that the underlying fluctuating configuration pertaining to the large N parity odd bubbles leads to an ill-defined statistical basis at the deconfining temperature $y=d$, as the determinant of the corresponding metric tensor $Hess\left(F\right(x,y\left)\right)$ vanishes identically. Such phenomena may well be expected to happen at this value of the temperature because the mass of the $\eta$ particle vanishes at the confining-deconfining temperature boundary; see [3] for a reasoning via scattering theory.

For the above ensemble of parity odd-bubble vacua with a given anomaly factor c, we notice that the Riemann Christoffel curvature tensor $R(x,y)$ in particular possesses a non-trivial global behavior over the entire parametric surface $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$. Namely, by the present intrinsic geometric analysis with free energy $F(x,y)$ as the real embedding map as in Equation (8), we conclude that a parity odd-bubble hot QCD vacuum configuration generically corresponds to an interacting regular statistical basis over $({\mathcal{M}}_2\left(\mathbb{R}\right),g)$ under fluctuations of the system parameters $\left\{(x,y)\right|x,y\in {\mathcal{M}}_2\left(\mathbb{R}\right)\}$, apart from (i) for a repeated pair of vacuum angles x as given by Equation (29) where the system goes under vacuum phase transitions; and (ii) for the constant temperature line $y=d$, where d is the decoherence temperature of an arbitrary vacuum system with $e\ne 2$. This is because the corresponding scalar curvature $R(x,y)$, as depicted in Equation (26) vanishes identically at this value of the temperature, viz. $y=d$, whereby the associated vacuum ensemble corresponds to a non-interacting statistical configuration. In fact, we notice also that the same conclusion holds further for an arbitrary vacuum ensemble of the unit-critical exponent parity odd hot QCD bubbles.

5. Conclusions and Outlook

Thermodynamic geometry as introduced by fluctuation theory models [7] renders local and global vacuum phase structures via the embedded intrinsic metric, hyper-scaling theories [11,12] and Widom’s approach to scaling theory where one defined Widom line as the locus of points in the space of parameters corresponding to the maximum correlation length [13]. Therefore, as mentioned in the introduction, the state-space geometric characterization has here been investigated for black holes and black branes in various string theory and M-theory vacuum configurations [29,30,31,32,33,34,35,36]. As one of the main subject matters of this paper, this has led us to explore the vacuum stability properties of an ensemble of large $N_c$ gauge theories as a collection of fluctuating meta-stable states concerning the parity odd bubbles [14]. Our leitmotif is further supported by observations concerning vacuum $SU\left(N\right)$ moduli fluctuations, thereby we find in particular that the statistical correlation functions arise solely due to anomalous meta-stable states, whereas a general statistical ensemble of vanishing anomaly states with $c=0$ parametrizes an interacting thermodynamic system of a negative curvature scalar for a negative value of the exponent e. From Equation (26), it follows that the vanishing anomaly configurations with $c=0$ corresponds to the following vacuum independent limiting scalar curvature

$$\begin{array}{c}\hfill R\left(y\right)=\frac{k}{(e-1)}{(d-y)}^{e-2}\end{array}$$

(30)

In particular, the present work analyzes the structures of an ensemble of $SU\left(N\right)$ gauge theory vacua from an intrinsic geometric perspective of a dynamic system. In the space of its parameters, our analysis is intended to examine the process of how one reaches the deconfining phase. Namely, we examine the physical and geometrical properties of confining-deconfining phase transitions via the intrinsic geometry of the parameter space. Scientifically, we have motivated the same with an introduction, overview, analysis, and conclusion and discussion of the vacuum stability. In this regard, the susceptibility arises as the second derivative of the free energy with respect to the vacuum parameter. On the other hand, the deconfining temperature may relate the temperature corresponding to the restoration of the chiral symmetry. However, it is worth mentioning that there are beliefs that it is still far from being understood—specifically, whether the two temperatures, viz. the one for deconfinement and the other for the chiral one, are the same or not? Such developments are left open for future research and developments.

Intrinsic geometrically, our exploration is useful in understanding the issues of QCD phenomenology, vacuum stabilities, phenomenology of heavy ion collisions, and LHC phenomenology. In a nutshell, it is worth mentioning that phase structures of QCD play an important role in understanding high-energy physics and its phenomenology. In this paper, we have highlighted this from the perspective of intrinsic Riemannian geometry. Here, we have computed local and global correlation properties of an ensemble of $SU\left(N\right)$ gauge theory vacuum configurations. Therefore, local stability is determined from the positivity of either of the fluctuation capacities that are defined as the auto-correlations of the free energy, viz. $\{F_{\theta \theta },F_{TT}\}$. On the other hand, global vacuum stability is determined via the positivity of the determinant of the intrinsic metric tensor on the space of parameters, viz. the vacuum angle $\theta$ and the temperature T. Under fluctuations of $\theta$ and T, this can be viewed as the Hessian matrix of the Kharzeev–Pisarski–Tytgat model of the free energy. Therefore, global stability requires examining the nature of cross-correlation $F_{\theta T}$, as well. Finally, we have performed global analysis, where corresponding phase transitions are examined via the signature and regularities of long-range correlation length. In our case, it follows that correlation length arises as the square root of the Ricci scalar curvature of the fluctuation surface.

Furthermore, we observe that the configurations with vanishing anomaly contributions have no global statistical correlation, viz. the configurations with $e=1$ corresponds to $R=0$ in the light of thermodynamic geometry. In other words, the global statistical correlations to party odd hot bubbles arise only because of an existence of meta-stable states. It is worth mentioning that meta-stable states arise only when the anomaly term becomes very small, which implies a strong variation to the topological susceptibility with respect to the system temperature. Moreover, we notice that the statistical system concerning an ensemble of parity odd bubbles undergoes a vacuum phase transition at the chiral symmetry restoration temperature as well as at an absolute value of the vacuum angle $\theta$. Interestingly, the long-range global correlation length becomes independent of both the temperature and decoherence temperature for theories with critical exponent $e=2$.

The above conclusion holds further for a particular choice of the temperature $T=T_d+1$, where $T_d$ is the decoherence temperature. On the other hand, we find that the unit-critical exponent vacuum configuration leads to a non-interacting statistical basis corresponding to a constant mass of ${\eta }^{\prime }$. Our consideration further leads to phenomenological investigations in the realm of hot QCD bubbles; for instance, see [14] for the maximal isospin violation. This proposal could further be explored towards the stability characterization of a rather technical subject, specifically, the formation of stable $\theta$ dependent YM configurations and its relation to statistical stability signatures concerning heavy ion collisions and standard model of physics at the LHC [17] towards the optimal design of accelerator experiments, LHC machines, and associated physical quantities.

Our consideration does not stop here, but continues further. For instance, we can extend the above setup into various dimensions of QCD research including nuclear collisions, parity conservation, CP violation, and others [73,74]. In this regard, we have addressed the vacuum stability criteria of gauge theory systems for both the critical and deconfining temperatures under the fluctuations of its model parameters. Following this, we have offered an intrinsic geometric examination of vacuum fluctuations in the space of parameters. In particular, for given values of the decoherence temperature and critical exponent, the relationship to CP odd meta-stable configurations of the YM vacuum at finite temperatures is anticipated through the parametric fluctuations in the space of the vacuum angle and temperature. Physically, the role of thermodynamic geometry arises by considering the system-embedding function as the free energy as a physical quantity.

Furthermore, we have provided the Legendre transformation $F^{★}$ of the free energy $F(x,y)$ in terms of the flow components. Indeed, it is shown that Legendre transform $F^{★}$ may not exist in general because of the inversion of a pair of nonlinear algebraic equations. Therefore, we have provided the concerned specific Legendre transforms of the free energy for the particular values of the critical exponent, viz. $e\in \{1,2,3\}$ that correspond to distinct sectors in the space of parameters. The concerned phase transitions are equally examined through the respective thermodynamic scalar curvatures as depicted above in Equations (26)–(28). The Legendre invariance and associated different metric structures of an ensemble of thermodynamic equilibrium states are relegated for a separate study.

On the other hand, it would be interesting to explore the notion of this paper for arbitrary finite N configurations possessing a definite periodicity in $\theta$, by considering for instance the fractional identification: $\theta \sim \theta +2\pi r$ with $0\le r\le 1$ in connection to the equation of motion of the effective theory. In this paper, we however largely concentrated on the analysis of integral vacuum fluctuations which are $2\pi$ periodic in $\theta$, viz. $r\in \{0,1\}$. The associated consideration concerning the (in)stability analysis of possible (fractional) vacua arising in the intermediate $\theta$ regime with $0<r:=p/q<1$ where $p,q\in \mathbb{Z}$ such that $p<q$ and $q\ne 0$, we leave open for a future investigation.

In this paper, for standard cases of $r=0,1$, the fluctuation theory analysis as examined in Section 3 and Section 4 shows that an ensemble of parity odd bubbles concerning YM meta-stable vacua generically leads to an interacting statistical basis, possessing an intriguing set of vacuum pair correlation functions and global phase transition curves. It is worth pointing out further that, for a precise prediction of vacuum statistical correlations, an exact calculation of the underlying $SU\left(N\right)$ gauge field theoretic potential U would be essential at a finite N to offer complete non-equilibrium statistical stability structures of fluctuating parity odd hot QCD bubble configurations. Concerning a class of finite N such backgrounds, we anticipate that the intrinsic geometric setup would render underlying vacuum stability properties and formation of an equilibrium thermodynamic configuration arising via the thermodynamic limit of an ensemble of meta-stable states, see [75] in the light of dynamic fermions. We leave this problem open for a future research development.