4.1. Observers in Rotational Motion
Consider a set of observers fixed to a ring that rotates at a fixed angular velocity in its own plane in the inertial lab. Traditionally, analyses of simultaneity on the rotating ring treat a set of
-D MCIFs of its observers. They chain together a set of one-space-dimensional Lorentz transforms from each one of these frames to the next, to construct a “helix of simultaneity” in the lab. But simultaneity is not transitive across frames: if you and I inhabit different frames, then if I say events
A and
B are simultaneous, and you say events
B and
C are simultaneous, I cannot maintain a priori that
A and
C are simultaneous. And yet this is precisely what conventional analyses do when they create a “helix of simultaneity”. They draw a cylindrical piece of spacetime and “unwrap” it to make a flat sheet—a nonsensical procedure that is supposed magically to turn two spatial dimensions into one. They then draw a straight line of simultaneity on this sheet, and wrap it back up into a cylinder. They follow this helix most of the way around this “world sheet” of the ring and note that it connects timelike events on any world line: clearly a contradiction [
19]. The conclusion is that rotation does not produce a valid frame. I maintain that although rotating frames do not exist, it is not for the above reason. First, constructing the above helix simply makes no sense: a
-dimensional analysis simply
doesn’t apply to a
-dimensional scenario. The inertial frames of special relativity have global extent, and the MCIFs that are chained together are of global extent. Hence each includes the entire ring; their spatial extent is not restricted to a small piece of the ring. It is simply not valid to chain together a series of “tiny”
-dimensional frames and wrap them around a cylinder in
spacetime as a substitute for what should have been done in the first place with global
-dimensional inertial frames. When we do apply a
-dimensional analysis in this section, we find that a common standard of simultaneity does not exist for all ring observers, and this is why a rotating frame does not exist.
In [
6], I have argued that to analyse a disk rotating in two dimensions, we must make the standard assumption for any non-inertial frame, that the plane of simultaneity at any event on the world line of an accelerated observer is identical to the plane of simultaneity of the MCIF at that event. (This is consistent with the footnote in [
20].) Light’s speed
is isotropic in any MCIF, and so an emitter’s plane of simultaneity in
-D becomes the true measure of simultaneity for that emitter, as opposed to a one-dimensional helix.
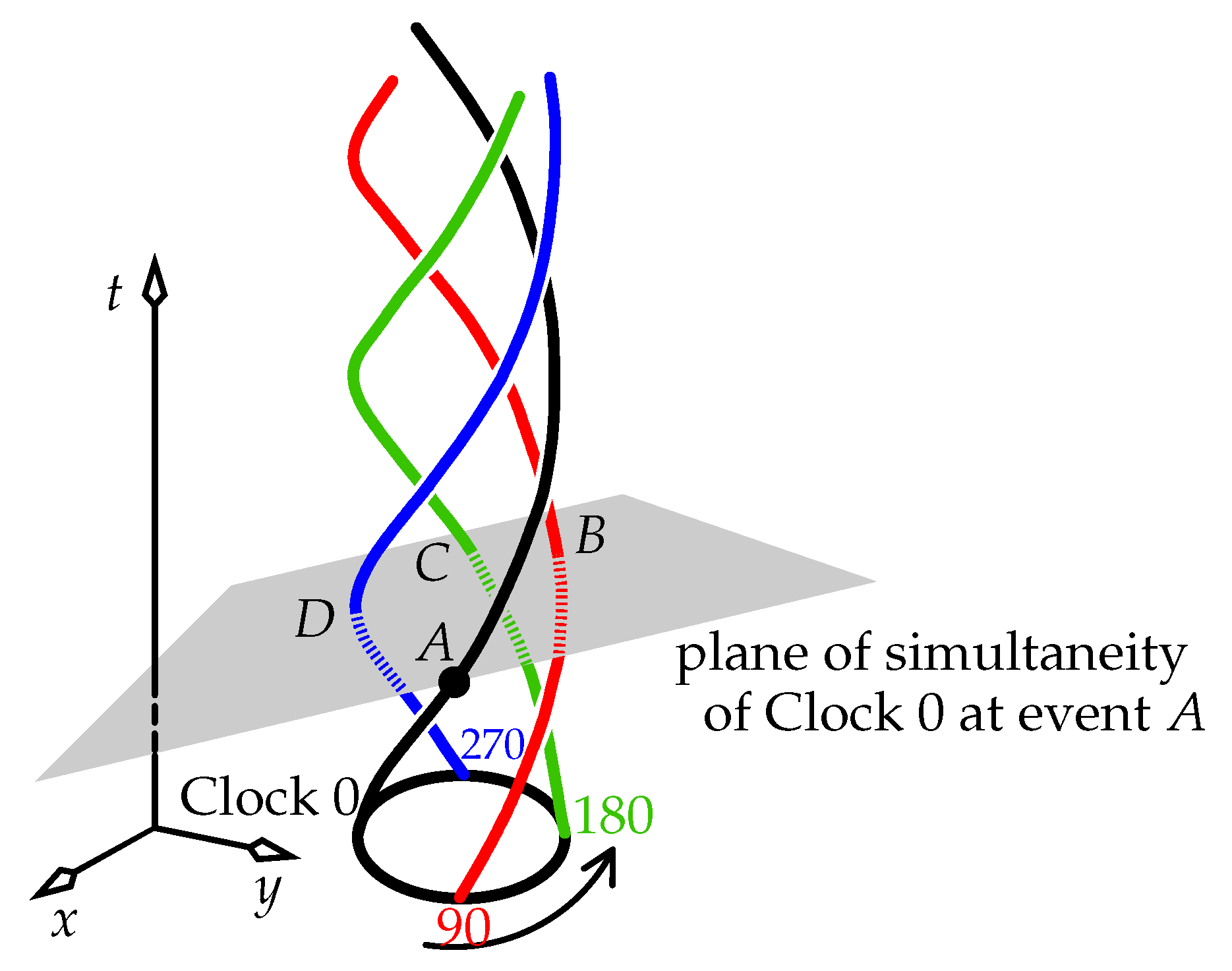
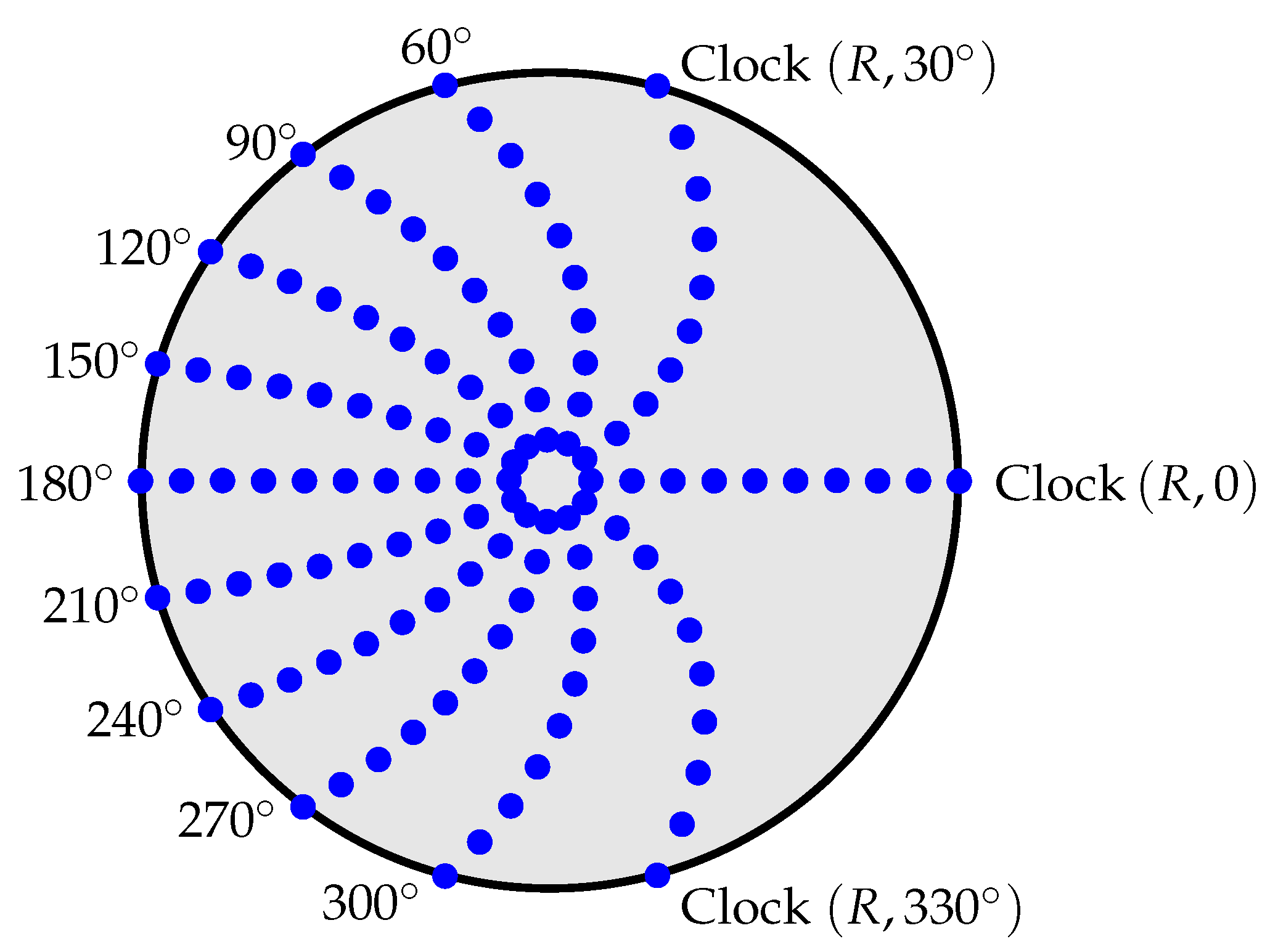
Figure 7.
Reproduced from [
6]. A set of helical world lines of four clocks on a rotating ring. Clock 0’s grey plane of simultaneity at the black-dot event
A is shown, constructed by the procedure of
Figure 6. It intersects the three world lines of Clocks 90, 180, and 270 at events
respectively.
Figure 7.
Reproduced from [
6]. A set of helical world lines of four clocks on a rotating ring. Clock 0’s grey plane of simultaneity at the black-dot event
A is shown, constructed by the procedure of
Figure 6. It intersects the three world lines of Clocks 90, 180, and 270 at events
respectively.
A typical plane of simultaneity for a clock on a rotating ring is shown in
Figure 7. We see the helical world lines of four clocks fixed to the ring at 90
intervals. The ring rotates in the inertial laboratory of the figure. Suppose these four clocks have been synchronised in the lab: this frame says that at all lab times, the four clocks all display the same value. But the clocks themselves give different meanings to “now”. Clock 0’s world line is black in
Figure 7; similarly, Clock 90 has a red world line, and so on. We construct Clock 0’s plane of simultaneity at event
A where it displays time zero, and find the intersection events
of this plane with the world lines of Clocks 90, 180, and 270 respectively. Event
B occurs in the laboratory future of
A, event
C occurs at the same lab moment as
A, and
D occurs in the lab past of
A:
For example, suppose the ring is Earth’s equator, “spinning east” in the ECI, but with no gravity present (as we are doing a special-relativity analysis here). The above four clocks are always synchronised in the ECI, which is the inertial frame of
Figure 7. Now recall the case in one space dimension, where a line of simultaneity for an observer of velocity
v has a slope on a
-versus-
x spacetime diagram of
. In two space dimensions, the plane of simultaneity has the analogous tilt in spacetime; thus, as it extends on Earth approximately a distance
R (Earth’s radius) to Clock 90’s world line, it rises along the time axis by
. The helical world lines of the comparatively slowly rotating clocks on Earth’s Equator (speed 465 m/s in the ECI) are almost parallel to the
t axis of
Figure 7 [proof: see the analysis around (
6)]. This rise is then
Hence, when Clock 0 displays
(event
A),
- –
Clock 90 displays approximately 33 nanoseconds (event B),
- –
Clock 180 displays 0 (event C), and
- –
Clock 270 displays ns (event D).
(Note this is not the Sagnac effect, since the Sagnac effect involves time differences that increase linearly with longitude, and incorporates no relativity.) If the four clocks have identical ages in the inertial frame, Clock 0 says “Clock 90 is the oldest, Clock 180 has the same age as me, and Clock 270 is the youngest”. This is all very well, but clock 180 constructs a different plane of simultaneity, and concludes “Clock 90 is the youngest, Clock 0 has the same age as me, and Clock 270 is the oldest”. The clocks cannot agree on simultaneity, and this is the reason that they cannot form a frame.
In the inertial frame (in which these clocks are moving with “gamma factor” ), the clocks’ proper times increase at a rate equal to the inertial frame’s clock rate reduced by a factor of . As time passes, each of the clocks says that the other clocks maintain the above time differences relative to itself. In particular, Clock 0 can do a one-off recalibration of them all to display the same time as Clock 0: subtract 33 ns from Clock 90 and add 33 ns to clock 270. This yields a set of clocks whose readings always agree for Clock 0 only. The other clocks on the ring will measure the set to be unsynchronised. But in this highly restricted sense, we now have a kind of rotating frame.
Clock 0’s plane of simultaneity cuts Clock 90’s world line 33 ns into Clock 0’s future. At this moment, Clock 90 is slightly east of exactly 90 from Clock 0, using the degree unit of the inertial lab. Hence Clock 0 measures Clock 90’s angular distance (using the degree unit of the inertial lab) to be slightly greater than 90; the true value for Earth’s size and spin rate is about . Similarly, Clock 0’s plane of simultaneity cuts the world line of Clock 180 such that Clock 0 says that its own time equals that shown on Clock 180 at this moment. Clock 0 then measures Clock 180’s angular distance to be exactly 180. Lastly, Clock 0 measures Clock 270’s angular distance as . Extending this argument to a continuum of clocks fixed to the perimeter, Clock 0 measures these clocks to crowd toward Clock 180. This is depicted later in Figure 14.
Now introduce a set of rulers, each of which links two neighbouring clocks. Clock 0 notes that nearby distances (rulers) on the ring are stretched, and remote distances are contracted. But ultimately all distances are determined by rulers linking clocks; and so we conclude that Clock 0 must measure a circumference of exactly
. This simple result hides a complicated spatial metric—Equation (
20) in [
6]—because for any clock on the ring, a ruler’s length now depends on its position relative to that clock.
From the earliest days of special relativity, researchers have approached rotation by making a rotational Galilei transform from an inertial frame. When treated as a possible change of frame, this transform runs contrary to relativity: after all, central to special relativity is the replacement of the Galilei transform with the Lorentz transform, because the Lorentz transform produces coordinates obeying the relativistic notion of simultaneity. The Galilei transform
is a valid change of
coordinates, but that does not make it a valid change of
frame. Instead, the transform produces a set of what might be called “rotating coordinates” for the
inertial frame. These coordinates need have no physical relevance to the rotating system—and they also are not necessarily useful for the inertial frame. In the context of Earth, they are a way of placing ECI coordinates on observers who are fixed in the ECEF, and this is certainly what is done to create our modern world’s “UTC time”. But they are not true coordinates of a rotating frame. My sentiments here echo those of Corum in [
21]. Corum decries the use of the Galilei transform—but perhaps doesn’t make the point that this transform is, at best, an attempt to create a set of rotating coordinates for the
inertial frame in lieu of the fact that rotating frames don’t exist.
The distinction that I am making here, of rotating coordinates for an inertial frame versus coordinates for a “rotating frame”, is probably completely unknown in the field of precise timing. The oblate Earth with its gravity is a much more complicated example of rotational motion than the above ring. But because analyses of the ring—or rather, rotating disk—have never produced a consensus, we should not expect the subject of precise timing on a rotating Earth to be in any advanced state. This is belied by the analyses found in many precise-timing papers, which simply assume that any arbitrary change of coordinates produces a new frame. See my further comments on this at the start of
Section 7.
4.2. Train on Circular Track, the Rotating Ring, and the Pole and Barn Again
Recall the meaning of Born rigidity: a body is accelerated in a Born-rigid way if it is continuously Lorentz contracted while always constituting a frame within which it retains its rest length. Born rigidity is tied to a frame being able to remain a frame once it has been accelerated. If we are willing to drop the requirement for an accelerated vehicle to qualify as a frame, then we can analyse a wider range of motions without demanding any behaviour such as a Lorentz contraction.
Consider accelerating a train in a straight line from rest by firing a set of minuscule rockets, each one attached to one of the train’s atoms, as described in
Section 2 and
Section 3.3, and shown for two atoms in
Figure 3. These rockets are all fired at equal times and by equal amounts in the inertial platform frame. This ensures that the train’s length in this frame remains at its rest length
for the duration of the burn, and the burn programme overrides the electromagnetic interaction between the atoms. The passengers say that the rockets fired non-simultaneously in their frame and
stretched the train for them by a factor of
, producing a new rest length of
. In the platform frame, this new rest length becomes Lorentz contracted by
to be
. So a “rest-to-moving” length contraction by the Lorentz factor of
certainly occurs, even though we arranged for the train’s length not to change in the platform frame.
This same idea applies to a train moving at constant speed on the circular track, where the train’s rear carriage is joined to its engine (i.e., this is a model of a rotating ring). The old questions are “Is each carriage Lorentz contracted, or are the links between the carriages Lorentz contracted? What happens to the train’s length?” In the same way that we were free to accelerate the straight train however we chose, and then ask what its passengers observed in the process, we are free to accelerate the train on the circular track however we choose, and then ask what its passengers observe. If we give all of the train’s atoms congruent helical world lines—the most democratic plan—then by construction, it retains its shape and rest length in the platform frame. But the passengers of the train say that the rockets are firing out of order, which stretches some parts of the train and compresses other parts according to the local standard of simultaneity of each passenger. Now they will generally disagree with each other about simultaneity, and hence will not qualify as a frame. So there will be no such thing as a “train frame”.
This, then is the rotating ring of
Figure 7. By rotating the ring in the inertial laboratory such that all of its particles follow congruent helical world lines, it is not deformed in the lab, but neither can its observers say that they occupy a well-defined frame. We are at liberty to arrange the world lines of all points in the ring to have any generally timelike shape, and so we might as well treat them all equally, and arrange all to be congruent helices. In that case nothing contracts in the lab frame. This is perhaps the closest that we can get to a “rotating frame” in relativity.
Return to our variant of the pole and barn paradox in
Section 2. The pole can certainly be guided into the barn using minuscule rockets and moved in circles indefinitely. But doing so means it will no longer constitute a single frame for the tiny bugs that live on its surface (so to speak). The planes of simultaneity of each of those bugs will be changing wildly, and we cannot treat the entire pole as a single frame in any analysis. (It is certainly not inertial, nor even uniformly accelerated). Any selected bug will observe most of the other bugs on the pole to be older or younger than itself, and will observe the pole to be compressed and coiled up inside the barn; and the barn has not been Lorentz contracted smaller than the pole’s extent. The pole was not accelerated in a Born-rigid way, and although its motion is completely valid, no part of it forms a frame. When the barn door opens, the tiny rockets guide the pole out and can even eventually move it parallel to its length at constant velocity. In that case, from that moment on, it will display the usual Lorentz contraction, and the bugs on it will say that they constitute a single frame.
4.3. The Extent of Disagreement on Simultaneity in the ECEF
In this section we examine the details of simultaneity on a rotating ring by using the example of a set of clocks on our rotating Earth, and satellites orbiting Earth. We focus on their ability to synchronise, given that they disagree on the meaning of “now”. By how much do their versions of “now” differ?
Equation (
4) and the discussion around it showed that if clocks fixed at longitudes 0, 90
, 180
, and 270
all have the same age in the ECI, then in the ECEF Clock 0 will say that in comparison to itself:
- –
Clock 90 is 33 ns older,
- –
Clock 180 is the same age, and
- –
Clock 270 is 33 ns younger.
This relative ageing holds true for all the clocks. In particular, Clock 180 will maintain that the ages of clocks 90 and 270 are the reverse of what Clock 0 says they are. Hence clocks 0 and 180 have a 66 ns disagreement about the ages of clocks 90 and 270. (And similarly, of course, these statements hold true if we swap the roles of the 0/180 pair with the 90/270 pair.) Now replace these clocks by four satellites at the distance of GPS satellites, but all orbiting in one plane and spaced 90
apart. We require the analogous calculation to (
4). The satellites are each at a distance of
km from Earth’s centre. A satellite’s speed in the ECI is
, where
G is the gravitational constant and
M is Earth’s mass (
SI units). Then, analogous to (
4), we write
From the viewpoint of one such satellite, the other satellites’ clocks are mismatched by up to
. This has no effect on the operation of satellites that use precise timing, because such satellites are synchronised in the ECI. For example, the calculations that a GPS receiver runs to establish its position are ECI calculations. That is, GPS is based on the ECI time of
emission of each satellite signal; it does not use (or even know) the time at each satellite that the receiver says is simultaneous with it receiving a signal.
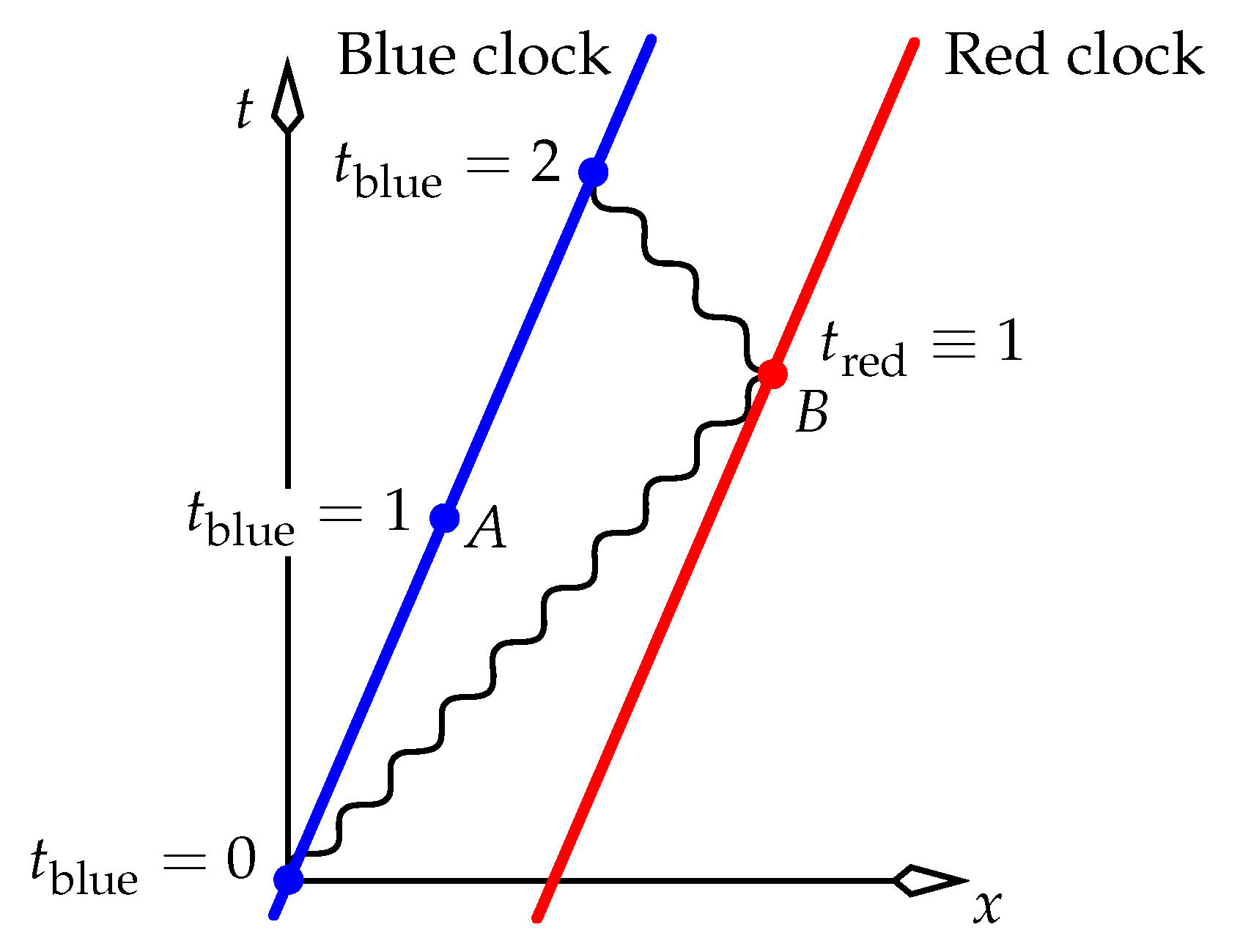
The above values of 33 nanoseconds and 1.1 microseconds refer to the time that one clocks says is displayed “now” on a distant clock. A different question—but one that is more pertinent to two clocks attempting to synchronise—is the extent to which these clocks agree on the meaning of “now”, since this affects their ability to even
define the meaning of the data hand-shake that normally forms part of a synchronisation procedure. To examine how closely two clocks on Earth’s Equator might be able to synchronise in the absence of gravity, we introduce an extra space dimension into the comparison of “nows” in
Figure 3. So we calculate the analogous quantity to what might be called
Figure 3’s “synchronisation disagreement” of 7 p.m. − 5 p.m. = 2 hours. Note that this is a different task than calculating the one-hour time difference between events
A and
B in
Figure 3, or the three-hour difference between events
B and
C. A time difference between two observers has no importance if it’s agreed upon by all (such as in an inertial frame), because they can adjust their clocks to correct for it. It only becomes important when observers have different standards of simultaneity: in that figure, Blue says
B is simultaneous with
A, whereas Red says
B is simultaneous with
C. No amount of clock adjustment can fix things when observers disagree on simultaneity, since then they simply don’t form a frame.
The two clocks on Earth’s Equator—but without gravity in our analysis—can be envisaged as fixed to a planar ring that rotates in an inertial frame: the ECI in this case. The lines of simultaneity in
Figure 3 become planes of simultaneity, such as the one drawn in
Figure 7.
To begin to compare the relative orientations of two such planes, a big simplification can be made.
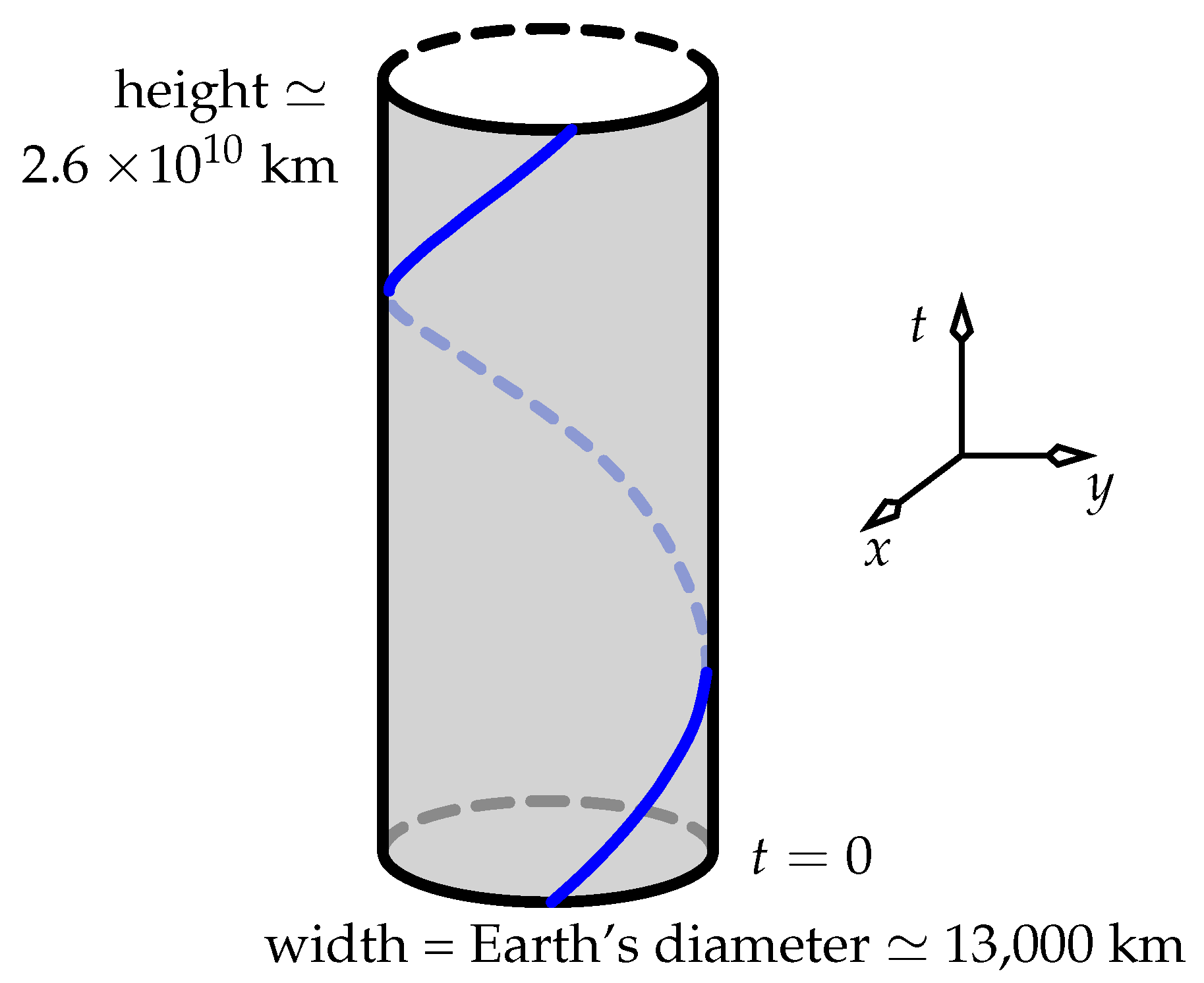
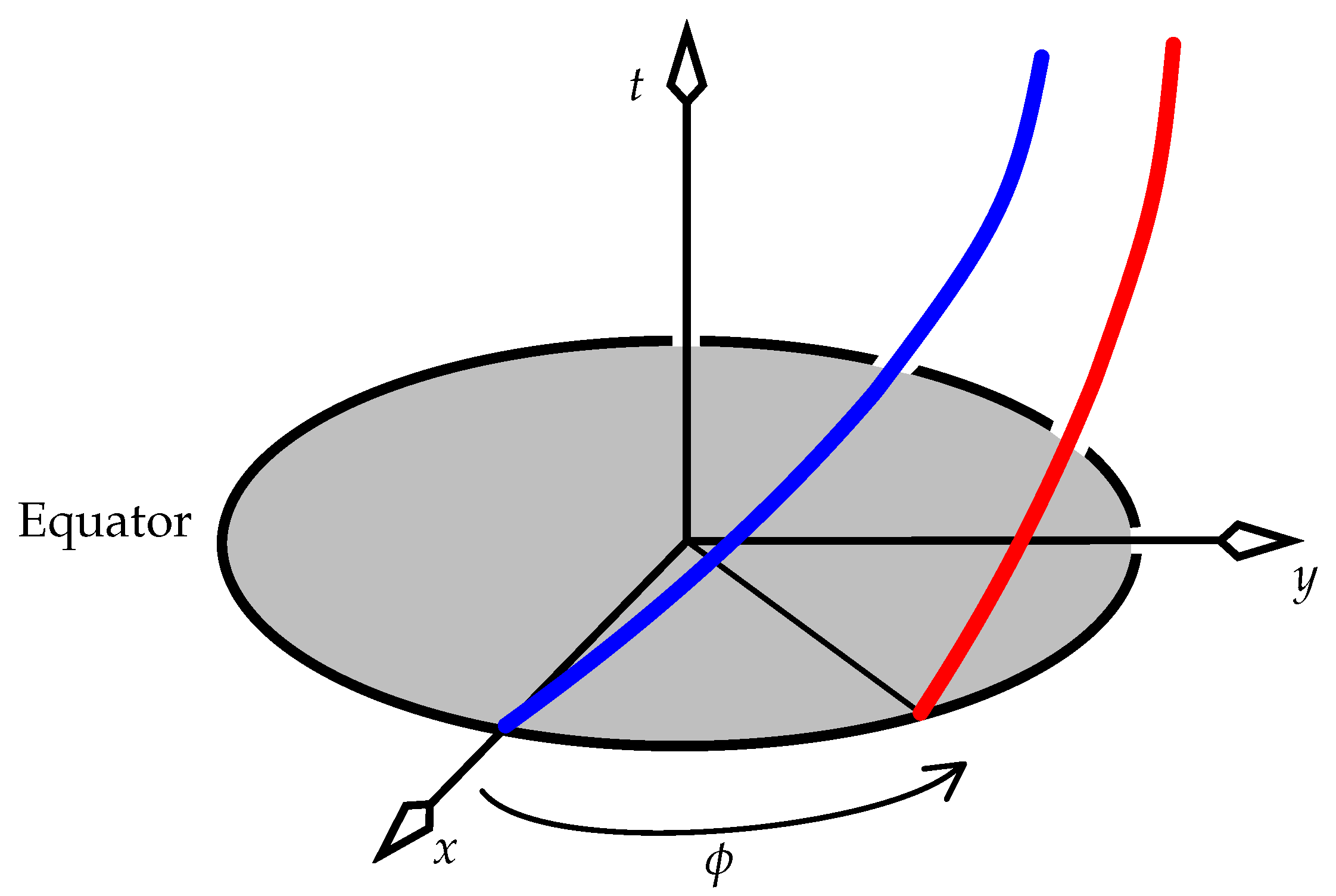
Figure 8 shows the helical world line of a single clock, drawn in the frame of the distant stars over the course of one sidereal day: the time (23 hours 56 minutes) taken by Earth to complete one rotation. The height of the cylinder on which this world line is drawn is
The width of the cylinder is
The cylinder thus has a height-to-diameter ratio of about 2 million. This enables us to approximate the helix as a straight line when analysing sloping planes of simultaneity that encompass a range of ECI times of much less than one day—which is valid here, because (
4) gives typical time increments of tens of nanoseconds at most. (A related analysis that uses the exactly helical world lines that are appropriate for any angular speed appears in [
6]; but it is far more complicated than the discussion here because it relies on the equations of
Section 5, which cannot be solved in terms of standard functions.)
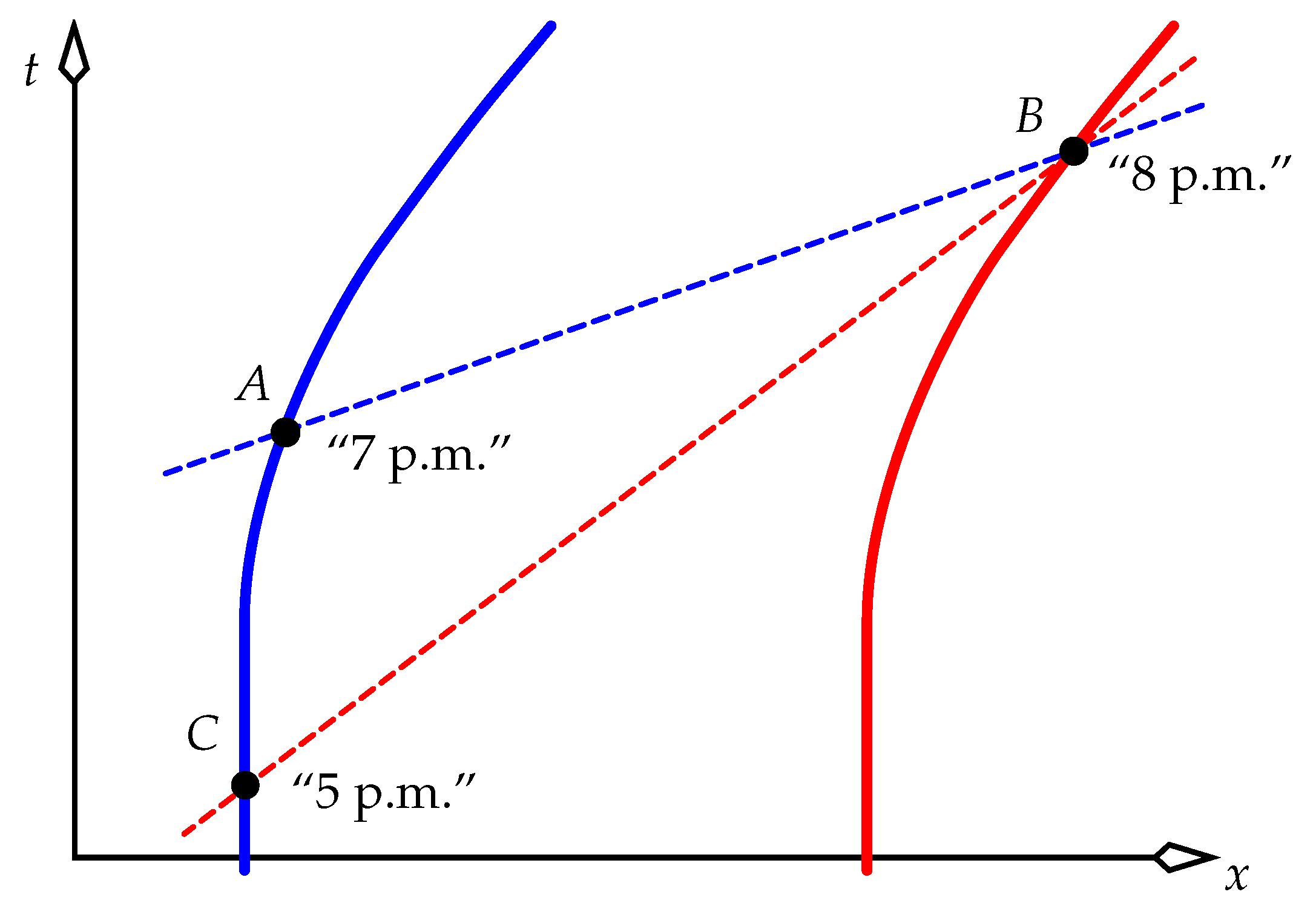
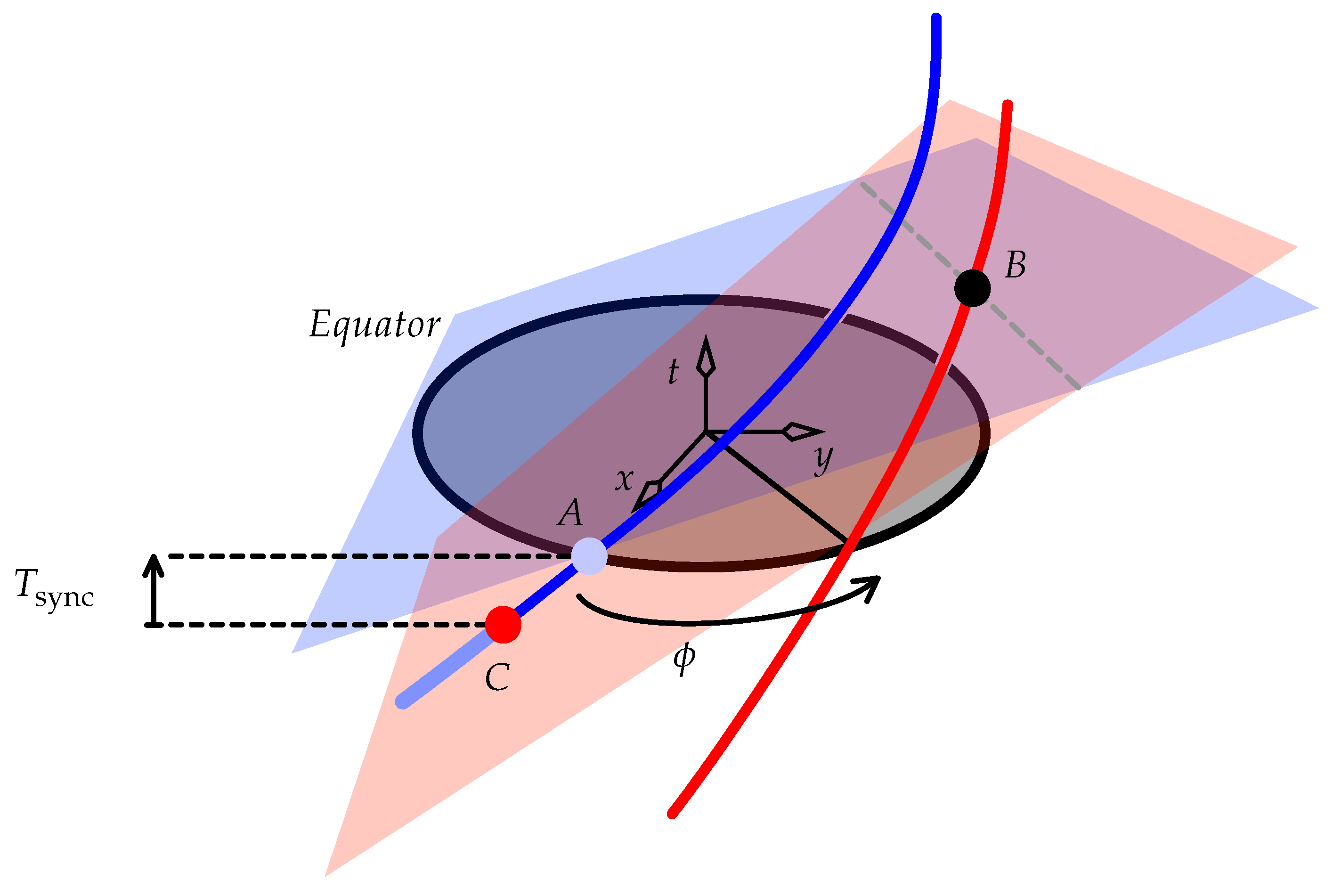
In
Figure 9 consider two clocks, Blue and Red, fixed to the Equator. Blue is at longitude 0, and Red is at longitude
. (We can ignore the tiny change to their perceived angular separation mentioned in
Section 4.1.) Parts of their world lines spanning a small time interval are drawn in
Figure 9 around the time
in the inertial frame of the distant stars. At this time, Blue is on the inertial frame’s
x axis, and its position together with this time define an event
A (analogous to event
A in
Figure 3). At event
A we will do the following (depicted in
Figure 10):
Construct the blue plane of simultaneity of Blue (analogous to the blue dashed line in
Figure 3).
Find the event
B where this blue plane intersects the red world line of Red (analogous to event
B in
Figure 3).
Construct the red plane of simultaneity of Red at event
B (analogous to the red dashed line in
Figure 3).
Find the event
C where this red plane intersects the blue world line of Blue (analogous to event
C in
Figure 3).
The difference between the times of events A and C in the ECI quantifies the extent to which Blue and Red don’t share a common “now”. We will calculate this difference.
In the equations that follow, we analyse the various planes and gradients using the standard 3-component cartesian formalism of vectors that is ubiquitous in three
spatial dimensions. That is, we order the components of coordinate vectors as
, because the
t axis here takes the place of the
z axis in standard geometric analyses of 3-space. The basic tool that we build on is the one-space-dimension picture in
Figure 11. The dashed
line of simultaneity in that figure is where the
plane of simultaneity in two spatial dimensions (
x and
y) cuts the
plane at
, at which moment the world line is in the
plane, as too is the normal to the plane of simultaneity. Using that idea, start with event
A in
Figure 10, which has coordinates (for a ring or Equator of radius
R)
Analogous to the dashed line of simultaneity with slope
v in
Figure 11, the blue plane of simultaneity is the set of the following events:
We must find
B, where this blue plane intersects the red world line. The red world line—approximated by a straight line—is the set of events
where the parameter
takes on all real values, and
is a direction vector of the red world line. This vector is found by rotating any direction vector of the blue world line (
) through angle
right-handed around the
t axis. Start with
Using the shorthand
we have
Hence, from (
10), the red world line has equation
What are the coordinates of event
B where this red world line is cut by the blue plane (
9)? Substituting the expressions for
t and
y from (
14) into “
” gives
Event
B’s coordinates now result from placing this value of
into (
14):
Next, we require the red plane of simultaneity at
B. Because we have approximated the blue and red world lines as straight, the red plane’s normal vector is a rotation by
of the normal to the blue plane of simultaneity. Referring to
Figure 11, start with
Rotate it by
to yield
This red plane thus has equation
The constant
is found by noting that event
B lies on this red plane. Specifically, place
from (
16) into (
19) to yield
Combining (
19) and (
20), the red plane of simultaneity through
B has equation
Last, we find event
C by intersecting this red plane with the blue world line. Referring to (
11), the blue world line has equation
for a parameter
that takes on all real values. Place the
coordinates of this into (
21) to give an expression for
at
C:
It follows that
Hence, (
22) and (
24) give
C’s coordinates as
In particular, the third element of (
25) is the time
of event
C in the inertial frame:
Clearly, for
(which corresponds to Earth’s natural spin) and
,
. Recall from (
8) that
. The difference between the times of events
A and
C for
is called
in
Figure 10. From now, drop the use of the “
” shorthand of (
12).
quantifies the fundamental disagreement in simultaneity or synchronisation for clocks that are a longitude
apart, fixed to a rotating ring of radius
R, and whose speed (in the inertial frame in which the ring’s centre is at rest) is much less than the speed of light, because we approximated the blue and red world lines as straight.
Clocks fixed to Earth’s Equator move at 465 m/s in the ECI. For these,
. Hence
. Equation (
27) becomes
This equation converts to conventional distance–time dimensions by dividing by
, where
c once again denotes the inertial-frame speed of light:
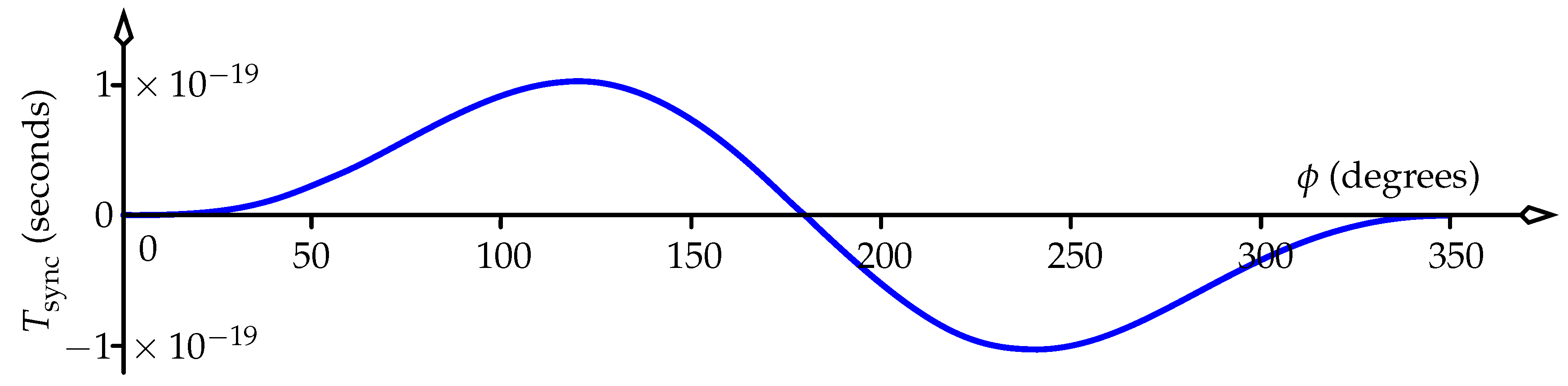
A plot of
versus longitude
is shown in
Figure 12, using a value of
km (Earth’s radius). The maximum value of around
seconds occurs at
, and it drops to zero very quickly as
tends to zero. Indeed, using the small-
approximations
it’s clear that
for small
. Such small values of
lie far beyond the accuracy of current communications technology, and so we conclude that a mismatch in the meaning of “now” will have no effect on any synchronisation handshakes currently being made between clocks on Earth.
The above calculation also applies to two satellites in circular orbits in Earth’s equatorial plane, each at a distance
R from Earth’s centre. What is the value of
for these? Circular motion is sufficient to analyse here, in which case a satellite’s speed in the ECI is
. [Note that the satellites’ world lines can be approximated as straight, as the above calculation demands. Also, their speed is far less than the speed of light, and so (
28) remains a valid approximation to (
27).] Substitute that value of
v into (
29) to yield
GPS satellites lie at a distance of
km from Earth’s centre. Use
SI units and choose the worst-case value of
. Then
For low Earth-orbit satellites (
km), a similar calculation gives a maximum
s.
The above values of
say that clocks fixed to Earth’s surface or on satellites have only a tiny mismatch in what they say is “happening now”. This presumably sets a limit to the efficacy of a handshake between their clocks to attempt a synchronisation procedure. But this analysis should not be construed as saying that two clocks for which
can be synchronised perfectly. For example, for
Figure 7’s Clock 0 and Clock 180 that lie on opposite sides of the Equator (
), (
29) says that
. (This value is easily seen without any mathematics, because the plane of simultaneity of Clock 0 at an ECI time of
in
Figure 7 will intersect the world line of Clock 180 at the same ECI time of
, and vice versa.) Thus events
A and
C in
Figure 10 coincide for clocks 0 and 180. Nonetheless, those clocks do not agree on the time displayed on a clock that is fixed at, say,
. Indeed, as stated in
Section 4.3, clocks 0 and 180 will disagree on the age of Clock 90 by 66 nanoseconds. Nothing can be done to “fix” this: it is inherent in relativity. So even though
is exactly zero for clocks 0 and 180, that only means that they agree on the meaning of “now” at each other’s location; but they disagree at the level of tens of nanoseconds on the simultaneity of events on Earth that are some distance from both of them—and even more so for events far from Earth. But as discussed just after (
5), this has no effect on the operation of GPS, because GPS uses the notion of simultaneity in the ECI, not simultaneity local to each clock.