A Modified Dynamical Model of Cosmology I Theory
Abstract
:1. Introduction
2. A New Model of Modified Dynamics
2.1. Fixing the Gauge and the Boundary Conditions
2.2. Trajectory of Particles
3. Modified Hubble Parameter
4. Cosmic Implications of the New Model
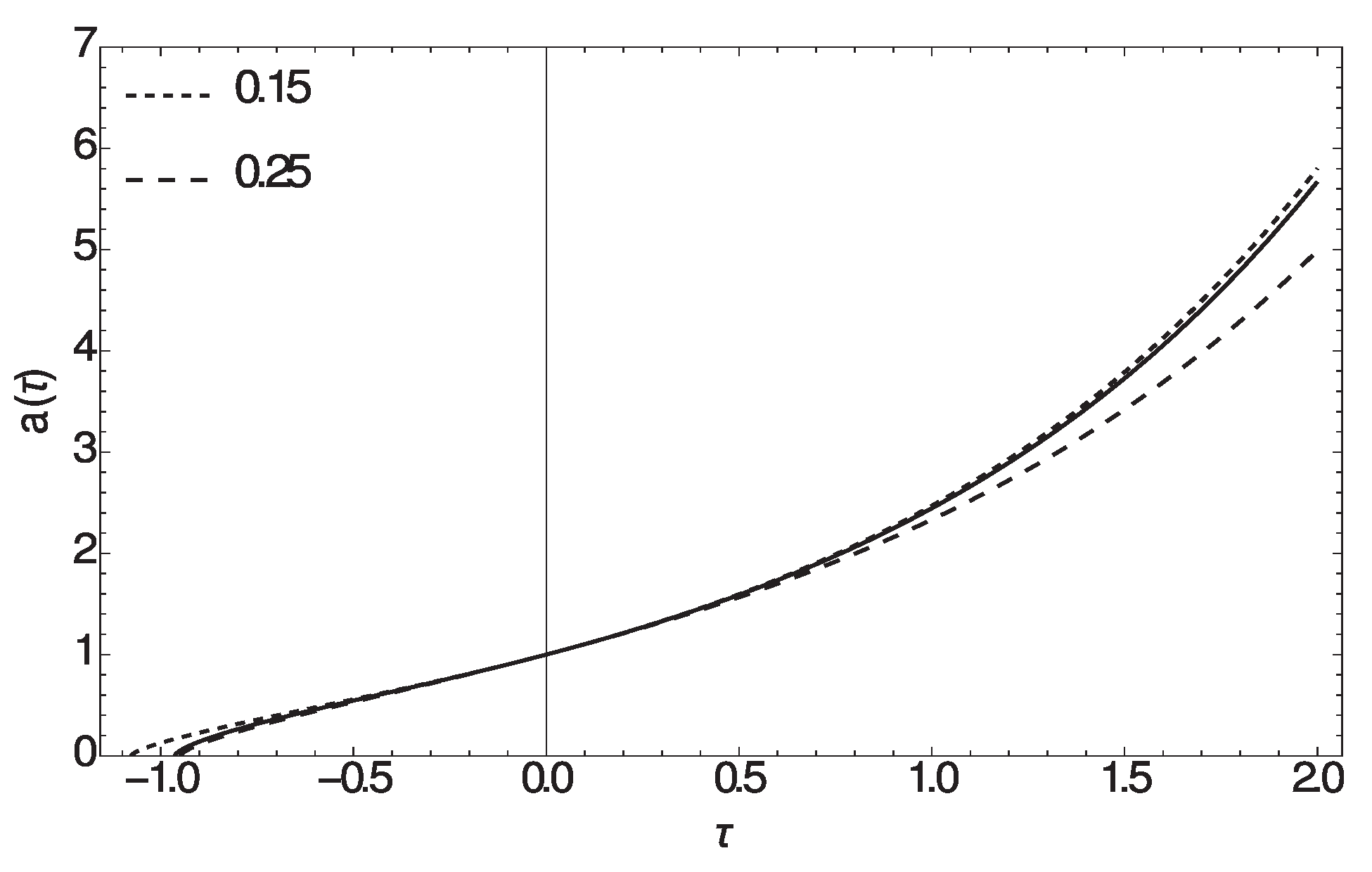
4.1. Evolution of the Scale Factor
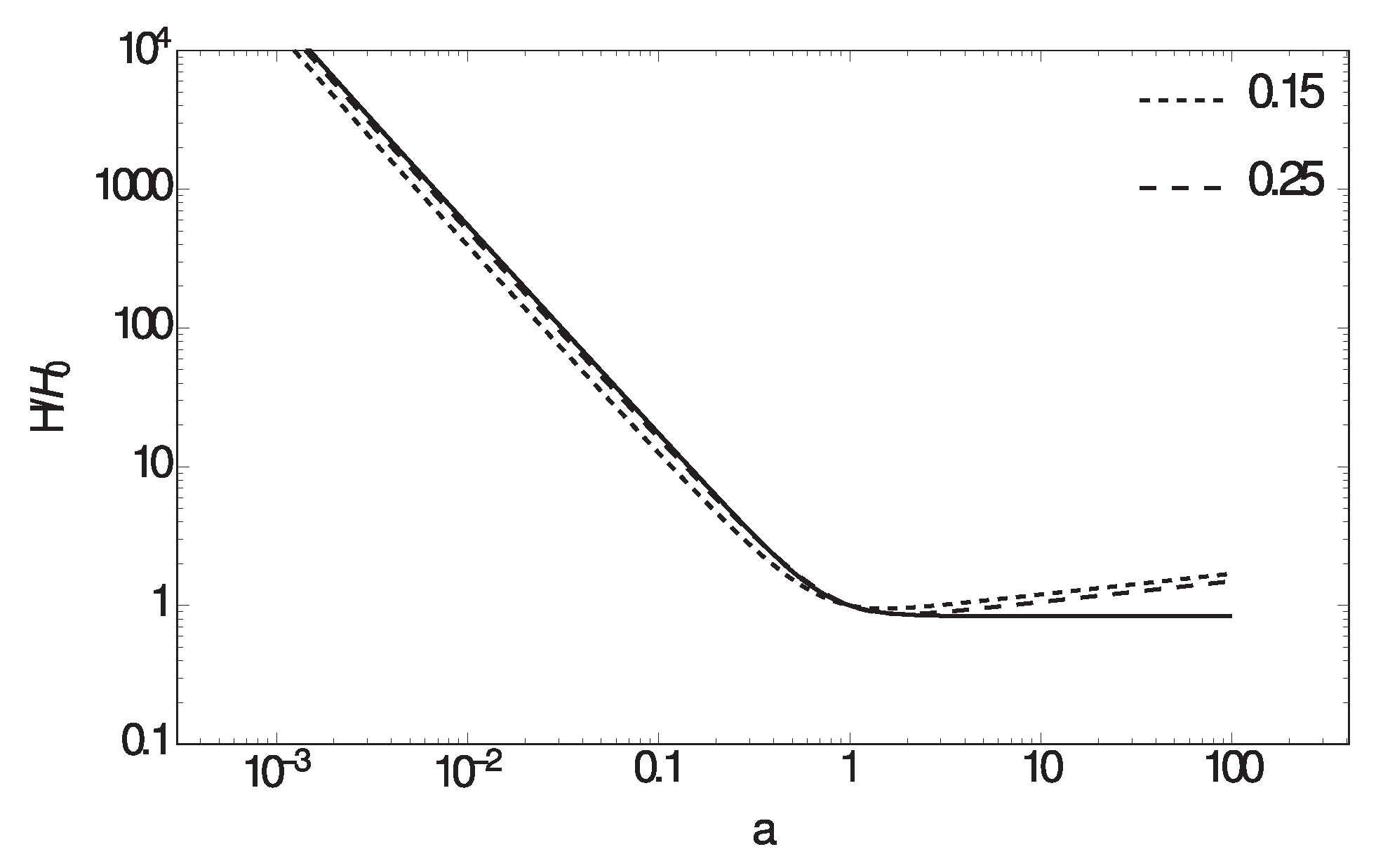
4.2. Hubble and Deceleration Parameter
4.3. Evolution of the Equation of State Parameter and the Sound Speed
4.4. Sequence of the Cosmological Epochs
4.5. Luminosity and Angular Diameter Distances
5. Discussion
5.1. Discussion on the Boundary Condition of GR
5.2. Discussion on Mach’s Principle as Boundary Condition
5.3. Discussion on the Averaging Procedure
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GR | General Relativity |
| PDE | Partial Differential Equation |
| CMB | Cosmic Microwave Background |
| ()CDM | Cold Dark Matter |
| B.C. | Boundary Condition |
| MOND | MOdified Newtonian Dynamics |
| MOD | Modified Dynamics |
| NFW | Navarro, Frenk, and White halo profile |
| SUSY | Supersymmetry |
| EPS | Ehlers, Pirani, and Schild |
| QCD | Quantum Chromodynamics |
| FLRW | Friedmann–Lemaitre–Robertson–Walker |
| YGH | York, Gibbons, and Hawking |
| WIMP | Weakly Interacting Massive Particles |
| MOG | MOdified Gravity |
| SNIa | Supernovae (type) Ia |
Appendix A. Time-Dependent Neumann Parameter
Appendix B. Discussion on the Trajectory of Massive Particles, GR Measurement Process, and the EPS Theorem

Appendix B.1. Trajectory of Massive Particles
| Solar System | Galaxies | Cluster of Galaxies | |
|---|---|---|---|
| 2 | |||
| 0.01 to 10 | 0.001 to 0.1 |

Appendix B.2. The EPS Theorem and the Structure of Spacetime
Appendix C. Discussion on the Dimensional Analysis of the Model
Appendix D. A Semi-Newtonian Model of Gravity: Some Properties and Issues
References
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Peebles, P.J.E.; Ratra, B. The Cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J.M. Gauge Invariant Cosmological Perturbations. Phys. Rev. 1980, D22, 1882–1905. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rept. 1992, 215, 203–333. [Google Scholar] [CrossRef] [Green Version]
- Bruni, M.; Matarrese, S.; Mollerach, S.; Sonego, S. Perturbations of space-time: Gauge transformations and gauge invariance at second order and beyond. Class. Quant. Grav. 1997, 14, 2585–2606. [Google Scholar] [CrossRef] [Green Version]
- Malik, K.A.; Wands, D. Cosmological perturbations. Phys. Rep. 2009, 475, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Sanders, R.H. The Dark Matter Problem; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jain, B.; Khoury, J. Cosmological Tests of Gravity. Ann. Phys. 2010, 325, 1479–1516. [Google Scholar] [CrossRef] [Green Version]
- Bertone, G.; Tait, T.M.P. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amendola, L.; Tsujikawa, S. Dark Energy; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, S. Boundary Terms of the Einstein–Hilbert Action. Fundam. Theor. Phys. 2017, 187, 43–59. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.A. Mach’s principle as boundary condition for Einstein’s equations. In Gravitation and Relativity; NASA Goddard Institute for Space Studies: New York, NY, USA, 1966; pp. 303–349. [Google Scholar]
- Raine, D.J. Mach’s principle and space-time structure. Rep. Prog. Phys. 1981, 44, 1151–1195. [Google Scholar] [CrossRef]
- Barbour, J.B.; Pfister, H. (Eds.) Mach’s Principle: From Newton’s Bucket to Quantum Gravity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Choquet-Bruhat, Y.; York, J.W., Jr. The Cauchy Problem. In General Relativity and Gravitation. Volume 1—One Hundred Years after the Birth of Albert Einstein; Held, A., Ed.; Plenum Press: New York, NY, USA, 1980; p. 99. [Google Scholar]
- Choquet-Bruhat, Y.; Geroch, R.P. Global aspects of the Cauchy problem in general relativity. Commun. Math. Phys. 1969, 14, 329–335. [Google Scholar] [CrossRef]
- Bondi, H.; Samuel, J. The Lense-Thirring effect and Mach’s principle. Phys. Lett. 1997, A228, 121. [Google Scholar] [CrossRef] [Green Version]
- Sciama, D.W.; Waylen, P.C.; Gilman, R.C. Generally covariant integral formulation of einstein’s field equation. Phys. Rev. 1969, 187, 1762–1766. [Google Scholar] [CrossRef]
- Thorne, K.S.; Lee, D.L.; Lightman, A.P. Foundations for a Theory of Gravitation Theories. Phys. Rev. D 1973, 7, 3563–3578. [Google Scholar] [CrossRef] [Green Version]
- Park, I.Y. Boundary dynamics in gravitational theories. arXiv 2018, arXiv:1811.03688. [Google Scholar] [CrossRef] [Green Version]
- Park, I. Foliation-Based Approach to Quantum Gravity and Applications to Astrophysics. Universe 2019, 5, 71. [Google Scholar] [CrossRef] [Green Version]
- Park, I.Y. Foliation-based quantization and black hole information. Class. Quant. Grav. 2017, 34, 245005. [Google Scholar] [CrossRef] [Green Version]
- Witten, E. A Note On Boundary Conditions In Euclidean Gravity. arXiv 2018, arXiv:1805.11559. [Google Scholar]
- Shenavar, H. Imposing Neumann boundary condition on cosmological perturbation equations and trajectories of particles. Astrophys. Space Sci. 2016, 361, 93. [Google Scholar] [CrossRef]
- Shenavar, H. Motion of particles in solar and galactic systems by using Neumann boundary condition. Astrophys. Space Sci. 2016, 361, 378. [Google Scholar] [CrossRef]
- Van Putten, M.H.P.M. Anomalous Galactic Dynamics by Collusion of Rindler and Cosmological Horizons. Astrophys. J. 2017, 837, 22. [Google Scholar] [CrossRef]
- Van Putten, M.H.P.M. Evidence for galaxy dynamics tracing background cosmology below the de Sitter scale of acceleration. Astrophys. J. 2017, 848, 28. [Google Scholar] [CrossRef] [Green Version]
- Milgrom, M. A Modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A Modification of the Newtonian dynamics: Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Rel. 2012, 15, 10. [Google Scholar] [CrossRef] [Green Version]
- Kroupa, P. The dark matter crisis: Falsification of the current standard model of cosmology. Publ. Astron. Soc. Austral. 2012, 29, 395–433. [Google Scholar] [CrossRef] [Green Version]
- Kroupa, P.; Pawlowski, M.; Milgrom, M. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. 2012, D21, 1230003. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S. Recovering a MOND-like acceleration law in mimetic gravity. Class. Quant. Grav. 2017, 34, 185006. [Google Scholar] [CrossRef]
- Rasanen, S. Dark energy from backreaction. JCAP 2004, 0402, 003. [Google Scholar] [CrossRef] [Green Version]
- Hirata, C.M.; Seljak, U. Can superhorizon cosmological perturbations explain the acceleration of the Universe? Phys. Rev. D 2005, 72, 083501. [Google Scholar] [CrossRef] [Green Version]
- Kolb, E.W.; Matarrese, S.; Notari, A.; Riotto, A. The Effect of inhomogeneities on the expansion rate of the universe. Phys. Rev. D 2005, 71, 023524. [Google Scholar] [CrossRef] [Green Version]
- Martineau, P.; Brandenberger, R.H. The Effects of gravitational back-reaction on cosmological perturbations. Phys. Rev. D 2005, 72, 023507. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J. Einstein Gravity from Conformal Gravity. arXiv 2011, arXiv:1105.5632. [Google Scholar]
- Anastasiou, G.; Olea, R. From conformal to Einstein Gravity. Phys. Rev. D 2016, 94, 086008. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, C.; Raju, A. A Neumann Boundary Term for Gravity. Mod. Phys. Lett. A 2017, 32, 1750077. [Google Scholar] [CrossRef] [Green Version]
- Ehlers, J.; Pirani, F.A.; Schild, A. Republication of: The geometry of free fall and light propagation. Gen. Relat. Grav. 2012, 44, 1587–1609. [Google Scholar] [CrossRef]
- Cai, R.G.; Tuo, Z.L.; Zhang, H.B.; Su, Q. Notes on Ghost Dark Energy. Phys. Rev. D 2011, 84, 123501. [Google Scholar] [CrossRef] [Green Version]
- Cai, R.G.; Tuo, Z.L.; Wu, Y.B.; Zhao, Y.Y. More on QCD Ghost Dark Energy. Phys. Rev. D 2012, 86, 023511. [Google Scholar] [CrossRef] [Green Version]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef] [Green Version]
- Scherrer, R.J. Purely kinetic k-essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef] [Green Version]
- Fukuyama, T.; Morikawa, M.; Tatekawa, T. Cosmic structures via Bose Einstein condensation and its collapse. JCAP 2008, 0806, 033. [Google Scholar] [CrossRef] [Green Version]
- Moffat, J.W. Scalar-tensor-vector gravity theory. JCAP 2006, 0603, 004. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Uzan, J.P. Causal structures in inflation. C. R. Phys. 2015, 16, 928–947. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological hints of modified gravity? Phys. Rev. D 2016, 93, 023513. [Google Scholar] [CrossRef] [Green Version]
- Shenavar, H.; Ghafourian, N. Local stability of galactic discs in modified dynamics. Mon. Not. R. Astron. Soc. 2018, 475, 5603–5617. [Google Scholar] [CrossRef]
- Pyne, T.; Birkinshaw, M. Beyond the thin lens approximation. Astrophys. J. 1996, 458, 46. [Google Scholar] [CrossRef] [Green Version]
- Pyne, T.; Carroll, S.M. Higher order gravitational perturbations of the cosmic microwave background. Phys. Rev. D 1996, D53, 2920–2929. [Google Scholar] [CrossRef] [Green Version]
- Ohanian, H. Gravitation and Spacetime; W. W. Norton: New York, NY, USA, 1976. [Google Scholar]
- Jacobs, M.W.; Linder, E.V.; Wagoner, R.V. Obtaining the metric of our Universe. Phys. Rev. D 1992, 45, R3292. [Google Scholar] [CrossRef]
- Zalaletdinov, R.M. Averaging out the Einstein equations and macroscopic space-time geometry. Gen. Relat. Grav. 1992, 24, 1015–1031. [Google Scholar] [CrossRef]
- Zalaletdinov, R. Towards a theory of macroscopic gravity. Gen. Rel. Grav. 1993, 25, 673–695. [Google Scholar] [CrossRef]
- Bagheri, S.; Schwarz, D.J. Light propagation in the averaged universe. J. Cosmol. Astropart. Phys. 2014, 1410, 073. [Google Scholar] [CrossRef] [Green Version]
- Overduin, J.M.; Cooperstock, F.I. Evolution of the scale factor with a variable cosmological term. Phys. Rev. D 1998, 58, 043506. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Dhawan, S.; Gerbino, M.; Freese, K.; Goobar, A.; Mena, O. Constraints on the sum of the neutrino masses in dynamical dark energy models with w(z) ≥ −1 are tighter than those obtained in ΛCDM. Phys. Rev. D 2018, 98, 083501. [Google Scholar] [CrossRef] [Green Version]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef] [Green Version]
- Jamali, S.; Roshan, M. The phase space analysis of modified gravity (MOG). Eur. Phys. J. C 2016, 76, 490. [Google Scholar] [CrossRef] [Green Version]
- Jamali, S.; Roshan, M.; Amendola, L. On the cosmology of scalar-tensor-vector gravity theory. J. Cosmol. Astropart. Phys. 2018, 1801, 048. [Google Scholar] [CrossRef] [Green Version]
- Balakrishna Subramani, V.; Kroupa, P.; Shenavar, H.; Muralidhara, V. Pseudo-evolution of galaxies in Λ CDM cosmology. Mon. Not. R. Astron. Soc. 2019, 488, 3876–3883. [Google Scholar] [CrossRef]
- Gurvits, L.I.; Kellermann, K.I.; Frey, S. The “angular size—Redshift” relation for compact radio structures in quasars and radio galaxies. Astron. Astrophys. 1999, 342, 378. [Google Scholar]
- Realdi, M.; Peruzzi, G. Einstein, de Sitter and the beginning of relativistic cosmology in 1917. Gen. Relat. Grav. 2009, 41, 225–247. [Google Scholar] [CrossRef]
- York, J.W., Jr. Role of conformal three geometry in the dynamics of gravitation. Phys. Rev. Lett. 1972, 28, 1082–1085. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action Integrals and Partition Functions in Quantum Gravity. Phys. Rev. D 1977, 15, 2752–2756. [Google Scholar] [CrossRef]
- Charap, J.M.; Nelson, J.E. Surface Integrals and the Gravitational Action. J. Phys. A 1983, 16, 1661. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Tully, R.B.; Shaya, E.J. A Dynamical Model of the Local Group. arXiv 2011, arXiv:1105.5596. [Google Scholar]
- Peebles, P. Dynamics of the Local Group: The Dwarf Galaxies. arXiv 2017, arXiv:1705.10683. [Google Scholar]
- Gourgoulhon, E. 3+ 1 Formalism in General Relativity: Bases of Numerical Relativity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 846. [Google Scholar]
- Arnowitt, R.L.; Deser, S.; Misner, C.W. The Dynamics of general relativity. Gen. Relat. Grav. 2008, 40, 1997–2027. [Google Scholar] [CrossRef] [Green Version]
- Kidder, L.E.; Lindblom, L.; Scheel, M.A.; Buchman, L.T.; Pfeiffer, H.P. Boundary conditions for the Einstein evolution system. Phys. Rev. D 2005, 71, 064020. [Google Scholar] [CrossRef] [Green Version]
- Szilagyi, B.; Gomez, R.; Bishop, N.T.; Winicour, J. Cauchy boundaries in linearized gravitational theory. Phys. Rev. D 2000, 62, 104006. [Google Scholar] [CrossRef] [Green Version]
- Brill, D.R. Observational contacts of general relativity. In Relativity, Astrophysics and Cosmology, Volume 38: Astrophysics and Space Science Library; Israel, W., Ed.; Springer: Dordrecht, The Netherland, 1973; pp. 127–152. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Weinberg, S. Adiabatic modes in cosmology. Phys. Rev. D 2003, 67, 123504. [Google Scholar] [CrossRef] [Green Version]
- Akhshik, M.; Firouzjahi, H.; Jazayeri, S. Cosmological Perturbations and the Weinberg Theorem. J. Cosmol. Astropart. Phys. 2015, 1512, 027. [Google Scholar] [CrossRef] [Green Version]
- Gasperini, M.; Marozzi, G.; Nugier, F.; Veneziano, G. Light-cone averaging in cosmology: Formalism and applications. J. Cosmol. Astropart. Phys. 2011, 1107, 008. [Google Scholar] [CrossRef] [Green Version]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of cold dark matter halos. Astrophys. J. 1996, 462, 563–575. [Google Scholar] [CrossRef] [Green Version]
- Dicke, R.H.; Peebles, P.J.E. Evolution of the Solar System and the Expansion of the Universe. Phys. Rev. Lett. 1964, 12, 435. [Google Scholar] [CrossRef]
- Pachner, J. Mach’s Principle in Classical and Relativistic Physics. Phys. Rev. 1963, 132, 1837–1842. [Google Scholar] [CrossRef]
- Pachner, J. Problem of Energy in an Expanding Universe. Phys. Rev. B 1965, 137, 1379. [Google Scholar] [CrossRef]
- Marzke, R.F.; Wheeler, J.A. Gravitation as geometry. I: The geometry of space-time and the geometrodynamical standard meter. In Gravitation and Relativity; WA Benjamin: New York, NY, USA, 1964; pp. 40–64. [Google Scholar]
- Ehlers, J. Survey of general relativity theory. In Relativity, Astrophysics and Cosmology; Springer: Berlin/Heidelberg, Germany, 1973; pp. 1–125. [Google Scholar]
- Kundt, W.; Hoffmann, B. Determination of gravitational standard time. In Recent Developments in General Relativity; Pergamon Press: New York, NY, USA, 1962; p. 303. [Google Scholar]
- Desloge, E.A. A simple variation of the Marzke-Wheeler clock. Gen. Relat. Grav. 1989, 21, 677–681. [Google Scholar] [CrossRef]
- Trautman, A. Editorial note to: J. Ehlers, F. A. E. Pirani and A. Schild, The geometry of free fall and light propagation. Gen. Relat. Grav. 2012, 44, 1581–1586. [Google Scholar] [CrossRef] [Green Version]
- Dodelson, S. Modern Cosmology; Academic Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Sofue, Y. Radial distributions of surface mass density and mass-to-luminosity ratio in spiral galaxies. Publ. Astron. Soc. Jpn. 2018, 70, 31. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation curve decomposition for size-mass relations of bulge, disk, and dark halo components in spiral galaxies. Publ. Astron. Soc. Jpn. 2016, 68, 2. [Google Scholar] [CrossRef] [Green Version]
- Pilyugin, L.S.; Grebel, E.K.; Zinchenko, I.A.; Kniazev, A.Y. The Abundance Properties of Nearby Late-Type Galaxies. II. the Relation between Abundance Distributions and Surface Brightness Profiles. Astron. J. 2014, 148, 134. [Google Scholar] [CrossRef] [Green Version]
- Courteau, S. Deep r-Band Photometry for Northern Spiral Galaxies. Astrophys. J. Suppl. Ser. 1996, 103, 363. [Google Scholar] [CrossRef]
- Courteau, S. Optical Rotation Curves and Linewidths for Tully-Fisher Applications. Astron. J. 1997, 114, 2402. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Dirac, P.A.M. New basis for cosmology. Proc. R. Soc. Lond. A 1938, 165, 199–208. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Gravitation and Cosmology; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schücking, E.L. Cosmology. In Relativity Theory and Astrophysics. Vol.1: Relativity and Cosmology; Ehlers, J., Ed.; American Mathematical Society: Providence, RI, USA, 1967; p. 218. [Google Scholar]
- Benisty, D.; Guendelman, E.I. Homogeneity of the universe emerging from the Equivalence Principle and Poisson equation: A comparison between Newtonian and MONDian cosmology. arXiv 2019, arXiv:1902.06511. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shenavar, H.; Javidan, K. A Modified Dynamical Model of Cosmology I Theory. Universe 2020, 6, 1. https://doi.org/10.3390/universe6010001
Shenavar H, Javidan K. A Modified Dynamical Model of Cosmology I Theory. Universe. 2020; 6(1):1. https://doi.org/10.3390/universe6010001
Chicago/Turabian StyleShenavar, Hossein, and Kurosh Javidan. 2020. "A Modified Dynamical Model of Cosmology I Theory" Universe 6, no. 1: 1. https://doi.org/10.3390/universe6010001
APA StyleShenavar, H., & Javidan, K. (2020). A Modified Dynamical Model of Cosmology I Theory. Universe, 6(1), 1. https://doi.org/10.3390/universe6010001





