Chiralspin Symmetry and Its Implications for QCD ^†

Abstract

In a local gauge-invariant theory with massless Dirac fermions, a symmetry of the Lorentz-invariant fermion charge is larger than a symmetry of the Lagrangian as a whole. While the Dirac Lagrangian exhibits only a chiral symmetry, the fermion charge operator is invariant under a larger symmetry group, $SU(2N_F)$, that includes chiral transformations as well as $SU{(2)}_{CS}$ chiralspin transformations that mix the right- and left-handed components of fermions. Consequently, a symmetry of the electric interaction, which is driven by the charge density, is larger than a symmetry of the magnetic interaction and of the kinetic term. This allows separating in some situations electric and magnetic contributions. In particular, in QCD, the chromo-magnetic interaction contributes only to the near-zero modes of the Dirac operator, while confining chromo-electric interaction contributes to all modes. At high temperatures, above the chiral restoration crossover, QCD exhibits approximate $SU{(2)}_{CS}$ and $SU(2N_F)$ symmetries that are incompatible with free deconfined quarks. Consequently, elementary objects in QCD in this regime are quarks with a definite chirality bound by the chromo-electric field, without the chromo-magnetic effects. In this regime, QCD can be described as a stringy fluid.

1. Introduction

Here, we review recent developments related to discovery of a new hidden symmetry in QCD—the chiralspin symmetry [1,2]. The chiralspin symmetry, while not a symmetry of the Dirac Lagrangian, is a symmetry of the Lorentz-invariant fermion charge. It allows separating in some situations electric and magnetic contributions. This has nontrivial implications on mechanism of hadron mass generation and on nature of the QCD matter at high temperatures.

2. Chiralspin Symmetry

The Dirac Lagrangian with $N_F$ massless flavors

$$\mathcal{L}=i\overline{\psi }{\gamma }_{\mu }{\partial }^{\mu }\psi =i{\overline{\psi }}_L{\gamma }_{\mu }{\partial }^{\mu }{\psi }_L+i{\overline{\psi }}_R{\gamma }_{\mu }{\partial }^{\mu }{\psi }_R,$$

(1)

where

$${\psi }_R=\frac{1}{2}\left(1+{\gamma }_5\right)\psi ,{\psi }_L=\frac{1}{2}\left(1-{\gamma }_5\right)\psi ,$$

(2)

is chirally symmetric

$$SU{(N_F)}_L\times SU{(N_F)}_R\times U{(1)}_A\times U{(1)}_V.$$

(3)

The fermion charge, which is Lorentz-invariant,

$$Q=\int d^{3}x\overline{\psi }(x){\gamma }_0\psi (x)=\int d^{3}x{\psi }^{†}(x)\psi (x)$$

(4)

is invariant with respect to any unitary transformation that can be defined in the Dirac spinor space. Previously known unitary transformations are those which leave the Dirac Lagrangian invariant:

$$SU(N_c),U{(N_F)}_L\times U{(N_F)}_R.$$

(5)

A new unitary transformation of Dirac spinors has recently been found [1,2]. It is a $SU(2)$ chiralspin (CS) transformation. The $SU{(2)}_{CS}$ chiralspin transformation and its generators ${\Sigma }^n$, $n=1,2,3$, are:

$$\psi \to {\psi }^{\prime }=exp\left(i\frac{{\epsilon }^n{\Sigma }^n}{2}\right)\psi ,$$

(6)

$${\Sigma }^n=\{{\gamma }_k,-i{\gamma }_5{\gamma }_k,{\gamma }_5\},$$

(7)

where ${\gamma }_k$ is any Hermitian Euclidean gamma-matrix:

$${\gamma }_i{\gamma }_j+{\gamma }_j{\gamma }_i=2{\delta }^{ij};{\gamma }_5={\gamma }_1{\gamma }_2{\gamma }_3{\gamma }_4.$$

(8)

The $su(2)$ algebra

$$[{\Sigma }^a,{\Sigma }^b]=2i{ϵ}^{abc}{\Sigma }^c$$

(9)

is satisfied with any $k=1,2,3,4$.

The $U{(1)}_A$ chiral symmetry is a subgroup of $SU{(2)}_{CS}$. The free massless Dirac Lagrangian is not invariant under the $SU{(2)}_{CS}$ chiralspin transformation. However, it is a symmetry of the fermion charge. The fermion charge has a larger symmetry than the Dirac equation.

The chiralspin transformations and generators can be presented in an equivalent form. With $k=4$, they are

$${\Sigma }^n=\{\mathbb{1}\otimes {\sigma }^1,\mathbb{1}\otimes {\sigma }^2,\mathbb{1}\otimes {\sigma }^3\}.$$

(10)

Here, the Pauli matrices ${\sigma }^i$ act in the space of spinors

$$\left(\begin{array}{c}R\\ L\end{array}\right),$$

(11)

where R and L represent the upper and lower components of the right- and left-handed Dirac bispinors (Equation (2)). The $SU{(2)}_{CS},k=4$ transformation can then be rewritten as

$$\psi \to {\psi }^{\prime }=exp\left(i\frac{{\epsilon }^n{\Sigma }^n}{2}\right)\psi =exp\left(i\frac{{\epsilon }^n{\sigma }^n}{2}\right)\left(\begin{array}{c}R\\ L\end{array}\right).$$

(12)

A fundamental irreducible representation of $SU{(2)}_{CS}$ is two-dimensional and the $SU{(2)}_{CS}$ transformations mix the R and L components of fermions.

An extension of the direct $SU{(2)}_{CS}\times SU(N_F)$ product leads to a $SU(2N_F)$ group. This group contains the chiral symmetry $SU{(N_F)}_L\times SU{(N_F)}_R\times U{(1)}_A$ as a subgroup. Its transformations are given by

$$\psi \to {\psi }^{\prime }=exp\left(i\frac{{ϵ}^m{T}^m}{2}\right)\psi ,$$

(13)

where $m=1,2,\dots ,{(2N_F)}^2-1$ and the set of ${(2N_F)}^2-1$ generators is

$$\begin{array}{c}\hfill T^m=\{({\tau }^a\otimes {\mathbb{1}}_D),({\mathbb{1}}_F\otimes {\Sigma }^n),({\tau }^a\otimes {\Sigma }^n)\}\end{array}$$

(14)

where $\tau$ is the flavor generators with the flavor index a and $n=1,2,3$ the $SU{(2)}_{CS}$ index. $SU(2N_F)$ is also a symmetry of the fermion charge, while not a symmetry of the Dirac equation.

The fundamental vector of $SU(2N_F)$ at $N_F=2$ is

$$\mathsf{\Psi }=\left(\begin{array}{c}{u}_R\\ u_L\\ d_R\\ d_L\end{array}\right).$$

(15)

The $SU(2N_F)$ transformations mix both flavor and chirality.

3. Symmetries of the QCD Action

Interaction of quarks with the gluon field in Minkowski space-time can be split into temporal and spatial parts:

$$\overline{\psi }{\gamma }^{\mu }{D}_{\mu }\psi =\overline{\psi }{\gamma }^0{D}_0\psi +\overline{\psi }{\gamma }^i{D}_i\psi ,$$

(16)

where $D_{\mu }$ is a covariant derivative that includes interaction of the matter field $\psi$ with the gauge field ${\mathit{A}}_{\mu }$,

$$D_{\mu }\psi =({\partial }_{\mu }-ig\frac{\mathit{t}·{\mathit{A}}_{\mu }}{2})\psi .$$

(17)

The temporal term includes an interaction of the color-octet charge density

$$\overline{\psi }(x){\gamma }^0\frac{\mathit{t}}{2}\psi (x)=\psi {(x)}^{†}\frac{\mathit{t}}{2}\psi (x)$$

(18)

with the chromo-electric part of the gluonic field. It is invariant under $SU{(2)}_{CS}$ and $SU(2N_F)$ [2]. The spatial part contains a quark kinetic term and interaction with the chromo-magnetic field. It breaks $SU{(2)}_{CS}$ and $SU(2N_F)$. We conclude that interaction of electric and magnetic components of the gauge field with fermions can be distinguished by symmetry. Such a distinction does not exist if the matter field is Bosonic, because a symmetry of the Klein–Gordon Lagrangian and of charge of the $J=0$ field is the same.

Of course, to discuss the notions “electric” and “magnetic”, one needs to fix the reference frame. An invariant mass of the hadron is by definition the rest frame energy. Consequently, to discuss physics of hadron mass generation, it is natural to use the hadron rest frame.

At high temperatures, the Lorentz invariance is broken and again a natural frame to discuss physics is the medium rest frame.

The quark chemical potential term $\mu \psi {(x)}^{†}\psi (x)$ in the Euclidean QCD action

$$S={\int }_0^{\beta }d\tau \int d^{3}x\overline{\psi }[{\gamma }_{\mu }{D}_{\mu }+\mu {\gamma }_4+m]\psi ,$$

(19)

is $SU{(2)}_{CS}$ and $SU(2N_F)$ invariant [3].

4. Observation of the Chiralspin Symmetry

New symmetries presented above were actually reconstructed [1] from lattice results on meson spectroscopy upon artificial subtraction of the near-zero modes of the Dirac operator from quark propagators [4]. An initial idea of these lattice experiments on low-mode truncation was to see whether hadrons survive an artificial restoration of chiral symmetry [5].

It is known that the quark condensate of the vacuum, an order parameter of chiral symmetry, is connected with the density of the near-zero modes of the Euclidean Dirac operator via the Banks–Casher relation [6]

$$<\overline{q}q>=-\pi \rho (0).$$

(20)

The hermitian Euclidean Dirac operator, $i{\gamma }_{\mu }{D}_{\mu }$, has in a finite volume V a discrete spectrum with real eigenvalues ${\lambda }_n$:

$$i{\gamma }_{\mu }{D}_{\mu }{\psi }_n(x)={\lambda }_n{\psi }_n(x).$$

(21)

Consequently, removing by hands the lowest lying modes of the Dirac operator from the quark propagators,

$$S=S_{Full}-\sum _{i=1}^k\frac{1}{{\lambda }_i}|{\lambda }_i⟩⟨{\lambda }_i|,$$

(22)

one artificially restores the chiral symmetry. This truncation of the near-zero modes makes the theory nonlocal, but it is not a big problem.

Hadron masses are extracted from the asymptotic slope of the rest frame t-direction Euclidean correlator

$$C_{\Gamma }(n_t)=\sum _{n_x,n_y,n_z}⟨{\mathcal{O}}_{\Gamma }(n_x,n_y,n_z,n_t){\mathcal{O}}_{\Gamma }{(\mathbf{0},0)}^{†}⟩,$$

(23)

where ${\mathcal{O}}_{\Gamma }(n_x,n_y,n_z,n_t)$ is an operator (see Figure 1) that creates a quark-antiquark pair with fixed quantum numbers. A priori, it was not clear whether hadrons would survive the above truncation. If they would, then one should expect a clean exponential decay of the Euclidean correlation functions.

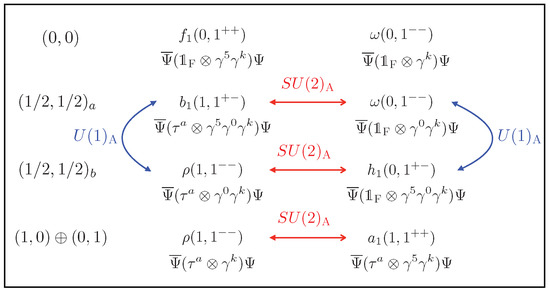
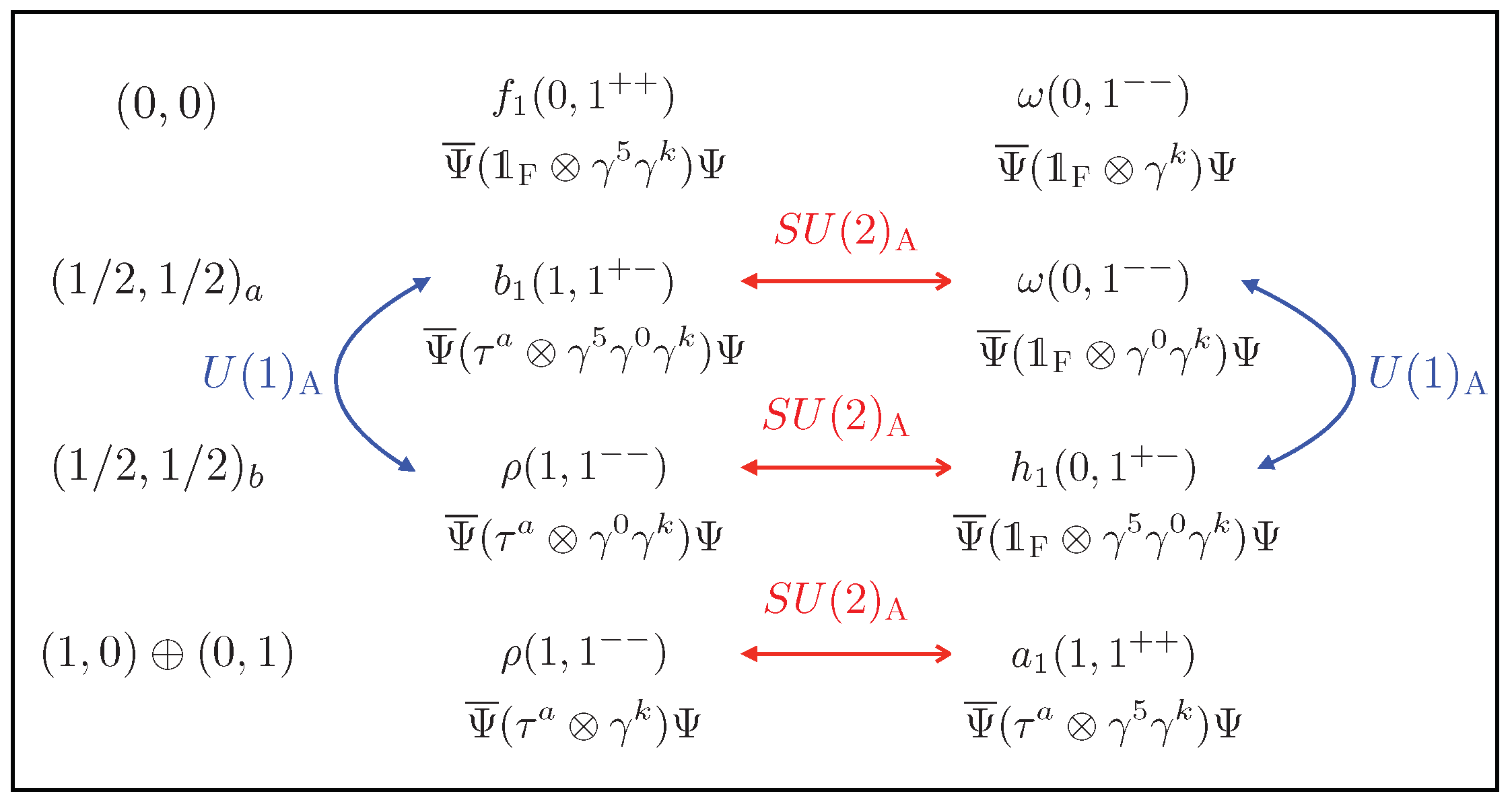
Figure 1. $SU{(2)}_L\times SU{(2)}_R$ classification of the $J=1$ meson operators. Operators that are connected by the $SU{(2)}_L\times SU{(2)}_R$ and $U{(1)}_A$ transformations are linked by the red and blue arrows, respectively. The figure is from Ref. [2].

A complete set of $J=1$ local meson operators for $N_F=2$ QCD is given in Figure 1.

The red arrows connect operators that transform into each other upon chiral $SU{(2)}_L\times SU{(2)}_R$. If hadrons survive the artificial chiral restoration, then mesons that are connected by the red arrows should be degenerate. If in addition the $U{(1)}_A$ symmetry is restored after low mode truncation, then there should be a degeneracy of mesons connected by the blue arrows. Consequently, from the symmetry of the QCD Lagrangian, one can expect degeneracy of mesons connected by the red and blue arrows. Beyond these arrows, there should be no degeneracy.

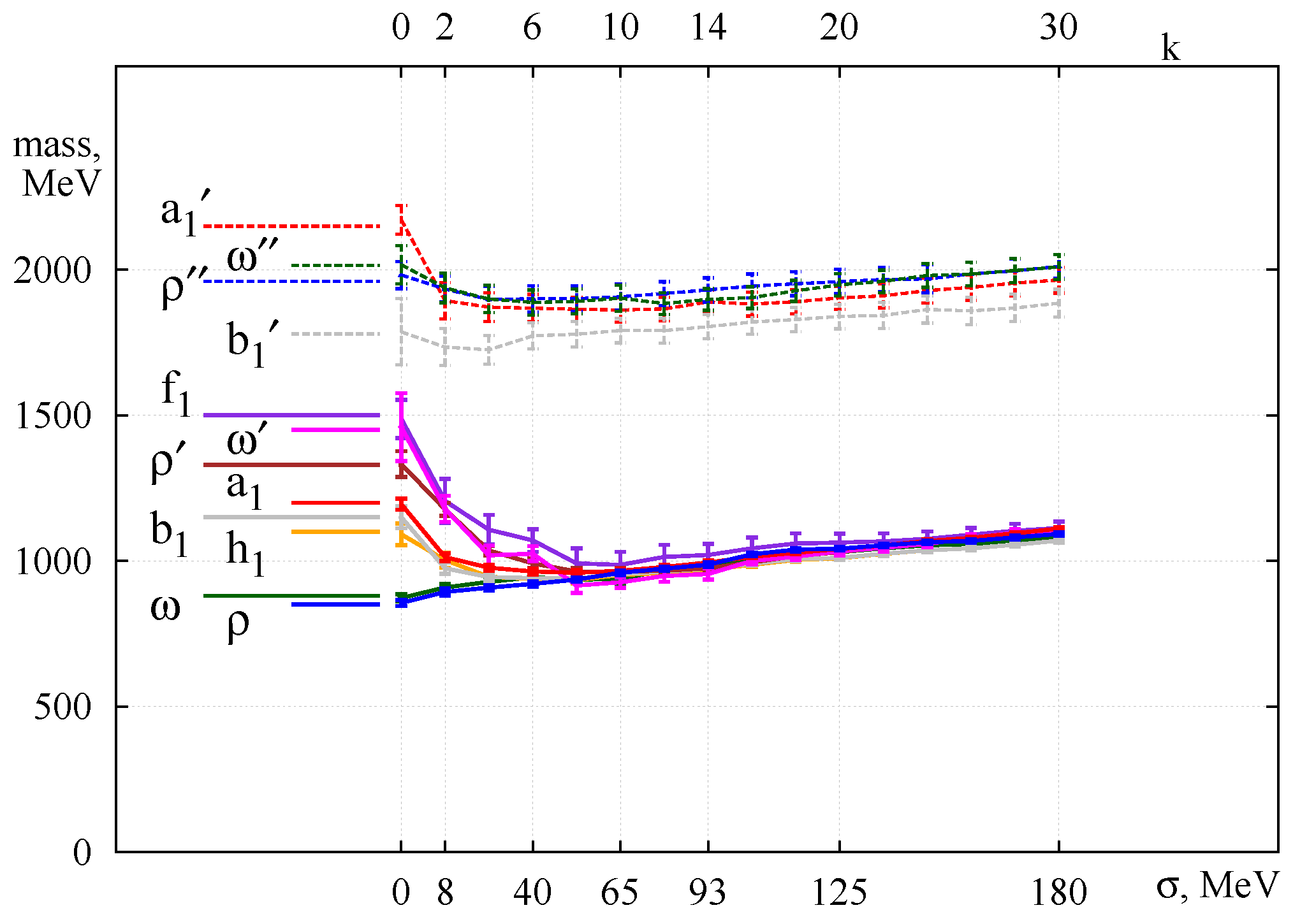
It was a big surprise when a larger degeneracy than the $SU{(2)}_L\times SU{(2)}_R\times U{(1)}_A$ symmetry of the QCD Lagrangian was found in actual lattice measurements [4,7] (see Figure 2).

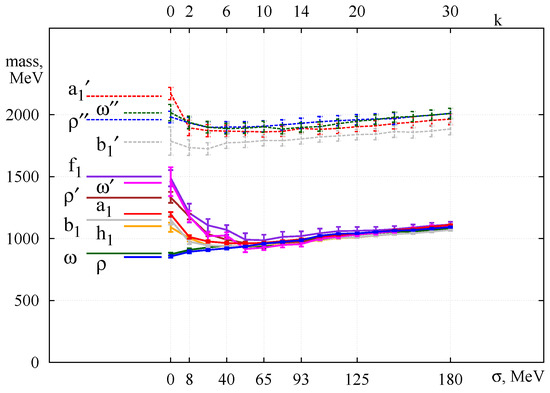
Figure 2. $J=1$ meson mass evolution as a function of the truncation number k. $\sigma$ shows the energy gap in the Dirac spectrum. The figure is from Ref. [7].

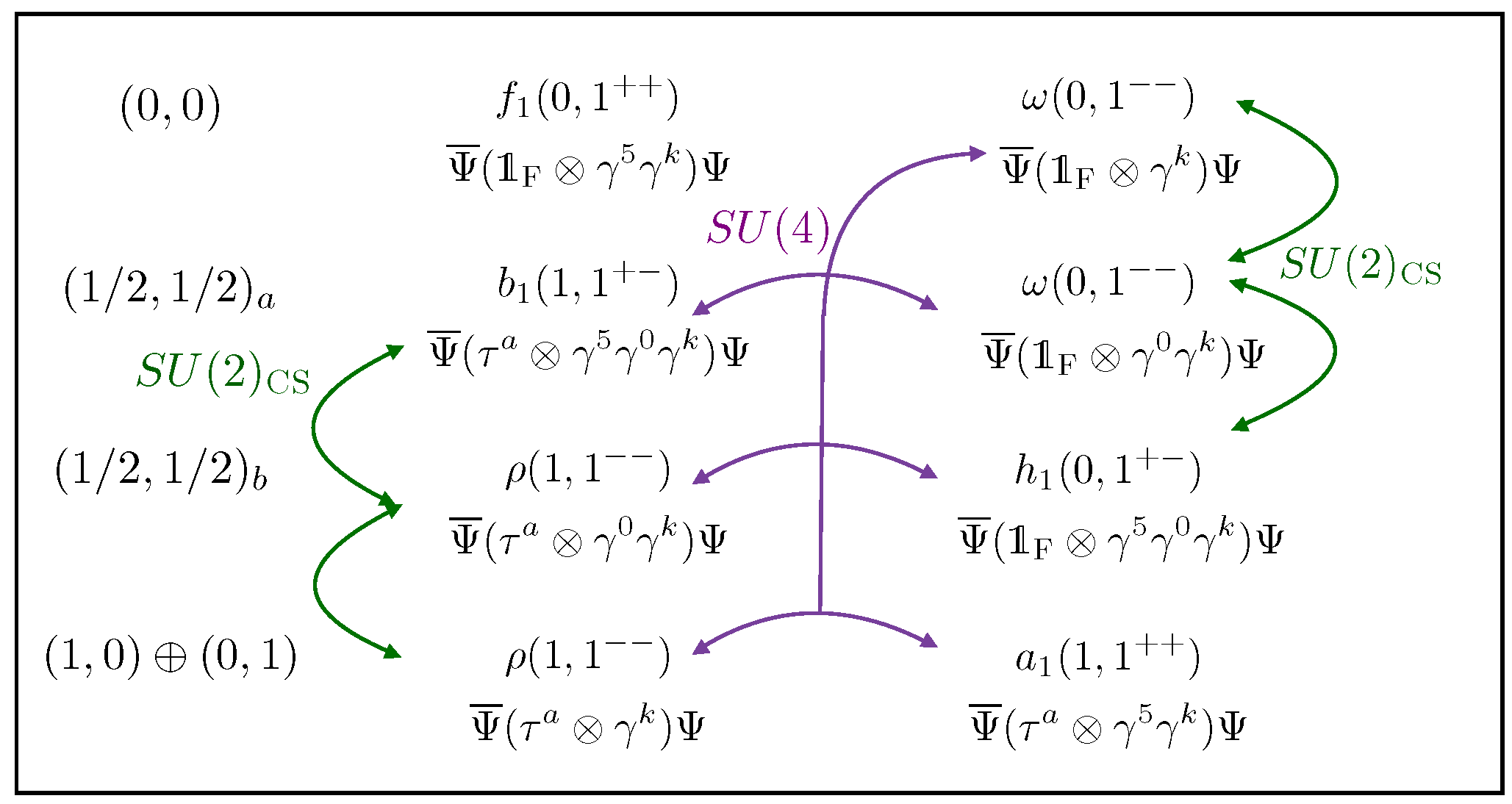
This degeneracy, presumably only approximate, represents the $SU{(2)}_{CS},k=4$ and the $SU(2N_F)$ symmetries because it contains irreducible representations of both groups (see Figure 3).

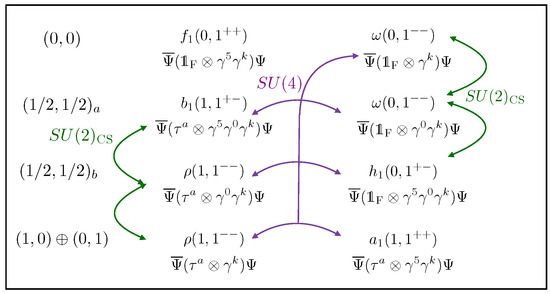
Figure 3. The green arrows connect operators that belong to $SU{(2)}_{CS}$ triplets. The purple arrow shows the $SU(4)$ 15-plet. The $f_1$ operator is a singlet of $SU(4)$. The figure is from Ref. [2].

The spatial $O(3)$ invariance is a good symmetry. The $SU{(2)}_{CS},k=4$ and $SU(2N_F)$ transformations do not mix bilinear operators from Figure 3 with operators of different spins and thus respect spin of hadrons as a good quantum number.

These lattice results suggest that, given the symmetry classification of the QCD Lagrangian (16), while the confining chromo-electric interaction, that is $SU{(2)}_{CS}$ and $SU(4)$ symmetric, contributes to all modes of the Dirac operator, the chromo-magnetic interaction, which breaks both symmetries, is located exclusively in the near-zero modes. Consequently, a truncation of the near-zero modes leads to emergence of $SU{(2)}_{CS}$ and $SU(4)$ in hadron spectrum. Similar results persist for $J=2$ mesons [8] and baryons [9].

The highly degenerate level seen in Figure 2 could be considered as a $SU(2N_F)$- symmetric level of the pure electric confining interaction. The hadron spectra in nature could be viewed as a splitting of the primary level of the dynamical QCD string by means of dynamics associated with the near zero modes of the Dirac operator, i.e., dynamics of chiral symmetry breaking that in addition includes all magnetic effects in QCD.

5. $\mathit{SU}(\mathbf{2}{\mathit{N}}_{\mathit{F}})\times \mathit{SU}(\mathbf{2}{\mathit{N}}_{\mathit{F}})$ Symmetry of Confining Interaction

In Figure 2, it is well visible that the $SU(4)$ 15-plet and the $SU(4)$ singlet ($f_1$) are also degenerate. This means that a confining interaction has a larger symmetry that includes the $SU(4)$ as a subgroup. What symmetry is it [10]?

The hadron mass is the energy in the rest frame. Consider the Minkowski QCD Hamiltonian in Coulomb gauge, which is suited to discuss the physics of the hadron mass generation in the rest frame [11]:

$$H_{QCD}=H_E+H_B+\int d^{3}x{\mathsf{\Psi }}^{†}(\mathit{x})[-i\mathit{\alpha }·\mathbf{\nabla }]\mathsf{\Psi }(\mathit{x})+H_T+H_C,$$

(24)

where the transverse (magnetic) and instantaneous “Coulombic” interactions are:

$$H_T=-g\int d^{3}x{\mathsf{\Psi }}^{†}(\mathit{x})\mathit{\alpha }·t^a{\mathit{A}}^a(\mathit{x})\mathsf{\Psi }(\mathit{x}),$$

(25)

$$H_C=\frac{g^2}{2}\int d^{3}x{d}^{3}y{J}^{-1}{\rho }^a(\mathit{x})F^{ab}(\mathit{x},\mathit{y})J{\rho }^b(\mathit{y}),$$

(26)

with J being Faddeev–Popov determinant, ${\rho }^a(\mathit{x})$ and ${\rho }^b(\mathit{y})$ are color-charge densities (that include both quark and glue charge densities) at the space points $\mathit{x}$ and $\mathit{y}$ and $F^{ab}(\mathit{x},\mathit{y})$ is a “Coulombic” kernel. Note that this Hamiltonian (Equation (24)) is not a model but represents QCD.

While the kinetic and transverse parts of the Hamiltonian are only chirally symmetric, the confining “Coulombic” part (Equation (26)) carries the $SU(2N_F)$ symmetry, because the charge density operator is $SU(2N_F)$ symmetric. However, both ${\rho }^a(\mathit{x})$ and ${\rho }^b(\mathit{y})$ are independently $SU(2N_F)$ symmetric because the $SU(2N_F)$ transformations at two different spatial points $\mathit{x}$ and $\mathit{y}$ can be completely independent, with different rotations angles. Thus, the integrand with $\mathit{x}\ne \mathit{y}$ is actually $SU(2N_F)\times SU(2N_F)$-symmetric. A contribution with $\mathit{x}=\mathit{y}$ with quarks of the same flavor vanishes because of the Grassmann nature of quarks. This means that confining “Coulombic” interaction is actually $SU(2N_F)\times SU(2N_F)$-symmetric [12]. Then, it follows that the confining “Coulombic” contributions to all hadrons from an irreducible representation of $SU(2N_F)\times SU(2N_F)$ must be the same.

The $SU(4)\times SU(4)$ has an irreducible representation of dim = 16 that is a direct sum of the 15-plet and of the singlet, $16=15\oplus 1$. Then, it becomes clear why the 15-plet mesons and the singlet in Figure 3 are degenerate in Figure 2.

6. Topology and the Near-Zero Modes Physics

The physics of the near-zero modes is not only responsible for chiral symmetry breaking in QCD but also for the breaking of higher symmetries $SU(2N_F)\supset SU{(2)}_{CS}$. The $SU{(2)}_{CS}$ transformations mix the right- and left-handed components of quarks. In other words, the physics of the near-zero modes should be associated not only with breaking of chiral and $U{(1)}_A$ symmetry, but also with asymmetry between the left and the right.

Below, we suggest a natural microscopic mechanism that induces an asymmetry between the left- and right-handed components of quarks in the near-zero modes. This mechanism is related to the local topological (instanton) fluctuations of the global gauge configuration.

In a gauge field with a nonzero topological charge, the massless fermion has exact zero modes

$${\gamma }_{\mu }{D}_{\mu }{\psi }_0(x)=0.$$

(27)

The zero mode is chiral, L or R. According to the Atiyah–Singer theorem, the difference of the number of the left- and right-handed zero modes of the Dirac operator is related to the topological charge Q of the gauge configuration,

$$Q=n_L-n_R.$$

(28)

With $|Q|\ge 1$, the numbers of right- and left-handed zero modes are not equal, which manifestly breaks the $SU{(2)}_{CS}$ symmetry. The topological configurations contain the chromo-magnetic field. What would be exact zero modes in a topological configuration with a nonzero topological charge become the near-zero modes of the Dirac operator in a global gauge configuration (with arbitrary global topological charge, zero or not zero) that contain local topological fluctuations, like in the Shuryak–Diakonov–Petrov theory of chiral symmetry breaking in the instanton liquid [13,14]. Consequently, on top of contributions from confining physics, which are manifestly $SU(2N_F)\supset SU{(2)}_{CS}$ symmetric, there appear contributions from the topological fluctuations that break $SU(2N_F)\supset SU{(2)}_{CS}$.

7. Observation of $\mathit{SU}{(\mathbf{2})}_{\mathit{CS}}$ and $\mathit{SU}(\mathbf{4})$ Symmetries at High Temperatures and Their Implication

Thus far, we have discussed $SU{(2)}_{CS}$ and $SU(4)$ symmetries in hadrons that emerge upon artificial truncation of the near-zero Dirac modes in $T=0$ calculations. The near-zero modes of the Dirac operator are naturally suppressed at high temperature above the chiral restoration crossover. Then, one can expect emergence of $SU{(2)}_{CS}$ and $SU(4)$ symmetries at high T without any artificial truncation [15].

Given this expectation, z-direction correlators

$$C_{\Gamma }(n_z)=\sum _{n_x,n_y,n_t}⟨{\mathcal{O}}_{\Gamma }(n_x,n_y,n_z,n_t){\mathcal{O}}_{\Gamma }{(\mathbf{0},0)}^{†}⟩$$

(29)

of all possible $J=0$ and $J=1$ local isovector operators ${\mathcal{O}}_{\Gamma }(x)=\overline{q}(x)\Gamma \frac{\mathit{\tau }}{2}q(x)$ have been calculated on the lattice at temperatures up to 380 MeV in $N_F=2$ QCD with the chirally symmetric domain wall fermions [16]. The operators and their $SU{(2)}_L\times SU{(2)}_R$ and $U{(1)}_A$ transformation properties are presented in Table 1.

Table 1. Bilinear operators and their $SU{(2)}_L\times SU{(2)}_R$, $U{(1)}_A$ transformation properties. This classification assumes propagation in z-direction. The index k denotes the components $1,2,4$, i.e., $x,y,t$.

Name	Dirac Structure	Abbreviation
Pseudoscalar	${\gamma }_5$	$PS$	$]U{(1)}_A$
Scalar	$\mathbb{1}$	S
Axial-vector	${\gamma }_k{\gamma }_5$	$\mathbf{A}$	$]SU{(2)}_A$
Vector	${\gamma }_k$	$\mathbf{V}$
Tensor-vector	${\gamma }_k{\gamma }_3$	$\mathbf{T}$	$]U{(1)}_A$
Axial-tensor-vector	${\gamma }_k{\gamma }_3{\gamma }_5$	$\mathbf{X}$

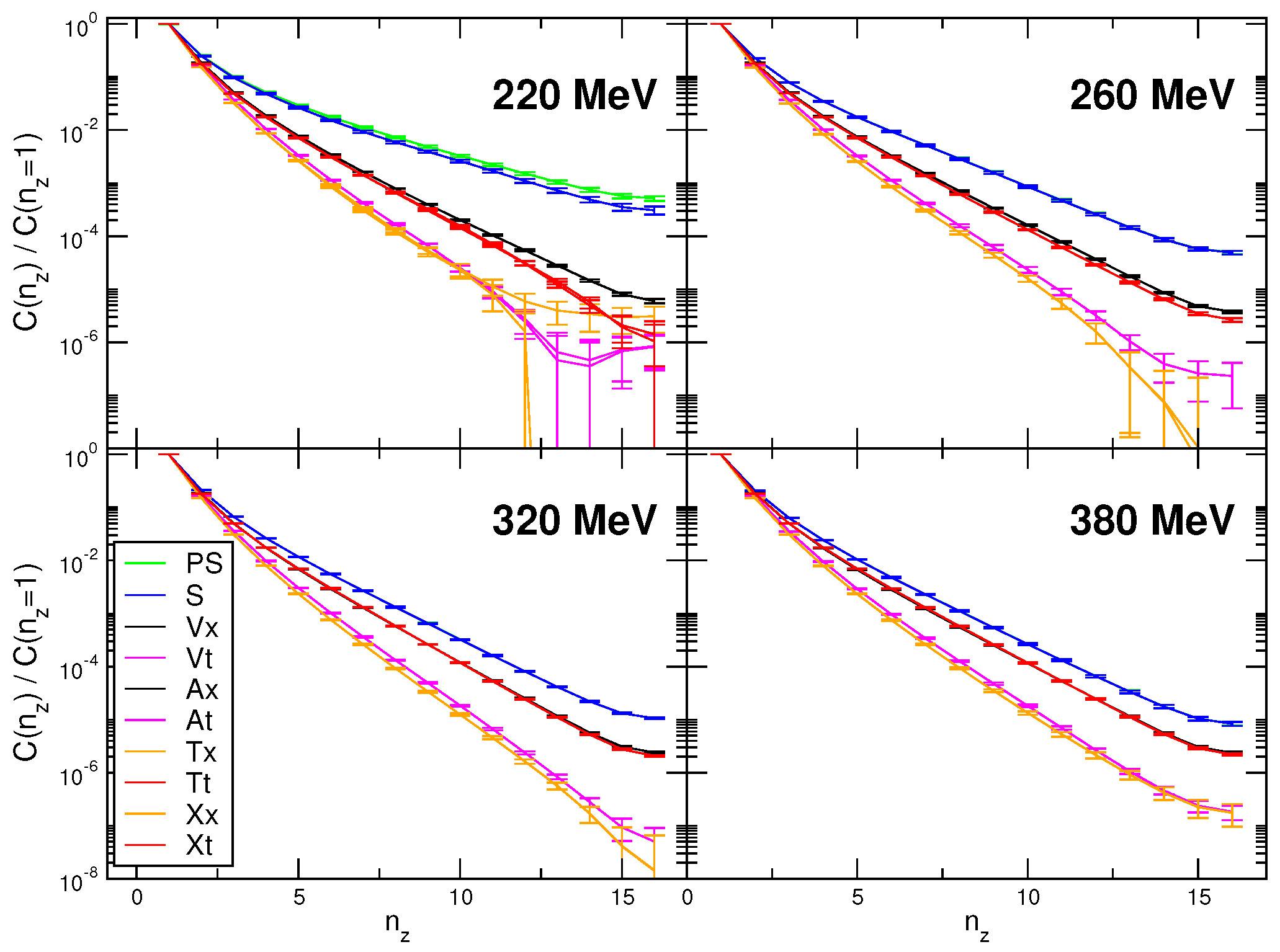
Figure 4 shows the correlators for all operators in Table 1. The argument $n_z$ is proportional to the dimensionless product $zT$.

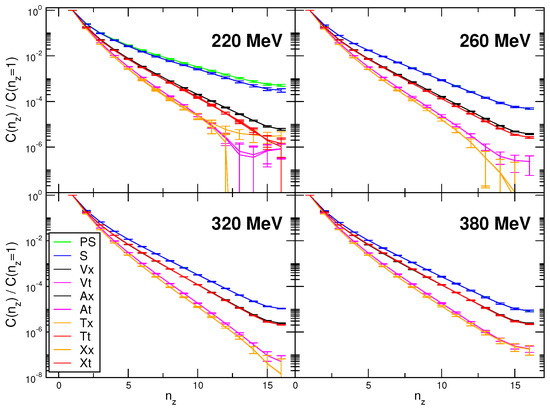
Figure 4. Normalized spatial correlators. The figure is from Ref. [16].

We observe three distinct multiplets:

$$\begin{array}{cc}\hfill E_1:& PS\leftrightarrow S\end{array}$$

(30)

$$\begin{array}{cc}\hfill E_2:& V_x\leftrightarrow T_t\leftrightarrow X_t\leftrightarrow A_x\end{array}$$

(31)

$$\begin{array}{cc}\hfill E_3:& V_t\leftrightarrow T_x\leftrightarrow X_x\leftrightarrow A_t.\end{array}$$

(32)

$E_1$ is the pseudoscalar-scalar multiplet connected by the $U{(1)}_A$ symmetry. The $E_2$ and $E_3$ multiplets contain, however, some operators that are not connected by $SU{(2)}_L\times SU{(2)}_R$ or $U{(1)}_A$ transformations. The symmetries responsible for emergence of the $E_2$ and $E_3$ multiplets are $SU{(2)}_{CS},k=1,2$ and $SU(4)$ (for details, see Ref. [16]). The $SU{(2)}_{CS},k=1,2$ transformations do not mix $J=0$ and $J=1$ operators in Table 1 and thus respect spin of mesons as a good quantum number at high T.

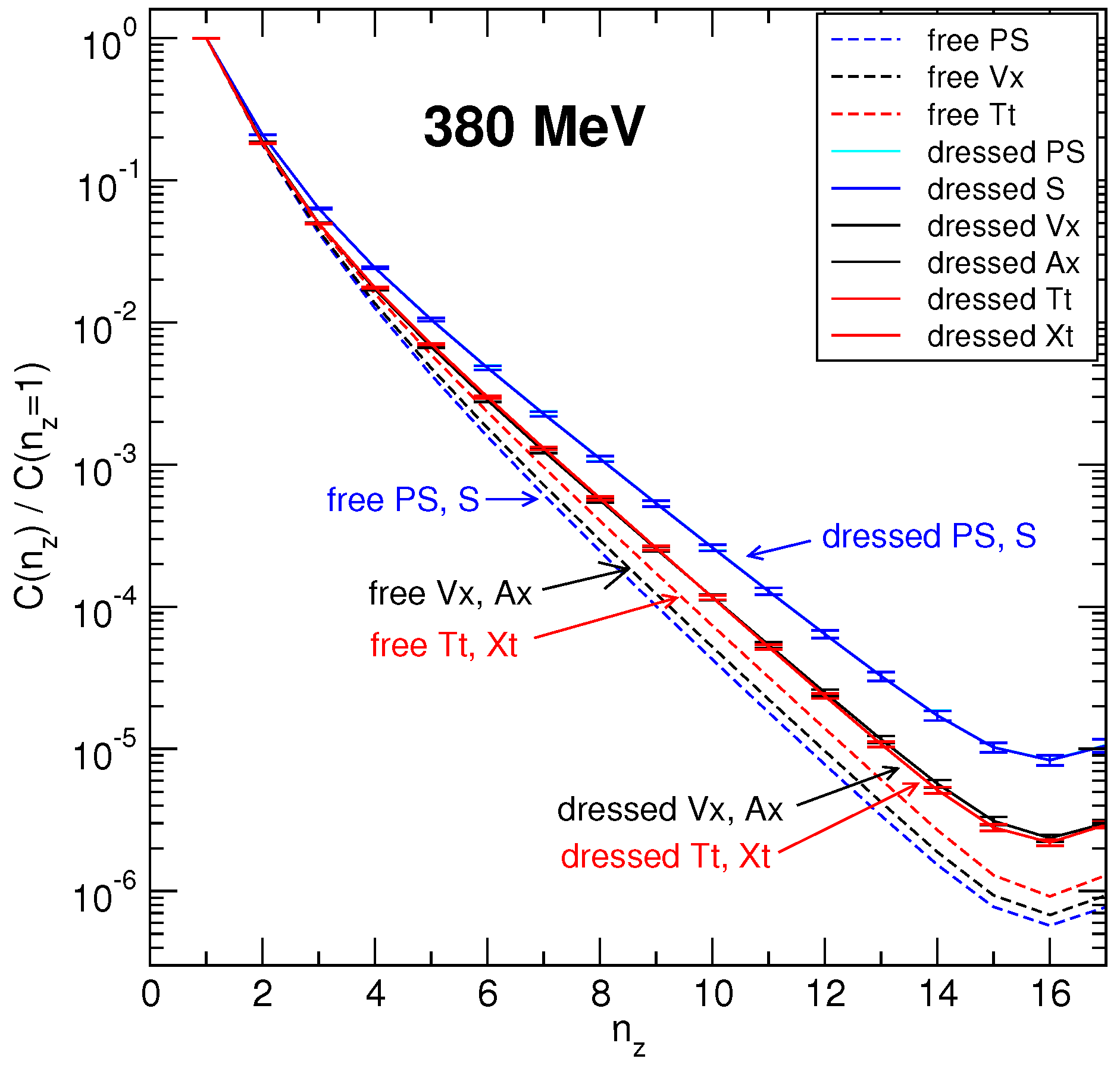
The $U{(1)}_A$ and $SU{(2)}_L\times SU{(2)}_R$ symmetries are exactly or almost exactly restored at temperatures above 220 MeV [17,18,19]. At the same time, the $SU{(2)}_{CS}$ and $SU(4)$ are only approximate. The correlators from the $E_1$ and $E_2$ multiplets at the highest available temperature 380 MeV are shown in Figure 5. A remaining $SU{(2)}_{CS}$ and $SU(4)$ breaking is at the level of 5%. We also show there correlators calculated with the noninteracting quarks (abbreviated as “free”). In the latter case, only $U{(1)}_A$ and $SU{(2)}_L\times SU{(2)}_R$ symmetries are seen in the correlators.

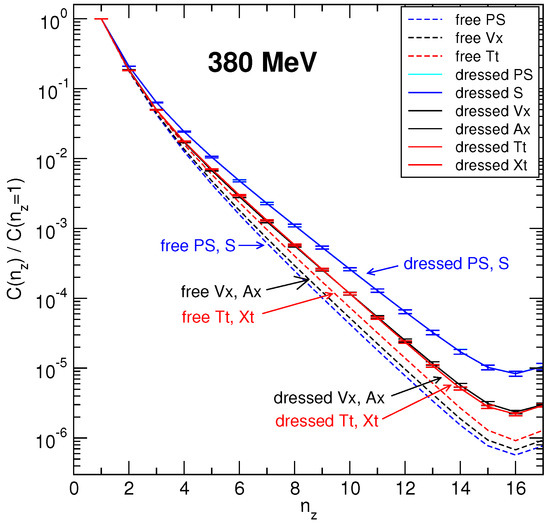
Figure 5. $E_1$ and $E_2$ multiplets in Equations (30) and (31) for interacting (dressed) and non-interacting (free) calculations at T= 380 MeV. The figure is from Ref. [16].

Scalar (S) and pseudoscalar (PS) systems are bound state systems because the slopes of the PS and S correlators are substantially smaller than for the free quark-antiquark pair [20,21]. In the free quark case, the minimal slope is determined by twice the lowest Matsubara frequency (because of the anti-periodic boundary conditions for quarks in time direction). If the quark-antiquark system is bound and of the Bosonic nature, the Bosonic periodic boundary conditions do allow the slope to be smaller. For the $J=1$ correlators, the difference of slopes of dressed and free correlators is smaller but is still visible. The observed approximate $SU{(2)}_{CS}$ and $SU(4)$ symmetries in $J=1$ correlators rule out asymptotically free deconfined quarks because free quarks do not have these symmetries. Correlators with such symmetries cannot be obtained in the weak coupling regime, because perturbation theory relies on a free Dirac equation that is not $SU{(2)}_{CS}$- and $SU(4)$-symmetric.

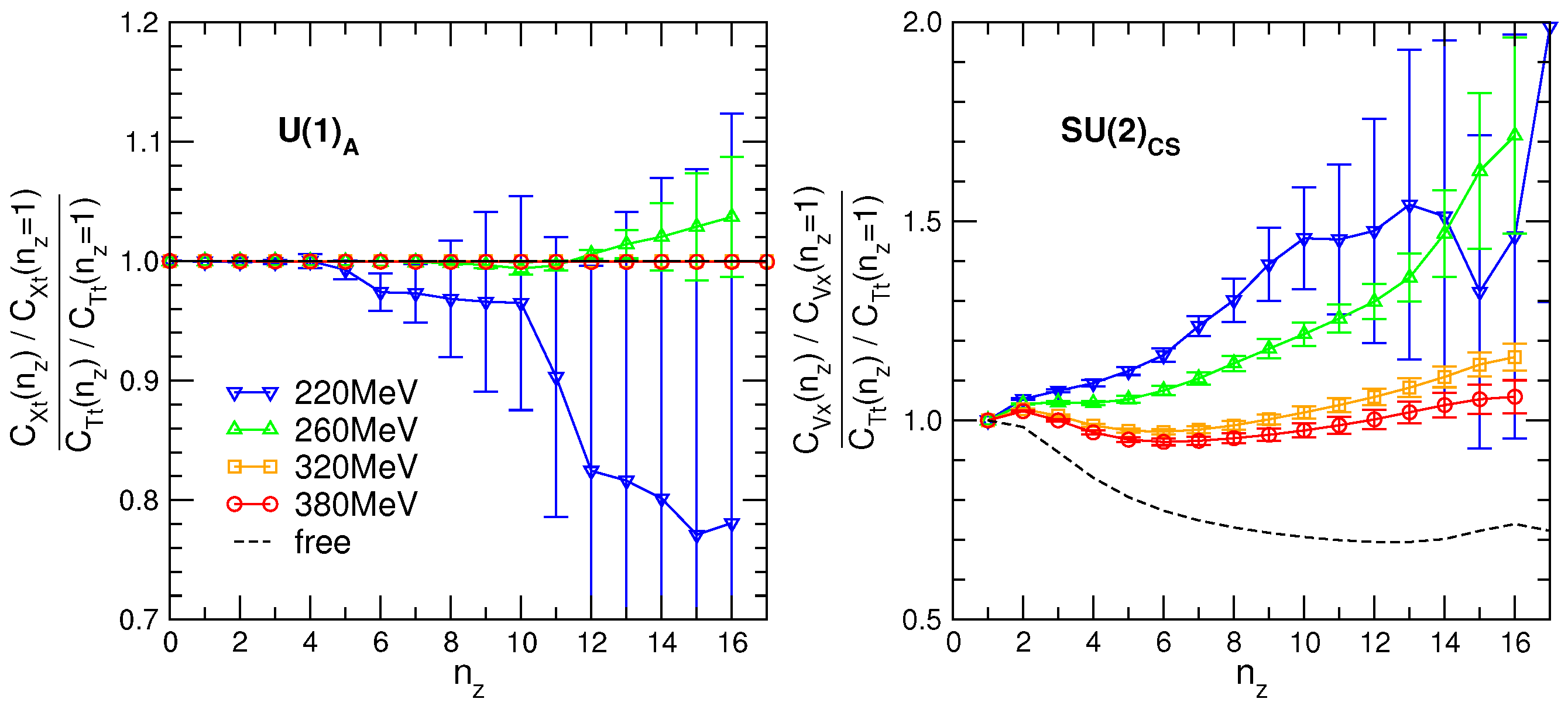
In Figure 6, we show a ratio of the correlators from the multiplet $E_2$ at different temperatures. We also show a ratio calculated with the free noninteracting quarks. For exact $SU{(2)}_{CS}$ symmetry, the ratio should be 1. At a temperature just above the chiral crossover, the ratio is essentially larger than 1. This can happen only if a contribution from the chromo-magnetic interaction is still large. Increasing the temperature, the role of the chromo-magnetic interaction is diminishing and the interaction between quarks is almost entirely chromo-electric. One concludes that elementary objects at T∼$2T_c$ are not free deconfined quarks, but rather quarks with a definite chirality bound by the chromo-electric field, something like a string. A remaining small $SU{(2)}_{CS}$ symmetry breaking is due to the quark kinetic term in the QCD action. This conclusion remains also true in matter with finite chemical potential [3].

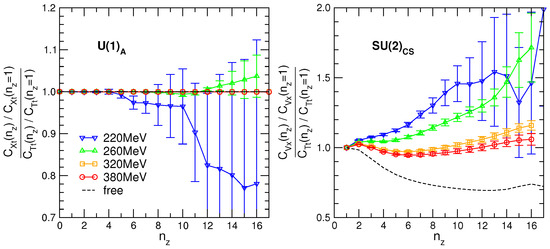
Figure 6. Ratios of normalized correlators that are related by $U{(1)}_A$ and $SU{(2)}_{CS}$ symmetries. The figure is from Ref. [16].

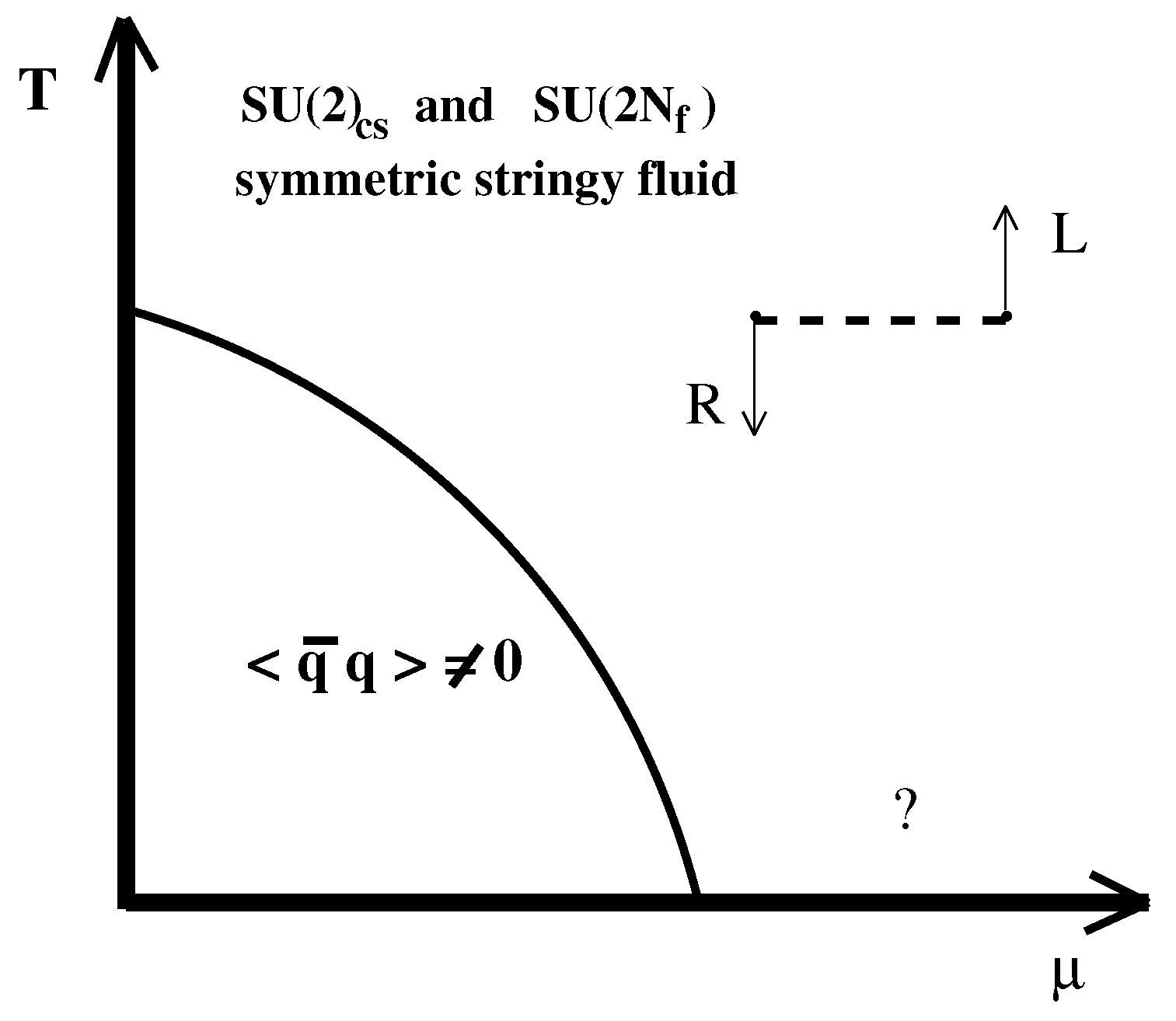
How should such a state of matter be called? It is not a plasma, because according to the standard definition plasma is a system of free charges with Debye screening of electric field. From our results, it follows that there are no free deconfined quarks and in addition it is a chromo-magnetic, but not a chromo-electric field, which is screened. Thus, conditionally, one could call this matter a stringy fluid (see Figure 7). However, elementary objects are not usual hadrons. This can be clearly deduced from the correlators in Figure 4. For example, at zero temperature, both $V_t$ and $V_x$ operators couple to one and the same $\rho$-meson. Above the cross-over, we observe that properties of objects that are created by $V_t$ and $V_x$ operators are very different, because these correlators are very different. This means that usual $\rho$-mesons get split into two independent objects with not yet known properties. This could explain observed fluctuations of conserved charges and could perhaps be experimentally detected via dileptons.

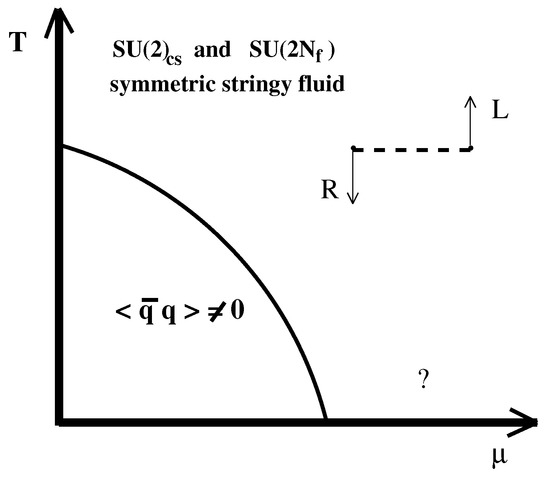
Figure 7. A schematic phase diagram.

Preliminary results on correlators at even higher temperatures, up to 1 GeV [22], suggest that at the very high temperatures the $SU{(2)}_{CS}$ and $SU(4)$ multiplet structure is washed away and one approaches to the asymptotic freedom regime.