Abstract
Gravity is the only force which is telling us about the existence of Dark Matter. I will review the idea that this must be the case because Dark Matter is nothing else than a manifestation of Gravity itself, in the guise of an additional, massive, spin-2 particle.
1. Where is Dark Matter?
Roughly 85% of all the matter of the Universe appears to be in the form of Dark Matter (DM). As of yet, we do not know what the origin and properties of DM are. That there is DM in our Universe we know from its gravitational effects [1]. Typically, DM is modeled as a cold relic density of some yet unknown particle, which was produced early in the evolution of the Universe, which possesses very weak interactions with Standard Model (SM) particles. Despite many efforts to debunk this field, DM remains very elusive. Here, I review the idea that DM is automatically built into the only known consistent extension of General Relativity (GR) to an additional interacting massive spin-2 field; since this field is engineered to interact only gravitationally, it escapes all non-gravitational detection methods [2,3,4,5,6].
2. Bimetric Theory
Multiple spin-2 particles in four dimensions have only recently been shown to be a consistent, ghost-free possibility, thanks to the construction of ghost-free bimetric theory (see [7] for a review). As the name says, this model describes, on top of the usual graviton with zero mass, a second, massive, propagating spin-2 particle [8]. We can begin with the (fully non-linear) action, which describes two dynamical tensor fields and [8]:
here, and are the mass scales that determine the strength of (self-)interaction for the two fields, whereas m tells the energy scale for the massive spin-2 field (see below). For the model to be consistent, the form of the potential is constrained to be [9,10]:
where are five free parameters. Of those five, two of them, and , act as vacuum energy terms for and , respectively. The are elementary symmetric polynomials constructed from the square-root matrix , which are defined by the totally anti-symmetric product:
In order to have a particle-physics feeling of the theory we are talking about, it is best to linearize it around some special (called proportional) backgrounds where :
where is the linearized quadratic Einstein–Hilbert Lagrangian (essentially describing usual gravity waves), plus a cosmological constant, i.e., , and . This linear theory at the quadratic level therefore describes a massless graviton , which mediates standard gravitational interactions with Planck mass , and an additional spin-2 field with non-zero Fierz–Pauli mass . Notice that matter, which appears in the stress-energy tensor , “sees” both linear fluctuations with the usual gravitational interaction strength of , but the massive spin-2 vertex has an additional factor of , which further suppresses these interactions. The and are free parameters of the theory.
3. Phenomenology
Bimetric theory contains a new massive and uncharged particle, which interacts with the SM only with gravitational strength. The most logical step is to check whether this new field is a good candidate for DM. The spin-2 DM, in particle physics terms, could be either heavy (think of TeV) or light (think of sub-eV masses), and I will review the two possibilities in turn in this section.
The first step is actually common to both cases, and that is to show that it gravitates as matter. This is easily proven if we expand the action to cubic order and consider the terms: the coefficient in front of them is , which tells us that the DM field responds to gravity (personified by the massless spin-2 field) identically to regular baryonic matter. An interesting point to note here is that there is no , so there is no tree-level decay of DM into two (or more, in fact) massless gravitons.
3.1. Heavy
Now, let us take a heavy spin-2 particle. The mechanism of choice to populate the Universe is a sort of slow “leakage” from the early Universe’s thermal bath, which goes under the name of freeze-in [11]. In practice, two SM particles from the thermal bath annihilate and produce a heavy spin-2 pair via an s-channel graviton [12,13]. This amplitude is extremely suppressed, so this leakage only happens very rarely; also, it is never counterbalanced by the opposite reaction, because the DM abundance remains well below the thermal one at all times. In our particular scenario, freeze-in can also proceed via the exchange of the DM field itself, and the two channels result in the same overall amplitude, due to the fact that the suppression for the vertex is compensated by an opposite enhancement of the self-interaction . We can summarize the result by:
where is the reheating temperature and is the Hubble parameter at the end of inflation. As usual, a large out-of equilibrium density of DM is bound to produce isocurvature perturbations, which are severely constrained. Taken at face value, the bound on isocurvature perturbations becomes either a lower limit on or on the scale of inflation at thermalization : . The next point is to make sure that the heavy spin-2 thingy resists until today. The DM in this setup does not carry any of the SM charges, but it possesses gravitational interactions with everything, and it would decay universally into all the kinematically allowed channels. The decay width into SM X pairs is easily obtained as [14],
Requiring that the lifetime of DM is longer than the age of the Universe Gyr, as it must be, we find that GeV. However, we also have constraints from the non-observation of the decay product of such a heavy DM particle. The strongest constraints come from -ray lines or high energy neutrinos [15,16]: these limits turn out to be roughly 10 orders of magnitude stronger than the Universe’s lifetime limit.
Figure 1 illustrates where we are with the parameter space of this spin-2 DM model. We plot the constraints on the total decay width, as well as the perturbativity limit beyond which the linear expansion we performed is no longer valid. We also report the different mass ranges available for freeze-in production. The available parameter space for bimetric spin-2 DM is interestingly restricted, for the mass, to the range:
Extensions of the current setup include the existence of multiple spin-2 particles [5], and another production mechanism that takes advantage of number-changing self-interactions [6], both of which turn out to open up some additional regions of available parameter space for this model.
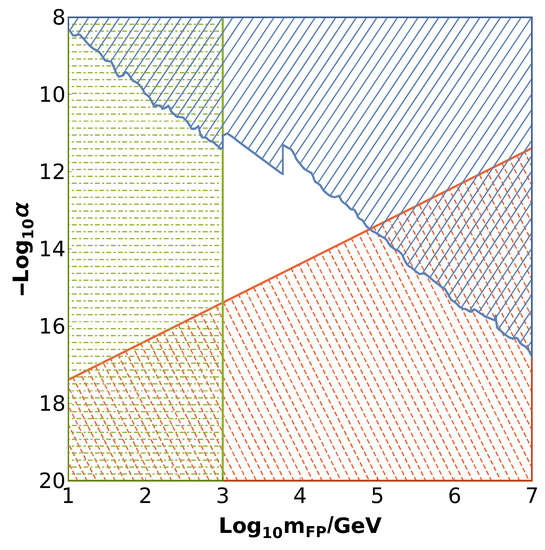
Figure 1.
Available parameter space for heavy bimetric DM. The solid blue lines mark the region excluded by the strongest lifetime constraints; the dashed red lines fill the region we cannot study perturbatively; finally, the dotted-dashed green lines delineate the range of masses for which the final abundance of DM produced in the early Universe cannot match the experimentally-observed value.
One peculiar feature of this model, which would tell it apart from, e.g., Kaluza–Klein models, is the universal decay of DM into all SM particles along with the absence of a decay channel into massless gravitons at the tree level. Moreover, we predict that the mass and interaction scale of the heavy spin-2 field are roughly of the same order of magnitude, and both are only slightly larger than the weak scale, so we have a heavy “wimp” particle, but with only gravitational interactions.
3.2. Light
Let us define a non-linear effective background as:
As we have mentioned previously, terms linear in and of any order in vanish in the expansion of the original action (1), so we can partially re-sum the expansion to separate the new background from the dynamics of the massive fluctuation , that is:
Seen in this way, the theory describes a propagating spin-2 particle, the massive field , on a generic background encoded in the metric .
In order for this “trick” to make sense, we need to ensure that , where is the Hubble parameter and the scale factor of the Universe. This is clearly satisfied for most reasonable at late enough times. Physically, this means that the background metric , the characteristic length and time scale of which is , behaves independently of the heavier field, which instead has a typical wavelength of .
Let us look at the Equation Of Motion (EOM) for the massive spin-2 field . These can as usual be obtained from Equation (9) via the variational derivative with respect to the field ,
where , and we now use the full non-linear metric to raise and lower indices; this metric also appears in the metric connection for the covariant derivative and of course in the curvature tensor. We can make further progress by taking into account the linearized Bianchi identities , which in turn mean . Therefore, looking at the trace of (10) we see that the massive spin-2 field is traceless, , and putting this fact back into the EOM, we obtain that this field is also transversal: . Hence, all in all, the massive spin-2 field propagates only five degrees of freedom. To make progress, we specialize to a Friedmann–Lemaître–Robertson–Walker background where t is cosmic time; now, given that is traceless and transverse, and , and going as usual to Fourier space, we obtain the EOM:
in which a dot stands for a time derivative. Consider the homogeneous modes only, that is :in the beginning, when , they appear practically massless and frozen due to Hubble friction. The field remains effectively massless until , since from this moment onward, it “sees” the appearance of a potential well and consequently starts to oscillate with frequency :
Hence, the behavior of each of the five degrees of freedom is identical to that of a typical scalar field with the mass term; therefore, we can borrow the entire machinery and cosmology from that of axion-like-particles; the only major difference, which however has little practical implications (or better: most likely unobservable cosmological implications), that this DM has spin-2. The main conclusion is that, due to the rapid oscillations around the minimum (), we can be sure that behaves as matter [17,18].
Using known results from axion cosmology, we can write the energy density of the DM as [17]:
notice that here, the initial field value at the onset of oscillations, let us call it , is determined by the misalignment mechanism. It is clear that, leaving aside other constraints for now, the observed DM abundance [19] can be matched for a wide range of ; the only limit here is that beyond eV, the field cannot be treated as homogeneous.
One of the, however, relevant differences between the scalar and spin-2 models is the fact that, because the spin-2 field is not in general background-compatible with isotropy, in principle, its energy density would have to be massively suppressed to respect the stringent microwave background anisotropies’ bound. Nonetheless, just like for a vector field [20], because the spin-2 DM field is oscillating very rapidly, the induced quadrupolar anisotropy is dynamically driven to nearly zero [21]. When the field was frozen, before oscillations began, its energy density was vastly subdominant, and therefore, the anisotropy it would imprint would be irrelevant. There is one perhaps unique way to test for this model, in that one can look at variations of, e.g., the elementary electric charge, induced by the oscillations of the spin-2 field acting as DM [22]; this would cause modulations in the emission lines of atoms, molecules and nuclei, which can be studied and probed with atomic and nuclear clocks, atomic spectroscopy, dedicated resonant mass detectors, laser interferometers and ALPdetectors. The peculiarity in our case is that the interactions with radiation are given by:
which return an effective couplings’ Maxwell fields as and . This is different from usual interactions [17,23,24,25,26,27,28,29,30,31] since in the scalar or pseudoscalar cases, the structures of the couplings are very different, being proportional to and , respectively. The induced non-trivial polarization correlations and the possible directional and temporal variations of electric charge therefore constitute a distinguishing signature of the scenario.
Funding
This research was funded by the European Regional Development Fund (ESIF/ERDF) and the Czech Ministry of Education, Youth and Sports (MEYS) through Project CoGraDS - CZ.02.1.01/0.0/0.0/15_003/0000437.
Conflicts of Interest
The author declares no conflict of interest.
References
- Olive, K.A.; Particle Data Group Collaboration. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Babichev, E.; Marzola, L.; Raidal, M.; Schmidt-May, A.; Urban, F.; Veermäe, H.; von Strauss, M. Bigravitational origin of dark matter. Phys. Rev. D 2016, 94, 084055. [Google Scholar] [CrossRef]
- Babichev, E.; Marzola, L.; Raidal, M.; Schmidt-May, A.; Urban, F.; Veermäe, H.; Von Strauss, M. Heavy spin-2 Dark Matter. J. Cosmol. Astropart. Phys. 2016, 2016, 09. [Google Scholar] [CrossRef]
- Marzola, L.; Raidal, M.; Urban, F.R. Oscillating Spin-2 Dark Matter. Phys. Rev. D 2018, 97, 024010. [Google Scholar] [CrossRef]
- González Albornoz, N.L.; Schmidt-May, A.; von Strauss, M. Dark matter scenarios with multiple spin-2 fields. J. Cosmol. Astropart. Phys. 2018, 2018, 014. [Google Scholar] [CrossRef]
- Chu, X.; Garcia-Cely, C. Self-interacting spin-2 dark matter. Phys. Rev. D 2017, 96, 103519. [Google Scholar] [CrossRef]
- Schmidt-May, A.; von Strauss, M. Recent developments in bimetric theory. J. Phys. A 2016, 49, 183001. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A. Bimetric gravity from ghost-free massive gravity. J. High Energy Phys. 2012, 2012, 126. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of massive gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.F.; Rosen, R.A. Resolving the ghost problem in non-linear massive gravity. Phys. Rev. Lett. 2012, 108, 041101. [Google Scholar] [CrossRef] [PubMed]
- Hall, L.J.; Jedamzik, K.; March-Russell, J.; West, S.M. Freeze-in production of FIMP dark matter. J. High Energy Phys. 2010, 2010, 080. [Google Scholar] [CrossRef]
- Garny, M.; Sandora, M.; Sloth, M.S. Planckian interacting massive particles as dark matter. Phys. Rev. Lett. 2016, 116, 101302. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Wu, Y.L. Pure gravitational dark matter, its mass and signatures. Phys. Rev. B 2016, 758, 402–406. [Google Scholar] [CrossRef]
- Han, T.; Lykken, J.D.; Zhang, R.J. On Kaluza-Klein states from large extra dimensions. Phys. Rev. D 1999, 59, 105006. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Anderson, B.; Atwood, W.B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; et al. Updated search for spectral lines from Galactic dark matter interactions with pass 8 data from the Fermi Large Area Telescope. Phys. Rev. D 2015, 91, 122002. [Google Scholar] [CrossRef]
- El Aisati, C.; Gustafsson, M.; Hambye, T. New search for monochromatic neutrinos from dark matter decay. Phys. Rev. D 2015, 92, 123515. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Maeda, K.I.; Volkov, M.S. Anisotropic universes in the ghost-free bigravity. Phys. Rev. D 2013, 87, 104009. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Nelson, A.E.; Scholtz, J. Dark light, dark matter and the misalignment mechanism. Phys. Rev. D 2011, 84, 103501. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Hallabrin, C.; Maroto, A.L.; Jareno, S.J.N. Isotropy theorem for cosmological vector fields. Phys. Rev. D 2012, 86, 021301. [Google Scholar] [CrossRef]
- Damour, T.; Donoghue, J.F. Equivalence principle violations and couplings of a light dilaton. Phys. Rev. D 2010, 82, 084033. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Huang, J.; Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 2015, 91, 015015. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Van Tilburg, K. Sound of dark matter: Searching for light scalars with resonant-mass detectors. Phys. Rev. D 2016, 116, 031102. [Google Scholar] [CrossRef] [PubMed]
- Stadnik, Y.V.; Flambaum, V.V. Improved limits on interactions of low-mass spin-0 dark matter from atomic clock spectroscopy. Phys. Rev. A 2016, 94, 022111. [Google Scholar] [CrossRef]
- Van Tilburg, K.; Leefer, N.; Bougas, L.; Budker, D. Search for ultralight scalar dark matter with atomic spectroscopy. Phys. Rev. Lett. 2015, 115, 011802. [Google Scholar] [CrossRef] [PubMed]
- Hees, A.; Guéna, J.; Abgrall, M.; Bize, S.; Wolf, P. Searching for an oscillating massive scalar field as a dark matter candidate using atomic hyperfine frequency comparisons. Phys. Rev. Lett. 2016, 117, 061301. [Google Scholar] [CrossRef] [PubMed]
- Stadnik, Y.V.; Flambaum, V.V. Enhanced effects of variation of the fundamental constants in laser interferometers and application to dark matter detection. Phys. Rev. A 2016, 93, 063630. [Google Scholar] [CrossRef]
- Stadnik, Y.V.; Flambaum, V.V. Searching for dark matter and variation of fundamental constants with laser and maser interferometry. Phys. Rev. Lett. 2015, 114, 161301. [Google Scholar] [CrossRef] [PubMed]
- Raffelt, G.G. Astrophysical methods to constrain axions and other novel particle phenomena. Phys. Rept. 1990, 198, 1–113. [Google Scholar] [CrossRef]
- Ringwald, A. Exploring the role of axions and other WISPs in the dark universe. Phys. Dark Univ. 2012, 1–2, 116–135. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).