Abstract
We review some of the recent results which can be useful for better understanding of the problem of stability of vacuum and in general classical solutions in higher derivative quantum gravity. The fourth derivative terms in the purely gravitational vacuum sector are requested by renormalizability already in both semiclassical and complete quantum gravity theories. However, because of these terms, the spectrum of the theory has unphysical ghost states which jeopardize the stability of classical solutions. At the quantum level, ghosts violate unitarity, and thus ghosts look incompatible with the consistency of the theory. The “dominating” or “standard” approach is to treat higher derivative terms as small perturbations at low energies. Such an effective theory is supposed to glue with an unknown fundamental theory in the high energy limit. We argue that the perspectives for such a scenario are not clear, to say the least. On the other hand, recently, there was certain progress in understanding physical conditions which can make ghosts not offensive. We survey these results and discuss the properties of the unknown fundamental theory which can provide these conditions satisfied.
Keywords:
higher derivatives; massive ghosts; stability; cosmological solutions; gravitational waves PACS:
04.62.+v; 98.80.-k; 04.30.-w
1. Introduction
Numerous tests and verifications performed during the last century have shown that General Relativity (GR) is a complete theory of classical gravitational phenomena. GR proved valid and useful in the wide range of energies and distances. At the same time, the presence of singular regions in physically relevant solutions of GR indicates the need for extending the theory. One can assume that GR is not valid at all scales, especially at very short distances and/or when the curvature becomes very large. In this situation, one can expect that the gravitational phenomena should be described by a more extensive and complicated theory. Indeed, one should expect that this unknown theory coincides with GR at large distances and/or in the weak field limit.
The dimensional arguments indicate that the origin of deviations from GR is most likely related to quantum effects. For example, the existence of fundamental Planck units () hints at the possibility of some sort of a new fundamental physics at the very high energy scale, where relativistic, quantum and gravitational effects become relevant at the same time. How can we interpret such a result of the dimensional analysis?
One can introduce a simple general classification of all possible approaches to Quantum Gravity (QG), which is based on the object of quantization. There are three distinct groups of approaches, namely
- (i)
- Quantize both gravity and matter fields. This is, definitely, the most fundamental possible approach.
- (ii)
- Quantize only matter fields on classical curved background (semiclassical approach). This is, in some sense, the most important approach, since we know for sure that matter fields should be quantized on a curved background. The main question is: What is the effect (back-reaction) of such a quantum theory on the gravitational equations of motion?
- (iii)
- Quantize “something else”. For example, in the case of (super)string theory, both matter and gravity are induced, and the fundamental object of quantization is the two-dimensional (2D) string, which lives in the external D-dimensional background and defines its geometry and dynamics.
Which of these approaches is “better”? The final verdict can be achieved only in experiments, and purely theoretical arguments can only help us to select what we regard more consistent, simple and natural. On the other hand, all these approaches have something in common, namely there are higher derivative terms in the gravitational action in all cases. In the next section, we briefly consider this issue in the framework of semiclassical approach. After that, in Section 3, we discuss that a very similar situation takes place in the theory of quantum gravity and also is quite similar in string theory. Starting from Section 4, we review the original results of Refs. [1,2] concerning recent advances in exploring the unitarity of quantum theory in the presence of complex conjugate pairs of higher derivative ghosts and in the study of stability on the cosmological backgrounds.
2. Semiclassical Approach and Higher Derivatives
Without quantization of gravity, at the quantum level, the classical action of vacuum is replaced by the effective action, that includes contributions of quantum matter fields [3,4] (see also [5] for a more recent review),
The form of the classical action of vacuum is defined by the consistency conditions, which means that the theory should be renormalizable. The simplest minimal vacuum action of renormalizable quantum field theory (QFT) in curved space is
where
is the Einstein–Hilbert action with the cosmological constant and
includes fourth derivatives, e.g., is the square of the Weyl tensor and
is the integrand of the Gauss–Bonnet topological term.
Without higher derivative (HD) terms in the vacuum sector, the semiclassical theory is not consistent due to the non-renormalizability. Even if these terms are not included into the classical action, they will emerge due to the renormalization group running in quantum theory. This can be explicitly seen using the conformal anomaly, as discussed in [5,6]. Formally, regarding semiclassical theory as fundamental (not effective) QFT, the higher derivative terms are not quantum corrections, for they should be introduced already at the classical level.
3. Two Sides of Higher Derivatives in Quantum Gravity
Consider now the situation in QG. The renormalizability of QG models strongly depend on the choice of the initial classical action. As the first example, let us consider quantum GR.
Using the standard power counting arguments (see some details below), one can easily obtain the relation
where D is the superficial degree of divergence of a diagram with p loops and d is the number of derivatives acting on the external lines of the diagram. One can easily see from Equation (7) and covariance of the counterterms that, at the one-loop level, there are logarithmically divergent term which are quadratic in curvatures [7,8], namely
At the two-loop level, we have [9],
Since the last of these structures does not vanish on-shell, the theory is not renormalizable in the usual sense. Of course, one can rely on the effective approach and make sound calculations (see, e.g., [10,11] and the review [12]), but the approximation behind this approach breaks down at the Planck scale, where QG is supposed to be especially relevant.
Within the standard perturbative approach, non-renormalizability means the theory has no predictive power. Every time we introduce a new type of a counterterm, it is necessary to fix renormalization condition and this means a measurement. Thus, before making a single prediction, it is necessary to have an infinite amount of experimental data.
What are the possible solutions of this problem? One of the options is to trade the standard perturbative approach in QFT to something different. Another way out is to modify or generalize the theory, i.e., start from another theory to construct QG. The first option is widely explored in the asymptotic safety scenarios, the effective approaches to QG (which is mentioned above), induced gravity approach (including string theory) and so on. Regardless of many options, their consistency and relation to the general targets of the QG program are not completely clear, in all cases. In what follows we concentrate on the second possibility and consider modified action of gravity as a starting point to construct QG.
The most natural choice is start from the four derivative gravity model, because we need fourth derivatives anyway to deal with the quantum matter field. Then, the starting action should be
where is the Einstein–Hilbert action (as mentioned before) and includes square of the Weyl tensor and R,
The propagators of metric and ghosts behave as (in the notations of [4,13] this means ) and we have , , and vertices with four, two and zero powers of momenta, respectively. The superficial degree of divergence D of the diagram with an arbitrary number of loops satisfies the relation
where d is the number of derivatives of external metric lines. Thus, this theory is definitely renormalizable and the dimensions of possible counterterms are 4, 2, and 0, depending on number of vertices with lower derivatives [13].
However, one has to pay a very high price for renormalizability, since this theory has massive ghosts. This can be seen from the spin-two sector of the propagator [13],
The tree-level spectrum includes massless graviton and massive spin-2 “ghost” with negative kinetic energy and a huge mass. The presence of a particle with negative energy means possible instability of the vacuum state of the theory. For instance, the Minkowski space is not protected from the spontaneous creation of massive ghost and (needed for energy conservation) compensating gravitons from the vacuum.
Indeed, there are different sides of the High Derivative Quantum Gravity (HDQG) problems with massive ghosts. For instance,
- (i)
- In classical systems, higher derivatives may generate exploding instabilities at the non-linear level [14] (see, e.g., recent review in [15]).
- (ii)
- Interaction between massive unphysical ghost and gravitons leads to massive emission of gravitons and unbounded acceleration of ghost. As a result, one should observe violation of energy conservation in the massless sector [16], which means an explosion of gravitons. In addition, ghosts produce violation of unitarity of the S-matrix, which also means similar instability at the quantum level.
Due to the great importance of the problem of higher derivatives and ghosts, there are many proposals to solve it (e.g., [17,18,19,20]). Let us consider another proposal, related to further generalization of the action of the QG theory. One can include more than four derivatives [21],
A simple analysis shows that in this theory massive ghost-like states are still present. For the real poles, case we can write
and it has been shown [21] that, for any sequence of poles with , the signs of the corresponding terms alternate, . This means that one can not make all but one particle in the spectrum healthy and provide an infinite mass of the ghost. In this sense, the theory in Equation (14) has the same level of problems with ghosts that the simpler fourth-derivative model.
However, the renormalization properties of these two theories are quite different. It is easy to see that the theory in Equation (14) is superrenormalizable if both higher order terms are present, . To check this fact, consider the power counting in this case. For the sake of simplicity, we can consider only the vertices with a maximal number of maximal derivatives, , which obviously provide the maximal power of divergences.
The propagators of gravitational modes and ghosts in this model are , where, combining the general expression for power counting for the diagram with n vertices and p loops,
with the topological relation for the number of internal lines,
one can easily arrive at the estimate of d for the logarithmic divergences with ,
For , we meet the standard HDQG result, . Due to the covariance, this means that the counterterms repeat the form of the four-derivative action in Equation (10). It is remarkable that the terms with six and higher derivatives do not get renormalized, but the coefficients of these terms define the divergences. Starting from , we have superrenormalizable theory, where the divergences show up only in loops. For , we have such a superrenormalizable theory, where divergences exist only for , that is at the one-loop level. Let us stress that the one-loop divergences are present for all N and that the logarithmic divergences always have zero, two and four derivatives of the metric, independent of N.
The low-energy effects of complex and real ghosts in these models are recently discussed in [22,23,24,25]. Another interesting possibility is that one can derive exact -functions in this superrenormalizable QG model, by means of one-loop level calculations [21,26]. These calculations, anyway, may be very difficult and for a while the results have been achieved only for the beta functions of cosmological and Newton constants. They have the form
Here, we used the standard notation for the density of the cosmological constant .
Different from four-derivative quantum gravity, these -functions do not depend on the choice of a gauge-fixing condition [21,26]. This important feature follows from the fact that the classical equations of motion and the the divergences in this theory have different number of metric derivatives. Again, for , these universal beta-functions are exact.
Overall, one can see that, from the theoretical side, there are positive and negative aspects of introducing the higher derivative terms in quantum gravity. A consistent theory which is supposed to work at arbitrary energy scale cannot be constructed without at least fourth derivatives. If the higher derivative terms are included, then the tree-level spectrum will include massless graviton and massive spin-2 “ghost” with negative kinetic energy and huge mass. If we do not include the higher derivative terms into classical action, they will emerge with infinite coefficients and (most relevant) with logarithmically running parameters. In any case, the nonphysical ghosts come back.
Thus, we can reach the following general conclusion: there is no way to live with ghosts and, on the other hand, there is no way to live without ghosts. The situation looks like a strange puzzle. However, parallel to this strange conclusion there is one absolutely certain thing. As a matter of fact the world exists, we live, and so there must be some explanation and resolution of the mentioned puzzle, of course.
The standard (for some people, at least) logic to solve this issue is to consider, by definition, all higher derivative terms to be small perturbations [27,28,29,30]. In this approach, all higher derivative terms, including the terms in the classical action which are subject of renormalization, local and nonlocal quantum corrections, running parameter, etc., are regarded as small perturbations over the basic Einstein–Hilbert term of GR. Certainly, this approach is efficient in fighting ghosts. However, the bad news is that it is a completely ad hoc approach. Furthermore, it is based on the approximation which is efficient only for the energies which are much below the Planck scale. This is not what we expect from the “theory of everything”, such as QG. As far as we approach the Planck energies, the higher derivative terms cannot be treated as small. Another disadvantage is that this ad hoc procedure brings a lot of ambiguity. For instance, how should we treat the term? Taking it as perturbation is somehow groundless, since it does not make ghosts. At the same time, from the dimensional and conceptual viewpoints, there is no apparent difference between and terms, so why should they be treated differently? Worst than that, by treating term as perturbation, we are forced to “forbid” the Starobinsky model of inflation, which is phenomenologically very successful. Let us stress that this inflationary model is essentially based on treating R and terms at the equal level, and not taking the last one as a perturbation.
Another important issue is what to do with , , and other similar terms. Why should we treat all such terms as perturbations? Because they have higher derivatives? Regardless of the fact they do not produce ghosts? What is the rule of splitting the action into the main part and perturbation?
We may think that, if the criterium is dimension, then this approach means that we assume that quantum gravitational phenomena are relevant only far below the Planck scale. Let us repeat, this is something opposite to what we expect from QG, since the original motivation was to deal with the Planck energies.
4. Ghosts in String Theory and in the Non-Polynomial Quantum Gravity
Let us consider two examples of ghost-free HD models of gravity. Both models can be seen as different representations of string or superstring theory. In string theory, the object of quantization is a kind of non-linear sigma-model in two space-time dimensions. In this case, both metric and matter fields are induced, implying unification of all fundamental forces. The sigma-model approach to string theory (we consider only bosonic case) is a QFT in curved space,
In the Polyakov approach, the conditions of anomaly cancellation emerge order by order in . This expansion corresponds to the special order of functional integration and to the low-energy effective action which corresponds to the growing orders of metric derivatives [31]. The critical dimensions are
At the first order in , the effective equations give induced GR [32,33,34], coming from the condition of Weyl invariance of string at the quantum level. In the second order in , the low-energy effective action already has the same fourth order in derivatives terms, which we already met in QG. However, in string theory there one extra possibility. Namely, one can use special reparameterization of the metric to remove ghosts at all orders in . In the simplest torsionless case, the effective action can can be written as
where the dilation is related to the in Equation (22). Now, to remove ghosts, one performs reparameterization of the background metric as follows:
where are specially tuned parameters [35,36,37].
It is important to note that the reparameterization in Equation (23) does not affect string S-matrix, because it does not concern quantum fields [35,36,37]. At the same time, the coefficients can be chosen in such a way that the effective low-energy theory of metric becomes free of massive unphysical ghosts. For instance, the fourth derivative terms combine into the Gauss–Bonnet term in Equation (5), namely
which is topological for but does not contribute to the propagator in any space-time dimension D. The same is true for the combination with extra factors of □,
which may be achieved in the higher orders in by correctly tuning higher order coefficients . As a result, the theory of string produces induced gravity which is free of ghosts and has no issues with renormalizability, since gravity is all induced. All this means that string theory solves the problem of QG in a satisfactory way, of course if we believe that gravity should be induced from string.
It is worthwhile, however, to look into further details of the scheme described above. The first observation is that the reparameterization in Equation (23) is ambiguous and this actually produce ambiguous physical solutions, e.g., in cosmology [38]. For instance, the terms of the form can be arbitrarily changed or removed by this transformation, and this ambiguity and, in general, , do not affect the presence of ghosts at all. One can note, for example, that the most successful model of inflation by Starobinsky [39] requires the term with the well-defined coefficient. Then we have to tune the parameter in Equation (23) such that, after the compactification of extra dimensions, one can provide this desirable value of the coefficient of , instead of making it zero.
Even more subtle point is that the effectively working ghost-killing transformation in Equation (23) must be absolutely precise. An infinitesimal change in the fine-tuning of the parameters would immediately create a ghost with a huge mass. Moreover, smaller violation of the absolutely precise fine-tuning leads to a greater mass of the ghost, hence (according to a “standard wisdom”) a smaller violation of the fine-tuning produces a greater gravitational instability.
Furthermore, we know from all our experience in Physics that at low energies quantum effects are described, e.g., by QFT, and not by string theory. Even higher loop corrections in QED eventually lead to the small violation of the absolutely precise ghost-killing transformation in Equation (23) and produce a huge destructive ghost, as explained above. Hence, string theory is ghost-free and unitary theory of QG, but only if it completely controls all QFT effects, even in the deep IR. It means that string theory must be a real and complete theory of everything to be a consistent theory of QG. The reality of such a control is not obvious, in our opinion.
The second example is an interesting alternative to the original Zwiebach transformation in Equation (23). In the non-local theory [40]
there are no ghosts, regardless of the presence of infinite derivatives in the action (an interesting discussion of physical spectrum and Cauchy problem in the theories of this kind is recently given in [41,42]).
In this and similar theories, propagator of metric perturbations has a single massless pole, corresponding to gravitons. With this choice, there are no ghosts. The idea is to use Zwiebach-like transformation in Equation (23), but arrive at the non-local theory in Equation (26), which is non-polynomial in derivatives, instead of “killing” all higher derivatives that one can kill. From the viewpoint of string theory, this means we have one more ambiguity in the effective low-energy action of gravity.
However, the same action can be used in a distinct way. There is a proposal to use the same kind of non-local models to construct superrenormalizable and unitary models of QG [43,44,45,46]. In such a theory, the propagator is defined by terms bilinear in curvature,
The equation for defining the poles is,
In this particular case, there is only a massless pole corresponding to gravitons. However, unfortunately, it is impossible to preserve the ghost-free structure at the quantum level [47]. Typically, after taking the loop corrections into account, in the dressed propagator, there are infinitely many poles on the complex plane. In this sense, the ghost-free structure of the theory cannot be preserved beyond the tree level.
Thus, we can make a conclusion that there is no way to live without ghosts in QG. In all three fundamental approaches to QG, namely semiclassical, legitimate QG, and induced gravity/strings, there is no reasonable way to get rid of massive ghost-like states.
At this stage, we can only repeat that there is apparently no way to live with ghosts, since their presence implies instability of all classical gravitational solutions and violation of unitarity. In other words, at both classical and quantum level, ghosts do not enable one to have a consistent theory. Therefore, we have a deep conflict between renormalizability and unitarity/stability. At the moment, there is no solution of this great puzzle, but in what follows we present some recent advances in its better understanding.
5. Complex Poles: Old Expectations in the New Setting
The importance of higher derivatives in semiclassical and quantum gravity has been fully recognized since the early 1960s [48], and the bad features of ghosts was completely clear more than 50 years ago [13]. Since then, there are numerous proposal on solving the contradiction between renormalizability and unitarity in QG. In particular, there is a promising idea that ghosts may become complex after taking the loop contributions into account. This means that there can be only complex “massive” poles in the dressed propagator [17,18,19]. Such poles always come in complex conjugate pair, which opens interesting possibilities, related to the Lee–Wick quantization scheme (let us note that another, different approach to deal with ghosts was suggested by Hawking and Hertog [20]). Similar approaches to solve the problem of higher derivative massive ghosts in fourth derivative QG are discussed in [49] and reviewed in [50]. In the last reference, it is shown that the definitive answer on whether this mechanism works can be obtained only on the basis of the full non-perturbative dressed propagator of the gravitational perturbations. One-loop effects of matter fields and proper gravity, large-N approximation and lattice-based considerations indicated an optimistic picture, but unfortunately all of these results are not conclusive, as explained in [50]. As we do not have completely reliable nonperturbative approach to QG, the chances of obtaining complete information about the exact dressed propagator look rather remote (let us mention an interesting attempt [51] to use Functional Renormalization group method for this end). However, do we always need so much to analyze the structure of the dressed propagator?
Starting from [17,18,19], the main hope for the “minimal” fourth-derivative QG was that the real ghost pole splits into a couple of complex conjugate poles under the effect of quantum corrections. We cannot control the position of these complex poles in the dressed propagator, since the higher loop corrections can be complicated, essential and difficult to evaluate. However, for the theory of QG with six or more derivatives [21], this is not necessary at all! In this case, one can simply start from the tree-level theory which has complex conjugate massive poles from the very beginning, and hence there is no need to rely on the precise knowledge of a dressed propagator. In this way, one can successfully construct the theory of quantum gravity which is both unitary and superrenormalizable [52] (see also generalization for an arbitrary dimension in [53]).
Furthermore, one can prove that, in this model, the unitary also holds at the quantum level, in particular because, in such a superrenormalizable model, one can guarantee that the position of the poles in the dressed propagator will be qualitatively the same as in the tree level theory. Further features of this kind of models, such as reflection positivity, has been discussed recently in Refs. [54,55], with somehow contradicting results. Therefore, in what follows we briefly review only the safe and certain result of [52].
For the sake of simplicity, we consider only six-derivative models, as done in [52]. It proves useful to write the six derivative action in a slightly different form,
where are polynomials of the first order. In the momentum representation, one can write
where and are constants of the -dimension.
The part of the action which is quadratic in the perturbations, , has the form
where
are projectors of the spin-0 (scalar) and spin-2 (tensor) modes, and
After the Wick rotation, the equations for the poles are
Now, the solution for the tensor part (scalar sector can be elaborated in a similar way) is
One can distinguish two possible cases in this solution.
- (i)
- Two real positive solutions .
- (ii)
- Two pairs of complex conjugate solutions for the mass.
In the theory of the field , the condition of unitarity of the S-matrix can be formulated in a usual way,
By defining the scattering amplitude as
we arrive at
If we assume that for the forward scattering amplitude , the previous equation simplifies to
The detailed analysis of tree-level, one-loop and multi-loop diagrams shows that the relation in Equation (39) is satisfied because massive poles always show up in complex conjugate pairs. The analysis performed in Reference [52] is mainly at the tree-level, but the complete proof of unitarity can be done on the basis of the scalar model within the Lee–Wick approach, as considered in [56,57], and especially in [58,59]. The proofs of [59] directly apply to the higher derivative gravity superrenormalizable QG with complex massive poles. Finally, we can conclude that this QG theory is unitary, but there may be a violation of causality at the microscopic time scales, defined by the magnitude of masses.
6. Ghost-Induced Instabilities in Cosmology
The unitarity of the S-matrix cannot be regarded as the unique condition of consistency of the QG theory. Even more than that: since gravity is essentially a non-polynomial theory, unitarity cannot be seen even as the most relevant consistency condition. The main requirement should be the stability of physically relevant solutions of classical general relativity in the presence of higher derivatives and massive ghosts.
The study of stability of the general gravitational solutions in the presence of higher derivatives does not appear to be a realistic problem to solve. There are a few publications [60,61] (see also [62]) with conflicting results concerning the stability of Schwarzschild solution in fourth-order gravity. The study of this subject is very complicated and cannot be described in this short review. Hence, we concentrate on the stability on the cosmological background which is much better explored.
The problem has been explored in several old and newer publications, for different cosmological backgrounds. In the case of gravitational waves on de Sitter space and the typical energy of the wave much below , the situation is described in [63,64,65] and in a more detailed and elaborated form, with the special attention to the role of higher derivatives, in [66]. Recently, the case of more general cosmological backgrounds has been reported in Ref. [1] (see also a short review in [67]). Let us start by explaining these results.
6.1. Perturbations: Low Values of k
The main conclusion of [1] is that the absence of growing modes in the fourth derivative theory holds if only if the initial seeds of the gravitational perturbations have frequencies below the threshold which is of the order of Planck mass. The situation is illustrated in Figure 1 for the specific case of radiation-dominated Universe.
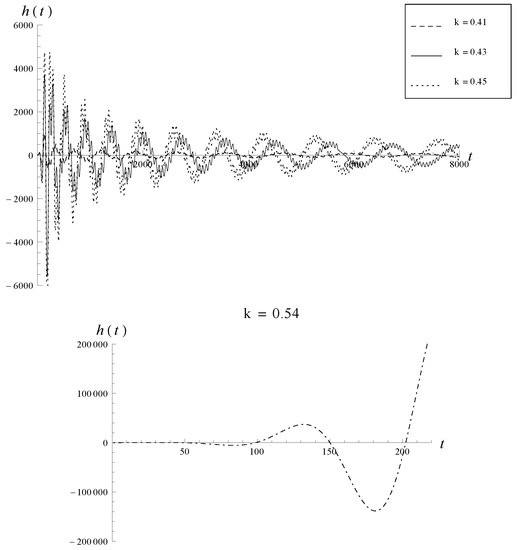
Figure 1.
The solution with growing modes appear only starting from .
One can observe in Figure 1 that there are no growing modes, until the frequency k achieves the value ≈ in the Planck units. Starting from this value, we observe instability due to the effect of massive ghost. Our interpretation of this result is that the ghost is present in the spectrum of the theory, but if there is no real ghost in the universe, there is no instability. The massive ghost cannot be created from the vacuum if the density of gravitons does not approach the Planck density which is required to create a ghost from the vacuum state.
Of course, the concentration of gravitons of the Planck order of magnitude is not forbidden by all known physical laws. Hence, we can expect that some new laws should be discovered to resolve the problem of consistent QG. We can see that these new laws must forbid the Planck order density of gravitons to resolve the issue, at least for the case of a cosmological background.
Let us note that the semiclassical (anomaly-induced) corrections were also considered [1]. As these corrections are at least , it is natural that the qualitative result for the Planck order threshold for stability does not change. The reason is that, until the energy of the gravitational perturbations does not approach the Planck order of magnitude, these corrections cannot compete with the classical -terms and, e.g., their running.
To illustrate better the existence of the Planck threshold, we included the 3D plot in Figure 2.
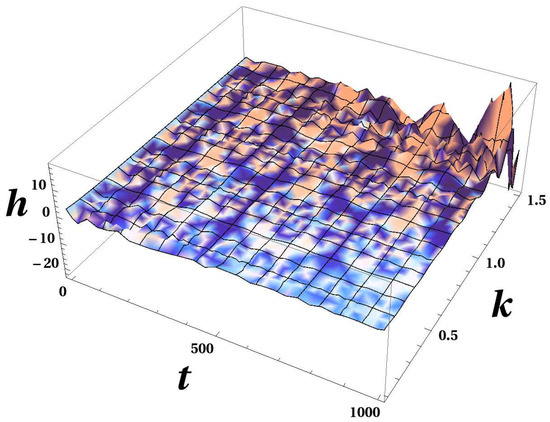
Figure 2.
In this plot, we use the units and the values and . The tensor perturbation mode h is shown as function of time t and of the initial frequency k. Until the values of k are small, there are no strongly growing solutions. However, when k gets closer to the Planck scale, the perturbations start to explode because of the high derivatives terms.
In this figure, one can observe perturbation h as function of time and of the initial frequency k. In the 3D plot, one can observe a “normal” oscillation for small values of k, and then the solution explodes abruptly for k close to the Planck mass scale. Apparently, for the values , there are run-away solutions.
6.2. Perturbations: High Values of k
Thus, we have a generally optimistic situation for the sub-Planckian frequencies. Indeed, this is not a really nice situation, from the general perspective. The remaining question is: What can we do with ghosts in the case of Planck order or greater frequencies? To answer this question, let us follow [2] and take a look at the simplest possible equation for the fourth-derivative gravity without quantum or semiclassical corrections,
It is easy to note that the space derivatives ∇ and hence the wave vector enter this equation only in the combination
When the universe expands, the frequency becomes smaller. This qualitative conclusion is supported by numerical analysis described in Ref. [2], including the model with semiclassical corrections taken into account.
In Figure 3, one can see that the growth of the gravitational waves with transplanckian frequencies really stops at some point. At least in the cosmological setting this may be a solution of the general problem.
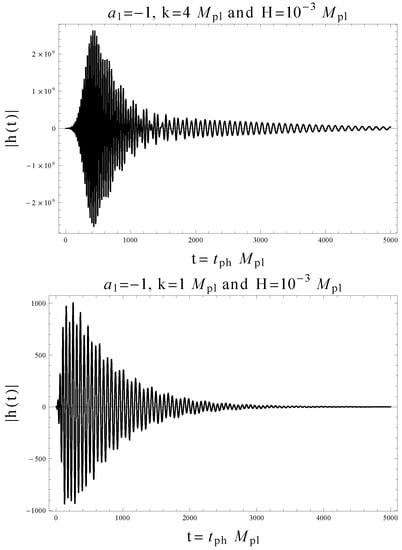
Figure 3.
In the case of radiation background and transplanckian frequencies, there is an explosive growth of perturbations that stabilize soon after they start. In these two plots, we use (normalized), , and .
In this case, we have in the gravitational theory with high derivatives terms. Unlike the previous case of relatively small frequencies, one can observe the effects of ghosts, since the run-away solutions almost instantly appear. However, after a while, these solutions become damped, because the effective frequency tends to decrease due to the fast expansion of the universe.
7. Conclusions
Let us make a few concluding statements about the situation with ghosts which was described above.
- (i)
- We know that there is no way to have semiclassical or quantum gravity without higher derivatives. The effective approaches imply treating higher derivatives as small perturbations over the basic theory which is GR with the cosmological constant. However, this treatment has several weak points. First, is it completely ad hoc and does not follow from the QFT logic, quite different from the situation in QED, where higher derivatives emerge only in the loop corrections, the corresponding terms do not run and treating them as small corrections does not lead to inconsistencies at the energy scales where the theory is supposed to work. The situation in QG is completely different, because the last is supposed to apply up to the Planck energies.
- (ii)
- Higher derivatives mean ghosts and instabilities. However, in the closed system, the problem can be solved because there is no energy to provide a global and total explosion of ghost or even tachyonic ghost modes (Lee–Wick approach). This way of thinking provides the theory which is formally superrenormalizable and unitary at the same time. However, this does not solve the problem of stability, which remains open. The main reason is that the real gravitational systems are not closed, and the metric perturbations propagate on the non-trivial backgrounds of classical gravitational solutions. Therefore, one needs an essential completion, or supplement to the proof of unitarity. This means we need a new insight about how the stability problem can be solved.
- (iii)
- The analysis of linear stability on the cosmological background shows that the perturbations with the initial seeds with the frequencies below the Planck-order threshold do not grow. The natural interpretation of this fact is that, without the Planck-order density of gravitons, one cannot create ghost from the vacuum.
Perhaps there is some unknown principle of Physics which forbids Planck-scale concentration of gravitons? Some discussion of the physical consequences of such a principle has been recently discussed in the literature [68,69].
The restriction on the initial frequencies can be violated for the Planck-scale background, which “opens” the phase space of quantum states and enables the production of instabilities. However, after that, the expansion of the universe reduces the frequencies and the instabilities become stabilized. This specific behaviour of perturbations in the theories with higher derivatives creates a hope to observe the traces of these theories in observations of transplanckian effects, as discussed in [70,71,72].
Author Contributions
The authors contributed equally to this work.
Funding
This research was partially funded by CNPq, grant number 303893/2014-1 and by FAPEMIG, grant number APQ-01205-16.
Acknowledgments
This review was based on the original works that were done in collaboration with Leonardo Modesto and Patrick Peter. We gratefully acknowledge these collaborations.
Conflicts of Interest
The author declares no conflict of interest.
References
- De O. Salles, F.; Shapiro, I.L. Do we have unitary and (super)renormalizable quantum gravity below the Planck scale? Phys. Rev. D 2014, 89, 084054, Erratum in 2014, 90, 129903. [Google Scholar]
- Peter, P.; De O. Salles, F.; Shapiro, I.L. On the ghost-induced instability on de Sitter background. Phys. Rev. D 2018, 97, 064044. [Google Scholar] [CrossRef]
- Birell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP Publishing: Bristol, UK, 1992. [Google Scholar]
- Shapiro, I.L. Effective Action of Vacuum: Semiclassical Approach. Class. Quantum Gravity 2008, 25, 103001. [Google Scholar] [CrossRef]
- Cusin, G.; De O. Salles, F.; Shapiro, I.L. Tensor instabilities at the end of the LCDM universe. Phys. Rev. D 2016, 93, 044039. [Google Scholar] [CrossRef]
- T’Hooft, G.; Veltman, M. One-loop divergences in the theory of gravitation. Ann. Inst. Henri Poincaré A 1974, 20, 69–94. [Google Scholar]
- Deser, S.; van Nieuwenhuisen, P. One-loop divergences of quantized Einstein-Maxwell fields. Phys. Rev. D 1974, 10, 401–410. [Google Scholar] [CrossRef]
- Goroff, M.H.; Sagnotti, A. The Ultraviolet Behavior of Einstein Gravity. Nucl. Phys. B 1986, 266, 709–736. [Google Scholar] [CrossRef]
- Donoghue, J. Leading quantum correction to the Newtonian potential. Phys. Rev. Lett. 1994, 72, 2996. [Google Scholar] [CrossRef] [PubMed]
- Donoghue, J. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874–3888. [Google Scholar] [CrossRef]
- Burgess, C.P. Quantum gravity in everyday life: General relativity as an effective field theory. Living Rev. Relativ. 2004, 7, 5–56. [Google Scholar] [CrossRef] [PubMed]
- Stelle, K.S. Renormalization of higher-derivative quantum gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Ostrogradsky, M.V. Mémoires sur les équations différentielles, relatives au problème des isopérimètres. Mem. Acad. St. Petersbg. 1850, 6, 385–517. [Google Scholar]
- Woodard, R.P. Avoiding dark energy with 1/r modifications of gravity. In The Invisible Universe: Dark Matter and Dark Energy; Lecture Notes in Physics Book Series; Springer: Berlin/Heidelberg, Germany, 2007; Volume 720, pp. 403–433. [Google Scholar]
- Veltman, M. Unitarity and causality in a renormalizable field theory with unstable particles. Physica 1963, 29, 186–207. [Google Scholar] [CrossRef]
- Tomboulis, E.T. Renormalizability and Asymptotic Freedom in Quantum Gravity. Phys. Lett. B 1977, 70, 77–80. [Google Scholar] [CrossRef]
- Tomboulis, E.T. Unitarity in Higher Derivative Quantum Gravity. Phys. Rev. Lett. 1984, 52, 1173–1176. [Google Scholar] [CrossRef]
- Salam, A.; Strathdee, J. Remarks on high-energy stability and renormalizability of gravity theory. Phys. Rev. D 1978, 18, 4480–4485. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hertog, T. Living with ghosts. Phys. Rev. D 2002, 65, 103515. [Google Scholar] [CrossRef]
- Asorey, M.; López, J.L.; Shapiro, I.L. Some remarks on high derivative quantum gravity. Int. J. Mod. Phys. A 1977, 12, 5711–5734. [Google Scholar] [CrossRef]
- Modesto, L.; de Paula Netto, T.; Shapiro, I.L. On Newtonian singularities in higher derivative gravity models. J. High Energy Phys. 2015, 2015, 98. [Google Scholar] [CrossRef]
- Giacchini, B.L. On the cancellation of Newtonian singularities in higher-derivative gravity. Phys. Lett. B 2017, 766, 306–311. [Google Scholar] [CrossRef]
- Accioly, A.; Giacchini, B.L.; Shapiro, I.L. Low-energy effects in a higher-derivative gravity model with real and complex massive poles. Phys. Rev. D 2017, 96, 104004. [Google Scholar] [CrossRef]
- Accioly, A.; Giacchini, B.L.; Shapiro, I.L. On the gravitational seesaw in higher-derivative gravity. Eur. Phys. J. C 2017, 77, 540. [Google Scholar] [CrossRef]
- Modesto, L.; Rachwal, L.; Shapiro, I.L. Renormalization group in super-renormalizable quantum gravity. Eur. Phys. J. C 2018, 78, 555. [Google Scholar] [CrossRef]
- Simon, J.Z. Higher-derivative Lagrangians, nonlocality, problems, and solutions. Phys. Rev. D 1990, 41, 3720. [Google Scholar] [CrossRef]
- Simon, J.Z. Stability of flat space, semiclassical gravity, and higher derivatives. Phys. Rev. D 1991, 43, 3308–3316. [Google Scholar] [CrossRef]
- Simon, J.Z. No Starobinsky inflation from selfconsistent semiclassical gravity. Phys. Rev. D 1992, 45, 1953–1960. [Google Scholar] [CrossRef]
- Parker, L.; Simon, J.Z. Einstein equation with quantum corrections reduced to second order. Phys. Rev. D 1993, 47, 1339–1355. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Shapiro, I.L.; Sibiryakov, A.G. On Weyl Invariance condition in string theory coupled with two-dimensional gravity. Nucl. Phys. B 1995, 445, 109–128. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Effective field theory from quantized strings. Phys. Lett. B 1985, 158, 316–322. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Quantum string theory effective action. Nucl. Phys. B 1985, 261, 1–27. [Google Scholar] [CrossRef]
- Callan, C.; Friedan, D.; Martinec, E.; Perry, M.J. Strings in background fields. Nucl. Phys. B 1985, 272, 593–609. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature squared terms and string theories. Phys. Lett. B 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Deser, S.; Redlich, A.N. String-induced gravity and ghost-freedom. Phys. Lett. B 1986, 176, 350–354. [Google Scholar] [CrossRef]
- Tseytlin, A.A. Ambiguity in the effective action in string theories. Phys. Lett. B 1986, 176, 92–98. [Google Scholar] [CrossRef]
- Maroto, A.L.; Shapiro, I.L. On the inflationary solutions in higher-derivative gravity with dilaton field. Phys. Lett. B 1997, 414, 34–44. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Tseytlin, A.A. On singularities of spherically symmetric backgrounds in string theory. Phys. Lett. B 1995, 363, 223–229. [Google Scholar] [CrossRef]
- Calcagni, G.; Modesto, L.; Nardelli, G. Nonperturbative spectrum of nonlocal gravity. arXiv, 2018; arXiv:1803.07848. [Google Scholar]
- Calcagni, G.; Modesto, L.; Nardelli, G. Initial conditions and degrees of freedom of non-local gravity. J. High Energy Phys. 2018, 2018, 87. [Google Scholar] [CrossRef]
- Tomboulis, E.T. Superrenormalizable gauge and gravitational theories. arXiv, 1997; arXiv:hep-th/9702146. [Google Scholar]
- Tomboulis, E.T. Nonlocal and quasilocal field theories. Phys. Rev. D 2015, 92, 125037. [Google Scholar] [CrossRef]
- Tomboulis, E.T. Renormalization and unitarity in higher derivative and nonlocal gravity theories. Mod. Phys. Lett. A 2015, 30, 1540005. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Shapiro, I.L. Counting ghosts in the “ghost-free” non-local gravity. Phys. Lett. B 2015, 744, 67–73. [Google Scholar] [CrossRef]
- Utiyama, R.; DeWitt, B.S. Renormalization of a classical gravitational field interacting with quantized matter fields. J. Math. Phys. 1962, 3, 608–618. [Google Scholar] [CrossRef]
- Antoniadis, I.; Tomboulis, E.T. Gauge Invariance And Unitarity In Higher Derivative Quantum Gravity. Phys. Rev. D 1986, 33, 2756–2779. [Google Scholar] [CrossRef]
- Johnston, D.A. Sedentary Ghost Poles In Higher Derivative Gravity. Nucl. Phys. B 1988, 297, 721–732. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R. Fixed points of higher derivative gravity. Phys. Rev. Lett. 2006, 97, 221301. [Google Scholar] [CrossRef] [PubMed]
- Modesto, L.; Shapiro, I.L. Superrenormalizable quantum gravity with complex ghosts. Phys. Lett. B 2016, 755, 279–284. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable or finite Lee–Wick quantum gravity. Nucl. Phys. B 2016, 909, 584–606. [Google Scholar] [CrossRef]
- Asorey, M.; Rachwal, L.; Shapiro, I.L. Unitary Issues in Some Higher Derivative Field Theories. Galaxies 2018, 6, 23. [Google Scholar] [CrossRef]
- Christodoulou, M.; Modesto, L. Reflection positivity in nonlocal gravity. arXiv, 2018; arXiv:1803.08843. [Google Scholar]
- Lee, T.D.; Wick, G.C. Finite Theory of Quantum Electrodynamics. Phys. Rev. D 1970, 2, 1033. [Google Scholar] [CrossRef]
- Lee, T.D.; Wick, G.C. Negative Metric and the Unitarity of the S Matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Cutkosky, R.E.; Landshoff, P.V.; Olive, D.I.; Polkinghorne, J.C. A non-analytic S matrix. Nucl. Phys. B 1969, 12, 281–300. [Google Scholar] [CrossRef]
- Grinstein, B.; O’Connell, D.; Wise, M.B. Causality as an emergent macroscopic phenomenon: The Lee-Wick O(N) model. Phys. Rev. D 2009, 79, 105019. [Google Scholar] [CrossRef]
- Whitt, B. Stability of Schwarzschild black holes in fourth-order gravity. Phys. Rev. D 1985, 32, 379–388. [Google Scholar] [CrossRef]
- Myung, Y.S. Stability of Schwarzschild black holes in fourth-order gravity revisited. Phys. Rev. D 2013, 88, 024039. [Google Scholar] [CrossRef]
- Mauro, S.; Balbinot, R.; Fabbri, A.; Shapiro, L. Fourth derivative gravity in the auxiliary fields representation and application to the black hole stability. Eur. Phys. J. Plus 2015, 130, 135. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Evolution of Small Excitation of Isotropic Cosmological Models With One Loop Quantum Gravitation Corrections. Pisma Zh. Eksp. Teor. Fiz. 1981, 34, 460–463. [Google Scholar]
- Hawking, S.W.; Hertog, T.; Real, H.S. Trace anomaly driven inflation. Phys. Rev. D 2001, 63, 083504. [Google Scholar] [CrossRef]
- Fabris, J.C.; Pelinson, A.M.; Shapiro, I.L. On the gravitational waves on the background of anomaly-induced inflation. Nucl. Phys. B 2001, 597, 539–560. [Google Scholar] [CrossRef]
- Fabris, J.C.; Pelinson, A.M.; de O. Salles, F.; Shapiro, I.L. Gravitational waves and stability of cosmological solutions in the theory with anomaly-induced corrections. J. Cosmol. Astropart. Phys. 2012, 2, 19. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Pelinson, A.M.; de O. Salles, F. Gravitational waves and perspectives for quantum gravity. Mod. Phys. Lett. A 2014, 29, 1430034. [Google Scholar] [CrossRef]
- Dvali, G.; Folkerts, S.; Germani, C. Physics of trans-Planckian gravity. Phys. Rev. D 2011, 84, 024039. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Black hole’s quantum N-portrait. Fortschr. Phys. 2013, 63, 742–767. [Google Scholar] [CrossRef]
- Martin, J.; Brandenberger, R.H. The TransPlanckian problem of inflationary cosmology. Phys. Rev. D 2001, 63, 123501. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Robustness of the inflationary perturbation spectrum to transPlanckian physics. Pisma Zh. Eksp. Teor. Fiz. 2001, 73, 415–418. [Google Scholar]
- Starobinsky, A.A. Robustness of the inflationary perturbation spectrum to trans-Planckian physics. J. Exp. Theor. Phys. Lett. 2001, 73, 371–374. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).