Prospects of Constraining the Dense Matter Equation of State from Timing Analysis of Pulsars in Double Neutron Star Binaries: The Cases of PSR J0737 ‒ 3039A and PSR J1757 ‒ 1854
Abstract
:1. Introduction
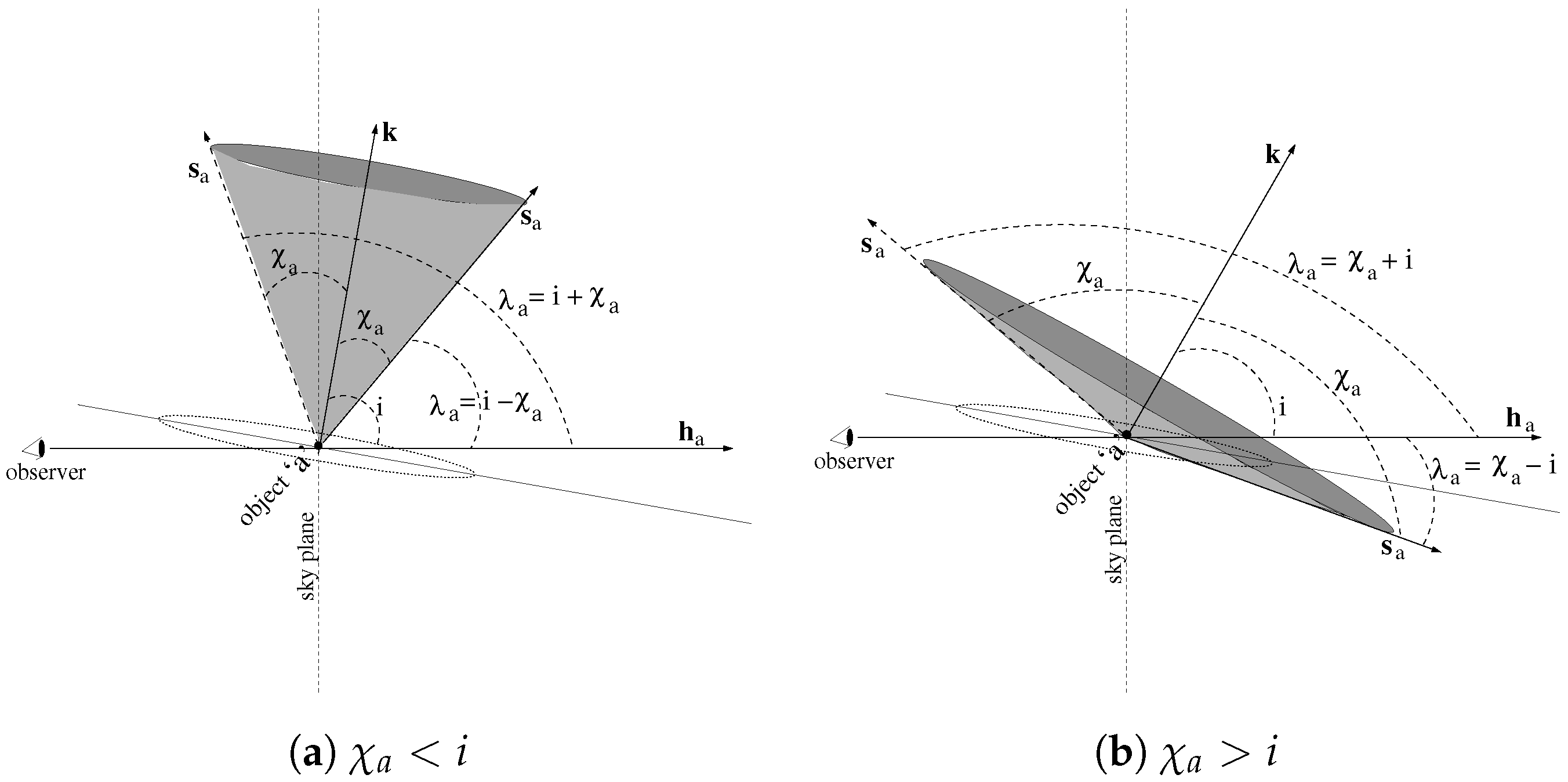
2. Precession in Double Neutron Star Binaries
Periastron Advance
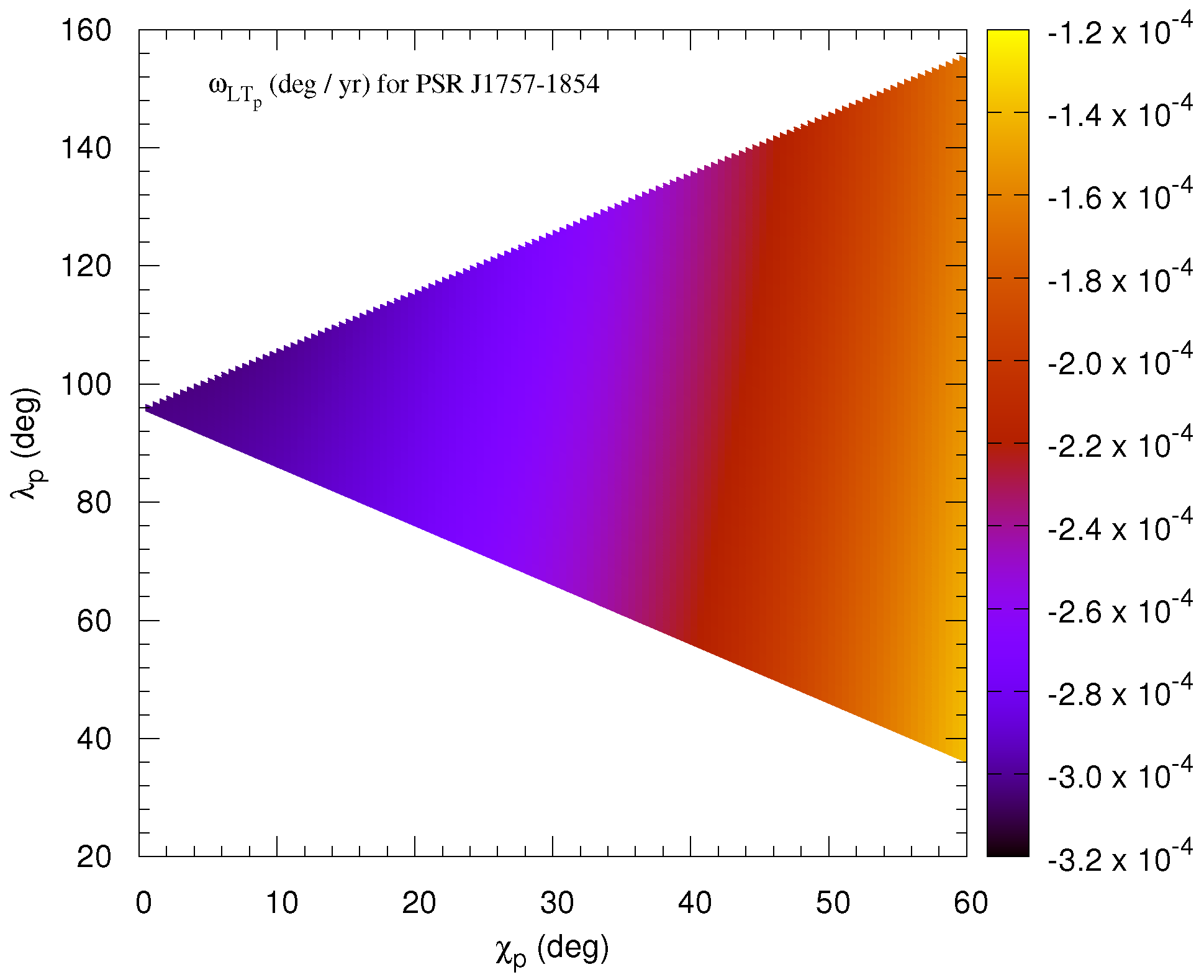
3. Results
4. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Van Straten, W.; Bailes, M.; Britton, M.; Kulkarni, S.R.; Anderson, S.B.; Manchester, R.N.; Sarkissian, J. A test of general relativity from the three-dimensional orbital geometry of a binary pulsar. Nature 2001, 412, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Deller, A.T.; Boyles, J.; Lorimer, D.R.; Kaspi, V.M.; McLaughlin, M.A.; Ransom, S.; Stairs, I.H.; Stovall, K. VLBI Astrometry of PSR J2222 − 0137: A Pulsar Distance Measured to 0.4% Accuracy. Astrophys. J. 2013, 770, 145. [Google Scholar] [CrossRef]
- Deller, A.T.; Vigeland, S.J.; Kaplan, D.L.; Goss, W.M.; Brisken, W.F.; Chatterjee, S.; Cordes, J.M.; Janssen, G.H.; Lazio, T.J.W.; Petrov, L.; et al. Microarcsecond VLBI Pulsar Astrometry with PSRπ. I. Two Binary Millisecond Pulsars with White Dwarf Companions. Astrophys. J. 2017, 828, 8. [Google Scholar] [CrossRef]
- Lorimer, D.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge Observing Handbooks for Research Astronomers; Cambridge University Press: Cambridge, UK, 2005; pp. 32–58. [Google Scholar]
- Freire, P.C.C.; Wex, N. The orthometric parametrization of the Shapiro delay and an improved test of general relativity with binary pulsars. Mon. Not. R. Astron. Soc. 2010, 409, 199–212. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N. Strong-field tests of gravity with the double pulsar. Annalen der Physik 2006, 15, 34–42. [Google Scholar] [CrossRef]
- Stairs, I. Testing General Relativity with Pulsar Timing. Living Rev. Relat. 2003, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M. Pulsars as probes of gravity and fundamental physics. Int. J. Mod. Phys. 2016, 25, 1630029–1630061. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. arXiv 2017, arXiv:1711.02644. [Google Scholar]
- Ayriyan, A.; Bastian, N.U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. How robust is a third family of compact stars against pasta phase effects? arXiv 2017, arXiv:1711.03926. [Google Scholar]
- Kurkela, A.; Romatschke, P.; Vuorinen, A. Cold quark matter. Phys. Rev. D 2010, 81, 105021. [Google Scholar] [CrossRef]
- Perera, B.B.P.; McLaughlin, M.A.; Kramer, M.; Stairs, I.H.; Ferdman, R.D.; Freire, P.C.C.; Possenti, A.; Breton, R.P.; Manchester, R.N.; Burgay, M.; et al. The Evolution of PSR J0737 − 3039B and a Model for Relativistic Spin Precession. Astrophys. J. 2010, 721, 1193–1205. [Google Scholar] [CrossRef]
- Cameron, A.D.; Champion, D.J.; Kramer, M.; Bailes, M.; Barr, E.D. The High Time Resolution Universe Pulsar Survey—XIII. PSR J1757 − 1854, the most accelerated binary pulsar. 2018, 475, L57–L61. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Chatterjee, S.; Demorest, P.B.; Lorimer, D.R. PALFA Discovery of a Highly Relativistic Double Neutron Star Binary. Astrophys. J. 2018, 231, 453. [Google Scholar]
- Barker, B.M.; O’Connell, R.F. The gravitational interaction: Spin, rotation, and quantum effects—A review. Gen. Relat. Gravit. 1979, 11, 149–175. [Google Scholar] [CrossRef]
- Perera, B.B.P.; Kim, C.; McLaughlin, M.A.; Ferdman, R.D.; Kramer, M.; Stairs, I.H.; Freire, P.C.C.; Possenti, A. Realistic Modeling of the Pulse Profile of PSR J0737 − 3039A. Astrophys J. 2014, 787, 51. [Google Scholar] [CrossRef]
- Pol, N.; McLaughlin, M.; Kramer, M.; Stairs, I.; Perera, B.B.P.; Possenti, A. A direct measurement of sense of rotation of PSR J0737 − 3039A. Astrophys. J. 2018, 853, 73. [Google Scholar] [CrossRef]
- Breton, R.P.; Kaspi, V.M.; Kramer, M. Relativistic Spin Precession in the Double Pulsar. Science 2008, 321, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Damour, T.; Schafer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo Cim. B 1988, 101, 127–176. [Google Scholar] [CrossRef]
- Kopeikin, S.M. Proper Motion of Binary Pulsars as a Source of Secular Variations of Orbital Parameters. Astrophys. J. 1996, 467, L93. [Google Scholar] [CrossRef]
- Bagchi, M. Rotational parameters of strange stars in comparison with neutron stars. New Astron. 2010, 15, 126–134. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Breton, R.P.; McLaughlin, M.A.; Freire, P.C.C.; Possenti, A.; Stappers, B.W.; Kaspi, V.M.; Manchester, R.N.; et al. The Double Pulsar: Evidence for Neutron Star Formation without an Iron Core-collapse Supernova. Astrophys. J. 2013, 767, 85. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Nozawa, T.; Stergioulas, N.; Gourgoulhon, E.; Eriguchi, Y. Construction of highly accurate models of rotating neutron stars—Comparison of three different numerical schemes. Astron. Astrophys. Suppl. Ser. 1998, 132, 431–454. [Google Scholar] [CrossRef]
- Deller, A.T.; Bailes, M.; Tingay, S.J. Implications of a VLBI Distance to the Double Pulsar J0737-3039A/B. Science 2009, 323, 1327–1329. [Google Scholar] [CrossRef] [PubMed]
- Pathak, D.; Bagchi, M. GalDynPsr: A package to estimate dynamical contributions in the rate of change of the period of radio pulsars. arXiv 2017, arXiv:1712.06590. [Google Scholar]
- Kramer, M.; Wex, N. TOPICAL REVIEW: The double pulsar system: A unique laboratory for gravity. Class. Quantum Gravity 2009, 26, 073001. [Google Scholar] [CrossRef]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future measurements of the Lense-Thirring effect in the Double Pulsar. In Proceedings of the Fourteenth Marcel Grossmann Meeting, Rome, Italy, 12–18 July 2015. [Google Scholar]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv 2001, arXiv:astro-ph/0207156. [Google Scholar]
- Cordes, J.M.; Lazio, T.J.W. NE2001. II. Using Radio Propagation Data to Construct a Model for the Galactic Distribution of Free Electrons. arXiv 2003, arXiv:astro-ph/0301598. [Google Scholar]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic measurements from timing the binary pulsar PSR B1913 + 16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Tauris, T.M.; Ridolfi, A.; Wex, N.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M. Pulsar J1411+2551: A Low-mass Double Neutron Star System. Astrophys. J. 2017, 851, L29. [Google Scholar] [CrossRef]
- Janssen, G.H.; Stappers, B.W.; Kramer, M.; Nice, D.J.; Jessner, A.; Cognard, I.M.B.; Purver, M.B. Multi-telescope timing of PSR J1518 + 4904. Astron. Astrophys. 2008, 490, 753–761. [Google Scholar]
- Fonseca, E.; Stairs, I.H.; Thorsett, S.E. A Comprehensive Study of Relativistic Gravity Using PSR B1534 + 12. Astrophys. J. 2014, 787, 82. [Google Scholar] [CrossRef]
- Keith, M.J.; Kramer, M.; Lyne, A.G.; Eatough, R.P.; Stairs, I.H.; Possenti, A.; Camilo, F.; Manchester, R.N. PSR J1753 − 2240: A mildly recycled pulsar in an eccentric binary system. Mon. Not. R. Astron. Soc. 2009, 393, 623–627. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Janssen, G.H.; Bassa, C.G.; Stappers, B.W.; Demorest, P.B.; Cognard, I.; Desvignes, G.; Theureau, G.; et al. PSR J1756 − 2251: A pulsar with a low-mass neutron star companion. Mon. Not. R. Astron. Soc. 2014, 443, 2183–2196. [Google Scholar] [CrossRef] [Green Version]
- Lynch, R.S.; Freire, P.C.C.; Ransom, S.M.; Jacoby, B.A. The Timing of Nine Globular Cluster Pulsars. Astrophys. J. 2012, 745, 109. [Google Scholar] [CrossRef]
- Corongiu, A.; Kramer, M.; Stappers, B.W.; Lyne, A.G.; Jessner, A.; Possenti, A.; D’Amico, N.; Löhmer, O. The binary pulsar PSR J1811 − 1736: Evidence of a low amplitude supernova kick. Astron. Astrophys. 2007, 462, 703–709. [Google Scholar] [CrossRef]
- Hobbs, G.; Lyne, A.G.; Kramer, M.; Martin, C.E.; Jordan, C. Long-term timing observations of 374 pulsars. Mon. Not. R. Astron. Soc. 2004, 353, 1311–1344. [Google Scholar] [CrossRef]
- Champion, D.J.; Lorimer, D.R.; McLaughlin, M.A.; Cordes, J.M.; Arzoumanian, Z.; Weisberg, J.M.; Taylor, J.H. PSR J1829 + 2456: A relativistic binary pulsar. Mon. Not. R. Astron. Soc. 2004, 350, L61–L65. [Google Scholar] [CrossRef]
- Van Leeuwen, J.; Kasian, L.; Stairs, I.H.; Lorimer, D.R.; Camilo, F. The Binary Companion of Young, Relativistic Pulsar J1906+0746. Astrophys. J. 2015, 798, 118. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Nice, D.J.; Taylor, J.H. Timing Measurements of the Relativistic Binary Pulsar PSR B1913 + 16. Astrophys. J. 2010, 722, 1030–1034. [Google Scholar] [CrossRef]
- Swiggum, J.K.; Rosen, R.; McLaughlin, M.A.; Lorimer, D.R.; Heatherly, S. PSR J1930 − 1852: A Pulsar in the Widest Known Orbit around Another Neutron Star. Astrophys. J. 2015, 805, 156. [Google Scholar] [CrossRef]
- Jacoby, B.A.; Cameron, P.B.; Jenet, F.A.; Anderson, S.B.; Murty, R.N.; Kulkarni, S.R. Measurement of Orbital Decay in the Double Neutron Star Binary PSR B2127 + 11C. Astrophys. J. 2006, 644, L113–L116. [Google Scholar] [CrossRef]
- Iorio, L. Prospects for measuring the moment of inertia of pulsar J0737-3039A. New Astron. 2009, 1, 40–43. [Google Scholar] [CrossRef]
- O’Connell, R.F. Proposed New Test of Spin Effects in General Relativity. Phys. Rev. Lett. 2004, 93, 081103. [Google Scholar] [CrossRef] [PubMed]
- Bejger, M.; Bulik, T.; Haensel, P. Constraints on the dense matter equation of state from the measurements of PSR J0737 − 3039A moment of inertia and PSR J0751 + 1807 mass. Mon. Not. R. Astron. Soc. 2005, 364, 635–639. [Google Scholar] [CrossRef]
- Iorio, L. General relativistic spin-orbit and spin-spin effects on the motion of rotating particles in an external gravitational field. Gen. Relat. Gravit. 2012, 44, 719–736. [Google Scholar] [CrossRef]
- Iorio, L. Post-Keplerian perturbations of the orbital time shift in binary pulsars: an analytical formulation with applications to the galactic center. Eur. Phys. J. C 2017, 77, 439. [Google Scholar] [CrossRef]
| 1. | |
| 2. | Although for the last few years, the slow pulsar of the system is not visible and is believed to be beaming away from the Earth due to its spin-precession [16]. |
| 3. | RNS stands for ‘Rapidly Rotating Neutron Star’, a package to calculate different properties of rotating neutron stars, freely available at http://www.gravity.phys.uwm.edu/rns/. |
| DNS | Masses | e | Refs. | |||||
|---|---|---|---|---|---|---|---|---|
| Days | ms | deg | ||||||
| J0453+1559 | 1.559 | 0.11251832 | 4.072468588 | 0.9671343 | 45.781816163093 | 0.0379412 | − | R1 |
| (DDGR) | 1.174 | |||||||
| J0737−3039A | 0.0877775 | 0.10225156248 | 0.99974 | 22.70 | 16.89947 | R2, R | ||
| J0737−3039B | 2773.46 | 138 | ||||||
| J1411+2551 | 0.1699308 | 2.61585677939 | − | 62.452895517590 | 0.0768 | − | R3 | |
| J1518+4904 | 0.24948451 | 8.6340050964 | 40.934988908 | 0.0113725 | − | R4 | ||
| B1534+12 | 0.27367740 | 0.420737298881 | 0.97496 | 37.9044411783 | 1.755795 | R5 | ||
| (DDGR) | ||||||||
| J1753−2240 † | − | 0.303582 | 13.6375668 | − | 95.1378086771 | − | − | R6 |
| J1756−2251 | 1.341 | 0.1805694 | 0.31963390143 | 0.93 | 28.4615890259983 | 2.58240 | R7 | |
| 1.230 | ( value) | |||||||
| J1757−1854 | 1.3384 | 0.6058142 | 0.18353783587 | 0.9945 | 21.497231890027 | 10.3651 | R8 | |
| 1.3946 | (theoretical) | |||||||
| J1807−2500B † | 1.3655 | 0.747033198 | 9.9566681588 | 0.9956 | 4.18617720284089 | 0.0183389 | − | R9 |
| 1.2064 | ||||||||
| J1811−1736 | 0.828011 | 18.7791691 | − | 104.1819547968 | 0.0090 | − | R10 | |
| B1820−11 † | − | 0.794608 | 357.76199 | − | 279.828696565349 | 0.00007 | − | R11 |
| J1829+2456 | 0.13914 | 1.176028 | − | 41.00982358 | 0.28 | − | R12 | |
| J1906+0746 | 1.291 | 0.0852996 | 0.16599304686 | 0.690882411 | 144.07315538 | 7.5844 | R13 | |
| (DDGR) | 1.322 | |||||||
| B1913+16 | 0.6171334 | 0.322997448911 | 0.68 ‡ | 59.03000322 | 4.226598 | 22 | R14, Rχ1 | |
| J1930−1852 | 0.39886340 | 45.0600007 | − | 185.52016047926 | 0.00078 | − | R15 | |
| J1946+2052 | − | 0.063848 | 0.07848804 | − | 16.9601753230 | 25.6 | − | R16 |
| B2127+11C | 1.358 | 0.681395 | 0.33528204828 | − | 30.52929614864 | 4.4644 | − | R17 |
| 1.354 |
| DNS | |||
|---|---|---|---|
| J0453+1559 | 0.03794 | ||
| J0737−3039A | 16.90312 | ||
| J1411+2551 | 0.07681 | − | |
| J1518+4904 | 0.01138 | − | |
| B1534+12 | 1.75533 | ||
| J1753−2240 | − | − | − |
| J1756−2251 | 2.58363 | ||
| J1757−1854 | 10.36772 | ||
| J1807−2500B | 0.01834 | ||
| J1811−1736 | 0.00895 | − | |
| B1820−11 | − | − | − |
| J1829+2456 | 0.29284 | − | |
| J1906+0746 | 7.58528 | ||
| B1913+16 | 4.22760 | ||
| J1930−1852 | 0.00079 | − | |
| J1946+2052 | − | − | − |
| B2127+11C | 4.46458 | − |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagchi, M. Prospects of Constraining the Dense Matter Equation of State from Timing Analysis of Pulsars in Double Neutron Star Binaries: The Cases of PSR J0737 ‒ 3039A and PSR J1757 ‒ 1854. Universe 2018, 4, 36. https://doi.org/10.3390/universe4020036
Bagchi M. Prospects of Constraining the Dense Matter Equation of State from Timing Analysis of Pulsars in Double Neutron Star Binaries: The Cases of PSR J0737 ‒ 3039A and PSR J1757 ‒ 1854. Universe. 2018; 4(2):36. https://doi.org/10.3390/universe4020036
Chicago/Turabian StyleBagchi, Manjari. 2018. "Prospects of Constraining the Dense Matter Equation of State from Timing Analysis of Pulsars in Double Neutron Star Binaries: The Cases of PSR J0737 ‒ 3039A and PSR J1757 ‒ 1854" Universe 4, no. 2: 36. https://doi.org/10.3390/universe4020036
APA StyleBagchi, M. (2018). Prospects of Constraining the Dense Matter Equation of State from Timing Analysis of Pulsars in Double Neutron Star Binaries: The Cases of PSR J0737 ‒ 3039A and PSR J1757 ‒ 1854. Universe, 4(2), 36. https://doi.org/10.3390/universe4020036





