Strangeness Production in Nucleus-Nucleus Collisions at SIS Energies
Abstract
:1. Introduction
2. Model Description
3. Results
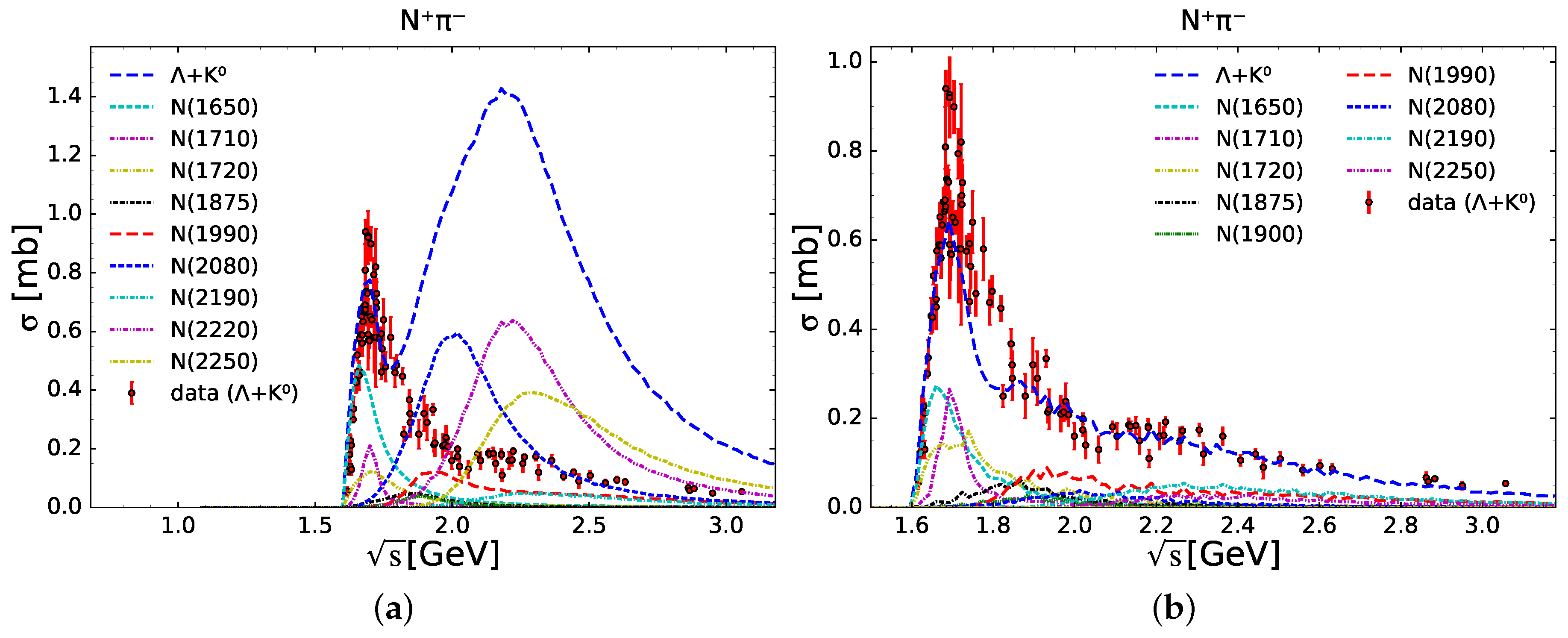
3.1. Hyperon Production via Resonances
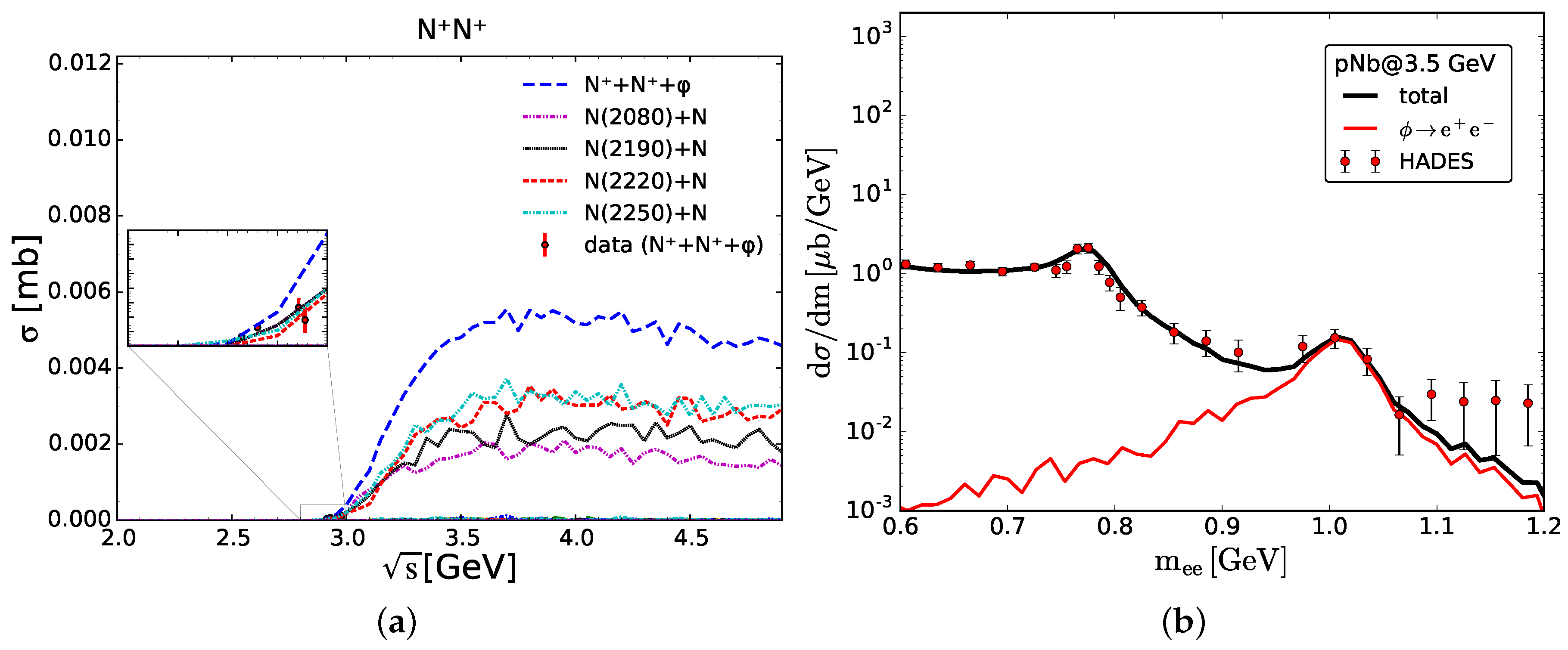
3.2. Production via Resonances
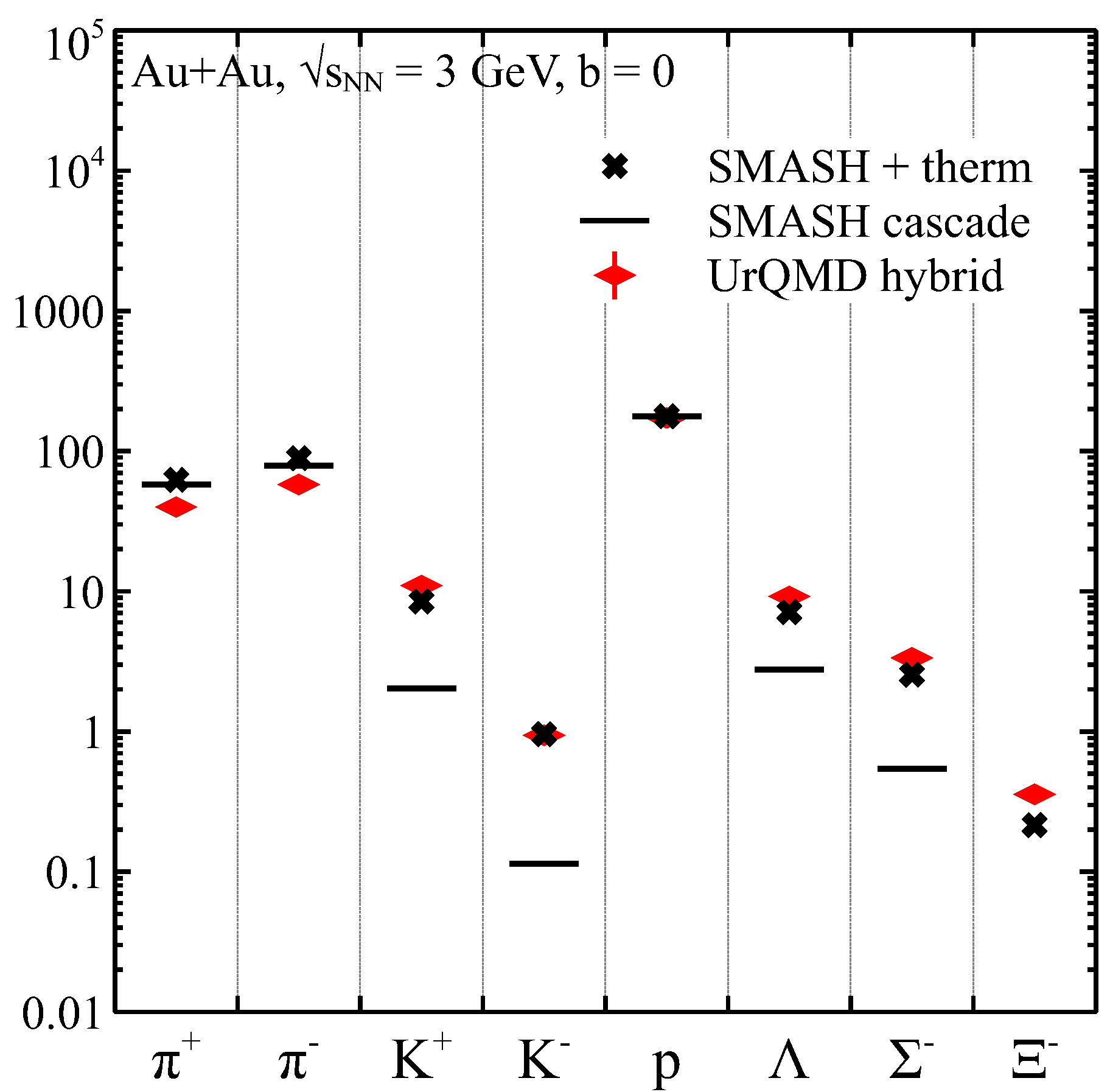
3.3. Strangeness Production via Thermalization
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blume, C. Open Questions in the Understanding of Strangeness Production in HIC -Experiment Perspective. In Proceedings of the 17th International Conference on Strangeness in Quark Matter (SQM 2017), Utrecht, The Netherlands, 10–15 July 2017. [Google Scholar]
- Blume, C.; Markert, C. Strange hadron production in heavy ion collisions from SPS to RHIC. Prog. Part. Nucl. Phys. 2011, 66, 834–879. [Google Scholar] [CrossRef]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M.; et al. Deep sub-threshold ϕ production and implications for the K+/K− freeze-out in Au+Au collisions. arXiv, 2017; arXiv:1703.08418. [Google Scholar]
- Agakishiev, G.; Balanda, A.; Bassini, R.; Belver, D.; Belyaev, A.V.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Braun-Munzinger, P.; Cabanelas, P.; et al. Deep sub-threshold Ξ− production in Ar+KCl reactions at 1.76A-GeV. Phys. Rev. Lett. 2009, 103, 132301. [Google Scholar] [CrossRef] [PubMed]
- Weil, J.; Steinberg, V.; Staudenmaier, J.; Pang, L.G.; Oliinychenko, D.; Mohs, J.; Kretz, M.; Kehrenberg, T.; Goldschmidt, A.; Bäuchle, B.; et al. Particle production and equilibrium properties within a new hadron transport approach for heavy-ion collisions. Phys. Rev. C 2016, 94, 054905. [Google Scholar] [CrossRef]
- Tindall, J.; Torres-Rincon, J.M.; Rose, J.B.; Petersen, H. Equilibration and freeze-out of an expanding gas in a transport approach in a Friedmann-Robertson-Walker metric. Phys. Lett. B 2017, 770, 532–538. [Google Scholar] [CrossRef]
- Patrignani, C. Particle Data Group. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Staudenmaier, J.; Weil, J.; Petersen, H. Non-equilibrium dilepton production in hadronic transport approaches. J. Phys. Conf. Ser. 2017, 832, 012037. [Google Scholar] [CrossRef]
- Weil, J.; Staudenmaier, J.; Petersen, H. Dilepton production with the SMASH model. J. Phys. Conf. Ser. 2016, 742, 012034. [Google Scholar] [CrossRef]
- Graef, G.; Steinheimer, J.; Li, F.; Bleicher, M. Deep sub-threshold Ξ and Λ production in nuclear collisions with the UrQMD transport model. Phys. Rev. C 2014, 90, 064909. [Google Scholar] [CrossRef]
- Baldini, A. Numerical Data and Functional Relationships In Science and Technology. Grp. 1: Nuclear and Particle Physics. Vol. 12: Total cross-sections for reactions of high-energy particles (including elastic, topological, inclusive and exclusive reactions). Subvol. In Landolt-Börnstein, New Series, 1/12B; Springer: Berlin, Germany, 1988. [Google Scholar]
- Steinheimer, J.; Bleicher, M. Sub-threshold ϕ and Ξ− production by high mass resonances with UrQMD. J. Phys. G Nucl. Part. Phys. 2016, 43, 015104. [Google Scholar] [CrossRef]
- Maeda, Y.; Hartmann, M.; Keshelashvili, I.; Barsov, S.; Büscher, M.; Drochner, M.; Dzyuba, A.; Hejny, V.; Kacharava, A.; Kleber, V.; et al. Kaon Pair Production in Proton-Proton Collisions. Phys. Rev. C 2008, 77, 015204. [Google Scholar] [CrossRef]
- Balestra, F.; Bedfer, Y.; Bertini, R.; Bland, L.C.; Brenschede, A.; Brochard, F.; Bussa, M.P.; Choi, S.; Debowski, M.; Dressler, R.; et al. ϕ and ω meson production in pp reactions at plab = 3.67 GeV/c. Phys. Rev. C 2001, 63, 024004. [Google Scholar] [CrossRef]
- Oliinychenko, D.; Petersen, H. Forced canonical thermalization in a hadronic transport approach at high density. J. Phys. G Nucl. Part. Phys. 2017, 44, 034001. [Google Scholar] [CrossRef]
- Hartnack, C.; Oeschler, H.; Leifels, Y.; Bratkovskaya, E.L.; Aichelin, J. Strangeness Production close to Threshold in Proton-Nucleus and Heavy-Ion Collisions. Phys. Rep. 2012, 510, 119–200. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinberg, V.; Oliinychenko, D.; Staudenmaier, J.; Petersen, H. Strangeness Production in Nucleus-Nucleus Collisions at SIS Energies. Universe 2018, 4, 37. https://doi.org/10.3390/universe4020037
Steinberg V, Oliinychenko D, Staudenmaier J, Petersen H. Strangeness Production in Nucleus-Nucleus Collisions at SIS Energies. Universe. 2018; 4(2):37. https://doi.org/10.3390/universe4020037
Chicago/Turabian StyleSteinberg, Vinzent, Dmytro Oliinychenko, Jan Staudenmaier, and Hannah Petersen. 2018. "Strangeness Production in Nucleus-Nucleus Collisions at SIS Energies" Universe 4, no. 2: 37. https://doi.org/10.3390/universe4020037
APA StyleSteinberg, V., Oliinychenko, D., Staudenmaier, J., & Petersen, H. (2018). Strangeness Production in Nucleus-Nucleus Collisions at SIS Energies. Universe, 4(2), 37. https://doi.org/10.3390/universe4020037



