Abstract
An extension of the relativistic density functional approach to the equation of state for strongly interacting matter is suggested that generalizes a recently developed modified excluded-volume mechanism to the case of temperature- and density-dependent available-volume fractions. A parametrization of this dependence is presented for which, at low temperatures and suprasaturation densities, a first-order phase transition is obtained. It changes for increasing temperatures to a crossover transition via a critical endpoint. This provides a benchmark case for studies of the role of such a point in hydrodynamic simulations of ultrarelativistic heavy-ion collisions. The approach is thermodynamically consistent and extendable to finite isospin asymmetries that are relevant for simulations of neutron stars, their mergers, and core-collapse supernova explosions.
1. Introduction
The simulation of astrophysical phenomena, such as core-collapse supernovae (CCSN) or neutron-star (NS) mergers, requires a careful modeling of strongly interacting matter in a wide range of densities and temperatures. The same applies to the theoretical description of heavy-ion collisions (HIC) that study compressed baryonic matter in the laboratory from low to high beam energies. The properties of such matter are represented by the equation of state (EoS) that provides information on pressure, entropy, energies, and other thermodynamic variables of interest.
A particular feature of QCD matter is the supposed phase transition (PT) from hadronic matter to quark matter when density or temperature increase to sufficiently high values. A strong first-order PT could allow for the existence of a third branch of compact stars and the occurrence of the twin-star phenomenon [1,2,3]. Signals of the PT might also have direct consequences in dynamical processes when matter in the quark phase expands and cools down, e.g., the release of a second neutrino burst in CCSN [4,5,6]. For a recent review on the role of the EoS in CCSN simulations, see [7].
The theoretical description of the hadron–quark PT in strongly interacting matter often relies on a construction employing different models for the two phases. With such an approach, the coexistence line of the first-order PT will usually connect a point on the zero-temperature axis at finite baryon chemical potential with a point at finite temperature T on the zero baryon chemical potential axis. By this construction, the QCD hadron–quark PT is of first order in the whole temperature–density plane, see for instance [8]. However, from lattice QCD studies, it is known that there is a smooth crossover at with increasing T [9,10], so at least one critical point at finite and T is expected to exist. Other possibilities are that the character of the transition is crossover all over the QCD phase diagram [11] or, as is advocated in studies of the BEC-BCS crossover transition in low-temperature QCD, that a second critical endpoint exists [12,13,14]. Since lattice QCD studies are presently incapable of exploring the EoS close to the presumed critical point with much confidence, unified models are needed that can account for the existence of these features, see, e.g., [15]. There are dedicated microscopic models available that incorporate the major expected features in the QCD phase diagram, e.g., chiral mean-field models [16] or parity-doublet quark–hadron models [17]. Simulations of CCSN or HIC that are based on a hydrodynamic description of matter during dynamical evolution use the thermodynamic properties of matter encoded in the EoS as an input. Such data can be provided by phenomenological models that do not need to incorporate all of the details of the underlying physics.
In this work, a novel approach is introduced to provide a phenomenological EoS of baryonic matter that exhibits a first-order PT and a critical point at densities and temperatures expected in QCD matter. The parameters of the model can be adjusted to place the coexistence line at arbitrary positions in the phase diagram. The description uses an extension of a relativistic energy density functional for hadronic matter assuming a medium-dependent change in the number of degrees of freedom. This approach employs a recently developed version of a modified excluded-volume (EV) mechanism that gives a thermodynamically consistent EoS with nuclear matter properties that are consistent with present constraints. Here, we concentrate on the hadron–quark transition but not on the liquid–gas PT, which is also contained in our model. The model allows us to study the PT for arbitrary isospin asymmetries; however, only isospin-symmetric matter is considered in this first exploratory study for simplicity. In the present work, no attempt was made to reproduce the EoS of QCD matter at vanishing baryon chemical potential obtained in lattice QCD studies. With appropriately chosen EV parameters, the crossover transition with increasing temperature can be well modeled, even for imaginary chemical potentials, e.g., in a hadron resonance gas model [18]. With improved parametrizations, the structure of the phase diagram in the full space of variables, i.e., temperature, baryon density/chemical potential, and isospin asymmetry, can be investigated in the future.
The theoretical formalism of the model is presented in Section 2, which includes the main equations that define the relevant thermodynamic quantities in Section 2.1. In Section 2.2, details of the parametrization of the interaction and of the effective degeneracy factors are given. They account for the change in the number of degrees of freedom with density and temperature. The phase transitions are explored in Section 3 for isospin-symmetric matter. Conclusions follow in Section 4.
2. Theoretical Model
The theoretical description of strongly interacting matter in the present work is adapted from the model introduced in [19]. It combines a relativistic mean-field (RMF) approach for hadronic matter with density-dependent nucleon–meson couplings and a modified EV mechanism. Here, it is sufficient to provide only the main equations without a detailed derivation. The essential quantities that determine the position of the PT and the critical point in the phase diagram are the effective degeneracy factors that depend on the number densities of the particles and the temperature.
2.1. Relativistic Energy Density Functional with Modified Excluded-Volume Mechanism
The present model assumes neutrons and protons as well as their antiparticles as the basic degrees of freedom. These particles interact by the exchange of mesons, and the model effectively describes the short-range repulsion ( meson), the intermediate-range attraction ( meson), and the isospin dependence of the nuclear interaction ( and mesons), as is common of RMF models. The contribution of leptons or other degrees of freedom like nuclei, hyperons or photons, as required for multi-purpose EoS for astrophysical applications [20], is not considered here.
The nucleons with rest masses are treated as quasi-particles of energy,
which depends on the particle momentum k and the scalar () and vector () potentials. Denoting the particle chemical potentials with , the contribution of the quasi-particles to the total pressure
of the system can be written as
where the medium-dependent effective degeneracy factors
are a product of the usual degeneracy factor for nucleons and the available-volume fraction , which is defined in Section 2.2.
The meson contribution
to the total pressure in Equation (2) contains the coupling factors of the mesons
given as a ratio of the density-dependent coupling functions and the meson masses . The source densities
for vector mesons () and
for scalar mesons () in Equation (5) are obtained from the quasi-particle vector densities
and scalar densities
with the Fermi-Dirac distribution function
The scaling factors
in Equations (7) and (8) determine the coupling between mesons and nucleons. They also appear in the vector potential
and the scalar potential
in the quasi-particle energy (Equation (1)). The rearrangement potential
contributes to the vector potential (Equation (16)) because the couplings in Equation (6) are assumed to depend on the baryon density , where is the baryon number of particle i, and the quantities are the derivatives of the coupling factors.
The dependence of the available-volume fractions in the effective degeneracy factor (Equation (4)) on the vector or scalar quasi-particle densities (9) and (10) also generates rearrangement contributions
and
in the potentials (Equations (16) and (17)), respectively. Furthermore, there is a rearrangement term
in the total pressure (Equation (2)) with two contributions from the density dependence of the couplings
and
from the EV effects.
The free energy density of the system
is obtained with the total pressure (Equation (2)) and the chemical potentials of the particles . They are not independent since, for nucleons with baryon number and charge number , they are given by
with the baryon chemical potential and the charge chemical potential . Only the latter two are independent quantities. For the internal energy density
the entropy density
is needed. Besides the standard contribution depending on the distribution functions , there is a term from the possible temperature dependence of the available-volume fractions . In order to guarantee the third law of thermodynamics, i.e., , the temperature derivative of the available-volume fractions has to vanish for . After solving the equations above for a given T, , and , a fully consistent thermodynamic EoS is obtained. For practical purposes, however, the baryon density and the hadronic charge fraction
are used as independent variables instead of and .
A possible shortcoming of models that consider EV effects is the potential appearance of a superluminal speed of sound in certain regions of the space of thermodynamic variables, see, e.g., [21,22]. This causality constraint has to be checked case by case depending on the specific implementation of the EV mechanism.
2.2. Available-Volume Fractions and Model Parameters
For a quantitative evaluation of the EoS in the present approach, the functional forms of the meson–nucleon couplings and the available-volume fractions have to be specified as well as all parameters. Here, we use the masses of nucleons and mesons and the coupling functions of the DD2 parametrization presented in [23]. It only considers , , and mesons for the effective description of the nuclear interaction but not the mesons. The parameters were obtained by fitting observables (binding energies, radii, etc.) of selected nuclei. With this set, the EoS of nuclear matter at zero temperature exhibits characteristic nuclear matter parameters, e.g., the saturation density ( fm−3), binding energy at saturation ( MeV), incompressibility ( MeV), symmetry energy ( MeV), and slope ( MeV), that are consistent with modern constraints from experiment and theory.
EV effects are frequently employed to describe an effective repulsive interaction between particles, in particular in calculations of the EoS in the framework of hadron resonance gas models, see, e.g., [24]. For zero baryon density, a comparison of the resulting EoS with results from lattice QCD calculations can be used to fix the volume parameters. If a finite volume is attributed to each particle i, the available volume for the motion of the particle is reduced from the total system volume V to with the classical available-volume fraction
Clearly, there is a limiting density above which a compression of the system becomes impossible. In general, the volumes and available-volume fractions can depend on the particle species, and the EV mechanism can be used to suppress particles, e.g., nuclei, in a mixture, causing them to disappear above a certain density, see, e.g., [25] for applications to the low-temperature and low-density EoS in astrophysical simulations.
In [19], the interpretation of the EV mechanism was changed by moving the factor from the system volume V to the degeneracy factor as in Equation (4) and allowing the available-volume fractions to be arbitrary functions of the particle densities and temperature. The medium dependence of the effective degeneracy factors is interpreted as a change in the effective number of degrees of freedom. A decrease in has the effect of a repulsive interaction between the particles, whereas an increase can be seen as the action of an attractive interaction, c.f., the softening of the nuclear EoS when hyperons are included, see, e.g., [26,27]. This freedom leaves the room to modify the properties of an EoS in a favored way.
In the present application of the modified EV mechanism, the available-volume fraction is defined to be identical for all particles i as
depending on the temperature T and an auxiliary quantity
depending on T and the quasi-particle vector densities with parameters s, v, and a cutoff density of . The function in Equation (30) guarantees that for and the EV mechanism has no effect on the EoS. The functions in Equation (30) and in Equation (31) are defined as
with parameters t and . In the limit , the function approaches one and it decreases with increasing temperature. Furthermore, the derivatives approach zero for , as required for the thermodynamic consistency, because of the choice of the function . For , the function vanishes very smoothly and there are no effects at higher temperatures because . In order to reproduce the correct high-temperature limit, given by a Stefan–Boltzmann-type behavior, a modification of the available-volume fractions for temperatures well above is required. This is left to future extensions of the model. According to Equation (31), the quantity x is only positive for baryon densities larger than , a quantity that decreases with increasing temperature. There are no artificial singularities due to the presence of the functions in Equations (30) and (32) because all derivatives of the exponential functions are zero when the arguments of the functions vanish. The actual values of the parameters for the modified EV mechanism used in the present study are , fm3, MeV, and of the DD2 parametrization.
3. Results
In order to illustrate the characteristic effects of the modified EV mechanism on the EoS, we limit the presentation to the case of symmetric matter, i.e., . The pressure p and baryon chemical potential are calculated as a function of the baryon density . Due to the increase in the available-volume fractions or the effective degeneracy factors , a considerable softening of the EoS is observed in a certain range of densities. Below the critical temperature , the pressure is not a monotonous function of the baryon chemical potential for an isotherm. A Maxwell construction is used to determine the two densities of the coexisting phases where p and are identical. The pressure p as a function of the baryon density is depicted in Figure 1 for selected temperatures. Note that an integral part of the underlying RMF model is a detailed description of the liquid–gas PT in nuclear matter and the formation and dissociation of nuclear clusters in compact-star matter. For details, see, e.g., [28].
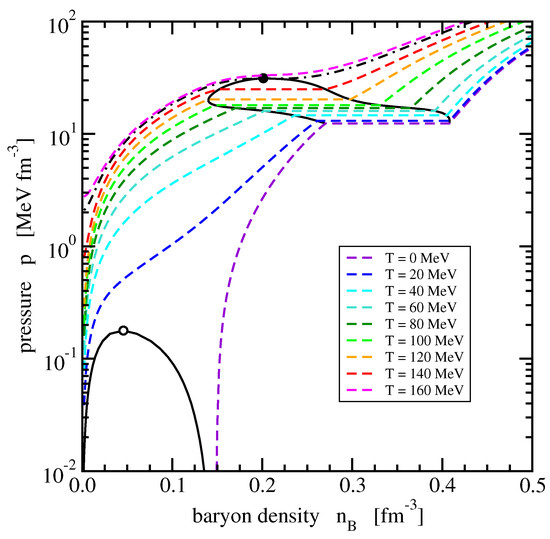
Figure 1.
Isotherms in isospin-symmetric strongly interacting matter in the pressure–baryon density diagram at temperatures from 0 to 160 MeV in steps of 20 MeV (dashed colored lines) and at the critical temperature of the pseudo hadron–quark phase transition (black dot-dashed line). The binodals and critical points are denoted by full black lines and a full (open) circle of the pseudo hadron–quark (liquid-gas) phase transition, respectively.
In the coexistence region of the pseudo hadron–quark PT between the low and high density phases, the pressure is constant as typical for a first-order PT. The area of coexistence is enclosed by the binodal, and, above the critical temperature MeV, there is no PT anymore. The peculiar shape of the binodal is a result of the specific form (30) of the available-volume fractions. It can be adjusted with appropriate changes in the functional form and parameters.
The binodals of the liquid–gas and pseudo hadron–quark PT in the temperature–baryon density plane are shown in panel (a) of Figure 2. At vanishing temperatures, the coexistence region of the pseudo hadron–quark PT covers a density range from 0.270 to 0.408 fm−3, well above the nuclear saturation density . At higher temperatures, it moves to lower densities with an almost constant extension in baryon density except for temperatures close to . Here, the critical density is found as 0.201 fm−3, still above . The dashed line in panel (a) marks the boundary between regions without (lower left) and with (upper right) effects of the modified EV mechanism in the present parametrization. It corresponds to the condition . There is another region in the phase diagram without modified EV effects at temperatures above , outside the figure.
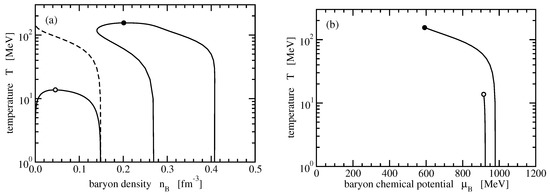
Figure 2.
Binodals (full lines) and critical points (full and open circles) of isospin-symmetric strongly interacting matter in (a) the temperature–baryon density diagram and (b) the temperature–baryon chemical potential diagram. The dashed line in panel (a) separates the region without effects of the modified excluded-volume mechanism (lower left) from the region with effects (upper right). Results for the liquid–gas phase transition are shown at subsaturation densities.
Panel (b) of Figure 2 depicts the lines of the first-order PT in the temperature–baryon chemical potential diagram ending in critical points. With increasing temperature, the baryon chemical potential at the pseudo hadron–quark PT reduces from 979.1 to 591.8 MeV at the critical point. By crossing the transition line, an abrupt change in the density occurs that becomes continuous at the critical point.
4. Conclusions
The extension of the modified EV approach to a density- and temperature-dependent parametrization of the available-volume fractions as introduced in this work was successful in achieving the main goal of this study: As a generic structure of the QCD phase diagram, a first-order pseudo hadron–quark phase transition at low temperatures and a crossover for low baryon densities could be modeled that also includes a critical endpoint at MeV and MeV. Other patterns of the QCD phase diagram that have been theoretically motivated could also be modeled within the present approach. Further extensions of the model are straightforward. They include the extension to a larger number of components of the hadron resonance gas in the underlying RMF model and an isospin dependence of the EV model. It would be worthwhile to study further thermodynamic quantities such as the speed of sound, heat capacities, or the susceptibilities in such an enlarged model. It would also be interesting to elaborate on a parametrization that would result in a second endpoint at low temperatures, as suggested by Hatsuda et al. [14]. The so-generalized parametrization of the QCD EoS can be used in Bayesian analysis studies for astrophysical applications pertaining to compact stars [29,30], their mergers, and core-collapse supernova explosions, as well as heavy-ion collisions analogous to those studied in [31].
Acknowledgments
This work was supported by the Russian Science Foundation under contract number 17-12-01427. S.T. was supported in part by the DFG through grant No. SFB1245.
Author Contributions
D.B. and S.T. conceived and designed the concept of this work. S.T. worked out the theoretical framework, performed the numerical calculations, and wrote the main body of the paper. D.B. wrote the abstract as well as the discussion, conclusions, and the references sections.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CCSN | core-collapse supernova |
| EoS | equation of state |
| EV | excluded-volume |
| HIC | heavy-ion collision |
| NS | neutron star |
| PT | phase transition |
| QCD | quantum chromodynamics |
| RMF | relativistic mean-field |
References
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, 88, 083013. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics—I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar]
- Alvarez-Castillo, D.E.; Blaschke, D.B. High-mass twin stars with a multipolytrope equation of state. Phys. Rev. C 2017, 96, 045809. [Google Scholar] [CrossRef]
- Sagert, I.; Fischer, T.; Hempel, M.; Pagliara, G.; Schaffner-Bielich, J.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. Signals of the QCD phase transition in core-collapse supernovae. Phys. Rev. Lett. 2009, 102, 081101. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.; Whitehouse, S.C.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. The neutrino signal from protoneutron star accretion and black hole formation. Astron. Astrophys. 2009, 499, 1–15. [Google Scholar] [CrossRef]
- Fischer, T.; Sagert, I.; Pagliara, G.; Hempel, M.; Schaffner-Bielich, J.; Rauscher, T.; Thielemann, F.K.; Käppeli, R.; Martinez-Pinedo, G.; Liebendörfer, M. Core-collapse supernova explosions triggered by a quark-hadron phase transition during the early post-bounce phase. Astrophys. J. Suppl. 2011, 194, 39. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cerniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The state of matter in simulations of core-collapse supernovae—Reflections and recent developments. Publ. Astron. Soc. Aust. 2017, 34, 67. [Google Scholar]
- Blaschke, D.B.; Sandin, F.; Skokov, V.V.; Typel, S. Accessibility of Color Superconducting Quark Matter Phases in Heavy-ion Collisions. Acta Phys. Pol. Suppl. 2010, 3, 741–746. [Google Scholar]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Equation of state in (2 + 1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Bratovic, N.M.; Hatsuda, T.; Weise, W. Role of Vector Interaction and Axial Anomaly in the PNJL Modeling of the QCD Phase Diagram. Phys. Lett. B 2013, 719, 131–135. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars. arXiv, 2017; arXiv:astro-ph.HE/1707.04966. [Google Scholar]
- Abuki, H.; Baym, G.; Hatsuda, T.; Yamamoto, N. The NJL model of dense three-flavor matter with axial anomaly: The low temperature critical point and BEC-BCS diquark crossover. Phys. Rev. D 2010, 81, 125010. [Google Scholar] [CrossRef]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N.; Baym, G. New critical point induced by the axial anomaly in dense QCD. Phys. Rev. Lett. 2006, 97, 122001. [Google Scholar] [CrossRef] [PubMed]
- Klähn, T.; Fischer, T. Vector interaction enhanced bag model for astrophysical applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Dexheimer, V.A.; Schramm, S. A Novel Approach to Model Hybrid Stars. Phys. Rev. C 2010, 81, 045201. [Google Scholar] [CrossRef]
- Mukherjee, A.; Steinheimer, J.; Schramm, S. Higher-order baryon number susceptibilities: Interplay between the chiral and the nuclear liquid-gas transitions. Phys. Rev. C 2017, 96, 025205. [Google Scholar] [CrossRef]
- Vovchenko, V.; Pasztor, A.; Fodor, Z.; Katz, S.D.; Stoecker, H. Repulsive baryonic interactions and lattice QCD observables at imaginary chemical potential. Phys. Lett. B 2017, 775, 71–78. [Google Scholar] [CrossRef]
- Typel, S. Variations on the excluded-volume mechanism. Eur. Phys. J. A 2016, 52, 16. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar]
- Rischke, D.H.; Gorenstein, M.I.; Stoecker, H.; Greiner, W. Excluded volume effect for the nuclear matter equation of state. Z. Phys. C 1991, 51, 485–490. [Google Scholar] [CrossRef]
- Satarov, L.M.; Dmitriev, M.N.; Mishustin, I.N. Equation of state of hadron resonance gas and the phase diagram of strongly interacting matter. Phys. Atom. Nucl. 2009, 72, 1390–1415. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Vovchenko, V.; Gorenstein, M.I.; Stoecker, H. Van der Waals Interactions in Hadron Resonance Gas: From Nuclear Matter to Lattice QCD. Phys. Rev. Lett. 2017, 118, 182301. [Google Scholar] [CrossRef] [PubMed]
- Hempel, M.; Schaffner-Bielich, J. Statistical Model for a Complete Supernova Equation of State. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef]
- Chatterjee, D.; Vidaña, I. Do hyperons exist in the interior of neutron stars? Eur. Phys. J. A 2016, 52, 29. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Hypernuclear Physics for Neutron Stars. Nucl. Phys. A 2008, 804, 309–321. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H.; Röpke, G.; Blaschke, D. Effects of the liquid-gas phase transition and cluster formation on the symmetry energy. Eur. Phys. J. A 2014, 50, 17. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33–54. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Ayriyan, A.; Benic, S.; Blaschke, D.; Grigorian, H.; Typel, S. New class of hybrid EoS and Bayesian M-R data analysis. Eur. Phys. J. A 2016, 52, 69. [Google Scholar] [CrossRef]
- Pratt, S.; Sangaline, E.; Sorensen, P.; Wang, H. Constraining the Equation of State of Superhadronic Matter from Heavy-Ion Collisions. Phys. Rev. Lett. 2015, 114, 202301. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).